Геометрия 7 класс, 3 признака равенства треугольников
#7 класс #Геометрия #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование
Предмет: геометрия (7 класс) Тема: Признаки равенства треугольников Подготовила материал: Учитель по математике, МБОУ СШ № 30 города Дзержинск: Кобякова Анна Викторовна
Введение: Понятие «Треугольник» Фигура «Треугольник» в геометрии является одной из самых простых и важных фигур. В большинстве случаев ей дают следующее определение: Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. В нашем случае вершинами выступают: А,В,С А отрезками: АВ, АС, ВС
Введение: Понятие «равенства треугольников»
Напомним что две фигуры, в частности два треугольника, называются равными если их можно совместить, наложив друг на друга.
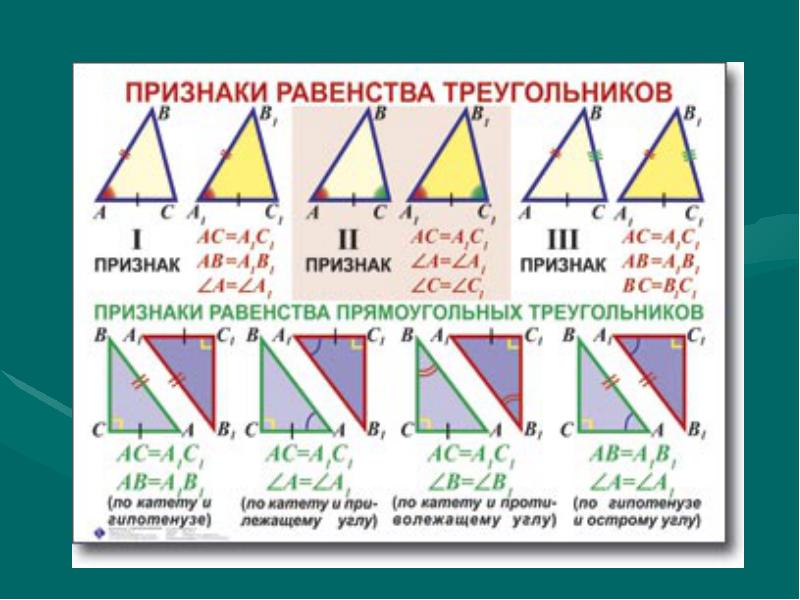
Первый признак равенства треугольников Теорема:(Первый признак равенства треугольников — по двум сторонам и углу между ними) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Первый признак равенства треугольников(доказательство)
Дано: ΔABC, ΔA1B1C1, AB=A1B1, AC=A1C1, ∠A=∠A1.
Доказать:ΔABC= ΔA1B1C1
Доказательство:Так как ∠A=∠A1, то можно треугольник A1B1C1 наложить на треугольник ABC так, чтобы точка A1 совместилась с точкой A, луч A1C1 наложился на луч AC, луч A1B1 — на луч AB. Так как AB=A1B1, то при таком наложении сторона A1B1 совместится со стороной AB, а значит, точка B1 совместится с точкой B. Аналогично, сторона A1C1 совместится со стороной AC, а точка C1 — с точкой C.
Первый признак равенства треугольников (Задача)
Второй признак равенства треугольников Теорема (Второй признак равенства треугольников — по стороне и двум прилежащим к ней углам) Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.
Второй признак равенства треугольников (доказательство)
Дано: ΔABC, ΔA1B1C1,AB=A1B1, ∠A=∠A1, ∠B=∠B1.
Доказать:ΔABC= ΔA1B1C1
Доказательство:
Так как AB=A1B1, то треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы:1)сторона A1B1 совместилась со стороной AB,2)точки C1 и С лежали по одну сторону от прямой AB.
Поскольку ∠A=∠A1, сторона A1С1 при этом наложится на луч AC.Так как ∠B=∠B1, сторона B1C1 наложится на сторону BC. Точка С1 принадлежит как стороне A1С1, так и стороне B1C1, поэтому С1 лежит и на луче AC, и на луче CB.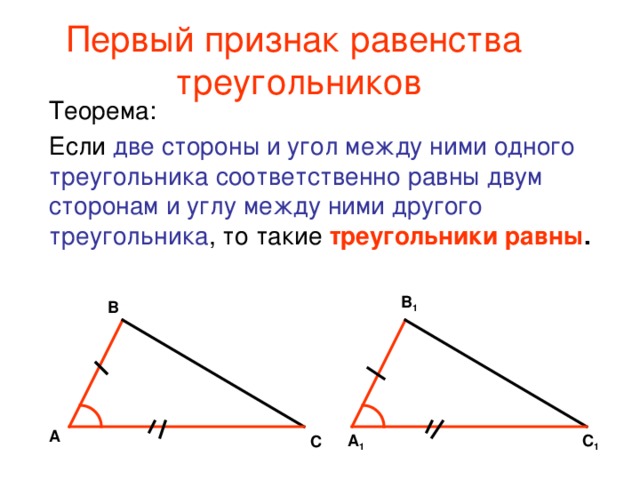
Второй признак равенства треугольников (задаача)
Третий признак равенства треугольников Теорема(Третий признак равенства треугольников — по трём сторонам) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников (доказательство)
Дано:ΔABC,ΔA1B1C1,AB=A1B1, AC=A1C1, BC=B1C1.
Доказать:ΔABC= ΔA1B1C1
Доказательство:Приложим треугольник A1B1C1 к треугольнику ABC так, чтобы:
вершина A1 совместилась с вершиной A,
вершина B1 совместилась с вершиной B,
точки C1 и C лежали по разные стороны от прямой AB.
При этом возможны три случая взаимного расположения луча CC1 и угла ACB.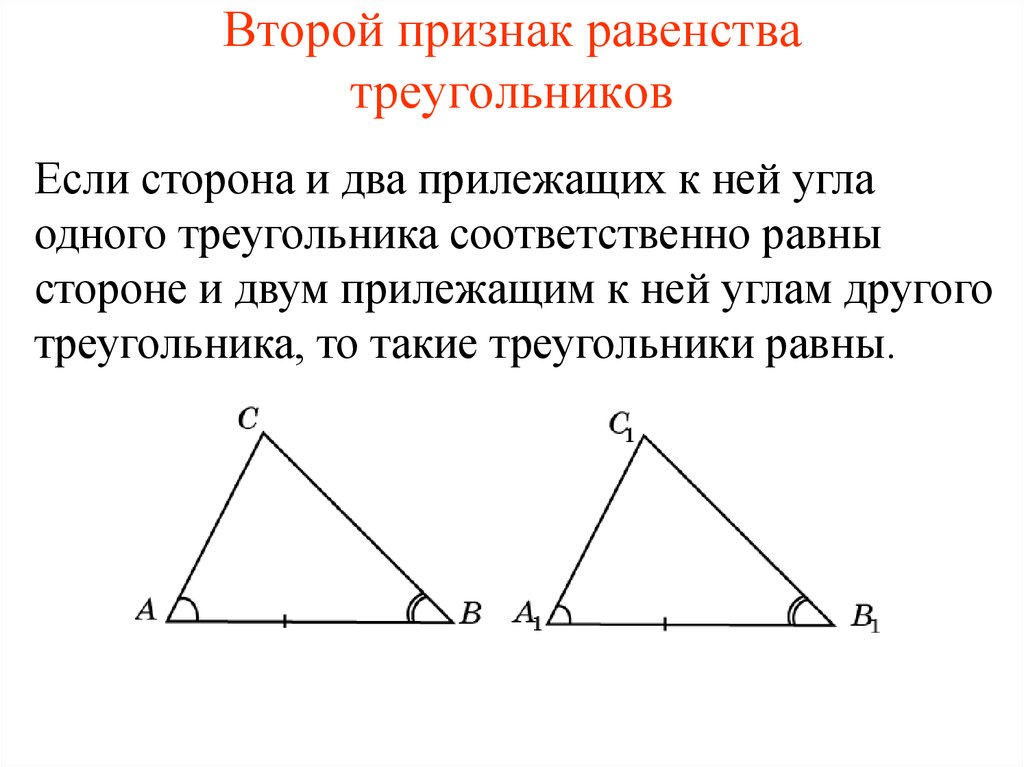
Третий признак равенства треугольников (доказательство) I. Луч CC1 проходит внутри угла ACB. Проведём отрезок CC1. По условию AC=A1C1 и BC=B1C1, поэтому треугольники ACC1 и BCC1 — равнобедренные с основанием CC1. По свойству равнобедренного треугольника, ∠ACC1=∠AC1C и ∠BCC1=∠BC1C. Если к равным углам прибывать равные углы, то получим равные углы: Таким образом, ∠ACB=∠AC1B. Точки A1 и A, B1 и B совмещены, то есть ∠AC1B и ∠A1C1B1 — один и тот же угол. Для треугольников ABC и A1B1C1 имеем: AC=A1C1, BC=B1C1 (по условию), ∠ACB=∠A1C1B1 (по доказанному). Следовательно, ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Третий признак равенства треугольников (доказательство)
II. Луч CC1 проходит внутри угла ACB.
Так как AC=A1C1 и BC=B1C1, треугольники ACC1 и BCC1 — равнобедренные с основанием CC1 и ∠ACC1=∠AC1C и ∠BCC1=∠BC1C (как углы при основании).
Если из равных углов вычесть равные углы, то получим равные углы:
Таким образом, ∠ACB=∠AC1B и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Третий признак равенства треугольников (доказательство) III. Луч CC1 совпадает со стороной угла ACB. По условию BC=B1C1, поэтому треугольник BCC1 — равнобедренный с основанием CC1. Отсюда ∠C1=∠C (как углы при основании) и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Повторение материала Задание: 1) назвать по какому признаку мы можем доказать равенство треугольников? 2)что не хватает для того чтобы применить теорему? И почему? 3)какие теоремы из раннее изученного материала мы используем чтобы это доказать?
Треугольники равны по двум углам и стороне. Третий признак равенства треугольников
Международная научно-практическая конференция «Первые шаги в науку»
«Новые» признаки равенства треугольников
Математика
9б класс МБОУ «Брянский городской
лицей №2 имени »
Руководитель: учитель математики
Брянск 2013
1. Введение
2. Создание каталога базовых задач на построение с помощью циркуля и линейки
3.
Сопоставление изученных признаков равенства треугольников и задач на построение треугольников. Отыскание нового метода доказательства признаков равенства треугольников
4. Доказательство новых признаков равенства треугольников
5. Обобщение полученных результатов
6. Применение новых признаков равенства треугольников при решении задач
7. Заключение
I. Введение
«Если две стороны и угол между ними одного треугольника…..». Заученные, как таблица умножения, признаки равенства треугольников. Сотни раз мы цитировали и применяли их при решении задач. Казалось бы, что может быть проще? Мы знаем об этом все!
Однако до сих пор остались вопросы, ответы на которые не дают нам покоя. Метод наложения, используемый для доказательства первого признака равенства, показался нам несколько искусственным. Не потому ли мы никогда не использовали его в решении задач? Почему так мало признаков равенства треугольников? В 8 классе строили треугольники по все тем же двум сторонам и углу между ними.
Возможно, обнаружив связь между решением задач на построение треугольников и признаками равенства, мы получим новый метод доказательства ПРТ. «Вооружившись» им мы сможем доказать другие признаки равенства треугольников. Мы уверены, что их гораздо больше, чем 3!
Чтобы убедиться в том, что ответы на эти вопросы волнуют не только нас, мы провели социологический опрос среди учащихся и учителей лицея (см. приложение 3).
Наши предположения подтвердились. Большинство учеников знают только 3 признака равенства треугольников. Метод наложения не пользуется большой популярностью. Задачи на построение также не кажутся интересной темой в геометрии. А этап исследования многие вообще считают лишним.
Таким образом, целью нашего исследования стало отыскание более понятного нам метода доказательства признаков равенства треугольников и новых признаков равенства треугольников.
Крайне важно было дополнить перечень простейших задач на построение, изученных в седьмом классе, другими элементарными построениями, которые мы проходили в курсе восьмого и девятого класса.
Всего получилось 12 базовых построений (см. приложение 1). В ходе дальнейшего исследования мы будем неоднократно обращаться к этому перечню.
Нужно отметить, что все задачи мы решали по алгоритму: дано-построить-анализ-построение-доказать-доказательство-исследование. Для простых задач и задач, решение которых известно, этап анализа мы опускали.
Больше всего внимание уделялось последнему этапу – исследованию, именно он дал нам возможность отыскать новый метод доказательства.
Чертежи было решено выполнять в программе Paint, поэтому возникла необходимость заранее научиться работать в ней.
II. Создание каталога базовых задач на построение с помощью циркуля и линейки
Большая часть нашей работы заключается в решении задач на построение треугольников, поэтому на первом этапе работы мы составили список простейших построений. Это позволило сделать решение задач более коротким и красивым.
Все задачи мы решали по плану: дано – построить – построение – доказать – доказательство — исследование.
Особое значение уделялось этапу исследования.
Базовые задачи на построение решались в различных разделах геометрии 7 и 8 класса. Мы их собрали в единый каталог.
1) Построение отрезка, равного данному;
2) Построение угла, равного данному;
3) Построение биссектрисы угла;
4) Построение середины отрезка;
5) Построение перпендикуляра через точку лежащую/не лежащую на данной прямой;
6) Построение прямой, параллельной данной;
7) Построение третьего угла, по двум известным;
8) Построение касательной к окружности, через точку не лежащую на данной окружности;
9) Деление отрезка в заданном отношении;
10) Деление отрезка в заданном отношении отрезков;
11) Деление отрезка на n равных отрезков.
Подробное решение этих задач представлено в приложении 1.
III. Сопоставление изученных признаков равенства треугольников и задач на построение треугольников. Отыскание нового метода доказательства признаков равенства треугольников.
Для поиска нового метода доказательства ПРТ мы сопоставили условие первого ПРТ с условием одной из задач на построение. Они оказались одинаковыми и мы предположили, что это не случайно и решение задачи на построение приведет нас к нахождению нового метода доказательства.
Построение треугольника по двум сторонам и углу между ними
https://pandia.ru/text/78/103/images/image003_23.jpg»497″>
ПРТ, доказанный в решении этой задачи, звучит так: «Если две стороны и медиана, проведенная к третьей, одного треугольника соответственно равны двум сторонам и медиане, проведенной к третьей, другого треугольника, то эти треугольники равны.»
Но не все задачи решались так просто. Например, задача на построение по двум сторонам и углу, прилежащему к одной из сторон, нового признака равенства не дала. Однако стоило нам немного изменить условие, и был получен еще один ПРТ. Решение этой задачи было особенно важно для нас, потому что ее условие мы придумывали сами.
https://pandia.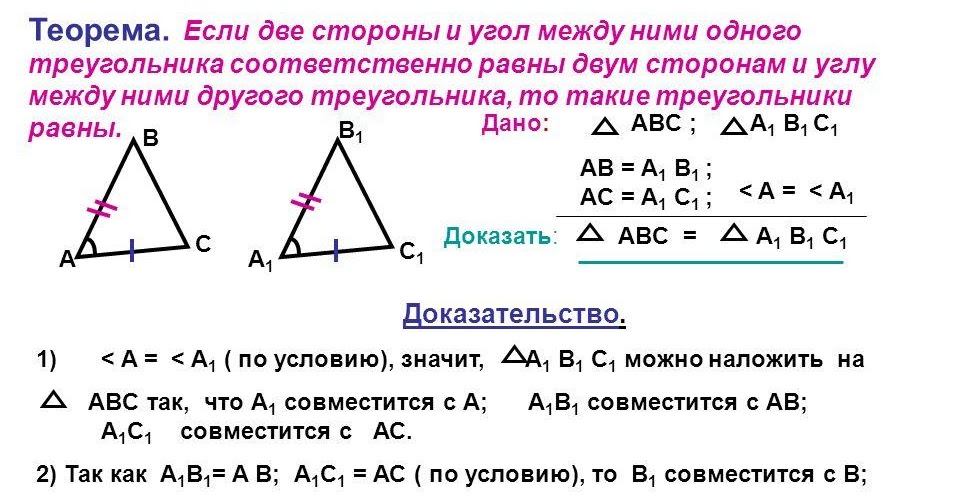
ru/text/78/103/images/image010_3.png»
Мы не сможем установить равенство двух треугольников по одному элементу, потому что неизвестно:»Будут ли равны остальные элементы?»
Так же невозможно установить равенство двух треугольников, используя два элемента по причине нехватки информации для установления равенства.
Возможно установление равенства двух треугольников, используя три элемента. Но при этом возникает вопрос: «Какие именно три элемента нужно назвать, для установления равенства треугольников?»
При изучении этого вопроса, я просмотрел школьные учебники геометрии различных авторов, а также словари и справочники. В учебниках за седьмой класс предложены к изучению только три признака равенства треугольников.
Θ1 Признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны . рис.1
Доказательство. Рассмотрим треугольники
ABC
и
A
1
B
1
C
1
, (рис.
1) у которых АВ = A
1
B
1
, АС = A
1
C
1
∠ А = ∠ А
1
. Докажем, что ΔABC = ΔA
1
B
1
C
1
.
Так как ∠А = ∠А 1 , то треугольник ABC можно наложить на треугольник А 1 В 1 С 1 так, что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А 1 В 1 и A 1 C 1 . Поскольку АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 а сторона АС — со стороной А 1 C 1 ; в частности, совместятся точки В и В 1 , С и C 1 . Следовательно, совместятся стороны ВС и В 1 С 1 . Итак, треугольники ABC и А 1 В 1 С 1 полностью совместятся, значит, они равны.
А вот как в Древнем Египте применили первый признак равенства треугольников
(по двум сторонам и углу между ними), создателем его также считается Фалес Милетский, для измерения высоты пирамиды: представим, что мы стоим перед огромной пирамидой, как же измерить её высоту? Ведь к ней не приложишь измерительные приборы! И тут на помощь Фалесу Милетскому приходит первый признак равенства треугольников: он подождал пока тень его точно совпадёт с его ростом, применил теорему, получилось, что высота пирамиды равна её тени (рис.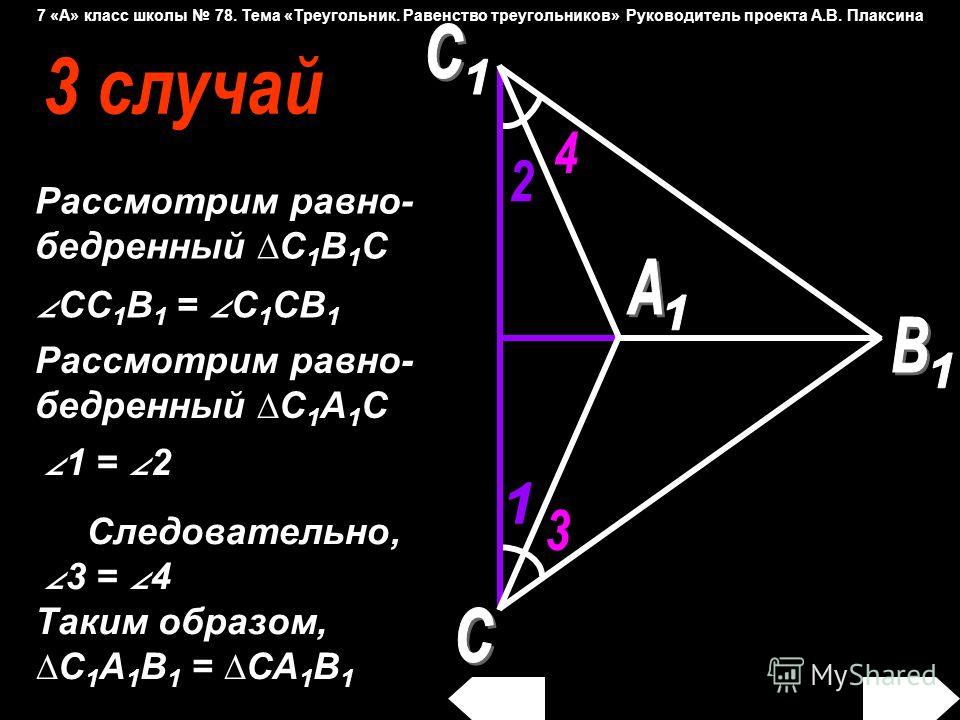
2).
Рис. 2
Θ2 Признак: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство: Если в △АВС и △А 1 В 1 С 1 будут иметь место следующие равенства AB=А 1 В 1 , ∠BAC=∠B 1 A 1 C 1 , ∠АВС= ∠А 1 В 1 С 1 . Наложим друг на друга треугольники А 1 В 1 С 1 и АВС таким образом, чтобы совпали равные стороны AB и А 1 В 1 и углы, которые к ним прилегают. Как и в уже рассмотренном предыдущем примере, если это необходимо, треугольник А 1 В 1 С 1 можно «перевернуть и приложить обратной стороной». Треугольники совпадут, следовательно, они могут считаться равными.
Θ3 Признак
: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Доказательство:Пусть для △ABC и △A
1
B
1
C
1
справедливы равенства А
1
В
1
=АВ, В
1
С
1
=ВС, С
1
А
1
=СА. Переместим треугольник А
1
В
1
С
1
таким образом, что сторона А
1
В
1
совпадет со стороной АВ, и вершины B
1
и B, A
1
и A, совпадут.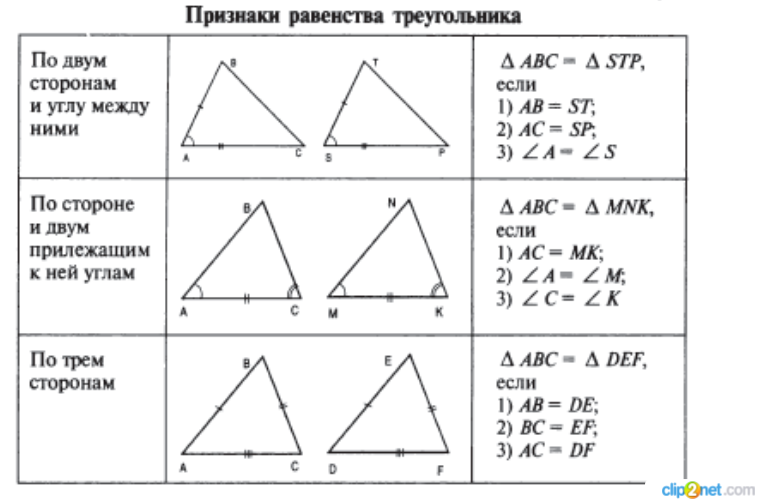
Возьмем окружность с центром в A и радиусом AC, и вторую окружность с центром B и радиусом BC. Эти окружности пересекутся в двух симметричных относительно отрезка AB точках: точкой C и точкой C
2
. Значит, C1 после переноса треугольника A1B1C1 должна совпасть или с точками C, или с C2. Любом случае, это будет означать равенство △ABC=△A
1
B
1
C
1
, так как треугольники △ABC=△ABC
2
равны (ведь эти треугольники являются симметричными относительно отрезка AB .
Это свойство – жесткость треугольника – широко используется на практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку; такой же принцип используется при установке кронштейна.
Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.
Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Потому, что: можно представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой, однако, сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними.
Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек. Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему
В справочнике по элементарной математике М. Я. Выгодского я нашел еще один признак.
Θ4 Признак: Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны.
Докажу этот признак.
Дано : ΔABC , ΔA1B1C1 , AB=A1B1,AC=A1C1, ∠ B= ∠ B1
Доказать: ΔABC=A1B1C1.
Расположим треугольники так, как на рисунке 1 . Соединим B и B1, тогда ΔАВВ1
Равнобедренный, значит
∠
1=
∠
2.
∠
3=
∠
4 как остатки равных углов.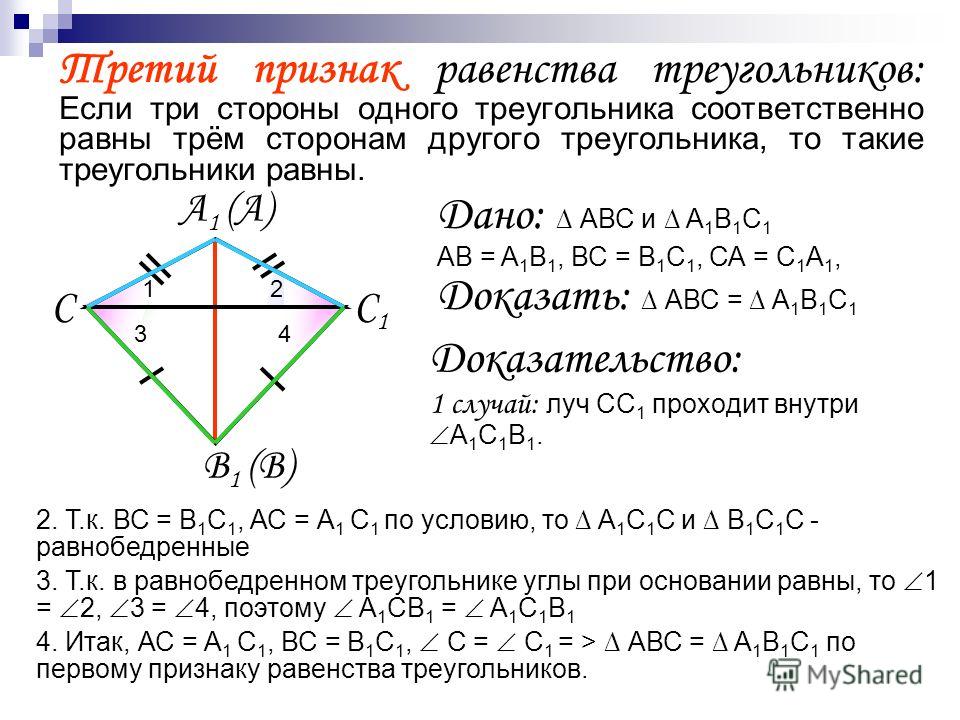
Получим ΔВСВ1- равнобедренный, отсюда ВС=В1С1. ΔАВС = ΔА1В1С1 по трем сторонам.
Также в школьном курсе рассматриваются 4 признака равенства прямоугольных треугольников:
Θ1 . Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Θ2 . Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Θ3 . Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Θ4 . Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Я решил теоретическую базу по признакам равенства треугольников, довавив к сторонам и углам, используемым в класических признаках равенства треугольников, другие компоненты: биссектрису, медиану и высоту.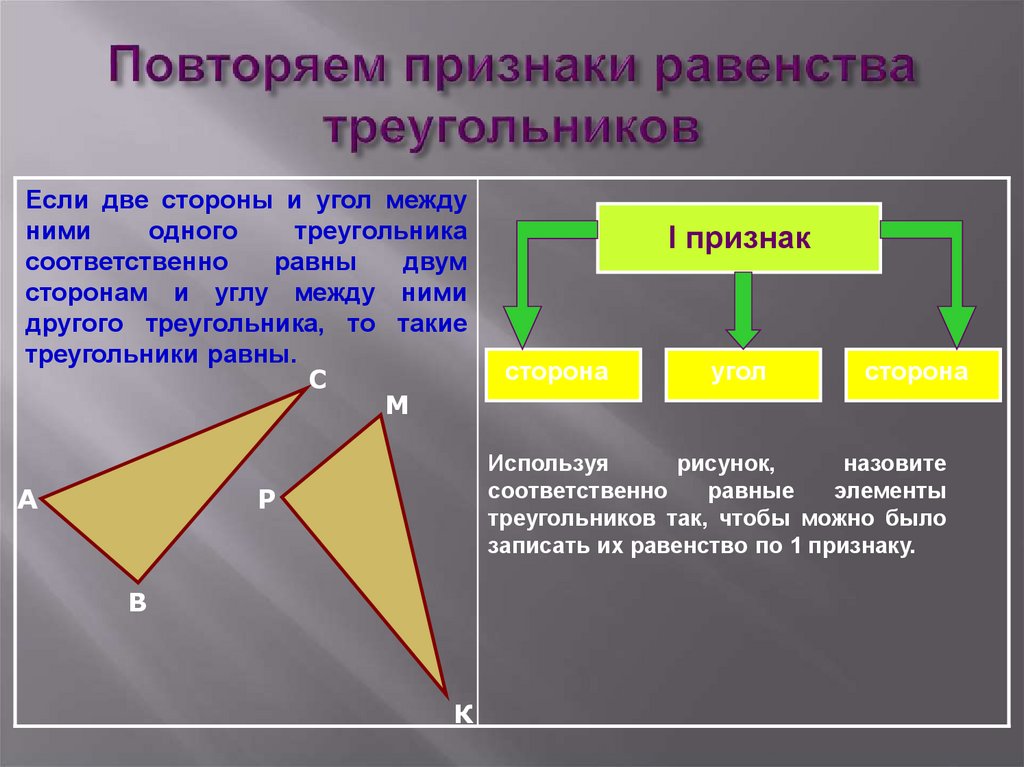
Нестандартные признаки равества треугольников.
1) По двум сторонам и высоте проведенной к одной из них.
Дано: AB=A1B1 , BC=B1C1 , AK=A1K1 ,
Доказать: ΔABC= ΔA1B1C1 .
Доказательство: ΔABK=ΔA1B1K1 по гипотенузе и катету, тогда ∠ B= ∠ B1 и получим ΔABC= ΔA1B1C1 по первому признаку.
2) По двум сторонам и медиане, проведенной к одной из них
Дано: AB=A1B1 , BC=B1C1 , AK=A1K1 , AK и A1K1 — медианы.
Доказать: ΔABC= ΔA1B1C1 .
Доказательство:ΔABK=ΔA1B1K1 по трем сторонам, значит ∠ B= ∠ B1 и ΔABC= ΔA1B1C1 по первому признаку.
3) По двум сторонам и высоте, проведенной из третьего угла.
Дано: ∠ B= ∠ B1 , ∠ C= ∠ C1 , AK=A1K1 .
Доказать: ΔABC= ΔA1B1C1 .
Доказательство: ΔABK=ΔA1B1K1 по катету и острому углу, значит BK=B1K1 ,
ΔACK=ΔA1C1K1 по катету и острому углу, значит KC=K1C1 , а следовательно BC=B1C1 , а ΔABC= ΔA1B1C1 по второму признаку.
4)По стороне и двум высотам, проведенным из углов, прилежащих к этой стороне.
Дано: АС=А1С1, СМ=С1М1, АК=А1К1.
Доказать: ΔСC= ΔA1B1C1 .
Доказательство: ΔAМC= ΔA1М1C1 по катету и гипотенузе, значит ∠ А= ∠ А1 , а ΔAКC= ΔA1К1C1 по катету и гипотенузе, значит ∠ С= ∠ С1 .
Итак, ΔABC= ΔA1B1C1 по второму признаку.
5)По двум сторонам и высоте, проведеннойк третьей стороне.
Дано: АВ=А1В1,ВС=В1С1,ВК=В1К1.
Доказать: ΔABC= ΔA1B1C1 .
Доказательство: ΔABK=ΔA1B1K1 по гипотенузе и катету, значит AK=A1K1,
ΔBКC= ΔB1К1C1 по катету и гипотенузе, значит KC=K1C1 .
Итак,ΔABC= ΔA1B1C1 по трем сторонам.
6)По стороне, одному из углов, прилежайщих к этой стороне и биссектрисе из этого угла.
Дано: АС=А1С1, АК=А1К1, ∠ А ∠ А1 .
Доказать: ΔABC= ΔA1B1C1 .
Доказательство: ΔКАС=ΔК1А1С1 по первому признаку, значит ∠ С= ∠ С1 ,
ΔABC= ΔA1B1C1 по второму признаку.
7) По двум высотам и углу, из которого провдена одна из высот.
Дано: СМ=С1М1, АК=А1К1, ∠ А ∠ А1 .
Доказать: ΔABC= ΔA1B1C1 .
Доказательство: ΔAМC= ΔA1М1C1 по катету и острому углу,ΔКАС=ΔК1А1С1 по катету и гипотенузе,ΔABC= ΔA1B1C1 по второму признаку.
Заключение.
В ходе исследования я выяснил, что помимо трех основных признаков равенства треугольников возможно указать немало других. Я сформулировал и доказал равенство треугольников по медиане, высоте, биссектрисе треугольника в сочетании со сторонами и углами треугольника, придерживаясь наличия трех элементов. Теперь я могу рассказать учащимся нашей школы, что существуют другие признаки равенства треугольников. Это позволит выпускникам школы применить результаты моих исследований при подготовке к ОГЭ и ЕГЭ и легко решать геометрические задачи на применение этих признаков.
Результат моего исследования : Доказаны несколько признаков равенства треугольников, не изучаемых в школьном курсе геометрии.
Список литературы
- Выгодский М.Я. Справочник по элементарной математике.
- Геометрия. 7-9 классы: учеб. Для общеобразоват.
учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – 19-е изд. – М. : Просвещение, 2009. - Погорелов А. В. Геометрия: Учеб. Для 7-9 кл. общеобразоват. Учреждений. – 3-е издание. – М.: Просвещение, 2002.
- . Энциклопедия «Аванта» по математике, Москва, 2004 г.
- 2. «Википедия» — свободная энциклопедия.
- 3. Глейзер Г.И. «История математики в школе», Москва, Просвещение, 1982 г.
- 4. Гусева Т.М. Признаки подобия треугольников.- Москва, Первое сентября, приложение «Математика», 1999 г., №28
- 5. Погорелов А.В. «Геометрия 7-9 классы», Москва, Просвещение, 2003 г.
учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – 19-е изд. – М. : Просвещение, 2009.Приложение 1
1.Как вы считаете, сколько существует признаков равенства треугольников?
А) 3 Б) более трех В) меньше трех
2. Хотели бы вы узнать новые признаки равенства треугольников?
А) да Б) нет
3 знака зодиака, которые, скорее всего, будут в любовном треугольнике
Астрология
Они могут оказаться в драме отношений.
по Кристин Феллизар
Shutterstock
. Сочный любовный треугольник может быть весело на в реальной жизни. Надеюсь, большинству людей не придется иметь дело с такой драмой отношений, но некоторые люди могут естественным образом оказаться в таких ситуациях из-за своего знака зодиака. По словам Терезы Рид, астролога и автора Искривь свою судьбу: добейся успеха с помощью астрологии и Таро , есть три знака зодиака, которые, скорее всего, окажутся в любовном треугольнике.
В астрологии личность каждого знака зодиака находится под влиянием его правящей планеты, модальности и элемента. Если вы хотите увидеть, кто может оказаться в любовном треугольнике, вам нужно взглянуть на элемент знака, который является основой личности знака. Например, земные знаки очень стабильны и приземлены, в то время как огненные знаки очень страстны, агрессивны и стремительны.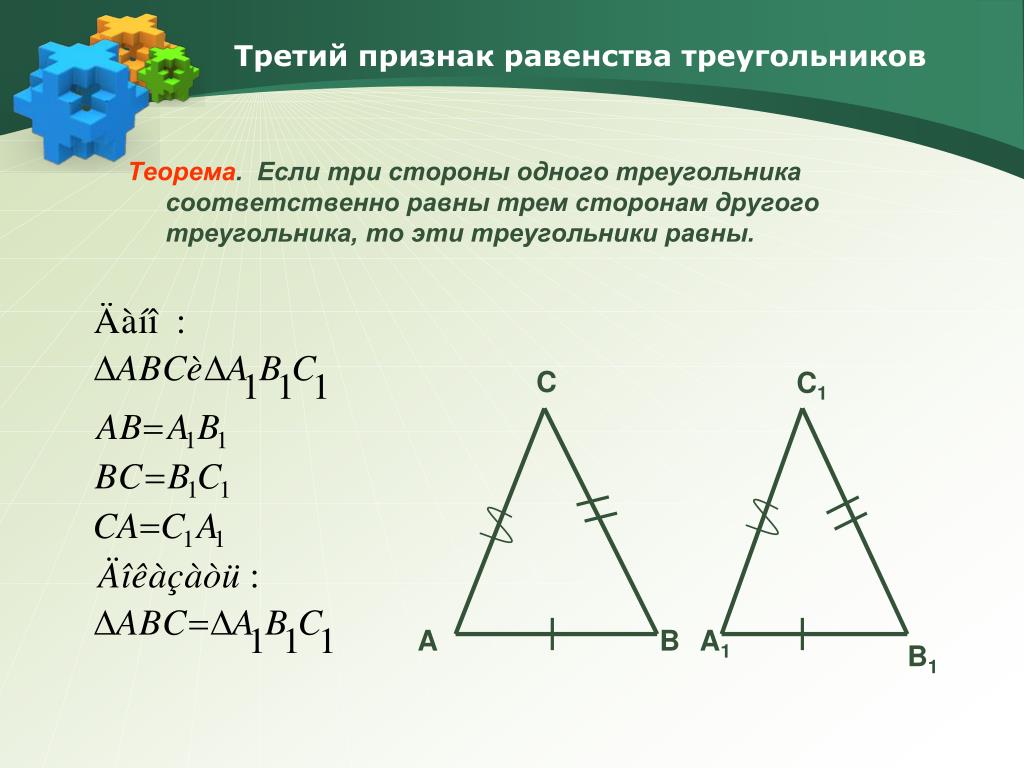
Из всех четырех стихий воздушные знаки чаще всего входят в любовный треугольник. По словам Рида, эти люди, как и воздух, не выносят изоляции. «Воздушным знакам нужна передышка, особенно в отношениях», — говорит она. «Если они этого не понимают, они становятся беспокойными и начинают искать другие, захватывающие переживания. Поэтому чаще всего они оказываются в середине треугольников или других сложных ситуаций».
Хотя воздушные знаки в целом могут попадать в любовные треугольники чаще, чем остальные представители зодиака, все они имеют разные причины оказаться в середине одного из них. С учетом сказанного, вот три знака зодиака, которые, скорее всего, попадут в любовный треугольник.
Близнецы (21 мая — 20 июня)
Ни для кого не секрет, что Близнецы имеют репутацию «плейбоя» зодиака. «Эти свободолюбивые заклинатели любят играть на поле», — говорит Рид. «Разнообразие — это их жизнь, поэтому неудивительно, что они часто жонглируют более чем одним человеком одновременно».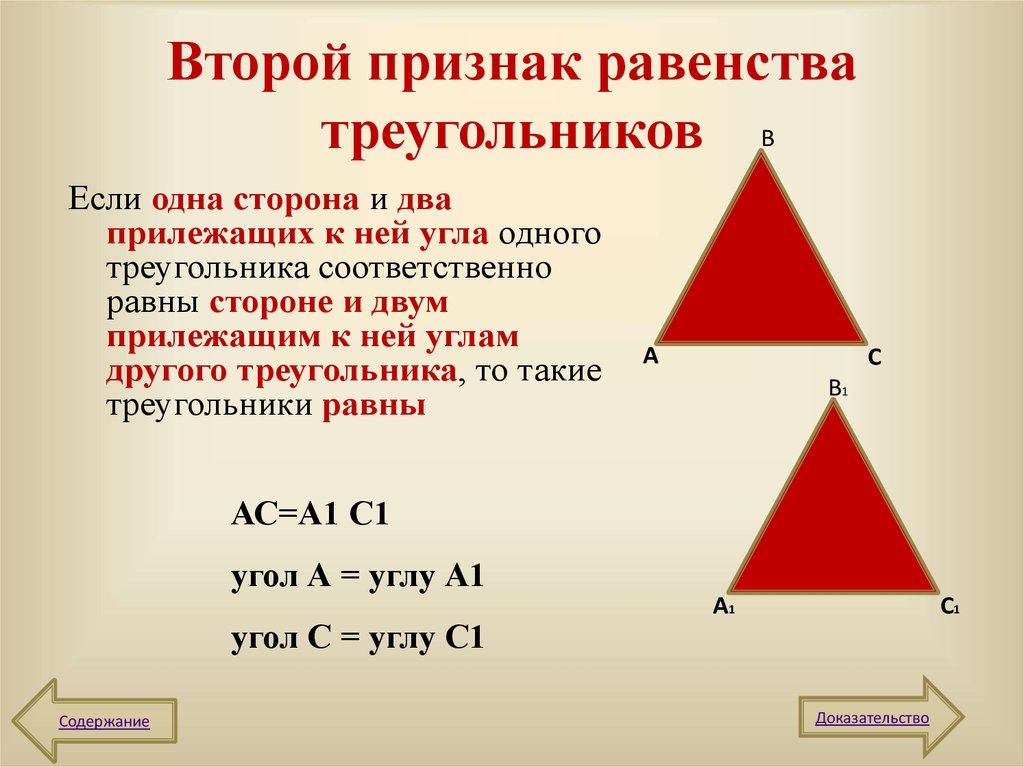
Они представлены близнецами и известны своей двойственной природой. Из-за этого им очень легко по-настоящему почувствовать, что они влюблены в двух человек одновременно.
Кроме того, Близнецы нуждаются в постоянной умственной стимуляции. Если это не так, им становится скучно. Если им скучно, они, скорее всего, будут искать стимуляцию в другом месте. «Из-за их двойственности и неугомонности с ними будет весело, но это также может привести к неприятностям», — говорит Рид. Для них важно быть искренними с людьми, с которыми они связаны, «если они не хотят оставлять за собой слезы».
Весы (23 сентября — 22 октября)
Весы представлены весами, что означает, что они всегда взвешивают вещи в уме. Из-за этого они, как правило, очень нерешительны, что может привести к тому, что они будут тянуть людей за собой, даже если они не собираются этого делать. Весами также управляет Венера, планета любви, поэтому они любят быть влюбленными.
«Они хотят романтических отношений, поэтому они будут более чем счастливы иметь более одного любовника, пытающегося завоевать их расположение», — говорит Рид.
«Их романтическая натура также означает, что их может сыграть хам, который хочет второстепенного. Если они получают достаточно внимания от этого человека, Весы будут ждать, надеясь, что в конце концов они станут «тем самым».
Водолей (20 января — 18 февраля)
Воздушный Водолей может оказаться в центре любовного треугольника по многим причинам. Во-первых, они могут быть эмоционально недоступны. По словам Рида, они предпочитают «друзей с выгодой» без каких-либо привязанностей. Если они не сообщают о своих намерениях, они могут попасть в ситуацию, когда они встречаются с несколькими людьми без их ведома.
«Водолеям также нравятся нетрадиционные товарищи по играм, что означает, что они могут быть в некоторой степени пансексуалами и открыты для полиамории», — говорит Рид. «Когда они находят кого-то, кто соответствует их странным стандартам, они более чем готовы быть моногамными. На самом деле, они могут стать отличными партнерами, как только посеют этот дикий овес».
Источник
Тереза Рид, астролог и автор книги Twist Your Fate: Manifest Success with Astrology and Tarot
HPD ЗНАКИ: ЗНАК треугольника (ЗНАК FDNY размер 1X1,3 RCNY §505-01 ЗНАК) | HPD SIGNS
Многоквартирные дома
Пансионаты (непереходные)
Монастыри
Общежития
Братства и женские клубы
Гостиницы (непереходные)
Жилые / рабочие единицы
Монастыри
Мотели (непереходные)
Недвижимость на время отпуска
0003
HPDsigns предлагает точные знаки, необходимые для соблюдения правил 3RCNY 505-01 «Идентификация квартир и гостевых комнат, а также указатели направления и знаки» и 3 RCNY 505-02 «Пожарная маркировка квартир, гостевых комнат и лестничных клеток».
Владельцы и управляющие жилой недвижимостью г. Нью-Йорк должны знать о новом требовании местного законодательства, касающемся их собственности.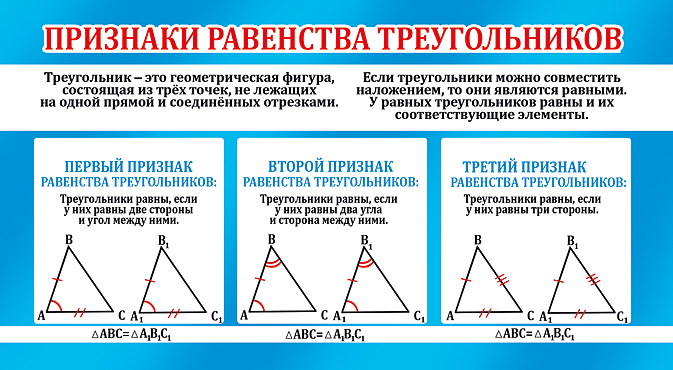
Владельцам жилых помещений необходимо будет установить новые необходимые «Обозначения квартир и гостевых комнат, а также указатели направления и знаки».
В июне 2016 года пожарная служба города Нью-Йорка (FDNY) приняла новое правило 3 RCNY §505-01, которое устанавливает новые требования к идентификационным знакам квартир и гостевых комнат, а также к указателям направления и указателям выхода.
Все многоквартирные дома и отели в Нью-Йорке должны соответствовать этому новому требованию в отношении маркировки дверей квартир и других знаков до 30 марта 2018 года.
Владельцам и управляющим рекомендуется соблюдать это новое требование безопасности, как можно скорее. Эта недорогая мера поможет контролировать реакцию на аварийное отключение электроэнергии, пожар или задымление и, возможно, поможет предотвратить гибель людей.
Собственники жилых домов теперь обязаны устанавливать таблички на входных дверях всех жилых помещений (квартир, гостевых и спальных комнат) в зданиях и помещениях групп Р-1 и Р-2, а также в вестибюлях и коридорах своего дома коридоры.
3 RCNY §505-01: Обозначения и указатели направления для зданий групп 1 и 2
В этом правиле излагаются требования к входным дверям и этажам, чтобы аварийный персонал мог определить, куда они направляются в конкретном здании. В требованиях указывается, где должны быть размещены знаки, на какой высоте они должны быть над полом и как должен выглядеть дизайн знаков. Подробности можно найти в тексте закона, начиная со страницы 4.
Требуемая маркировка должна быть размещена в здании до 30 марта 2017 г. или ранее. Маркировка для зданий, требующих окончательного или временного ЦО 01.06.16 или после этой даты, должна соответствовать требованиям до выдачи. То есть, согласно 3 RCNY §505-01
, все знаки и вывески должны поддерживаться в рабочем состоянии и устанавливаться своевременно. Кроме того,
3 RCNY §505-02: Противопожарная маркировка квартир, гостевых комнат и лестничных клеток для зданий групп 1 и 2. Что это такое?
Настоящие правила определяют аварийную маркировку для жилых единиц Р-1 и Р-2 (квартир, гостевых и спальных комнат) и дверей лестничных клеток с исключениями.
Маркировка расположена низко над землей (не более 12 дюймов над полом) и размещена на дверных косяках. Схемы можно увидеть начиная с 13 страницы закона.
Дата вступления в силу?
30 марта 2018 г. Новые здания должны соответствовать требованиям до их заселения.
Как выглядит соответствие?
Как и в предыдущем постановлении, ежегодные проверки должны проводиться и регистрироваться. Хотя в настоящее время в законе не перечислены какие-либо нарушения за несоблюдение требований, можно с уверенностью сказать, что несоблюдение маркировки, вывесок, а также проведение и запись проверок могут привести к штрафным санкциям.
Группа знаков: Знаки квартир, Указатели направления здания, Знаки идентификации квартир, Знаки дверей, Знаки номеров квартир, Фотолюминесцентные знаки, Светящиеся в темноте знаки, Фотолюминесцентные знаки идентификации дверей, Светящиеся в темноте идентификационные знаки, Светящиеся в темноте двери Опознавательные знаки, Фотолюминесцентные опознавательные знаки, Фотолюминесцентные опознавательные знаки с номером, Фотолюминесцентные дверные опознавательные знаки, Номерные указатели, Квартирная и аварийная маркировка, Знаки с номерами дверей, Знаки пожарной охраны, Знаки с номерами квартир, Светящиеся знаки, Фотолюминесцентные знаки, Знаки с номерами дверей, Знаки местного законодательства, 3 RCNY §505-01, Буквенные знаки, Цифровые треугольные знаки, Треугольные знаки аварийной маркировки, Буквенные указатели, Цифровые буквенные знаки
Стоимость доставки и обработки:
Наша доставка фиксирована, независимо от того, покупаете ли вы 1 или 20 штук (мы отправляем только в пределах США ) — не упустите эту возможность купить все необходимые знаки без дополнительной стоимости доставки .
Налог с продаж:
Мы обязаны взимать налог с продаж с любого продукта, продаваемого на этом сайте и доставляемого по адресу в Нью-Йорке. Налог с продаж составляет 8,875 процента.
Примечание:
Требования к содержанию знаков определяются предполагаемым использованием и применимыми нормами. ПОКУПАТЕЛЬ несет ответственность за определение соответствующего содержания знака или пакета знаков. HPDSigns.com не дает никаких гарантий или заявлений о пригодности знака для какого-либо конкретного применения. ЗАКАЗЧИК НЕСЕТ ОТВЕТСТВЕННОСТЬ ЗА СООТВЕТСТВИЕ ЗНАКОВ ЗАКАЗА ЗАКАЗЧИКА ВСЕМ ЗАКОНАМ ШТАТА, ФЕДЕРАЛЬНЫМ, МЕСТНЫМ И МУНИЦИПАЛЬНЫМ ЗАКОНАМ. Пожалуйста, ознакомьтесь с условиями перед покупкой.
Мы предоставляем знаки для квартир , указатели направления здания , знаки для идентификации квартир , дверные знаки , знаки с числовым треугольником , знаки с номером квартиры , фотолюминесцентные знаки , светящиеся в темноте знаки , цифровые указатели , светящиеся в темноте знаки , дверные знаки с номерами , Знаки пожарной охраны , Знаки с номерами квартир , Светящиеся знаки , Фотолюминесцентные знаки , Знаки с номерами дверей , ЗНАКИ-указатели и Знаки местного законодательства
Для получения дополнительной информации о том, что требуется, см.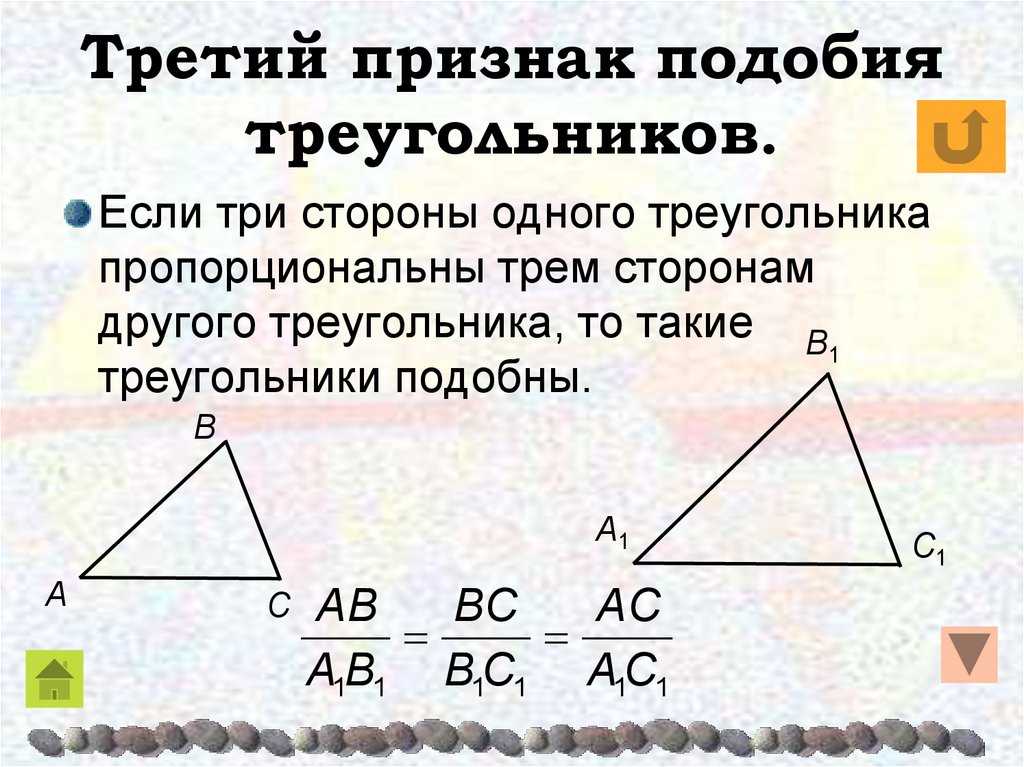
соответствующие законы и правила, применимые к вашему городу. и государство. Эта страница предназначена только для информационных целей и не предназначена в качестве юридической консультации, профессиональной консультации или изложения закона. Возможно, вы захотите проконсультироваться с юристом.
Find us on:
Google Map , YELP , Bing Map , MapQuest , Yellow Pages , Google Plus , Amazon.com , Buildingsigns.com , 0111
В HPDsigns мы специализируемся на всех вывесках Департамента строительства Нью-Йорка (DOB), вывесок Департамента жилищного строительства Нью-Йорка (HPD) и вывесок Департамента транспорта Нью-Йорка (DOT). Наша цель — предоставить управляющим недвижимостью, операторам строительных площадок и владельцам зданий знаки, требуемые агентствами Нью-Йорка и пожарной службой Нью-Йорка, алюминиевые знаки, предупреждения и уведомления для быстрой и тяжелой установки, алюминиевые знаки для установки в зданиях с надлежащим обозначением HPD, квартира Дверные знаки , Светящиеся в темноте знаки , Светящиеся знаки , Фотолюминесцентные знаки , Знаки местного закона 26 , Светящиеся знаки Нью-Йорка , Дверные знаки , Фотолюминесцентные знаки , Фотолюминесцентные знаки , Строительные светящиеся в темноте знаки , Дверные знаки , необходимые строительные знаки , Строительные фотолюминесцентные знаки , Светящиеся в темноте знаки , Знаки входной двери квартиры , Знаки идентификации дверей , Светящиеся в темноте знаки и Светящиеся в темноте знаки безопасности, а также знаки «Треугольник»
Этот фотолюминесцентный знак «Символ треугольника» представляет собой светящийся в темноте знак, который часто усиливает светящееся обозначение дверей квартир в зданиях с помощью светящихся в темноте знаков, которые служат в качестве опознавательных знаков здания/квартиры и опознавательных знаков безопасных дверей.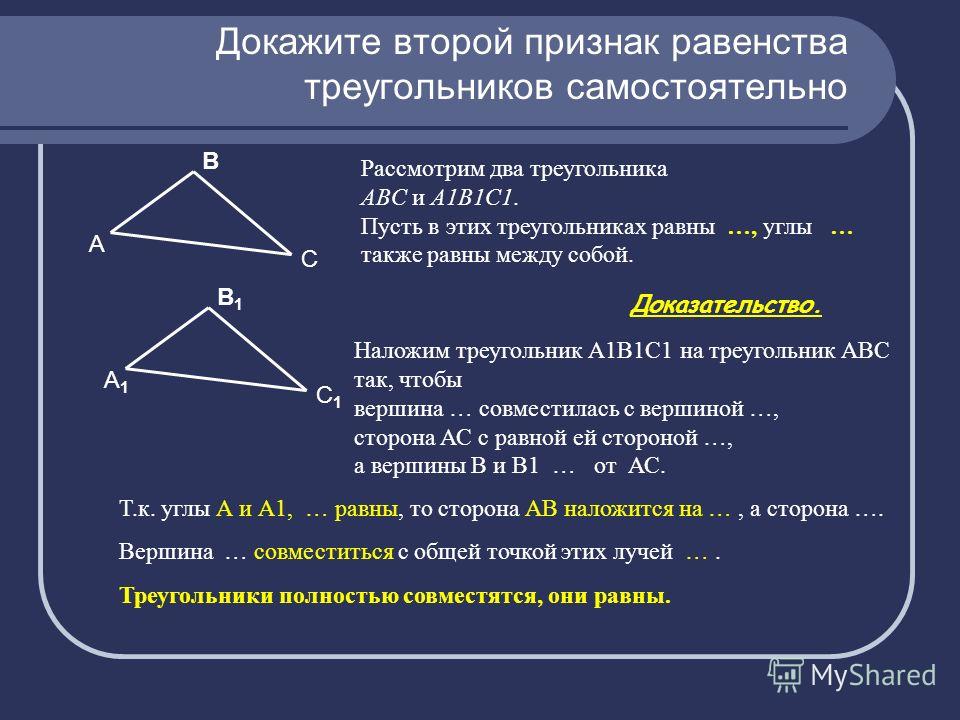
на объекте с надлежащим обозначением FDNY, обозначением HPD и алюминиевыми знаками
знаками HPD является безопасным сайтом McAfee!
Мы с гордостью сообщаем, что HPD подписывает сертификат McAfee Secure Site. Каждый день он проходит ежедневные обширные тесты безопасности. HPD подписывает ценности защиты потребителей. HPD указывает, что это не взломанный сайт**. Знаки HPD не используют преднамеренные вирусы, шпионское ПО и другие онлайн-угрозы. HPD указывает, что это не фишинговый сайт и не сайт для атак* с вредоносным ПО или вредоносными ссылками. Действительные тесты SSL-сертификата. Знаки HPD – это сертифицированный веб-сайт McAfee Secure. Каждый день знаки HPD проходят интенсивное ежедневное сканирование системы безопасности, которое позволяет использовать знак доверия McAfee SECURE™ только на знаках HPD. Каждый день знаки HPD проходят интенсивные тесты безопасности на предмет возможного доступа к личной информации, ссылок на опасные сайты, фишинга и других онлайн-угроз.