«Чтение свойств функции по графику функции»
Конденко Любовь Николаевна
Учитель высшей квалификационной категории
Средней школы № 1 г. Елабуга
ТЕМА: «ЧТЕНИЕ СВОЙСТВ ФУНКЦИИ ПО ГРАФИКУ ФУНКЦИИ»
“График – это говорящая линия,
которая может о многом рассказать”
М.Б. Балк
Цели:
- Образовательные
Продолжить формирование у учащихся понятия, что функция- математическая модель, позволяющая описывать изучать разнообразные зависимости между реальными величинами.
- Развивающие
Развитие всех познавательных процессов, в частности функционального стиля мышления. Развитие графической культуры.
- Воспитательные
Вырабатывать внимание, самостоятельность при работе на уроке. Воспитывать гордость за учёных, инженеров, конструкторов, создавших теорию графиков, применивших теорию к практической деятельности .Осуществлять профессиональную ориентацию учащихся.
1.Актуализация знаний
2.
 Формирование умений , навыков.
Формирование умений , навыков.
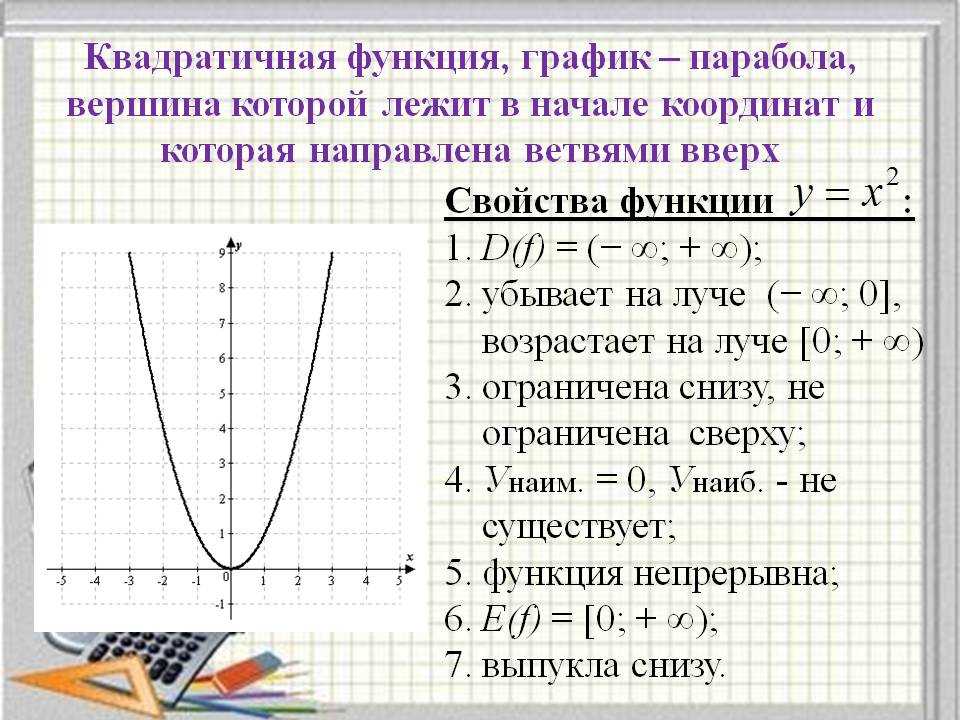
Функция – одно из основных математических общенаучных понятий, зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает различные законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении у = х2 геодезист или геометр увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может усмотреть в нем зависимость силы у сопротивления воздуха или воды от скорости х движения. Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение х в 2 раза приведет к увеличению у в 4 раза, и это заключение может применяться в любой конкретной ситуации. В школьном курсе изучается немало функций.
 Они еще не умели считать , но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя не будет голодать; чем сильнее натянуть тетиву лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее в пещере.
Они еще не умели считать , но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя не будет голодать; чем сильнее натянуть тетиву лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее в пещере.
Оно сыграло и поныне играет большую роль в познании реального мира .Идея функциональной зависимости присутствует уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами.
Функция является одним из основных понятий математики, в частности математического анализа, так как математические модели реальных ситуаций, изучаемые на протяжении всего курса алгебра, напрямую связаны с функциями.
В технике и физике часто пользуются именно графическим способом задания функции. Более того , по- мере развития математики все активнее проникает графический метод в самые различные области жизни человека. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике.
Задание № 1.
Само слово «функция» (от латинского functio — совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673 году в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати он его ввел с1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа». В восемнадцатом веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во «Введении в анализ бесконечного»): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств». Так понимали функцию на протяжении почти всего восемнадцатого века.
Так понимали функцию на протяжении почти всего восемнадцатого века.
Как видно из представленных определений, само понятие функции фактически отождествлялось с аналитическим выражением. Новые шаги в развитии естествознания и математики вызвали и дальнейшее обобщение понятия функции.
Графиком функции — называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции.
График функции у =f(x)) строиться по точкам; чем больше точек вида (х;f(Х)) мы возьмем, тем более точное представление о графике получим. Если этих точек взять достаточно много, то и представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает нам, что график нужно изобразить в виде сплошной линии.
Находясь на выставке картин, мы рассматриваем произведения искусств и обращаем внимание на то, сумел ли художник предать глубину, завершенность образного содержания. Картина является итогом длительных наблюдений и размышлений художника над жизнью. График функции это своего рода «портрет» функции. Чтобы научиться видеть и создавать такие картины необходимо знать основные математические функции и их свойства.
Картина является итогом длительных наблюдений и размышлений художника над жизнью. График функции это своего рода «портрет» функции. Чтобы научиться видеть и создавать такие картины необходимо знать основные математические функции и их свойства.
Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения.
По графику можно прочитать многие свойства функции, можно решать неравенства и уравнения.
Читая ,график функции мы можем делать выводы об :
-
Области определения
-
Области значений
-
Нулях функции
-
Знакопостоянстве
-
Монотонности
-
Четности
-
Периодичности
-
Экстремумах
-
Ограниченности
- Непрерывности
Выполним задание:
Множество всех значений независимой переменной, которые она может принимать называют областью определения функции.
Если известен график функции, то область ее определения найти нетрудно. Для этого достаточно спроецировать график на ось абсцисс. То числовое множество, геометрическая модель которого получится на оси абсцисс в результате указанного проецирования, и будет представлять собой область определения функции.
Ответ: (-9;9]
Выполним задание:
Множество всех значений зависимой переменной называют областью значений функции.
Если известен график функции, то область значений найти сравнительно нетрудно. Для этого достаточно спроецировать график на ось ординат. То числовое множество, геометрическая модель которого получится на оси ординат в результате указанного проецирования, и будет представлять собой область значений функции.
Ответ: [-4;6).
Выполним задание:
Функция у равное f(х) достигает на промежутке Х своего наибольшего значения, если существует такая точка х0 Î Х, что для всех х Î Х выполняется неравенство f(x) ≤ f(x0).
Из рисунка видим, что при х =-3, f(-3)=3 и это значение больше других значений функции.
Ответ: 3.
На практике удобнее пользоваться следующей формулировкой: функция возрастает, если большему значению аргумента соответствует большее значение функции. Или используя геометрическое истолкование понятий возрастания: двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в гору.
Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Или используя геометрическое истолкование понятий убывания: двигаясь по графику убывающей функции слева направо, мы как бы спускаемся в горы.
Или используя геометрическое истолкование понятий убывания: двигаясь по графику убывающей функции слева направо, мы как бы спускаемся в горы.
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
Выполним задание:
Найти промежутки монотонности функции у=f (x), заданной графиком.
Для определения промежутков монотонности будем использовать геометрическое истолкование : двигаясь по графику убывающей функции слева направо, мы как бы спускаемся в горы ,а двигаясь по графику возрастающей функции слева направо, мы как бы поднимаемся в гору.
Функция возрастает на промежутках [-5;-2) и на (-2; 1]
Функция у=f(x ) убывает на промежутках (-9;- 5] и на [1; 9].
На слайде 13 представлено задание из единого государственного экзамена: На каком из следующих рисунков изображен график функции, возрастающей на промежутке [-1;2].
Функцию y=f(x) называют периодической с периодом Т, Т≠0, если для любого х из области определения функции выполняются равенства f(x-T) = f(x)= =f(x+T).
Число Т, удовлетворяющее указанному условию, называется периодом функции y= f (x).
Если функция у=f(x) имеет период Т, то для построения графика функции нужно сначала построить часть графика на любом промежутке длины Т, а затем сдвинуть эту часть по оси Ох вправо и влево на Т, 2Т, 3Т и так далее.
Обычно стараются, если это возможно, выделить наименьший положительный период, его и называют основным периодом.
Задание 1.
Функция у =f (x), имеющая период Т = 4 задана графиком на промежутке [-1; 3].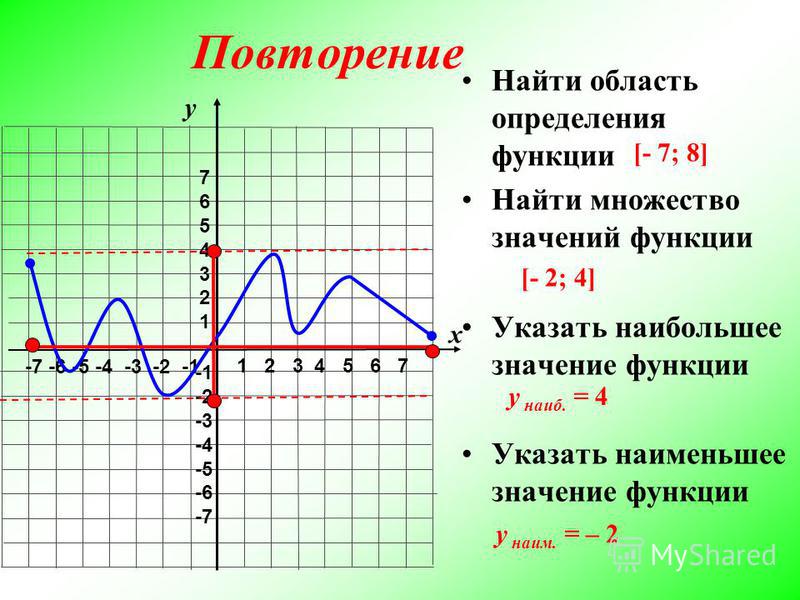 Найдите значение этой функции при х = 10.
Найдите значение этой функции при х = 10.
Задание2.
Функция у=f(x) определена на всей числовой прямой и является периодической с периодом 4. На рисунке изображен график этой функции при -3≤х≤1. Найдите значение выражения f(-6)∙f(-3)∙f(13).
Выполнить эти задания можно двумя способами.
1 способ:
Используя определение периодической функции достраиваем график функции с учетом периода вдоль оси абсцисс. Затем по графику находим значение функции для указанных значений аргументов.
2 способ:
Используя равенство f(x-T)= f(x)= f(x+T).
Решение можно посмотреть в презентации на слайдах 15, 16.
Определение четной и нечетной функции.
Функция y= f(x) называется четной, если область ее определения симметрична относительно нуля и для любого значения х, из области определения верно равенство f(-х)=f(x). График четной функции симметричен относительно оси ординат.
График четной функции симметричен относительно оси ординат.
На слайде приведены примеры четных функций и примеры симметрии относительно прямой.
Функция y=f(x) называется нечетной, если ее область определения симметрична относительно нуля и для любого значения х из области определения верно равенство f(-х)=-f(x).
График нечетной функции симметричен относительно начала координат.
На слайде приведен пример симметрии относительно точки и на следующем слайде примеры графиков нечетных функций, изучаемых в школьном курсе алгебры. На графиках показана симметрия точек графика относительно начала координат. (Слайды 17-19).
На 20 слайде предложено задание:
Укажите график четной функции. (Решение можно посмотреть на слайде 20).
Определение промежутков знакопостоянства.
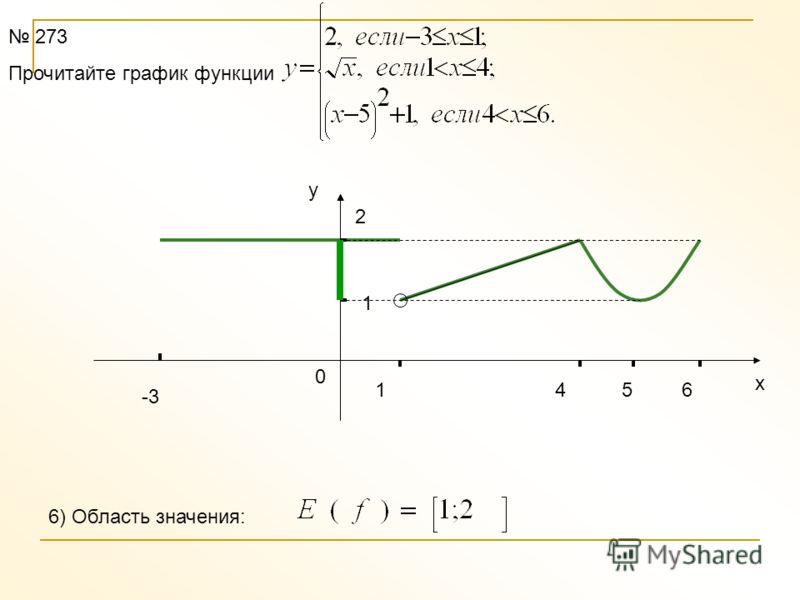
Решите неравенство f(x)≥0, если на рисунке изображен график функции у=f(x).
Решите неравенство f(x)≤0, если на рисунке изображен график функции у=f(x).
Другими словами нужно найти промежутки знакопостоянства функции у равное f(x).Функция принимает значение, равное нулю в тех точках, в которых график функции пересекает ось абсцисс. Функция принимает отрицательные значения на множестве тех значений аргумента, которым соответствуют части графика, расположенные ниже оси абсцисс, то есть f(x) меньше или равно нулю. Функция принимает положительные значения на множестве тех значений аргумента, которым соответствуют части графика, расположенные выше оси абсцисс, те есть f(x) больше или равно нуля.
f(x) ≥0 на промежутках хÎ (-9;-7,2]U(-1,8;5,8]
f(x)≤0 на промежутках хÎ [7,2;-1,8)U[5,8;9,2].
Как читать графики на бирже для новичка
Главная
Блог
Вопрос-ответ
Как читать графики на бирже: краткое руководство для начинающих инвесторов
21 июня 2022 11 минут
Следить за стоимостью ценных бумаг на фондовом рынке помогают графики. Как их читать и зачем они нужны инвесторам — в статье.
Как их читать и зачем они нужны инвесторам — в статье.
Графики помогают инвесторам наблюдать за тем, как меняется стоимость определенной ценной бумаги, принимать правильные инвестиционные решения и избегать убытков.
- Зачем инвесторам нужны биржевые графики
- Какие существуют виды графиков
- Как правильно читать графики и что они показывают
- Кратко
Зачем инвесторам нужны биржевые графики
Графики выполняют две важные функции.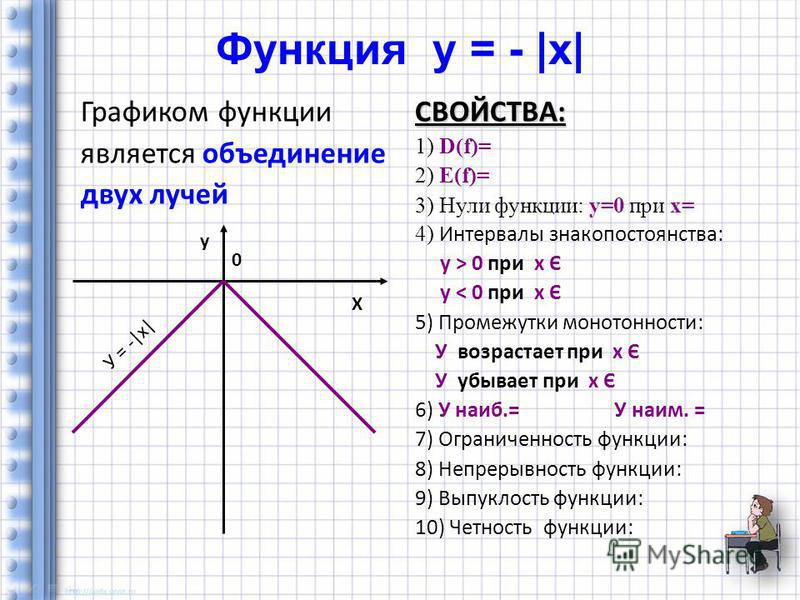 Они показывают текущую стоимость акции и отражают изменения ее стоимости в течение определенного промежутка времени. Инвестор может сам выставлять временной интервал, например один день, месяц или год. Цена акций на биржевых графиках обновляется раз в секунду. Это помогает инвесторам, которые совершают большое количество операций в день, выгодно продавать свои активы и получать доход.
Они показывают текущую стоимость акции и отражают изменения ее стоимости в течение определенного промежутка времени. Инвестор может сам выставлять временной интервал, например один день, месяц или год. Цена акций на биржевых графиках обновляется раз в секунду. Это помогает инвесторам, которые совершают большое количество операций в день, выгодно продавать свои активы и получать доход.
Консервативные инвесторы покупают акции на длительный срок и могут использовать графики для технического анализа. Они смотрят, как изменялась цена актива, и пытаются ответить на два основных вопроса: насколько хорошо в прошлом шли дела компании и что произойдет с ценой акций в будущем. Подробнее о техническом анализе читайте в нашей статье — Для чего нужен метод скользящей средней и как его используют инвесторы.
График акций Apple. Синяя линия показывает изменения стоимости акций компании в течение пяти дней. В зеленом прямоугольнике справа или в белом поле в верхнем левом углу отображается текущая стоимость одной акции.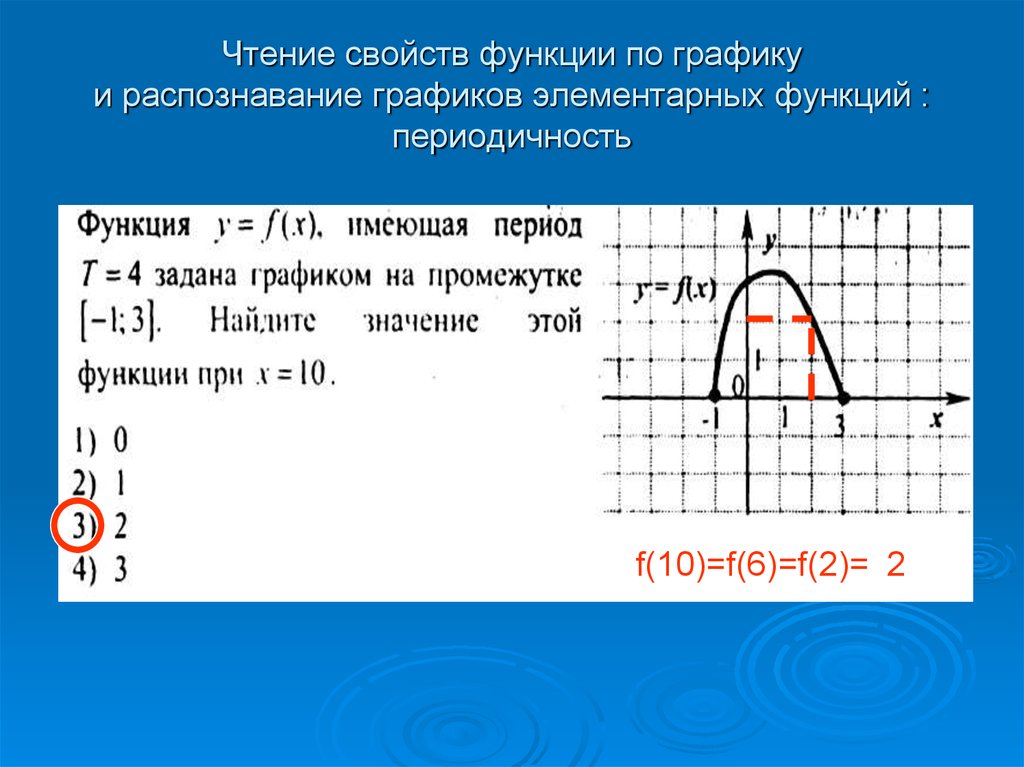 Красные и зеленые полосы снизу показывают объем торгов за день. Источник: сервис Yahoo Finance
Красные и зеленые полосы снизу показывают объем торгов за день. Источник: сервис Yahoo Finance
Какие существуют виды графиков
Есть три основных типа графиков. Они отличаются по виду и в зависимости от отображаемых данных. Многие инвестиционные сервисы позволяют пользователям переключаться между разными типами графиков.
Линейный график. Это самый простой способ отобразить колебания стоимости акций определенной компании. Линейный график показывает только цену акции на момент закрытия. По линейному графику инвесторы не могут проследить, как именно изменилась цена в течение торговой сессии.
Линейный график акций Яндекса. Он отражает только цены закрытия и поэтому изображается в виде сплошной линии. Источник: сервис Yahoo Finance
Вопрос-ответ 08 апреля 2022 Фундаментальный анализ фондового рынка — минимум, который должен знать каждый инвестор 13 минут
Свечной график.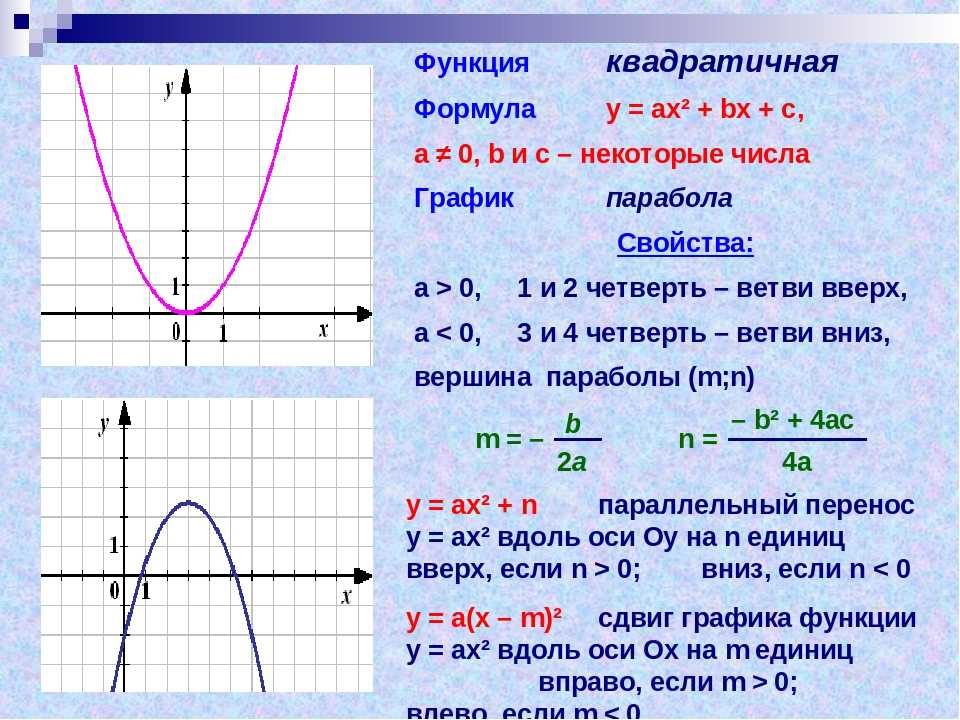 Иногда его называют японскими свечами. Он показывает дополнительную информацию о стоимости акций. Кроме цены закрытия торгов, инвестор видит цену открытия, а также максимальное и минимальное значения цены акции. Существует три вида свеч: растущие, падающие и дожи.
Иногда его называют японскими свечами. Он показывает дополнительную информацию о стоимости акций. Кроме цены закрытия торгов, инвестор видит цену открытия, а также максимальное и минимальное значения цены акции. Существует три вида свеч: растущие, падающие и дожи.
Как отображаются данные о цене акций на японских свечах. Источник данных: аналитический отдел ООО «Ньютон Инвестиции»
Растущие свечи означают, что цена акции выросла. Их отражают зеленым цветом. Падающие свечи означают, что цена акции упала. Дожами называют те свечи, на которых цены открытия и закрытия совпали.
Свечной график акций Яндекса. С помощью стоимости акций на вертикальной оси справа можно анализировать, как изменялись цены открытия и закрытия. Многие сервисы показывают цены открытия, закрытия и другие данные, если направить курсор на определенное место графика. Источник: сервис Yahoo Finance
Источник: сервис Yahoo Finance
Барный график. Он выглядит сложнее японских свечей, но отличается от них только внешним видом. Его предпочитают использовать западные трейдеры. Чтобы определить по барному графику изменение цены одной акции, нужно смотреть на две горизонтальные линии по бокам. Их называют «ушами».
Как отображаются данные на барном графике. Источник данных: аналитический отдел ООО «Ньютон Инвестиции»
Левое ухо — цена открытия, правое ухо — цена закрытия. Если левое ухо выше правого — цена упала, и бар будет красным. Если левое ухо ниже — цена выросла, и бар будет зеленым.
Барный график акций Яндекса. С помощью стоимости акций на вертикальной оси справа можно анализировать, как изменялись цены открытия и закрытия. Многие сервисы показывают цены открытия, закрытия и другие данные, если направить курсор на определенное место графика. Источник: сервис Yahoo Finance
Многие сервисы показывают цены открытия, закрытия и другие данные, если направить курсор на определенное место графика. Источник: сервис Yahoo Finance
Как правильно читать графики и что они показывают
Существует очень много биржевых индикаторов, которые можно наносить на графики акций.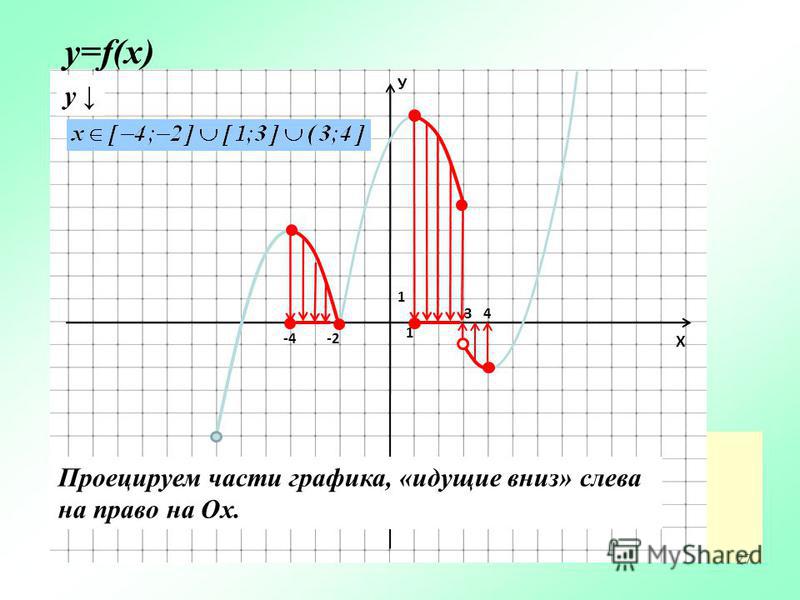 Но чтобы понять основную информацию о ценных бумагах, в техническом анализе используют четыре основных показателя.
Но чтобы понять основную информацию о ценных бумагах, в техническом анализе используют четыре основных показателя.
Линия тренда. Она помогает инвестору понять, растет стоимость акции или нет. Если линия графика уходит вверх — тренд положительный, если линия уходит вниз — тренд отрицательный. Иногда линия тренда выглядит как горизонтальная прямая. Она растет или падает в зависимости от изменения цены актива. В этом случае линия показывает, как изменилась цена акции за определенный промежуток времени.
Стоимость акций всегда меняется и может резко увеличиться или упасть. Обычно инвесторы не начинают продавать акции при отрицательном тренде или покупать их при положительном. В такие периоды они часто ищут дополнительную информацию, например смотрят отчетность или читают новости. Это помогает понять, что происходит с компанией и принять инвестиционное решение.
На графике отображена стоимость акций Apple с 2009 по 2015 год. Сплошная синяя и пунктирные фиолетовые линии показывают тренд. Видно, как с 2009 по 2012 год цена акций росла. Тренд был положительный. С 2012 по 2013 год стоимость акций резко упала — тренд стал отрицательным. В пунктирных прямоугольниках видно, на сколько процентов выросла или упала стоимость акций за определенный отрезок времени. Источник: сервис Yahoo Finance
Сплошная синяя и пунктирные фиолетовые линии показывают тренд. Видно, как с 2009 по 2012 год цена акций росла. Тренд был положительный. С 2012 по 2013 год стоимость акций резко упала — тренд стал отрицательным. В пунктирных прямоугольниках видно, на сколько процентов выросла или упала стоимость акций за определенный отрезок времени. Источник: сервис Yahoo Finance
Поддержка и сопротивление. Уровень поддержки показывает цену, ниже которой акция не упадет. Линия сопротивления показывает цену, выше которой акция не поднимется. Каждый инвестор самостоятельно определяет уровни поддержки и сопротивления. Они помогают понять, стоит ли покупать акцию в определенный момент или нет.
Некоторые акции в течение долгого времени торгуются в определенных ценовых границах. Инвесторы используют такие акции, чтобы увеличивать прибыль. Когда ценная бумага достигла уровня сопротивления — акцию продают. Когда она достигла уровня поддержки — ее покупают.
Когда она достигла уровня поддержки — ее покупают.
График акций Яндекса. Красные линии показывают уровни сопротивления, зеленые — уровни поддержки. Источник сервис Yahoo Finance
Вопрос-ответ 15 июня 2022 Дивидендные аристократы США: список и их особенности 9 минут
Дивиденды и дробление акций. Крупные и устойчивые компании периодически выплачивают дивиденды. То есть они распределяют часть прибыли между всеми держателями акций. Дивиденды выплачивают раз в месяц, квартал, полгода или год. Такие компании предпочитают инвесторы, которые хотят получать пассивный доход. График на бирже показывает, выплачивает ли компания дивиденды акционерам.
Крупные и устойчивые компании периодически выплачивают дивиденды. То есть они распределяют часть прибыли между всеми держателями акций. Дивиденды выплачивают раз в месяц, квартал, полгода или год. Такие компании предпочитают инвесторы, которые хотят получать пассивный доход. График на бирже показывает, выплачивает ли компания дивиденды акционерам.
Дробление акций — это ситуация, когда компания увеличивает количество акций в обращении. Например, в 2020 году Apple провела дробление акций в соотношении 4 к 1. То есть каждая акция превратилась в четыре акции. Обычно дробление проводят, чтобы привлечь больше инвесторов, повысить спрос и таким образом увеличить стоимость акций.
График акций Apple. Внизу по горизонтали располагаются буквы D — Dividends. Они обозначают даты дивидендных выплат. Apple выплачивает дивиденды раз в квартал. 30 июля 2020 года компания произвела дробление акций. Оно обозначается буквой S — Splits.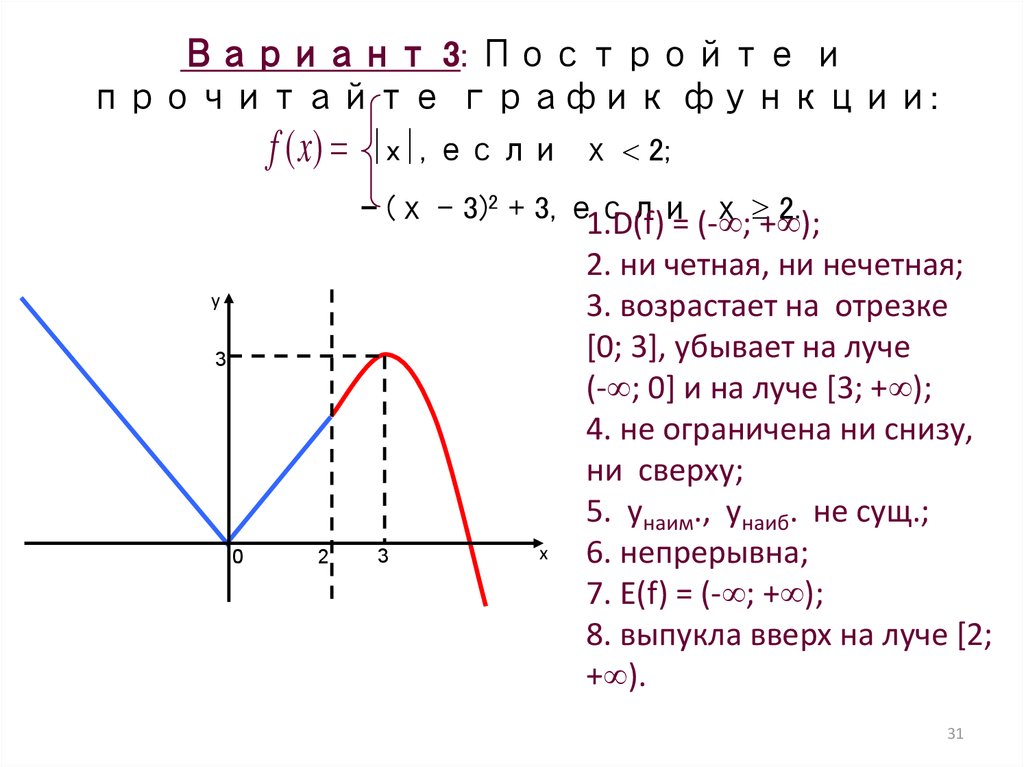 После дробления цена упала. Но затем выросла, потому что больше людей начало инвестировать в Apple. Источник: сервис Yahoo Finance
После дробления цена упала. Но затем выросла, потому что больше людей начало инвестировать в Apple. Источник: сервис Yahoo Finance
Объем торгов. Эта денежная сумма, на которую все инвесторы продали или купили акции определенной компании за одну торговую сессию. Объем торгов может напрямую влиять на стоимость акций. Если инвесторы приобрели большое количество ценных бумаг компании — их стоимость вырастет. Если продали — их стоимость снизится.
Основная доля торгов на фондовом рынке приходится на крупных институциональных инвесторов: фонды и банки. Когда они совершают крупные покупки, то формируют большой объем торгов и двигают цену акций вверх или вниз. Частные инвесторы следят за такими операциями, чтобы предсказывать стоимость акций.
График акций Apple. Вертикальные полосы снизу показывают объем торгов.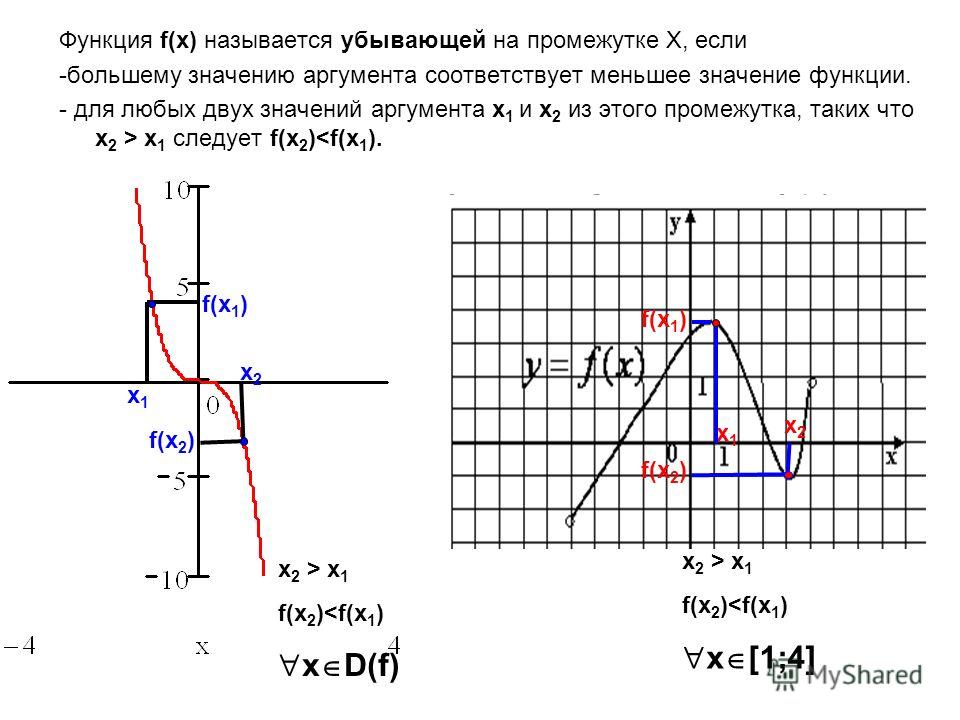 Красный цвет означает, что большое количество акций продали. Зеленый — большое количество акций купили. Две зеленые стрелки показывают на дни с самыми большими объемами торгов. Видно, как после крупного приобретения акций в феврале их стоимость резко увеличилась. В середине мая произошла крупная продажа и стоимость акций упала. Источник: сервис Yahoo Finance
Красный цвет означает, что большое количество акций продали. Зеленый — большое количество акций купили. Две зеленые стрелки показывают на дни с самыми большими объемами торгов. Видно, как после крупного приобретения акций в феврале их стоимость резко увеличилась. В середине мая произошла крупная продажа и стоимость акций упала. Источник: сервис Yahoo Finance
Кратко
- 1
Графики на бирже отражают цены определенных акций или других ценных бумаг.
 Инвесторы используют графики, чтобы следить за изменением стоимости активов из своего портфеля, вовремя их продавать и получать потенциальную прибыль.
Инвесторы используют графики, чтобы следить за изменением стоимости активов из своего портфеля, вовремя их продавать и получать потенциальную прибыль. - 2 Существует три основных вида графиков: линейный, свечной и барный. Линейный график показывает только цену акции на момент закрытия торгов. Свечной и барный график показывают цену открытия, цену закрытия, максимальное и минимальное значения цены акции. Они отличаются только по виду.
- 3 Есть несколько важных индикаторов, за которыми инвесторы следят с помощью графиков. Это линия тренда, уровни поддержки и сопротивления, дата дивидендных выплат, дробление акций и объем торгов.
Данный справочный и аналитический материал подготовлен компанией ООО «Ньютон Инвестиции» исключительно в информационных целях. Оценки, прогнозы в отношении финансовых инструментов, изменении их стоимости являются выражением мнения, сформированного в результате аналитических исследований сотрудников ООО «Ньютон Инвестиции», не являются и не могут толковаться в качестве гарантий или обещаний получения дохода от инвестирования в упомянутые финансовые инструменты. Не является рекламой ценных бумаг. Не является индивидуальной инвестиционной рекомендацией и предложением финансовых инструментов. Несмотря на всю тщательность подготовки информационных материалов, ООО «Ньютон Инвестиции» не гарантирует и не несет ответственности за их точность, полноту и достоверность.
Оценки, прогнозы в отношении финансовых инструментов, изменении их стоимости являются выражением мнения, сформированного в результате аналитических исследований сотрудников ООО «Ньютон Инвестиции», не являются и не могут толковаться в качестве гарантий или обещаний получения дохода от инвестирования в упомянутые финансовые инструменты. Не является рекламой ценных бумаг. Не является индивидуальной инвестиционной рекомендацией и предложением финансовых инструментов. Несмотря на всю тщательность подготовки информационных материалов, ООО «Ньютон Инвестиции» не гарантирует и не несет ответственности за их точность, полноту и достоверность.
Харлампий Эмеретли
Автор
Поделиться статьей
Читайте также
01 августа 2017 Какие бывают виды графиков 12 минут 08 апреля 2022 Фундаментальный анализ фондового рынка — минимум, который должен знать каждый инвестор 13 минут 14 апреля 2022 Для чего нужен метод скользящей средней и как его используют инвесторы 9 минут 19 мая 2022 Что такое демосчет на бирже: как инвестировать без риска 14 минут 15 июня 2022 Дивидендные аристократы США: список и их особенности 9 минутКак читать график
Графики используются повсеместно в нашей повседневной жизни, от прогнозов погоды до тенденций фондового рынка и бизнес-отчетов.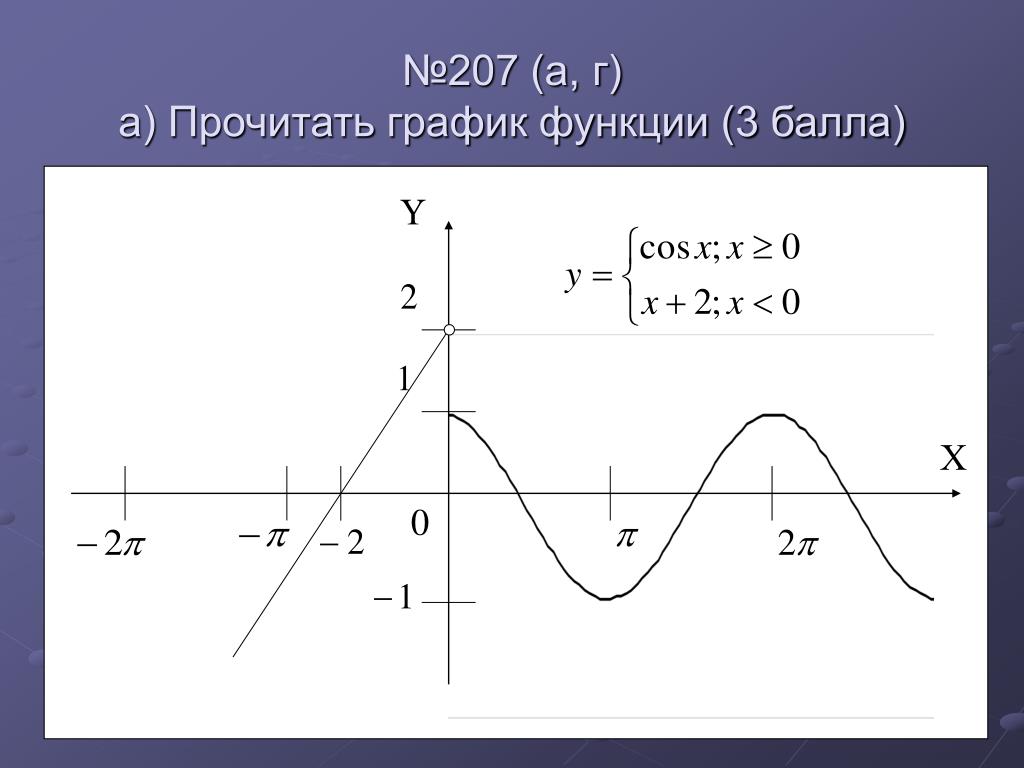 Они представляют собой визуальное представление данных или отношений между переменными. Некоторые графики труднее читать, чем другие, но, тем не менее, все они важны для изучения.
Они представляют собой визуальное представление данных или отношений между переменными. Некоторые графики труднее читать, чем другие, но, тем не менее, все они важны для изучения.
Чтение и понимание различных графиков является важным навыком для любого человека. Если вы используете их в своих таблицах PPT и Excel, вы должны знать, какие графики подходят для того или иного типа данных. В этой статье мы рассмотрим некоторые из различных типов графиков и диаграмм и способы их чтения.
Различные типы графиков и диаграмм
Термины «графики» и «диаграммы» иногда используются взаимозаменяемо, но это не совсем одно и то же. Графики представляют отношения между двумя или более переменными. Диаграммы представляют собой набор данных. Проще говоря, все графики — это диаграммы, но не все диаграммы — это графики.
Давайте рассмотрим 10 наиболее часто используемых графиков и диаграмм, а также способы их чтения.
1. Линейный график
Линейный график является одним из наиболее часто используемых графиков.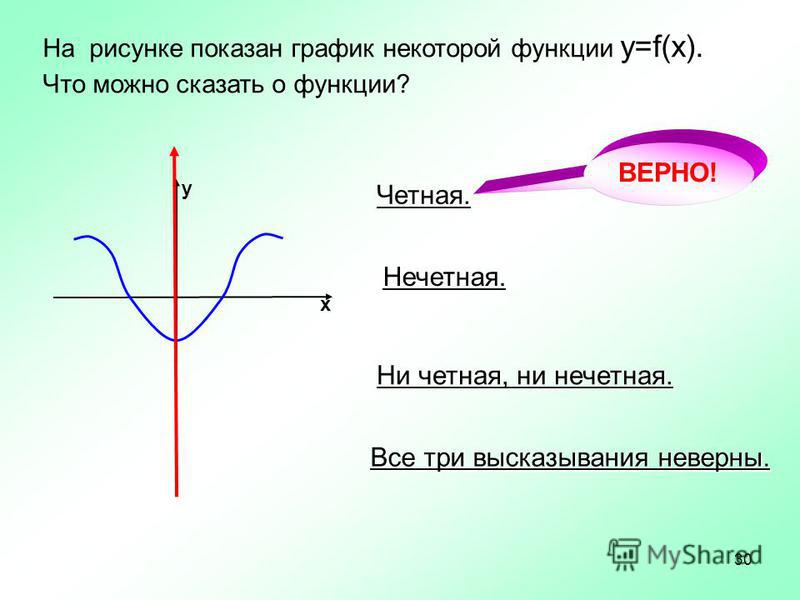 Он показывает, как две переменные изменяются по отношению друг к другу. Простейшая форма линейного графика — это та, которая иллюстрирует, как конкретная переменная изменяется во времени.
Он показывает, как две переменные изменяются по отношению друг к другу. Простейшая форма линейного графика — это та, которая иллюстрирует, как конкретная переменная изменяется во времени.
Положение точки на линейном графике определяется ее соответствующими значениями на оси x и оси y. Например, на приведенном выше линейном графике точка B указывает, что средняя температура в понедельник составляет 8 ° F. Точно так же, глядя на данные по обеим осям, вы можете интерпретировать, что означает конкретный экземпляр на графике.
Связанный: Как сделать линейный график в Excel
2. Гистограмма
Гистограмма представляет две или более переменных с использованием высоты прямоугольных столбцов. Чем выше полоса, тем выше значение, которое она представляет. Гистограммы сравнивают элементы одной категории по отношению к набору фиксированных значений. Чтобы лучше понять это, давайте посмотрим на приведенный ниже пример.
Здесь мы сравниваем рейтинги шести фильмов. На оси X у нас есть просмотренные фильмы, высота прямоугольников которых соответствует рейтингу каждого из них. На оси Y у нас есть шкала оценок — от одной до пяти звезд.
На оси X у нас есть просмотренные фильмы, высота прямоугольников которых соответствует рейтингу каждого из них. На оси Y у нас есть шкала оценок — от одной до пяти звезд.
Таким образом, гистограмма позволяет сравнивать элементы похожих категорий. Обратите внимание, что существует несколько видов гистограмм. Тот, который мы использовали на иллюстрации выше, называется вертикальной гистограммой. Другие виды гистограмм включают в себя:
- Горизонтальные гистограммы
- Гистограммы с накоплением
- Сгруппированные гистограммы
Связанные: Как сделать гистограмму в Excel
3. Круговые диаграммы
Круговая диаграмма — это круговая диаграмма, разделенная на несколько частей или секторов. Каждый кусочек представляет собой уникальную долю целого. Круговые диаграммы очень распространены, учитывая, насколько легко их интерпретировать.
Например, на изображении выше мы видим распределение дохода человека в виде частей всего круга. Это дает нам четкое представление о том, сколько денег человек тратит на определенную вещь.
Это дает нам четкое представление о том, сколько денег человек тратит на определенную вещь.
4. Гистограммы
Гистограмма похожа на гистограмму по внешнему виду и функциям, но содержащиеся в ней прямоугольные столбцы расположены рядом друг с другом. Это связано с тем, что столбцы здесь отображают значения, пропорциональные определенным числовым интервалам на оси x.
Приведенная выше гистограмма представляет возрастное распределение посетителей ресторана. Количество людей в возрасте от 20 до 29 лет равно 10, что соответствует высоте прямоугольной полосы. Гистограммы используются для представления больших наборов данных, и каждый диапазон переменных называется «сегментом» или «ячейкой».
5. Диаграммы с областями
Диаграммы с областями или графики с областями аналогичны линейным графикам; единственное дополнение состоит в том, что пространство между осью x и линейным графиком заполнено цветами или текстурами. Они представляют собой смесь линейного графика и гистограммы и используются для подчеркивания величины.
Диаграммы с площадями часто используются для сравнения объемов двух или более величин. На приведенном выше графике показаны тенденции выручки двух компаний с 1980 по 2020 год.
6. Пиктограммы
Пиктограмма или пиктограмма — это визуальное представление числовых данных с помощью значков. Обратите внимание на пиктограмму выше, чтобы лучше понять это. В нем количество учеников, которым нравится тот или иной фрукт, представлено значками самого фрукта.
Например, пять учеников в классе любят яблоки, поэтому к пиктограмме примыкают пять значков яблок. Хотя пиктограммы очень легко интерпретировать, они не идеальны для представления больших наборов данных или сложных отчетов.
Связанный: Как создавать мощные графики и диаграммы в Microsoft Excel
7. Точечная диаграмма
Графики рассеяния показывают, насколько сильно две переменные коррелируют друг с другом. Точки или точки, упомянутые на графике, представляют их значения. Если корреляция сильная, точки образуют отчетливый узор, который кажется близким к линии или кривой. Они обычно используются, когда набор данных велик, и вы пытаетесь проверить кажущуюся тенденцию.
Если корреляция сильная, точки образуют отчетливый узор, который кажется близким к линии или кривой. Они обычно используются, когда набор данных велик, и вы пытаетесь проверить кажущуюся тенденцию.
Приведенный выше график рассеяния показывает, как цены на продукт меняются в течение 20 недель. Хотя это выглядит как линейный график, мы можем видеть, что точки не связаны, а используются для рисования линии, представляющей тренд.
8. Сплайн-диаграмма
Сплайн-диаграмма основана на идее, что изменения следуют траектории. В отличие от линейного графика, который использует прямые линии и делает резкие повороты от одной точки к другой, сплайновая диаграмма использует изогнутые линии, чтобы показать приблизительное приближение отсутствующих точек данных.
Чтобы упростить сравнение, мы построили кривую сплайновой диаграммы поверх предыдущего примера линейного графика.
9. Воронкообразная диаграмма
Воронкообразная диаграмма используется для представления стадий линейного процесса, которые образуют воронкообразную форму.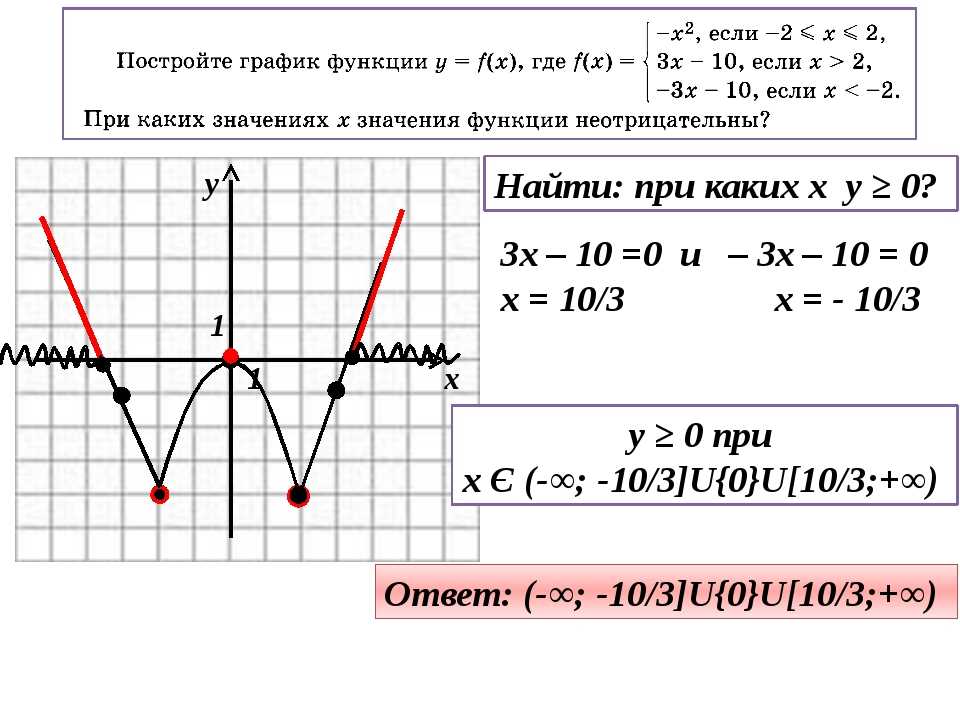 Он используется для визуального отображения того, как количество уменьшается или теряется на каждом этапе. Каждый этап воронки представляет собой процент от целого.
Он используется для визуального отображения того, как количество уменьшается или теряется на каждом этапе. Каждый этап воронки представляет собой процент от целого.
Возможно, вы уже слышали термин «воронка продаж». это наиболее распространенное изображение воронкообразной диаграммы. В приведенном выше примере представлены продажи продукта. Мы видим, что только 3% людей, получивших рекламное уведомление, действительно купили продукт.
10. Диаграмма Венна
Диаграмма Венна — это графическая иллюстрация, содержащая два или более перекрывающихся круга, которые показывают логическую связь между двумя или более наборами элементов. По сути, это помогает визуализировать различия и сходства между двумя или более вещами.
Научитесь читать график
Графики могут показаться простыми для понимания, но точно интерпретировать то, что они представляют, может быть сложно, особенно если вы имеете дело со сложным графиком.
Если вы профессионально пользуетесь графиками, очень важно выбирать правильные графики, чтобы читатели могли легко интерпретировать их.
GNU gprof — Как читать график вызовов
GNU gprof — Как читать график вызовов Перейти к первому, предыдущему, следующему, последнему разделу, оглавлению.График вызовов показывает, сколько времени было потрачено на каждую функцию и его дети. Из этой информации вы можете найти функции, которые, в то время как сами они, возможно, не использовали много времени, называемого другими функции, которые использовали необычное количество времени.
Вот пример вызова из небольшой программы. Этот звонок поступил из
тот же gprof работает как пример плоского профиля в предыдущем
глава.
гранулярность: каждое попадание выборки покрывает 2 байта на 20,00% от 0,05 секунды
index % времени, когда сами дочерние элементы вызываются name
<спонтанно>
[1] 100,0 0,00 0,05 пуск [1]
0,00 0,05 1/1 основной [2]
0,00 0,00 1/2 при_выходе [28]
0,00 0,00 1/1 выход [59]
--------------------------------------------------------------
0,00 0,05 1/1 пуск [1]
[2] 100,0 0,00 0,05 1 основной [2]
0,00 0,05 1/1 отчет [3]
--------------------------------------------------------------
0,00 0,05 1/1 основной [2]
[3] 100,0 0,00 0,05 1 отчет [3]
0,00 0,03 8/8 местное время [6]
0,00 0,01 1/1 печать [9]
0,00 0,01 9/9 fgets [12]
0,00 0,00 12/34 strncmp <цикл 1> [40]
0,00 0,00 Поиск 8/8 [20]
0,00 0,00 1/1 fоткрыт [21]
0,00 0,00 8/8 времени жевания [24]
0,00 0,00 8/16 пробел [44]
--------------------------------------------------------------
[4] 59,8 0,01 0,02 8+472 <цикл 2 в целом> [4]
0,01 0,02 244+260 время простоя <цикл 2> [7]
0,00 0,00 236+1 tzset <цикл 2> [26]
--------------------------------------------------------------
Строки, полные дефисов, делят эту таблицу на записей , по одной на каждую. функция. Каждая запись имеет одну или несколько строк.
функция. Каждая запись имеет одну или несколько строк.
В каждой записи основная строка начинается с порядкового номера. в квадратных скобках. Конец этой строки указывает, к какой функции относится запись. за. Предыдущие строки в записи описывают вызывающих абонентов этого функции, а следующие строки описывают ее подпрограммы (также называемые детей , когда мы говорим о графе вызовов).
Записи отсортированы по времени, проведенному в функции и ее подпрограммах.
Внутренняя функция профилирования mcount (см. раздел Как понять плоский профиль)
никогда не упоминается в графе вызовов.
- Первичный: Подробная информация о содержимом основной строки.
- Звонящие: Подробная информация о содержании линий вызывающих абонентов.
- Подпрограммы: Подробная информация о содержимом строк подпрограмм.
- Циклы: При наличии циклов рекурсии,
например
aзвонкиbзвонкиa. ..
..
Основная строка в записи графа вызовов — это строка, которая описывает функцию, о которой идет речь, и дает общее Статистика по этой функции.
Для справки повторим основную строку из записи для функции сообщает в нашем основном примере вместе со строкой заголовка, которая
показывает имена полей:
index % времени, когда сами дочерние элементы вызываются name ... [3] 100,0 0,00 0,05 1 отчет [3]
Вот что означают поля в основной строке:
-
индекс - Записи нумеруются последовательными целыми числами. Каждая функция поэтому имеет порядковый номер, который появляется в начале его первичная линия. Каждая перекрестная ссылка на функцию, как вызывающую программу или подпрограмму другой, дает свой порядковый номер, а также свое имя. Номер индекса поможет вам, если вы хотите найти запись для этой функции.
-
% времени - Это процент от общего времени, проведенного в этом
функции, включая время, проведенное в подпрограммах, вызываемых из этой
функция.
 Время, проведенное в этой функции, снова подсчитывается для вызывающих
эта функция. Поэтому складывать эти проценты бессмысленно.
Время, проведенное в этой функции, снова подсчитывается для вызывающих
эта функция. Поэтому складывать эти проценты бессмысленно. -
сам - Это общее количество времени, проведенного в этой функции. Этот
должно совпадать с числом, напечатанным в поле
секунддля этой функции в плоском профиле. -
детский - Это общее время, затраченное на вызовы подпрограмм, сделанные
эта функция. Это должно быть равно сумме всех
selfидетейзапись детей, перечисленных непосредственно под этим функция. -
по телефону - Это количество вызовов функции.
Если функция вызвала себя рекурсивно, есть два числа,
разделенные `+’ . Первое число считает нерекурсивные вызовы,
а второй считает рекурсивные вызовы.
В приведенном выше примере функция
отчетбыл вызван один раз изосновной. -
наименование - Это имя текущей функции.
 Номер индекса
повторяется после него.
Если функция является частью цикла рекурсии, номер цикла
печатается между именем функции и порядковым номером
(see section Как описываются взаимно рекурсивные функции). Например, если функция
Номер индекса
повторяется после него.
Если функция является частью цикла рекурсии, номер цикла
печатается между именем функции и порядковым номером
(see section Как описываются взаимно рекурсивные функции). Например, если функция gnurrявляется частью цикл номер один и имеет индекс двенадцать, его основная линия будет заканчиваться так:gnurr <цикл 1> [12]
Запись функции имеет строку для каждой функции, из которой она была вызвана. Поля этих строк соответствуют полям основной строки, но их значения различны из-за разницы в контексте.
Для справки повторим две строки из записи для функции отчет , основная линия и одна предшествующая ей линия вызывающего абонента вместе
со строкой заголовка, которая показывает имена полей:
index % времени, когда сами дочерние элементы вызываются name
...
0,00 0,05 1/1 основной [2]
[3] 100,0 0,00 0,05 1 отчет [3]
Вот значения полей в звонилке для отчет звонил с основной :
-
сам - Оценка количества времени, проведенного в отчете
о самом отчете, когда он был звонил сосновной.
-
дети - Оценка количества времени, проведенного в подпрограммах отчета
отчетбыл вызван сосновной. Суммаselfидетейполя — это оценка о количестве времени, затраченного на звонки наотчетсосновной. -
по телефону - Два числа: количество вызовов
отчетс основного , за которым следует общее количество нерекурсивных вызововс отчетомиз все его абоненты. -
наименование и порядковый номер - Имя звонящего по номеру
, отчет, к которому относится эта линия, за которым следует порядковый номер вызывающего абонента. Не все функции имеют записи в графе вызовов; некоторый варианты доgprofзапрос на пропуск некоторых функций. Когда у вызывающего абонента нет собственной записи, у него все еще есть линии вызывающего абонента. в записях функций, которые он вызывает.
Если вызывающий объект является частью цикла рекурсии, номер цикла
печатается между именем и порядковым номером.
в записях функций, которые он вызывает.
Если вызывающий объект является частью цикла рекурсии, номер цикла
печатается между именем и порядковым номером.
Если личность вызывающих функцию не может быть определена,
печатается фиктивная вызывающая линия, которая имеет `
Запись функции имеет строку для каждой из ее подпрограмм — в других слова, строки для каждой функции, которую он вызвал. Эти линии поля соответствуют полям основной строки, но их значения различаются из-за разницы в контексте.
Для справки повторим две строки из записи для функции main , основная строка и строка для подпрограммы вместе
со строкой заголовка, которая показывает имена полей:
index % времени, когда сами дочерние элементы вызываются name
...
[2] 100,0 0,00 0,05 1 основной [2]
0,00 0,05 1/1 отчет [3]
Вот значения полей в строке подпрограммы для main вызов отчет :
-
сам - Оценка количества времени, затраченного непосредственно в отчете
отчетбыл вызван сосновной.
-
дети - Оценка количества времени, проведенного в подпрограммах отчета
отчетбыл вызван сосновной. Сумма полейselfиchildrenявляется оценкой от общего времени звонков наотчетсосновной. -
по телефону - Два номера, количество звонков на
отчетсосновнойза которым следует общее количество нерекурсивных вызововс отчетом. -
наименование - Имя подпрограммы
main, к которой относится эта строка, за которым следует порядковый номер подпрограммы. Если вызывающий объект является частью цикла рекурсии, номер цикла печатается между именем и порядковым номером.
Граф может быть усложнен наличием циклов
рекурсия в графе вызовов. Цикл существует, если функция вызывает
другая функция, которая (прямо или косвенно) вызывает (или кажется, что
call) исходная функция. Например: если
Например: если a вызывает b ,
и b вызывает a , затем a и b образуют цикл.
Всякий раз, когда есть двусторонние пути вызова между парой функций, они
относятся к одному и тому же циклу. Если a и b звонят друг другу и b и c вызывают друг друга, все три делают один цикл. Обратите внимание, что
даже если b вызывает только a , если он не был вызван с a , gprof не может это определить, поэтому a и b до сих пор
считается циклом.
Циклы нумеруются последовательными целыми числами. Когда функция принадлежит циклу, каждый раз, когда имя функции появляется в графе вызовов за ним следует `<цикл номер >’ .
Причина, по которой циклы имеют значение, заключается в том, что они делают значения времени в вызове
график парадоксальный. «Время, проведенное у детей»
«Время, проведенное у детей» и должно
включить время, проведенное в его подпрограмме b и в b подпрограммы — но одна из подпрограмм b — это a ! Сколько из время должно быть включено в детей , когда и косвенно рекурсивны?
Способ gprof разрешает этот парадокс путем создания единственной записи
для цикла в целом. Первая строка этой записи описывает
общее время, проведенное непосредственно в функциях цикла.
«подпрограммы» цикла — это отдельные функции цикла, и
все другие функции, которые вызывались непосредственно ими. «звонившие» из
цикл — это функции вне цикла, которые вызывали функции в
цикл.
Вот пример части графа вызовов, который показывает цикл, содержащий
функции а и б . Цикл был введен вызовом и из основной ; оба a и b называются c .
index % времени, когда сами дочерние элементы вызываются name
----------------------------------------
1,77 0 1/1 основной [2]
[3] 91,71 1,77 0 1+5 <цикл 1 в целом> [3]
1.02 0 3 б <цикл 1> [4]
0,75 0 2 а <цикл 1> [5]
----------------------------------------
3 а <цикл 1> [5]
[4] 52,85 1,02 0 0 б <цикл 1> [4]
2 а <цикл 1> [5]
0 0 3/6 в [6]
----------------------------------------
1,77 0 1/1 основной [2]
2 б <цикл 1> [4]
[5] 38,86 0,75 0 1 а <цикл 1> [5]
3 б <цикл 1> [4]
0 0 3/6 в [6]
----------------------------------------
(Весь граф вызовов для этой программы содержит, кроме того, запись для основной , который вызывает a , и запись для c , с вызывающими абонентами а и б . )
)
index % времени, когда сами дочерние элементы вызываются name
<спонтанно>
[1] 100,00 0 1,93 0 пуск [1]
0,16 1,77 1/1 основной [2]
----------------------------------------
0,16 1,77 1/1 пуск [1]
[2] 100,00 0,16 1,77 1 основной [2]
1,77 0 1/1 а <цикл 1> [5]
----------------------------------------
1,77 0 1/1 основной [2]
[3] 91,71 1,77 0 1+5 <цикл 1 в целом> [3]
1.02 0 3 б <цикл 1> [4]
0,75 0 2 а <цикл 1> [5]
0 0 6/6 в [6]
----------------------------------------
3 а <цикл 1> [5]
[4] 52,85 1,02 0 0 б <цикл 1> [4]
2 а <цикл 1> [5]
0 0 3/6 в [6]
----------------------------------------
1,77 0 1/1 основной [2]
2 б <цикл 1> [4]
[5] 38,86 0,75 0 1 а <цикл 1> [5]
3 б <цикл 1> [4]
0 0 3/6 в [6]
----------------------------------------
0 0 3/6 б <цикл 1> [4]
0 0 3/6 a <цикл 1> [5]
[6] 0,00 0 0 6 в [6]
----------------------------------------
Поле self основной строки цикла — это общее время
расходуется на все функции цикла. Он равен сумме
Он равен сумме самостоятельных полей для отдельных функций в цикле, найдено
в записи в строках подпрограмм для этих функций.
дочерних полей основной строки цикла и строк подпрограммы
считать только подпрограммы вне цикла. Хотя звонит b , время, проведенное в этих звонках до б не учитывается детей время. Таким образом, мы не сталкиваемся с проблемой
что делать, когда время в этих звонках на b включает косвенные
рекурсивные вызовы a .
Поле детей линии вызывающего абонента в оценках ввода цикла
количество времени, затраченное на весь цикл , и другие его
подпрограммы, когда этот вызывающий вызывал функцию в цикле.
звонки Поле в основной линии для цикла имеет два номера:
во-первых, количество раз, когда функции в цикле вызывались функциями
вне цикла; во-вторых, количество раз, когда им звонили
функции в цикле (включая моменты, когда функция в цикле вызывает
сам).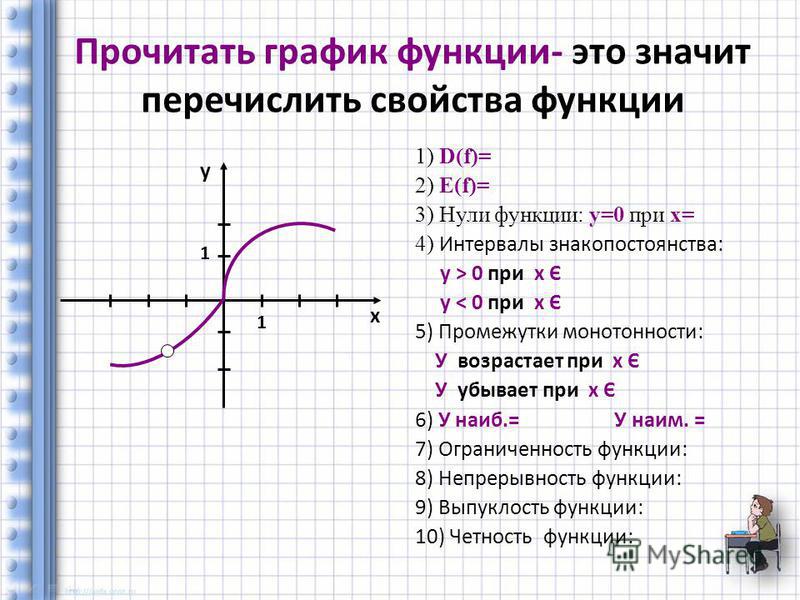

 Инвесторы используют графики, чтобы следить за изменением стоимости активов из своего портфеля, вовремя их продавать и получать потенциальную прибыль.
Инвесторы используют графики, чтобы следить за изменением стоимости активов из своего портфеля, вовремя их продавать и получать потенциальную прибыль. ..
.. Время, проведенное в этой функции, снова подсчитывается для вызывающих
эта функция. Поэтому складывать эти проценты бессмысленно.
Время, проведенное в этой функции, снова подсчитывается для вызывающих
эта функция. Поэтому складывать эти проценты бессмысленно. Номер индекса
повторяется после него.
Если функция является частью цикла рекурсии, номер цикла
печатается между именем функции и порядковым номером
(see section Как описываются взаимно рекурсивные функции). Например, если функция
Номер индекса
повторяется после него.
Если функция является частью цикла рекурсии, номер цикла
печатается между именем функции и порядковым номером
(see section Как описываются взаимно рекурсивные функции). Например, если функция 
 в записях функций, которые он вызывает.
Если вызывающий объект является частью цикла рекурсии, номер цикла
печатается между именем и порядковым номером.
в записях функций, которые он вызывает.
Если вызывающий объект является частью цикла рекурсии, номер цикла
печатается между именем и порядковым номером.