Произведение длин векторов: Скалярное произведение векторов — урок. Геометрия, 9 класс.

Скалярное произведение векторов

Угол между векторами   может принимать значения от 0 до 180 градусов (от 0 до   радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства:   либо   (в радианах).

В литературе значок угла   часто пропускают и пишут просто  .

Определение: Скалярным произведением двух векторов   и   называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:

Обозначение: скалярное произведение обозначается через   или просто  .

Результат операции является ЧИСЛОМ: Умножается вектор на вектор, а получается число. Действительно, если длины векторов   – это числа, косинус угла – число, то их произведение   тоже будет числом.

Пример

Найти скалярное произведение векторов   и  , если 

Решение: 

Ответ: 

Угол между векторами и значение скалярного произведения

Длины ненулевых векторов всегда положительны:  , поэтому знак может зависеть только от значения косинуса.

1) Если угол между векторами острый:    (от 0 до 90 градусов), то  , и скалярное произведение будет положительным:  . Особый случай: если векторы сонаправлены, то угол между ними считается нулевым  , и скалярное произведение также будет положительным. Поскольку  , то формула упрощается:  .

2) Если угол между векторами тупой:    (от 90 до 180 градусов), то  , и, соответственно, скалярное произведение отрицательно:  . Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым:   (180 градусов). Скалярное произведение тоже отрицательно, так как 

3) Если угол между векторами прямой:   (90 градусов), то   и скалярное произведение равно нулю:  .

Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: 

Третий случай имеет большую практическую значимость

, поскольку позволяет проверить, ортогональны векторы или нет.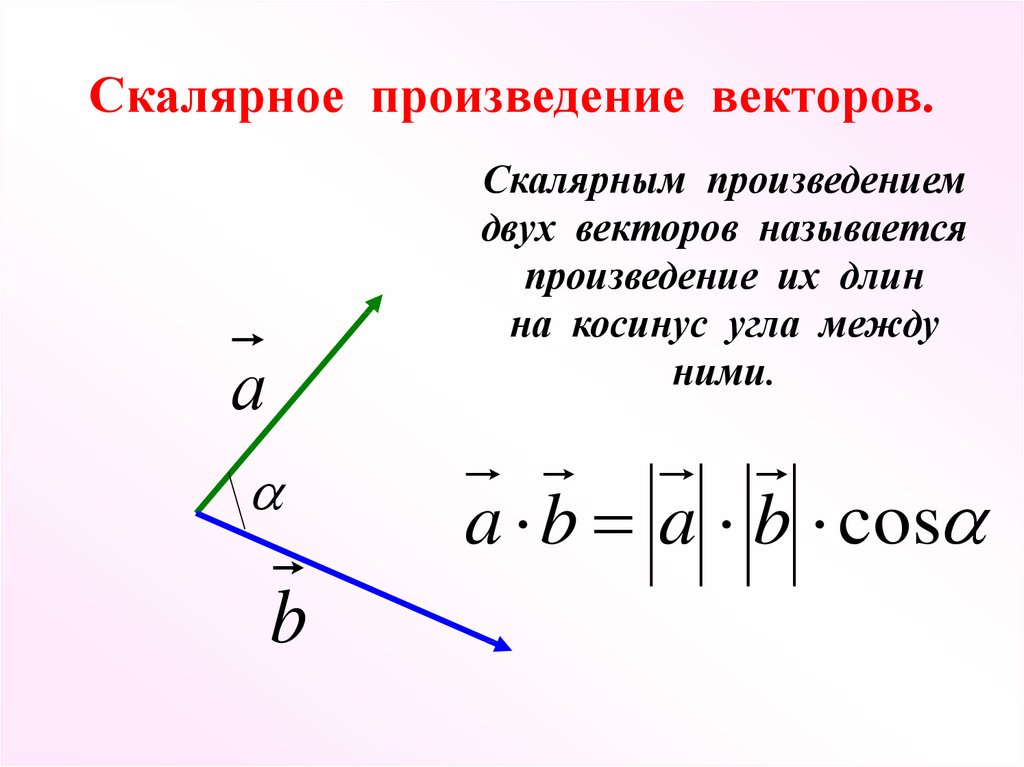

Скалярный квадрат вектора Что будет, если вектор умножить на самого себя?

Или: 

Число   называется скалярным квадратом вектора  , и обозначатся как  .

Таким образом, скалярный квадрат вектора   равен квадрату длины данного вектора:

Из данного равенства можно получить формулу для вычисления длины вектора:

Свойства скалярного произведения.

Для произвольных векторов   и любого числа   справедливы следующие свойства:

1)   – переместительный или коммутативный закон скалярного произведения.

2)   – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.

3)   – сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.

Пример

Найти скалярное произведение векторов   и  , если известно, что  .

Решение: 

(1) Подставляем выражения векторов  .

(2) Раскрываем скобки по правилу умножения многочленов. Раскрыть скобки нам позволяет дистрибутивное свойство скалярного произведения.

(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов:  . Во втором слагаемом используем перестановочность скалярного произведения:  .

(4) Приводим подобные слагаемые:  .

(5) В первом слагаемом используем формулу скалярного квадрата  , о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука:  . Второе слагаемое раскладываем по стандартной формуле  .

(6) Подставляем данные условия  , и ВНИМАТЕЛЬНО проводим окончательные вычисления.

Ответ: 

Пример

Найти длину вектора  , если  .

Решение:

 

(1) Поставляем выражение вектора  .

(2) Используем формулу длины:  , при этом в качестве вектора «вэ» у нас выступает целое выражение  .

(3) Используем школьную формулу квадрата суммы  .

(4) Дальнейшее аналогично действиям из двух предыдущих задач.

Ответ: 

Скалярное произведение векторов / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
5. Скалярное произведение векторов

Определение

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Пусть нам даны векторы и , тогда их скалярное произведение будет обозначаться так: или .

Из определения мы можем записать:

             (1)

Утверждение:

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Доказательство:

Пусть , т.е. = 90⁰, тогда , а, значит, = 0.

Пусть и ненулевые, при этом = 0, тогда из равенства (1) получаем, что , а, значит, = 90⁰, т.е. . Следовательно, утверждение верно.

Так как при ( при ) тогда из формулы (1) следует, что скалярное произведение ненулевых векторов и положительно (отрицательно) тогда и только тогда, когда ().

Пусть векторы и будут являться сонаправленными, тогда угол между ними будет равен 0⁰ и , тогда из формулы (1) получим . Частным случаем является произведение вектора на себя, т.е.

Скалярное произведение называется скалярным квадратом вектора и обозначается . Скалярный квадрат вектора равен квадрату его длины.

Советуем посмотреть:

Синус, косинус, тангенс, котангенс

Основное тригонометрическое тождество. Формулы приведения.

Формулы для вычисления координат точки

Теорема о площади треугольника

Теорема синусов

Теорема косинусов

Решение треугольников

Измерительные работы

Угол между векторами

Скалярное произведение в координатах

Свойства скалярного произведения векторов

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Правило встречается в следующих упражнениях:

7 класс

Задание 1041, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1042, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1044, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1051, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 16, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 22, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1068, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

линейная алгебра — скалярное произведение для нахождения длины вектора в сравнении с законом косинуса

При использовании скалярного произведения для нахождения длины вектора должен ли ответ всегда быть таким же, как и при применении закона косинуса? Я делал обзор линейной алгебры и решил решить некоторые вопросы о длинах векторов, используя как скалярное произведение, так и закон косинуса.

Допустим, у вас есть вектор $\vec u = 2\vec a + 3\vec b$ и $\vec v = 3\vec a -\vec b$, где $\|\vec a\| = 3$, $\|\vec b\| = 4$ и $\vec a \cdot \vec b = 5$. Найдите $\|\vec u\|$ и угол между $\vec u$ и $\vec v$. 9{\circ}= \theta$$

Я пытаюсь понять, почему метод закона косинусов и скалярное произведение дают разные величины для $\|\vec v\|$. Это приводит к другому углу между двумя векторами.

Извините, если это было опубликовано ранее. Я пытался найти что-то подобное, но ничего не нашел. Любая помощь приветствуется!

Векторы и скалярные произведения. Учебные пособия по работе с изображениями, вычислениям и математике

\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{# 1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)

Вектор представляет собой упорядоченную последовательность значений:

\[\begin{split}\vec{v} = [ v_1, v_2, \cdots v_n ] \\\end{split}\]

Видео

См. эти видео Академии Хана для хорошего введения в векторные скалярные произведения:

• математические свойства скалярных произведений,
• длина вектора,
• единичных векторов

Масштабирование вектора

Вектор может быть масштабирован скаляром \(c\):

\[c \vec{v} \triangleq [ c v_1, c v_2, \cdots c v_n ]\]

Добавление вектора

Допустим, у нас есть два вектора, содержащие значения \(n\):

\[\begin{split}\vec{v} = [ v_1, v_2, \cdots v_n ] \\ \vec{w} = [ w_1, w_2, \cdots w_n ]\end{split}\]

Вектор дополнение дает новый вектор со значениями \(n\):

\[\vec{v} + \vec{w} \triangleq [ v_1 + w_1, v_2 + w_2, \cdots v_n + w_n ]\]

Сложение векторов является коммутативным, поскольку \(v_i + w_i = w_i + v_i\):

\[\vec{ v} + \vec{w} = \vec{w} + \vec{v}\] 92 }\).

Исходя из определения длины вектора и скалярного произведения, квадратный корень из скалярное произведение вектора на самого себя дает длину вектора:

\[\VL{v} = \sqrt{ \vec{v} \cdot \vec{v} }\]

Свойства скалярных произведений

We будет использовать результаты из Some алгебра с суммированием.

Коммутативный

\[\vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v}\]

потому что \(v_i w_i = w_i v_i\).

Распределение над сложением векторов

\[\vec{v} \cdot (\vec{w} + \vec{x}) = \vec{v} \cdot \vec{w} + \vec{v} \cdot \vec{x}\]

, потому что:

\[\begin{split}\vec{v} \cdot (\vec{w} + \vec{x}) = \\ \Sigma{ v_i ( w_i + x_i) } = \\ \Sigma{ (v_i + w_i)} + \Sigma{ (v_i + x_i)} = \\ \vec{v} \cdot \vec{w} + \vec{v} \cdot \vec{x}\end{split}\]

Скалярное умножение

Допустим, у нас есть два скаляра, \(c\) и \(d\):

\[(c \vec{v}) \cdot (d \vec{w}) = c d ( \vec{v} \cdot \vec{w} )\]

, потому что:

\[\begin{split}(c \vec{v}) \cdot (d \vec{w}) = \\ \Sigma{ c v_i d w_i } = \\ c d \Sigma{ v_i w_i }\end{split}\]

Из свойств распределения по сложению и скалярному умножению:

\[\vec{v} \cdot (c \vec{w} + \vec{x }) = c (\vec{v} \cdot \vec{w}) + (\vec{v} \cdot \vec{x})\]

См.: свойства скалярных произведений.