Произведение векторов как найти – формула, примеры, свойства, геометрический смысл

Как найти векторное произведение векторов — энциклопедический справочник и словарь для студента от А до Я

ФОРМУЛА

Чтобы найти векторное произведение \(\ [\overline{a}, \overline{b}] \) двух векторов, заданных их координатами \(\ \overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right) \quad{и}\quad \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \)соответственно, необходимо вычислить следующий определитель

\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{x}} & {a_{y}} & {a_{z}} \\ {b_{x}} & {b_{y}} & {b_{z}}\end{array}\right| \)

Как правило, такой определитель вычисляется путем разложения первой строки. Также обратите внимание, что результатом векторного произведения является вектор.

ПРИМЕРЫ РАСЧЕТА ВЕКТОРНОЙ ПРОДУКЦИИ ВЕКТОРОВ

ПРИМЕР

Задание: Найти векторное произведение векторов \(\ \overline{a}=(1 ; 0 ; 0) \quad{и}\quad \overline{b}=(0 ; 1 ; 0) \)

Решение: Для расчета векторного произведения указанных векторов используем формулу

\(\ [\overline{a}, b]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{x}} & {a_{y}} & {a_{z}} \\ {b_{x}} & {b_{y}} & {b_{z}}\end{array}\right| \)

Подставляя координаты указанных векторов, получаем:

\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {1} & {0} & {0} \\ {0} & {1} & {0}\end{array}\right| \)

Разобьем определитель по первой строке:

\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {1} & {0} & {0} \\ {0} & {1} & {0}\end{array}\right|= \)

\(\ =\overline{i} \cdot \left| \begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right|-\overline{j} \cdot \left| \begin{array}{cc}{1} & {0} \\ {0} & {0}\end{array}\right|+\overline{k} \cdot \left| \begin{array}{cc}{1} & {0} \\ {0} & {1}\end{array}\right|= \)

\(\ =0 \cdot \overline{i}-0 \cdot \overline{j}+1 \cdot \overline{k} \)

Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляется как определитель второго порядка: мы берем произведение вторичных элементов из произведения элементов главной диагонали.

Итак, координаты искомого вектора равны коэффициентам ортов, то есть

\(\ [\overline{a}, \overline{b}]=(0 ; 0 ; 1) \)

Ответ: \(\ [\overline{a}, \overline{b}]=(0 ; 0 ; 1) \)

ПРИМЕР

Задание: Даны векторы \(\ \overline{a}=(5 ; 3 ;-4) \quad{и}\quad \overline{b}=(6 ; 7 ;-8) \) . Найти координаты векторного произведения \(\ [\overline{a}, \overline{b}] \)

Решение: Координаты векторного произведения \(\ [\overline{a}, \overline{b}] \) рассчитываются по формуле

\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{x}} & {a_{y}} & {a_{z}} \\ {b_{x}} & {b_{y}} & {b_{z}}\end{array}\right| \)

Подставляя координаты указанных векторов, получаем:

\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {5} & {3} & {-4} \\ {6} & {7} & {-8}\end{array}\right|= \)

Разобьем полученный определитель по первой строке:

\(\ =\vec{i} \cdot \left| \begin{array}{cc}{3} & {-4} \\ {7} & {-8}\end{array}\right|-\overline{j} \cdot \left| \begin{array}{cc}{5} & {-4} \\ {6} & {-8}\end{array}\right|+\overline{k} \cdot \left| \begin{array}{cc}{5} & {3} \\ {6} & {7}\end{array}\right|= \)

\(\ =[3 \cdot(-8)-7 \cdot(-4)] \cdot \overline{i}-[5 \cdot(-8)-6 \cdot(-4)] \cdot \overline{j}+ \)

\(\ +[5 \cdot 7-6 \cdot 3] \cdot \overline{k}=(-24+28) \overline{i}-(-40+24) \overline{j}+(35-18) \overline{k}= \)

\(\ =4 \cdot \overline{i}+16 \cdot \overline{j}+17 \cdot \overline{k} \)

Тогда

\(\ [\overline{a}, \overline{b}]=(4 ; 16 ; 17) \)

Ответ: \(\ [\overline{a}, \overline{b}]=(4 ; 16 ; 17) \)

sciterm.ru

Что такое векторное произведение векторов и как его найти?

Не менее полезное и широко используемое в геометрии, чем скалярное произведение векторов есть векторное произведение. Так что, и на эту тему я решил написать небольшую онлайн программку, которая будет вам помогать с вычислениями и в понимании формул.

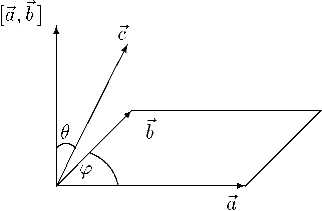
Также хочу вам немножко рассказать, что такое векторное произведение и где оно используется? Векторным произведением двух векторов, является вектор, длина которого равна произведению длин этих векторов на синус угла между ними, также этот вектор должен быть перпендикулярен к плоскости, в которой лежат два других вектора, и все они должны образовывать правый репер.

То есть тройка векторов {a, b, c} будет правой, если посмотреть с конца вектора c на плоскость векторов a и b, то движение от a к b по меньшему углу должна происходить против часовой стрелки.

Очень интересны и геометрические свойства векторного произведения:

• Первое сформулируем теоремой:
  

  Векторное произведение двух векторов равно нулю тогда и только тогда, когда угол между ними ноль, то есть когда эти векторы коллинеарные.

  Основываясь на эту теорему, и доводят, что векторы или прямые коллинеарные.

• Второе – это то, что длина векторного произведения равна площади параллелограмма, построенного на перемножаемых векторах. Именно это часто используют для вычисления площади параллелограмма, треугольника и некоторых других геометрических фигур.

Сама программа вычисляет двумя способами длину векторного произведения, в первом случае по определению, а во втором для ортонормированного базиса. В последнем, она также находит и координаты вектора векторного произведения. Как всегда, выводятся все формулы и матрицы с пошаговыми шагами решения. Вам надо только выбрать подходящий для вас вариант и ввести данные вашей задачи и через секунду перед вами полное решение.

Пользуйтесь программкой и вы сможете не просто проверить своё решение, но и увидеть, где вы допустили ошибку, если она будет. Всё расписано до мельчайших подробностей.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

Как найти векторное произведение векторов?

Пусть два вектора заданы координатами и .

Векторное произведение данных векторов обозначается или и равно следующему определителю:

   

В результате расчета векторного произведения получается вектор.
Данный определитель чаще всего раскладывают по элементам первой строки.

Пример
Даны векторы , . Найдем их векторное произведение.

Решение. Используем формулу для нахождения векторного произведения:

   

Подставим соответствующие координаты данных векторов и получим:

   

Выполним разложение определителя по элементам первой строки:

   

   

   

Координаты вектора, который получают в результате векторного произведения, будут равны коэффициентам при единичных векторах , и соответственно:

   

Ответ: .

Рассмотрим векторное произведение со стороны его геометрической интерпретации:
Площадь параллелограмма, который можно построить на векторах и , равна модулю векторного произведения данных векторов:

   

или половине треугольника, который построен та данных векторах:

   

ru.solverbook.com

Лекция 5. произведения векторов

Лекция 5. ПРОИЗВЕДЕНИЯ ВЕКТОРОВ

ОПРЕДЕЛЕНИЕ 1. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ ОПРЕДЕЛЯЕТСЯ ФОРМУЛОЙ

, (1)

ГДЕУГОЛ МЕЖДУ ВЕКТОРАМИ, ИМЕЮЩИМИ ОБЩЕЕ НАЧАЛО.

ИЗ ОПРЕДЕЛЕНИЯ (4.1) СЛЕДУЕТ, ЧТО ДЛЯ БАЗИСНЫХ ВЕКТОРОВ ВЫПОЛНЯЮТСЯ РАВЕНСТВА

(2)

КРОМЕ ТОГО ИЗ ФОРМУЛ (1), (2) СЛЕДУЮТ СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ

(3)

ТЕОРЕМА 1. ВЫЧИСЛЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ В КООРДИНАТАХ ДАЁТСЯ ФОРМУЛАМИ

В ПРОСТРАНСТВЕ (4)

НА ПЛОСКОСТИ (5)

ДОКАЗАТЕЛЬСТВО. ДОКАЖЕМ ФОРМУЛУ (4) ДЛЯ ПРОСТРАНСТВА. ФОРМУЛА (5) ДОКАЗЫВАЕТСЯ АНАЛОГИЧНО

ПУСТЬ , ТОГДА

С ПОМОЩЬЮ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ МОЖНО РЕШАТЬ ТИПОВЫЕ ЗАДАЧИ:

1) ВЫЧИСЛЯТЬ ДЛИНУ ВЕКТОРА

ИЗ ФОРМУЛЫ (1) СЛЕДУЕТ

(6)

₂₎

ВЫЧИСЛЯТЬ ПРОЕКЦИЮ ВЕКТОРА НА НАПРАВЛЕНИЕ ЗАДАВАЕМОЕ ВЕКТОРОМ

_{ИЗ ОПРЕДЕЛЕНИЯ ПРОЕКЦИИ (ФОРМУЛА (3.9)) И СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ (4.1) ПОЛУЧАЕМ}

(7)

УГОЛ -ЭТО УГОЛ МЕЖДУ НЕНУЛЕВЫМИ ВЕКТОРАМИ .

3) ВЫЧИСЛЯТЬ УГ0Л МЕЖДУ ВЕКТОРАМИ И

(8)

4) ВЫЧИСЛЯТЬ РАБОТУ

ПОСТОЯННАЯ СИЛА ПРИЛОЖЕНА К ТЕЛУ И ПЕРЕМЕЩАЕТ ЕГО ВДОЛЬ ОТРЕЗКА ПРЯМОЙ ОТ ТОЧКИ К ТОЧКЕ

.В ЭТОМ СЛУЧАЕ РАБОТА ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ:

(9)

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ КООРДИНАТ ВЕКТОРА

ТЕОРЕМА 2. КООРДИНАТЫ ВЕКТОРА ЭТО ПРОЕКЦИИ ВЕКТОРА НА ОСИ ОХ, ОУ, ОZ СООТВЕТСТВЕННО

(10)

ДОКАЗАТЕЛЬСТВО. ПУСТЬ

АНАЛОГИЧНО ДОКАЗЫВАЮТСЯ, ЧТО КОРДИНАТЫ -это ПРОЕКЦИИ ВЕКТОРА НА ОСИ ОУ, ОZ .

ИЗ ТЕОРЕМЫ СЛЕДУЕТ, ЧТО:

1) КООРДИНАТЫ ЛЮБОГО ЕДИНИЧНОГО ВЕКТОРА ИМЕЮТ ВИД

(11)

называют направляющими косинусами вектора.

2) КООРДИНАТЫ ЛЮБОГО ВЕКТОРА ИМЕЮТ ВИД

(12)

ГДЕ и .

ПРАВИЛО 1. ВЕКТОРЫ И ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ ТОГДА И ТОЛЬКО ТОГДА, КОГДА

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ

ОПРЕДЕЛЕНИЕ 2. ТРИ ВЕКТОРА НАЗОВЁМ НЕКОМПЛАНАРНЫМИ, ЕСЛИ ОНИ НЕ ЛЕЖАТ НИ В КАКОЙ ОДНОЙ И ТОЙ ЖЕ ПЛОСКОСТИ.

Например, базисные векторы некомпланарные.

ОПРЕДЕЛЕНИЕ 3. ТРИ УПОРЯДОЧЕННЫХ НЕКОМПЛАНАРНЫХ ВЕКТОРА С ОБЩИМ НАЧАЛОМ ОБРАЗУЮТ В ТАКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПРАВУЮ ТРОЙКУ ВЕКТОРОВ, ЕСЛИ КРАТЧАЙШИЙ ПОВОРОТ ВЕКТОРА К ВЕКТОРУ , НАБЛЮДАЕМЫЙ ИЗ КОНЦА ВЕКТОРА, СОВЕРШАЕТСЯ ПРОТИВ ЧАСОВОЙ СТРЕЛКИ.

ОПРЕДЕЛЕНИЕ 4. ПУСТЬ ЗАДАНЫ ДВА НЕНУЛЕВЫХ ВЕКТОРА И ТОГДА ВЕКТОРНЫМ ПРОИЗВЕДЕНИЕМ НАЗЫВАЕТСЯ ВЕКТОР , ОПРЕДЕЛЯЕМЫЙ ТРЕМЯ СВОЙСТВАМИ:

2) ВЕКТОРА ОБРАЗУЮТ ПРАВУЮ ТРОЙКУ ВЕКТОРОВ (13)

3) ДЛИНА ВЕКТОРА ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ

СЛЕДУЮЩИЕ РАВЕНСТВА ЛЕГКО ПРОВЕРИТЬ, ПОЛЬЗУЯСЬ ОПРЕДЕЛЕНИЕМ 4.4

ВЫЧИСЛЕНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ В КООРДИНАТАХ. ПРАВИЛО .

ТЕОРЕМА 3 ПУСТЬ ЗАДАНЫ ДВА ВЕКТОРА , ТОГДА КООРДИНАТЫ

ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЫЧИСЛЯЮТСЯ ПО ФОРМУЛЕ (14)

ДОКАЗАТЕЛЬСТВО. ПРИ УМНОЖЕНИИ ИСПОЛЬЗУЕМ СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ

(15)

Получили известную формулу вычисления определителя разложением по первой строке.

Теорема доказана.

С помощью векторного произведения можно решать следующие задачи :

1. ВЫЧИСЛЯТЬ ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА , ПОСТРОЕН0ГО НА ВЕКТОРАХ И КАК НА СТОРОНАХ . ДВУХШАГОВЫЙ АЛГОРИТМ ДАЁТСЯ ФОРМУЛОЙ

(16)

_{1 ШАГ. ВЫЧИСЛЯЕМ ПО ФОРМУЛЕ (}14) ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

_{2 ШАГ. НАХОДИМ ДЛИНУ ПОЛУЧЕННОГО ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ПО ФОРМУЛЕ (6).}

2. ВЫЧИСЛЯТЬ МОМЕНТ СИЛЫ , ПРИЛОЖЕНОЙ К ТОЧКЕ , ОТНОСИТЕЛЬНО ТОЧКИ _.

СПРАВЕДЛИВА ФОРМУЛА

(17)

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

ОПРЕДЕЛЕНИЕ 5. СМЕШАННЫМ ПРОИЗВЕДЕНИЕМ ВЕКТОРОВ НАЗОВЁМ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРА НА ВЕКТОР , ТО ЕСТЬ (). БУДЕМ ОБОЗНАЧАТЬ СМЕШАННОЕ ПРОИЗВЕДЕНИЕ СИМВОЛОМ

(18)

ВЫЧИСЛЕНИЕ СМЕШАННОГО ПРОИЗВЕДЕНИЯ В КООРДИНАТАХ

ТЕОРЕМА 4. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЁХ ВЕКТОРОВ

ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ (19)

ДОКАЗАТЕЛЬСТВО. ПО ОПРЕДЕЛЕНИЮ СМЕШАННОЕ ПРОИЗВЕДЕНИЕ РАВНО .

1 ШАГ. ВЫЧИСЛЯЕМ СНАЧАЛА ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ПО ПРАВИЛУ (14)

2 ШАГ. УМНОЖАЯ ПОЛУЧЕННОЕ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ СКАЛЯРНО НА ВЕКТОР , ПОЛУЧАЕМ

ЗДЕСЬ СООТВЕТСТВУЮЩИЕ МИНОРЫ (СМ. ГЛАВА1 ФОРМУЛА (2)).

ТЕОРЕМА ДОКАЗАНА.

МОДУЛЬ ВЕЛИЧИНЫ СМЕШАННОГО ПРОИЗВЕДЕНИЯ ТРЁХ ВЕКТОРОВ РАВЕН ОБЪЁМУ ПАРАЛЛЕЛЕПИПЕДА ПОСТРОЕННОГО НА ЭТИХ ВЕКТОРАХ КАК НА СТОРОНАХ.

(20)

ЗАМЕЧАНИЕ. ОБЪЁМ ПИРАМИДЫ, ПОСТРОЕННОЙ НА ВЕКТОРАХ КАК НА СТОРОНАХ, РАВЕН (21)

ЕСЛИ

Контрольные вопросы

1. Сформулируйте определение скалярного произведения и правила его вычисления в координатах. От чего зависит знак скалярного произведения. Как определяется проекция вектора на направление с помощью скалярного произведения?

2. Какие задачи можно решать, используя скалярное произведение?

3. Дайте определение правой тройки векторов.

4. Сформулируйте определение векторного произведения и правила его вычисления в координатах. Какие задачи можно решать, используя векторное произведение?

5. Сформулируйте правила вычисления площадей параллелепипедов и треугольников

с помощью векторного произведения.

6. Сформулируйте определение смешанного произведения и правила его вычисления в координатах. Какие задачи можно решать, используя смешанное произведение?

7. Сформулируйте правило вычисление объёмов пирамид и параллелепипедов

с помощью смешанного произведения.

studfiles.net

Векторное произведение векторов и его свойства — Мегаобучалка

Определение. Векторным произведением векторов и (обозначается ) называется новый вектор , удовлетворяющий условиям:

1) перпендикулярен обоим векторам, т.е. плоскости этих векторов: .

2) Направлен он так, что если смотреть с его конца, то поворот от первого вектора ко второму на наименьший угол видится происходящим против часовой стрелки.

3) , т.е. длина векторного произведения равна произведению длин векторов на синус угла между ними. Иначе говоря, длина векторного произведения численно равна площади параллерограмма, построенного на векторах как на сторонах.

Вектор является математическим объектом, характеризуемым величиной (длиной) и направлением. В приведённом определении условия 1) и 2) определяют направление, а условие 3) – длину векторного произведения.

Из определения следуют свойства векторного произведения.

Условие 2) определения означает, что Это свойство названо антикоммутативностью.

Для любого числа выполняется

Первые три свойства позволяют оперировать с векторным произведением как с многочленами, не забывая только об антикоммутативности.

Из условия 3) следует, что и, следовательно, равенство нулю векторного произведения есть условие коллинеарности векторов, т.е. получено ещё одно условие коллинеарности:

(14)

(Векторное произведение в координатной форме). Пусть векторы заданы своими координатами:

Как и в случае скалярного произведения, здесь также всё сводится к векторному произведению базисных векторов. Нетрудно убедится в справедливости следующей базисной таблицы векторного произведения.

Руководствуясь этой таблицей, получим:

(15)

Эта формула громоздка для запоминания, зато легко запоминается формула

(16)

Легко убедиться в совпадении формул (15) и (16), надо лишь разложить определитель по первой строке.

Например, если то

Переходя к примерам заметим, что в геометрии векторное произведение используется для нахождения площадей.

Пример 3. Дано:

Найти

Решение. Отметим, что задача задана в бескоординатной форме, поэтому воспользуемся свойствами векторного произведения, позволяющими оперировать как с многочленами (не забывая об антикоммутативности

Раскроем сначала скобки под знаком модуля:

Мы учли, что

Теперь переходим к модулям:

Пример 4. Дано: Вычислить площадь треугольника, построенного на векторах и

Решение. Вспоминаем пункт 3 определения векторного определения: , т.е. модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах.

Следовательно,

.

Ответ:

Пример 5. Найти вектор , который перпендикулярен векторам и и удовлетворяет условию , где .

Решение. Можно, конечно, решать бесхитростно: ввести координаты вектора и для нахождения координат использовать три условия: – условия перпендикулярности векторов и , а так же . В результате получим систему трёх уравнений с тремя неизвестными относительно

Решив эту систему, получим , т.е.

Изящнее и проще решать иначе. Обратим внимание на условие, что перпендикулярен векторам и . Но ведь и векторное произведение тоже вектор, который перпендикулярен векторам и , следовательно, вектора и коллинеарны, т.е. Найдём

следовательно, Тогда из условия получим

поэтому ,-24,-14).

Ответ: ,-24,-14).

 

megaobuchalka.ru