Произведение векторов как найти: Как найти скалярное произведение векторов? Ответ на webmath.ru

Содержание

Скалярное произведение между векторами. Как найти скалярное произведение векторов. Косинус угла между векторами a b.

Альфашкола
Статьи
Скалярное произведение векторов

Векторы — это величины, которые описываются как величиной, так и направлением.

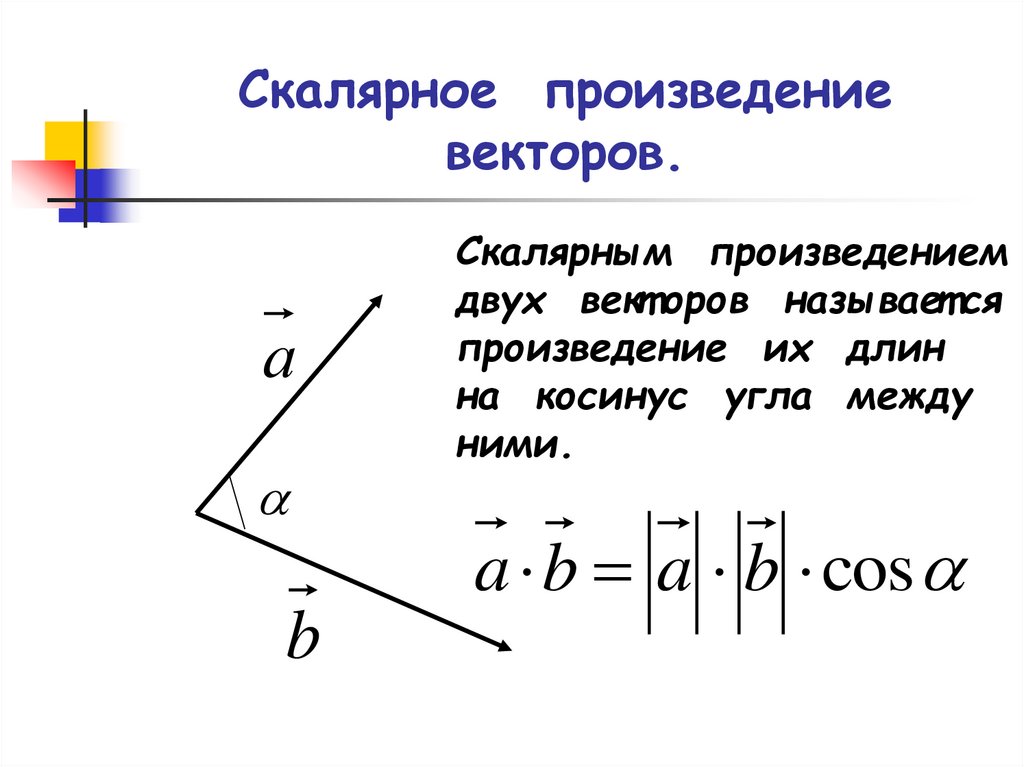
Скалярное произведение \( \overline{a }\) и \( \overline{b }\) определяется как
\( \overline{a }· \overline{b }\) \(= |a| |b|· ∠ (\overline{a }\overline{b })\)
где \(| a |-\) модуль, или величина \( a\),
\(| b |-\) модуль \(b\),
\(∠ (\overline{a }\overline{b })\)-угол между \(a\) и \(b\):

Если два вектора сонаправены, то \( ∠cos (\overline{a }\overline{b })= ∠cos \;0=1\) скалярное произведение равно \( \overline{a }· \overline{b }\)\(=\)\( \overline{|a| }· \overline{|b| }\).

Пример 1. Рассмотрим два вектора \( \overline{a }\) и \( \overline{b }\) модуль \( \overline{a }\) равен \(4\), а \( \overline{b }\) равен \(5\), а угол между ними равен \(60◦\). Найдите скалярное произведение \( \overline{a }· \overline{b }\).

Решение: \( 4 × 5 × cos 60◦ = 4 × 5 ×\frac{1}{2}= 10 \).

Ответ: \(10\).

Если угол между \( \overline{a }\) и \( \overline{b }\) меньше \(90◦\) , то есть распаложен на промежутке \(0<∠ (\overline{a }\overline{b })<\frac{\pi}{2}\), то результат скалярного произведения будет больше \(0\) , то есть положительным.

Если угол между \( \overline{a }\) и \( \overline{b }\) больше \(90◦\) , то есть распаложен на промежутке \(\frac{\pi}{2}<∠ (\overline{a }\overline{b })<\pi\) , то результат скалярного произведения будет меньше \(0\) , то есть отрицательным.

Если угол между \( \overline{a }\) и \( \overline{b }\) равен \(90◦\), то результат скалярного произведения будет равен \(0\), так как \(cos\frac{\pi}{2}=0\).
2=-64+96\sqrt{2}*\frac{\sqrt{2}}{2}-64=32\).
Ответ: \(32\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Ирина Александровна Бащиванжи
Репетитор по математике
Стаж (лет)
Образование:

Кишинёвский Государственный Педагогический Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике и информатике 5-8 классы. Также готовлю учеников по профориентации. Математика прекрасна своей необычностью, многогранностью. Каждая задача, каждый пример обладают своей собственной изюминкой. Обучаю учащегося смотреть с разных сторон на одну и ту же задачу, находить нестандартные решения, с помощью математики анализировать окружающий мир.
Оксана Александровна Анцыферова

Репетитор по математике
Стаж (лет)
Образование:
Саратовский государственный университет им. Н. Г. Чернышевского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике и русскому языку 1-4 классов. Очень легко и с интересом к предметам: математика, русский язык можно относиться, если это тебе понятно! А когда педагог в доступной форме, с учетом дифференцированного подхода к каждому ребенку, может помочь освоить материал, справиться со всеми заданиями по предметам- значимый результат для современного ребенка! Подготовить ребенка к школе, помочь освоить основы грамоты, дать первоначальные математические представления — первостепенная задача для педагога, работающего профессионально и качественно!

Юлиана Евгеньевна Соловьёва
Репетитор по математике
Стаж (лет)
Образование:
Воронежский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)

Репетитор по математике для 4-9 классов и химии для 8-11 классов. Умею хорошо организовать педагогический процесс с точки зрения возрастных особенностей детей, а также с точки зрения способа восприятия информации. Стабильно и эффективно готовлю к ОГЭ и ЕГЭ. Использую только свой «отработанный» контент для презентаций: рисунки, видеоразбор. Также разбираю сложные темы, повышаю текущую успеваемость. Занимаюсь с учениками разного уровня. Хорошо умею объяснять сложный материал простыми словами.

Похожие статьи
- Как быстро умножить число на 1,5
- Как перевести км/час в м/с?
- Как перевести квадратные километры в квадратные метры
- Как перевести килограммы в тонны?
- Как перевести дециметры в сантиметры
- НИУ ВШЭ (Программная инженерия): проходной балл, отзывы
- Планиметрическая задача
- Как по координатам вершин треугольника записать уравнения сторон и уравнение биссектрисы
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как найти скалярное произведение векторов
ФОРМУЛА
Чтобы найти скалярное произведение двух векторов, заданных их координатами, необходимо вычислить сумму произведений соответствующих координат этих векторов. Для случая, если векторы заданы на плоскости координатами \(\ \overline{a}=\left(a_{x} ; a_{y}\right) \quad{и}\quad \overline{b}=\left(b_{x} ; b_{y}\right) \), формула верна:

\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y} \)
Если векторы заданы в пространстве их координатами: \(\ \overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right) \quad{и}\quad \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \) , соответственно, их скалярное произведение вычисляется по формуле:
\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z} \)
ПРИМЕРЫ РАСЧЕТА СКАЛЯРНОЙ ПРОДУКЦИИ ВЕКТОРОВ
ПРИМЕР
Задание: Найти скалярное произведение векторов \(\ \overline{a}=(1 ;-3) \quad{и}\quad \overline{b}=(-2 ;-3) \)
Решение: Векторы даны на плоскости, поэтому для вычисления их скалярного произведения воспользуемся формулой
\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y} \)
Подставляя координаты указанных векторов, получим

\(\ (\overline{a}, \overline{b})=1 \cdot(-2)+(-3) \cdot(-3)=-2+9=7 \)
Ответ: \(\ (\overline{a}, \overline{b})=7 \)
ПРИМЕР
Задание: Есть точки в пространстве \(\ A(-1 ;-2 ; 5), B(-3 ; 2 ; 1) \quad{и}\quad C(0 ; 1 ;-1) \) . Найти скалярное произведение векторов \(\ \overline{A B} и \overline{A C} \)
Решение: Сначала мы находим координаты векторов \(\ \overline{A B} {и} \overline{A C} \) . Для этого из координат конца мы вычисляем соответствующие координаты начала, получаем:
\(\ \overline{A B}=(-3-(-1) ; 2-(-2) ; 1-5)=(-2 ; 4 ;-4) \)
\(\ \overline{A C}=(0-(-1) ; 1-(-2) ;-1-5)=(1 ; 3 ;-6) \)
Далее мы используем формулу для вычисления скалярного произведения векторов, заданных в пространстве:
\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z} \)

Получите
\(\ (\overline{A B}, \overline{A C})=(-2) \cdot 1+4 \cdot 3+(-4)(-6)=-2+12+24=34 \)
Ответ: \(\ (\overline{A B}, \overline{A C})=34 \)

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Как найти угол между векторами Как найти координаты вектора Как найти длину вектора Как найти проекцию вектора

Узнать цену работы

Узнай цену

своей работы

Имя

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Скалярное произведение векторов.

Навигация по странице:

Геометрическая интерпретация скалярного произведения векторов
Алгебраическая интерпретация скалярного произведения векторов
Формулы скалярного произведения векторов заданных координатами
- для плоских задач
- для пространственных задач
- для n -мерных векторов
Свойства скалярного произведения векторов
Примеры задач на скалярное произведение векторов
- плоские задачи
- пространственные задачи
- задачи в n -мерном пространстве

Онлайн калькулятор. Скалярное произведение векторов.

Онлайн упражнения на тему скалярное произведение двух векторов на плоскости.

Онлайн упражнения на тему скалярное произведение двух векторов в пространстве.

Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В случае плоской задачи скалярное произведение векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Формула скалярного произведения n -мерных векторов

В случае n-мерного пространства скалярное произведение векторов a = {a₁ ; a₂ ; . .. ; a_n} и b = {b₁ ; b₂ ; … ; b_n} можно найти воспользовавшись следующей формулой:

a · b = a₁ · b₁ + a₂ · b₂ + … + a_n · b_n

Свойства скалярного произведения векторов

Скалярное произведение вектора самого на себя всегда больше или равно нуля:
a · a ≥ 0
Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
a · a = 0 <=> a = 0
Скалярное произведение вектора самого на себя равно квадрату его модуля:
a · a = |a|²
Операция скалярного умножения коммуникативна:
a · b = b · a
Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:
a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b
(αa) · b = α(a · b)
Операция скалярного умножения дистрибутивна:
(a + b) · c = a · c + b · c

Примеры задач на вычисление скалярного произведения векторов

Примеры вычисления скалярного произведения векторов для плоских задач

Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.

Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.

Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.

Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.

Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.

Решение:

p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =

= 5 |a|² + 12 a · b — 9 |b|² = 5 · 3² + 12 · 3 · 2 · cos 60˚ — 9 · 2² = 45 +36 -36 = 45.

Пример вычисления скалярного произведения векторов для пространственных задач

Пример 4. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.

Пример вычисления скалярного произведения для n -мерных векторов

Пример 5. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Точечные и перекрестные произведения векторов

Величина, которая характеризуется не только величиной, но и направлением, называется вектором. Скорость, сила, ускорение, импульс и т. д. являются векторами.

Векторы можно умножать двумя способами:

Скалярное произведение или скалярное произведение
Векторное произведение или векторное произведение

Скалярное произведение/скалярное произведение векторов

Произведение вектора/скалярного произведения двух скалярных всегда является скалярной величиной. Рассмотрим два вектора а и б . Скалярное произведение вычисляется как произведение величин a, b и косинуса угла между этими векторами.

Скалярное произведение = |a||b| cos α

Здесь |a| = величина вектора a |b| = величина вектора b α = угол между векторами

Векторы a и b с углом α между ними

Проекция одного вектора на другой Вектор

Вектор a можно спроецировать на прямую l, как показано ниже:

CD = проекция вектора a на вектор b

Из приведенного выше рисунка видно, что мы можем проецировать один вектор на другой вектор. AC — величина вектора A. На приведенном выше рисунке AD нарисовано перпендикулярно линии l. CD представляет собой проекцию вектора a на вектор b .

Треугольник ACD, таким образом, является прямоугольным треугольником, и мы можем применить тригонометрические формулы.

Если α – мера угла ACD, то
cos α = CD/AC
Или, CD = AC cos α

Из рисунка видно, что CD – проекция вектора a на вектор b

Итак, мы можем сделать вывод, что один вектор можно спроецировать на другой вектор на косинус угла между ними.

Свойства скалярного произведения:

Скалярное произведение двух векторов всегда является действительным числом (скаляром).
Скалярное произведение коммутативно, т. е. a.b =b.a= |a||b| cos α
Если α равно 90°, то скалярное произведение равно нулю, поскольку cos(90) = 0. Итак, скалярное произведение единичных векторов в направлениях x, y равно 0.
Если α равно 0°, то скалярное произведение равно произведение величин a и b |a||b|.
Скалярное произведение единичного вектора на самого себя равно 1.
Скалярное произведение вектора a на самого себя равно |a| ²
Если α равно 180 ⁰ , скалярное произведение векторов a и b равно -|a||b|
Скалярное произведение является распределительным над сложением

a. ( b + c ) = a.b + a.c

(M B ) = км A.B
- Если компонентная форма векторов приведена как:
A = A1X + A2Y + A3Z
A = A1X + A2Y + A3Z
.0013 B = B1X + B2Y + B3Z
. Затем скалярный продукт дается как
A.B = A1B1 + A2B2 + A3B3
- Расскарный продукт равен нулю в следующих случаях:
  - . ноль
  - Модуль вектора b равен нулю
  - Векторы a и b перпендикулярны друг другу
Неравенства, основанные на скалярном произведении
Неравенство Коши – Шварца
В соответствии с этим принципом для любых двух векторов a и b величина скалярного произведения всегда меньше или равна произведению величин вектора a и вектора b
|a.b| ≤ |а| |б|
Доказательство:
Поскольку, a.b = |a| |б| cos α
Мы знаем, что 0 < cos α < 1
Таким образом, мы заключаем, что |a.b| ≤ |а| |б|
Неравенство треугольника
Для любых двух векторов a и b мы всегда имеем
| а + б | ≤ | и | + | б |
Неравенство треугольника
Доказательство:
| а + б | ² =| а + б || а + б |
= a. a. + a.b + b.a + b.b
= | и | ² + 2 а.б +| б | ² (точечный продукт коммутативен)
≤ | и | ² + 2| а||б | + | б | ²
≤ ( |a | + | b| ) ²
Это доказывает, что | а + б | ≤ | и | + | б|
Примеры скалярного произведения векторов
Вопрос 1. Рассмотрим два вектора, для которых |a|=6 и |b|=3 и α = 60°. Найдите их скалярное произведение.
Решение:
a.b = |a| |б| cos α
SO, A.B = 6.3.COS (60 °)
= 18 (1/2)
A. B = 9
Вопрос 2. Докажите, что векторы A = 3I+J- 4k и вектор b = 8i-8j+4k перпендикулярны.
Решение :
Мы знаем, что векторы перпендикулярны, если их скалярное произведение равно нулю.0003
= (3)(8) +(1)(-8)+(-4)(4)
=24-8-16 =0
Поскольку скалярное произведение равно нулю, мы можем заключить, что векторы перпендикулярны друг другу.
Перекрестное произведение/векторное произведение векторов
Читатели уже знакомы с трехмерной правосторонней прямоугольной системой координат. В этой системе поворот оси x против часовой стрелки в положительную ось y указывает на то, что правый (стандартный) винт будет продвигаться в направлении положительной оси z, как показано на рисунке.
Трехмерная прямоугольная система координат
Векторное произведение двух векторов a и b с углом α между ними математически вычисляется как
a × b = |a| |б| sin α
Следует отметить, что перекрестное произведение представляет собой вектор с заданным направлением. Равнодействующая всегда перпендикулярна и к a, и к b.
В случае, если a и b являются параллельными векторами, результирующая должна быть равна нулю, поскольку sin(0) = 0
Свойства перекрестного произведения:
- Перекрестное произведение создает векторную величину. Равнодействующая всегда перпендикулярна и к a, и к b.
- Перекрестное произведение параллельных/коллинеарных векторов равно нулю, поскольку sin(0) = 0.
i × i = j × j = k × k = 0 величина каждого есть единица. (Поскольку sin(0)=1)
Перекрестное произведение не коммутативно.

a × b не равно b × a

Cross product is distributive over addition

a × ( b + c ) = a × b + a × c

If k is скаляр, тогда векторов мы получаем третий и в направлении против часовой стрелки, мы получаем отрицательную результирующую.

Поперечный продукт по часовой стрелке и в направлении против часовой стрелки

Следующие результаты могут быть установлены:

I × j = k j × k = i k × i = j

j × i = -k i × k = -j k × j = -i

Перекрестное произведение в определяющей форме
Если вектор a представлен как a = a1x + a2y + a3z , а вектор b представлен как b = b1x + b2y + б3з
Тогда перекрестное произведение a × b может быть вычислено с помощью определителя: a и b — смежные стороны параллелограмма OXYZ, α — угол между векторами a и b.
Тогда площадь параллелограмма равна | а × б | = |а| |b|sin.α
Векторы a и b как смежные стороны параллелограмма
Примеры of C ross product of Vectors
Вопрос 1. Найдите векторное произведение двух векторов a и b, если их величины равны 5 и 10 соответственно. Учитывая, что угол между ними равен 30°.
Решение:
A × B = A.B.SIN (30) = (5) (10) (1/2) = 25 перпендикулярных до A и B
. , Найдите площадь параллелограмма, смежные стороны которого равны
a = 4i+2j -3k
b= 2 i +j-4k
Решение :
Площадь вычисляется путем нахождения векторного произведения смежных сторон
a2b3 – b2a3) + y(a3b1 – a1b3) + z(a1b2 – a2b1)
= i(-8+3) + j(-6+16) + k(4-2)
= -5i +10j + 2k
Следовательно, величина площади равна
=
=
Применение: Скалярные произведения и перекрестные произведения широко используются в инженерных приложениях.

Точечное и кросс-произведение
Точечное и кросс-произведение
Скалярный продукт
Определение
Определим скалярное произведение двух векторов
v = а i + b j и w = c i + d j
быть
против ^. w = ac + bd

Обратите внимание, что скалярное произведение двух векторов — это число, а не вектор. Для трехмерных векторов скалярное произведение определяется аналогично:
Скалярное произведение в R ³
Если
v = i + b j + c k и w = d i + e j + ф к
затем
v ^. ш = объявление + быть + ср
Примеры:
Если
        v = 2 и + 4 и

и
        w = i + 5 j

, затем
         против 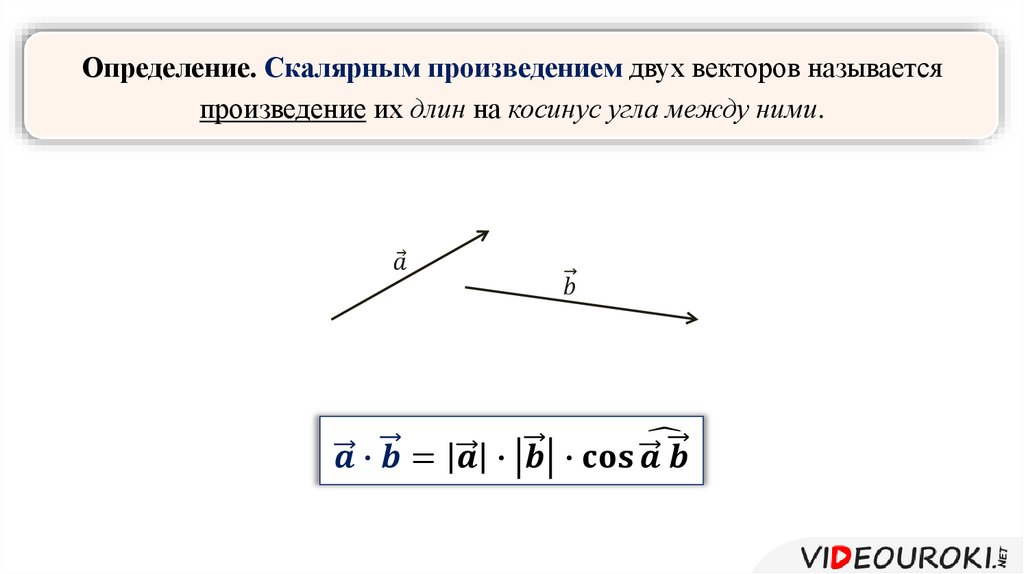^. ш = (2)(1) + (4)(5) = 22
Упражнение

Найдите скалярное произведение
2 и + и — к     и     и + 2 и

Угол между двумя векторами
Определим угол тета между двумя векторами v и w по формуле
против ^. с
потому что q =
|| против || || ш ||

так что

v ^. ш = || В| | || ш || cosq

Два вектора называются ортогональными , если их угол прямой.
Мы видим, что углы ортогональны тогда и только тогда, когда
        v ^. с = 0
Пример
Чтобы найти угол между
        v = 2i + 3j + k

и
        w = 4i + j + 2k

вычисляем:

и
и
         v ^. с = 8 + 3 + 2 = 13

Отсюда

Углы направления
     Определение направляющих косинусов
Пусть
          v = a i + b j + c k
будет вектором, тогда мы определим направляющие косинусы быть следующим:

cos a =
|| против ||
б
cos b =
|| против ||
с
cos g =
|| против ||
Выступы и компоненты Предположим, что автомобиль остановился на крутом холме, и пусть g будет силой сила тяжести, действующая на него. Мы можем разбить вектор g на компонент который толкает машину по дороге, и компонент, который толкает машину на дорогу. Мы определяем
Определение
Пусть u и v — векторы. затем и можно разделить на два компонента, р и с такие что r параллельно v и s перпендикулярно против . р называется проекция ты на против и s называется компонентом u перпендикулярно против .

Мы видим, что || и || || против || ||проект _v и ||
у ^. против = || и || || против || cos q   =
||у||
= || против || ||проект _v и ||

следовательно
ты ^. против
||проект _v и || знак равно
|| против ||

Мы можем вычислить проекцию u на v по формуле:
и ^. против
проект _v u = v
|| против || ²
Обратите внимание, что это работает, поскольку, если мы возьмем величины обеих сторон, мы получим что
и ^. против
| |продж _в у|| = ||в||
|| против || ²
а правая часть упрощается до приведенной выше формулы. Направление верно, так как правая часть формулы есть постоянное кратное v , поэтому вектор проекции находится в направление v по мере необходимости.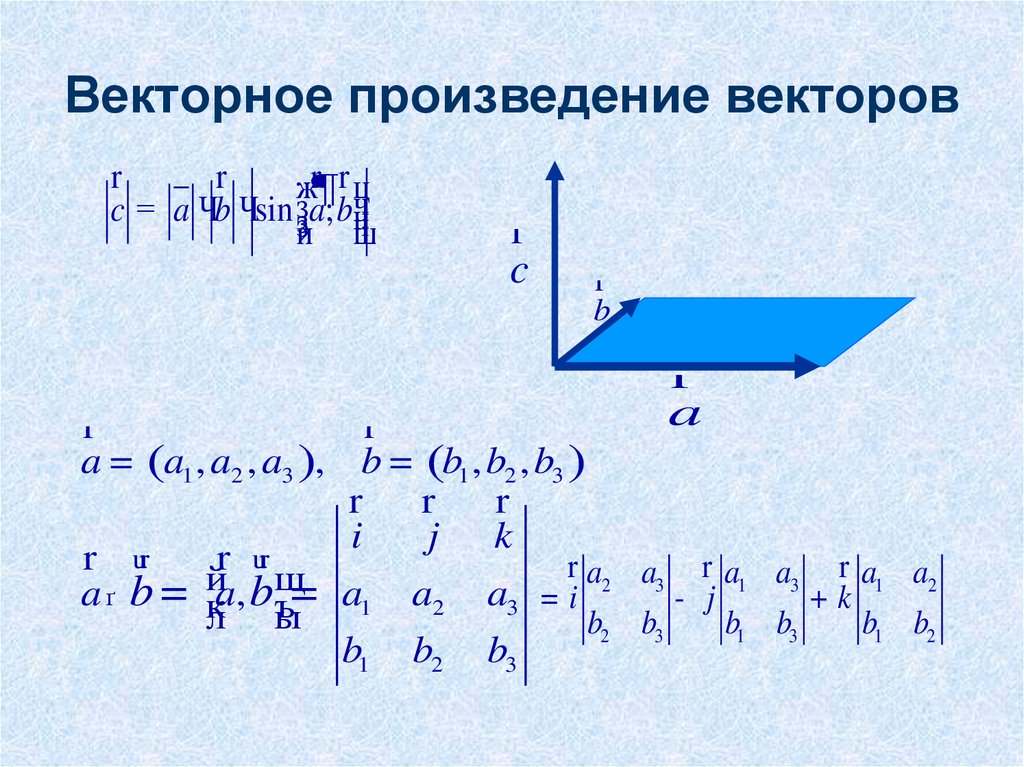
Чтобы найти вектор s , обратите внимание на диаграмму, что
проект _v u + s = у
так что
с = у — проект _v у
Работа
Работа, совершаемая постоянной силой F вдоль PQ определяется как
W = F ^. PQ
Пример
Найдите работу, совершенную против силы тяжести, чтобы переместить груз массой 10 кг. ребенка из точки (2,3) в точку (5,7)?
Решение
Имеем, что вектор силы равен
Ф = m a = (10)(-9,8 j ) = -98 j
а вектор смещения равен
против = (5 — 2) i + (7 — 3) j = 3 i + 4 и
Работа — это точечный продукт
W = F ^. v = (-98 j ) ^. (3 я + 4 и )
= (0)(3) + (-98)(4) = -392
Обратите внимание, что отрицательный знак подтверждает, что работа выполняется против силы тяжести. Следовательно, чтобы сдвинуть ребенка с места, требуется 392 Дж работы.
Крутящий момент
Предположим, вы катаетесь на лыжах и ужасно падаете. Ваше тело вращается вокруг и лыжи остаются на месте (не пытайтесь повторить это дома). С правильными креплениями ваши крепления будут отпустите, и ваша лыжа оторвется. Привязки признают, что сила был применен. Эта сила называется крутящим моментом. Чтобы вычислить это мы используем перекрестное произведение двух векторов, которое не только дает крутящий момент, но также создает направление, перпендикулярное как силе, так и направление ноги.
Перекрестное произведение двух векторов
Определение
Пусть u = a i + b j + c k и v = d i + e j + f k — векторы, тогда мы определяем перекрестное произведение v x w на определитель матрицы:
Мы можем вычислить этот определитель как

     = (bf – ce) и + (кд — аф) и + (а-э-бд) к

Пример
Найдите векторное произведение u x v если
u = 2 i + j — 3 k v = 4 j + 5 k
Решение
Мы рассчитываем
= 17 i — 10 j + 8 k
Если вам нужна дополнительная помощь, см. конспекты лекций по математике 103 B по матрицам.
Упражнения
Найти u x v когда
u = 3 i + j — 2 k ,      v = i — к

u = 2 i — 4 j — k ,      v = 3 i — дж + 2 к

Обратите внимание, что с момента изменения порядка двух строк определителя знак определителя, имеем
         u x v = — v x и

Геометрия и векторное произведение
Пусть у и у — векторы, и рассмотрим параллелограмм, который два вектора составляют. Затем
|| u x v || = Площадь параллелограмма

а направление u x v является прямым углом к параллелограмму что следует правилу правой руки
Примечание.    Для i x j величина равна 1 и направление k , следовательно, i x j = k .
Упражнение
Найти j x k и i x к
Новый взгляд на крутящий момент
Определим крутящий момент (или момент M силы F относительно точки Q) как
М = PQ x F

Пример
Гаечный ключ на 20 дюймов расположен под углом 30 градусов с земля. Сила в 40 фунтов, которая составляет и угол 45 градусов с гаечным ключом поворачивает гаечный ключ. Найдите крутящий момент.
Решение
Мы можем записать ключ как вектор
20 cos 30 i + 20 sin 30 j = 17,3 i + 10 j

и сила как
-40 cos 75 i — 40 sin 75 j = -10,3 i — 38,6 j

следовательно, крутящий момент равен величине их векторного произведения:

= -564 дюйм фунты

Параллелепипеды
Чтобы найти объем параллелепипеда, натянутого на три вектора и , v и w , находим тройное произведение:
Объем = u ^. ( v x w )
Это можно найти, вычислив определитель трех векторов:

Пример
Найти объем параллелепипеда, натянутого на векторы
u = <1,0,2>        В = <0,2,3>         w = <0,1,3>
Решение
Мы найти
Назад на векторную страницу
Назад на домашнюю страницу Math 107
Назад на домашнюю страницу математического факультета
электронная почта Вопросы и предложения
Объяснение урока: скалярное произведение в 3D
В этом объяснении мы узнаем, как найти скалярное произведение двух векторов в 3D.
Скалярное произведение, также называемое скалярным произведением, поскольку оно дает скалярную величину, не вектор, это один из способов перемножения векторов.
Возможно, вы уже знакомы с нахождением скалярного произведения на плоскости. (2Д). Возможно, вы узнали, что скалярное произведение ⃑𝐴 и ⃑𝐵 определяется как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖×‖‖⃑𝐵‖‖×𝜃cos, где 𝜃 — угол между двумя векторами ⃑𝐴 и ⃑𝐵.
Немного поэкспериментировав с геометрией, можно показать, что его можно вычислить из компоненты обоих векторов: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵, где 𝐴 и 𝐵 — 𝑥-компоненты ⃑𝐴 и ⃑𝐵, а 𝐴 и 𝐵 — их 𝑦-компоненты.
Рассмотрим два вектора ⃑𝐴 и ⃑𝐵, которые образуют углы 𝜃 и 𝜃 с положительное направление оси 𝑥 соответственно.
Тогда угол между ними равен 𝜃=𝜃−𝜃. При условии 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴𝜃, 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴, 𝐵 = ‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵, 𝐵 = ‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵, cossincossin мы находим, что 𝐴𝐵+𝐴𝐵 = ‖⃑𝐴⃑𝐴⃑𝐴‖⋅ ‖⃑𝐵⃑𝐵⃑𝐵𝜃𝜃𝜃𝜃+‖⃑𝐴⃑𝐴⃑𝐴⋅ ⋅ ‖⃑𝐵⃑𝐵𝜃𝜃 = ‖⃑𝐴⃑𝐴‖⋅‖⃑𝐵⃑𝐵⃑𝐵 coscossinsincoscossinsin
Используя тригонометрическое тождество вычитания coscoscossinsin(𝛼−𝛽)=𝛼𝛽+𝛼𝛽, находим, заменив 𝛼 на 𝜃 и 𝛽 с 𝜃, что coscoscossinsincoscossinsin(𝜃−𝜃)=𝜃𝜃+𝜃𝜃=𝜃𝜃+𝜃𝜃.0003
Поскольку 𝜃=𝜃−𝜃, имеем 𝐴𝐵+𝐴𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖𝜃=⃑𝐴⋅⃑𝐵.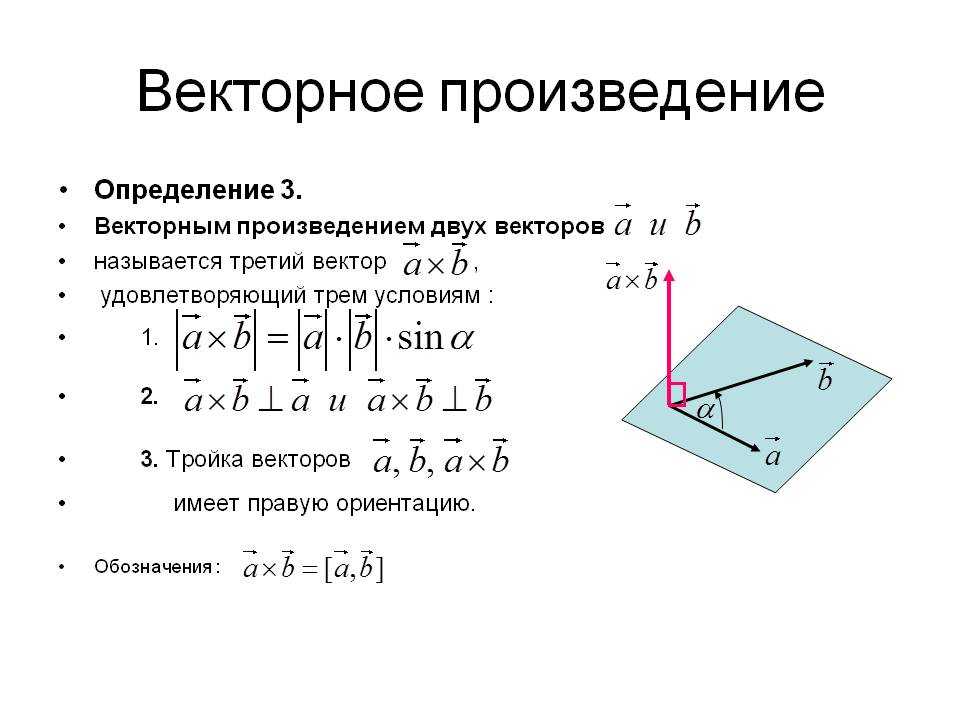 cos
Переходя к 3D-векторам, определение скалярного произведения не изменилось.
Определение: скалярное произведение двух трехмерных векторов где 𝜃 — угол между ⃑𝐴 и ⃑𝐵.
Давайте посмотрим на наш первый пример и применим определение скалярного произведения.
Пример 1. Нахождение скалярного произведения двух векторов по данным Норма одного из них, составные части другого и Угол между ними
Предположим, ⃑𝐴=(−1,2,7), ‖‖⃑𝐵‖‖=13, а угол между двумя векторов составляет 135∘. Найдите ⃑𝐴⋅⃑𝐵 с точностью до сотых.
Ответить
Мы знаем, что ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖𝜃cos. Мы уже знаем ‖‖⃑𝐵‖‖ и угол 𝜃. Поэтому нам нужно найти ‖‖⃑𝐴‖‖ используя компоненты ⃑𝐴: ‖‖⃑𝐴‖‖=𝐴+𝐴+𝐴=√(−1)+2+7=√54.
Теперь, подставив это значение в наше уравнение для ⃑𝐴⋅⃑𝐵, мы нашли ⃑𝐴⋅⃑𝐵=√54⋅13⋅135≃−67.55.cos∘
Практическое руководство. Вычисление скалярного произведения с использованием компонентов вектора
Скалярное произведение трехмерных векторов вычисляется с использованием компонентов вектора так же, как и в 2D, а именно, ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, где индексы 𝑥, 𝑦 и 𝑧 обозначим компоненты вдоль 𝑥-, 𝑦-, и 𝑧-оси.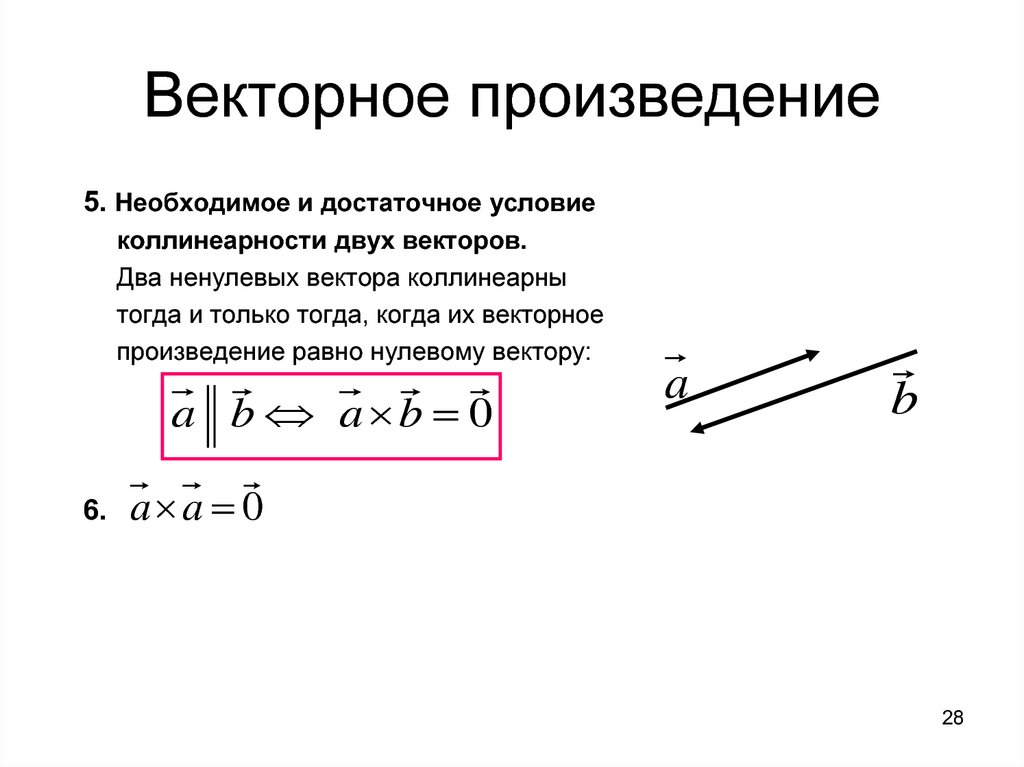
Применим этот метод на следующем примере.
Пример 2. Нахождение скалярного произведения двух заданных векторов Их компоненты
Учитывая, что ⃑𝐴=(−6,−3,5) и ⃑𝐵=(7,−4,−1), определить ⃑𝐴⋅⃑𝐵.
Ответ
Здесь мы вычисляем скалярный продукт, используя ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, где индексы 𝑥, 𝑦 и 𝑧 обозначим компоненты вдоль 𝑥-, 𝑦-, и 𝑧-оси. Таким образом, мы имеем ⃑𝐴⋅⃑𝐵=(−6)⋅7+(−3)⋅(−4)+5⋅(−1)=−42+12+(−5)=−35.
Теперь, когда мы знаем, как определяется скалярный продукт и как его вычислить, используя компонентов векторов, давайте посмотрим на свойства скалярного произведения.
Поскольку скалярное произведение является произведением величин векторов, умноженных косинусом угла между ними, он равен нулю, когда косинус угла между обоими векторами равен нулю. Это происходит, когда угол между ними 90∘ или −90∘ (или 270∘), то есть, когда они перпендикулярны.
Свойство: скалярное произведение двух перпендикулярных векторов
Скалярное произведение двух перпендикулярных векторов равно нулю. И наоборот, когда скалярное произведение двух векторов равно нулю, то эти два вектора перпендикулярны.
Чтобы вспомнить, у каких углов косинус равен нулю, вы можете визуализировать единичный круг, помня, что косинус — это 𝑥-координата точки P, связанная с угол 𝜃.
Мы собираемся использовать это свойство в следующих двух примерах.
Пример 3. Поиск недостающих компонентов ортогональных векторов
Для какого значения 𝑘 являются векторами ⃑𝐴=(7,−7𝑘,−6) и ⃑𝐵=(7,−3,𝑘) перпендикуляр?
Ответ
Если два вектора перпендикулярны, то угол между ними равен 90∘ или −90∘ (или 270∘). В обоих случаях косинус угла между ними равен нуль. Следовательно, скалярное произведение двух векторов равно нулю. В этом вопрос, значит ⃑𝐴⋅⃑𝐵=0; то есть, 𝐴𝐵+𝐴𝐵+𝐴𝐵=0.
Следовательно, имеем 7⋅7+(−7𝑘)⋅(−3)+(−6)⋅𝑘=049+21𝑘−6𝑘=0𝑘=−4915.
Пример 4. Определение перпендикулярных и параллельных векторов
Что из следующего верно для векторов ⃑𝐴=(−3,7,−8) и ⃑𝐵=(−6,−1,−1)?
Они параллельны.
Они перпендикулярны.
Они не параллельны и не перпендикулярны.
Ответ
Если ⃑𝐴 и ⃑𝐵 параллельны, то существует число 𝑘 такое, что ⃑𝐴=𝑘⃑𝐵. Мы было бы −3=−6𝑘7=−𝑘−8=−𝑘.
Очевидно, нет значения 𝑘, которое бы подтверждало три уравнения, поскольку мы получить три различных решения для каждого из них 12,−7,8а. Следовательно, ⃑𝐴 и ⃑𝐵 не параллельны.
Если ⃑𝐴 и ⃑𝐵 перпендикулярны, то их скалярное произведение равно нулю. Давайте работать их точечный продукт: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵=(−3)⋅(−6)+7⋅(−1)+(−8)⋅(−1)=18+(−7)+8=19.
Их скалярное произведение не равно нулю; следовательно, ⃑𝐴 и ⃑𝐵 не перпендикулярны .
Правильный ответ: ⃑𝐴 и ⃑𝐵 не параллельны и не перпендикулярны.
Другие свойства скалярного произведения возникают из-за того, что косинус угол между двумя векторами является одним из его факторов. Например, учитывая, что функция косинуса четная с периодом 360∘, это означает, что не имеет значения, если берем угол от ⃑𝐴 к ⃑𝐵 или с ⃑𝐵 на ⃑𝐴, потому что coscoscos𝜃=(−𝜃)=(360−𝜃).
Следовательно, скалярное произведение коммутативно: ⃑𝐴⋅⃑𝐵=⃑𝐵⋅⃑𝐴.
Кроме того, скалярное произведение двух коллинеарных векторов равно плюс или минус произведению их величины. Действительно, рассмотрим сначала два коллинеарных вектора ⃑𝐴 и ⃑𝐵, угол между которыми равен нулю: ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖⋅0=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖, потому что поскольку cos0=1.
Теперь рассмотрим два коллинеарных вектора ⃑𝐴 и ⃑𝐵, причем угол между ними 180∘ (т. е. два вектора указывают в противоположных направлениях): ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖⋅180=−‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖, cos∘ поскольку cos180=−1∘.
Отсюда следует, что скалярное произведение вектора на самого себя дает квадрат его величины. Это можно легко проверить с помощью того, как мы вычисляем скалярное произведение: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, так ⃑𝐴om⃑𝐴 = 𝐴𝐴+𝐴𝐴+𝐴𝐴 = 𝐴+𝐴+𝐴.
, так как ‖⃑𝐴⃑𝐴⃑𝐴 = 𝐴+𝐴+𝐴, мы находим, что ⃑𝐴⋅⃑𝐴=‖‖⃑𝐴‖‖.
Как и умножение, скалярное произведение является дистрибутивным: (⃑𝐴+⃑𝐵)⋅⃑𝐶=⃑𝐴⋅⃑𝐶+⃑𝐴⋅⃑𝐶.
Кроме того, у нас есть (𝑘⃑𝐴)⋅⃑𝐵=⃑𝐴⋅(𝑘⃑𝐵)=𝑘⃑𝐴⋅⃑𝐵.
Воспользуемся этими свойствами, чтобы ответить на следующий вопрос.
Пример 5. Использование распределения скалярного произведения
Если ⃑𝐴 и ⃑𝐵 — два перпендикулярных единичных вектора, найти (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵).
Ответ
Во фразе «⃑𝐴» есть две части информации и ⃑𝐵 два перпендикулярные единичные векторы». Во-первых, векторы перпендикулярны, что означает, что их скалярное произведение равно нулю. Второй что они являются единичными векторами, что означает, что они имеют величину 1. Теперь, используя распределительное свойство скалярного произведения, мы находим, что (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵)=−6⃑𝐴⋅⃑𝐴+3⃑𝐴⋅⃑𝐵+2⃑𝐵⋅⃑𝐴−⃑𝐵⋅⃑𝐵.
Поскольку векторы перпендикулярны, члены 3⃑𝐴⋅⃑𝐵 и 2⃑𝐵⋅⃑𝐴 равны нулю.
Также мы знаем, что ⃑𝐴⋅⃑𝐴=‖‖⃑𝐴‖‖=1 так как ⃑𝐴 является единичным вектором. То же самое относится к ⃑𝐵. Следовательно, мы находим, что (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵)=−6−1=−7.
Ключевые точки
Скалярное произведение векторов ⃑𝐴 и ⃑𝐵 определяется как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖×‖‖⃑𝐵‖‖×𝜃, потому что где 𝜃 — угол между двумя векторами ⃑𝐴 и ⃑𝐵.
No related posts.