Производная arcsin(x) равна производной 1/sin(x)? : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| ult1m |
| ||
10/09/12 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| ИСН |
| |||
18/05/06 |
| |||
| ||||
| ult1m |
| |
| ||
| ИСН |
| |||
18/05/06 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
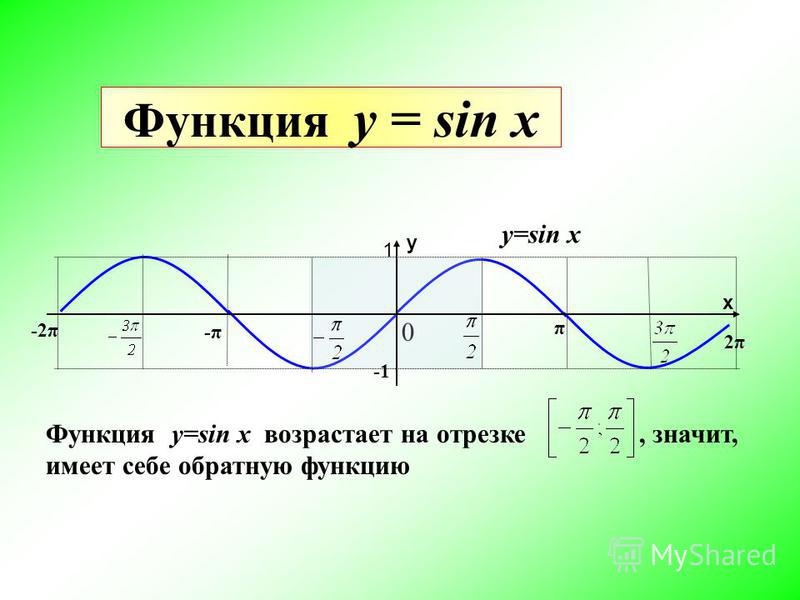
Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′.
 Производная сложной функции Производные с пи
Производная сложной функции Производные с пиПредставлено доказательство и вывод формулы для производной косинуса — cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка.
Содержание
См. также: Синус и косинус — свойства, графики, формулы
Производная по переменной x от косинуса x равна минус синусу x:
(cos
x)′ = — sin
x
.
Доказательство
Чтобы вывести формулу производной косинуса, воспользуемся определением производной:
.
Преобразуем это выражение, чтобы свести его к известным математическим законам и правилам. Для этого нам нужно знать четыре свойства.
1) Тригонометрические формулы . Нам понадобится следующая формула:
(1) ;
2) Свойство непрерывности функции синус:
(2) ;
3) Значение первого замечательного предела:
(3) ;
4) Свойство предела от произведения двух функций:
Если и ,
то
(4) .
Применяем эти законы к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(1) ;
В нашем случае
;
.
Тогда
;
;
;
.
Сделаем подстановку .
При ,
.
Используем свойство непрерывности (2):
Сделаем такую же подстановку и применим первый замечательный предел (3):
.
Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):
.
Тем самым мы получили формулу производной косинуса.
Примеры
Рассмотрим простые примеры нахождения производных от функций, содержащих косинус. Найдем производные от следующих функций:
y = cos 2x; y = cos 3x; y = cos nx; y = cos 2
x
;
y = cos 3
x
и y = cos n
x
.
Пример 1
Найти производные от cos 2x, cos 3x и cos nx .
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = cos nx . Затем, в производную от cos nx , подставим n = 2
и n = 3
. И, тем самым, получим формулы для производных от cos 2x и cos 3x .
И, тем самым, получим формулы для производных от cos 2x и cos 3x .
Итак, находим производную от функции
y = cos nx
Представим эту функцию от переменной x как сложную функцию, состоящую из двух функций:
1)
2)
Тогда исходная функция является сложной (составной) функцией, составленной из функций и :
.
Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем .
.
Подставим :
(П1) .
Теперь, в формулу (П1) подставим и :
;
.
;
;
.
Пример 2
Найти производные от косинуса в квадрате, косинуса в кубе и косинуса в степени n:
y = cos 2
x
;
y = cos 3
x
;
y = cos n
x
.
В этом примере также функции имеют похожий вид. Поэтому мы найдем производную от самой общей функции — косинуса в степени n:
y = cos n
x
.
Затем подставим n = 2
и n = 3
. И, тем самым, получим формулы для производных от косинуса в квадрате и косинуса в кубе.
Итак, нам нужно найти производную от функции
.
Перепишем ее в более понятном виде:
.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции ,
зависящей от переменной :
;
2) Функции ,
зависящей от переменной :
.
Тогда исходная функция является сложной функцией, составленной из двух функций и :
.
Находим производную от функции по переменной x:
.
Находим производную от функции по переменной :
.
Применяем правило дифференцирования сложной функции .
.
Подставим :
(П2) .
Теперь подставим и :
;
.
;
;
.
Производные высших порядков
Заметим, что производную от cos x первого порядка можно выразить через косинус следующим образом:
.
Найдем производную второго порядка, используя формулу производной сложной функции :
.
Здесь .
Заметим, что дифференцирование cos x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
Тогда производная n-го порядка имеет вид:
(5) .
Более строго эту формулу можно доказать с помощью метода математической индукции. Доказательство для n-й производной синуса изложено на странице “Производная синуса ”. Для n-й производной косинуса доказательство точно такое. Нужно только во всех формулах заменить sin на cos.
См. также:
При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :
Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким
образом, производная
постоянной функции равна
нулю на всей области определения .
Производная степенной функции.
Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Следовательно,
Этим доказана формула производной степенной функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним подстановку в исходный предел:
Если
вспомнить второй
замечательный предел, то придем к
формуле производной показательной
функции:
Производная логарифмической функции.

Докажем
формулу производной логарифмической
функции для всех x из
области определения и всех допустимых
значениях основания a логарифма.
По определению производной имеем:
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.
Производные тригонометрических функций.
Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.
По определению производной для функции синуса имеем .
Воспользуемся
формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким образом, производная функции sin x есть cos x .
Абсолютно
аналогично доказывается формула
производной косинуса.
Следовательно, производная функции cos x есть –sin x .
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.
Производная обратной функции.
Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, — это производная функции f(x) по x .
Теперь сформулируем правило нахождения производной обратной функции.
Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x) , то в точке существует конечная производная обратной функции g(y) , причем . В другой записи .
Можно это правило переформулировать для любого x из промежутка , тогда получим .
Давайте
проверим справедливость этих формул.
Найдем обратную функцию для натурального логарифма (здесь y – функция, а x — аргумент). Разрешив это уравнение относительно x , получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.
Из таблицы производных видим, что и .
Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:
Как видите, получили такие же результаты как и в таблице производных.
Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.
Начнем с производной арксинуса.
. Тогда по формуле производной обратной функции получаем
Осталось провести преобразования.
Так как областью значений арксинуса является интервал , то (смотрите раздел основные элементарные функции, их свойства и графики). Поэтому , а не рассматриваем.
Следовательно, .
Областью определения производной
арксинуса является промежуток (-1;
1) .
Для
арккосинуса все делается абсолютно
аналогично:
Найдем производную арктангенса.
Для обратной функцией является .
Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.
Пусть arctgx
= z ,
тогда
Следовательно,
Схожим
образом находится производная
арккотангенса:
Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами.
Содержание
См. также: Арксинус, арккосинус — свойства, графики, формулы
Здесь мы полагаем, что нам известны производные синуса и косинуса. Далее мы выводим производные арксинуса и арккосинуса, учитывая, что они являются обратными функциями к синусу и косинусу, соответственно.
Вывод производной арксинуса
Рассмотрим функцию арксинус от переменной x
:
y = arcsin
x
.
— 1
до + 1
:
.
— π/2
до + π/2
:
.
Функция арксинус является обратной к функции синус:
x = sin
y
.
Для определения производной арксинуса, применим формулу производной обратной функции:
(1) .
Производная синуса нам известна. Обычно ее записывают в следующем виде:
.
Здесь .
,
где .
Подставим в формулу (1):
(2) .
Здесь
y = arcsin
x
;
x = sin
y
.
Теперь выразим правую часть формулы (2) через переменную x
.
Для этого заметим, что поскольку ,
то .
Тогда
.
Подставим в формулу (2):
.
Тем самым мы вывели формулу производной арксинуса:
.
Второй способ
Поскольку арксинус и синус являются обратными функциями по отношению друг к другу, то
(3) .
Здесь .
Продифференцируем это уравнение по переменной x
.
То есть найдем производные левой и правой части и приравняем их друг к другу:
(4) .
Производную правой части находим из таблицы производных :
.
Производную левой части находим по формуле производной сложной функции :
.
Здесь .
Поскольку ,
то .
Поэтому
.
Тогда
.
Подставим в (4):
.
Отсюда
.
Вывод производной арккосинуса
Используя связь между арксинусом и арккосинусом
Производную арккосинуса легко получить из производной арксинуса, если воспользоваться связью между арксинусом и арккосинусом :
.
Отсюда
.
По формуле производной обратной функции
Также производную арккосинуса можно найти по формуле производной обратной функции.
Рассмотрим функцию арккосинус:
y = arccos
x
.
Здесь независимая переменная x
может принимать значения от — 1
до + 1
:
.
Зависимая переменная y
может принимать значения от 0
до π
:
.
Функция арккосинус является обратной к функции косинус:
x = cos
y
.
Применим формулу производной обратной функции:
(1) .
Производная косинуса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x
и y
.
Тогда
,
где .
Подставим в формулу (1):
(5) .
Здесь
y = arccos
x
;
x = cos
y
.
Теперь выразим правую часть формулы (5) через переменную x
.
Поскольку ,
то .
Тогда
.
Подставим в формулу (5):
.
Таким образом, мы вывели формулу производной арккосинуса:
.
Основа доказательства ― определение предела функции. Можно воспользоваться другим способом, используя тригонометрические формулы приведения для косинуса и синуса углов. Выразить одну функцию через другую — косинус через синус, и продифференцировать синус со сложным аргументом.
Рассмотрим первый пример вывода формулы (Cos(х))»
Даем ничтожно малое приращение Δх аргументу х функции у = Cos(х). При новом значении аргумента х+Δх получаем новое значение функции Cos(х+Δх). Тогда приращение функции Δу будет равно Cos(х+Δx)-Cos(x).
Отношение же приращения функции к Δх будет таким: (Cos(х+Δx)-Cos(x))/Δх. Проведем тождественные преобразования в числителе получившейся дроби. Вспомним формулу разности косинусов углов, результатом будет произведение -2Sin(Δх/2) умножить на Sin(х+Δх/2).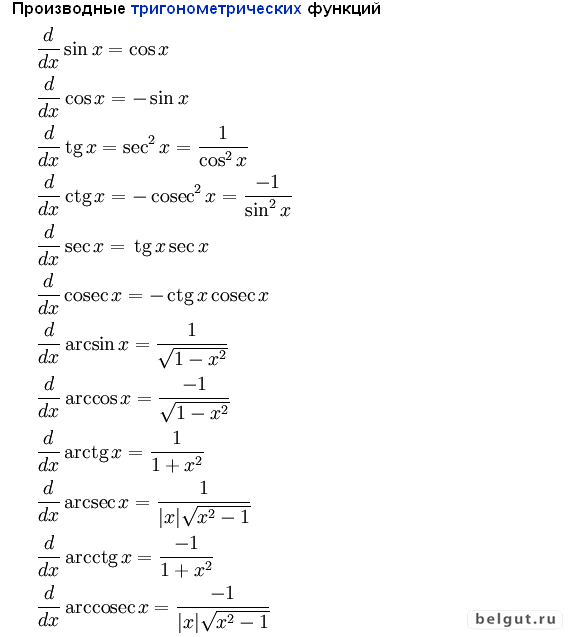 Находим предел частного lim этого произведения на Δх при Δх, стремящемся к нулю. Известно, что первый (его называют замечательным) предел lim(Sin(Δх/2)/(Δх/2)) равен 1, а предел -Sin(х+Δх/2) равен -Sin(x) при Δx, стремящемся к нулю.
Находим предел частного lim этого произведения на Δх при Δх, стремящемся к нулю. Известно, что первый (его называют замечательным) предел lim(Sin(Δх/2)/(Δх/2)) равен 1, а предел -Sin(х+Δх/2) равен -Sin(x) при Δx, стремящемся к нулю.
Запишем результат: производная (Cos(х))» равна — Sin(х).
Некоторым больше нравится второй способ вывода той же формулы
Из курса тригонометрии известно: Cos(х) равно Sin(0,5·∏-х), аналогично Sin(х) равно Cos(0,5·∏-x). Тогда дифференцируем сложную функцию — синус дополнительного угла (вместо косинуса икс).
Получим произведение Cos(0,5·∏-х)·(0,5·∏-х)», потому что производная синуса х равна косинусу х. Обращаемся ко второй формуле Sin(х) = Cos(0,5·∏-x) замены косинуса на синус, учитываем, что (0,5·∏-х)» = -1. Теперь получаем -Sin(x).
Итак, найдена производная косинуса, у» = -Sin(х) для функции у = Cos(х).
Часто используемый пример, где употребляется производная косинуса. Функция y = Cos 2 (x) сложная. Находим сначала дифференциал степенной функции с показателем 2, это будет 2·Cos(x), затем умножаем его на производную (Cos(x))», которая равна -Sin(х). Получаем y» = -2·Cos(х)·Sin(x). Когда применим формулу Sin(2·х), синуса двойного угла, получим окончательный упрощенный
Получаем y» = -2·Cos(х)·Sin(x). Когда применим формулу Sin(2·х), синуса двойного угла, получим окончательный упрощенный
ответ y» = -Sin(2·х)
Гиперболические функции
Применяются при изучении многих технических дисциплин: в математике, например, облегчают вычисления интегралов, решение Выражаются они через тригонометрические функции с мнимым аргументом, так, гиперболический косинус ch(х) = Cos(i·х), где i ― мнимая единица, гиперболический синус sh(x) = Sin(i·x).
Производная гиперболического косинуса вычисляется достаточно просто.
Рассмотрим функцию у = (e x +e -x)/2, это и есть гиперболический косинус ch(х). Используем правило нахождения производной суммы двух выражений, правило выноса постоянного множителя (Const) за знак производной. Второе слагаемое 0,5·е -х ― сложная функция (ее производная равна -0,5·е -х), 0,5·е х ― первое слагаемое. (ch(х)) «=((e х +e — x)/2)» можно записать по другому: (0,5·e х +0,5·е — х)» = 0,5·e х -0,5·e — х, потому что производная (e — x)» равна -1, умнноженная на e — x . Получилась разность, а это есть гиперболический синус sh(x).
Получилась разность, а это есть гиперболический синус sh(x).
Вывод: (ch(х))» = sh(x).
Рассмитрим на примере, как вычислить производную функции у = ch(x 3 +1).
По гиперболического косинуса со сложным аргументом у» = sh(x 3 +1)·(x 3 +1)», где (x 3 +1)» = 3·x 2 +0.
Ответ: производная данной функции равна 3·х 2 ·sh(х 3 +1).
Производные рассмотренных функций у = ch(х) и y = Cos(х) табличные
При решении примеров нет необходимости каждый раз дифференцировать их по предложенной схеме, достаточно использовать вывод.
Пример. Продифференцировать функцию у = Cos(x)+Cos 2 (-x)-Ch(5·х).
Легко вычислить (воспользуемся табличными данными), у» = -Sin(x)+Sin(2·х)-5·Sh(5·х).
Производная arcctg. Вывод производных арксинуса (arcsin x)′ и арккосинуса (arccos x)′
При
выводе самой первой формулы таблицы
будем исходить из определения
производнойфункции в точке. Возьмем ,
где x –
любое действительное число, то есть, x –
любое число из области определения
функции . Запишем предел отношения приращения
функции к приращению аргумента при :
Запишем предел отношения приращения
функции к приращению аргумента при :
Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Производная степенной функции.
Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Следовательно,
Этим
доказана формула производной степенной
функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним подстановку в исходный предел:
Если
вспомнить второй
замечательный предел, то придем к
формуле производной показательной
функции:
Производная логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x из
области определения и всех допустимых
значениях основания a логарифма.
По определению производной имеем:
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.
Производные тригонометрических функций.
Для
вывода формул производных тригонометрических
функций нам придется вспомнить некоторые
формулы тригонометрии, а также первый
замечательный предел.
По определению производной для функции синуса имеем .
Воспользуемся
формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким образом, производная функции sin x есть cos x .
Абсолютно
аналогично доказывается формула
производной косинуса.
Следовательно, производная функции cos x есть –sin x .
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.
Производная обратной функции.
Чтобы
при изложении не было путаницы, давайте
обозначать в нижнем индексе аргумент
функции, по которому выполняется
дифференцирование, то есть, —
это производная функции f(x) по x .
Теперь сформулируем правило нахождения производной обратной функции.
Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x) , то в точке существует конечная производная обратной функции g(y) , причем . В другой записи .
Можно это правило переформулировать для любого x из промежутка , тогда получим .
Давайте проверим справедливость этих формул.
Найдем обратную функцию для натурального логарифма (здесь y – функция, а x — аргумент). Разрешив это уравнение относительно x , получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.
Из таблицы производных видим, что и .
Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:
Самые часто задаваемые вопросы
Возможно ли, изготовить печать на документе по предоставленному образцу?
Ответ
Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.
Какие виды оплаты вы принимаете?
Ответ
Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.
Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами?
Ответ
В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.
Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.
Что делать при обнаружении в документе опечаток и ошибок?
Ответ
Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.
Что нужно сделать, чтобы заказать диплом в вашей компании?
Ответ
Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.
Последние отзывы
Алексей:
Мне нужно было приобрести диплом для устройства на работу по профессии менеджер. И самое главное, что и опыт, и навыки у меня есть, но без документа я не могу, никуда устроится. Попав на ваш сайт, все-таки решился на покупку диплома. Диплом был выполнен за 2 дня!! Теперь у меня есть работа, о которой я раньше и не мечтал!! Спасибо!
И самое главное, что и опыт, и навыки у меня есть, но без документа я не могу, никуда устроится. Попав на ваш сайт, все-таки решился на покупку диплома. Диплом был выполнен за 2 дня!! Теперь у меня есть работа, о которой я раньше и не мечтал!! Спасибо!
Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции.
Вывод формул производных натурального логарифма и логарифма по основанию a
Производная натурального логарифма от x равна единице, деленной на x:
(1) (ln
x)′ =
.
Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a
:
(2) (log
a x)′ =
.
Доказательство
Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию :
.
Эта функция определена при .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:
А) Свойства логарифма . Нам понадобятся следующие формулы:
(4) ;
(5) ;
(6) ;
Б) Непрерывность логарифма и свойство пределов для непрерывной функции:
(7) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
В) Значение второго замечательного предела:
(8) .
Применяем эти факты к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим свойства (4) и (5).
.
Воспользуемся свойством (7) и вторым замечательным пределом (8):
.
И, наконец, применим свойство (6):
.
Логарифм по основанию e называется натуральным логарифмом . Он обозначается так:
Он обозначается так:
.
Тогда ;
.
Тем самым мы получили формулу (2) производной логарифма.
Производная натурального логарифма
Еще раз выпишем формулу производной логарифма по основанию a
:
.
Эта формула имеет наиболее простой вид для натурального логарифма, для которого ,
.
Тогда
(1) .
Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
.
Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:
.
Другие способы доказательство производной логарифма
Здесь мы предполагаем, что нам известна формула производной экспоненты:
(9) .
Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.
Докажем формулу производной натурального логарифма, применив формулу производной обратной функции :
.
В нашем случае .
Обратной функцией к натуральному логарифму является экспонента:
.
Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:
.
Поскольку ,
то
.
Тогда
.
Формула доказана.
Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции . Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x
:
(10) .
Производная от икса равна единице:
.
Применяем правило дифференцирования сложной функции :
.
Здесь .
Подставим в (10):
.
Отсюда
.
Пример
Найти производные от ln 2x, ln 3x и ln nx .
Решение
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = ln nx . Затем подставим n = 2
и n = 3
. И, тем самым, получим формулы для производных от ln 2x и ln 3x .
Затем подставим n = 2
и n = 3
. И, тем самым, получим формулы для производных от ln 2x и ln 3x .
Итак, ищем производную от функции
y = ln nx .
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции ,
зависящей от переменной :
;
2) Функции ,
зависящей от переменной :
.
Тогда исходная функция составлена из функций и :
.
Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции .
.
Здесь мы подставили .
Итак, мы нашли:
(11) .
Мы видим, что производная не зависит от n
.
Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:
.
— это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:
.
Ответ
; ; .
Производная логарифма модуля x
Найдем производную от еще одной очень важной функции — натурального логарифма от модуля x
:
(12) .
Рассмотрим случай .
Тогда и функция имеет вид:
.
Ее производная определяется по формуле (1):
.
Теперь рассмотрим случай .
Тогда и функция имеет вид:
,
где .
Но производную этой функции мы также нашли в приведенном выше примере. Она не зависит от n
и равна
.
Тогда
.
Объединяем эти два случая в одну формулу:
.
Соответственно, для логарифма по основанию a
,
имеем:
.
Производные высших порядков натурального логарифма
Рассмотрим функцию
.
Мы нашли ее производную первого порядка:
(13) .
Найдем производную второго порядка:
.
Найдем производную третьего порядка:
.
Найдем производную четвертого порядка:
.
Можно заметить, что производная n-го порядка имеет вид:
(14) .
Докажем это методом математической индукции.
Доказательство
Подставим в формулу (14) значение n = 1:
.
Поскольку ,
то при n = 1
,
формула (14) справедлива.
Предположим, что формула (14) выполняется при n = k . Докажем, что из этого следует, что формула справедлива при n = k + 1 .
Действительно, при n = k
имеем:
.
Дифференцируем по переменной x
:
.
Итак, мы получили:
.
Эта формула совпадает с формулой (14) при n = k + 1
.
Таким образом, из предположения, что формула (14) справедлива при n = k
следует, что формула (14) справедлива при n = k + 1
.
Поэтому формула (14), для производной n-го порядка, справедлива для любых n .
Производные высших порядков логарифма по основанию a
Чтобы найти производную n-го порядка от логарифма по основанию a
,
нужно выразить его через натуральный логарифм:
.
Применяя формулу (14), находим n-ю производную:
.
Представлен вывод производных первого порядка арксинуса (arcsin x)′ и арккосинуса (arccos x)′. Для каждой из функций, вывод дан двумя способами.
Здесь мы полагаем, что нам известны производные синуса и косинуса. Далее мы выводим производные арксинуса и арккосинуса, учитывая, что они являются обратными функциями к синусу и косинусу, соответственно.
Вывод производной арксинуса
Рассмотрим функцию арксинус от переменной x
:
y = arcsin
x
.
— 1
до + 1
:
.
— π/2
до + π/2
:
.
Функция арксинус является обратной к функции синус:
x = sin
y
.
Для определения производной арксинуса, применим формулу производной обратной функции:
(1) .
Производная синуса нам известна. Обычно ее записывают в следующем виде:
.
Здесь .
,
где .
Подставим в формулу (1):
(2) .
Здесь
y = arcsin
x
;
x = sin
y
.
Теперь выразим правую часть формулы (2) через переменную x
.
Для этого заметим, что поскольку ,
то .
Тогда
.
Подставим в формулу (2):
.
Тем самым мы вывели формулу производной арксинуса:
.
Второй способ
Поскольку арксинус и синус являются обратными функциями по отношению друг к другу, то
(3) .
Здесь .
Продифференцируем это уравнение по переменной x
.
То есть найдем производные левой и правой части и приравняем их друг к другу:
(4) .
Производную правой части находим из таблицы производных :
.
Производную левой части находим по формуле производной сложной функции :
.
Здесь .
Поскольку ,
то .
Поэтому
.
Тогда
.
Подставим в (4):
.
Отсюда
.
Вывод производной арккосинуса
Используя связь между арксинусом и арккосинусом
Производную арккосинуса легко получить из производной арксинуса, если воспользоваться связью между арксинусом и арккосинусом :
.
Отсюда
.
По формуле производной обратной функции
Также производную арккосинуса можно найти по формуле производной обратной функции.
Рассмотрим функцию арккосинус:
y = arccos
x
.
Здесь независимая переменная x
может принимать значения от — 1
до + 1
:
.
Зависимая переменная y
может принимать значения от 0
до π
:
.
Функция арккосинус является обратной к функции косинус:
x = cos
y
.
Применим формулу производной обратной функции:
(1) .
Производная косинуса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x
и y
.
Тогда
,
где .
Подставим в формулу (1):
(5) .
Здесь
y = arccos
x
;
x = cos
y
.
Теперь выразим правую часть формулы (5) через переменную x
.
Поскольку ,
то .
Тогда
.
Подставим в формулу (5):
.
Таким образом, мы вывели формулу производной арккосинуса:
.
Как вычислить арксинус вручную? – Обзоры Вики
чтобы вычислить x из sin (x). arcsin определяется как инверсия sin, но ограничивается определенным диапазоном. Следовательно, arcsin(sin (x)) = x, если x находится в этом диапазоне (обычно от 0 до 2π или от −π до π) или значение y такое, что sin (y) = sin (x), т.е. y = x + 2πn или y = π − x + 2πm для некоторого n∈Z или m∈Z и y находится в этом диапазоне.
Точно так же можно ли вычислить арксинус без калькулятора? Арксинус — это обратная функция синуса, то есть она смотрит на отношение и спрашивает, какой угол может создать это отношение. … Мы можем выразить это соотношение грехов как грех=опфип=1 .
… Мы можем выразить это соотношение грехов как грех=опфип=1 .
Что означает Арккос? Определение арккосинуса
: обратная функция косинус, если y — косинус θ, то θ — это арккосинус y — сокращение arccos.
Что такое арксинус 2? Как функция с действительным знаком arcsin2 не определено, поскольку sin (x) ∈ [−1,1] для всех x∈R.
Во-вторых, что такое производная от arcsin? Что такое производная от arcsin? Производная arcsin x равна 1/√1-x². Записывается как d/dx(arcsin x) = 1/√1-x². Это также можно записать как d/dx(sin–1х) = 1/√1-x².
Как найти арккосинус?
Попробуйте это Перетащите любую вершину треугольника и посмотрите, как вычисляется угол C с помощью функции arccos (). Значит: угол, косинус которого равен 0.866, равен 30 градусам. Используйте arccos, если вы знаете косинус угла и хотите узнать фактический угол.
…
Для y = arccos x:
| Диапазон | 0 ≤ у ≤ π 0 ° ≤ у ≤ 180 ° |
|---|---|
| Домен | — 1 ≤ х ≤ 1 |
тогда что такое csc? Чай косеканс (csc ) (csc) (csc)
Косеканс обратен синусу. Это отношение гипотенузы к стороне, противоположной заданному углу в прямоугольном треугольнике.
Это отношение гипотенузы к стороне, противоположной заданному углу в прямоугольном треугольнике.
Как мне узнать, есть ли у меня SOH CAH TOA? SOHCAHTOA — это мнемоническое устройство, помогающее запомнить, какое соотношение соответствует какой функции.
- SOH = Синус противоположен гипотенузе.
- CAH = косинус смежен с гипотенузой.
- TOA = Касательная противоположна соседнему.
Как решить арксинус?
Что такое арксинус числа 3? Однако в реальных цифрах arcsin 3 не определен, и многие калькуляторы выдадут вам ошибку. (Синус действительного числа может быть только между 1 и -1.)
Как найти arcsin из 2?
- iz = iπ2 + 2πki + ln (a ± √a2−1)
- z = (π2 + 2πk) −iln (a ± √a2−1)
- z = (π2 + 2πk) ± iln (a − √a2−1)
- arcsin2=(π2+2πk)±iln(2−√3) integer k.
 2 а потом умножить на производную от 2х.
2 а потом умножить на производную от 2х.Что означает арксин?
Определение арксинуса
: обратная функция синуса если y является синусом θ, то θ является арксинусом y — сокращением arcsin.
Как найти арксинус на единичной окружности?
Что такое решение arccos 0.5? арккосинус (0.5) = 60°
Как написать косеканс?
Косеканс (косеканс) — функция тригонометрии
В прямоугольном треугольнике косеканс угла — это длина гипотенузы, деленная на длину противоположной стороны. В формуле он сокращается до «csc».
Как решить косеканс? Секанс x равен 1, деленному на косинус x: sec x = 1 cos x , а косеканс x определяется как 1 делится на синус x: csc x = 1 sin x .

Что такое косеканс окружности?
Функция косеканса является обратной величиной функции синуса (cscx=1sinx) Икс знак равно 1 грех . Его можно найти для угла t, используя координату y связанной точки на единичной окружности: csct=1г т = 1г .
Sohcahtoa только для прямоугольных треугольников?
В: Сохчатоа только для прямоугольных треугольников? А: Да, это относится только к прямоугольным треугольникам. Если у нас есть наклонный треугольник, мы не можем предположить, что эти триггерные отношения будут работать. … A: У прямоугольного треугольника гипотенуза всегда противоположна углу 90 градусов и является самой длинной стороной.
Производная функция y=2 arccos x в точке x0=0 равна.
 ..
..Ответы
30.  01.17
01.1730.  01.17
01.17Михаил Александров
Читать ответы Андрей Андреевич
Читать ответы Eleonora Gabrielyan
Читать ответы Посмотреть всех экспертов из раздела Учеба и наука
Похожие вопросы В баллоне объёмом 1,66^3 м находится 2 кг азота при давлении 10^5 Па.
 -3 кг/моль.
-3 кг/моль.В зале 89 стульев. сначала из зала вынесли 2стула потом1.на сколько меньше стульев вынесли, чем их осталось?
Напишите сочинение о том как вы выполняете любимую или необходимую работу готовите какое-то блюдо убираете Квартиру комнату заботьтесь И домашних животных например чистить аквариум ухаживать
дано: угол A= углу В, СО= 4, DО=6, АО =5. найти: а) ОВ; АС: ВD; в) S AOC:S BOD
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
Пользуйтесь нашим приложением
Производная арксинуса — формула, доказательство, примеры arcsin (который также может быть записан как sin
-1 ) является обратной функцией синуса. т. е. если y = sin -1 x, то sin y = x. По определению обратных функций, если f и f -1 являются обратными функциями друг друга, то f(f -1 (x)) = f -1 (f(x)) = x. Отсюда sin(arcsin x) = arcsin(sin x) = x в соответствующих областях. Мы используем эти факты, чтобы найти производную от arcsin x.
Отсюда sin(arcsin x) = arcsin(sin x) = x в соответствующих областях. Мы используем эти факты, чтобы найти производную от arcsin x.Давайте посмотрим формулу производной от arcsin вместе с доказательством (двумя разными методами) и несколькими примерами решения.
1. Что такое производная от arcsin? 2. Производная арксинуса Доказательство по цепному правилу 3. Производная арксинуса Доказательство по первому принципу 4. Часто задаваемые вопросы о производной от arcsin Что такое производная от arcsin?
Производная от arcsin x обозначается как d/dx(arcsin x) (или) d/dx(sin -1 x) (или) (arcsin x)’ (или) (sin -1 x) ‘. Его значение равно 1/√1 — x². Мы докажем это двумя методами в следующих разделах. Два метода:
- Использование цепного правила
- Использование первых принципов
Производная функции arcsin x Формула
Производная функции arcsin равна
- d/dx(угловой синус x) = 1/√1 — x² (ИЛИ)
- d/dx(sin -1 x) = 1/√1 — x²
Мы докажем эту формулу сейчас в следующих разделах в каждом из вышеупомянутых методов.

Производная арксинуса Доказательство по цепному правилу
Чтобы найти производную от arcsin с помощью цепного правила, предположим, что y = arcsin x. Принимая sin с обеих сторон,
sin y = sin (arcsin x)
По определению обратной функции sin (arcsin x) = x. Таким образом, приведенное выше уравнение принимает вид
sin y = x … (1)
Дифференцируя обе части по x,
d/dx (sin y) = d/dx(x)
Имеем d/ dx (sinx) = cosx. Кроме того, по цепному правилу
cos y · dy/dx = 1
dy/dx = 1/cos y
Используя одно из тригонометрических тождеств, cos y = √1 — sin²y = √1 — x² (из ( 1))
Таким образом, dy/dx = 1/√1 — x²
Подставив здесь y = arcsin x,
d/dx (arcsin x) = 1/√1 — x²
Отсюда доказано.
Производная арксинуса Доказательство по первому принципу
Напомним, что производная функции f(x) по первому принципу (определение производной) дается пределом, f'(x) = limₕ→₀ [f(x + h) — f( х)] / ч.
 Чтобы найти производную от arcsin x, предположим, что f(x) = arcsin x. Тогда f(x + h) = arcsin (x + h). Тогда из приведенного выше предела
Чтобы найти производную от arcsin x, предположим, что f(x) = arcsin x. Тогда f(x + h) = arcsin (x + h). Тогда из приведенного выше пределаf'(x) = limₕ→₀ [arcsin (x + h) — arcsin x] / h
Предположим, что arcsin (x + h) = A и arcsin x = B.
Тогда sin A = x + h и sin B = x.
Вычитание второго уравнения из первого,
sin A — sin B = (x + h) — x
sin A — sin B = h
Так как h → 0, (sin A — sin B) → 0 Отсюда sin A → sin B (или) A → B (или) A — B → 0.
Тогда приведенный выше предел становится следующим:
f'(x) = lim\(_{AB → 0}\ ) (A — B) / (sin A — sin B)
Имеем sin A — sin B = 2 sin [(A — B)/2] cos [(A + B)/2]. Подставляя это в приведенный выше предел,
f'(x) = lim\(_{A-B→ 0}\) (A — B) / [2 sin [(A — B)/2] cos [(A + B)/2] ]
Когда A — B → 0, мы можем иметь (A — B)/2 → 0.
f'(x) = lim\(_{\frac{AB}{2}→ 0}\) [(A — B)/2] / sin [(A — B)/2] lim\(_{A → B}\) cos[(A + B)/2]
f'(x) = lim\(_{ \frac{A-B}{2}→ 0}\) 1/ (sin [(A — B)/2] / [(A — B)/2] ) lim\(_{A → B}\) cos[ (A + B)/2]
Мы знаем, что lim ₓ→₀ (sin x)/x = 1.
 Отсюда
Отсюдаf'(x) = (1/1) cos[(B + B)/ 2] = cos B … (2)
Имеем sin B = x.
Итак, cos B = √1 — sin²B = √1 — x²
Следовательно, f'(x) = 1/√1 — x²
Отсюда доказано.
Статьи по теме:
Вот некоторые темы, связанные с производной от arcsin x.
- Производные формулы
- Калькулятор производных
- Тригонометрические формулы
- Расчетный калькулятор
Часто задаваемые вопросы о производной Arcsin
Что такое производная от arcsin?
Производная от arcsin x равна 1/√1-x². Записывается как d/dx(arcsin x) = 1/√1-x². Это также можно записать как d/dx(sin -1 x) = 1/√1-x².
Как найти производную от arcsin?
Чтобы получить производную от arcsin, предположим, что y = arcsin x, тогда sin y = x. Дифференцируя обе части по y, тогда cos y = dx/dy. Взяв обратные величины, dy/dx = 1/(cos y) = 1/√1 — sin²y = 1/√1-x².

Что такое производная от arcsin √x?
Мы знаем, что производная от arcsin x равна 1/√1 — x². Используя эту формулу и цепное правило, d/dx(arcsin √x) = 1/√1 — (√x)² d/dx (√x) = 1/√1 — x · (1/2√x) = 1/(2√ х- х²)).
Что такое производная от arcsin x/2?
Производная от arcsin x равна 1/√1 — x². Используя это и цепное правило, d/dx(arcsin x/2) = √1 — (x/2)² d/dx (x/2) = √1 — x²/4 · (1/2) = 2 /√4 — х² · (1/2) = 1/√4 — х².
Является ли arcsin производной от Sin?
Нет, производная от arcsin НЕ является sin. Производная arcsin x равна 1/√1 — x².
Что такое производная от arcsin x/a?
Производная от arcsin x равна 1/√1 — x². Используя это и цепное правило, d/dx(arcsin x/a) = 1/√1 — (x/a)² d/dx (x/a) = 1/√1 — (x²/a²) · ( 1/а) = [а/√а² — х²] · (1/а) = 1/√а² — х².
В чем разница между производными sin x и arcsin x?
Производная sin x равна cos x, тогда как производная arcsin x равна 1/√1-x².
Мэтуэй | Популярные проблемы
1 92)21 Оценка интеграла интеграл от 0 до 1 кубического корня из 1+7x относительно x 22 Найдите производную — d/dx грех(2x) 23 Найдите производную — d/dx 9(3x) по отношению к x41 Оценка интеграла интеграл от cos(2x) по x 42 Найдите производную — d/dx 1/(корень квадратный из х) 43 Оценка интеграла 9бесконечность 45 Найдите производную — d/dx х/2 46 Найдите производную — d/dx -cos(x) 47 Найдите производную — d/dx грех(3x) 92+168 Оценка интеграла интеграл от sin(x) по x 69 Найдите производную — d/dx угловой синус(х) 70 Оценить предел предел, когда x приближается к 0 из (sin(x))/x 92 по отношению к х 85 Найдите производную — d/dx лог х 86 Найдите производную — d/dx арктан(х) 87 Найдите производную — d/dx натуральное бревно 5х92 Производные обратных тригонометрических функций
Подход
к
C A L C U L U S
Содержание | Дом
13
Производная от y = arcsin x
Производная от y = arccos x
Производная от y = арктангенс x
Производная от y = arccot x
Производная от y = угловая секунда x
Производная от y = arccsc x
НЕ НУЖНО запоминать производные этого Урока.
 Скорее, ученик должен знать, как их вывести.
Скорее, ученик должен знать, как их вывести.В теме 19 тригонометрии мы ввели обратные тригонометрические функции. По обратным соотношениям:
y = arcsin x подразумевает sin y = x .
И аналогично для каждой из обратных тригонометрических функций.
Задача 1. Если y = arcsin x , покажите:
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!Начало:
г = arcsin x подразумевает 1) sin y = х . Следовательно, согласно тождеству Пифагора a’ : потому что у = = согласно строке 1). 
Мы берем положительный знак, потому что cos y положительно для всех значений y в диапазоне y = arcsin x , то есть 1-й и 4-й квадранты. (Тема 19 тригонометрии.)
Задача 2. Если y = arcsec x , покажите:
Начало:
г = угловая секунда x подразумевает сек г = х . Значит, согласно тождеству Пифагора b : 1
желто-коричневый у = ± = ± Производная от y = arcsin x
Производная арксинуса по его аргументу
равна 1 на квадратный корень
из 1 минус квадрат аргумента.
Вот доказательство:
г = arcsin x подразумевает грех г = х . Поэтому, взяв производную по x : = 1; = = по Задаче 1.
Именно это мы и хотели доказать.
Примечание: Мы могли бы напрямую использовать теорему урока 8:
Мы будем использовать эту теорему в следующих доказательствах.

Задача 3. Вычислите эти производные. [В частях а) и б) используйте цепное правило.]
а) д
дхarcsin x 2 = б) д
дх= в) д
дхx 2 arcsin x = Производная от y = arccos x
Производная arccos x является отрицательным производной
arcsin x . Это будет верно для обратной каждой пары кофункций.Производная от arccot x будет минусом
производной арктана x .Производная arcscsc x будет минусом
производной arcsec x .
Для, начиная с arccos x :
Угол, косинус которого равен x , является дополнением
угла, синус которого равен x .арккос х = №
2− угловой угол 91 133 x 91 134 . Поскольку производная №
2равно 0, результат следующий. Задача 4. Вычислите эти производные.
а) д
дхарккос x
а= б) д
дхx arccos 2 x = Производная от y = arctan x
д
дхарктический x = 1
1 + x 2Первый,
y = arctan x подразумевает tan y = x .

Следовательно, по теореме урока 8:
Урок 12. , согласно пифагорейскому тождеству
б ,Что мы и хотели доказать.
Следовательно, производная от arccot x является отрицательным:
д
дхарккот x = — 1
1 + x 2Задача 5. Вычислите эти производные.
а) д
дхарктан ( a x 2 ) = 2 топор
1 + a 2 x 4б) д
дхарккот x
а= − а
а 2 + x 2в) д
дхарктан 2
х= −2
x 2 + 4г) д
дхдуга 2 x = −2
4 x 2 + 1*
Остальные производные редко встречаются в исчислении.
 Тем не менее, вот доказательства.
Тем не менее, вот доказательства.Производная от y = угловая секунда x
Еще раз,
y = угловая секунда x подразумевает секунды y = x .
Следовательно, по теореме урока 8:
, Урок 12. Теперь, согласно теореме из темы 19 тригонометрии: это произведение никогда не бывает отрицательным. Поэтому для обеспечения того, чтобы вместо замены раздела y на x , мы заменим его на | х |. А в задаче 2 возьмем только положительный корень из тангенса y .
Следовательно,
Что мы и хотели доказать.
Если мы возьмем диапазон угловых секунд x в качестве угла третьего квадранта между −π и −π/2, когда x отрицательно, то нам не нужно будет записывать абсолютное значение, и доказательство будет простым.
 . Мы бы просто заменили сек y с x и возьмите положительный корень из tan y , потому что тангенс y положителен в первом и третьем квадрантах. На графике y = arcsec x с этим диапазоном наклон для отрицательных x отрицательный. Недостатком выбора этого диапазона является то, что, когда x отрицательно, arcsec x не будет равняться arccos 1/ x , потому что arccos 1/ x будет углом 2-го квадранта. Но тогда в доказательстве мы должны написать абсолютное значение.
. Мы бы просто заменили сек y с x и возьмите положительный корень из tan y , потому что тангенс y положителен в первом и третьем квадрантах. На графике y = arcsec x с этим диапазоном наклон для отрицательных x отрицательный. Недостатком выбора этого диапазона является то, что, когда x отрицательно, arcsec x не будет равняться arccos 1/ x , потому что arccos 1/ x будет углом 2-го квадранта. Но тогда в доказательстве мы должны написать абсолютное значение.Таким образом, производная от arcccsc x является отрицательной:
д
дхarccsc x = − Следующий урок: Производные экспоненциальной и логарифмической функций
Содержание | Главная
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.

Даже 1 доллар поможет.Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Производные обратных тригонометрических функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17554
- Пол Сибургер
- Общественный колледж Монро
Определение производных обратных тригонометрических функций
Теперь найдем производные обратных тригонометрических функций, \(y = \arcsin x,\) \(y = \arccos x,\) \(y = \arctan x, \) \( y = \text{arccot}\, x,\) \(y = \text{arcsec}\, x,\) и \(y = \text{arccsc}\, x. \)
\)
Одним из способов сделать это, особенно полезным для понимания того, как получаются эти производные, является использование комбинации неявного дифференцирования и прямоугольных треугольников. Дополнительным преимуществом этого подхода является то, что он подготовит вас к более успешному изучению будущей темы, называемой тригонометрической подстановкой.
Пример \(\PageIndex{1}\): найти производную от \(y = \arcsin x\)
Найти производную от \(y = \arcsin x\).
Решение:
Чтобы найти производную \(y = \arcsin x\), мы сначала перепишем это уравнение в терминах его обратной формы. То есть \[ \sin y = x \label{inverseEqSine}\]
Теперь это уравнение показывает, что \(y\) можно считать острым углом в прямоугольном треугольнике с отношением синусов \(\dfrac{x {1}\). Поскольку отношение синуса дает нам длину противоположной стороны по длине гипотенузы, это означает, что противоположная сторона имеет длину \(х\), а гипотенуза имеет длину \(1\). См. рисунок \(\PageIndex{1}\).
См. рисунок \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\)
Теперь давайте неявно продифференцируем уравнение \ref{inverseEqSine} относительно \(x\).
\[\cos y \cdot \frac{dy}{dx} = 1\]
Затем мы решаем это для \(\dfrac{dy}{dx}\).
\[\frac{dy}{dx} =\frac{1}{\cos y}\]
Глядя на рисунок \(\PageIndex{1}\), мы видим, что \(\cos y = a \). Теперь воспользуемся теоремой Пифагора, чтобы найти выражение для \(а\) через \(х\), используя известные нам другие стороны прямоугольного треугольника. 92} \end{выравнивание*} \]
Пример \(\PageIndex{2}\): найти производную от \(y = \text{arcsec}\, x\)
Найти производную от \(y = \text{arcsec}\, x\ ).
Решение:
Чтобы найти производную от \(y = \text{arcsec}\, x\), мы сначала перепишем это уравнение в терминах его обратной формы. То есть \[ \sec y = x \label{inverseEqSec}\]
Как и прежде, пусть \(y\) считается острым углом в прямоугольном треугольнике с отношением секущих \(\dfrac{x}{ 1}\). Поскольку отношение секущей является обратным отношением косинуса, оно дает нам длину гипотенузы по длине прилежащей стороны, так что это означает, что гипотенуза имеет длину \(x\), а прилежащая сторона имеет длину из \(1\). См. рисунок \(\PageIndex{3}\).
Поскольку отношение секущей является обратным отношением косинуса, оно дает нам длину гипотенузы по длине прилежащей стороны, так что это означает, что гипотенуза имеет длину \(x\), а прилежащая сторона имеет длину из \(1\). См. рисунок \(\PageIndex{3}\).
Рисунок \(\PageIndex{3}\)
Дифференцирующее уравнение \ref{inverseEqSec} неявно относительно \(x\), дает нам:
\[\sec y\tan y \ cdot \frac{dy}{dx} = 1\]
Решая это для \(\dfrac{dy}{dx}\), мы получаем:
\[\frac{dy}{dx} =\frac{ 1}{\sec y\tan y}\]
Чтобы найти \(\tan y\) через \(x\), нам нужно найти длину противоположной стороны, \(a\) , в терминах \(x\). По теореме Пифагора имеем: 92 — 1}}.\]
Но это не совсем правильно, по крайней мере, не для отрицательных значений \(x\). Рассматривая график \(y = \text{arcsec}\, x\) на рисунке \(\PageIndex{5}\), мы видим, что его наклон всегда положителен. Но при отрицательных значениях \(х\) указанный выше вид производной был бы отрицательным (и явно неверным).
Рисунок \(\PageIndex{5}\)
Как мы докажем ниже, фактическая формула производной для этой функции: 92 — 1}}\]
Рассмотрим домен и диапазон исходной функции, \(y = \text{arcsec}\, x:\)
\[\text{Домен: } (-\infty, — 1] \cup [1, \infty) \quad \text{or} \quad |x| \geq 1\]
\[\text{Диапазон: } \big[0, \frac{\pi}{2}\big) \cup \big(\frac{\pi}{2}, \pi\big ] \quad \text{or} \quad 0 \leq y \leq \pi, y \ne \frac{\pi}{2}\]
Обратите внимание, что область определения производной является подмножеством области определения исходная функция, исключая конечные точки, \(x = -1\) и \(x = 1.\) 92 y}{\sin y}\]
Мы видим, что эта функция позволяет \(y\) принимать все значения между \(0\) и \(\pi\), за исключением \(y = \frac{ \pi}{2}\), где исходное выражение \(\dfrac{1}{\sec y\tan y}\) не определено. Это подмножество диапазона исходной функции \(y = \text{arcsec}\, x.\). Обратите внимание, что в производной \(y\) не может принимать значения конечных точек этого интервала, а они были частью диапазона \(y = \text{arcsec}\, x. \)
\)
Теперь рассмотрим, что для всех значений \(y\) в этом диапазоне между \(0\) и \(\pi \), выражение для \(\dfrac{dy}{dx}\) положительно, так как оба 92} = |x|.\]
Это означает, что на самом деле здесь мы получаем нечто более интересное: \[ \frac{d}{dx}\big(\arcsin(\cos x) \big) = \frac{ -\sin x}{|\sin x|}\]
Эта функция чередует значения \(-1\) и \(1\), когда \(\sin x\) положительное и отрицательное значение соответственно.
См. график функции \( y = \arcsin(\cos x)\) ниже на рисунке \(\PageIndex{6}\).
Рисунок \(\PageIndex{6}\): График \(y = \arcsin(\cos x)\).
Формулы производных
Точно так же мы можем инкапсулировать цепное правило в производной \(\ln u\) как \(\dfrac{d}{dx}\big(\ln u\big) = \ dfrac{u’}{u}\), мы можем написать формулы для производной обратных тригонометрических функций, которые инкапсулируют цепное правило. Обратите внимание, что \(u\) представляет собой функцию \(x\) в этих формулах, а \(u’\) представляет собой производную \(u\) по \(x\). 2}} \\ 92-1}} \end{align*} \]
2}} \\ 92-1}} \end{align*} \]
Авторы
- Пол Сибургер (Общественный колледж Монро)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Пол Сибургер
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- нет
- Метки
- расчетный график: да
Производная арксинуса с доказательством и формулой, частным и цепными правилами
Производная арксинуса является частью Дифференциации, которая является подтемой исчисления. В производной от arcsinx это чистая тригонометрическая функция. В этой статье мы узнаем, как различать дуговые синусоиды, используя различные правила дифференцирования, такие как первый принцип производной, дифференцировать дуговые синусоиды, используя цепное правило, и дифференцировать дуговые синусоиды, используя правило частных.
В производной от arcsinx это чистая тригонометрическая функция. В этой статье мы узнаем, как различать дуговые синусоиды, используя различные правила дифференцирования, такие как первый принцип производной, дифференцировать дуговые синусоиды, используя цепное правило, и дифференцировать дуговые синусоиды, используя правило частных.
Что такое арксинус?
Функция арксинуса обратна функции синуса. Это чистая тригнометрическая функция. Мы можем легко найти производные алгебраической функции и производные тригонометрических функций. Он возвращает угол, синус которого является заданным числом. Арксинус x определяется как функция обратного синуса x, когда -1 ≤ x ≤ 1.
Когда синус y равен x:
sin y = x
Тогда арксинус x равен функция обратного синуса от x, равная y: 9{-1} 1 = π/2 рад = 90°\)
График арксинуса
Арксинус можно представить в графической форме следующим образом:
Прочтите эту статью о пределах и непрерывности.
Значения Arcsin
| x | ARCSIN (x) (RAD) | ARCSIN (X) (°)| 2121 (x) (°) | 2921 | | 9 2 | 1929 2 | 921. /2 | -90° |
| \(-\sqrt3\over2\) | -π/3 | -60° | ||
| \(-\sqrt2\over2\) | -π/4 | -45° | \(-\- | π/6 | -30° |
| 0 | 0 | 0° | ||
| \(1\over2\) | π/6 | 30° | ||
| \(\sqrt2\over2 \) | π/4 | 45° | ||
| \(\sqrt3\over2\) | π/3 | 60° | ||
| 1 | π/2 | 90° |
Properties of Arcsine
| Rule name | Rule |
| Sine of arcsine | sin( arcsin x ) = x |
| Arcsine of Sine | ARCSIN (SIN x ) = x +2 K π, когда K ∈ 42158 888888888888 г.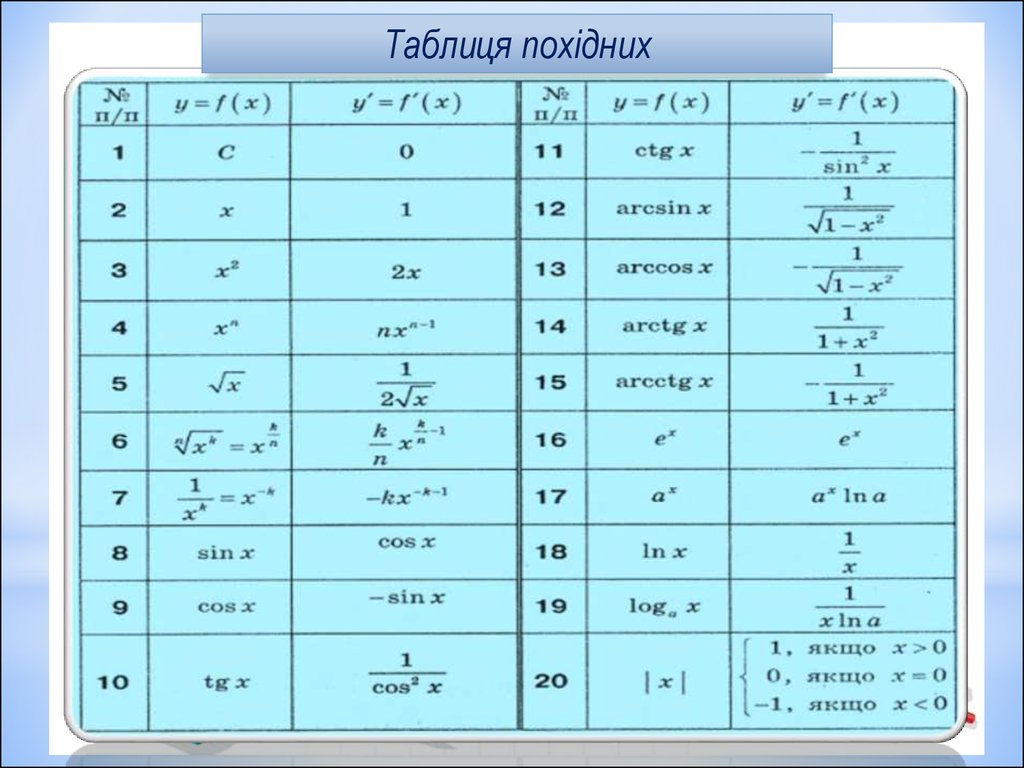 88888888 гг.2} }\) 88888888 гг.2} }\) |
Также читайте об арифметических прогрессиях в этой статье.
Доказательство производной Arcsinx
Мы узнаем, как дифференцировать arcsinx, используя различные правила дифференцирования, такие как первый принцип производной, дифференцировать arcsinx, используя цепное правило, и дифференцировать arcsinx, используя правило частных.
Производная арксинуса по правилу частных
Давайте посмотрим, как найти производную арксинуса в деталях
Шаги для нахождения производной от arcsin x:
Шаг 1: Запишите sin y = x,
Шаг 2: Дифференцируйте обе части этого уравнения по x.
\(\begin{matrix}
{d\over{dx}}sin y = {d\over{dx}}x\\
уютный {d\over{dx}} y = 1
\end{matrix }\)
Шаг 3: Найдите \({dy\over{dx}}\)
\({d\over{dx}} y = {1\over{cosy}}\)
Шаг 4: Определите cos y через x, используя опорный треугольник. 92)}}}\)
92)}}}\)
Доказательство производной arcsin по цепному правилу
Вот доказательство производной arcsin по цепному правилу
\(\begin{matrix}
\text{ Let } y = arcsin x\\
\text{ Принимая sin с обеих сторон, }\\
sin y = sin (arcsin x)\\
\text{ По определению обратной функции имеем, }\\
sin (arcsin x) = x\\
\text{ Итак, уравнение принимает вид }
sin y = x \\
\text{ Дифференцируя обе части по x,}\\
{d\over{dx}} (sin y) = {d\over{ дх}} (х)\\ 92}}}
\end{matrix}\)
Доказательство производной от arcsin по первому принципу
Вот доказательство производной от arcsin по первому принципу.
\(\begin{matrix}
f'(x)={dy\over{dx}}=\lim _{h{\rightarrow}0}{f(x+h)–f(x)\over {h}}
f(x)=arcsinx\\
f(x+h)=arcsin(x+h)\\
f(x+h)–f(x)= tan(x+h) – tan (x) = arcsin (x + h) – arcsinx\\
{f(x+h) – f(x)\over{h}}={ arcsin (x + h) – arcsinx\over{h}}\ \
\ lim _ {h {\ rightarrow} 0} {f (x + h) -f (x) \ over {h}} = \ lim _ {h {\ rightarrow} 0} {arcsin (x + h) – arcsinx\over{h}}\\
\text{ Предположим, что arcsin (x + h) = A и arcsin x = B }\\
sin A = x + h\\
sin B = x\\
sin A – sin B = (x + h) – x\\
sin A – sin B = h\\
If \text{ h → 0, (sin A – sin B) → 0 sin A → sin B или A → B или A – B → 0}\\
\lim _{AB{\rightarrow}0}{f(x+h) -f(x)\over{h}} = \lim _{AB{\rightarrow}0} {(A — B)\over {(sin A – sin B)}}\\
\text{ sin A – sin B = 2 sin [(A – B)/2] cos [(A + B)/2] }\\
\lim _ {AB {\ rightarrow} 0} {f (x + h) -f (x) \ over {h}} = \ lim _ {AB {\ rightarrow} 0} {(A — B) \ over {[2 sin [(А – В)/2] cos [(А + В)/2]]}}\\ 92}}}
\end{matrix}\)
Надеюсь, что эта статья о производной Arcsinx была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о производной от Arcsinx
В.1 Что такое производная от Arcsinx?
Ответ 1 Функция арксинуса является обратной функцией синуса. Он возвращает угол, синус которого является заданным числом. Арксинус x определяется как функция обратного синуса x, когда -1 ≤ x ≤ 1. 92}}}\)
Q.2 Какова производная функции синуса?
Ответ 2 Производная синуса записывается как sin′(a) = cos(a), что означает, что скорость изменения sin(x) при определенном угле x = a определяется выражением косинус этого угла. Если f(x) = sinx, найдите f'(x)
\(\begin{matrix}
f(x) = sinx = cos({\pi\over{2}} -x)\\
\text{ Используя цепное правило, }\\
f'(x) = – sin({\pi\over{2}} -x) · {d\over{dx}} ({\pi\over{2}} -x )\\
= – sin({\pi\over{2}} -x) · (-1)\\
= sin({\pi\over{2}} -x)\\
= cosx
\end{matrix }\)
Q. 3 Как найти производную функции arcsinx?
3 Как найти производную функции arcsinx?
Ответ 3 \(\begin{matrix}
\text{ Пусть } y = arcsin x\\
\text{ Принимая sin с обеих сторон, }\\
sin y = sin (arcsin x )\\
\text{ По определению обратной функции имеем }\\
sin (arcsin x) = x\\
\text{ Таким образом, уравнение принимает вид }
sin y = x \\ 92} }\)
6.2.2 Дифференцирование обратных тригонометрических функций
Исчисление одной действительной переменной Автор Pheng Kim
Винг |
6.2.2
|
Возврат
К содержанию
Перейти к проблемам и решениям
1. |
Производные арксинуса и Арккосинус
Следовательно:
|
Аналогично:
|
Обратите внимание, что ( d / dx ) arccos x является минусом ( d / dx ) arcsin x .
Производные арктангенса И арккотангенс
|
Обратите внимание, что уравнение [1. 3] действует для всех x в R . Это
согласуется с тем фактом, что dom(arctan x ) равен R .
3] действует для всех x в R . Это
согласуется с тем фактом, что dom(arctan x ) равен R .
Аналогично:
|
Обратите внимание, что ( d / dx ) arccot x это негатив ( d / dx ) арктангенс х .
Производные арксинуса и Арккосеканс
Итак, поскольку sec y = х , получаем:
|
Аналогично:
|
Обратите внимание, что ( d / dx )
arccsc x — это
минус ( d / dx ) угл. сек х .
сек х .
Пример 1.1
Дифференцируйте каждую из следующих функций, упрощая ответ, когда соответствующий.
Решение
EOS
900 Решение проблем Страница
2. Соотношения между обратными тригонометрическими функциями |
для всех x в (1, 1). Мы видели в разделе
4.1 Теорема 6.1: если функция f непрерывна на [ a , b ] и ее
производная равна 0 на
Перейти к проблемам и решениям Вернуться к началу Страница
3. Избегайте путаницы при запоминании производных |
Заметим, что:
Производная от | — это просто отрицательная производная от . |
arccos x [уравнение. [1.2]] | дуги x [экв. [1.1]], |
arccot x [уравнение. [1.4]] | arctan x [уравнение. [1.3]], |
arccsc x [уравнение. [1.6]] | угловых секунды x [уравнение. [1.5]]. |
Как для ( d / dx ) арктан x , не должно быть путаницы ни с каким другим производная.
Перейти к проблемам и решениям Вернуться к началу Страница
4. Зачем возиться со всеми этими обратными вещами? |
Производная от arcsin х равно:
У нас есть три новых первообразных: arcsin, arctan,
и угл. сек. Ну вот поэтому мы и заморачиваемся со всеми этими обратными
сек. Ну вот поэтому мы и заморачиваемся со всеми этими обратными
вещи.
Обратите внимание, что мы не
хвастаться
о производных обратных кофункций arccos x , arccot x и arccsc x . Причина
заключается в том, что они просто отрицательные производные от arcsin x , arctan x и arcsec x соответственно, как указано в части
3, и, таким образом, не дают новых первообразных. Например, мы знаем, что:
Вернуться к началу страницы
Проблемы и решения |
1. Найдите производную каждой из следующих функций, упрощая ответ, когда это уместно.
Решение
Возврат на вершину стр.
2. Найдите уравнение линии, касающейся кривой y = Arcsin ( x /2) в точке x ( x /2) в точке x ( x /2) в точке .
= 1.
Найдите уравнение линии, касающейся кривой y = Arcsin ( x /2) в точке x ( x /2) в точке x ( x /2) в точке .
= 1.
Решение
Возврат на вершину стр.
3. 2
3. 2
3. 2
Пусть f ( x ) = sin arcsin х .
а. Покажите, что f ‘( x ) = 1 с помощью
вычисляя его непосредственно из заданного выражения.
б. Упростить f ( x ). Найдите f ‘( x ), используя это
упрощенная форма f ( x ).
с. Нарисуйте график f ( x ).
Примечание: См. также Проблема и решение 4.
Решение
c. Домен
из ф есть [1, 1]; его диапазон также [1, 1].


 -1 не равно 1/sin ? это какую тему нужно перечитывать?
-1 не равно 1/sin ? это какую тему нужно перечитывать? http://mathworld.wolfram.com/InverseSine.html
http://mathworld.wolfram.com/InverseSine.html Ну обозначения у них такие: минус единичка в подобных случаях означает не степень, а обратную функцию. А у нас это (применительно к конкретным функциям, не к абстрактным) не принято.
Ну обозначения у них такие: минус единичка в подобных случаях означает не степень, а обратную функцию. А у нас это (применительно к конкретным функциям, не к абстрактным) не принято. Ну, например, здесь: http://ru.wikipedia.org/wiki/Обратная_функция .
Ну, например, здесь: http://ru.wikipedia.org/wiki/Обратная_функция .

 2 а потом умножить на производную от 2х.
2 а потом умножить на производную от 2х.
 ..
.. 01.17
01.17 01.17
01.17 -3 кг/моль.
-3 кг/моль. Отсюда sin(arcsin x) = arcsin(sin x) = x в соответствующих областях. Мы используем эти факты, чтобы найти производную от arcsin x.
Отсюда sin(arcsin x) = arcsin(sin x) = x в соответствующих областях. Мы используем эти факты, чтобы найти производную от arcsin x.
 Чтобы найти производную от arcsin x, предположим, что f(x) = arcsin x. Тогда f(x + h) = arcsin (x + h). Тогда из приведенного выше предела
Чтобы найти производную от arcsin x, предположим, что f(x) = arcsin x. Тогда f(x + h) = arcsin (x + h). Тогда из приведенного выше предела Отсюда
Отсюда
 Скорее, ученик должен знать, как их вывести.
Скорее, ученик должен знать, как их вывести.



 Тем не менее, вот доказательства.
Тем не менее, вот доказательства. . Мы бы просто заменили сек y с x и возьмите положительный корень из tan y , потому что тангенс y положителен в первом и третьем квадрантах. На графике y = arcsec x с этим диапазоном наклон для отрицательных x отрицательный. Недостатком выбора этого диапазона является то, что, когда x отрицательно, arcsec x не будет равняться arccos 1/ x , потому что arccos 1/ x будет углом 2-го квадранта. Но тогда в доказательстве мы должны написать абсолютное значение.
. Мы бы просто заменили сек y с x и возьмите положительный корень из tan y , потому что тангенс y положителен в первом и третьем квадрантах. На графике y = arcsec x с этим диапазоном наклон для отрицательных x отрицательный. Недостатком выбора этого диапазона является то, что, когда x отрицательно, arcsec x не будет равняться arccos 1/ x , потому что arccos 1/ x будет углом 2-го квадранта. Но тогда в доказательстве мы должны написать абсолютное значение.