Урок по математика. 11 класс. Тема: «Правило вычисления производной частного»
Дата 15.11
Тема: Правило вычисления производной частного
Цели:
- Ввести правила дифференцирования производной частного
- Повторить правила нахождения(f(x)+g(x))΄, (f(x)-g(x))΄ и (c f(x))΄
- Учиться применять новое знание при решении задач
- развивать творческую и мыслительную деятельность учащихся
- развивать способность к «видению» проблемы
- формировать умения чётко и ясно излагать свои мысли
- формировать познавательные интересы и мотивы самосовершенствования
- воспитывать умение работать с имеющейся информацией
- воспитывать культуру труда общения, на выки самоконтроля, взаимоконтроля и взаимопомощи
Ход урока.
I. Организационный момент. Проверка домашнего задания.
II. Актуализация опорных знаний.
Мы несколько раз уже использовали слово “ производная “.
1. Так, кто скажет определение производной функции в точке?
Ответ: Производной функции в точке Х0 называется число к которому стремится разностное отношение .
2. Как называется операция нахождения производной ?
Ответ: дифференцированием.
3. При решении каких задач применяется производная?
Ответ при решении задач на нахождении мгновенной
скорости при неравномерном движении тела.
Есть еще другие задачи, где необходимо использовать производную;
Например: При решение квадратного уравнения ах2 +вх+с = 0 количество корней определяем с помощью дискриминанта. А если нам потребуется определить количество корней уравнения вида Какими формулами можно здесь воспользоваться? Тут и нам поможет производная. На это мы не будем останавливаться, т.к. при изучении дальнейших тем, вы вернетесь к этой задаче.
Мы вернемся к нашей теме и вспомним правила нахождения производных:
Правило 1 (производная от произведения числа на функцию). Справедливо равенство
(c f (x))’ = c f ‘ (x) ,
где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
На
Правило 2 (производная суммы функций). Производная суммы функций вычисляется по формуле
(f (x) + g (x))’ = f ‘ (x) + g’ (x),
то есть производная от суммы функций равна сумме производных этих функций.
Правило 3 (производная разности функций). Производная разности функций вычисляется по формуле
(f (x) – g (x))’ = f ‘ (x) – g’ (x),
то есть производная от разности функций равна разности производных этих функций.
Правило 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле
(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x),
Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
(U+V)1
(UV)1
Изучение нового материала
Производная частного равна разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, деленной на квадрат знаменателя.
Закрепление изученного материала
Выполнение №28.18 (работа в группах)
Отработка прототипов заданий №9 нахождение физического смысла производной открытого банка задач ЕГЭ по математике
Задание В9 (№119979)
Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Решение.
Найдем производную функции :
По условию, скорость точки равна 2 м/с, значит, значение производной в момент времени равно 2.
Получаем уравнение:
Решим его:
, — не подходит по смыслу задачи: время не может быть отрицательным.
Ответ: 7
Решим задание В9 (№ 119975) из Открытого банка заданий для подготовки к ЕГЭ по математике.
Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени .
Решение.
1. Найдем производную функции :
2. Найдем значение производной в точке :
Ответ: 60 м/с.
Рефлексия
Выберите 1 фразу для соседа по парте:
Ты молодец.
Я доволен твоей работой на уроке.
Ты мог бы поработать лучше.
Домашнее задание:
Повторить основные правила дифференцирования
карточки
Опубликовано в группе «УРОК.РФ: группа для участников конкурсов»
Производная частного — интернет энциклопедия для студентов
ОПРЕДЕЛЕНИЕ
Производная от частного равна разности произведения производной числителя по знаменателю и произведению числителя на производную знаменателя, деленную на квадрат знаменателя.
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Производная произведения Производная разности Производная суммы Производная степенной функции
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Производная произведения двух дифференцируемых функций определяется формулой.
 Формулы производных. Защита персональной информации
Формулы производных. Защита персональной информацииС правочные материалы по теме «производная». Базовый школьный уровень.
Теоретические сведения для учеников, преподавателей и репетиторов по математике. В помощь к проведению занятий.
Определение: производной функции в точке называется предел отношения приращения функции к приращению переменной, то есть
Таблица производных основных математических функций:
Правила вычисления производных
Производная суммы двух любых выражений равна сумме производных этих выражений (производная суммы равна сумме производных)
Производная разности двух любых выражений равна разности производных этих слагаемых (производная разности равна разности производных).
Производная от произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго (сумма поочередно взятых производных от множителей).
Комментарий репетитора по математике: когда я короткими фразами напоминаю ученику о правиле вычисления производной от произведения, я говорю так: производная первого множителя на второй плюс обмен штрихами!
Производная от частного двух выражений равна частному разности поочередно взятых производных от множителей и квадрата знаменателя.
Производная от произведения числа на функцию . Чтобы найти производную от произведения числа на буквенное выражение (на функцию) нужно умножить это число на производную этого буквенного выражения.
Для вычисления производной сложной функции необходимо найти производную внешней функции и умножить ее на производную внутренней функции.
Ваши комментарии и отзывы к странице с производными:
Александр С.
Очень нужна была таблица. В интернете одна из самых. За пояснения и правила тоже огромное спасибо. Хотя бы по одному примеру ещё к ним и вообще было бы отлично было. Еще раз огромное спасибо.
Еще раз огромное спасибо.
Колпаков А.Н, репетитор по математике: хорошо, постараюсь в ближайшее время дополнить страницу примерами.
Виртуальный математический справочник.
Колпаков Александр Николаевич, репетитор по математике.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Что такое производная функция — это основное математическое понятие, находится на одном уровне с интегралами, при анализе. Данная функция в определенной точке дает характеристику скорости изменений функции в данной точке.
Такие понятия как дифференцирование и интегрирование, первое расшифровывается как действие поиска производной, второе наоборот, восстанавливает функцию отталкиваясь от данной производной.
Вычислениям производной отводится важная часть в дифференциальных расчетах.
Для наглядного примера, изобразим производную на координатной плоскости.
в функции у=f(х) фиксируем точки М в которой (х0; f(X0)) и N f (x0+?x) к каждой абсциссе есть приращение в виде?x. Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как?у.
Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как?у.
Найдем тангенс угла в треугольнике MPN используя для этого точки М и N.
tg? = NP/MP = ?у/?x.
При?x идущем к 0. Пересекающая МN все ближе к касательной МТ и угол? будет?. Следовательно, tg ? максимальное значение для tg ?.
tg ? = lim от?x-0 tg ? = lim от?x-0 ?у/?x
Таблица производных
Если проговаривать формулировку каждой формулы производных . Таблица будет проще запоминаться.
1) Производная от постоянного значения равняется 0.
2) Х со штрихом равняется единице.
3) Если есть постоянный множитель, просто выносим ео за производную.
4) Чтобы найти производную степень, нужно показатель данной степени умножить на степень с таким же основанием, у которого показатель на 1 меньше.
5) Поиск корня равен одному, деленному 2 этих корня.
6) Производная одного, деленного на Х равняется одному разделенному на Х возведенный в квадрат, со знаком минус.
7) П синус равняется косинусу
8) П косинус равняется синусу со знаком минус.
9) П тангенс равняется одному, деленному на косинус в квадрате.
10) П котангенс равняется одному со знаком минус, деленная на синус в квадрате.
В дифференцировании также существуют правила, которые тоже проще выучить проговаривая их в слух.
1) Очень просто, п. слагаемых равняется их сумме.
2) Производная в умножении равняется умножению первого значения на второе, прибавляя к себе умножение второго значения на первое.
3) Производная в делении равняется умножению первого значения на второе, отнимая от себя умножение второго значения на первое. Дробь деления на второе значение в квадрате.
4) Формулировка является частным случаем третьей формулы.
В этом уроке мы продолжаем изучать производные функций и переходим к более сложной теме, а именно, к производным произведения и частного. Если вы смотрели предыдущий урок, то наверняка поняли, что мы рассматривали лишь самые простые конструкции, а именно, производную степенной функции, суммы и разности. {\prime }}=1\cdot \left(\sqrt{x}-1 \right)+x\frac{1}{3\sqrt{x}}= \\& =\sqrt{x}-1+\sqrt{x}\cdot \frac{1}{3}=\frac{4}{3}\sqrt{x}-1 \\\end{align}\]
{\prime }}=1\cdot \left(\sqrt{x}-1 \right)+x\frac{1}{3\sqrt{x}}= \\& =\sqrt{x}-1+\sqrt{x}\cdot \frac{1}{3}=\frac{4}{3}\sqrt{x}-1 \\\end{align}\]
Ответ найден.
Зачем раскладывать производные на множители?
Только что мы использовали несколько очень важных математических фактов, которые сами по себе не имеют отношения к производным, однако без их знания все дальнейшее изучение этой темы просто не имеет смысла.
Во-первых, решая самую первую задачу и, уже избавившись от всех знаков производных, мы зачем-то начали раскладывать это выражение на множители.
Во-вторых, решая следующую задачу, мы несколько раз переходили от корня к степени с рациональным показателем и обратно, при этом используя формулу 8-9-го класса, которую стоило бы повторить отдельно.
По поводу разложения на множители ― зачем вообще нужны все эти дополнительные усилия и преобразования? На самом деле, если в задаче просто сказано «найти производную функции», то эти дополнительные действия не требуются. Однако в реальных задачах, которые ждут вас на всевозможных экзаменах и зачетах, просто найти производную зачастую недостаточно. Дело в том, что производная является лишь инструментом, с помощью которой можно узнать, например, возрастание или убывание функции, а для этого требуется решать уравнение, раскладывать его на множители. И вот здесь этот прием будет очень уместен. Да и вообще, с функцией, разложенной на множители, гораздо удобней и приятней работать в дальнейшем, если требуются какие-то преобразования. Поэтому правило № 1: если производную можно разложить на множители, именно так и стоит поступать. И сразу правило № 2 (по сути, это материал 8-9-го класса): если в задаче встречается корень n -ной степени, причем, корень явно больше двух, то этот корень можно заменить обычной степенью с рациональным показателем, причем в показателе появится дробь, где n ― та самая степень ― окажется в знаменателе этой дроби.
Однако в реальных задачах, которые ждут вас на всевозможных экзаменах и зачетах, просто найти производную зачастую недостаточно. Дело в том, что производная является лишь инструментом, с помощью которой можно узнать, например, возрастание или убывание функции, а для этого требуется решать уравнение, раскладывать его на множители. И вот здесь этот прием будет очень уместен. Да и вообще, с функцией, разложенной на множители, гораздо удобней и приятней работать в дальнейшем, если требуются какие-то преобразования. Поэтому правило № 1: если производную можно разложить на множители, именно так и стоит поступать. И сразу правило № 2 (по сути, это материал 8-9-го класса): если в задаче встречается корень n -ной степени, причем, корень явно больше двух, то этот корень можно заменить обычной степенью с рациональным показателем, причем в показателе появится дробь, где n ― та самая степень ― окажется в знаменателе этой дроби.
Разумеется, если под корнем присутствует какая-то степень (в нашем случае это степень k ), то она никуда не девается, а просто оказывается в числителе этой самой степени. {2}}}\]
{2}}}\]
Мы нашли ответ. Как и предполагалось, объем вычисления оказался существенно меньше, чем для первой функции.
В чем разница между обозначениями?
У внимательных учеников наверняка уже возник вопрос: почему в одних случаях мы обозначаем функцию как $f\left(x \right)$, а в других случаях пишем просто $y$? На самом деле, с точки зрения математики нет абсолютно никакой разницы ― вы вправе использовать как первое обозначение, так и второе, при этом никаких штрафных санкций на экзаменах и зачетах не последует. Для тех, кому все-таки интересно, поясню, почему авторы учебников и задач в одних случаях пишут $f\left(x \right)$, а в других (гораздо более частых) ― просто $y$. Дело в том, что записывая функцию в виде\, мы неявно намекаем тому, кто будет читать наши выкладки, что речь идет именно об алгебраической интерпретации функциональной зависимости. Т. е., есть некая переменная $x$, мы рассматриваем зависимость от этой переменной и обозначаем ее $f\left(x \right)$. При этом, увидев вот такое обозначение, тот, кто будет читать ваши выкладки, например, проверяющий, будет подсознательно ожидать, что в дальнейшем его ждут лишь алгебраические преобразования ― никаких графиков и никакой геометрии.
С другой стороны, используя обозначения вида\, т. е., обозначая переменную одной единственной буквой, мы сразу даем понять, что в дальнейшем нас интересует именно геометрическая интерпретация функции, т. е., нас интересует, в первую очередь, ее график. Соответственно, столкнувшись с записью вида\, читатель вправе ожидать графических выкладок, т. е., графиков, построений и т. д., но, ни в коем случае, не аналитических преобразований.
Еще хотел бы обратить ваше внимание на одну особенность оформления задач, которые мы сегодня рассматриваем. Многие ученики считают, что я привожу слишком подробные выкладки, и многие из них можно было бы пропустить или просто решить в уме. Однако именно такая подробная запись позволит вам избавится от обидных ошибок и значительно увеличит процент правильно решенных задач, например, в случае самостоятельной подготовки к контрольным или экзаменам. Поэтому если вы еще неуверенны в своих силах, если вы только начинаете изучать данную тему, не спешите ― подробно расписывайте каждый шаг, выписывайте каждый множитель, каждый штрих, и очень скоро вы научитесь решать такие примеры лучше, чем многие школьные учителя. {2}}x} \\\end{align}\]
{2}}x} \\\end{align}\]
Теперь, если мы сравним полученный результат с тем, что мы получили ранее, при вычислении по другому пути, то мы убедимся, что получили одно и то же выражение. Таким образом, каким бы путем мы не шли при вычислении производной, если все посчитано верно, то ответ будет одним и тем же.
Важные нюансы при решении задач
В заключении хотел бы рассказать вам еще одну тонкость, связанную с вычислением производной частного. То, что я вам сейчас расскажу, не было в изначальном сценарии видеоурока. Однако за пару часов до съемок я занимался с одним из своих учеников, и мы как раз разбирали тему производных частного. И, как выяснилось, этот момент многие ученики не понимают. Итак, допустим, нам нужно посчитать снять штрих следующей функции:
В принципе, ничего сверхъестественного на первый взгляд в ней нет. Однако в процессе вычисления мы можем допустить много глупых и обидных ошибок, которые я бы хотел сейчас разобрать.
Итак, считаем эту производную. {\prime }}$ можно рассматривать и как производную частного, и как производную степенной функции. При этом если все вычисления выполнены верно, то ответ всегда получится одним и тем же. Во-вторых, при вычислении производных, содержащих и переменную, и константу, принципиально важным является то, где находится переменная ― в числителе или в знаменателе. В первом случае, когда переменная находится в числителе, мы получаем простую линейную функцию, которая элементарно считается. А в случае, если переменная стоит в знаменателе, то мы получаем более сложное выражение с сопутствующими выкладками, приведенными ранее.
{\prime }}$ можно рассматривать и как производную частного, и как производную степенной функции. При этом если все вычисления выполнены верно, то ответ всегда получится одним и тем же. Во-вторых, при вычислении производных, содержащих и переменную, и константу, принципиально важным является то, где находится переменная ― в числителе или в знаменателе. В первом случае, когда переменная находится в числителе, мы получаем простую линейную функцию, которая элементарно считается. А в случае, если переменная стоит в знаменателе, то мы получаем более сложное выражение с сопутствующими выкладками, приведенными ранее.
На этом урок можно считать законченным, поэтому если вам что-то непонятно по производным частного или произведения, да и вообще, если у вас есть любые вопросы по этой теме, не стесняйтесь ― заходите на мой сайт, пишите, звоните, и я обязательно постараюсь вам помочь.
Сами по себе производные ― тема отнюдь не сложная, но очень объемная, и то, что мы сейчас изучаем, будет использоваться в будущем при решении более сложных задач. Именно поэтому все недопонимания, связанные с вычислениями производных частного или произведения, лучше выявить немедленно, прямо сейчас. Не когда они представляют собой огромный снежный ком недопонимания, а когда представляют собой маленький теннисный шарик, с которым легко разобраться.
Именно поэтому все недопонимания, связанные с вычислениями производных частного или произведения, лучше выявить немедленно, прямо сейчас. Не когда они представляют собой огромный снежный ком недопонимания, а когда представляют собой маленький теннисный шарик, с которым легко разобраться.
Правило отношения — формула, доказательство, определение, примеры
Правило отношения в исчислении — это метод нахождения производной или дифференцирования функции, заданной в виде отношения или деления двух дифференцируемых функций. Это означает, что мы можем применить правило отношения, когда нам нужно найти производную функции вида: f(x)/g(x), такую, что и f(x), и g(x) дифференцируемы, а g (x) ≠ 0. Факторное правило непосредственно следует правилу произведения и понятию пределов вывода при дифференцировании. Давайте разберемся в формуле для частного правила, ее доказательстве с использованием решенных примеров подробно в следующих разделах.
1. | Что такое частное правило? |
| 2. | Формула частного правила |
| 3. | Вывод формулы частного правила |
| 4. | Как применить правило отношения в дифференциации? |
| 5. | Часто задаваемые вопросы о правиле частных |
Что такое частное правило?
Правило отношения в математическом анализе — это метод, используемый для нахождения производной любой функции, заданной в виде частного, полученного в результате деления двух дифференцируемых функций. Правило частного в словах гласит, что производная частного равна отношению результата, полученного при вычитании числителя, умноженного на производную знаменателя из знаменателя, умноженного на производную числителя, на квадрат знаменателя. Это означает, что если нам дана функция вида: f(x) = u(x)/v(x), мы можем найти производную этой функции, используя производную частного правила как,
f'(x) = [u(x)/v(x)]’ = [v(x) × u'(x) — u(x) × v'(x)]/[v(x) ] 2
Формула частного правила
Мы можем вычислить производную или вычислить дифференцирование частного двух функций, используя формулу производной правила отношения. Формула производной частного правила задается следующим образом:
Формула производной частного правила задается следующим образом:
x)]/[v(x)] 2
где,
- f(x) = функция вида u(x)/v(x), для которой вычисляется производная.
- u(x) = дифференцируемая функция, составляющая числитель функции f(x).
- u'(x) = производная функции u(x).
- v(x) = дифференцируемая функция, которая составляет знаменатель данной функции f(x).
- v'(x) = производная функции v(x).
Вывод формулы частного правила
В предыдущем разделе мы узнали о формуле отношения для нахождения производных отношения двух дифференцируемых функций. Давайте посмотрим на доказательство формулы частного правила здесь. Существуют различные методы доказательства формулы правила отношения, заданной как
- Использование производных и предельных свойств
- Использование неявного дифференцирования
- Использование цепного правила
Доказательство формулы частного правила с использованием свойств производной и предела
Чтобы доказать формулу частного правила с использованием определения производной или пределов, пусть функция f(x) = u(x)/v(x).
⇒ f'(x) = \(\mathop {\lim }\limits_{h \to 0}\) [f(x + h) — f(x)]/h
= \(\ mathop { \lim }\limits_{h \to 0}\) \(\ frac {\ frac {u (x + h)} {v (x + h)} — \ frac {u (x)} {v (x) }}{ч}\)
= \(\ mathop {\lim }\limits_{h \to 0}\) \(\frac{u(x+h)v(x) — u(x)v(x+h)}{h \cdot v(x) \cdot v(x+h)}\)
= \( \left(\mathop {\lim }\limits_{h \to 0} \frac{u(x+h)v( x) — u (x) v (x + h)} {h} \ right) \ left (\ mathop {\ lim} \ limit_ {h \ to 0} \ frac {1} {v (x) \ cdot v (x+h)}\right)\)
= \(\left(\mathop {\lim }\limits_{h \to 0} \frac{u(x+h)v(x) — u(x) )v(x) + u(x)v(x) — u(x)v(x + h)}{h}\right) \) [1/v(x) 2 ]
= \( \left[\!\left(\ mathop {\lim}\limits_{h \to 0} \frac{u(x+h)v(x) — u(x)v(x)}{h}\right )\!\!\! -\!\!\left(\mathop {\lim }\limits_{h \to 0} \frac{u(x)v(x + h) — u(x)v(x )}{h}\вправо)\!\вправо]\) [1/v(x) 92}\)
Доказательство формулы частного правила с использованием неявного дифференцирования
Чтобы доказать формулу частного правила с помощью формулы неявного дифференцирования, возьмем дифференцируемую функцию f(x) = u(x)/v(x), поэтому u( х) = f(x)⋅v(x). 2}\) 92}\)
2}\) 92}\)
Как применить правило частного в дифференциации?
Чтобы найти производную функции вида f(x) = u(x)/v(x), обе функции u(x) и v(x) должны быть дифференцируемыми. Мы можем применить следующие данные шаги, чтобы найти вывод дифференцируемой функции f (x) = u (x) / v (x), используя правило отношения.
- Шаг 1: Запишите значения u(x) и v(x).
- Шаг 2: Найдите значения u'(x) и v'(x) и примените формулу правила отношения, заданную как: f'(x) = [u(x)/v(x)]’ = [и'(х) × v(х) — и(х) × v'(х)]/[v(х)] 2
Давайте посмотрим на следующий пример, приведенный ниже, чтобы лучше понять правило отношения.
Пример: Найдите f'(x) для следующей функции f(x), используя правило частных: f(x) = x 2 /(x+1).
Решение:
Здесь f(x) = x 2 /(x + 1)
u(x) = x 2
v(1) = (x0 + 03
⇒ и'(х) = 2х
⇒v'(x) = 1
⇒f'(x) = [v(x)u'(x) — u(x)v'(x)]/[v(x)] 2
⇒f'(x) = [(x+1)•2x — x 2 •1]/(x + 1) 2
⇒ f'(x) = (2x 2 + 2x — x 2 )/(x + 1) 2
⇒f'(x) = (x 2 + 2x)/(x + 1) 2
Ответ: производная от x 2 /(x + 1) равна (x 2 + 2x)/(x + 1) 2 . 2}\) 92}\).
2}\) 92}\).
Пример 3. Применение правила отношения для дифференцирования \(\frac{1-2x}{x}\).
Решение:
Пусть f(x) = (1-2x)/x
f'(x) = \(\frac{d}{dx}\) \(\frac{(1-2x)}{x}\) = [x \(\frac{d}{dx}\) ( 1-2x) — (1-2x) \(\frac{d}{dx}\) x]/x 2
f'(x) = [x(-2) — (1-2x) ( x)]/x 2 = (-2x — 1 + 2x)/x 2 = -1/x 2
Ответ: производная от \(\frac{(1-2x)}{ х}\) равно -1/х 2 .
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по правилу частных
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о частном правиле
Что такое частное правило дифференцирования в исчислении?
Факторное правило — это одно из производных правил, которое мы используем для нахождения производной функций вида P(x) = f(x)/g(x). Производная функции P(x) обозначается через P'(x). Если производная функции P(x) существует, мы говорим, что P(x) дифференцируема. Итак, дифференцируемые функции — это те функции, у которых существуют производные. Функция P(x) дифференцируема в точке x = a, если существует следующий предел.
Производная функции P(x) обозначается через P'(x). Если производная функции P(x) существует, мы говорим, что P(x) дифференцируема. Итак, дифференцируемые функции — это те функции, у которых существуют производные. Функция P(x) дифференцируема в точке x = a, если существует следующий предел.
\(P'(x) = \mathop {\lim }\limits_{h \to 0} \frac{P(a+h)-P(a)}{h}\)
Как найти производную, используя правило частных?
Производные от отношения двух дифференцируемых функций могут быть вычислены в математических вычислениях с использованием правила отношения. Нам нужно применить формулу правила отношения для дифференцирования функции f(x) = u(x)/v(x). Формула частного правила имеет вид 90 107.
f'(x) = [u(x)/v(x)]’ = [u'(x) × v(x) — u(x) × v'(x)]/[v(x)] 2
где f'(x), u'(x) и v'(x) — производные функций f(x), v(x) и u(x).
Что такое формула частного правила?
Формула производной частного правила — это правило дифференциального исчисления, которое мы используем для нахождения производной рациональной функции. Предположим, что две функции, u(x) и v(x), дифференцируемы, тогда можно применить правило отношения, чтобы найти (d/dx)[u(x)/v(x)] как,
Предположим, что две функции, u(x) и v(x), дифференцируемы, тогда можно применить правило отношения, чтобы найти (d/dx)[u(x)/v(x)] как,
f'(x) = [u(x)/v(x)]’ = [u'(x) × v(x) — u(x) × v'(x)]/[v(x)] 2
Как вывести формулу частного правила?
Формула правила отношения может быть получена с использованием различных методов. Они даны как, 92}\)
Как вывести правило частных, используя определение пределов и производных?
Доказательство правила отношения может быть дано с использованием определения и свойств пределов и производных. Для функции f(x) = u(x)/v(x) производная f'(x) может быть задана как
⇒ f'(x) = \(\ mathop {\lim }\limits_{ ч \к 0}\) [f(x + h) — f(x)]/h
= \ (\ mathop {\ lim} \ limit_ {h \ to 0} \) \ (\ frac {\ frac {u (x + h)} {v (x + h)} — \ frac {u (x) }{в(х)}}{ч}\)
= \(\ mathop {\lim}\limits_{h \to 0}\) \(\frac{u(x+h)v(x)\) — \(u(x)v(x+h)} {ч \cdot v(x) \cdot v(x+h)}\)
= \( \left(\ mathop {\lim}\limits_{h \to 0} \frac{u(x+h)v(x)\) — \(u(x)v(x+h)}{ h} \ right) \ left (\ mathop {\ lim } \ limit_ {h \ to 0} \ frac {1} {v (x) \ cdot v (x + h)} \ right) \)
= \(\left(\ mathop {\lim}\limits_{h \to 0} \frac{u(x+h)v(x) — u(x)v(x) + u(x)v(x) ) — u(x)v(x + h)}{h}\right) \) [1/v(x) 2 ]
= \(\ влево [\ влево (\ mathop {\ lim} \ limit_ {h \ to 0} \ frac {u (x + h) v (x) — u (x) v (x)} {h} \ вправо) \) — \(\ влево (\ mathop {\ lim} \ limit_ {h \ to 0} \ frac {u (x) v (x + h) — u (x) v (x)} {h} \право)\право]\) [1/v(x) 2 ]
= \(\left[v(x)\left(\mathop {\lim }\limits_{h \to 0} \frac{u(x+h) — u(x)}{h}\right)\) -\(u(x)\left(\mathop {\lim }\limits_{h \to 0} \frac{v(x + h) — v(x)}{h} \right)\right]\) [1/v(x) 2 ]
Каковы применения формулы производной частного правила? Приведите примеры.

Мы можем применить правило частных, чтобы найти дифференцирование функции вида u(x)/v(x). Например, для функции f(x) = sin x/x мы можем найти производную как f'(x) = [x \(\frac{d}{dx}\) sin x — sin x \( \frac{d}{dx}\) x]/x 2 , f'(x) = (x•cos x — sin x)/x 2 .
Как доказать правило частных с помощью неявного дифференцирования?
Мы можем использовать метод неявного дифференцирования, чтобы вывести правило отношения для дифференцируемой функции f(x) = u(x)/v(x), поэтому u(x) = f(x)⋅v(x). Используя правило произведения, мы имеем u'(x) = f'(x)⋅v(x) + f(x)v'(x). Решая для f'(x), получаем
f'(x) = \(\frac{u'(x) — f(x)v'(x)}{v(x)}\)
Подставьте f(x),
⇒ f'(x) = \(\frac{u'(x) — \frac{u(x)}{v(x)}v'(x)}{v(x) )}\) 92}\).
Скачать БЕСПЛАТНЫЕ учебные материалы
Расчетный лист
Правило частного — DerivativeIt
В исчислении правило частного используется для нахождения производной функции, которая может быть выражена как отношение двух дифференцируемых функций. Другими словами, факторное правило позволяет нам дифференцировать функции, имеющие дробную форму.
Другими словами, факторное правило позволяет нам дифференцировать функции, имеющие дробную форму.
Допустим, у нас есть две функции:
f(x) = x 2 и
g(x) = x
Теперь допустим, что мы хотим найти производную от
Один из подходов к нахождению производной состоит в том, чтобы упростить функцию, а затем продифференцировать ее.
Итак, производная дроби f(x)/g(x) равна всего 1.
Теперь ради интереса вычислим f'(x)/g'(x) (дифференцируя числитель, а затем знаменатель)
Итак, мы видим, что (f(x)/g(x))’ = 1, а это не равно (f'(x)/g'(x)) = 2x
Производная частного не равно частному производных.
Чтобы дифференцировать частное, нельзя просто взять производную от числителя и разделить ее на производную от знаменателя. Вместо этого нам нужно использовать правило отношения , чтобы найти производную от частного (аналогично тому, как правило произведения необходимо использовать для нахождения производной от произведения).
Формула правила отношения для дифференцирования
Если две функции f(x) и g(x) дифференцируемы (т. е. существуют производные от f(x) и g(x)), то их частное (f(x)/ g(x)) дифференцируема, и производная находится следующим образом:
Формула правила частного в словах
Правило частного гласит, что производная частного равна произведению знаменателя на производную от числителя минус числитель, умноженному на производную от знаменателя, все это делится на квадрат знаменатель.
Две хитрости для запоминания правила отношения
Подобно правилу произведения, вам нужно найти производную от f(x), а затем умножить ее на g(x), а затем найти производную от g(x) и умножить ее. через f(x). Однако, поскольку члены вычитаются, порядок имеет значение, а также необходимо выполнить деление.
Это усложняет запоминание правила отношения по сравнению с правилом произведения.
Вот два метода, которые могут помочь вам запомнить правило отношения:
1. Вы всегда начинаете с нижней функции (знаменателя) и заканчиваете нижней функцией в квадрате.
Вы всегда начинаете с нижней функции (знаменателя) и заканчиваете нижней функцией в квадрате.
И если это не сработает…
2. Вот мелодия, которую вы можете использовать:
Lo d hi минус hi d low, по всему квадрату того, что ниже.
Здесь lo относится к знаменателю, hi относится к числителю, а d относится к производной от. Это действительно глупо, но именно поэтому это работает!
Когда использовать правило отношения
В исчислении правило отношения может применяться, когда функция, которую вы хотите дифференцировать, состоит из частного (или дроби), а числитель и знаменатель частного являются дифференцируемыми функциями сами по себе .
Например, функция f(x) = x/x 2 можно дифференцировать, используя правило отношения для производных, потому что:
- Числитель (x) дифференцируем – его производная равна 1
- Знаменатель (x 2 ) дифференцируем – его производная равна x
(Конечно вы также можете сначала упростить функцию до 1/x, а затем продифференцировать ее и получить тот же результат)
Примеры использования правила отношения
Лучший способ увидеть, как работает правило отношения, — это рассмотреть несколько примеров.
Используя правило отношения
Для первого примера найдем производную от
Назовем числитель f(x), так что f(x) = x 2 + 1
Назовем знаменатель g(x) , поэтому g(x) = x 3
Это означает, что:
f'(x) = 2x
g'(x) = 3x 2
Теперь мы можем применить правило частных, чтобы найти производную f(x)/g(x). Формула для правила отношения:
Теперь мы можем подставить f(x), f'(x), g(x) и g'(x) в формулу
А затем мы просто упрощаем использование факторизации и правил возведения в степень, чтобы найти окончательный ответ
Использование правила отношения с тригонометрическими функциями
В качестве другого примера, мы можем использовать правило отношения для нахождения производной tan(x)
Сначала напомним, что tan(x) можно выразить как sin(x), деленное на cos(x)
Назовем числитель f(x), так что f(x) = sin(x)
Назовем знаменатель g( x), поэтому g(x) = cos(x)
Это означает, что:
f'(x) = cos(x)
g'(x) = -sin(x)
Теперь мы можем применить правило частных, чтобы найти производную от f(x)/g(x). Формула для частного правила:
Формула для частного правила:
Теперь мы можем подставить f(x), f'(x), g(x) и g'(x) в формулу:
Тогда упростим запоминание тождества триггера sin 2 (x) + cos 2 (x) = 1 и учитывая, что 1/cos(x) равно sec(x).
Используя правило частных, производная tan(x) равна sec 2 (x)
Доказательство правила частных
Есть несколько способов доказать правило частных. Здесь мы рассмотрим доказательство частного правила, используя:
- Первые принципы – определение производной и свойства пределов.
- Неявное дифференцирование и правило произведения.
Определение производной F(x) равно
Затем мы помещаем F(x+h) и F(x) в
Это можно переписать, найдя наименьший общий знаменатель в числителе (g(x+h).g(x)) и взяв 1/ ч вне.
Следующий шаг нужен для облегчения жизни чуть позже. Что мы делаем, так это добавляем 0 к числителю, что совсем не меняет значение. Но вместо того, чтобы добавлять прямой 0, мы добавляем его в виде -f(x)g(x) + f(x)g(x)
.
 умножают дроби.
умножают дроби.Далее мы используем одно из свойств пределов, которое гласит, что предел произведения двух функций равен произведению их пределов. Затем мы также используем тот факт, что предел, когда h приближается к нулю для g(x+h), равен просто g(x)
. обычный -f(x) из второй части.
Другим свойством пределов является то, что предел суммы равен сумме пределов. Таким образом, мы можем взять предел каждой дроби отдельно.
И тогда мы можем взять предел каждой части произведения
Теперь вы можете заметить, что два из приведенных выше пределов выглядят знакомыми – это точные определения для f'(x) и g'(x).
Наконец, при приближении h к 0 предел g(x) и f(x) остается g(x) и f(x) (поскольку они не зависят от h). А дальше остается все переписать в простейшем виде. И вот она у нас есть — формула для частного правила.Доказательство частного правила с использованием неявного дифференцирования и правила произведения
Пусть y = f(x)/g(x), тогда мы хотим найти y’.

Сначала давайте изменим уравнение:
Теперь мы можем взять производную в левой и правой частях уравнения (используя правило произведения в правой части)
Затем подставим y = f(x)/ g(x) в приведенное выше уравнение
В конечном счете мы хотим найти производную от y (y’), поэтому теперь мы находим y’ и находим формулу для правила отношения.
Доказательство частного правила с использованием правил произведения и цепочки
Пусть F(x) = f(x)/g(x).
Мы можем переписать это частное как произведение
Мы можем найти F'(x), используя правило произведения
Чтобы найти (g(x) -1 )’, мы можем применить цепное правило. Цепное правило гласит, что мы сначала берем производную от g(x) -1 через g(x) (= (-1)g(x) -2 ), а затем умножаем ее на производную от g( x) через x (= g'(x)).
Затем мы приводим отрицательные показатели к знаменателю, а затем упрощаем, находя наибольший общий знаменатель.
 У нас осталась формула правила отношения.
У нас осталась формула правила отношения.Доказательство частного правила с использованием ln и цепного правила
Пусть y = f(x)/g(x)
Для начала возьмем натуральный логарифм (ln) с обеих сторон
Затем применим свойства бревен к разделить частное правой части на разность бревен
Теперь возьмем производную с обеих сторон. Напомним, что производная от ln(x) по x равна 1/x. Аналогичным образом производная ln(y) по y равна 1/y, производная ln(f(x)) по f(x) равна 1/f(x), а производная ln (g(x)) относительно g(x) равно 1/g(x).
Чтобы найти производные каждого члена по x, мы можем применить цепное правило, сначала продифференцировав по внутренней функции ln, а затем умножив ее на производную от внутренней функции.
Наконец, изолируйте y’, подставьте y = f(x)/g(x) и затем упростите решение для y’
Правило частных в терминах u и v Правило иногда легче выразить, если использовать u и v для представления числителя и знаменателя соответственно.
 Это может быть более компактно, чем использование обозначений функций f(x) и g(x).
Это может быть более компактно, чем использование обозначений функций f(x) и g(x).Используя переменную u в качестве числителя и v в качестве знаменателя, частное правило для нахождения производной функции u/v может быть выражено как:
Урок Видео: правило частного Правило
В этом видео мы научимся найти производную функции по правилу частных. Мы будем рассматривать различные примеры того, как это можно использовать.
Предположим, что функция 𝑦 равна минус три 𝑥 в квадрате минус два 𝑥 плюс 17 сверх квадратного корня из 𝑥.
Если бы мы хотели найти производную этой функции, существуют различные методы, которые мы могли бы использовать. Мы могли бы разделить числитель на знаменатель и просто продифференцируем полученную функцию. В качестве альтернативы мы могли бы написать дробь как произведение и найти производную по правилу произведения. Есть и альтернативный метод который мы можем использовать, чтобы найти эту производную.
 И это не требует упрощения или
переписывание уравнения. Мы называем это частным правилом. Вывод частного правила
немного длинноват для этого видео. Поэтому мы не будем это освещать
здесь.
И это не требует упрощения или
переписывание уравнения. Мы называем это частным правилом. Вывод частного правила
немного длинноват для этого видео. Поэтому мы не будем это освещать
здесь.Правило частных говорит, что дано две дифференцируемые функции, 𝑢 от 𝑥 и 𝑣 от 𝑥, производная их частное задается 𝑑 на d𝑥 из 𝑢 из 𝑥 над 𝑣 из 𝑥 равно 𝑣 из 𝑥 раз 𝑑 на d𝑥 из 𝑢 из 𝑥 минус 𝑢 из 𝑥 раз 𝑑 на d𝑥 из 𝑣 из 𝑥 по всему 𝑣 из 𝑥 в квадрате. Мы можем написать это намного больше кратко в простых обозначениях. Это дает нам 𝑢 над 𝑣 простым числом. равно 𝑣𝑢 простому минус 𝑢𝑣 простому числу по всему 𝑣 в квадрате.
Я нахожу простой способ запомнить Частное правило с рифмой. Рифма идет LO 𝑑 HI минус HI 𝑑 LO над квадратом того, что ниже. Где HI — числитель рациональная функция, которую мы дифференцируем. И LO является знаменателем этого рациональная функция.
 И 𝑑s, которые находятся внутри
рифмовать показать, где мы должны различать. Таким образом, 𝑑 HI будет дифференциалом
числителя нашей функции. А 𝑑 LO — дифференциал
знаменатель нашей функции. Вам может быть легче запомнить
через другое средство. Но не стесняйтесь использовать этот метод
слишком.
И 𝑑s, которые находятся внутри
рифмовать показать, где мы должны различать. Таким образом, 𝑑 HI будет дифференциалом
числителя нашей функции. А 𝑑 LO — дифференциал
знаменатель нашей функции. Вам может быть легче запомнить
через другое средство. Но не стесняйтесь использовать этот метод
слишком.Теперь мы готовы взглянуть на некоторые Примеры.
Найдите первую производную от 𝑦 равно 8𝑥 плюс пять больше трех 𝑥 плюс 22.
Здесь мы видим, что наша функция 𝑦 — рациональная функция. Таким образом, мы можем найти его производную по формуле с помощью частного правила. Факторное правило говорит нам, что если мы дифференцируем частное двух функций, поэтому 𝑢 по 𝑣 по отношению к 𝑥. Тогда это равно 𝑣, умноженному на дифференциал 𝑢 относительно 𝑥 минус 𝑢, умноженный на дифференциал 𝑣 относительно 𝑥 по всему 𝑣 в квадрате.
 Для того, чтобы найти первый
производная от 𝑦, начнем с обозначения 𝑢 и 𝑣 из нашего уравнения. 𝑢 будет равно числителю
функции, поэтому восемь 𝑥 плюс пять. И 𝑣 будет равно
знаменатель функции, так что это три 𝑥 плюс 22,
Для того, чтобы найти первый
производная от 𝑦, начнем с обозначения 𝑢 и 𝑣 из нашего уравнения. 𝑢 будет равно числителю
функции, поэтому восемь 𝑥 плюс пять. И 𝑣 будет равно
знаменатель функции, так что это три 𝑥 плюс 22,Далее мы должны найти d на d𝑥 из 𝑢 и d на d𝑥 из 𝑣, или d𝑢 на d𝑥 и d𝑣 на d𝑥. 𝑢 и 𝑣 оба являются полиномами. Таким образом, мы можем просто различать их срок за сроком. Написание 𝑢 в терминах степеней 𝑥, можно сказать, что оно равно восьми 𝑥 в степени один плюс пять 𝑥 в сила нуля. Для дифференциации мы просто умножьте на мощность и уменьшите мощность на единицу. В первый раз умножаем на мощность, так что это один, и уменьшить мощность на единицу, до нуля. Оставив нас с одним разом восемь 𝑥 в нулевой степени. Для второго члена умножаем на мощность, так что это ноль, и уменьшить мощность на единицу, до отрицательной единицы.
 Давая нам ноль, умноженный на пять
𝑥 в минус.
Давая нам ноль, умноженный на пять
𝑥 в минус.В первом члене 𝑥 в степени из нуля — это только один. Таким образом, получается восемь. Во втором семестре мы умножение на ноль. Так что этот член становится равным нулю. Следовательно, мы находим, что d𝑢 по d𝑥 равно восьми. Мы можем использовать аналогичный метод, чтобы найти д𝑣 от д𝑥. И мы находим, что он равен три. Теперь, когда мы нашли d𝑢 по d𝑥 и d𝑣 на d𝑥, мы готовы использовать правило частных. Мы находим, что d𝑦 по d𝑥 равно 𝑣, то есть три 𝑥 плюс 22, умноженные на d𝑢 на d𝑥, так что восемь минус 𝑢, так что это восемь 𝑥 плюс пять, умноженное на d𝑣 на d𝑥, так что это три. И это все 𝑣 в квадрате, так что это три 𝑥 плюс 22 в квадрате.
Далее мы можем расширить скобки. А затем упростить, чтобы найти, что наш решение состоит в том, что первая производная от 𝑦 равна 161 по трем 𝑥 плюс 22 все в квадрате.

Теперь рассмотрим немного более сложный пример.
Найдите первую производную функция 𝑦 равна четырем 𝑥 в квадрате плюс пять 𝑥 плюс пять на четыре 𝑥 в квадрате минус два 𝑥 плюс три.
Мы видим, что наша функция является рациональная функция. Следовательно, мы можем использовать частное Правило для нахождения производной. Факторное правило говорит нам, что 𝑢 над 𝑣 тире равно 𝑣𝑢 тире минус 𝑢𝑣 тире по всему 𝑣 в квадрате. Где 𝑢 — числитель нашего функция, а 𝑣 — знаменатель. В нашем случае 𝑢 равно четырем 𝑥 в квадрате плюс пять 𝑥 плюс пять. А 𝑣 равно четырем 𝑥 в квадрате. минус два 𝑥 плюс три. Теперь мы должны найти 𝑢 простое число и 𝑣 основной. Мы делаем это, дифференцируя 𝑢 и 𝑣 относительно 𝑥.
Так как 𝑢 и 𝑣 полиномиальны функций, мы можем найти их производные, взяв каждый член и умножив термин в силу 𝑥.
 И тогда, уменьшая мощность
𝑥 по одному. И делая это, мы находим, что 𝑢
простое равно восьми 𝑥 плюс пять. А 𝑣 простое равно восьми 𝑥
минус два. Подставив их в наш
формулы, находим, что первая производная от 𝑦 или 𝑦 простого числа равна 𝑣
умножить на 𝑢 простое минус 𝑢 умножить на 𝑣 простое число по всему 𝑣 в квадрате. Теперь результат здесь выглядит довольно
устрашающий. Тем не менее, мы все еще можем расширить
скобки, а затем упростить. Вот что мы получаем после
раскрывая скобки в числителе.
И тогда, уменьшая мощность
𝑥 по одному. И делая это, мы находим, что 𝑢
простое равно восьми 𝑥 плюс пять. А 𝑣 простое равно восьми 𝑥
минус два. Подставив их в наш
формулы, находим, что первая производная от 𝑦 или 𝑦 простого числа равна 𝑣
умножить на 𝑢 простое минус 𝑢 умножить на 𝑣 простое число по всему 𝑣 в квадрате. Теперь результат здесь выглядит довольно
устрашающий. Тем не менее, мы все еще можем расширить
скобки, а затем упростить. Вот что мы получаем после
раскрывая скобки в числителе.Наш последний шаг — упростить числитель. Теперь мы достигли нашего решение. что это за первая производная 𝑦 или 𝑦 простых чисел равно минусу 28𝑥 в квадрате минус 16𝑥 плюс 25 всех четырех 𝑥 в квадрате минус два 𝑥 плюс три все в квадрате.
Теперь давайте взглянем на немного другой тип вопроса.

Предположим, что 𝑓 из 𝑥 равно 𝑥 в квадрате плюс 𝑎𝑥 плюс 𝑏 по всему 𝑥 в квадрате минус семь 𝑥 плюс четыре. Учитывая, что 𝑓 нуля равно единица и 𝑓 простые числа равны четырем, найдите 𝑎 и 𝑏.
Наш первый шаг в этом вопросе может нужно заменить 𝑥 равным нулю в 𝑓 из 𝑥. Поскольку нам дано, что 𝑓 нуля равен единице. Получаем, что 𝑓 нуля равно до нуля в квадрате плюс 𝑎 умножить на ноль плюс 𝑏 всего на ноль в квадрате минус семь раз ноль плюс четыре. Теперь все эти термины пойдут на ноль, кроме 𝑏 и четыре. У нас осталось 𝑓 нуля равно до 𝑏 более четырех. Далее воспользуемся тем, что вопрос сказал нам, что 𝑓 нуля равно единице. Итак, мы можем установить это равным один. Отсюда мы находим, что 𝑏 равно до четырех. Далее мы можем использовать тот факт, что 𝑓 простое число нуля равно четырем. Однако, прежде всего, мы должны найти 𝑓 премьера 𝑥.
 Чтобы сделать это, нам нужно
дифференцировать 𝑓. Поскольку 𝑓 — рациональная функция, мы
можно использовать правило отношения, чтобы найти его производную.
Чтобы сделать это, нам нужно
дифференцировать 𝑓. Поскольку 𝑓 — рациональная функция, мы
можно использовать правило отношения, чтобы найти его производную.Факторное правило говорит нам, что 𝑢 над 𝑣 простым числом равно 𝑣 умноженному на 𝑢 простое минус 𝑢 умноженное на 𝑣 простое на всем протяжении 𝑣 в квадрате. Установка нашей функции 𝑓 of 𝑥 равной к 𝑢 над 𝑣, мы получаем, что 𝑢 равно 𝑥 в квадрате плюс 𝑎𝑥 плюс 𝑏. А 𝑣 равно 𝑥 в квадрате минус семь 𝑥 плюс четыре. Мы можем найти 𝑢 простых и 𝑣 простых путем дифференциации этих двух функций. Давая нам, что 𝑢 простое число равно два 𝑥 плюс 𝑎 и 𝑣 простое число равно двум 𝑥 минус семь. Теперь мы можем заменить их на факторное правило. Получаем, что 𝑓 простое число 𝑥 есть равно 𝑥 в квадрате минус семь 𝑥 плюс четыре умножить на два 𝑥 плюс 𝑎 минус 𝑥 в квадрате плюс 𝑎𝑥 плюс 𝑏 умножить на два 𝑥 минус семь всего 𝑥 в квадрате минус семь 𝑥 плюс четыре в квадрате.

Теперь мы можем упростить 𝑓 простое число 𝑥 на данный момент. Однако мы собираемся быть подстановка в 𝑥 равна нулю. Таким образом, многие из этих терминов просто исчезнуть. Давайте просто заменим 𝑥 равно ноль здесь. Получаем это. Однако многие термины будут равны нулю, что оставляет нам четыре 𝑎 плюс семь 𝑏 на всех 16. Теперь мы обнаружили, что 𝑏 равно до четырех ранее. Итак, мы можем заменить это на, что дает нам четыре 𝑎 плюс 28 всего 16.
Так как вопрос сказал нам, что 𝑓 простое число равно четырем, мы можем установить это равным четырем. Затем мы просто переставляем это в порядок решения для 𝑎. Теперь мы получаем наше решение, что 𝑎 равно девяти. Теперь мы нашли значения обоих 𝑎 и 𝑏, что завершает решение этого вопроса.
В следующем примере мы будем глядя на немного другой тип вопроса.

Пусть 𝑔 из 𝑥 равно 𝑓 из 𝑥 больше минус четыре ℎ от 𝑥 минус пять. Учитывая, что 𝑓 отрицательных двух равно отрицательной единице, 𝑓 простое число от отрицательной двойки равно отрицательной восьмерке, ℎ отрицательная двойка равна отрицательной двойке, а ℎ штрих от отрицательной двойки равен пяти, найти 𝑔 простое число отрицательных двух.
В этом вопросе нас просят найти 𝑔 простое число отрицательных двух. Итак, начнем с дифференциации 𝑔 из 𝑥. 𝑔 от 𝑥 — рациональная функция, поэтому нам нужно будет использовать частное правило. Факторное правило говорит нам, что 𝑢 над 𝑣 простым числом равно 𝑣𝑢 простым минус 𝑢𝑣 простым числом во всем 𝑣 в квадрате. Установка 𝑔 из 𝑥 равным 𝑢 более 𝑣, мы видим, что 𝑢 равно 𝑓 из 𝑥. А 𝑣 равно минус четырем ℎ 𝑥 минус пять. 𝑢 простое число будет равно 𝑓 из 𝑥 основной. Теперь штрих просто представляет дифференцирование по 𝑥.
 Следовательно, 𝑓 из 𝑥 простых чисел равно
идентично 𝑓 простому числу 𝑥. Далее нам нужно найти 𝑣 простое число. Итак, минус четыре ℎ от 𝑥
минус пять простых.
Следовательно, 𝑓 из 𝑥 простых чисел равно
идентично 𝑓 простому числу 𝑥. Далее нам нужно найти 𝑣 простое число. Итак, минус четыре ℎ от 𝑥
минус пять простых.Опять же, поскольку простое число просто представляет дифференцирование по 𝑥, мы можем применить нормальное дифференцирование правила здесь. И так, дифференцируя постоянный член минус пять приведет к нулю. Таким образом, мы можем сказать, что это равно минус четыре ℎ из 𝑥 простых чисел. Теперь, поскольку наша функция ℎ от 𝑥 равна умножается на постоянную отрицательную четверку. Мы можем использовать наши производные правила и из производной вычесть минус четыре. Давая нам отрицательные четыре умноженные на ℎ из 𝑥 простых чисел.
И теперь мы можем применить то же самое логика, как мы делали для 𝑓 из 𝑥 простых чисел. И мы можем сказать, что 𝑣 простое число равно отрицательному четырем ℎ простому числу 𝑥.
 Теперь мы можем заменить в
частное правило, чтобы найти 𝑔 простое число 𝑥. Теперь, когда мы нашли 𝑔 простое число
𝑥, мы можем заменить в 𝑥 равно минус два. Теперь мы составили уравнение в
термины 𝑓 отрицательной двойки, 𝑓 штрих отрицательной двойки, ℎ отрицательной двойки и ℎ
простое число отрицательных двух. Все это нам дано
значение в вопросе. Итак, мы можем заменить в
эти значения здесь.
Теперь мы можем заменить в
частное правило, чтобы найти 𝑔 простое число 𝑥. Теперь, когда мы нашли 𝑔 простое число
𝑥, мы можем заменить в 𝑥 равно минус два. Теперь мы составили уравнение в
термины 𝑓 отрицательной двойки, 𝑓 штрих отрицательной двойки, ℎ отрицательной двойки и ℎ
простое число отрицательных двух. Все это нам дано
значение в вопросе. Итак, мы можем заменить в
эти значения здесь.Теперь наш последний шаг в поиске 𝑔 первое число отрицательных двух должно упростить это. Раскрывая скобки, получаем минус 24 минус 20 всего девять. Это дает нам решение, которое 𝑔 простое число от минус двух равно минус 44 больше девяти.
Далее мы посмотрим, как мы можем дифференцировать функцию, состоящую из двух рациональных выражений.
Если 𝑦 равно 𝑥 плюс пять больше 𝑥 минус пять минус 𝑥 минус пять сверх 𝑥 плюс пять, найти d𝑦 по d𝑥.

Наша функция 𝑦 состоит из двух рациональные выражения, 𝑥 плюс пять на 𝑥 минус пять и 𝑥 минус пять на 𝑥 плюс пять. И мы могли бы найти d𝑦 по d𝑥 по используя правило отношения для этих двух рациональных выражений. Однако для этого потребуется использовать частное правило дважды. Мы можем сделать нашу работу немного проще, если объединить два рациональных выражения в одно. Получаем, что 𝑦 равно 𝑥 плюс пять в квадрате минус 𝑥 минус пять в квадрате всего 𝑥 минус пять раз 𝑥 плюс пять. Мы можем раскрыть скобки и тогда упростить, чтобы получить, что 𝑦 равно 20𝑥 на 𝑥 в квадрате минус 25.
Теперь наша функция состоит из только одно рациональное выражение. Мы готовы использовать частное Правило дифференцирования этой функции. Факторное правило говорит нам, что 𝑢 над 𝑣 простым числом равно 𝑣𝑢 простым минус 𝑢𝑣 простым числом над 𝑣 в квадрате.
 Установив 𝑦 равным 𝑢 над 𝑣, мы
получаем, что 𝑢 равно 20𝑥, а 𝑣 равно 𝑥 в квадрате минус 25. Затем мы можем найти 𝑢 простое число и 𝑣
простое, что дает нам, что 𝑢 простое равно 20, а 𝑣 простое равно двум
𝑥.
Установив 𝑦 равным 𝑢 над 𝑣, мы
получаем, что 𝑢 равно 20𝑥, а 𝑣 равно 𝑥 в квадрате минус 25. Затем мы можем найти 𝑢 простое число и 𝑣
простое, что дает нам, что 𝑢 простое равно 20, а 𝑣 простое равно двум
𝑥.Теперь мы можем подставить их в правило частного, чтобы найти, что d𝑦 на d𝑥 равно 𝑥 в квадрате минус 25 умножить на 20 минус 20𝑥 раз на два 𝑥 по всему 𝑥 в квадрате минус 25 в квадрате. Мы упрощаем это, чтобы получить, что d𝑦 на d𝑥 равно минусу 20𝑥 минус 500 по всему 𝑥 в квадрате минус 25 в квадрате.
В нашем последнем примере мы увидим как вычислить производную рациональной функции в точке.
Вычислите 𝑓 простое число из трех, где 𝑓 из 𝑥 равно 𝑥 на 𝑥 плюс два минус 𝑥 минус три на 𝑥 минус два.
Теперь наша функция — разница двух рациональных выражений. Мы можем начать с объединения двух рациональные выражения в одно.
 Получаем, что 𝑓 из 𝑥 равно
минус 𝑥 плюс шесть по всему 𝑥 в квадрате минус четыре. И мы написали 𝑓 как
рациональная функция. И мы готовы использовать частное
правило, которое говорит нам, что 𝑢 над 𝑣 простым числом равно 𝑣𝑢 простым минус 𝑢𝑣 простым числом
во всем 𝑣 в квадрате. Установка 𝑓 из 𝑥 равным 𝑢 более
𝑣, получаем, что 𝑢 равно отрицательному 𝑥 плюс шесть, а 𝑣 равно 𝑥
в квадрате минус четыре. Затем мы находим, что 𝑢 простое число равно
на отрицательную единицу, а 𝑣 простое число равно двум 𝑥.
Получаем, что 𝑓 из 𝑥 равно
минус 𝑥 плюс шесть по всему 𝑥 в квадрате минус четыре. И мы написали 𝑓 как
рациональная функция. И мы готовы использовать частное
правило, которое говорит нам, что 𝑢 над 𝑣 простым числом равно 𝑣𝑢 простым минус 𝑢𝑣 простым числом
во всем 𝑣 в квадрате. Установка 𝑓 из 𝑥 равным 𝑢 более
𝑣, получаем, что 𝑢 равно отрицательному 𝑥 плюс шесть, а 𝑣 равно 𝑥
в квадрате минус четыре. Затем мы находим, что 𝑢 простое число равно
на отрицательную единицу, а 𝑣 простое число равно двум 𝑥.Замена 𝑢, 𝑣, 𝑢 простых и 𝑣 вернуться к частному правилу. Мы находим, что 𝑓 простое число 𝑥 равно равно 𝑥 в квадрате минус четыре, умноженное на минус один минус минус 𝑥 плюс шесть умножить на два 𝑥 по всему 𝑥 в квадрате минус четыре в квадрате. Чтобы найти 𝑓 простое число из трех, мы просто подставляем 𝑥 равно трем в 𝑓 простое число 𝑥.
 Получаем, что 𝑓 тире из трех равно
равно трем в квадрате минус четыре умножить на минус один минус минус три
плюс шесть умножить на два три три в квадрате минус четыре
в квадрате. Что упрощает до минус пять
минус 18 на 25. Это дает нам решение, которое 𝑓
простое число из трех равно минусу 23 больше 25.
Получаем, что 𝑓 тире из трех равно
равно трем в квадрате минус четыре умножить на минус один минус минус три
плюс шесть умножить на два три три в квадрате минус четыре
в квадрате. Что упрощает до минус пять
минус 18 на 25. Это дает нам решение, которое 𝑓
простое число из трех равно минусу 23 больше 25.Итак, мы видели множество Примеры частного правила. Остановимся на некоторых ключевых моментах видео. Чтобы найти производную от отношение двух дифференцируемых функций, 𝑢 от 𝑥 и 𝑣 от 𝑥, мы можем использовать Правило частных, которое гласит, что d на d𝑥 из 𝑢 из 𝑥 над 𝑣 из 𝑥 равно 𝑣 из 𝑥 раз d на d𝑥 из 𝑢 из 𝑥 минус 𝑢 из 𝑥 раз d на d𝑥 из 𝑣 из 𝑥 по всему 𝑣 𝑥 в квадрате. Об этом чаще всего пишут кратко, используя простые обозначения, следующим образом. 𝑢 над 𝑣 простым числом равно 𝑣𝑢 простое минус 𝑢𝑣 простое число по всему 𝑣 в квадрате.



 умножают дроби.
умножают дроби.
 У нас осталась формула правила отношения.
У нас осталась формула правила отношения.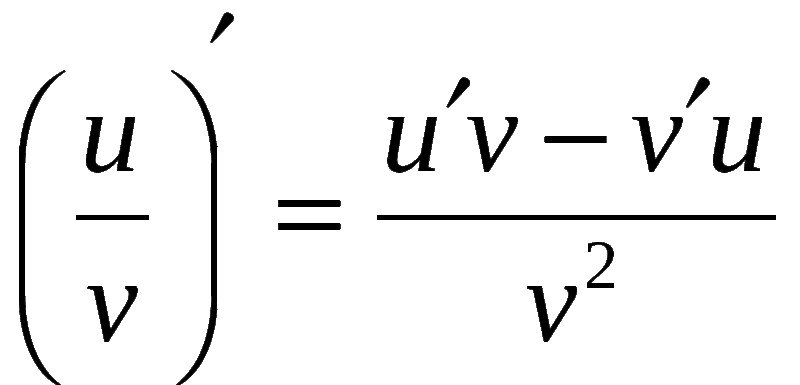 Это может быть более компактно, чем использование обозначений функций f(x) и g(x).
Это может быть более компактно, чем использование обозначений функций f(x) и g(x). И это не требует упрощения или
переписывание уравнения. Мы называем это частным правилом. Вывод частного правила
немного длинноват для этого видео. Поэтому мы не будем это освещать
здесь.
И это не требует упрощения или
переписывание уравнения. Мы называем это частным правилом. Вывод частного правила
немного длинноват для этого видео. Поэтому мы не будем это освещать
здесь. И 𝑑s, которые находятся внутри
рифмовать показать, где мы должны различать. Таким образом, 𝑑 HI будет дифференциалом
числителя нашей функции. А 𝑑 LO — дифференциал
знаменатель нашей функции. Вам может быть легче запомнить
через другое средство. Но не стесняйтесь использовать этот метод
слишком.
И 𝑑s, которые находятся внутри
рифмовать показать, где мы должны различать. Таким образом, 𝑑 HI будет дифференциалом
числителя нашей функции. А 𝑑 LO — дифференциал
знаменатель нашей функции. Вам может быть легче запомнить
через другое средство. Но не стесняйтесь использовать этот метод
слишком. Для того, чтобы найти первый
производная от 𝑦, начнем с обозначения 𝑢 и 𝑣 из нашего уравнения. 𝑢 будет равно числителю
функции, поэтому восемь 𝑥 плюс пять. И 𝑣 будет равно
знаменатель функции, так что это три 𝑥 плюс 22,
Для того, чтобы найти первый
производная от 𝑦, начнем с обозначения 𝑢 и 𝑣 из нашего уравнения. 𝑢 будет равно числителю
функции, поэтому восемь 𝑥 плюс пять. И 𝑣 будет равно
знаменатель функции, так что это три 𝑥 плюс 22, Давая нам ноль, умноженный на пять
𝑥 в минус.
Давая нам ноль, умноженный на пять
𝑥 в минус.
 И тогда, уменьшая мощность
𝑥 по одному. И делая это, мы находим, что 𝑢
простое равно восьми 𝑥 плюс пять. А 𝑣 простое равно восьми 𝑥
минус два. Подставив их в наш
формулы, находим, что первая производная от 𝑦 или 𝑦 простого числа равна 𝑣
умножить на 𝑢 простое минус 𝑢 умножить на 𝑣 простое число по всему 𝑣 в квадрате. Теперь результат здесь выглядит довольно
устрашающий. Тем не менее, мы все еще можем расширить
скобки, а затем упростить. Вот что мы получаем после
раскрывая скобки в числителе.
И тогда, уменьшая мощность
𝑥 по одному. И делая это, мы находим, что 𝑢
простое равно восьми 𝑥 плюс пять. А 𝑣 простое равно восьми 𝑥
минус два. Подставив их в наш
формулы, находим, что первая производная от 𝑦 или 𝑦 простого числа равна 𝑣
умножить на 𝑢 простое минус 𝑢 умножить на 𝑣 простое число по всему 𝑣 в квадрате. Теперь результат здесь выглядит довольно
устрашающий. Тем не менее, мы все еще можем расширить
скобки, а затем упростить. Вот что мы получаем после
раскрывая скобки в числителе.
 Чтобы сделать это, нам нужно
дифференцировать 𝑓. Поскольку 𝑓 — рациональная функция, мы
можно использовать правило отношения, чтобы найти его производную.
Чтобы сделать это, нам нужно
дифференцировать 𝑓. Поскольку 𝑓 — рациональная функция, мы
можно использовать правило отношения, чтобы найти его производную.

 Следовательно, 𝑓 из 𝑥 простых чисел равно
идентично 𝑓 простому числу 𝑥. Далее нам нужно найти 𝑣 простое число. Итак, минус четыре ℎ от 𝑥
минус пять простых.
Следовательно, 𝑓 из 𝑥 простых чисел равно
идентично 𝑓 простому числу 𝑥. Далее нам нужно найти 𝑣 простое число. Итак, минус четыре ℎ от 𝑥
минус пять простых. Теперь мы можем заменить в
частное правило, чтобы найти 𝑔 простое число 𝑥. Теперь, когда мы нашли 𝑔 простое число
𝑥, мы можем заменить в 𝑥 равно минус два. Теперь мы составили уравнение в
термины 𝑓 отрицательной двойки, 𝑓 штрих отрицательной двойки, ℎ отрицательной двойки и ℎ
простое число отрицательных двух. Все это нам дано
значение в вопросе. Итак, мы можем заменить в
эти значения здесь.
Теперь мы можем заменить в
частное правило, чтобы найти 𝑔 простое число 𝑥. Теперь, когда мы нашли 𝑔 простое число
𝑥, мы можем заменить в 𝑥 равно минус два. Теперь мы составили уравнение в
термины 𝑓 отрицательной двойки, 𝑓 штрих отрицательной двойки, ℎ отрицательной двойки и ℎ
простое число отрицательных двух. Все это нам дано
значение в вопросе. Итак, мы можем заменить в
эти значения здесь.
 Установив 𝑦 равным 𝑢 над 𝑣, мы
получаем, что 𝑢 равно 20𝑥, а 𝑣 равно 𝑥 в квадрате минус 25. Затем мы можем найти 𝑢 простое число и 𝑣
простое, что дает нам, что 𝑢 простое равно 20, а 𝑣 простое равно двум
𝑥.
Установив 𝑦 равным 𝑢 над 𝑣, мы
получаем, что 𝑢 равно 20𝑥, а 𝑣 равно 𝑥 в квадрате минус 25. Затем мы можем найти 𝑢 простое число и 𝑣
простое, что дает нам, что 𝑢 простое равно 20, а 𝑣 простое равно двум
𝑥. Получаем, что 𝑓 из 𝑥 равно
минус 𝑥 плюс шесть по всему 𝑥 в квадрате минус четыре. И мы написали 𝑓 как
рациональная функция. И мы готовы использовать частное
правило, которое говорит нам, что 𝑢 над 𝑣 простым числом равно 𝑣𝑢 простым минус 𝑢𝑣 простым числом
во всем 𝑣 в квадрате. Установка 𝑓 из 𝑥 равным 𝑢 более
𝑣, получаем, что 𝑢 равно отрицательному 𝑥 плюс шесть, а 𝑣 равно 𝑥
в квадрате минус четыре. Затем мы находим, что 𝑢 простое число равно
на отрицательную единицу, а 𝑣 простое число равно двум 𝑥.
Получаем, что 𝑓 из 𝑥 равно
минус 𝑥 плюс шесть по всему 𝑥 в квадрате минус четыре. И мы написали 𝑓 как
рациональная функция. И мы готовы использовать частное
правило, которое говорит нам, что 𝑢 над 𝑣 простым числом равно 𝑣𝑢 простым минус 𝑢𝑣 простым числом
во всем 𝑣 в квадрате. Установка 𝑓 из 𝑥 равным 𝑢 более
𝑣, получаем, что 𝑢 равно отрицательному 𝑥 плюс шесть, а 𝑣 равно 𝑥
в квадрате минус четыре. Затем мы находим, что 𝑢 простое число равно
на отрицательную единицу, а 𝑣 простое число равно двум 𝑥. Получаем, что 𝑓 тире из трех равно
равно трем в квадрате минус четыре умножить на минус один минус минус три
плюс шесть умножить на два три три в квадрате минус четыре
в квадрате. Что упрощает до минус пять
минус 18 на 25. Это дает нам решение, которое 𝑓
простое число из трех равно минусу 23 больше 25.
Получаем, что 𝑓 тире из трех равно
равно трем в квадрате минус четыре умножить на минус один минус минус три
плюс шесть умножить на два три три в квадрате минус четыре
в квадрате. Что упрощает до минус пять
минус 18 на 25. Это дает нам решение, которое 𝑓
простое число из трех равно минусу 23 больше 25.