Производная cos x 2 y 2: Найти производную y’ = f'(x) = cos(x)^(2) (косинус от (х) в степени (2))

2. Вычислите сумму всех частных производных второго порядка функции

Тесты

Вариант 1.

1. Найдите частные производные первого порядка функции z=sin x ln(1+y)

а)=cos x, = б) =-cos y ln(1+y), =

в) = -cos x, = г) = cos x ln(1+y),=

2. Вычислите сумму всех частных производных второго порядка функции

z=x³-4x²y+5y²

а) -10x-8y+10 б) -2x-8y+10 в) -2x-8y+20 г) -10x-8y+30

3. Найдите функции e^y-e^x+xy=0

а) б) в) г)

4. Найдите дифференциал первого порядка функции z=x²+xy²+sin y

а) dz=(2x+y²)dx+(2xy+cos y)dy б) dz=(2x+2y)dx+(2xy+cos y)dy

в) dz=(2x+y²)dx+(2xy-cos y)dy г) dz=(2x+y²)dx+(2x-cos y)dy

5. Найдите полную производную функции z=x³y³+x, x=cos t, y=t²sin t

а) б)

в) г)

6. Найдите производную функции z=5x²-3x-y-1 в точке M(2;1) по направлению от этой точки к точке N(5;5)

а) 11,5 б)27,4 в) 13 г) 9,4

Вариант 2.

1. Найдите частные производные первого порядка функции

z=2sin x ln(3+y)

а)=2cos x, = б) =-2cos y ln(3+y), =

в) = -2cos x, = г) = 2cos x ln(3+y),=

z=2x³-3xy²+5x²

а) 6x-12y+10 б) 6x-6y+10 в) 6x-12y+20 г) 6x-6y+20

3. Найдите функции e

—^y-e^x+xy=0

а) б) в) г)

4. Найдите дифференциал первого порядка функции z=2x²+3xy²+sin y

а) dz=(4x+3y²)dx+(6xy+cos y)dy б) dz=(4x+6y)dx+(6xy+cos y)dy

в) dz=(4x+3y²)dx+(6xy-cos y)dy г) dz=(4x+3y²)dx+(6x-cos y)dy

5. Найдите полную производную функции z=x²y+x, x=sin t, y=2t²

а) б)

в) г)

6. Найдите производную функции z=2x²-4x-2y+1 в точке M(3;2) по направлению от этой точки к точке N(4;3)

а) б) в) г)

Вариант 3.

1. Найдите частные производные первого порядка функции

z=sin 2x ln(5+y)

а)=cos 2x, = б) =-2cos y ln(5+y), =

в) = -cos 2x, = г) = 2cos 2x ln(5+y),=

2.

Вычислите сумму всех частных производных второго порядка функции

z=y³+4x²y+3x²

а) 16x+8y+12 б) 16x+8y+6 в) 16x+14y+6 г) 16x+14y+12

3. Найдите функции e^y-e^—x+xy=0

а) б) в) г)

4. Найдите дифференциал первого порядка функции z=x²-3xy²-sin y

а) dz=(2x-3y²)dx+(6xy-cos y)dy б) dz=(2x-3y²)dx-(6xy+cos y)dy

в) dz=(2x-3y²)dx-(6xy-cos y)dy г) dz=(2x+3y²)dx+(6xy-cos y)dy

5. Найдите полную производную функции z=2xy+x², x=2sin t, y=t sin t

а) б)

в) г)

6. Найдите производную функции z=-3x²+5x-y+2 в точке M(-1;1) по направлению от этой точки к точке N(2;4)

а) б) в) г)

Вариант 4.

1. Найдите частные производные первого порядка функции

z=cos 3x ln(y+3)

а)=-3cos 3x, = б) =-3sin 3x ln(y+3), =

в) = -3sin 3x, = г) = 3cos 3x ln(y+3),=

2. Вычислите сумму всех частных производных второго порядка функции

z=3x³-2x²y-3y²

а) 10x-4y-12 б) 10x-4y-6 в) 14x-4y-6 г) 14x-4y-12

3. Найдите функции e^y-e^x+2xy=0

а) б) в) г)

4. Найдите дифференциал первого порядка функции z=2x

2-3x²y+cos y

а) dz=(4x+6xy)dx+(3x²-sin y)dy б) dz=(4x-6xy)dx+(3x²+sin y)dy

в) dz=(4x-6xy)dx-(3x²+sin y)dy г) dz=(4x+6xy)dx-(3x²-sin y)dy

5. Найдите полную производную функции z=x³y²+3x, x=cos t, y=2t²+t

а)

б)

в)

г)

6. Найдите производную функции z=x²+4x-3y-4 в точке M(2;0) по направлению от этой точки к точке N(3;5)

а) б) в) г)

Вариант 5.

1. Найдите частные производные первого порядка функции

z=sin x ln(2+3y)

а)=cos x, = б) =-cos x ln(2+3y), =

в) = -cos x, = г) =cos x ln(2+3y),=

2. Вычислите сумму всех частных производных второго порядка функции

z=4x²+xy²+3y³

а) 8+2x+20y б) 8+2x-20y в) -8+2x+22y г) 8+2x+22y

3. Найдите функции e^y+e^x-3xy=0

а) б) в) г)

4. Найдите дифференциал первого порядка функции z=4x²+4xy²-cos y

а) dz=(8x+4y²)dx+(8xy+sin y)dy б) dz=(8x+4y²)dx-(8xy+sin y)dy

в) dz=(8x-4y²)dx+(8xy-sin y)dy г) dz=(8x+4y²)dx-(8xy-sin y)dy

5. 5x; 2)y=1/x cosx — вопрос №2252050 — Учеба и наука

Лучший ответ по мнению автора

19. 12.16 Лучший ответ по мнению автора

Eleonora Gabrielyan Читать ответы

Владимир Читать ответы

Михаил Александров Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Через 2 года мой братишка будет в 2 раза старше, чем 2 года назад, а я через 3 года буду в 3 раза старше, чем 3 года назад.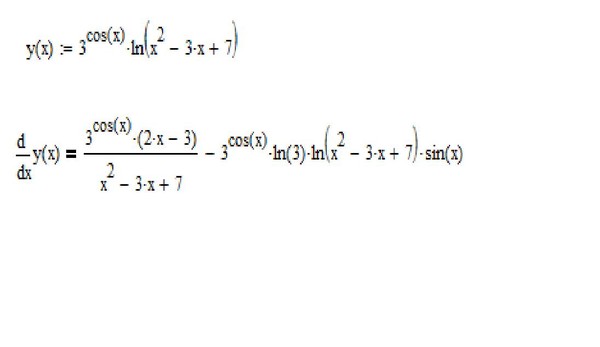 Сколько лет брату и сколько мне сейчас?

Решено

Высота конуса равна 6 см, угол при вершин осевого сечения равен 120 градусов. Найдите 1) площадь сечения конуса плоскостью проходящей через две…

Решено

На каждые 1000 лампочек в среднем приходится 2 бракованные. Какова вероятность купить исправную лампочку?

Решено

В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.

на тарелке было 16 пирожков…

Пользуйтесь нашим приложением

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92 + (x + 2y) потому что (x + y) = (x + 2y + cos (x + y)) y’? Исчисление Вопрос задан 10. 05.19 Подписаться І 1 Подробнее Отчет 2 ответа от опытных наставников Лучший Новейшие Самый старый Автор: ЛучшиеНовыеСамыеСтарые Марк Дж. ответил 11.05.19 Репетитор 4,8 (108) Инженер-механик и математик наполовину на пенсии Об этом репетиторе › Об этом репетиторе › Если вы относитесь к y’ в уравнении так же, как к x в квадратном уравнении, вы найдете 2 ответа для y’: y’ = cos(x+y) показано как правильный ответ, если вы напрямую его в приведенное выше уравнение. однако это сложное уравнение для решения в закрытой форме! другое решение: y’ = x + 2y или y’ — 2y = x (Вы также можете показать, что это y’ также удовлетворяет уравнению!) Начальные условия не заданы, поэтому предположим, что y(0) = A Тогда, это уравнение решается как y = Ae 2x + (1/4)e 2x — (1/2)x — (1/4) Голосовать за 0 Понизить Подробнее Отчет Дибьенду Д. ответил 20.05.19 Репетитор 4,8 (64) Опыт преподавания математики в старших и средних классах более 2 лет См. таких репетиторов Смотрите таких репетиторов (y’) 2 + (x + 2y) cos(x + y) = (x + 2y + cos(x + y)) y’ ⇒ (y’) 2 + (x + 2y ) cos(x + y) = (x + 2y) y’ + cos(x + y) y’ ⇒ (y’) 2 — cos(x + y) y’ = (x + 2y) y ‘ — (x + 2y) cos(x + y) ⇒ y’ [y’ — cos(x + y)] = (x + 2y) [y’ — cos(x + y)] ⇒ ( y’ — x — 2y) [y’ — cos(x + y)] = 0 y’ — x — 2y = 0 ———-(1) или y’ — cos (х + у) = 0 ———-(2) Из (1) получаем: y’ — 2y = x Пусть, коэффициент интегрирования µ(x) = e ∫-2 dx = e -2x Умножая обе части на µ(x) : e -2x (y’) — 2e -2x (y) = e -2x (x) ———(3) Пусть, e -2x (y) = z ∴ z’ = e -2x (y’) — 2e -2x (y) Итак, уравнение (3) принимает вид: z’ = e -2x ( х) ⇒ dz/dx = e -2x (x) ⇒ z = ∫e -2x (x) dx + C 1 ⇒ z = -(1/4)e -2x (2x + 1) + C 1 [интегрирование по частям] ⇒ e -2x (y) = -(1/4)e -2x (2x + 1) + C 1 ⇒ y = C 1 4 e 2x — x/2 — 1/4 Из (2) получаем: y’ = cos(x + y) ———(4) Пусть, z = x + y ∴ z’ = y’ + 1 Итак, уравнение (4) принимает вид: z’ — 1= cos(z) ⇒ dz/dx = 1 + cos(z) ⇒ ∫dz/(cos(z) + 1) = x + C 2 ⇒ tan( z/2) = x + C 2 [интегрирование путем замены tan(z/2) некоторой произвольной переменной u] ⇒ z = 2 tan -1 (x + C 2 ) ⇒ x + у = 2 тангенс -1 (х + С 2 ) ⇒ у = 2 тангенс -1 (х + С 2 ) — х у = С 9 9 4 0 9 9 9 x 3 3 3 1 1 — х/2 — 1/4 или у = 2 тангенс -1 (х + С 2 ) — х Голосовать за 0 Понизить Подробнее Отчет Все еще ищете помощи? Получите правильный ответ, быстро. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт