Производная cos x 3: Производная cos(x/3)

2+1}.$$

3) $ y-x=\varepsilon\sin y $

Решение.

$$\frac{d}{dx}(y-x-\varepsilon\sin y)=0\Rightarrow\,\, y’-1-\varepsilon\cos y\cdot y’=0 \Rightarrow y’=\,\frac{1}{1-\varepsilon\cos y}.$$

Найдите производную функции y = cosx + 3tgx в точке с абсциссой x0= п/… — Учеба и наука

Лучший ответ по мнению автора

02. 05.17 Лучший ответ по мнению автора

Другие ответы

Функция y=tgx в точке x=pi/2 не определена и ее производная в этой точке не существует. 02.05.17

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Отрезок длиной 13 см не пересекает плоскость. Концы отрезка удалены от плоскости на 2 и 7 см. Найдите длину проекции отрезка на плоскость.

Решено

В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.

Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81%

В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DE.

Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площад

Пользуйтесь нашим приложением

Производная функция. 122-151 Найти производную функцию.

№122. a) y=5x⁴+3sin x –cos x+9

б) f (x)=(x³-2x+7) ⁴ f ′ (2)-?

№123. а) y=x

³_*⁴√x^-3_* ³√x^-2

б) f (x)=3sin²x f ′ ( П/6)-?

№124. а) 3x²-8/3x²+8

б) f (x)=arcos 2x f ′ (1/4)-?

№125. а) y=(5x³-3)_*(6x²+1) y′(2)-?

б) f (x)=cos(3x²-1)

№126. а) y=⁴√x³_*x²

_*√x^-1_* ⁵√x^-2

б) f (x)=sin²3x f ′ (П/18)-?

№127.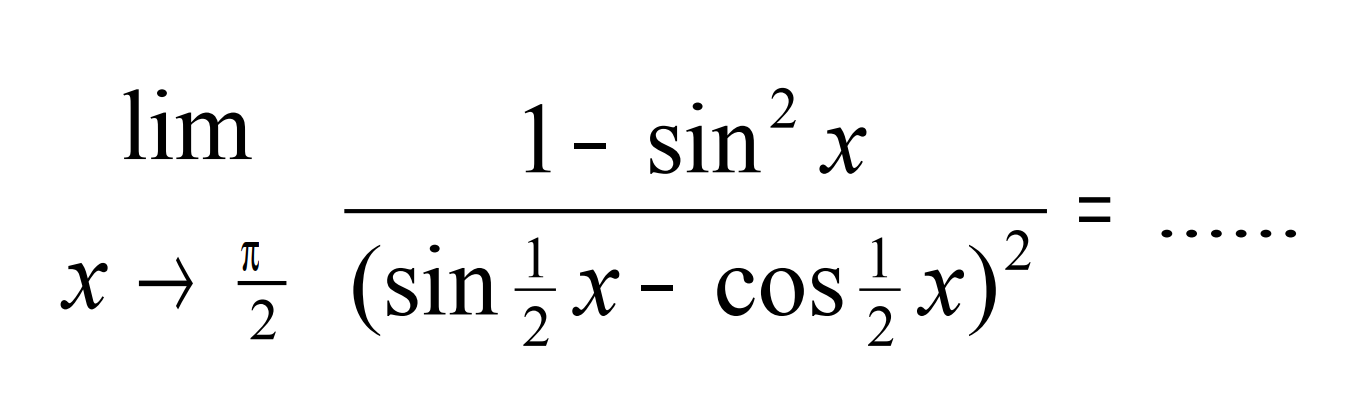 а) y=x³_*√x²/⁴√x³_*√x

б) y=sin²5x y′(П/20)-?

№128. а) y=(x³+4)_*(x²+x-1) y

′(2)-?

б) f (x)=cos(x³-2)

№129. а) y=x⁴-3/x⁴+3

б) f(x)=cos3x_*(sin3x+1) f ′ (П/24)-?

№130. а) y=x⁴-3cos x+3sin x—ln x+29

б) f (x)=sin x_*tg x f ′ (П/4)-?

№131.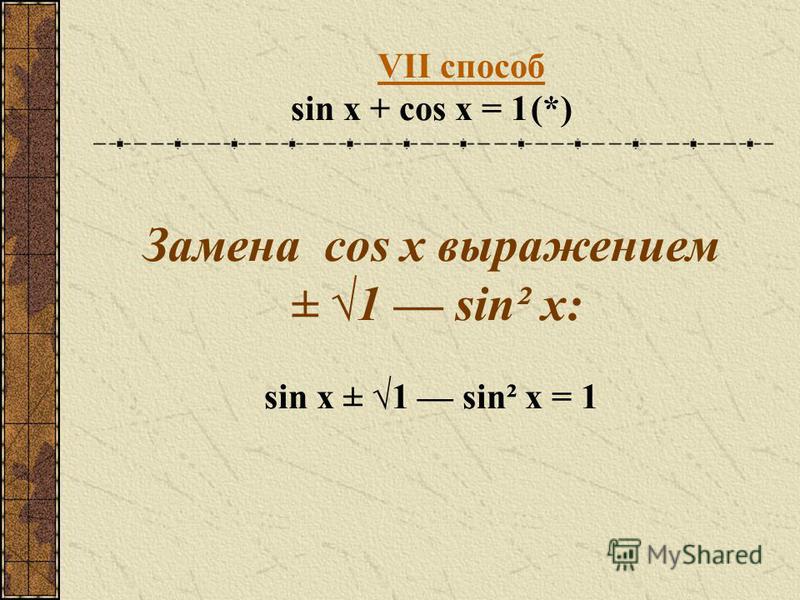 а) y=3√x+2/3_*³√

x²-3/³√x+25

б) y=ctg x-sin3x y′(П/6)-?

№132. а) y=4ln x+x³ y′(2)-?

б) y=5sin³x

№133. а) y=x⁵+2ln x y′(-2)-?

б) f (x)=3sin(2x²-1)

№134. а) y=(2+sin x)/sin x y′(П/4)-?

б) y=(x²+3)_*√(x²-3)

№135. а) y=arcos x+arcsin x y′(1/√2)-?

б) y=ln(4x³+x)⁵

№136.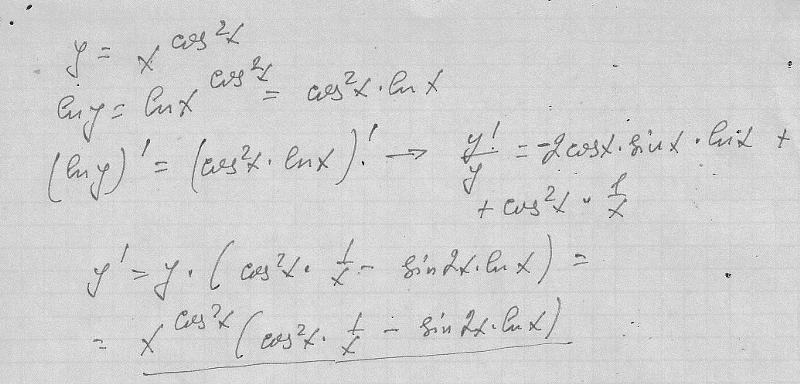 а) y=2arcsin x+3arccos x y′(1/2)-?

б) f (x)=ln (x²+3)/(x²-3)

№137. а) y=(ln x+2)/(2-ln x)

б) y=5^2x-1

№138. а) y=(e^x-1)/(e^x+1)

б) y=tg²4x

№139. а) y=(2-sin x)/(2+sin x) y′(П/3)-?

б) y=ln(3x²-2)⁶

№140. а) y=cos x-sin x y′(П/4)-?

б) y=ln((x³-3)/(x³+3))

№141. а) y=cos x_*(2+sin x)

б) f (x)=3_*⁵√(3x²-1)³ f ′(0)-?

№142. а) y=5x⁴-3sin x+6cos x-ln x+11

б) f (x)=(x³+1)_* ³√(x²-1)² f ′(1)-?

№143. а) y=(3+sin x)_*(3-sin x) y′(П/4)-?

б) y=ln(x³+5)⁴

№144. а) f (x)=(e ^x+2)/(e^x-2)

б) y=sin x_*cos x

№145. а) f (x)=2sin x_*(1-cos x) f ′(П/3)-?

б) y=ln(x²-4)/(x²+4)

№146. а) f (x)=(x²-3x+1)/(x²+1) f ′(-1)-?

б) y=(sin x+2)_*cos x

№147. а) y=10x⁴—e^2x+√2

б) y=(x³-1)/(x³+1) y′(0,5)-?

№148. а) y=x²_*e^x*x+3x y′(0)-?

б) f (x)=ln ⁷√x³/(x-1)

№149. а) y=⁵√(4x²-3)

б) y=5^sin2x y′(0)-?

№150. а) y=sin³ (8x²-1)

б) y=(3x²-1)/(2x+1) y′(0)-?

№151. а) y=(8x²-1)_*(4x-3) y′(1)-?

б) y=ln (3-x²)/(3+x²)

№152. y=3x²—x+2 при x=2, x=0,01

№153. y=2x²+3x-2 при x=3, x=0,002

№154.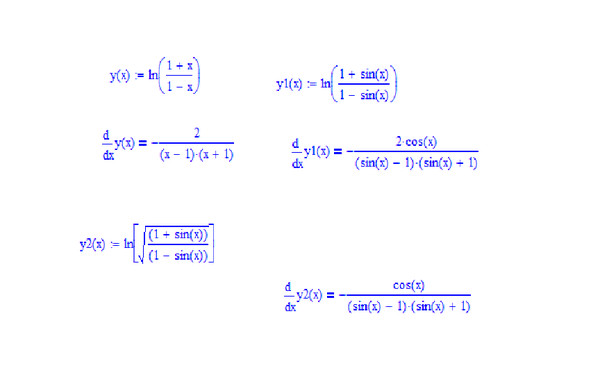 y=3x²+2x+10 при x=5, x=0,001

№155. y=3x²+4x при x=10, x=0,001

№156. y=4x²-5x при x=5, x=0,001

№157. y=2x³—x+10 при x=2, x=0,001

№158. y=5x²-3x+5 при x=5, x=0,02

№159. y=4x³-2x при x=5, x=0,001

№160. y=6x²+2x-1 при x=10, x=0,001

№161. y=6x³-2x при x=10, x=0,01

№162. y=4x²+2x при x=2, x=0,001

№163. y=5x³-2x при x=2, x=0,002

№164. y=4x²-3x при x=3, x=0,001

№165. y=5x³-2x при x=2, x=0,002

№166.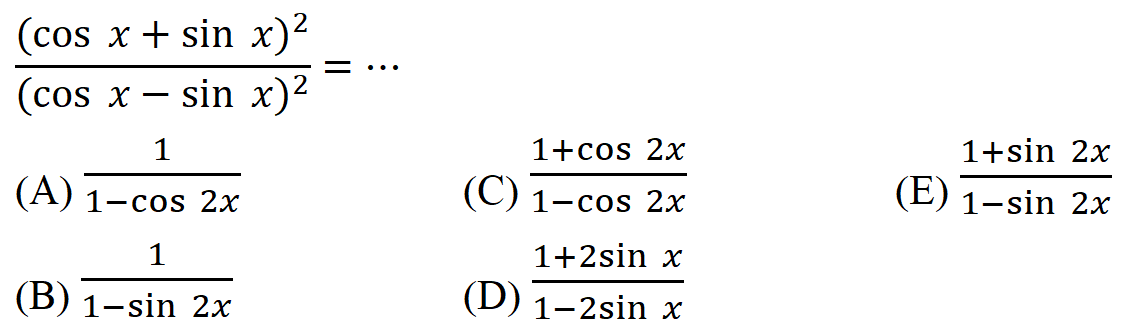 y=7x³—x при x=2, x=0,002

№167. y=3x²+5x+1 при x=3, x=0,001

№168. y=x³+2x при x=2, x=0,1

№169. y=x²-2x при x=1, x=0,01

№170. y=2x³+5 при x=2, x=0,001

№171. y=x³ при x=10, x=0,03

№172. y=2x²-3x при x=5, x=0,01

№173. y=3x²-2x+4 при x=4, x=0,02

№174. y=2x²+2x-1 при x=3, x=0,02

№175. y=3x²+2x-3 при x=2, x=0,01

№176. y=3x³-2x при x=2, x=0,01

№177. y=2x²—x+3 при x=1, x=0,1

№178. y=3x²+2x-2 при x=3, x=0,02

№179.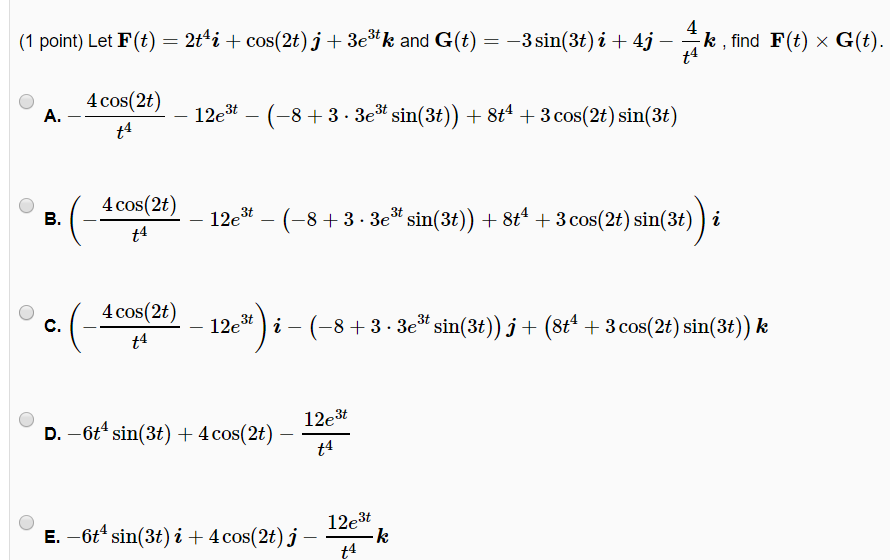 y=5x³+2x при x=2, x=0,001

№180. y=3x²+2x-1 при x=5, x=0,02

№181. y=2x²+3x-4 при x=3, x=0,01

Равна производная cos x. Найти производную: алгоритм и примеры решений

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.

Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».

Пошаговые примеры — как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

А проверить решение задачи на производную можно на .

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Проверить решение задачи на производную можно на калькуляторе производных онлайн .

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Представлено доказательство и вывод формулы для производной косинуса — cos(x). Примеры вычисления производных от cos 2x, cos 3x, cos nx, косинуса в квадрате, в кубе и в степени n. Формула производной косинуса n-го порядка.

Содержание

См. также: Синус и косинус — свойства, графики, формулы

Производная по переменной x от косинуса x равна минус синусу x:
(cos x)′ = — sin x .

Доказательство

Чтобы вывести формулу производной косинуса, воспользуемся определением производной:
.

Преобразуем это выражение, чтобы свести его к известным математическим законам и правилам. Для этого нам нужно знать четыре свойства.
1) Тригонометрические формулы . Нам понадобится следующая формула:
(1) ;
2) Свойство непрерывности функции синус:
(2) ;
3) Значение первого замечательного предела:
(3) ;
4) Свойство предела от произведения двух функций:
Если и , то
(4) .

Применяем эти законы к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(1) ;
В нашем случае
; . Тогда
;
;
;
.

Сделаем подстановку . При , . Используем свойство непрерывности (2):
.

Сделаем такую же подстановку и применим первый замечательный предел (3):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

.

Тем самым мы получили формулу производной косинуса.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих косинус. Найдем производные от следующих функций:
y = cos 2x; y = cos 3x; y = cos nx; y = cos 2 x ; y = cos 3 x и y = cos n x .

Пример 1

Найти производные от cos 2x, cos 3x и cos nx .

Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = cos nx . Затем, в производную от cos nx , подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от cos 2x и cos 3x .

Итак, находим производную от функции
y = cos nx .
Представим эту функцию от переменной x как сложную функцию, состоящую из двух функций:
1)
2)
Тогда исходная функция является сложной (составной) функцией, составленной из функций и :
.

Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем .
.
Подставим :
(П1) .

Теперь, в формулу (П1) подставим и :
;
.

;
;
.

Пример 2

Найти производные от косинуса в квадрате, косинуса в кубе и косинуса в степени n:
y = cos 2 x ; y = cos 3 x ; y = cos n x .

В этом примере также функции имеют похожий вид. Поэтому мы найдем производную от самой общей функции — косинуса в степени n:
y = cos n x .
Затем подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от косинуса в квадрате и косинуса в кубе.

Итак, нам нужно найти производную от функции
.
Перепишем ее в более понятном виде:
.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции , зависящей от переменной : ;
2) Функции , зависящей от переменной : .
Тогда исходная функция является сложной функцией, составленной из двух функций и :
.

Находим производную от функции по переменной x:
.
Находим производную от функции по переменной :
.
Применяем правило дифференцирования сложной функции .
.
Подставим :
(П2) .

Теперь подставим и :
;
.

;
;
.

Производные высших порядков

Заметим, что производную от cos x первого порядка можно выразить через косинус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции :

.
Здесь .

Заметим, что дифференцирование cos x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5) .

Более строго эту формулу можно доказать с помощью метода математической индукции. Доказательство для n-й производной синуса изложено на странице “Производная синуса ”. Для n-й производной косинуса доказательство точно такое. Нужно только во всех формулах заменить sin на cos.

См. также:

При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :

Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.

Таким образом, производная постоянной функции равна нулю на всей области определения .

Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:

Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.

Производная показательной функции.

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

Производная логарифмической функции.

Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:

Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.

Производные тригонометрических функций.

Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.

По определению производной для функции синуса имеем .

Воспользуемся формулой разности синусов:

Осталось обратиться к первому замечательному пределу:

Таким образом, производная функции sin x есть cos x .

Абсолютно аналогично доказывается формула производной косинуса.

Следовательно, производная функции cos x есть –sin x .

Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби).

Производные гиперболических функций.

Правила дифференцирования и формула производной показательной функции из таблицы производных позволяют вывести формулы производных гиперболического синуса, косинуса, тангенса и котангенса.

Производная обратной функции.

Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, — это производная функции f(x) по x .

Теперь сформулируем правило нахождения производной обратной функции.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x) , то в точке существует конечная производная обратной функции g(y) , причем . В другой записи .

Можно это правило переформулировать для любого x из промежутка , тогда получим .

Давайте проверим справедливость этих формул.

Найдем обратную функцию для натурального логарифма (здесь y – функция, а x — аргумент). Разрешив это уравнение относительно x , получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.

Из таблицы производных видим, что и .

Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:

Как видите, получили такие же результаты как и в таблице производных.

Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.

Начнем с производной арксинуса.

. Тогда по формуле производной обратной функции получаем

Осталось провести преобразования.

Так как областью значений арксинуса является интервал , то (смотрите раздел основные элементарные функции, их свойства и графики). Поэтому , а не рассматриваем.

Следовательно, . Областью определения производной арксинуса является промежуток (-1; 1) .

Для арккосинуса все делается абсолютно аналогично:

Найдем производную арктангенса.

Для обратной функцией является .

Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.

Пусть arctgx = z , тогда

Следовательно,

Схожим образом находится производная арккотангенса:

Дата: 20.11.2014

Таблица производных.

Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств.

Это знакомство позволит:

Понимать суть несложных заданий с производной;

Успешно решать эти самые несложные задания;

Подготовиться к более серьёзным урокам по производной.

Сначала — приятный сюрприз.)

Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!

Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует.

Приступим к знакомству?)

Термины и обозначения.

В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках.

Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная.

Дифференцирование — действие над функцией.

Производная — результат этого действия.

Так же, как, например, сумма — результат сложения. Или частное — результат деления.

Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т. п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.

Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее.

Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…)

Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.

Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного.

Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:

1. Таблица производных (формулы дифференцирования).

3. Производная сложной функции.

Начнём по порядку. В этом уроке рассмотрим таблицу производных.

Таблица производных.

В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.

Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)

Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.

	Функция y	Производная функции y y»
1	C (постоянная величина)	C» = 0
2	x	x» = 1
3	x n (n — любое число)	(x n)» = nx n-1
	x 2 (n = 2)	(x 2)» = 2x
4	sin x	(sin x)» = cosx
	cos x	(cos x)» = — sin x
	tg x
	ctg x
5	arcsin x
	arccos x
	arctg x
	arcctg x
4	a x
	e x
5	log a x
	ln x (a = e )

Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)

Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету…

Рассмотрим несколько примеров:

1. Найти производную функции y = x 3

Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:

(x 3) » = 3·x 3-1 = 3x 2

Вот и все дела.

Ответ: y» = 3x 2

2. Найти значение производной функции y = sinx в точке х = 0.

Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.

По табличке находим синус и соответствующую производную:

y» = (sin x)» = cosx

Подставляем ноль в производную:

y»(0) = cos 0 = 1

Это и будет ответ.

3. Продифференцировать функцию:

Что, внушает?) Такой функции в таблице производных и близко нет.

Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает…

Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается!

Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:

Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем:

Ответ: y» = — sin x .

Пример для продвинутых выпускников и студентов:

4. Найти производную функции:

Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так:

А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:

Вот и всё. Это будет ответ.

Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.

Навигация по странице.

Производная постоянной.

При выводе самой первой формулы таблицы будем исходить из определения производной функции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :

Следует заметить, что под знаком предела получается выражение , которое не является , так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.

Таким образом, производная постоянной функции равна нулю на всей области определения .

Пример.

Найти производные следующих постоянных функций

Решение.

В первом случае мы имеем производную натурального числа 3 , во втором случае нам приходится брать производную от параметра а , который может быть любым действительным числом, в третьем — производную иррационального числа , в четвертом случае имеем производную нуля (ноль является целым числом), в пятом – производную рациональной дроби .

Ответ:

Производные всех этих функций равны нулю для любого действительного x (на всей области определения)

Производная степенной функции.

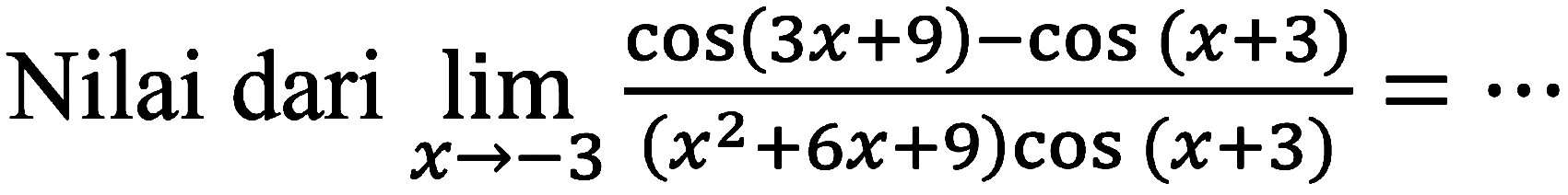
Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле :

Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.

Следует рассмотреть два случая: при положительных x и отрицательных x .

Сначала будем полагать . В этом случае . Выполним логарифмирование равенства по основанию e и применим свойство логарифма:

Пришли к неявно заданной функции. Находим ее производную:

Осталось провести доказательство для отрицательных x .

Когда показатель p представляет собой четное число, то степенная функция определена и при , причем является четной (смотрите раздел ). То есть, . В этом случае и также можно использовать доказательство через логарифмическую производную.

Когда показатель p представляет собой нечетное число, то степенная функция определена и при , причем является нечетной. То есть, . В этом случае и логарифмическую производную использовать нельзя. Для доказательства формулы в этом случае можно воспользоваться правилами дифференцирования и правилом нахождения производной сложной функции:

Последний переход возможен в силу того, что если p — нечетное число, то p-1 либо четное число, либо нуль (при p=1 ), поэтому, для отрицательных x справедливо равенство .

Таким образом, формула производной степенной функции доказана для любого действительного p .

Пример.

Найти производные функций .

Решение.

Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции:

Производная показательной функции.

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

По определению производной для функции синуса имеем .

Воспользуемся формулой разности синусов:

Осталось обратиться к первому замечательному пределу:

Таким образом, производная функции sin x есть cos x .

Абсолютно аналогично доказывается формула производной косинуса.

При решении задач дифференцирования мы будем постоянно обращаться к таблице производных основных функций, иначе зачем мы ее составляли и доказывали каждую формулу. Рекомендуем запомнить все эти формулы, в дальнейшем это сэкономит Вам массу времени.

Copyright by cleverstudents

Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Производная Cos3x — формула, доказательство, примеры

Производная cos3x задается как -3 sin3x. Мы можем оценить дифференцирование cos3x, используя различные методы дифференцирования. Производная функции дает скорость изменения функции при небольшом изменении переменной функции. Мы знаем, что производная от cosx равна -sinx. Следовательно, используя цепное правило дифференцирования, мы можем вычислить производную от cos3x, взяв произведение производной от cos3x по 3x и производной от 3x по x, что математически записывается как d(cos3x)/dx = d(cos3x)/d(3x) × d(3x)/dx = -3 sin3x. 93x, используя метод цепного правила. Мы докажем, что производная cos3x равна -3 sin3x, используя первый принцип производных и метод цепного правила вместе с некоторыми решенными примерами для лучшего понимания концепции.

1.	Что такое производная от Cos3x?
2.	Производная формулы Cos3x
3.	Производная от Cos3x с использованием метода цепного правила 93 раза?
6.	Часто задаваемые вопросы о производной Cos3x

Что такое производная от Cos3x?

Производная cos3x равна -3 sin3x. Производная функции дает скорость изменения этой функции по отношению к изменению переменной. Мы можем вычислить производную cos3x, используя различные методы дифференцирования, такие как цепное правило и первый принцип производных. Мы знаем, что производная от cos(ax) равна -a sin(ax), используя метод цепного правила. Подставив в эту формулу a = 3, мы можем получить производную от cos3x, равную -3 cos3x. В следующем разделе давайте рассмотрим формулу производной от cos3x.

Производная формулы Cos3x

Формула для производной cos3x определяется как d(cos 3x)/dx = -3 sin 3x. Мы можем вычислить дифференцирование cos3x, используя тот факт, что производная составной функции h(x) = cos(ax) равна -a sin(ax), поскольку cos(ax) является композицией функций f(x) = cosx и г(х) = 3х. На изображении ниже показана формула производной cos3x:

Производная от Cos3x с использованием метода цепного правила

Метод цепного дифференцирования используется для нахождения производных сложных функций. Мы можем вычислить производную от cos3x, используя метод цепного правила. Чтобы вычислить дифференцирование cos3x, возьмем произведение производной cos3x по 3x и производной 3x по x следующим образом:

d(cos3x)/dx = d(cos3x)/d(3x) × d(3x)/dx

= -sin3x × 3

= -3 sin3x

Таким образом, мы доказали, что производная cos3x равна -3 sin3x.

Производная от Cos3x с использованием первого принципа

Мы можем вычислить производную от cos3x, используя первый принцип производных. Чтобы найти дифференцирование cos3x, мы берем предельное значение, когда x приближается к x + h. Чтобы упростить это, мы устанавливаем x = x + h и хотим взять предельное значение, когда h приближается к 0. Мы будем использовать определенные тригонометрические и предельные формулы для определения производной cos3x:

• d(f(x)) /dx = lim _{ч → 0} [f(x+h) — f(x)]/ч
• cos (a + b) = cos a cos b — sin a sin b
• lim _x→0 (sinx)/ x = 1
• lim _x→0 (cos x — 1) / x = 0

Используя приведенные выше формулы, мы имеем

d(cos3x)/dx = lim _h→0 [cos3(x+h) — cos3x]/h

= lim _h→0 [cos(3x + 3h) — cos3x]/h

= lim _h→0 [cos3x cos3h — sin3x sin3h — cos3x]/h

= cos3x lim _h→0 (cos3h — 1)/h × (-sin3x) lim _h→0 (sin3h)/h

= cos3x lim _h→0 3 (cos3h — 1)/3h × (-sin3x) lim _h→0 3 (sin3h)/3h — [Умножение и делением предела на 3]

= 3 cos3x lim _h→0 (cos3h — 1)/3h × 3(-sin3x) lim _h→0 (sin3h)/3h

= 3 cos3x × 0 — 3 sin3x × 1 → [Используя формулы пределов sin и cos]

= -3 sin3x

Таким образом, мы доказали, что дифференцирование cos3x равно -3 sin3x. 3x? 93x с использованием первого принципа производных и метода цепного правила.

☛ Похожие темы:

• Дифференциация и интеграция
• Антипроизводные правила
• Формула Sin2x

Часто задаваемые вопросы о производной Cos3x

Что такое производная Cos3x в исчислении?

Производная от cos3x равна -3 sin3x. Мы можем оценить дифференцирование cos3x, используя различные методы дифференцирования. Математически это записывается как d(cos3x)/dx = d(cos3x)/d(3x) × d(3x)/dx = -3 sin3x.

Как найти производную Cos3x?

Мы знаем, что производная от cos(ax) равна -a sin(ax), используя метод цепного правила. Подставив в эту формулу a = 3, мы можем получить производную от cos3x, равную -3 cos3x. Мы можем доказать, что производная cos3x равна -3 sin3x, используя первый принцип производных и метод цепного правила

Что такое вторая производная Cos3x?

Вторая производная cos3x равна -9 cos3x. Вторую производную от cos3x можно определить, дифференцируя первую производную от cos3x. 93x, используя метод цепного правила, степенное правило дифференцирования и формулу для производной cosx.

Какая производная от Cos3x относительно Син3х?

Производная cos3x по sin3x равна -tan3x.

Что такое первообразная Cos3x?

Первообразная cos3x равна (1/3) sin3x + C, где C — постоянная интегрирования. Первообразная функции есть не что иное, как ее интеграл.

Какова формула производной Cos3x?

Формула для производной cos3x: d(cos 3x)/dx = -3 sin 3x. Мы можем определить дифференцирование cos3x, используя тот факт, что производная составной функции h(x) = cos(ax) равна -a sin(ax), поскольку cos(ax) есть композиция функций f(x) = cosx и г(х) = 3х.

3.5 Производные тригонометрических функций. Исчисление, том 1

Цели обучения

• 3.5.1 Найдите производные функции синуса и косинуса.
• 3.5. 2 Найдите производные стандартных тригонометрических функций.
• 3.5.3 Вычислите высшие производные синуса и косинуса.

Одним из важнейших видов движения в физике является простое гармоническое движение, которое связано с такими системами, как объект с массой, колеблющейся на пружине. Простое гармоническое движение может быть описано с помощью функции синуса или косинуса. В этом разделе мы расширим наши знания о формулах производных, включив в них производные этих и других тригонометрических функций. Мы начнем с производных функций синуса и косинуса, а затем используем их для получения формул для производных оставшихся четырех тригонометрических функций. Способность вычислять производные функций синуса и косинуса позволит нам найти скорость и ускорение простого гармонического движения.

Производные функций синуса и косинуса

Мы начнем исследование производной функции синуса, используя формулу, чтобы сделать обоснованное предположение о ее производной. Напомним, что для функции f(x),f(x)

f′(x)=limh→0f(x+h)−f(x)h.f′(x)=limh→0f(x+h)−f(x)h.

Следовательно, для значений hh, очень близких к 0, f′(x)≈f(x+h)−f(x)h.f′(x)≈f(x+h)−f(x)h. Мы видим, что, используя h=0,01,h=0,01,

ddx(sinx)≈sin(x+0,01)−sinx0,01ddx(sinx)≈sin(x+0,01)−sinx0,01

Установив D(x)=sin(x+0,01)−sinx0,01D(x)=sin(x+0,01)−sinx0,01 и используя графическую утилиту, мы можем получить график аппроксимации производной sinxsinx (рис. 3.25).

Рисунок 3,25 График функции D(x)D(x) очень похож на косинусоидальную кривую.

При осмотре график D(x)D(x) оказался очень близким к графику функции косинуса. Действительно, мы покажем, что

ddx(sinx)=cosx.ddx(sinx)=cosx.

Если бы мы проделали те же шаги для аппроксимации производной функции косинуса, мы бы обнаружили, что

ddx(cosx)=-sinx.ddx(cosx)=-sinx.

Теорема 3,8

Производные sin

x и cos x

Производной функции синуса является косинус, а производной функции косинуса является отрицательный синус.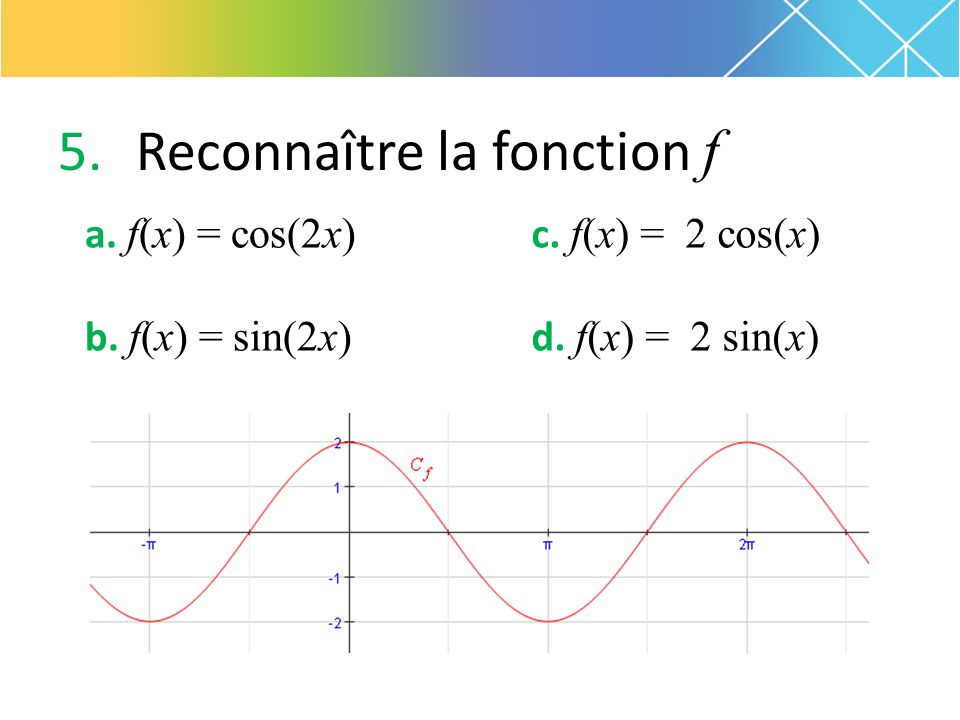

ddx(sinx)=cosxddx(sinx)=cosx

(3.11)

ddx(cosx)=-sinxddx(cosx)=-sinx

(3.12)

Доказательство

Поскольку доказательства для ddx(sinx)=cosxddx(sinx)=cosx и ddx(cosx)=-sinxddx(cosx)=-sinx используют аналогичные методы, мы приводим только доказательство для ddx(sinx)=cosx.ddx(sinx )=cosx. Прежде чем начать, вспомните два важных тригонометрических предела, которые мы изучили в разделе «Введение в пределы»:0909

limh→0sinhh=1andlimh→0cosh−1h=0.limh→0sinhh=1andlimh→0cosh−1h=0.

Графики y=(sinh)hy=(sinh)h и y=(cosh-1)hy=(cosh-1)h показаны на рис. 3.26.

Рисунок 3,26 Эти графики показывают два важных предела, необходимых для установления формул производных для функций синуса и косинуса.

Напомним также следующее тригонометрическое тождество для синуса суммы двух углов:

sin(x+h)=sinxcosh+cosxsinh.sin(x+h)=sinxcosh+cosxsinh.

Теперь, когда мы собрали все необходимые уравнения и тождества, приступим к доказательству.

ddxsinx=limh→0sin(x+h)−sinxhПрименить определение производной.=limh→0sinxcosh+cosxsinh−sinxhИспользовать тождество триггера для синуса суммы двух углов.=limh→0(sinxcosh−sinxh+cosxsinhh)Перегруппировать .=limh→0(sinx(cosh−1h)+cosx(sinhh)) Фактор outsinxandcosx.=sinx·0+cosx·1Применить формулы тригонометрического предела.=cosxSimplify.ddxsinx=limh→0sin(x+h)−sinxhПрименить определение производная.=limh→0sinxcosh+cosxsinh−sinxhИспользовать тождество триггера для синуса суммы двух углов.=limh→0(sinxcosh−sinxh+cosxsinhh)Перегруппировать.=limh→0(sinx(cosh−1h)+cosx( sinhh)) Фактор outsinxandcosx.=sinx·0+cosx·1Применить формулы триггерного предела.=cosxSimplify.

□

На рис. 3.27 показано соотношение между графиком f(x)=sinxf(x)=sinx и его производной f′(x)=cosx.f′(x)=cosx. Обратите внимание, что в точках, где f(x)=sinxf(x)=sinx имеет горизонтальную касательную, ее производная f′(x)=cosxf′(x)=cosx принимает нулевое значение. Мы также видим, что где f(x)=sinxf(x)=sinx возрастает, f′(x)=cosx>0f′(x)=cosx>0 и где f(x)=sinxf(x)=sinx равно убывает, f′(x)=cosx<0.f′(x)=cosx<0.

Рисунок 3,27 Где f(x)f(x) имеет максимум или минимум, f′(x)=0f′(x)=0, то есть f′(x)=0f′(x)=0, где f(x) f(x) имеет горизонтальную касательную. Эти точки отмечены точками на графиках.

Пример 3,39

Дифференцирование функции, содержащей sin

x

Найдите производную f(x)=5x3sinx.f(x)=5x3sinx.

Решение

Используя правило произведения, мы имеем

f′(x)=ddx(5×3)·sinx+ddx(sinx)·5×3=15×2·sinx+cosx·5×3.f′(x)=ddx(5×3)·sinx +ddx(sinx)·5×3=15×2·sinx+cosx·5×3.

После упрощения получаем

f′(x)=15x2sinx+5x3cosx.f′(x)=15x2sinx+5x3cosx.

Контрольно-пропускной пункт 3,25

Найдите производную f(x)=sinxcosx.f(x)=sinxcosx.

Пример 3,40

Нахождение производной функции, содержащей cos

x

Найдите производную g(x)=cosx4x2. g(x)=cosx4x2.

Решение

Применяя правило частных, мы имеем

)2.

Упрощая, получаем

g′(x)=−4x2sinx−8xcosx16x4=−xsinx−2cosx4x3.g′(x)=−4x2sinx−8xcosx16x4=−xsinx−2cosx4x3.

Контрольно-пропускной пункт 3,26

Найдите производную f(x)=xcosx.f(x)=xcosx.

Пример 3,41

Приложение к скорости

Частица движется вдоль координатной оси таким образом, что ее положение в момент времени tt определяется выражением s(t)=2sint−ts(t)=2sint−t для 0≤t≤2π. 0≤t≤2π. В какие моменты времени частица покоится?

Решение

Чтобы определить, когда частица находится в состоянии покоя, установите s′(t)=v(t)=0.s′(t)=v(t)=0. Начните с нахождения s′(t).s′(t). Получаем

s′(t)=2cost−1,s′(t)=2cost−1,

поэтому мы должны решить

2cost−1=0for0≤t≤2π.2cost−1=0for0≤t≤2π.

Решениями этого уравнения являются t=π3t=π3 и t=5π3.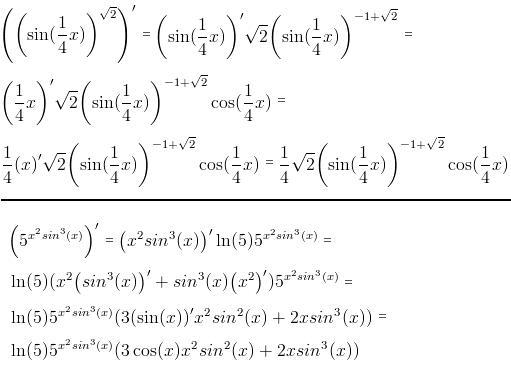 t=5π3. Таким образом, частица покоится в моменты времени t=π3t=π3 и t=5π3.t=5π3.

Контрольно-пропускной пункт 3,27

Частица движется вдоль координатной оси. Его положение в момент времени tt определяется выражением s(t)=3t+2costs(t)=3t+2cost для 0≤t≤2π.0≤t≤2π. В какие моменты времени частица покоится?

Производные других тригонометрических функций

Поскольку оставшиеся четыре тригонометрические функции могут быть выражены в виде частных, содержащих синус, косинус или и то, и другое, мы можем использовать правило частных, чтобы найти формулы для их производных.

Пример 3,42

Производная функции касательной

Найдите производную f(x)=tanx.f(x)=tanx.

Решение

Начните с выражения tanxtanx как частного sinxsinx и cosx:cosx:

f(x)=tanx=sinxcosx.f(x)=tanx=sinxcosx.

Теперь примените правило частных, чтобы получить

f′(x)=cosxcosx−(−sinx)sinx(cosx)2. f′(x)=cosxcosx−(−sinx)sinx(cosx)2.

Упрощая, получаем

f′(x)=cos2x+sin2xcos2x.f′(x)=cos2x+sin2xcos2x.

Признав, что cos2x+sin2x=1,cos2x+sin2x=1, по теореме Пифагора мы теперь имеем

f′(x)=1cos2x.f′(x)=1cos2x.

Наконец, используйте тождество secx=1cosxsecx=1cosx, чтобы получить

f′(x)=sec2x.f′(x)=sec2x.

Контрольно-пропускной пункт 3,28

Найдите производную f(x)=cotx.f(x)=cotx.

Производные остальных тригонометрических функций могут быть получены с использованием аналогичных методов. Мы приводим эти формулы в следующей теореме.

Теорема 3,9

Производные tanx,cotx,secx,tanx,cotx,secx и cscxcscx

Производные остальных тригонометрических функций следующие: (cotx)=-csc2xddx(cotx)=-csc2x

(3.14)

ddx(secx)=secxtanxddx(secx)=secxtanx

(3.15)

ddx(cscx)=-cscxcotx. ddx(cscx)=-cscxcotx.

(3.16)

Пример 3,43

Нахождение уравнения касательной

Найдите уравнение касательной к графику f(x)=cotxf(x)=cotx в точке x=π4.x=π4.

Решение

Чтобы найти уравнение касательной, нам нужна точка и наклон в этой точке. Чтобы найти точку, вычислите

f(π4)=cotπ4=1.f(π4)=cotπ4=1.

Таким образом, касательная проходит через точку (π4,1).(π4,1). Затем найдите наклон, найдя производную f(x)=cotxf(x)=cotx и оценив ее в π4:π4:

f′(x)=−csc2xandf′(π4)=−csc2(π4)= −2.f′(x)=−csc2xandf′(π4)=−csc2(π4)=−2.

Используя уравнение точки-наклона линии, получаем 1+π2.y=−2x+1+π2.

Пример 3,44

Нахождение производной тригонометрических функций

Нахождение производной f(x)=cscx+xtanx.f(x)=cscx+xtanx.

Решение

Чтобы найти эту производную, мы должны использовать как правило сумм, так и правило произведения. Используя правило сумм, находим

f′(x)=ddx(cscx)+ddx(xtanx).f′(x)=ddx(cscx)+ddx(xtanx).

В первом члене ddx(cscx)=−cscxcotx,ddx(cscx)=−cscxcotx, и, применяя правило произведения ко второму члену, мы получаем

ddx(xtanx)=(1)(tanx)+( sec2x)(x).ddx(xtanx)=(1)(tanx)+(sec2x)(x).

Следовательно, мы имеем

f′(x)=−cscxcotx+tanx+xsec2x.f′(x)=−cscxcotx+tanx+xsec2x.

Контрольно-пропускной пункт 3,29

Найдите производную f(x)=2tanx−3cotx.f(x)=2tanx−3cotx.

Контрольно-пропускной пункт 3.30

Найдите наклон прямой, касательной к графику f(x)=tanxf(x)=tanx в точке x=π6.x=π6.

Производные высшего порядка

Производные sinxsinx и cosxcosx более высокого порядка следуют повторяющемуся шаблону. Следуя шаблону, мы можем найти любую производную высшего порядка от sinxsinx и cosx.cosx.

Пример 3,45

Нахождение производных высшего порядка от y=sinxy=sinx

Найдите первые четыре производные от y=sinx.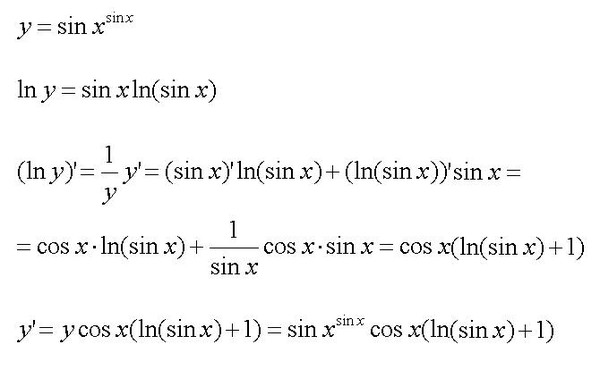 y=sinx.

Решение

Каждый шаг в цепочке прост:

y=sinxdydx=cosxd2ydx2=-sinxd3ydx3=-cosxd4ydx4=sinx.y=sinxdydx=cosxd2ydx2=-sinxd3ydx3=-cosxd4ydx4=sinx.

Анализ

Как только мы распознали модель производных, мы можем найти любую производную более высокого порядка, определив шаг в модели, которой она соответствует. Например, каждая четвертая производная sin x равно sin x , поэтому

=d4n+1dx4n+1(sinx)=cosx.d4dx4(sinx)=d8dx8(sinx)=d12dx12(sinx)=…=d4ndx4n(sinx)=sinxd5dx5(sinx)=d9dx9(sinx)=d13dx13(sinx)=… =d4n+1dx4n+1(sinx)=cosx.

Контрольно-пропускной пункт 3.31

Для y=cosx,y=cosx найдите d4ydx4.d4ydx4.

Пример 3,46

Использование шаблона для производных высшего порядка от y=sinxy=sinx

Найдите d74dx74(sinx).d74dx74(sinx).

Решение

Сразу видно, что для 74-й производной sinx,74=4(18)+2,sinx,74=4(18)+2, поэтому

d74dx74(sinx)=d72+2dx72+2(sinx) =d2dx2(sinx)=-sinx. d74dx74(sinx)=d72+2dx72+2(sinx)=d2dx2(sinx)=-sinx.

Контрольно-пропускной пункт 3,32

Для y=sinx,y=sinx найдите d59dx59(sinx).d59dx59(sinx).

Пример 3,47

Приложение к ускорению

Частица движется вдоль координатной оси таким образом, что ее положение в момент времени tt определяется выражением s(t)=2−sint.s(t)=2−sint. Найдите v(π/4)v(π/4) и a(π/4).a(π/4). Сравните эти значения и решите, ускоряется или замедляется частица.

Решение

Сначала найдите v(t)=s′(t):v(t)=s′(t):

v(t)=s′(t)=−cost.v(t)=s′(t )=-стоимость.

Таким образом,

v(π4)=−12.v(π4)=−12.

Затем найдите a(t)=v′(t).a(t)=v′(t). Таким образом, a(t)=v′(t)=sinta(t)=v′(t)=sint, и мы имеем

a(π4)=12.a(π4)=12.

Поскольку v(π4)=−12<0v(π4)=−12<0 и a(π4)=12>0,a(π4)=12>0, мы видим, что скорость и ускорение действуют в противоположных направлениях ; то есть объект ускоряется в направлении, противоположном направлению, в котором он движется.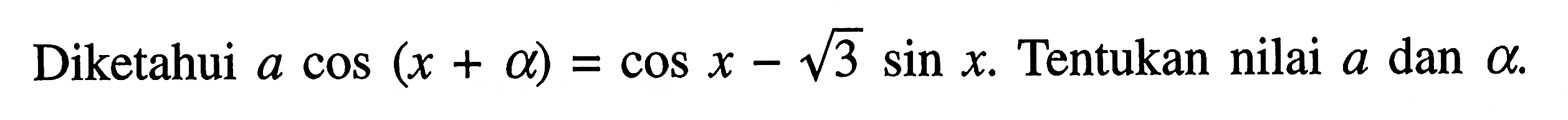 Следовательно, частица замедляется.

Контрольно-пропускной пункт 3,33

Блок, прикрепленный к пружине, движется вертикально. Его положение в момент времени tt определяется выражением s(t)=2sint.s(t)=2sint. Найдите v(5π6)v(5π6) и a(5π6).a(5π6). Сравните эти значения и решите, ускоряется блок или замедляется.

Раздел 3.5 Упражнения

Для следующих упражнений найдите dydxdydx для заданных функций.

175.

y=x2-secx+1y=x2-secx+1

176.

у=3cscx+5xy=3cscx+5x

177.

y=x2cotxy=x2cotx

178.

y=x−x3sinxy=x−x3sinx

179.

у=секхху=секхх

180.

y=sinxtanxy=sinxtanx

181.

y=(x+cosx)(1−sinx)y=(x+cosx)(1−sinx)

182.

y=tanx1-secxy=tanx1-secx

183.

y=1-cotx1+cotxy=1-cotx1+cotx

184.

у=cosx(1+cscx)y=cosx(1+cscx)

Для следующих упражнений найдите уравнение касательной к каждой из заданных функций при указанных значениях x.x. Затем используйте калькулятор, чтобы построить график функции и касательной, чтобы убедиться, что уравнение для касательной правильное.

185.

[T] f(x)=-sinx,x=0f(x)=-sinx,x=0

186.

[Т] f(x)=cscx,x=π2f(x)=cscx,x=π2

187.

[T] f(x)=1+cosx,x=3π2f(x)=1+cosx,x=3π2

188.

[Т] f(x)=secx,x=π4f(x)=secx,x=π4

189.

[T] f(x)=x2-tanx,x=0f(x)=x2-tanx,x=0

190.

[Т] f(x)=5cotx,x=π4f(x)=5cotx,x=π4

Для следующих упражнений найдите d2ydx2d2ydx2 для заданных функций.

191.

y=xsinx-cosxy=xsinx-cosx

192.

у=sinxcosxy=sinxcosx

193.

у=х-12sinxy=x-12sinx

194.

y=1x+tanxy=1x+tanx

195.

у=2cscxy=2cscx

196.

у=сек2ху=сек2х

197.

Найдите все значения xx на графике f(x)=−3sinxcosxf(x)=−3sinxcosx, где касательная горизонтальна.

198.

Найдите все значения xx на графике f(x)=x−2cosxf(x)=x−2cosx для 0

199.

Пусть f(x)=cotx. f(x)=cotx. Определите точки на графике функции ff для 0

200.

[T] Масса на пружине подпрыгивает вверх и вниз в простом гармоническом движении, моделируемом функцией s(t)=−6costs(t)=−6cost, где ss измеряется в дюймах, а tt измеряется в секундах . Найдите скорость, с которой пружина колеблется в момент времени t=5t=5 с.

201.

Пусть положение качающегося маятника в простом гармоническом движении определяется как s(t)=acost+bsints(t)=acost+bsint, где aa и bb — константы, tt измеряет время в секундах, а ss измеряет положение в сантиметрах . Если положение равно 0 см, а скорость равна 3 см/с при t=0t=0, найдите значения aa и bb.

202.

После того, как ныряльщик прыгнул с трамплина, край трамплина колеблется с положением, заданным s(t)=−5costs(t)=−5cost см через tt секунд после прыжка.

1. Нарисуйте один период функции положения для t≥0.t≥0.
2. Найдите функцию скорости.
3. Нарисуйте один период функции скорости для t≥0.t≥0.
4. Определите моменты времени, когда скорость равна 0 за один период.
5. Найдите функцию ускорения.
6. Нарисуйте один период функции ускорения для t≥0.t≥0.

203.

Количество гамбургеров, проданных в ресторане быстрого питания в Пасадене, Калифорния, определяется как y=10+5sinxy=10+5sinx, где yy — количество проданных гамбургеров, а xx — количество часов после открытия ресторана в с 11:00 до 23:00, когда магазин закрывается. Найдите y′y′ и определите интервалы, в течение которых количество продаваемых гамбургеров увеличивается.

204.

[T] Количество осадков в месяц в Финиксе, штат Аризона, можно приблизительно оценить как y(t)=0,5+0,3cost, y(t)=0,5+0,3cost, где tt — количество месяцев, начиная с января. Найдите y′y′ и с помощью калькулятора определите интервалы, в течение которых количество осадков уменьшается.

В следующих упражнениях используйте правило частных для вывода данных уравнений.

205.

ddx(cotx)=-csc2xddx(cotx)=-csc2x

206.

ddx(secx)=secxtanxddx(secx)=secxtanx

207.

ddx(cscx)=-cscxcotxddx(cscx)=-cscxcotx

208.

Используйте определение производной и тождество

cos(x+h)=cosxcosh-sinxsinhcos(x+h)=cosxcosh-sinxsinh, чтобы доказать, что d(cosx)dx=-sinx.d(cosx)dx=- синкс.

В следующих упражнениях найдите требуемую производную высшего порядка для заданных функций.

209.

d3ydx3d3ydx3 из y=3cosxy=3cosx

210.

d2ydx2d2ydx2 из y=3sinx+x2cosxy=3sinx+x2cosx

211.

d4ydx4d4ydx4 из y=5cosxy=5cosx

212.

d2ydx2d2ydx2 из y=secx+cotxy=secx+cotx

213.

d3ydx3d3ydx3 из y=x10-secxy=x10-secx

Решения Бальбхарати для математики и статистики 2 (искусства и науки) 12-й стандарт Совета штата Махараштра HSC, глава 1 — Дифференциация [Последнее издание] Упражнение 1.1 [Страницы 11 — 13] 9((3x + 2) +  5)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 2.03 | Страница 12

Различайте следующие w.r.t.x: `log[tan(x/2)]`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.1 | Вопрос 2.04 | Page 12

Дифференцируйте следующий W.R.T.X: `SQRT (TANSQRT (x)`

Просмотр решения

Упражнение 1.1 | Q 2,05 | Page 12

Дифференцируйте следующее W.R.X: Cot ^{366 (x} [x [x [x [x [x [x [x [x [x [x [x . ]

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 1 | ВОПРОС 2.06 | Страница 12 92x)`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.1 | Вопрос 2.1 | Страница 12

Дифференцируйте следующие w.r.t.x: cos ² [log(x ² + 7)]

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 2.11 | Страница 12

Дифференцируйте следующие w.r.t.x: tan[cos (sinx)]

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.1 | Вопрос 2.12 | Страница 12

Различают следующие w.r.t.x: sec[tan (x ⁴ + 4)]

ПОСМОТРЕТЬ РЕШЕНИЕ

9092))]`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.1 | Вопрос 2.16 | Страница 12

Различайте следующие w.r.t.x: loge ² (logx)

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 2.17 | Страница 12

Дифференцируйте следующие w.r.t.x: [log {log(logx)}] ²

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 2.18 | Страница 12

Дифференцируйте следующие w.r.t.x: sin ² x ² – cos ² x ²  

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 1 | Вопрос 3.01 | Страница 12

Дифференцируйте следующие w.r.t.x: (x ² + 4x + 1) ³ + (x ³ − 5x − 2) ⁴  

90 РЕШЕНИЕ Вопрос 3.02 | Страница 12

Дифференцируйте следующие w.r.t.x: (1 + 4x) ⁵ (3 + x −x2) ⁸ 

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 3.03 | Страница 12

Различайте следующие w.r.t.x: `x/(sqrt(7 — 3x)` 93`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 3.05 | Страница 12

Дифференцируйте следующие w.r.t.x: (1 + sin ² x) ² (1 + cos ² x) ³  

ПРОСМОТР РЕШЕНИЯ

9

9

| Вопрос 3.06 | Страница 12

Дифференцируйте следующие w.r.t.x: `sqrt(cosx) + sqrt(cossqrt(x)` 9sqrt(x) — 1)`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.1 | Вопрос 3.12 | Страница 12

Дифференцируйте следующие w.r.t.x: log[tan ³ x.sin ⁴ x.(x ² + 7) ⁷ ]

ПРОСМОТР РЕШЕНИЯ

6

6 | Вопрос 3. 13 | Страница 12

Дифференцируйте следующие w.r.t.x: `log(sqrt((1 — cos3x)/(1 + cos3x)))`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 3.14 | Страница 12

Дифференцируйте следующие w.r.t.x: `(sqrt((1 + cos((5x)/2))/(1 — cos((5x)/2))))` 92 + 5)`

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 4.1 | Страница 12

Приведена таблица значений f, g, f’ и g’:

x	ф(х)	г(х)	ф'(х)	г'(х)
2	1	6	–3	4
4	3	4	5	-6
6	5	2	–4	7

Если r(x) =f [g(x)] найти r’ (2).

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 4.2 | Страница 12

Приведена таблица значений f, g, f’ и g’:

x	ф(х)	г(х)	ф'(х)	г'(х)
2	1	6	–3	4
4	3	4	5	-6
6	5	2	–4	7

Если R(x) =g[3 + f(x)] найти R'(4).

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 4.3 | Страница 12

Приведена таблица значений f, g, f’ и g’:

x	ф(х)	г(х)	ф'(х)	г'(х)
2	1	6	–3	4
4	3	4	5	-6
6	5	2	–4	7

Если s(x) = f[9 − f (x)], найдите s'(4).

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 4.4 | Страница 12

Приведена таблица значений f, g, f’ и g’:

x	ф(х)	г(х)	ф'(х)	г'(х)
2	1	6	–3	4
4	3	4	5	-6
6	5	2	–4	7

Если S(x) =g [g(x)] найти S'(6).

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 5 | Страница 12

Предположим, что `f'(3) = -1,»g»‘(2) = 5, «g»(2) = 3 и y = f[«g»(x)], «тогда» [«dy»/»dx»]_(x = 2) = ?`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 6 | Страница 12

Если h(x) = `sqrt(4f(x) + 3″g»(x)), f(1) = 4, «g»(1) = 3, f'(1) = 3 , «g»‘(1) = 4, «найти h»‘(1)`.

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 7 | Страница 12

Найдите координаты x всех точек кривой y = sin 2x − 2 sin x, 0 ≤ x < 2π, где `"dy"/"dx"` = 0.

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.1 | Вопрос 8 | Страница 13

Выберите подходящую подсказку из корзины подсказок и заполните пустые места в следующем абзаце. [Активность]:

«Пусть f (x) = x ² + 5 и g (x) = e ^x + 3, тогда
f[g(x)] = ………. и g[ f(x)] = ……
Теперь f'(x) = ………. и g'(x) = …….. ..
Производная f[g(x)] w.r.t.x через f и g равна ……….

Поэтому `»d»/»dx»[f[«g»( x)]]` = . ……… и

`[«d»/»dx»[f[«g»(x)]]]_(x  =  0)` = .. ……..
Производная g[f(x)] w.r.t.x через f и g равна

Поэтому `»d»/»dx»[«g»[f(x)]] ` = ………. и 9x}`

ПОСМОТРЕТЬ РЕШЕНИЕ

Решения Balbharati для математики и статистики 2 (искусства и науки) 12-й стандарт HSC Maharashtra State Board Глава 1 Дифференциация Упражнение 1.2 [Страницы 29 — 30]

Упражнение 1.2 | Вопрос 1.1 | Страница 29

Найдите производную функции y = f(x), используя производную обратной функции x = f ^-1 (y) в следующем: y = `sqrt(x)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 1.2 | Страница 29

Найдите производную функции y = f(x), используя производную обратной функции x = f ^-1 (y) в следующем виде: y = `sqrt(2 — sqrt(x)`

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 1.3 | Страница 29

Найдите производную функции y = f(x) ) с использованием производной обратной функции x = f ^-1 (y) в следующем виде: y = `root(3)(x — 2)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 2 | Q 1.4 | Страница 29

Найдите производную функции y = f(x), используя производную обратной функции x = f ^–1 (y) в следующем: y = log(2x – 1)

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 1,5 | Страница 29

Найдите производную функции y = f(x), используя производную обратной функции x = f ^–1 (y) в следующем: y = 2x + 3

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.2 | Вопрос 1.6 | Страница 29

Найдите производную функции y = f(x), используя производную обратной функции x = f ^–1 (y) в следующем: y = e ^x – 3

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 1.7 | Страница 29

Найдите производную функции y = f(x), используя производную обратной функции x = f ^–1 (y) в следующем: y = e ^2x-3  

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 1.8 | Страница 29

Найдите производную функции y = f(x), используя производную обратной функции x = f ^–1 (y) в следующем: y = `log_2(x/2)`

VIEW РЕШЕНИЕ

Упражнение 1. 2 | Вопрос 2.1 | Страница 29

Найдите производную обратной функции: y = x ² ·e ^x  

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.2 | Вопрос 2.2 | Страница 29

Найдите производную от обратной функции: y = x cos x

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 2.3 | Страница 29

Найдите производную обратной функции следующего уравнения: y = x ·7 ^x 

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.2 | Вопрос 2.4 | Страница 29

Найдите производную обратной функции: y = x ² + log x

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.2 | Вопрос 2.5 | Page 29

Найдите производную обратной функции следующего уравнения: y = x log x

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 3.1 | Страница 29

Найдите производную от обратной следующих функций, а также найдите их значение в указанных напротив них точках. у = х ⁵ + 2х ³ + 3x, при x = 1

ПРОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 2 | Вопрос 3.2 | Страница 29

Найдите производную от обратной следующих функций, а также найдите их значение в указанных напротив них точках. y = e ^x + 3x + 2

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 3.3 | Страница 29

Найдите производную от обратной следующих функций, а также найдите их значение в указанных напротив них точках. у = 3x ² + 2logx ³  

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.2 | Вопрос 3.4 | Страница 29

Найдите производную от обратной следующих функций, а также найдите их значение в указанных напротив них точках. y = sin(x – 2) + x ²  

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 4 |

Если f(x) = x ³ + x – 2, найдите (f ^–1 )'(–2).

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 5.1 | Страница 29

Используя производную, докажите, что: tan ^–1 x + кроватка ^–1 x = `pi/(2)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 2 | Вопрос 5.2 | Страница 29

Используя производную, докажите, что: sec ^–1 x + cosec ^–1 x = `pi/(2)`    …[для |x| ≥ 1]

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.2 | Вопрос 6.01 | Стр. 29

Различайте следующие з.р.т. x : tan ^–1 (log x)

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.2 | Вопрос 6.02 | Стр. 29

Различайте следующие з.р.т. х : косек 9(-1)x`

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 1.7 | Стр. 39

Различайте следующие з.р.т. x : (sin x) ^x  

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 1.8 | Стр. 39

Различайте следующие з.р.т. x : (sin x ^x )

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 2.1 | Стр. 40

Проведите дифференциацию следующих з.р.т. х : х ^е + х ^х + е ^х + е ^е   909(tanx) «at» x = pi/(4)`

ПРОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 3. 01 | Страница 40

Найдите `»dy»/»dx»`, если `sqrt(x) + sqrt(y) = sqrt(a)`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.3 | Вопрос 3.02 | Страница 40

Найдите `»dy»/»dx»`, если `xsqrt(x) + ysqrt(y) = asqrt(a)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 3.03 | Страница 40

Найдите `»dy»/»dx»`, если `x + sqrt(xy) + y ` = 1

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 3.04 | Страница 40 9092))`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.3 | Вопрос 3.06 | Страница 40

Найдите `»dy»/»dx»`, если xe ^y + ye ^x = 1

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 3.07 | Страница 40

Найдите `»dy»/»dx»`, если e ^x+y = cos(x – y)

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 3.08 | Страница 40

Найдите `»dy»/»dx», если cos (xy) = x + y

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.3 | Вопрос 3.09 | Страница 40

Найдите `»dy»/»dx»`, если `e^(e^(x — y)) = x/y`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 3 | Вопрос 4.1 | Страница 40

Покажите, что `»dy»/»dx» = y/x` в следующем примере, где a и p — константы: ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 4.2 | Страница 40

Покажите, что `»dy»/»dx» = y/x` в следующем, где a и p — константы: x ^p y ⁴ = (x + y) ^p+4 , p ∈ N

ПРОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.3 | Вопрос 4.3 | Страница 40 92/(log у — 1)`.

ПОСМОТРЕТЬ РЕШЕНИЕ

Решения Balbharati для математики и статистики 2 (искусства и науки) 12-й стандарт HSC Maharashtra State Board Глава 1 Дифференциация Упражнение 1.4 [Страницы 48 — 49]

Упражнение 1.4 | Вопрос 1.1 | Страница 48

Найдите `»dy»/»dx»`, если x = at ² , y = 2at

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.4 | Вопрос 1.2 | Страница 48

Найдите `»dy»/»dx»`, если x = a cot θ, y = b cosec θ

ПОСМОТРЕТЬ РЕШЕНИЕ

9092)`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.4 | Вопрос 1.4 | Страница 48

Найдите `»dy»/»dx»`, если: x = sinθ, y = tanθ

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 4 | Вопрос 1,5 | Страница 48

Найдите `»dy»/»dx»`, если: x = a(1 – cosθ), y = b(θ – sinθ)

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.4 | Вопрос 1.6 | Страница 48

Найти `»dy»/»dx»`, если: x = `(t + 1/t), y = a(t + 1/t)`, где a > 0, a ≠ 1, t ≠ 0.

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.4 | Вопрос 1.7 | Страница 48 92)/т)`.

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.4 | Вопрос 2.1 | Страница 48

Найдите «dy»/»dx», если: x = cosec ² θ, y = cot ³ θ at θ= `pi/(6)`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.4 | Вопрос 2.2 | Страница 48

Найдите «dy»/»dx»`, если: x = a cos <sup>3</sup> θ, y = a sin <sup>3</sup> θ at θ = `pi/(3)`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.4 | Вопрос 2.3 | Страница 48

Найдите `»dy»/»dx»`, если: x = t ² + t + 1, y = `sin((pit)/2) + cos((pit)/2) «at» т = 1`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.4 | Вопрос 2.4 | Страница 48

Найдите `»dy»/»dx»`, если: x = 2 cot t + cos 2t, y = 2 sin t – sin 2t при t = `pi/(4)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1. 4 | Вопрос 2.5 | Страница 48

Найдите `»dy»/»dx»`, если: x = t + 2sin (πt), y = 3t – cos (πt) при t = `(1)/(2)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.4 | Вопрос 3.1 | Страница 48

Если x = `asqrt(secθ — tanθ), y = asqrt(secθ + tanθ), «покажите, что» «dy»/»dx» = y/x`.

ПОСМОТРЕТЬ РЕШЕНИЕ 92 — 9`

ПРОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 1.2 | Страница 60

Найдите производные второго порядка от следующего: e ^2x . tan x

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 1.3 | Страница 60

Найдите производные второго порядка от следующего: e ^4x . cos 5x

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 1.4 | Страница 60

Найдите производные второго порядка от следующего: x ³ .logx

9093)`.

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 4.01 | Страница 60

Найдите n ^th производную от следующего: (ax + b) ^m  

ПРОСМОТР РЕШЕНИЯ

Упражнение 1. 5 | Вопрос 4.02 | Страница 60

Найдите n ^th производную от следующего: `(1)/x`

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.5 | Вопрос 4.03 | Страница 60

Найдите n ^th производную от следующего: e ^ax+b  

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 4.04 | Страница 60

Найдите n-ю производную от следующего: a ^px+q  

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 4.05 | Страница 60

Найдите n ^th производную от следующего: log (ax + b)

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.5 | Вопрос 4.06 | Страница 60

Найдите производную n ^th следующего выражения: cos x

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 4.07 | Страница 60

Найдите n ^th производную от следующего: sin (ax + b)

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 4.08 | Страница 60

Найдите производную n ^th следующего выражения: cos (3 – 2x)

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1. 5 | Вопрос 4.09 | Страница 60

Найдите n ^th производную от следующего: log (2x + 3)

ПРОСМОТР РЕШЕНИЯ

Упражнение 1.5 | Вопрос 4.1 | Страница 60

Найдите n ^th производную от следующего: `(1)/(3x — 5)`

ПОСМОТРЕТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 4.11 | Страница 60

Найдите n ^th производную от следующего: y = e ^x . cos (bx + c)

ПОКАЗАТЬ РЕШЕНИЕ

Упражнение 1.5 | Вопрос 4.12 | Страница 60

Найдите n ^th производную от следующего: y = e ^8x . cos (6x + 7)

ПОСМОТРЕТЬ РЕШЕНИЕ

Решения Balbharati для математики и статистики 2 (искусства и науки) 12-й стандарт HSC Maharashtra State Board Глава 1 Дифференциация Разное Упражнение 1 [Страницы 61 — 63] 92` в.р.т. х при х = 1 равно

• `-(29)/(15)`

• `(7)/(3)`

• `(31)/(15)`

  0 `(29)/(15)`

ПРОСМОТР РЕШЕНИЯ

Разное Упражнение 1 | вопрос 2 | Страница 62

Выберите правильный вариант из предложенных вариантов:

Если y = sec (tan ^–1 x), то `»dy»/»dx»` при x = 1 равно

• `(1)/(2)`

• 92)`

ПРОСМОТРЕТЬ РЕШЕНИЕ

Разное Упражнение 1 | Вопрос 7 |

Выберите правильный вариант из предложенных вариантов:

Если y является функцией x и log (x + y) = 2xy, то значение y'(0) = . ….. ….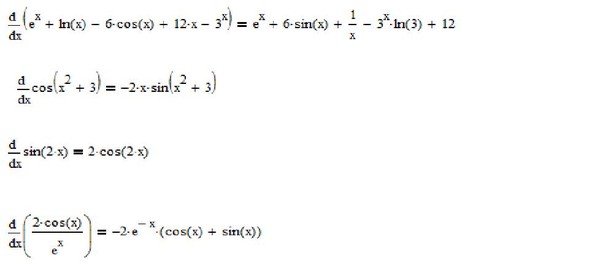

• 2

• 0

• –1

• 1

. Вопрос 8 | Страница 62

9092) + «B»»dy»/»dx» + «C»` = 0, тогда значения A, B, C равны

• x ² , – x, – y

• x ² , x, y

• x ² , x, — y

• x ² , –x, Y

9095. View Solid и наука) 12-й стандарт HSC Maharashtra State Board Глава 1 Дифференциация Разное Упражнение 2 [Страницы 63 — 64]

Разное Упражнение 2 | Вопрос 1 | Страница 63

Решите следующее: 

f(x) = –x, для – 2 ≤ x < 0
= 2x, для 0 ≤ x < 2
= `(18 — x)/(4)` , для 2 < x ≤ 7
g(x) = 6 – 3x, для 0 ≤ x < 2
= `(2x — 4)/(3)`, для 2 < x ≤ 7
Пусть u (x) = f[g(x)], v(x) = g[f(x)] и w(x) = g[g(x)]. Найдите каждую производную при x = 1, если она существует, т.е. найдите u'(1), v'(1) и w'(1). Если его нет, то объясните почему?

ПОСМОТРЕТЬ РЕШЕНИЕ

Разное Упражнение 2 | вопрос 2 | Страница 63

Решите следующее: 

Значения f(x), g(x), f'(x) и g'(x) приведены в следующей таблице:

x	ф(х)	г(х)	ф'(х)	фг'(х)
– 1	3	2	– 3	4
2	2	– 1	– 5	– 4

Совпадение со следующим:

Группа A – Функция	Группа B – производная
(A)`»d»/»dx»[f(g(x))]»at» x = -1`	1. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт