1.2. Производная сложной функции
Пусть y=f(u), где и является не независимой переменной, а функцией независимой переменной х: и=(х). Таким образом, у=f((х)).
В этом случае функция у называется сложной функцией х, а переменная и — промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы:
Теорема: Если у=f(и) и и=(х) – дифференцируемые функции своих аргументов, то производная сложной функции у=f((х)) существует и равна производной функции у по промежуточному аргументу и на производную промежуточного аргумента и по независимой переменной х:
Эта теорема
распространяется и на сложные функции,
которые задаются с помощью цепочки,
содержащей три звена и более.
Например, если у=f(и), и=(v), v=(x), т.е. у=f(((х))), то
1.3. Формулы дифференцирования
Во всех приведенных ниже формулах буквами и и v обозначены дифференцируемые функции независимой переменной х: и=и(х), v=v(x), а буквами а, с, п – постоянные:
.
Остальные формулы написаны как для функций независимой переменной, так и для сложных функций:
7. 7а.
8. 8а.
9. 9а.
10. 10а.
11. 11а.
12. 12а.
13. 13а.
14. 14а.
15.
(ех )=ех.
15а.
(еи)=еии.
16. 16а.
17. 17а.где а>0, а1.
При решении приведенных ниже примеров сделаны подробные записи. Однако следует научиться дифференцировать без промежуточных записей.
Пример 1. Найти производную функции у=5х3-2х+
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3, 5, 7 и 8:
Пример 2. Найти производную функции
Решение. Применяя формулы 6, 3, 7 и 1, получим
Пример
3. Найти
производную функции у=sin
Решение. Это сложная функция с промежуточным аргументом sin. Используя формулы 7а и 10, имеем
f ()
= 3 sin2
(sin )=3
sin2
cos .
Вычислим значение производной при =/3:
Пример 4. Найти производную функции
Решение. Это сложная функция с промежуточным аргументом cos х. Применяя формулы 3, 5, 7а, 11, 16а, получим
Пример 5. Найти производную функции
Решение. Дифференцируем данную функцию по формулам 6, 12, 3 и 1:
Пример 6. Найти производную функции и вычислить ее значение приt=2.Решение. Сначала преобразуем функцию, используя свойства логарифмов:
Теперь дифференцируем по формулам 3, 16а, 7 и 1:
Вычислим значение производной при t=2:
Пример
7.
Найти
производную функции
и вычислить ее значение прих=0.
Решение. Используем формулы 6, 3, 14а, 9а, 5 и 1:
Вычислим значение производной при х=0:
1.4. Геометрический смысл производной
Производная функции имеет простую и важную геометрическую интерпретацию.
Если функция y=f(x) дифференцируема в точке x,
Угловой коэффициент касательной, проведенной к графику функции y=f{x) в точке (х0, у0), равен значению производной функции при х=х0, т.е. kкас=у (х0).
Уравнение этой касательной имеет вид:
у-у0 = f (х0)
(х-х0).
Пример 8. Составить уравнение касательной к графику функции в точкеА(3, 6).
Решение. Для нахождения углового коэффициента касательной найдем производную данной функции:
Угловой коэффициент касательной равен значению производной функции при х=3:
k=у (3)=232-23-2=18-6-2=10.
Уравнение касательной имеет вид
у-6 = 10 (х-3), или у-6 = 10х-30, т.е.
10х—у-24 = 0.
Пример 9. Составить уравнение касательной, проведенной к графику функции в точке с абсциссойх=2.
Решение. Сначала найдем ординату точки касания А (2, у). Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т. е.
А (2, 2).
Уравнение
касательной, проведенной к кривой в
точке
Угловой коэффициент касательной равен значению производной функции при х=2:
Тогда уравнение касательной:
у-2 = — (х-2), у-2=-х+2, т. е. х+у-4 = 0.
Сложная функция. Производная сложной функции – методическая разработка для учителей, Маукешева Менсулу Бурангалиевна
|
Общая цель: |
1) образовательная – сформировать понятие сложной функции, изучить алгоритм вычисления производной сложной функции, показать его применение при вычислении производных. 2) развивающая – продолжить развитие умений логически и аргументировано рассуждать, используя обобщения, анализ, сравнение при изучении производной сложной функции. 3) воспитательная – воспитывать наблюдательность в ходе отыскания математических зависимостей, продолжить формирование самооценки при осуществлении дифференцированного обучения, повышать интерес к математике. |
|
Ожидаемый результат: |
— Знает формулы сложных функций, алгоритм вычисления производной сложной функции. — Умеет применять их при вычислении производных . — Уметь применять применение формул из сайта BilimLand.kz в разных ситуациях. — Уметь представлять и защищать индивидуальные задания. |
|
Тип урока: |
Комбинированный с применением элементов 7 модулей, Элементы Полиязычья в обучении и ресурсов BilimLand.kz, ресурсы: iTest.kz, Видеоколлекция. Математика, Познавательные фильмы. видео Большие люди (Эйлер). |
|
Задания: |
Карточки с упр. из сайта BilimLand.kz, карточки с формулами, упражнения для выполнения заданий. |
|
Источники, оснащение и оборудование, ресурсы: |
BilimLand.kz: Видеоколлекция + iTest.kz + Начальная математика + Познавательные фильмы. Компьютер, проектор, ноутбуки на каждой парте, планшет, смартфоны, стикеры, карточки для светофора, листы оценивания, критерии оценивания светофора и заданий iTest.kz, девиз, тема урока, итог урока на русском, казахском и английском языках, бэйджики. |
Ход урока
|
Этапы урока |
Действия учителя |
Ресурсы и модули |
Действия учеников |
|
|
Вводная часть 2 мин |
1. Здравствуйте, ребята! Стратегия «пять пальцев» Сегодня будем продолжать работать в парах. Обращение внимания учащихся на листы оценивания по критериям, которые выполняют оценивание взаимно. Повторить критерии оценивания по светофорам.  И нам снова будет помогать сайт BilimLand.kz. Хочу напомнить, что это онлайн образовательный портал для дошкольной подготовки младших классов, средних классов и старших классов. BILIM – знание. Материалы сайта помогут подготовиться к различным экзаменам, ВОУДу и ЕНТ, повторить забытый материал за предыдущие классы. Цель сайта – сделать качественное образование доступным для всех.
|
Создание коллаборативной среды Модуль Новые подходы, Парная работа Вовлечение всех
Модуль Лидерство |
Учащиеся приветствуют учителя. Поднимают палец
Слушают
Читает Кристина |
|
|
5 минут |
3. Проверка пройденного материала — Горячий стул (Знание основных формул производной) Проверка дом задания заранее на доске, а другой из класса проверяет (красным мелом). Задания из вариантов итоговой аттестации (экзаменационный материал) Вариант 13 и14 (3)
Найти производную функции. Теперь давайте вспомним, как вычисляется производная различных функций. Для этого вы должны выполнить 7 заданий. К каждому заданию предложены варианты ответов, зашифрованные буквами. Правильное решение каждого задания позволяет открыть нужную букву фамилии ученого, который ввел обозначение y‘, f ‘(x). Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс. Видеоколлекция. Телевизионные программы. Большие люди. 28. Айтеке би Байбекулы. Леонард Эйлер. Мария Тальони Белоусова Женя iTest.kz Понятие производной. Производная основных функций Каждая пара учащихся выбирает задание и решает, готовятся отвечать на основном экране. Другие оценивают. В Листы оценивания заносятся баллы. |
Модуль Критическое мышление iTest.kz модуль ИКТ
Диалоговое обучение
Модуль «Талантливые и одаренные» модуль «ИКТ»
|
Отвечает кто на «горячем стуле», остальные задают вопросы
Решают и прикрепляют соответствующую букву
Слушают и задают вопросы, оценивают светофором |
|
|
|
А теперь прочитаем тему урока Тема урока: Сложная функция. Күрделі функция. Күрделі функцияның туындысы. Complex function. Derivative of complex function. Наш девиз урока: BilimLand, iTest, Twig.kz С вами к знаниям нам преграды нет!
BilimLand, iTest, Twig.kz Сіздермен бірге бізге білімге кедергі жоқ!
BilimLand, iTest, Twig.kz With your knowledge we are no obstacles! Как вы думаете: Какова же цель нашего урока? |
Элементы полиязычья |
Все вместе произносят тему урока и девиз (на трех языках), автором которых являются сами учащиеся и учитель отвечают |
|
|
Основная часть (2 мин)
|
iTest. Записывают формулы 1,3,5,6,7,8 Глава Производная сложной функции. Прослушивание видеолекции №1 на стр. 4 знакомятся с внутренней и внешней функциями
Глава Производная сложной функции, упр. 4 стр. 4 Выполняют Алгоритм вычисления производной сложной функции f(x) = h(g(x)).
Каждому дается памятника с алгоритмом. 4. Учитель у доски: f(x) = (3-5x)5
Выполняют упр. 5 стр. 4 ответы на основной экран по желанию Остальные оценивают светофорами Стр. 5 Видеолекция. Упр 7 — 4 учащихся у доски по желанию, остальные в тетрадях Упр. 8 еще 4 учащихся у доски |
BilimLand.kz курс Математика Раздел Начала анализа. Производная сложной функции. модуль «ИКТ»
Диалоговое обучение
BilimLand. курс Математика Раздел Начала анализа. Производная Производная сложной функции. модуль «ИКТ»
Диалоговое обучение
Модуль «Возрастные особенности»
модуль «ИКТ»
Диалоговое обучение
Модуль Критическое мышление
|
Слушают, делают записи и отвечают на поставленные вопросы
Слушают, делают записи
Решают на ноутбуках, хлопают по завершении работы, Пары оценивают
Решают на ноутбуках, хлопают по завершении работы, Пары оценивают
Получают карточки с формулами
Решают и выводят ответы на основном экране, оценивают
Решают и выводят ответы на основном экране, оценивают
|
|
|
Подведение итогов (2 мин)
|
Рефлексия 3 мин. Чемодан, мясорубка, корзина На доске вывешиваются рисунки чемодана, мясорубки, корзины. Чемодан – все пригодится в дальнейшем. Мясорубка – информацию переработаю. Корзина – все выброшу. Ученикам предлагается выбрать, как они поступят с информацией, полученной на уроке. Организация работы дома: 2 мин. Ученики: заполняют домашнее задание в дневник Дом задание стр. 6 упр. 9 и 10 BilimLand.kz. Производная. Производная сложной функции. |
Модуль «Новые подходы в преподавании и обучении» «Оценивание»
|
Прикрепляют стикеры
Запись в дневники |
|
|
Сдать листы оценивания |
Модуль «Новые подходы в преподавании и обучении» Модуль «Оценивание» |
Оценивание Сдают лидеры листы оценивания |
||
|
Оценки объявить с обоснованием каждому ученику |
Модули «Лидерство» «Оценивание» |
Учитель выставляет итоговую оценку |
||
|
Изменения по уроку |
Урок показал, что вполне можно совмещать несколько современных технологий на одном уроке, BilimLand. Урок получился плотным, интересным, содержательным и главное понравился моим ученикам. Мы с детьми убедились, что учащиеся самостоятельно могут изучать учебный материал и решать упражнения на закрепление BilimLand.kz . |
|||
Орг. момент.
Актуализация знаний учащихся. 
Производная сложной функции.
kz изучают конспект лекции к тесту, выписывают главное (формулу вычисления производной сложной функции) и взаимно проверяют задают друг другу вопросы, Таблица производных сложной функции 
kz
Индивидуальная работа. Рефлексия
kz применять в дальнейшем ежедневно. Какие изменения по уроку?Приложение № 1
Критерии оценивания по светофору
|
критерии |
Вид смайлика |
|
|
Все решено верно и доступно |
|
|
|
Допущены ошибки и не все понятно |
|
|
|
Не выполнено задание и не понятно объяснение |
|
Приложение № 2
|
№ |
Ф И |
опрос |
iTest |
BilimLand. Упр 4 стр 4
|
BilimLand.kz упр 5 стр 4 |
BilimLand.kz упр 7 стр 5 |
BilimLand.kz упр 8стр 5 |
итог |
|
1 |
Азбергенев Диаз |
|
|
|
|
|
|
|
|
2 |
Белоусова Евгения |
|
|
|
|
|
|
|
|
3 |
Гаврилина Ксения |
|
|
|
|
|
|
|
|
4 |
Головченко Максим |
|
|
|
|
|
|
|
|
5 |
Зверева Кристина |
|
|
|
|
|
|
|
|
6 |
Каиржанов Тимур |
|
|
|
|
|
|
|
|
7 |
Каиржанов Райымбек |
|
|
|
|
|
|
|
|
8 |
Куксова Анастасия |
|
|
|
|
|
|
|
|
9 |
Мамедов Родион |
|
|
|
|
|
|
|
|
10 |
Меньшова Елизавета |
|
|
|
|
|
|
|
|
11 |
Кучкина Валерия |
|
|
|
|
|
|
|
|
12 |
Старкова Александра |
|
|
|
|
|
|
|
|
13 |
Цыпленков Данил |
|
|
|
|
|
|
|
kz
|
Баллы |
Оценка |
|
|
31 и более |
«5» |
|
|
от 16 до 30 |
«4» |
|
|
от 8 до 15 |
«3» |
|
|
от 5 до 8 |
«2 « |
|
|
+ и — |
0,5 балл |
|
+ 1 балл
— 0 баллов
Лидер группы:
Учитель математики: Маукешева М.
Б.
Приложение № 3
Критерии оценивания выполнения теста
|
Процент выполнения |
Оценка |
|
От 90% до 100 % |
5 |
|
От 70% до 90 % |
4 |
|
От 50% до 70 % |
3 |
|
Ниже 50% |
2 |
Приложение № 4
Тема урока:
Сложная функция.
Производная сложной функции.
Күрделі функция. Күрделі функцияның туындысы.
Complex function. Derivative of complex function.
Наш девиз урока:
BilimLand, iTest, Twig.kz
С вами к знаниям нам преграды нет!
BilimLand, iTest, Twig.kz
Сіздермен бірге бізге білімге кедергі жоқ!
BilimLand, iTest, Twig.kz
With your knowledge we are no obstacles!
Итог урока
BilimLand.kz iTest.kz Twig.kz
Спасибо вам за наш успех!!!
Біздін жетістіктерімізге алгысымызды білдіреміз!!!
Thank you for our success!!!
Физический или геометрический смысл комплексной производной
Задай вопрос
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 5к раз
$\begingroup$
Производная функции с действительным знаком в точке — это наклон функции в этой точке.
Аналогично, каков физический или геометрический смысл производной комплекснозначной функции в точке?
- комплекс-анализ
- комплекс-геометрия
$\endgroup$
2
$\begingroup$
Вы можете думать о производной как о выражении локального/мгновенного растяжения и вращения. 9{i\theta}$ говорит, что вблизи $a$ мы (приблизительно) растягиваем/сокращаем расстояния на коэффициент $r$, а также поворачиваем на угол $\theta$. Например, $f'(a)=i$ означает, что мы просто вращаемся против часовой стрелки на $\pi/2$ радиан. А $f'(a)=-i/2$ означает, что мы сжимаемся в 2 раза и поворачиваемся против часовой стрелки на $3\pi/2$ радиан.
$\endgroup$
$\begingroup$
Один ясный физический смысл дает теория гармонических функций.
В частности, если $f=u+iv$ комплексно-дифференцируема на открытом множестве, то обе составляющие функции удовлетворяют уравнению Лапласа. Другими словами, их можно рассматривать как возможные функции потенциальной энергии для силового поля, консервативного в домене, или как функции напряжения для электростатического поля в домене. Однако есть еще кое-что, связь между $u$ и $v$ заключается в том, что они определяют кривые уровня, которые пересекаются под прямым углом. То есть $u$ и $v$ — ортогональные функции. Следовательно, если мы будем думать об одном как о потенциальной энергии, то другое будет играть роль силы. Касательные линии к силовому полю перпендикулярны эквипотенциальным линиям потенциала. Все это заключено в простом предположении, что $f'(z)$ существует и не равно нулю.
$\endgroup$
$\begingroup$
$\endgroup$
Прекрасный мир сложных функций | Каспер Мюллер
Фракталы как результат рекурсивных сложных функцийИсследование скрытой структуры в высших измерениях
Это первая часть небольшой серии статей, предназначенных для описания наиболее интересных результатов комплексного анализа в доступной форме.
Даже если вы не проходили курс теории сложных функций, вы сможете получить ценное представление об этой фантастической области. Если вы изучаете математику или освежаете свои навыки, я считаю, что это также хорошее место, так как я познакомлю вас со многими замечательными взглядами на эту теорию.
Прежде чем исследовать эту плодотворную и красивую тему, давайте начнем с некоторых основ.
При изучении вещественных функций одной действительной переменной непрерывность и дифференцируемость зависят от некоторых условий, использующих пределы только с двух направлений. Одно направление слева направо и другое справа налево. Разумеется, других направлений на реальной прямой нет, так как она одномерна.
Например, чтобы проверить непрерывность, можно проверить, что предел значения функции в качестве аргумента приближается к некоторому числу, скажем, a слева равно тому же значению, когда аргумент приближается к a справа, т.е.
В том же смысле дифференцируемость также имеет двустороннее условие, но это более сильное условие, чем непрерывность.
То, что предел можно взять только с двух сторон, делает эти свойства довольно слабыми в том смысле, что в реальном анализе у нас может быть много вредоносных функций, удовлетворяющих критерию дифференцируемости в некоторой точке реальной линии, но если функция удовлетворяет этому, то ее производная не обязательно дифференцируема в этой точке. На самом деле, даже не гарантируется, что предел к этой точке существует!
Более того, слабые условия на самом деле делают нашу жизнь довольно сложной в том смысле, что у нас есть ограниченное понимание этих функций, и поэтому количество мощных инструментов для них не очень впечатляет.
Однако, в мире комплексных чисел и их функций, это совсем другая история, как вы скоро увидите. Оказывается, условия намного сильнее, и поэтому в нашем распоряжении множество полезных инструментов и много красивых теорем.
На самом деле, в реальном анализе есть много проблем, которые мы можем решить (на момент написания статьи) только используя методы комплексного анализа.
Прежде чем мы углубимся в некоторые интересные факты, давайте договоримся о нескольких вещах. В реальном анализе мы обычно сопоставляем возможный бесконечный интервал (или их объединение) реальной линии с собой. В частности, области определения этих функций одномерны.
Прежде чем перейти к сложным функциям, я очень кратко напомню вам о некоторых свойствах комплексных чисел, их геометрии и топологии.
Отправной точкой является воображаемая единица измерения. Это число i , которое удовлетворяет тому, что i² = -1 .
Ни одно действительное число не обладает этим свойством!
Комплексные числа можно понимать как двумерное действительное векторное пространство, натянутое на базис 1 и i. Другими словами. Комплексное число имеет вид a+bi и удовлетворяет обычным законам векторных пространств, т.е. распределительный закон, коммутативный закон и т. д.
Следовательно, существует геометрия, связанная с комплексными числами.
У них есть величина и направление (поскольку они являются векторами), и их следует визуализировать как лежащие в плоскости (называемой комплексной плоскостью), изоморфной (что означает ту же алгебраическую структуру) ℝ².
Так, например, комплексное число 3+4i является точкой (или вектором) (3, 4) на этой плоскости. В более общем смысле комплексное число a + bi — это точка (a, b) на комплексной плоскости.
Хорошо, что у нас есть векторное представление комплексных чисел, очень похожее на ℝ², но на самом деле здесь больше структуры, потому что мы, конечно, можем также перемножать комплексные числа. То есть это то, что математики называют кольцо , потому что векторные пространства являются абелевыми группами относительно их операции сложения .
Оказывается, это даже больше, чем кольцо. Поскольку каждый ненулевой элемент (комплексное число) имеет обратный, т. е. вы также можете делить комплексные числа, это особый вид кольца, называемый полем .
Когда вы умножаете два комплексных числа, вы используете закон распределения и помните, что i² = -1 .
Отлично. Теперь у нас есть понимание сложной плоскости.
В комплексном анализе мы обычно изучаем функции с подмножествами комплексной плоскости в качестве доменов. В уме вы можете представить себе возможно деформированный диск с нулем или большим количеством отверстий, который иногда представляет собой всю сложную плоскость.
В частности, области определения функции двумерны, и это приводит к некоторым интересным последствиям.
Отправной точкой комплексного анализа является понятие сложных дифференцируемых функций, также называемых голоморфными функциями.
Как упоминалось во введении, дифференцируемость означает, что существует определенный предел, но когда функция определена в двумерной области, существует бесконечно много направлений, из которых можно приближаться к числу. Это накладывает большое ограничение на набор голоморфных функций и придает этим функциям некоторые замечательные свойства.
Перед тем, как объявить их, давайте немного изучим этот всенаправленный предел.
Поскольку сложная функция одной комплексной переменной отображает комплексное число в комплексное число, мы могли бы записать ввод и вывод следующим образом
Чтобы дать простой пример этого, рассмотрим
То, что направление предела не имеет значения, подразумевает, что, в частности, если мы возьмем предел вдоль действительной оси, мы получим тот же результат, что и если мы возьмем предел вдоль мнимой оси.
Посмотрим, что это значит.
где δ и η проходят вдоль действительной оси. Эти два предела должны быть одинаковыми, что дает
. Когда мы расширим f в реальных функциях u и v , как указано выше, так что f = u+iv, и подставим это в дифференциальное уравнение, которое мы только что нашли, мы получим систему дифференциальных уравнений в частных производных, известную как уравнения Коши-Римана .
Наш вывод показывает, что каждая голоморфная функция должна удовлетворять этим уравнениям, что накладывает на них строгое требование.
Обратное почти верно. Но нам нужны некоторые аргументы, связанные с непрерывностью, чтобы это работало.
Также оказывается, что в точке, где производная данной голоморфной функции отлична от нуля, функция сохраняет угол. Это называется конформной картой и является важным и хорошим обменом этими функциями.
Первым признаком того, что эти функции обладают некоторыми интересными свойствами, является следующее. Оказывается, если функция голоморфна, т.е. комплексно дифференцируема в некоторой области, содержащей некоторую точку, скажем, p , то она комплексно дифференцируема бесконечно много раз в p .
Это можно сформулировать немного более компактно, а именно, что производная комплексной дифференцируемой функции комплексно дифференцируема.
Это, конечно, неверно для реальных функций вообще.
Аналитические функции
Это также означает, что голоморфные функции являются аналитическими , то есть имеют сходящийся степенной ряд вокруг любой точки своей области определения с некоторым радиусом сходимости.
На самом деле верно и обратное. Любая аналитическая функция голоморфна. Поэтому мы иногда называем их аналитическими функциями вместо голоморфных функций. Эти два определения математически эквивалентны, хотя мы подразумеваем под этими двумя выражениями что-то другое. Мы сохраняем оба определения, так как существует также понятие вещественных аналитических функций, которое как определение не эквивалентно вещественной дифференцируемости.
Как упоминалось выше, голоморфная функция имеет степенной ряд разложения. Степенные ряды имеют так называемый радиус сходимости. Вы должны попытаться представить диск на комплексной плоскости как область определения такого ряда, а радиус этого диска — это его радиус сходимости. Это означает, что на границе круга есть хотя бы одна точка, из-за которой ряд расходится.
Как вы увидите в следующей части, есть способы обойти эти раздражающие точки, опять же из-за двумерности сложной плоскости!
Прежде чем погрузиться в суть голоморфии, я хочу поделиться с вами особенно приятной забавой, а именно геометрией укоренения.
И я говорю не о корнях многочленов, а о квадратных корнях, кубических корнях и т. д.
Со школы мы все знаем о квадратном корне. Что квадратный корень, скажем, из 4 равен 2. Но что это за операция на самом деле? Если вопрос, эквивалентный «, чему равен квадратный корень из 4?» » равно « какое число в квадрате равно 4? », то, конечно, вопрос некорректен, потому что есть, конечно, два числа, удовлетворяющих этому.
По соглашению мы имеем в виду положительный квадратный корень из , но есть два квадратных корня из 4, а именно 2 и -2.
Как насчет кубического корня? Что ж, в какой-то момент мы все узнали, что существует ровно один кубический корень из действительного числа. А на самом деле это правда с доработками. Это правда, что существует только один реальный кубический корень из вещественных чисел, но на самом деле есть два других корня, скрывающихся в другом измерении! Есть три различных кубических корня из любых 9номер 0062 кроме 0 .
На самом деле существует n различных n-ых корней любого комплексного (включая действительное, конечно) числа!
Как всегда, аддитивная идентичность 0 является особым числом в мультипликативном мире. Если мы посчитаем то, что известно как множественность, то вышесказанное верно и для 0, , в противном случае мы должны исключить 0 из утверждения.
Но что еще более удивительно, эти n корни комплексного числа z лежат симметрично на окружности с радиусом, равным положительному корню n из длины z , с центром в точке 0.
Это объясняет, почему существует только один действительный кубический корень и два действительных квадратных корня. корни вещественного числа, потому что если их надо расположить симметрично по окружности, то один корень определяет положение остальных. Например, один из квадратных корней из 1 равен 1, но поскольку квадратных корней ровно два, а другой корень должен располагаться симметрично вокруг единичной окружности, он должен быть равен -1.
Таким же образом один кубический корень из 1 равен 1, но тогда два других корня лежат в вершинах равностороннего треугольника, вписанного в единичную окружность с одной вершиной в 1.
В общем, n корни из 1 образуют вершины правильного n-угольника (многоугольника с n сторонами), и все они лежат на единичной окружности. Они называются корнями единства .
Пятые корни из единицыn корни из единицы на самом деле образуют абелеву группу (относительно умножения) и вообще обладают многими интересными свойствами, но это для другой статьи.
Это уже показывает, что, расширив реальные числа на другое измерение, многие тайны, которые были скрыты во тьме, теперь становятся ясными, и это только начало нашего просветления.
Почти кажется (извините меня за мое философское мнение, которое я навязываю вам здесь), что воображаемое измерение необходимо для того, чтобы действительно понять многие из реальных понятий, таких как извлечение корней или умножение на -1 (вы можете взглянуть в этой истории для обсуждения этого).
Как будто он был там все время, и мы изо всех сил пытались видеть в темноте, в более низком измерении — но мы видели только тени реальных вещей, из-за чего мы не могли их правильно понять. Однако дополнительное измерение дало нам свет, в котором мы так отчаянно нуждались.
Здесь все становится по-настоящему интересным.
Когда мы интегрируем действительные функции, мы делаем это по интервалу (возможно, бесконечному интервалу) реальной линии, и здесь снова из-за одномерности, когда заданы конечные точки, у нас нет особого выбора интервала, кроме направления .
Это не относится к комплексным интегралам. Когда у нас есть две конечные точки на комплексной плоскости (которые могут быть одной и той же точкой), тогда у нас есть бесконечно много кривых (или объединения определенных связанных кривых, называемых контурами), по которым мы можем интегрировать, поскольку область является двумерной.
Это может показаться устрашающим (и трудным для визуализации), но это не так плохо, как кажется.
В самом деле, для голоморфных функций справедлива следующая удивительная вещь.
Когда два контура (вы можете думать о контурах как о кривых на комплексной плоскости) выбираются между одними и теми же двумя конечными точками, то, если мы можем непрерывно деформировать один контур в другой (т.е. если они гомотопны — см. ниже gif), то интегралы по ним равны.
Это интуитивно означает, что если в области между контурами нет дыр, то не имеет значения, какой контур мы выберем.
Два гомотопически эквивалентных контура в комплексной плоскостиЭто имеет некоторые интересные следствия по чисто топологическим причинам.
Это означает, например, что если две конечные точки контура совпадают (так что мы имеем замкнутый контур), то если пространство, которое вписывает контур, стягиваемо, т.е. гомотопно точке (постоянная кривая), то интеграл по этому контуру равен нулю. Это известно как теорема Коши в честь Огюстена-Луи Коши.
Итак, если функция голоморфна в этой области, то интеграл равен нулю.
вместо f голоморфная функция в области D, содержащей γ.
Напомним, что голоморфные функции не имеют полюсов в своей области определения, т. е. не взрываются и не обращаются в бесконечность ни в одной точке. С ними очень приятно работать, но иногда вы хотите работать с функциями, которые голоморфны во всей своей области, за исключением исчисляемого количества точек.
Эти функции называются мероморфный . Вы можете думать о них как об обобщении дробей многочленов. Самое замечательное в них то, что они обладают голоморфными свойствами, но также могут иметь полюса или сингулярности. Некоторыми из наиболее важных функций в математике являются мероморфные функции, включая дзета-функцию Римана , гамма-функцию, 1/z и т. д.
Некоторые из интересных вопросов, касающихся этих функций, конечно, связаны с полюсами и нулями этих функций. и получается, что контурный интеграл в сочетании с логарифмическая производная дает нам инструмент для вычисления именно этого.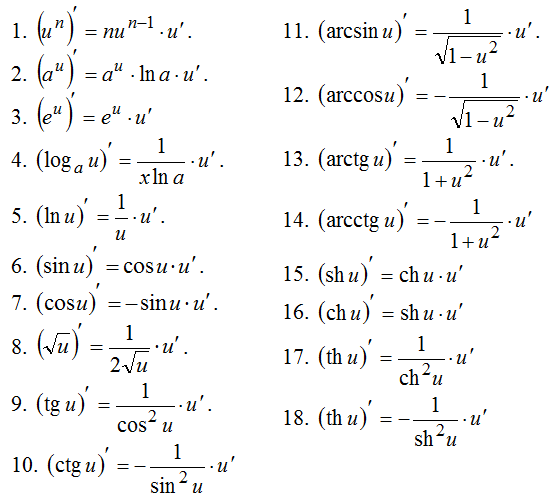
Если f мероморфная функция внутри и на замкнутом контуре C, и f не имеет ни нулей, ни полюсов на C, , то
Где Z P число нулей1 и число полюсов в C.
Очень интересно видеть, что интеграл касается только топологии, а не геометрии! Площадь и положение кривой не имеют значения, но важно то, что она замкнута и что функция имеет полюсы и нули в подмножестве, вписанном контуром комплексной плоскости — это важно!
Этот результат связан с теорией, называемой исчислением остатков , которая тесно связана с расширением ряда Тейлора , называемого рядом Лорана , но это для другой статьи.
Вы можете прочитать больше о ряде Тейлора здесь и изучить некоторые интересные свойства логарифмической производной вместе со мной здесь .
Прежде чем закончить эту часть, давайте подытожим то, что мы узнали.
Из-за разницы между геометрией и топологией в 1 и 2 измерениях на сложные функции накладываются более строгие ограничения, чем на реальные функции, если они должны удовлетворять некоторым условиям, включающим ограничения.
Это, в свою очередь, приводит к сильным свойствам функций, удовлетворяющих этим условиям, что делает голоморфные функции чрезвычайно полезными при решении задач как комплексного, так и реального анализа.
Кроме того, оказывается, что область топологии становится полезной, потому что комплексные интегралы, известные как контурные интегралы, зависят только от классов гомотопической эквивалентности контура, а не от самих путей.
Это привело к прекрасным открытиям Огюстена-Луи Коши и может быть использовано для вычисления нулей и полюсов мероморфных функций, которые мы скоро исследуем.
В следующей части мы продолжим изучение красоты голоморфных и мероморфных функций, потому что, как вы увидите, у них есть некоторые свойства, применение которых в квантовой физике еще не совсем понятно. Это связано с приданием значений расходящимся рядам и извлечением глубокой информации из функций даже за пределами их области определения.
Многие, кто имел возможность узнать больше о математике, путают ее с арифметикой и считают сухой наукой.
