Производные математические функции (Visual Basic для приложений)
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 2 мин
Ниже приводится список неинтринзивных математических функций, которые можно извлечь из внутренних математических функций.
| Функция | Производные эквиваленты |
|---|---|
| Secant | Sec(X) = 1 / Cos(X) |
| Cosecant | Cosec(X) = 1 / Sin(X) |
| Cotangent | Cotan(X) = 1 / Tan(X) |
| Арксинус | Arcsin(X) = Atn(X / Sqr(-X * X + 1)) |
| Арккосинус | Arccos(X) = Atn(-X / Sqr(-X * X + 1)) + 2 * Atn(1) |
| Арксеканс | Arcsec(X) = Atn(X / Sqr(X * X - 1)) + Sgn((X) - 1) * (2 * Atn(1)) |
| Арккосеканс | Arccosec(X) = Atn(X / Sqr(X * X - 1)) + (Sgn(X) - 1) * (2 * Atn(1)) |
| Арккотангенс | Arccotan(X) = Atn(X) + 2 * Atn(1) |
| Гиперболический синус | HSin(X) = (Exp(X) - Exp(-X)) / 2 |
| Гиперболический косинус | HCos(X) = (Exp(X) + Exp(-X)) / 2 |
| Гиперболический тангенс | HTan(X) = (Exp(X) - Exp(-X)) / (Exp(X) + Exp(-X)) |
| Гиперболический секанс | HSec(X) = 2 / (Exp(X) + Exp(-X)) |
| Гиперболический косеканс | HCosec(X) = 2 / (Exp(X) - Exp(-X)) |
| Гиперболический котангенс | HCotan(X) = (Exp(X) + Exp(-X)) / (Exp(X) - Exp(-X)) |
| Ареасинус | HArcsin(X) = Log(X + Sqr(X * X + 1)) |
| Ареакосинус | HArccos(X) = Log(X + Sqr(X * X - 1)) |
| Ареатангенс | HArctan(X) = Log((1 + X) / (1 - X)) / 2 |
| Ареасеканс | HArcsec(X) = Log((Sqr(-X * X + 1) + 1) / X) |
| Ареакосеканс | HArccosec(X) = Log((Sgn(X) * Sqr(X * X + 1) + 1) / X) |
| Ареакотангенс | HArccotan(X) = Log((X + 1) / (X - 1)) / 2 |
| Логарифм с основанием N | LogN(X) = Log(X) / Log(N) |
- Функции (Visual Basic для приложений)
Поддержка и обратная связь
Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.
в статье Поддержка Office VBA и обратная связь.
Обратные гиперболические функции их графики и формулы
Определения обратных гиперболических функций, их области определений и значений
arsh x — обратный гиперболический синус
- Обратный гиперболический синус (ареасинус),
- – это функция, обратная к гиперболическому синусу ( x = sh y ), имеющая область определения –∞ < x < +∞ и множество значений –∞ < y < +∞.
Ареасинус строго возрастает на всей числовой оси.
arch x — обратный гиперболический косинус
- Обратный гиперболический косинус (ареакосинус),
- – это функция, обратная к гиперболическому косинусу ( x = сh y ), имеющая область определения 1 ≤ x < +∞ и множество значений 0 ≤ y < +∞.
Ареакосинус строго возрастает на своей области определения.
Вторая ветвь ареакосинуса также определена при x ≥ 1 и расположена симметрично относительно оси абсцисс, – ∞ < y ≤ 0 :
. Она строго убывает на области определения.
Она строго убывает на области определения.
arth x — обратный гиперболический тангенс
- Обратный гиперболический тангенс (ареатангенс),
- – это функция, обратная к гиперболическому тангенсу ( x = th y ), имеющая область определения – 1 < x < 1 и множество значений –∞ < y < +∞.
Ареатангенс строго возрастает на своей области определения.
arcth x — обратный гиперболический котангенс
- Обратный гиперболический котангенс (ареакотангенс),
- – это функция, обратная к гиперболическому котангенсу ( x = cth y ), имеющая область определения |x| > 1 и множество значений y ≠ 0.
Ареакотангенс строго убывает на своей области определения.
Графики обратных гиперболических функций
График обратного гиперболического синуса (ареасинуса) y = arsh x График обратного гиперболического косинуса (ареакосинуса) y = arch x , x ≥ 1Пунктиром показана вторая ветвь ареакосинуса. График обратного гиперболического тангенса (ареатангенса) y = arth x , |x| < 1 График обратного гиперболического котангенса (ареакотангенса) y = arcth x , |x| > 1
Формулы с обратными гиперболическими функциями
Связь с тригонометрическими функциями
Arsh iz = i Arcsin z; Arch z = i Arccos z;
Arcsin iz = i Arsh z; Arccos z = – i Arch z;
Arth iz = i Arctg z; Arcth iz = – i Arcctg z;
Arctg iz = i Arth z; Arcctg iz = – i Arcth z;
Здесь i – мнимая единица, i2 = –1.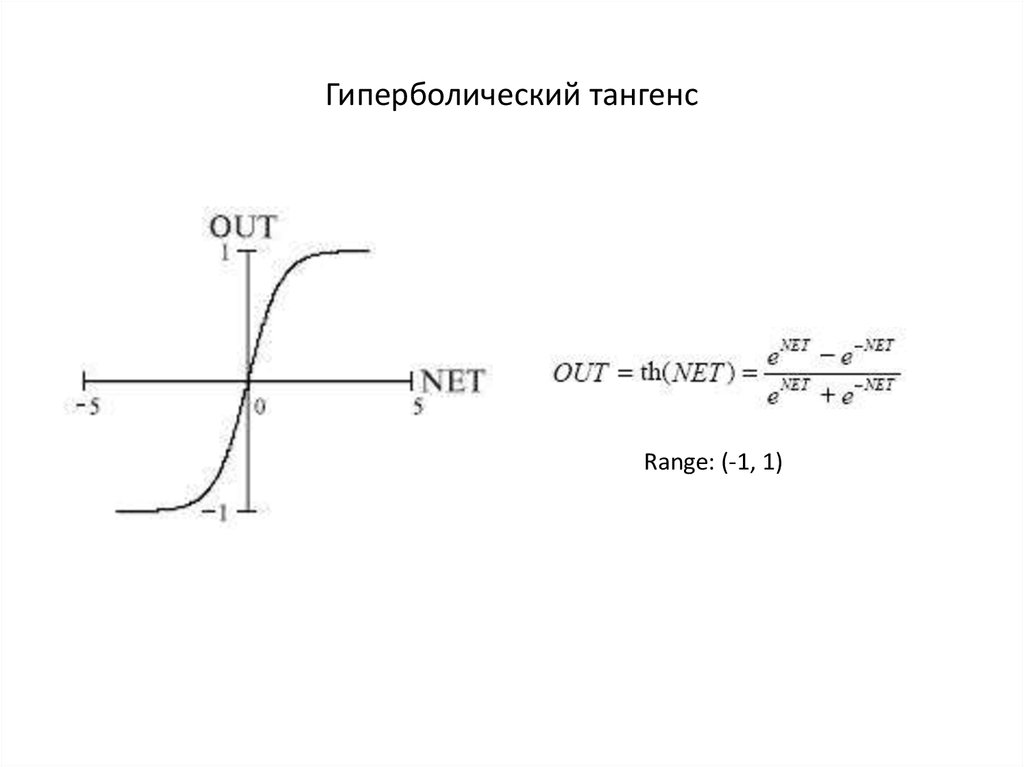
Четность
arsh(–x) = – arsh x; arch(–x) ≠ ± arch x;
arth(–x) = – arth x; arcth(–x) = – arcth x.
Функции arsh(x), arth(x), arcth(x) – нечетные. Функция arch(x) – не является четной или нечетной.
Формулы связи обратных гиперболических синусов через тангенсы и косинусов через котангенсы
;
;
;
.
Формулы суммы и разности
;
;
;
.
Производные обратных гиперболических функций
;
.
Интегралы от arsh x, arch x, arth x, arcth x
arsh x
Для вычисления интеграла от гиперболического арксинуса, делаем подстановку x = sh t и интегрируем по частям:
.
arch x
Аналогично, для гиперболического арккосинуса. Делаем подстановку x = ch t и интегрируем по частям учитывая, что t ≥ 0:
.
arth x
Делаем подстановку x = th t и интегрируем по частям:
;
;
;
.
arcth x
Аналогично получаем:
.
Разложения в ряды
arsh x
При |x| < 1 имеет место следующее разложение:
arth x
При |x| < 1 имеет место следующее разложение:
arcth x
При |x| > 1 имеет место следующее разложение:
Обратные функции
Гиперболический синус
При – ∞ < y < ∞ и – ∞ < x < ∞ имеют место формулы:
,
.
Гиперболический косинус
При 1 ≤ y < ∞ и 0 ≤ x < ∞ имеют место формулы:
,
.
Гиперболический тангенс
При – 1 < y < 1 и – ∞ < x < ∞ имеют место формулы:
,
.
Гиперболический котангенс
При – ∞ < y < – 1 или 1 < y < ∞ и x ≠ 0 имеют место формулы:
,
.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Производные обратных гиперболических функций — Криста Кинг Математика
Шесть обратных гиперболических производных
Чтобы построить наши обратные гиперболические функции, нам нужно знать, как найти обратную функцию в целом, поэтому давайте повторим.
Чтобы найти обратную функцию, мы обращаем ???x??? И они??? в функции. 9{-1}{х}???
Помните, что вы также можете увидеть эту функцию в виде ???y={\text{arccosh}}{(x)}???. Это оба представления функции аркгиперболического косинуса, и они могут использоваться взаимозаменяемо.
Теперь, когда мы поняли, как найти обратную гиперболическую функцию, когда мы начинаем с гиперболической функции, давайте поговорим о том, как найти производную обратной гиперболической функции.
Ниже приведен график, на котором показаны шесть обратных гиперболических функций и их производные.
Как использовать неявное дифференцирование для поиска формул для обратных гиперболических производных
Пройти курс
Хотите узнать больше об исчислении 1? У меня есть пошаговый курс для этого. 🙂
Учить больше
Дифференцирование аркгиперболического котангенса 97???
Получите доступ к полному курсу исчисления 1
Начать
Изучайте математикуКриста Кинг
