Производная и дифференциал
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Производная функции
2. Дифференцирование
3. Дифференциал
Центральные понятия дифференциального исчисления — производная и дифференциал возникли при рассмотрении множества задач естествознания и математики, каждая из которых приводила к вычислению пределов одного типа.
Производная функции
Определение
Если отношение
\[\frac{\Delta y}{\Delta x} =\frac{f(x+\Delta x)-f(x)}{\Delta x} \]
имеет конечный предел при стремлении приращения независимой переменной к 0, то такой предел называется производной функции f(х) при заданном х.
Производная функции — одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место.
Дифференцирование
Процесс нахождения производной называется дифференцированием. Обратная операция — восстановление функции по известной производной —интегрированием.
Для нахождения производной функции f(x) в точке x0 на основе определения следует выполнить следующие действия:
- Записать отношение \[\frac{\Delta y}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \]
- Упростить дробь, сократив ее, если возможно, на $\Delta x$;
- Найти производную f'(x0), вычисляя предел полученного выражения. Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x0.
Производная сложной функции равна произведению производной по промежуточной переменной по независимой переменной:
\[Z’x=F`\left(y\right)f’\left(x\right)\]
Пример 1
Найти производную функции
\[y=\ln x\]
Решение. {x} \sin xdx\]
{x} \sin xdx\]
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 09.12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Дифференциал функции
- Понятие и геометрический смысл дифференциала
- О разных формах записи дифференциала
- Свойства дифференциала
- Применение дифференциала в приближенных вычислениях
- Абсолютная и относительная погрешности приближенных вычислений
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
или
или же
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(
Почему дифференциал можно использовать в приближенных вычислениях?
Дифференциал, является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть.
В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см.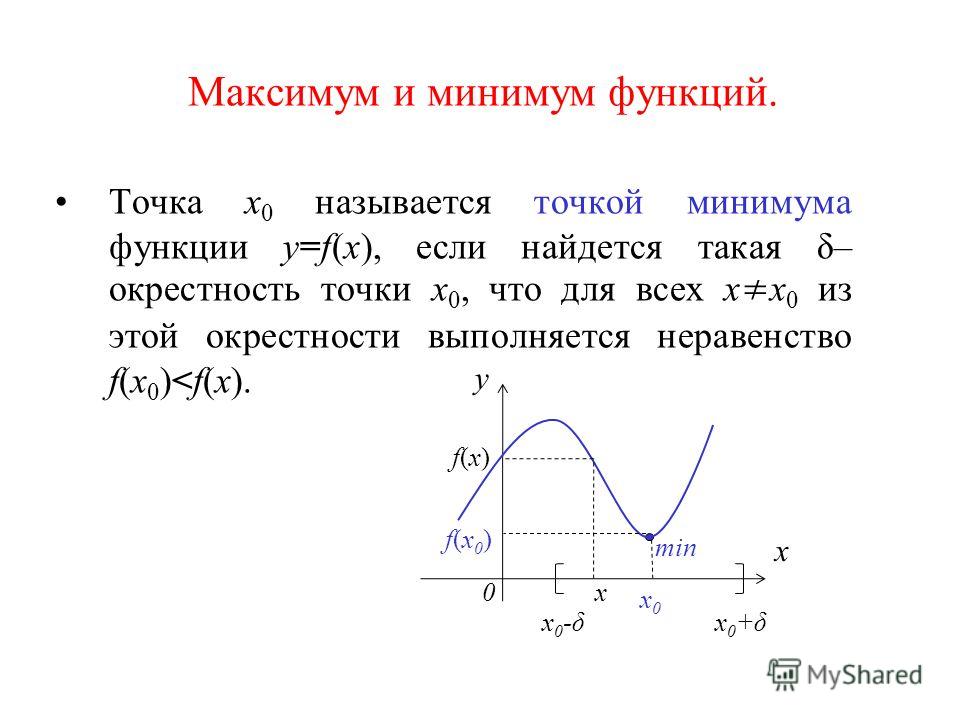 рисунок) к оси Ox, ближе к началу
координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.
рисунок) к оси Ox, ближе к началу
координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.
Дифференциал функции в точке x и обозначают
или
Следовательно,
(1)
или
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а — наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
(3)
или
(4)
Пример 1. Найти дифференциалы функций:
Найти дифференциалы функций:
1) ;
2) ;
3) ;
4) .
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) ;
2) ;
3) ;
4) .
Найти дифференциалы самостоятельно, а затем посмотреть решения
Пример 2. Найти дифференциал функции
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Пример 3. Найти дифференциал функции
в точке x.
Пример 4. Найти дифференциал функции
в точках x = 0 и x = 1.
Посмотреть правильные решения примеров 2, 3, 4.
В основном же задачи на дифференциалы — это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
(С – постоянная величина) (5)
(6)
(7)
(8)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .
Одно из особеннейших свойств дифференциала — инвариантность
формы дифференциала в случае сложных функций.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Установленное во втором параграфе приближенное равенство
или
(10)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
а
то
или
(11)
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном случае примет вид
Положим
тогда
Следовательно,
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 6. Пользуясь понятием дифференциала, вычислить приближенно
Решение. Число
является одним из значений функции
Так как производная этой функции
то формула (11) примет вид
Полагая
и
получаем
(табличное значение
Вычислить приближенно самостоятельно, а затем посмотреть решение
Пример 7. Вычислить приближенно:
1) ;
2) .
Посмотреть правильное решение и ответ.
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:
(12)
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
(13)
Если точное число неизвестно, то
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина была достаточно малой по сравнению с , так как чем меньше , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина вычислялась просто.
Пример 8. Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.
Оценить точность полученного результата.
Решение. Рассмотрим функцию
Её производная равна
а формула (11) примет вид
В данном случае было бы нерационально вычислять приближенно следующим образом:
так как значение
не является малым по сравнению со значением производной в точке
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда
Теперь, полагая
получим
Умножая на 4/3, находим
Принимая табличное значение корня
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Правило Лопиталя
- Частные производные
Поделиться с друзьями
Разница между дифференциальным и производным (Математика и статистика)
Чтобы лучше понять разницу между дифференциалом и производной функции, вам нужно сначала понять концепцию функции.
Функция — это одно из основных понятий в математике, которое определяет взаимосвязь между набором входов и набором возможных выходов, где каждый вход связан с одним выходом. Одна переменная является независимой переменной, а другая переменная является зависимой переменной.
Понятие функции — одна из самых недооцененных тем в математике, но она необходима для определения физических отношений. Возьмем, к примеру: утверждение «у есть функция х» означает, что что-то, связанное с у, напрямую связано с х по некоторой формуле. Скажем, если на входе 6 и функция добавить 5 на вход 6. Результат будет 6 + 5 = 11, что является вашим выходом.
Есть несколько исключений в математике, или вы можете сказать, проблемы, которые не могут быть решены с помощью обычных методов геометрии и алгебры. Новая ветвь математики, известная как исчисление, используется для решения этих проблем..
Исчисление принципиально отличается от математики, которая не только использует идеи из геометрии, арифметики и алгебры, но также имеет дело с изменением и движением.
Исчисление как инструмент определяет производную функции как предел определенного вида. Понятие производной функции отличает исчисление от других разделов математики. Дифференциал — это подполе исчисления, которое относится к бесконечно малой разнице в некоторой изменяющейся величине и является одним из двух фундаментальных делений исчисления. Другая ветвь называется интегральным исчислением.
Что такое дифференциал?
Дифференциал является одним из основных разделов исчисления наряду с интегральным исчислением. Это подполе исчисления, которое имеет дело с бесконечно малым изменением в некоторой изменяющейся величине. Мир, в котором мы живем, полон взаимосвязанных величин, которые периодически меняются.
Например, площадь круглого тела, которое изменяется по мере изменения радиуса, или снаряда, который изменяется со скоростью. Эти изменяющиеся объекты в математических терминах называются переменными, и скорость изменения одной переменной по отношению к другой является производной.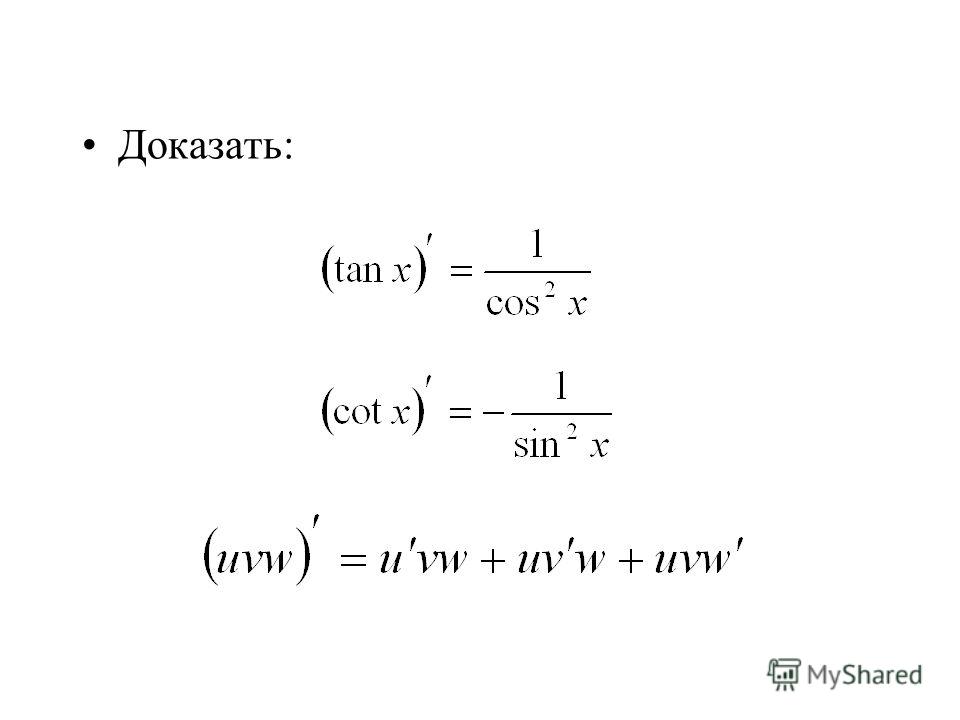 И уравнение, которое представляет отношения между этими переменными, называется дифференциальным уравнением.
И уравнение, которое представляет отношения между этими переменными, называется дифференциальным уравнением.
Дифференциальные уравнения — это уравнения, которые содержат неизвестные функции и некоторые их производные.
Что такое производная?
Понятие производной функции является одним из самых мощных понятий в математике. Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости.
Производная функции представляет собой мгновенную скорость изменения значения зависимой переменной относительно изменения значения независимой переменной. Это фундаментальный инструмент исчисления, который также можно интерпретировать как наклон касательной линии. Он измеряет, насколько крутой график функции находится в некоторой заданной точке на графике..
Проще говоря, производная — это скорость, с которой функция изменяется в определенной точке..
Разница между дифференциальным и производным
Определение дифференциала против.
 производный
производныйТермины дифференциальный и производный тесно связаны друг с другом с точки зрения взаимосвязи. В математике изменяющиеся объекты называются переменными, а скорость изменения одной переменной по отношению к другой называется производной.
Уравнения, которые определяют связь между этими переменными и их производными, называются дифференциальными уравнениями. Дифференциация — это процесс поиска производной. Производная функции — это скорость изменения выходного значения по отношению к ее входному значению, тогда как дифференциал — это фактическое изменение функции..
Дифференциальные отношения против. производный
Дифференцирование — это метод вычисления производной, которая представляет собой скорость изменения выхода y функции по отношению к изменению переменной x.
Проще говоря, производная относится к скорости изменения y относительно x, и это соотношение выражается как y = f (x), что означает, что y является функцией от x. Производная функции f (x) определяется как функция, значение которой генерирует наклон функции f (x), где она определена и f (x) является дифференцируемой. Это относится к наклону графика в данной точке.
Это относится к наклону графика в данной точке.
Представление Дифференциала Vs. производный
Дифференциалы представлены как dИкс, dY, dт, и так далее, где dх представляет небольшое изменение в х, dу представляет небольшое изменение у, и dт небольшое изменение т. При сравнении изменений в связанных величинах, где у — функция х, дифференциал dу можно записать как:
dу = ф‘(Икс) dИкс
Производная функции является наклоном функции в любой точке и записывается как d/dИкс. Например, производная от sin (x) может быть записана как:
d/dх грех (х) = грех (х)‘ = cos (x)
Дифференциальный и производный: Сравнительная таблица
Краткое изложение дифференциала производный
В математике скорость изменения одной переменной по отношению к другой переменной называется производной, а уравнения, выражающие взаимосвязь между этими переменными и их производными, называются дифференциальными уравнениями. В двух словах, дифференциальные уравнения включают производные, которые фактически указывают, как величина изменяется по отношению к другой. Решая дифференциальное уравнение, вы получаете формулу для количества, которое не содержит производных. Метод вычисления производной называется дифференцированием. Проще говоря, производная функции — это скорость изменения выходного значения относительно его входного значения, тогда как дифференциал — это фактическое изменение функции..
В двух словах, дифференциальные уравнения включают производные, которые фактически указывают, как величина изменяется по отношению к другой. Решая дифференциальное уравнение, вы получаете формулу для количества, которое не содержит производных. Метод вычисления производной называется дифференцированием. Проще говоря, производная функции — это скорость изменения выходного значения относительно его входного значения, тогда как дифференциал — это фактическое изменение функции..
Математика и статистика
Дифференциал и производная разница
Чтобы лучше понять разницу между дифференциалом и производной функции, вам нужно сначала понять концепцию функции.
Функция является одной из основных концепций математики, которая определяет взаимосвязь между набором входов и множеством возможных выходов, где каждый вход связан с одним выходом. Одной переменной является независимая переменная, а другая переменная — зависимая переменная.
Концепция функции является одной из самых недооцененных тем в математике, но имеет важное значение для определения физических отношений. Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x по какой-либо формуле. Скажем, если входной сигнал равен 6, а функция — добавить 5 к входу 6. Результат будет 6 + 5 = 11, что является вашим выходом.
Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x по какой-либо формуле. Скажем, если входной сигнал равен 6, а функция — добавить 5 к входу 6. Результат будет 6 + 5 = 11, что является вашим выходом.
В математике есть несколько исключений, или вы можете сказать о проблемах, которые не могут быть решены обычными методами геометрии и алгебры. Для решения этих проблем используется новая ветвь математики, известная как исчисление.
Исчисление принципиально отличается от математики, которая не только использует идеи из геометрии, арифметики и алгебры, но также имеет дело с изменением и движением.
Исчисление как инструмент определяет производную функции как предел определенного вида. Понятие производной функции отличает исчисление от других отраслей математики. Дифференциал — это подполе исчисления, которое относится к бесконечно малой разности в некоторой переменной величине и является одним из двух фундаментальных делений исчисления. Другая ветвь называется интегральным исчислением.
Другая ветвь называется интегральным исчислением.
Что такое Дифференциал?
Дифференциал — одно из фундаментальных делений исчисления, а также интегральное исчисление. Это подполе исчисления, которое имеет дело с бесконечно малым изменением в некоторой переменной величине. Мир, в котором мы живем, наполнен взаимосвязанными количествами, которые меняются периодически.
Например, площадь кругового тела, которая изменяется при изменении радиуса или снаряд, который изменяется со скоростью. Эти изменяющиеся сущности в математических терминах называются переменными, а скорость изменения одной переменной по отношению к другой является производной. И уравнение, представляющее связь между этими переменными, называется дифференциальным уравнением.
Читайте также: Bloodborne 2 дата выхода на ps4
Дифференциальные уравнения — это уравнения, содержащие неизвестные функции и некоторые их производные.
Что такое производная?
Понятие производной функции является одним из самых мощных понятий в математике.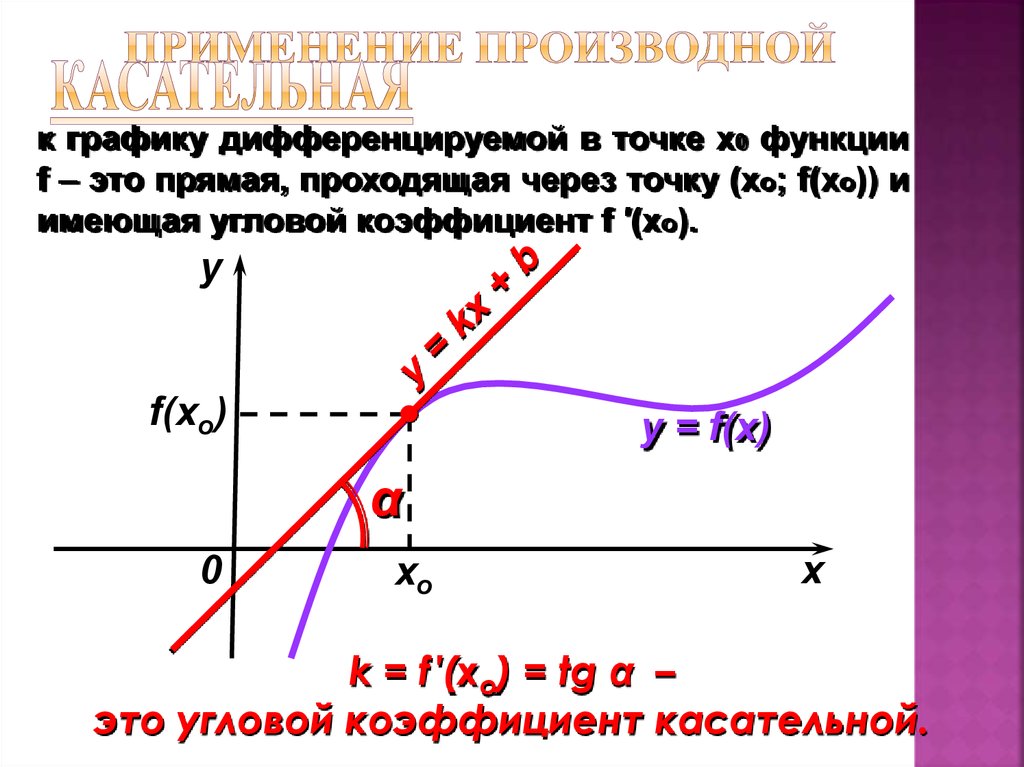 Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости.
Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости.
Производная функции представляет собой мгновенную скорость изменения значения зависимой переменной по отношению к изменению значения независимой переменной. Это фундаментальный инструмент исчисления, который также можно интерпретировать как наклон касательной линии. Он измеряет, насколько крутой график функции находится в некоторой заданной точке графика.
Проще говоря, производная — это скорость, с которой функция изменяется в какой-то определенной точке.
Разница между дифференциальными и производными
Определение дифференциального Vs. производный
Оба термина дифференциальные и производные тесно связаны друг с другом с точки зрения взаимосвязи. В математике меняющиеся сущности называются переменными, а скорость изменения одной переменной по отношению к другой называется производной.
Уравнения, определяющие связь между этими переменными и их производными, называются дифференциальными уравнениями. Дифференциация — это процесс нахождения производной. Производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.
Дифференциация — это процесс нахождения производной. Производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.
Связь дифференциальных Vs. производный
Дифференциация — это метод вычисления производной, которая является скоростью изменения выхода y функции относительно изменения переменной x.
Проще говоря, производная относится к скорости изменения y по х, и это соотношение выражается как y = f (x), что означает, что y является функцией x. Производные функции f (x) определяются как функция, значение которой порождает наклон f (x), где она определена, и f (x) дифференцируема. Это относится к наклону графика в данной точке.
Представление дифференциального Vs. производный
Дифференциалы представлены как dИкс, dу, dt и т. д., где dx представляет собой небольшое изменение x, dy представляет собой небольшое изменение y и dt — небольшое изменение t. При сравнении изменений связанных величин, где y — функция x, дифференциал dy может быть записана как:
При сравнении изменений связанных величин, где y — функция x, дифференциал dy может быть записана как:
Читайте также: Excel найти номер строки по значению
Производной функции является наклон функции в любой точке и записывается как d/dИкс. Например, производную от sin (x) можно записать в виде:
d/dx sin (x) = sin (x) ’ = cos (x)
Дифференциальная и производная: Сравнительная таблица
Резюме дифференциальных Vs. производный
В математике скорость изменения одной переменной по отношению к другой переменной называется производной, а уравнения, выражающие связь между этими переменными и их производными, называются дифференциальными уравнениями.В двух словах, дифференциальные уравнения включают производные, которые фактически определяют, как изменяется количество относительно другого. Решая дифференциальное уравнение, вы получаете формулу для количества, не содержащего производных. Метод вычисления производной называется дифференцированием. Проще говоря, производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.
Проще говоря, производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.
Центральные понятия дифференциального исчисления — производная и дифференциал возникли при рассмотрении множества задач естествознания и математики, каждая из которых приводила к вычислению пределов одного типа.
Производная функции
имеет конечный предел при стремлении приращения независимой переменной к 0, то такой предел называется производной функции f(х) при заданном х.
Производная функции — одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место.
Дифференцирование
Процесс нахождения производной называется дифференцированием. Обратная операция — восстановление функции по известной производной —интегрированием.
Для нахождения производной функции f(x) в точке x0 на основе определения следует выполнить следующие действия:
- Записать отношение [frac<Delta y><Delta x>=mathop<lim >limits_ <Delta x o 0>frac<Delta x>]
- Упростить дробь, сократив ее, если возможно, на $Delta x$;
- Найти производную f'(x0), вычисляя предел полученного выражения.
 Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x0.
Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x0.
Производная сложной функции равна произведению производной по промежуточной переменной по независимой переменной:
Попробуй обратиться за помощью к преподавателям
Найти производную функции
Введем новую переменную u = x/$Delta $х которая стремится к бесконечности и найдем предел новой функции
Читайте также: В 10 раз быстрее это сколько
Вычислить производную функции
По формуле разности функций вычислим производную
За f(x) примем числитель, а за g(x) — знаменатель
Найдем производные отдельные множителей и упростим дробь
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Найти производную сложной функции
По правилу нахождения производной сложной функции вычислим производную и умножим ее на производную подкоренного выражения.
Дифференциал
Дифференциалом функции называется произведение производной этой функции на приращение независимой переменной.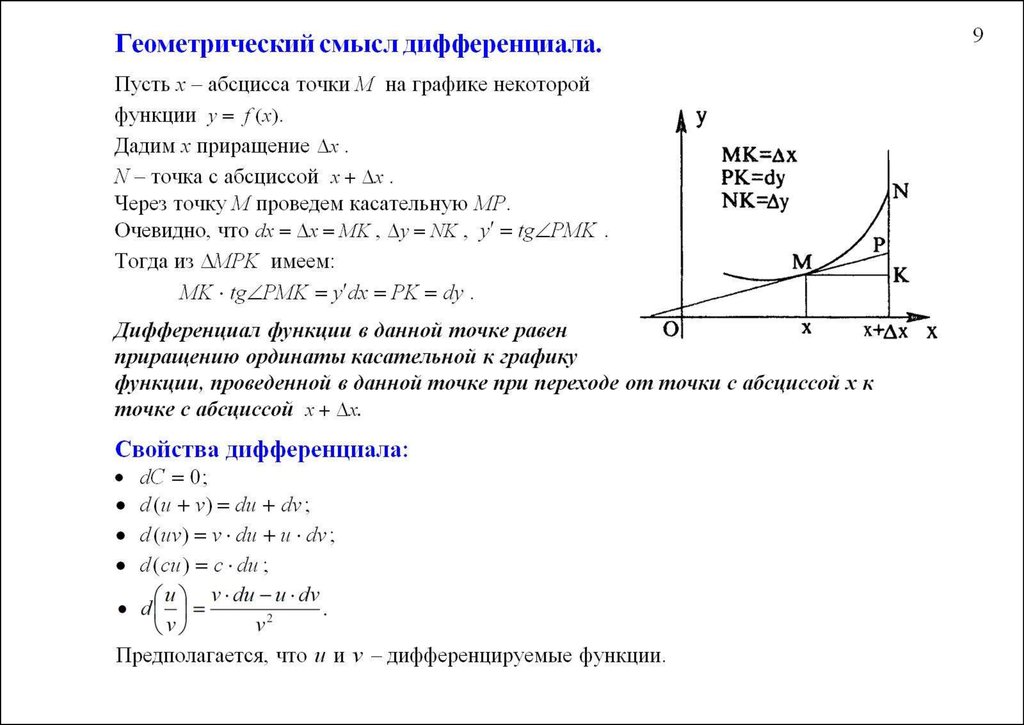 sin xdx]
sin xdx]
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
| Hellhammer 29 декабря 2005 года |
Производная и оператор дифференцирования. | LightCone
Значение дифференциального и интегрального исчислений сложно переоценить. {-35}\)м.). Несмотря на это вся современная наука (в том числе квантовая механика и теория струн) пропитана дифференциальным исчислением. Даже дискретные результаты типа квантования энергетических уровней атомов получаются из рассмотрения непрерывных функций и дифференциальных уравнений.
{-35}\)м.). Несмотря на это вся современная наука (в том числе квантовая механика и теория струн) пропитана дифференциальным исчислением. Даже дискретные результаты типа квантования энергетических уровней атомов получаются из рассмотрения непрерывных функций и дифференциальных уравнений.
Производная функции в какой-либо точке по определению это отношение интервала \( \displaystyle \Delta y\) к интервалу \( \displaystyle \Delta x\) в окрестности этой точки, когда длины этих интервалов стремятся к нулю. На рисунке для примера показаны две точки с соответствующими интервалами.
Хотя сами интервалы в пределе бесконечно малы, их отношение в общем случае имеет конечную величину:
\( \displaystyle f'(x)=\frac{dy}{dx}=\frac{\Delta y}{\Delta x}\) при \( \Delta x\rightarrow 0\)
где через \( \displaystyle dx\) и \( \displaystyle dy\) обозначают дифференциалы (difference — разность), то есть те самые бесконечномалые интервалы — разность декартовых координат текущей и следующей точек.
В научной литературе обозначение производной штрихами практически не используется, а запись в виде отношения дифференциалов общепринята. По сути это и есть определение производной.
Из рисунка видно, что даже при одинаковом \( \displaystyle \Delta x\) соответствующая величина \( \displaystyle \Delta y\) будет разной. Каждой точке непрерывной функции \( \displaystyle f(x)\) можно сопоставить число — производную функции в этой точке. Совокупность этих точек тоже будет непрерывной функцией — производной исходной функции.
Физическим смыслом производной является скорость изменения исходной функции. Достаточно взглянуть на рисунок выше чтобы понять. В районе первой точки функция быстро меняется. Производная будет иметь большую величину потому что \( \displaystyle \Delta y\) большое. И она будет отрицательной, так как \( \displaystyle y(x_{1}+\Delta x)<y(x_{1})\) и их разница \( \displaystyle \Delta y = y(x_{1}+\Delta x)-y(x_{1})\) будет отрицательной. Для второй точки, где функция почти не меняется, производная мала так как \( \displaystyle \Delta y\) мало. 2}{\Delta x}=\) \( \displaystyle 2x+\Delta x=2x\) при \( \displaystyle \Delta x\rightarrow 0\)
2}{\Delta x}=\) \( \displaystyle 2x+\Delta x=2x\) при \( \displaystyle \Delta x\rightarrow 0\)
В реальной жизни, при численных вычислениях на компьютере, к пределу \( \displaystyle \Delta x\rightarrow 0\) вообще не переходят. Скажем, с микрофона поступает аналоговый сигнал \( \displaystyle f(t)\), который необходимо оцифровать с частотой \( \displaystyle 1/\Delta t\) и произвести цифровую обработку в которой как раз и используются производные. Сигнал (функция) разбивается на конечное число точек (дискретизация):
Декартовы y-координаты этой дискретной функции можно записать в вектор-столбец:
\( \displaystyle f(t)=\begin{pmatrix}
y_{1}\\
y_{2}\\
y_{3}\\
…\\
y_{n}
\end{pmatrix}\)
А взятие производной можно записать в виде умножения матриц:
\( \displaystyle \frac{d}{dt}f(t)=\) \( \displaystyle \frac{1}{\Delta t}\begin{pmatrix}
-1&1 &0 &… &0 \\
0&-1 &1 &… &0 \\
0&0 &-1 &… &0 \\
…&… &… &… &…\\
0& 0& 0& …&1
\end{pmatrix}\begin{pmatrix}
y_{1}\\
y_{2}\\
y_{3}\\
…\\
y_{n}
\end{pmatrix}=\) \( \displaystyle \frac{1}{\Delta t}\begin{pmatrix}
y_{2}-y_{1}\\
y_{3}-y_{2}\\
y_{4}-y_{3}\\
…\\
y_{n}-y_{n-1}
\end{pmatrix}\)
Кажется громоздко, но смысл прост. Это просто произведение квадратной матрицы на вектор-столбец (исходная функция), которое дает другой вектор-столбец (производная функция). То есть получившийся вектор-столбец как раз будет являться аппроксимацией производной исходной функции. Проверьте, что умножая приведенную матрицу по стандартному правилу «строка на столбец» мы получим вектор, состоящий из разниц значений функции в соседних точках, например: \( \displaystyle \Delta y_{12}=y_{2}-y_{1}\) и т.п., что по определению и есть производная (если поделить на \( \displaystyle \Delta t\)). Это еще одна наглядная демонстрация откуда пошло название дифференциал (разность по-русски), достаточно посмотреть на вектор-столбец результата.
Это просто произведение квадратной матрицы на вектор-столбец (исходная функция), которое дает другой вектор-столбец (производная функция). То есть получившийся вектор-столбец как раз будет являться аппроксимацией производной исходной функции. Проверьте, что умножая приведенную матрицу по стандартному правилу «строка на столбец» мы получим вектор, состоящий из разниц значений функции в соседних точках, например: \( \displaystyle \Delta y_{12}=y_{2}-y_{1}\) и т.п., что по определению и есть производная (если поделить на \( \displaystyle \Delta t\)). Это еще одна наглядная демонстрация откуда пошло название дифференциал (разность по-русски), достаточно посмотреть на вектор-столбец результата.
Заметьте, что мы свели операцию взятия производной к простому умножению матриц. Если вектор-столбец является аппроксимацией функции, то приведенная матрица (деленная на \( \displaystyle \Delta t\)) — это аппроксимация самого оператора дифференцирования \( \displaystyle \frac{d}{dt}\).
То есть при \( \displaystyle \Delta t \rightarrow 0\) матрица и вектор-столбец будут бесконечномерными и мы перейдем от аппроксимации к действительным величинам: функциям и операторам над ними. То есть оператор и матрица фактически одно и тоже в нашем контексте. Кстати, матрицами можно представлять и более простые операции.
Одной из точек зрения на процесс взятия производной (дифференцирования) является взгляд с позиции линейных операторов. Оператор (operator — выполняющий операцию) это то, что действует на функцию в результате чего получается другая функция. По прямой аналогии примера с матрицами, алгебраически можно записать:
\( \displaystyle \hat{D}f(t)=f'(t)\)
где за \( \displaystyle \hat{D}\) обозначен оператор дифференцирования \( \displaystyle \frac{d}{dt}\).
Читать следует так: оператор \( \displaystyle \hat{D}\) действует на исходную функцию \( \displaystyle f \) в результате чего получается другая функция \( \displaystyle f’\). Действие оператора можно представить графически как изменение сигнала неким преобразователем:
Действие оператора можно представить графически как изменение сигнала неким преобразователем:
Поскольку другие операторы, в том числе и элементарные (сложение, умножение), можно записать в подобном графическом виде, данная парадигма позволяет наглядно отображать дифференциальные уравнения в виде схем и производить их численный анализ на компьютере. Известный пример реализации — Simulink в составе MATLAB.
— дифференциальная и производная
спросил
Изменено 3 года, 2 месяца назад
Просмотрено 743 раза
$\begingroup$
Я пытаюсь научиться $u$-подстановке в рамках подготовки к исчислению $2$, и я не думаю, что вполне понимаю разницу между производной и дифференциалом.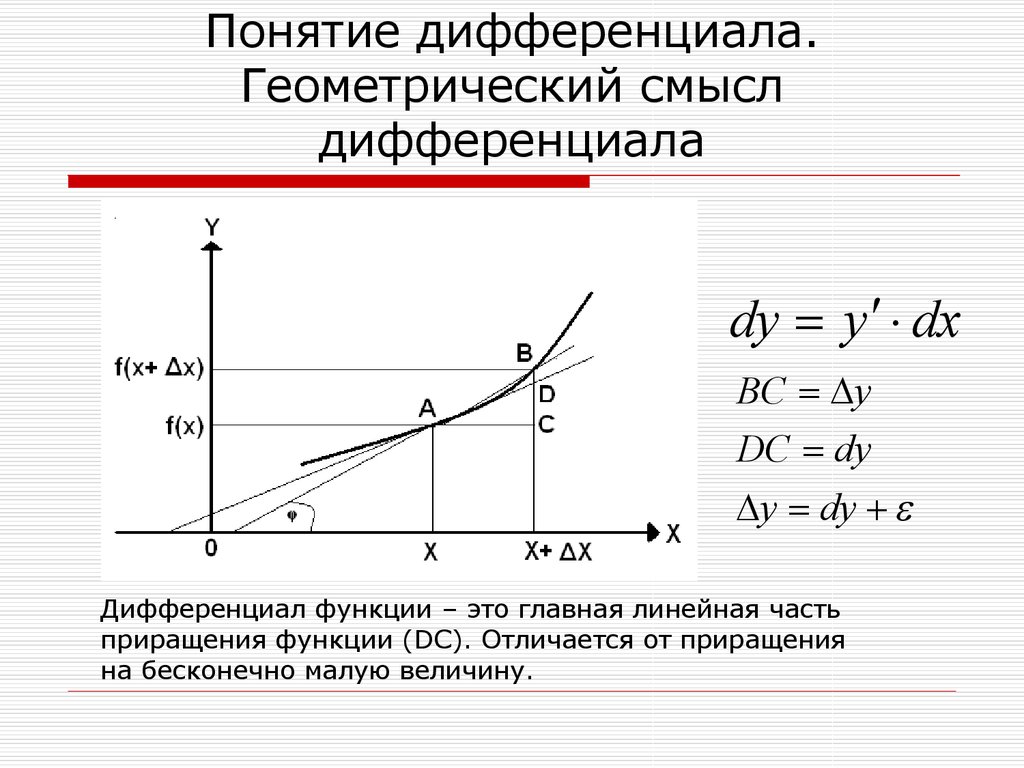 2$. 9{n — 1} f (t_i) (x_ {i + 1} — x_i),
$$
где предел берется по всем размеченным разделам $\mathscr P = (a = x_0 \le t_0 \le x_1 \le t_1 \le \dotsb \le t_{n — 1} \le x_n = b)$ как $\lVert \mathscr P\rVert = \sup \{x_{i + 1} — x_i : 0 \le i < n\}$ сжимается до $0$, если предел существует; и, если прищуриться, можно увидеть $\int$ как обобщенную $\sum$ (действительно, Лейбниц выбрал оператор, чтобы предложить $\int\text{um}$), и $\Delta x_i = x_{i + 1 } - x_i$ как макроскопическое приращение, которое в пределе становится бесконечно малым приращением $\mathrm dx$. 92=27, тогда вы можете провести касательную к этой точке функции.
2$. 9{n — 1} f (t_i) (x_ {i + 1} — x_i),
$$
где предел берется по всем размеченным разделам $\mathscr P = (a = x_0 \le t_0 \le x_1 \le t_1 \le \dotsb \le t_{n — 1} \le x_n = b)$ как $\lVert \mathscr P\rVert = \sup \{x_{i + 1} — x_i : 0 \le i < n\}$ сжимается до $0$, если предел существует; и, если прищуриться, можно увидеть $\int$ как обобщенную $\sum$ (действительно, Лейбниц выбрал оператор, чтобы предложить $\int\text{um}$), и $\Delta x_i = x_{i + 1 } - x_i$ как макроскопическое приращение, которое в пределе становится бесконечно малым приращением $\mathrm dx$. 92=27, тогда вы можете провести касательную к этой точке функции.
С другой стороны, очень хорошо, что вы пытаетесь понять, что на самом деле означает dx. Когда мы интегрируем, с точки зрения графика, мы на самом деле берем площадь под кривой таким образом, что складываем бесконечно много прямоугольников, так что их сумма приближается к площади под кривой. Вы можете думать о знаке интеграла как о сумме любых границ, которые вы выберете, и о f(x) как о длине, а dx как о ширине. dx на самом деле является очень небольшим изменением x, и именно это и означает интегрирование. Когда мы берем бесконечно много прямоугольников, наше приближение становится все лучше и лучше.
dx на самом деле является очень небольшим изменением x, и именно это и означает интегрирование. Когда мы берем бесконечно много прямоугольников, наше приближение становится все лучше и лучше.
Это также дает небольшой намек на то, почему дифференцирование и интегрирование противоположны друг другу, как если бы вы интегрировали функцию и взяли производную от интеграла. Вы фактически возвращаете функцию.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Разница между дифференциалом и производным
Последнее обновление: 7 сентября 2022 г. / Автор Piyush Yadav / Факт проверен / 5 минут
Производные содержатся в дифференциальных уравнениях. Они представляют скорость изменения переменных. При изменении независимой переменной необходимо отметить соответствующее изменение зависимой переменной.
Производные обозначают эту скорость изменения, изучая наклон функции на графике.
Дифференциал и производная Основное различие между дифференциалом и производной заключается в функциях, которые каждая из них выполняет, и значениях, которые каждая из них представляет. Дифференциалы представляют собой наименьшие различия в величинах, которые являются переменными, как площадь тела. Это позволяет вычислить взаимосвязь между независимыми и зависимыми переменными в уравнении.
| Parameters of Comparison | Differentials | Derivatives |
| Definition | Differentials represent the smallest of differences в количествах, которые являются переменными. | Производные представляют скорость изменения переменных в дифференциальном уравнении. |
| Вычисленная разница | Вычисляется линейная разница. | Вычисляется наклон графика в определенной точке. |
| Связь | Дифференциальные уравнения используют производные, чтобы прийти к окончательным решениям. Производные содержатся в дифференциальных уравнениях. | Производные просто означают скорость изменения зависимой переменной по отношению к независимой переменной. |
| Функциональные коннотации | Функциональные коннотации между переменными неизвестны | Функциональные коннотации между переменными известны. |
| Представлено | Дифференциальные уравнения представлены многими формулами. Один из часто используемых: dy/dx = f(x) | Существуют различные степени производных с различными формулами представления. Наиболее часто используемое формульное представление производной: d /dx |
Как раздел исчисления, дифференциальные уравнения представляют бесконечно малую разницу в определенных флуктуирующих величинах. Дифференциальные уравнения содержат производные и их функции.
Дифференциалы измеряют линейную траекторию изменения зависимой переменной как следствие изменения количества независимой переменной. Существует несколько различных типов дифференциальных уравнений разного порядка и степени математической сложности.
Дифференциальные уравнения используются для описания движения тепловых волн, изменения численности населения, распада радиоактивных материалов, движения электричества, движения маятника и т. д. изменение одной переменной вызывается изменением другой.
Это методологический инструмент, используемый для вычисления производных функций. Следовательно, это репрезентативное уравнение. Дифференциальные уравнения часто представляются как:
db/dy = f(a)
Где b — зависимая, а a — независимая переменная.
Что такое производная?Проще говоря, производные относятся к скорости изменения переменных, когда изменение регистрируется в независимой переменной, а соответствующее изменение производится в зависимой переменной. Следовательно, он подчеркивает изменение выхода из-за изменения входного значения.
Производные чаще всего используются в дифференциальных уравнениях. Дифференциация — это процесс, используемый для нахождения производных. Они используются для обозначения наклона касательной. В течение заданного периода времени производные измеряют крутизну наклона функции.
Они используются для обозначения наклона касательной. В течение заданного периода времени производные измеряют крутизну наклона функции.
Подобно дифференциалам, производные также могут быть классифицированы как производные первого и второго порядка. В то время как первое можно напрямую предсказать по наклону линии, второе учитывает вогнутость графика.
Они являются важной частью математических расчетов. Часто наклон представлен как:
d /dx
Например, производная определяется как скорость изменения b по отношению к a. Это отношение выражается как b = f(a), где b — функция a. Значение этой функции создает наклон f(a).
Производные часто используются учеными-исследователями в дифференциальных уравнениях для измерения изменений значений переменных, чтобы можно было точно предсказать поведение изменяющихся систем.
Основные различия между дифференциалами и производными- Основное различие между дифференциалами и производными заключается в их определениях, которые, таким образом, влияют на их функциональность в математической сфере.
 Первый — это подобласть исчисления, которая означает бесконечно малую разницу в некоторой флуктуирующей величине. Производные, с другой стороны, относятся к изменению выходной стоимости из-за соответствующего изменения входной стоимости. Это означает скорость этого изменения.
Первый — это подобласть исчисления, которая означает бесконечно малую разницу в некоторой флуктуирующей величине. Производные, с другой стороны, относятся к изменению выходной стоимости из-за соответствующего изменения входной стоимости. Это означает скорость этого изменения. - Дифференциальные уравнения содержат производные или функции производных. Принимая во внимание, что производные просто относятся к мгновенному изменению, которое происходит с изменением независимой переменной, которое вызывает соответствующее изменение значения зависимой переменной.
- Функциональная связь между зависимой и независимой переменными известна в случае производной и неизвестна в случае дифференциала. Это представляет собой еще одно важное различие между двумя математическими понятиями.
- Формулы дифференциального уравнения и уравнения производной также существенно различаются. dy/dx = f(x) представляет первую, где y — зависимая, а x — независимая переменная. Производные представлены d/dx.

- Дифференциалы представляют изменение реального значения на линейной карте, а производные представляют то же изменение на карте наклона. Производные вычисляют наклон функции на графике в любой заданный момент времени.
Дифференциалы и производные являются основополагающими математическими понятиями, незаменимыми при решении сложных математических задач. Они оба часто используются в сочетании друг с другом и часто могут быть неправильно истолкованы, если их значения или функции остаются неясными.
Различия между двумя понятиями минимальны, но в то же время их важно осознавать. Эти две концепции различаются с точки зрения их реализации и использования в уравнениях.
В то время как дифференциальное уравнение содержит производные или функции производных, производные являются мерой мгновенного изменения, происходящего в зависимой переменной, которое вызывается соответствующим изменением независимой переменной.
Дифференциалы представляют отношения, существующие между двумя переменными. Они используют производные, чтобы четко определить эту связь и измерить бесконечно малые изменения.
Они используют производные, чтобы четко определить эту связь и измерить бесконечно малые изменения.
Представление каждого из них существенно отличается. Кроме того, дифференциалы отображают изменение реальной стоимости посредством линейного отображения, в то время как производные отображают наклон изменения. Каждое понятие также воплощает в себе значимые вариативные формы.
Ссылки- https://ieeexplore.ieee.org/abstract/document/8579172/
- https://www.tandfonline.com/doi/abs/10.4169/074680210X4802290 Любая разница» в Google. Оцените этот пост!
[Всего: 0]
Один запрос?
Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы быть полезным для вас. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/семьей. SHARING IS ♥️
Содержание
сообщите об этом объявлении
Дифференциал функции
Определение дифференциала функции
Рассмотрим функцию y = f ( x ), которая непрерывна в интервале [ a , b ].
 Предположим, что в какой-то момент x 0 ∈ [ a , b ] независимая переменная увеличивается на Δ х . Приращение функции Δ y , соответствующее изменению независимой переменной Δ x , равно
Предположим, что в какой-то момент x 0 ∈ [ a , b ] независимая переменная увеличивается на Δ х . Приращение функции Δ y , соответствующее изменению независимой переменной Δ x , равно\[\Delta y = \Delta f\left( {{x_0}} \right) = f\left( {{x_0} + \Delta x} \right) — f\left( {{x_0}} \right ).\]
Для любой дифференцируемой функции приращение Δ y можно представить в виде суммы двух слагаемых:
\[\Delta y = A\Delta x + \omicron\left( {\Delta x} \right),\]
, где первый член (называемый главной частью приращения) линейно зависит от приращения \(\Delta x,\), а второй член имеет более высокий порядок малости по отношению к \(\Delta x.\) выражение \(A\Delta x\) называется дифференциалом функции и обозначается \(dy\) или \(df\left( {{x_0}} \right).\) 92.\)
Обратите внимание, что в этом примере коэффициент \(A\) равен значению производной \(S\) в точке \({x_0}:\)
\[А = 2{х_0}.
 \]
\]Оказывается, для любой дифференцируемой функции справедлива следующая теорема:
Коэффициент \(A\) при главной части приращения функции в точке \({x_0}\) равен значению производной \(f’\left( {{x_0}} \right )\) в этот момент, то есть приращение \(\Delta y\) равно
\[\Delta y = A\Delta x + \omicron\left( {\Delta x} \right) = f’\left({{x_0}} \right)\Delta x + \omicron\left( {\ Дельта х} \справа).\]
Деление обеих частей уравнения на \(\Delta x \ne 0\) дает
\[\frac{{\Delta y}}{{\Delta x}} = A + \frac{{\omicron\left({\Delta x} \right)}}{{\Delta x}} = f ‘\left( {{x_0}} \right) + \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}}.\]
В пределе при \(\Delta x \to 0\) мы получаем значение производной в точке \({x_0}:\)
\[y’\left( {{x_0}} \right) = \lim\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = A = f’ \влево( {{x_0}} \вправо).\]
Здесь мы учли, что для малой величины \(\omicron\left( {\Delta x} \right)\) более высокого порядка малости, чем \(\Delta x,\), предел равен
\[\lim\limits_{\Delta x \to 0} \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}} = 0.
 \]
\]Предполагая, что дифференциал независимой переменной \(dx\) равен ее приращению \(\Delta x:\)
\[дх = \Дельта х,\]
получаем из соотношения
\[dy = A\Delta x = y’dx\]
то
\[y’ = \frac{{dy}}{{dx}},\]
, поэтому производную функции можно представить как отношение двух дифференциалов.
Геометрический смысл дифференциала функции
На рис. \(2\) схематично показано разбиение приращения \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член более высокого порядка малости \(\ омикрон\влево( {\Delta x} \вправо).\)
Рис. 2.Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M,\), как известно, имеет угол наклона \(\alpha,\) тангенс которой равен производной:
\[\tan \alpha = f’\left( {{x_0}} \right).\]
Когда независимая переменная изменяется на \(\Delta x\), тангенс увеличивается на \(A\Delta x.\) Это линейное приращение, образованное тангенсом, является просто дифференциалом функции.
 Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\)
Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\)Свойства дифференциала
Пусть \(и\) и \(v\) — функции переменной \(х\). Дифференциал имеет следующие свойства:
- Константа может быть вынесена за знак дифференциала:
\[d\влево( {Cu} \вправо) = Cdu,\]
где \(С\) — постоянное число. - Дифференциал суммы (разности) двух функций равен сумме (разности) их дифференциалов:
\[d\left( {u \pm v} \right) = du \pm dv.\]
- Дифференциал константы равен нулю:
\[d\влево(С\вправо) = 0.\]
- Дифференциал независимой переменной \(x\) равен ее приращению:
\[dx = \Дельта x.\]
- Дифференциал линейной функции равен ее приращению:
\[d\left( {ax + b} \right) = \Delta \left( {ax + b} \right) = a\Delta x.\]
- Дифференциал произведения двух функций:
\[d\left( {uv} \right) = du \cdot v + u \cdot dv.
 \] 9{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\]
\] 9{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\]и так далее.
Формоинвариантность дифференциала
Рассмотрим композицию двух функций \(y = f\left( u \right)\) и \(u = g\left( x \right).\). Ее производную можно найти по цепному правилу:
\[{y’_x} = {y’_u} \cdot {u’_x},\]
, где субиндекс обозначает переменную дифференцирования.
Дифференциал «внешней» функции \(y = f\left( u \right)\) можно записать как
\[dy = {y’_u}\,du.\]
Дифференциал «внутренней» функции \(u = g\left( x \right)\) может быть представлен аналогичным образом:
\[du = {u’_x}\,dx.\]
Если в последнюю формулу подставить \(du\), то получится
\[dy = {y’_u}\,du = {y’_u}{u’_x}\,dx.\]
Поскольку \({y’_x} = {y’_u} \cdot {u’_x},\), то
\[dy = {y’_x}\,dx.\]
Видно, что в случае сложной функции мы получаем выражение для дифференциала в том же виде, что и для «простой» функции.
 Это свойство называется формоинвариантностью дифференциала.
Это свойство называется формоинвариантностью дифференциала.Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Найти дифференциал функции \[y = \sin x — x\cos x.\]
Пример 2
Найти дифференциал функции \[y = \cot {\frac{{\ pi x}}{4}}\] в точке \(x = 1.\) 9\prime}} \right) = \cos x — \left( {\cos x + x\left( { — \sin x} \right)} \right) = \cancel{\cos x} — \cancel{\ cos x} + x\sin x = x\sin x.\]
Дифференциал имеет следующий вид:
\[dy = y’dx = x\sin x\,dx.\]
Пример 2.
Найти дифференциал функции \[y = \cot {\frac{{\pi x}}{4}}\] в точке \(x = 1.\)
Раствор.
Находим производную и вычисляем ее значение в данной точке: 92}дх.\]
Дополнительные проблемы см. на стр. 2.
Дифференциальное определение и значение — Merriam-Webster
1 из 2
дифференциал ˌdi-fə-ˈren(t)-shəl
1
а
: относящиеся к или составляющие различие : отличительные
дифференциальные характеристики
б
: проведение различия между отдельными лицами или классами
дифференцированные налоговые ставки
с
: на основе или в результате дифференциала
д
: функционируют или работают иначе или с другой скоростью
дифференциальная плавка
2
математика : являющийся, относящийся к дифференциалу или включающий его (см.
 раздел 2, смысл 1) или дифференциал
раздел 2, смысл 1) или дифференциал3
физика
а
: относящиеся к количественным различиям (по движению или давлению)
б
: производящие эффекты вследствие количественных различий
дифференциально
ˌdi-fə-ˈren(t)-shə-lē
наречие
дифференциал
2 из 2
1
математика
а
: произведение (см.
 значение произведения 1) производной функции одной переменной на приращение независимой переменной
значение произведения 1) производной функции одной переменной на приращение независимой переменнойб
: сумма произведений, в которой каждое произведение состоит из частной производной данной функции нескольких переменных, умноженной на соответствующее приращение, и которая содержит столько произведений, сколько независимых переменных в функции
2
: разница между сопоставимыми индивидуумами или классами
разница в цене
также : сумма такой разницы
3
а
: узел шестерни трансмиссии, соединяющий два коллинеарных вала или оси (например, задних колес автомобиля) и позволяющий одному валу вращаться быстрее, чем другому
Блокировка заднего дифференциала
б
: случай, покрывающий такую сборку
Синонимы
Прилагательное
- различающий
- дискриминационный
- дискриминационный
- дискриминационный
Посмотреть все синонимы и антонимы в тезаурусе
Примеры предложений
Прилагательное отменили дифференцированные шкалы заработной платы для мужчин и женщин, выполняющих одинаковую работу
Последние примеры в Интернете
Части тождества Эйлера появляются в решениях задачи 9.
 0165 дифференциальных уравнений, как в колебательных контурах, и решения уравнения Шрёдингера в квантовой механике.
Ретт Аллен, Wired , 14 марта 2022 г.
С этой точки зрения дифференциальная конфиденциальность делает данные переписи более точными и прозрачными, а не менее. New York Times , 21 апреля 2022 г.
Меньшая машина активна 9Дифференциал 0165 передает крутящий момент на внешнее колесо во время энергичного прохождения поворотов, создавая забавное ощущение надвигающейся избыточной поворачиваемости даже за пределами точки, в которой задние шины фактически теряют сцепление с дорогой.
Майк Дафф, Автомобиль и водитель , 11 мая 2022 г.
Хотя подкачка является грубым способом маскировки данных, дифференциальные алгоритмы конфиденциальности могут быть настроены для точного удовлетворения требований конфиденциальности.
0165 дифференциальных уравнений, как в колебательных контурах, и решения уравнения Шрёдингера в квантовой механике.
Ретт Аллен, Wired , 14 марта 2022 г.
С этой точки зрения дифференциальная конфиденциальность делает данные переписи более точными и прозрачными, а не менее. New York Times , 21 апреля 2022 г.
Меньшая машина активна 9Дифференциал 0165 передает крутящий момент на внешнее колесо во время энергичного прохождения поворотов, создавая забавное ощущение надвигающейся избыточной поворачиваемости даже за пределами точки, в которой задние шины фактически теряют сцепление с дорогой.
Майк Дафф, Автомобиль и водитель , 11 мая 2022 г.
Хотя подкачка является грубым способом маскировки данных, дифференциальные алгоритмы конфиденциальности могут быть настроены для точного удовлетворения требований конфиденциальности. New York Times , 21 апреля 2022 г.
В программе поощрения говорится, что больницы, которые обязуются постоянно предоставлять отчеты о пропускной способности, будут иметь право на дифференцированную скорректированную выплату, увеличенную на 0,25%.
Стефани Иннес, , Республика Аризона, , 12 апреля 2022 г.
А теперь, когда прибывают первые беженцы из Украины, мало где более ярко иллюстрирует дифференциал 9Получают лечение 0166 беженцев. Washington Post , 11 марта 2022 г.
Уровень избирательности приема также был связан с дифференциальным ростом объема заявлений.
Майкл Т. Нитцель, Forbes , 26 января 2022 г.
Таким образом, цифра 99 процентов не является репрезентативной для реального использования, поскольку минимальное измерение фильтрации маски N95 составляет 9.
New York Times , 21 апреля 2022 г.
В программе поощрения говорится, что больницы, которые обязуются постоянно предоставлять отчеты о пропускной способности, будут иметь право на дифференцированную скорректированную выплату, увеличенную на 0,25%.
Стефани Иннес, , Республика Аризона, , 12 апреля 2022 г.
А теперь, когда прибывают первые беженцы из Украины, мало где более ярко иллюстрирует дифференциал 9Получают лечение 0166 беженцев. Washington Post , 11 марта 2022 г.
Уровень избирательности приема также был связан с дифференциальным ростом объема заявлений.
Майкл Т. Нитцель, Forbes , 26 января 2022 г.
Таким образом, цифра 99 процентов не является репрезентативной для реального использования, поскольку минимальное измерение фильтрации маски N95 составляет 9. 5 процентов (что составляет перепад давления, посадку, утечку и т. д.).
Кори Гаскин, Ars Technica , 18 декабря 2021 г.
5 процентов (что составляет перепад давления, посадку, утечку и т. д.).
Кори Гаскин, Ars Technica , 18 декабря 2021 г.Критически важно, чтобы внутренняя часть полуоси (ближайшая к дифференциал ) мог изгибаться, позволяя задним колесам поворачиваться под экстремальными углами, когда задняя подвеска находилась под нагрузкой. Мэтт Крисара, Popular Mechanics , 10 августа 2022 г. Спартанцы допустили только один из своих промахов в тайме, совершив восемь потерь, что привело к дифференциалу из пяти бросков в пользу «Ниттани Лайонс».
 Крис Солари, 9 лет0165 Detroit Free Press , 16 февраля 2022 г.
Эта чудовищная мельница с шестиступенчатой автоматической коробкой передач Ford, соединенной с 9-дюймовым дифференциалом Strange Engineering , встроена в точную копию корпуса фастбэка Dynacorn Classic Bodies от Mustang 1967 года.
Роберт Росс, Robb Report , 20 декабря 2021 г.
Шесть разных бомбардиров привели «Иглз» к доминирующему голу 14:0 дифференциал в трех турнирных играх.
Кэм Керри, BostonGlobe.com , 15 ноября 2021 г.
Не потренировавшись с США, Букеру, Миддлтону и Холидей пришлось преодолевать долгий перелет и приспосабливаться к времени дифференциал для игры.
Дуэйн Рэнкин, , Республика Аризона, , 6 августа 2021 г.
Крис Солари, 9 лет0165 Detroit Free Press , 16 февраля 2022 г.
Эта чудовищная мельница с шестиступенчатой автоматической коробкой передач Ford, соединенной с 9-дюймовым дифференциалом Strange Engineering , встроена в точную копию корпуса фастбэка Dynacorn Classic Bodies от Mustang 1967 года.
Роберт Росс, Robb Report , 20 декабря 2021 г.
Шесть разных бомбардиров привели «Иглз» к доминирующему голу 14:0 дифференциал в трех турнирных играх.
Кэм Керри, BostonGlobe.com , 15 ноября 2021 г.
Не потренировавшись с США, Букеру, Миддлтону и Холидей пришлось преодолевать долгий перелет и приспосабливаться к времени дифференциал для игры.
Дуэйн Рэнкин, , Республика Аризона, , 6 августа 2021 г. Задний двигатель идентичен переднему блоку, но коробка передач добавляет электронный блокирующий механизм к 9.Дифференциал 0165 для обеспечения дополнительного сцепления при движении по бездорожью.
Сэм Абуэльсамид, Forbes , 20 мая 2021 г.
Нотр-Дам должен был закрыться со счетом 41-0, чтобы вернуться к этой точке дифференциал .
Том Нойе, The Indianapolis Star , 11 марта 2021 г.
Сохранение и улучшение этого числа может стать решающим фактором, если конференц-стол или «Щит болельщиков» сведутся к цели 9.0165 дифференциал .
Джулия По, orlandosentinel.com , 5 октября 2020 г.
Узнать больше
Задний двигатель идентичен переднему блоку, но коробка передач добавляет электронный блокирующий механизм к 9.Дифференциал 0165 для обеспечения дополнительного сцепления при движении по бездорожью.
Сэм Абуэльсамид, Forbes , 20 мая 2021 г.
Нотр-Дам должен был закрыться со счетом 41-0, чтобы вернуться к этой точке дифференциал .
Том Нойе, The Indianapolis Star , 11 марта 2021 г.
Сохранение и улучшение этого числа может стать решающим фактором, если конференц-стол или «Щит болельщиков» сведутся к цели 9.0165 дифференциал .
Джулия По, orlandosentinel.com , 5 октября 2020 г.
Узнать большеЭти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «дифференциальный».
 Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.История слов
Этимология
Прилагательное
заимствовано из средневековой латыни Differentialis, из Латинского Differentia Различие запись 1 + -ālis -al запись 1
Существительное
существительное, производное от дифференциальной записи 1
Первое известное употребление
Прилагательное
1615, в значении, определенном в смысле 1a
Существительное
1871, в значении, определенном в смысле 1a
Путешественник во времени
Первое известное использование дифференциала было в 1615 году
Другие слова того же года дифференциация
дифференциал
дифференциальный анализатор
Посмотреть другие записи поблизости
Процитировать эту запись «Дифференциал».
 Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/дифференциал. По состоянию на 16 сентября 2022 г.
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/дифференциал. По состоянию на 16 сентября 2022 г.Ссылка на копию
Медицинское определение
Дифференциал
дифференциал ˌdif-ə-ˈren-chəl
1
: из, относящихся к разнице или составляющей ее
дифференциальная рождаемость на разных экономических уровнях
2
: проведение различия между отдельными лицами или классами
дифференциальное количество клеток
дифференциальное окрашивание
Еще от Merriam-Webster о
дифференциальномНглиш: перевод дифференциального для говорящих на испанском языке
0002 Britannica.
 com: Энциклопедическая статья о дифференциал
com: Энциклопедическая статья о дифференциал Последнее обновление: 21 июля 2022
Подпишитесь на крупнейший словарь Америки и получите тысячи других определений и расширенный поиск без рекламы!
Мерриам-Вебстер полный
Дифференциальное исчисление — термины, формулы, правила, примеры
Дифференциальное исчисление изучает скорость изменения двух величин. Исчисление можно разделить на две части, а именно дифференциальное исчисление и интегральное исчисление. В дифференциальном исчислении производное уравнение используется для описания скорости изменения функции, тогда как в интегральном исчислении изучается площадь под кривой.
Одно из основных применений дифференциального исчисления — нахождение минимального или максимального значения заданной функции в рамках задачи оптимизации. В этой статье мы узнаем больше о дифференциальном исчислении, важных формулах и различных связанных примерах.
1. 
Что такое дифференциальное исчисление? 2. Термины, относящиеся к дифференциальному исчислению 3. Формулы дифференциального исчисления 4. Правила дифференциального исчисления 5. Дифференциальное исчисление против интегрального исчисления 6. Часто задаваемые вопросы по дифференциальному исчислению Что такое дифференциальное исчисление?
Дифференциальное исчисление включает в себя нахождение производной функции в процессе дифференцирования. Производная функции при определенном значении даст скорость изменения функции вблизи этого значения. Производная используется для измерения наклона касательной к графику функции.
Термины, относящиеся к дифференциальному исчислению
Дифференциальное исчисление — это изучение скорости изменения зависимой величины по отношению к изменению независимой величины.
 Например, скорость движущегося объекта можно интерпретировать как скорость изменения расстояния во времени. Если y = f(x) — функция, которая дифференцируется, то, согласно дифференциальному исчислению, используется обозначение f'(x) = dy/dx. Некоторые важные термины, связанные с дифференциальным исчислением, перечислены ниже:
Например, скорость движущегося объекта можно интерпретировать как скорость изменения расстояния во времени. Если y = f(x) — функция, которая дифференцируется, то, согласно дифференциальному исчислению, используется обозначение f'(x) = dy/dx. Некоторые важные термины, связанные с дифференциальным исчислением, перечислены ниже:Функция — Функция определяется как бинарное отношение, в котором каждый вход отображается ровно на один выход. y = 5x + 1 является примером функции. Здесь x (вход) — независимая переменная, а y (выход) — зависимая переменная.
Независимая переменная — В функции переменная, которая действует как вход, называется независимой переменной. В математической модели переменная, которой манипулируют, является независимой переменной.
Зависимая переменная — Переменная в функции, которая представляет результат, называется зависимой переменной. Значение этой переменной изменяется по отношению к изменению зависимой переменной.
 Другими словами, значение зависимой переменной определяется независимой переменной.
Другими словами, значение зависимой переменной определяется независимой переменной.Домен и диапазон — В дифференциальном исчислении домен может быть определен как список всех входных значений, а диапазон — это все выходные значения, полученные после применения входных данных к функции. Например, y = 5x + 1. Пусть домен будет {0, 1, 2}, тогда диапазон будет следующим:
y = 5(0) + 1 = 1
y = 5(1) + 1 = 6
y = 5(2) + 1 = 11
Диапазон = {1, 6, 11}
Пределы — Производная может быть определена концепцией предела. В дифференциальном исчислении предел описывает значение функции по мере приближения к определенному входному значению.
Производные — В дифференциальном исчислении производные используются для нахождения скорости изменения функции. Если касательную провести к точке, лежащей на графике функции, то наклон касательной даст производную функции в точке, где касательная касается кривой.
 Производная функции f(x) представляется как f'(x), dy/dx, df/dx.
Производная функции f(x) представляется как f'(x), dy/dx, df/dx.Пример дифференциального исчисления
Предположим, существует функция, заданная как f(x) = x 2 . Наклон этой функции в конкретной точке, скажем, 3, можно определить с помощью дифференциального исчисления. Производная этой функции будет f'(x) = 2x. Теперь в это уравнение подставляется x = 3, чтобы получить f'(x) = 6. Таким образом, наклон касательной при x = 3 равен 6.
Формулы дифференциального исчисления
Различные формулы дифференциального исчисления используются для нахождения производных различных типов функций. Согласно определению, производная функции может быть определена следующим образом:
f'(x) = \(lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}\)
Важные формулы дифференциального исчисления для различных функций приведены ниже. :
Элементарные функции
- d/dx e x = e x
- d/dx a x = a x .
 ln .a , где a > 0, a ≠ 1
ln .a , где a > 0, a ≠ 1 - d/dx ln x = 1/x, x > 0
- д/дх √х = 1/(2 √х)
Тригонометрические функции
- d/dx sin x = cos x
- d/dx cos x = -sin x
- d/dx tan x = sec 2 x , x ≠ (2n + 1) π / 2 , n ∈ I
- d/dx ctg x = — cosec 2 x, x ≠ nπ, n ∈ I
- d/dx сек х = сек х тангенс х, х ≠ (2n + 1) π / 2 , n ∈ I
- d/dx cosec x = — cosec x ctg x, x ≠ nπ, n ∈ I
Гиперболические функции
- d/dx sinx = chx
- d/dx coshx = sin hx
- d/dx tan hx = сек ч 92}}\)
Производные высшего порядка
Производная используется для определения скорости изменения функции. Чтобы найти скорость изменения этой производной, используются производные более высокого порядка. В приведенной ниже таблице перечислены наиболее часто используемые производные высшего порядка для функции y = f(x) в дифференциальном исчислении:
Порядок производной Производная первого порядка Производная второго порядка 9{3}}\)Пример: sinx f'(x) = cosx f»(x) = — sinx f»'(x) = — cosx Уравнения дифференциального исчисления
Уравнения дифференциального исчисления или просто дифференциальные уравнения — это уравнения, связывающие функции с их производными.
 Существуют два основных типа дифференциальных уравнений, а именно, обыкновенные дифференциальные уравнения и уравнения в частных производных. Обыкновенное дифференциальное уравнение — это уравнение, в котором есть только одна независимая переменная и уравнение содержит одну или несколько производных по этой переменной. Уравнение в частных производных состоит из одной или нескольких независимых переменных и их частных производных.
Существуют два основных типа дифференциальных уравнений, а именно, обыкновенные дифференциальные уравнения и уравнения в частных производных. Обыкновенное дифференциальное уравнение — это уравнение, в котором есть только одна независимая переменная и уравнение содержит одну или несколько производных по этой переменной. Уравнение в частных производных состоит из одной или нескольких независимых переменных и их частных производных.В дифференциальном исчислении есть три общие формулы для дифференциальных уравнений. Они приведены ниже:
- \(\frac{\mathrm{d} y}{\mathrm{d} x}\) = f(x)
- \(\frac{\mathrm{d} y}{\mathrm{d} x}\) = f(x, y)
- \(x_{1}\frac{\partial y}}{\partial x_{1}} + x_{2}\frac{\partial y}}{\partial x_{2}} = y\)
Правила дифференциального исчисления
Если известны производные некоторых простых функций, то правила дифференциального исчисления можно использовать для нахождения производных сложных функций.
 Правила дифференциального исчисления перечислены в таблице, приведенной ниже.
Правила дифференциального исчисления перечислены в таблице, приведенной ниже.Правило дифференциального исчисления Форма функции Интерпретация Постоянное правило у = с dy / dx = 0 Постоянное множественное правило у = ср(х) dy / dx = cf'(x) Силовое правило у = х н dy / dx = n · x n-1 Обобщенное правило мощности у = [f(x)] п dy / dx = n[f(x)] n-1 f'(x) Сумма двух функций у = е(х) + г(х) dy / dx = f'(x) + g'(x) Разница двух функций у = f(x) — g(x) dy / dx = f'(x) — g'(x) 9{2}}\) Цепное правило для составных функций у = f[g(x)]; y = f(u), u = g(x) dy / dx = \(\ frac {\ mathrm {d} y} {\ mathrm {d} u}.  \ frac {\ mathrm {d} u} {\ mathrm {d} x} \) = f'[ г(х)]г'(х)
\ frac {\ mathrm {d} u} {\ mathrm {d} x} \) = f'[ г(х)]г'(х)Дифференциальное исчисление против интегрального исчисления
Дифференциальное исчисление использует дифференцирование для нахождения производной функции, а интегральное исчисление использует интегрирование для нахождения интеграла функции. Интеграция есть обратный процесс дифференциации. Основные различия между дифференциальным исчислением и интегральным исчислением перечислены в таблице, приведенной ниже:
Дифференциальное исчисление Интегральное исчисление В дифференциальном исчислении производные используются для определения мгновенной скорости изменения функции. Интегральное исчисление использует интегралы для определения площади под кривой. Интегралы также известны как первообразные. Интуитивно дифференциация — это процесс разделения чего-либо на более мелкие части для отслеживания изменений. 
Интегрирование суммирует бесконечно малые части, чтобы получить общую площадь под кривой. Дифференциальное исчисление используется для определения возрастания или убывания функции. Интегральное исчисление используется для нахождения площадей, объемов и центральных точек. Пример: Дифференцировать f(x) = x 3
f'(x) = 3x 2Пример: интегрирование f(x) = x 3 9{4}}{4}+С\)
где, C — постоянная интегрированияПриложения для дифференциального исчисления
Существует множество приложений для дифференциального исчисления. Большинство количественных областей используют дифференциальное исчисление, такое как комплексный анализ, функциональный анализ, абстрактная алгебра и дифференциальная геометрия.
- В финансах дифференциальное исчисление используется при оптимизации портфеля для выбора лучших акций.
- В биологии дифференциальное исчисление используется для определения эволюции популяций хищников и жертв с течением времени.

- В механике скорость и ускорение могут быть получены из функции положения с помощью дифференциального исчисления.
- Художники-графики используют дифференциальное исчисление, чтобы увидеть, как модель ведет себя в быстро меняющихся условиях.
☛ Связанные темы:
- Формулы дифференцирования и интегрирования
- Формула неявного дифференцирования
- Формула УФ-дифференциации
Важные примечания по дифференциальному исчислению:
- Дифференциальное исчисление включает использование производных для определения скорости изменения зависимой переменной по отношению к независимой переменной.
- Правило констант, правило разностей, правило сумм, правило степеней и т. д. — это различные правила дифференциального исчисления.
- Существует два типа уравнений дифференциального исчисления — обыкновенные уравнения и уравнения в частных производных. Эти уравнения помогают связать функции с их производными.

- Интегральное исчисление включает интегрирование, которое является обратным процессом дифференцирования.
Часто задаваемые вопросы по дифференциальному исчислению
Что такое определение дифференциального исчисления?
Дифференциальное исчисление — это раздел исчисления, включающий изучение производных, которые используются для нахождения мгновенной скорости изменения функции с помощью процесса дифференцирования.
Насколько сложно дифференциальное исчисление?
Решение задач по дифференциальному исчислению становится простым благодаря кристально четким концепциям и постоянному пересмотру. Понимание и изучение формул является ключом к получению хорошей оценки на экзамене по дифференциальному исчислению.
Как решить дифференциальное исчисление?
Различные правила и формулы дифференциального исчисления используются для решения простых и сложных задач. Шаги для решения задачи дифференциального исчисления следующие:
- Определите тип функции.

- Применить требуемое правило дифференцирования и формулу.
- Результатом будет производная заданной функции.
Как понять дифференциальное исчисление?
Лучший способ получить четкое представление о дифференциальном исчислении — привить глубокие знания о предварительном исчислении. Следующим шагом является чтение теории дифференциального исчисления. Наконец, вопросы разного уровня сложности необходимо решать с использованием формул и теоретических понятий, необходимых для освоения этой темы.
Дифференциальное исчисление — это то же самое, что и дифференциальные уравнения?
Дифференциальные уравнения составляют часть дифференциального исчисления. Дифференциальные уравнения можно определить как уравнения, содержащие функцию с одной или несколькими переменными, а также производные или частные производные по этой переменной (переменным).
В чем разница между дифференциальным и интегральным исчислением?
Интеграция – это обратный процесс дифференциации.
 Дифференциальное исчисление связано с нахождением скорости изменения функции, в то время как интегральное исчисление связано с нахождением площади под кривой.
Дифференциальное исчисление связано с нахождением скорости изменения функции, в то время как интегральное исчисление связано с нахождением площади под кривой.Каковы применения дифференциального исчисления?
Дифференциальное исчисление используется почти во всех областях. Он используется для просмотра скорости роста или убывания функций, а также для нахождения оптимального значения (максимума или минимума) математических моделей.
17.1 Дифференциальные уравнения первого порядка
Начнем с рассмотрения уравнений, в которых только первая производная функции.
Определение 17.1.1 Дифференциал первого порядка уравнение представляет собой уравнение форма $F(t, y, \dot{y})=0$. Решением дифференциального уравнения первого порядка является функция $f(t)$, которая делает $\ds F(t,f(t),f'(t))=0$ для каждого значения $t$. $\квадрат$
Здесь $F$ — функция трех переменные, которые мы обозначаем как $t$, $y$ и $\dot{y}$. Это понятно что $\dot{y} $ явно появится в уравнении, хотя $t$ и $y$ не нужно.
 Термин «первый порядок» означает, что первый
появляется производная от $y$, но не производные более высокого порядка.
93/3+t+8/3$.
$\квадрат$
Термин «первый порядок» означает, что первый
появляется производная от $y$, но не производные более высокого порядка.
93/3+t+8/3$.
$\квадрат$Общее уравнение первого порядка слишком общее, т. е. мы не можем описать методы, которые будут работать на всех, или даже на большом количестве часть из них. Мы можем добиться прогресса в конкретных видах дифференциальные уравнения первого порядка. Например, многое можно сказать об уравнениях вида $\ds \dot{y} = \phi (t, y)$, где $\phi $ является функцией двух переменных $t$ и $y$. При разумных условиях на $\phi$ такой уравнение имеет решение и соответствующее задача с начальным значением имеет единственное решение. Однако в целом эти уравнения могут быть очень сложными или невозможно решить в явном виде.
Пример 17.1.6. Рассмотрим этот конкретный пример задачи с начальным значением. для закона охлаждения Ньютона: $\dot y = 2(25-y)$, $y(0)=40$. Мы первые обратите внимание, что если $y(t_0) = 25$, правая часть дифференциала уравнение равно нулю, поэтому постоянная функция $y(t)=25$ является решением к дифференциальному уравнению.
 2}$,
позволяя $A$ быть равным нулю.
$\квадрат$
2}$,
позволяя $A$ быть равным нулю.
$\квадрат$Определение 17.1.8. Дифференциальное уравнение первого порядка имеет вид разъемный если он можно записать в виде $\dot{y} = f(t)g(y)$. $\квадрат$
Как и в примерах, мы можем попытаться решить разделимое уравнение с помощью преобразование в форму $$\int {1\over g(y)}\,dy=\int f(t)\,dt.$$ Этот метод называется разделением переменные . Самый простой (в принцип) своего рода разделимое уравнение такое, в котором $g(y)=1$, в какой случай мы пытаемся решить $$\int 1\,dy=\int f(t)\,dt.$$ Мы можем это сделать, если найдем антипроизводную $f(t)$.
Кроме того, как мы уже видели, дифференциальное уравнение обычно имеет бесконечное число решений. В идеале, но обязательно не всегда соответствующая задача с начальными значениями будет иметь только один решение. Решение, в котором не осталось неизвестных констант называется конкретное решение .
Общий подход к разделимым уравнениям таков: Предположим, мы хотим решить $\dot{y} = f(t) g(y) $, где $f$ и $g$ — непрерывные функции.
 2-1$ имеет постоянные решения $y(t)=1$ и $y(t)=-1$.
2-1$ имеет постоянные решения $y(t)=1$ и $y(t)=-1$.Для нахождения непостоянных решений заметим, что функция $1/g(y)$ непрерывна, где $g\not=0$, поэтому $1/g$ имеет первообразную $G$. Пусть $F$ будет первообразная $f$. Теперь мы пишем $$G(y) = \int {1\over g(y)}\,dy = \int f(t)\,dt=F(t)+C,$$ поэтому $G(y)=F(t)+C$. Теперь решим это уравнение относительно $y$.
Конечно, есть несколько мест, где это идеальное описание могло бы быть использовано. неверно: нужно уметь находить первообразные $G$ и $F$, а нам нужно решить окончательное уравнение относительно $y$. В результате решения исходного дифференциального уравнения постоянные решения, если они есть, и все функции $y$, удовлетворяющие $G(y)=F(t)+C$.
Пример 17.1.9 Рассмотрим дифференциальное уравнение $\dot y=ky$. Когда $k>0$, это описывает некоторые простые случаи роста населения: это говорит о том, что изменение населения $y$ пропорционально Население. Основное предположение состоит в том, что каждый организм в текущая популяция воспроизводится с фиксированной скоростью, поэтому чем больше популяции, тем больше образуется новых организмов.
 Пока это слишком
просто для моделирования большинства реальных популяций, в некоторых случаях это полезно
ограниченное время. Когда $k 9\circ$?
(отвечать)
Пока это слишком
просто для моделирования большинства реальных популяций, в некоторых случаях это полезно
ограниченное время. Когда $k 9\circ$?
(отвечать)Пример 17.1.13 Решать Логистическое уравнение $\dot{y} = ky(M-y)$. (это несколько более разумная модель населения в большинстве случаев, чем более простая $\dot y=ky$.) Нарисуйте график решения этого уравнения при $M=1000$, $k=0,002$, $y(0)=1$. (отвечать)
Пример 17.1.14 Предположим, что $\dot{y} = ky$, $y(0)=2$ и $\dot{y}(0)=3$. Что такое $y$? (отвечать)
Пример 17.1.15 Радиоактивное вещество подчиняется уравнению $\dot{y} =ky$, где $k0$. Через какое время останется половина массы? (Это известно как период полураспада. Обратите внимание, что период полураспада зависит от $k$, но не на $M$.) (отвечать)
Пример 17.1.16 Висмут-210 имеет период полураспада пять дней. Если там есть изначально 600 миллиграмм, сколько осталось через 6 дней? Когда будет осталось всего 2 миллиграмма? (отвечать)
Пример 17.

- Константа может быть вынесена за знак дифференциала:

 Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x0.
Если данный предел существует, то говорят, что функция f(x) дифференцируема в точке x0. Первый — это подобласть исчисления, которая означает бесконечно малую разницу в некоторой флуктуирующей величине. Производные, с другой стороны, относятся к изменению выходной стоимости из-за соответствующего изменения входной стоимости. Это означает скорость этого изменения.
Первый — это подобласть исчисления, которая означает бесконечно малую разницу в некоторой флуктуирующей величине. Производные, с другой стороны, относятся к изменению выходной стоимости из-за соответствующего изменения входной стоимости. Это означает скорость этого изменения.
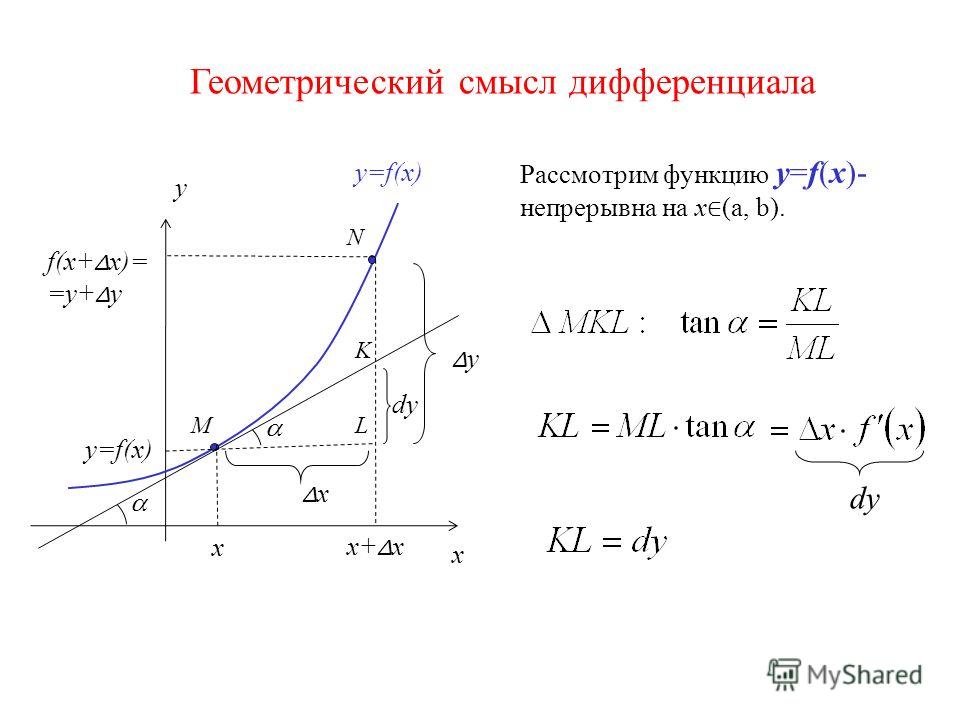 Предположим, что в какой-то момент x 0 ∈ [ a , b ] независимая переменная увеличивается на Δ х . Приращение функции Δ y , соответствующее изменению независимой переменной Δ x , равно
Предположим, что в какой-то момент x 0 ∈ [ a , b ] независимая переменная увеличивается на Δ х . Приращение функции Δ y , соответствующее изменению независимой переменной Δ x , равно \]
\]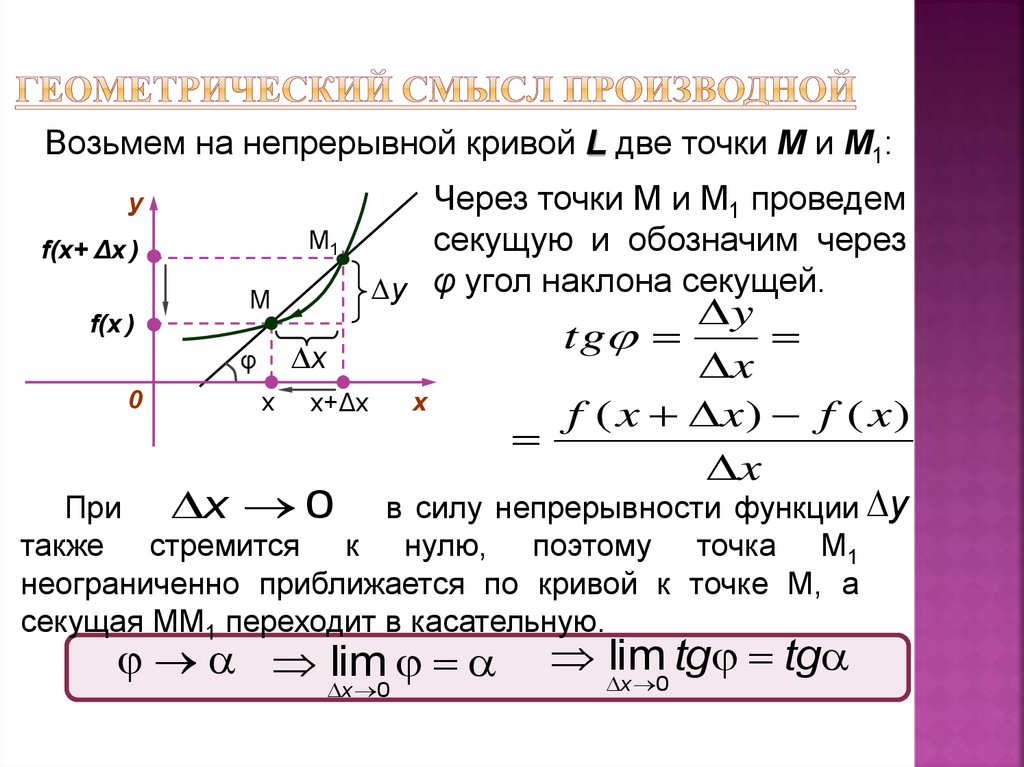 \]
\] Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\)
Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\) \] 9{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\]
\] 9{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\] Это свойство называется формоинвариантностью дифференциала.
Это свойство называется формоинвариантностью дифференциала. раздел 2, смысл 1) или дифференциал
раздел 2, смысл 1) или дифференциал значение произведения 1) производной функции одной переменной на приращение независимой переменной
значение произведения 1) производной функции одной переменной на приращение независимой переменной 0165 дифференциальных уравнений, как в колебательных контурах, и решения уравнения Шрёдингера в квантовой механике.
Ретт Аллен, Wired , 14 марта 2022 г.
С этой точки зрения дифференциальная конфиденциальность делает данные переписи более точными и прозрачными, а не менее. New York Times , 21 апреля 2022 г.
Меньшая машина активна 9Дифференциал 0165 передает крутящий момент на внешнее колесо во время энергичного прохождения поворотов, создавая забавное ощущение надвигающейся избыточной поворачиваемости даже за пределами точки, в которой задние шины фактически теряют сцепление с дорогой.
Майк Дафф, Автомобиль и водитель , 11 мая 2022 г.
Хотя подкачка является грубым способом маскировки данных, дифференциальные алгоритмы конфиденциальности могут быть настроены для точного удовлетворения требований конфиденциальности.
0165 дифференциальных уравнений, как в колебательных контурах, и решения уравнения Шрёдингера в квантовой механике.
Ретт Аллен, Wired , 14 марта 2022 г.
С этой точки зрения дифференциальная конфиденциальность делает данные переписи более точными и прозрачными, а не менее. New York Times , 21 апреля 2022 г.
Меньшая машина активна 9Дифференциал 0165 передает крутящий момент на внешнее колесо во время энергичного прохождения поворотов, создавая забавное ощущение надвигающейся избыточной поворачиваемости даже за пределами точки, в которой задние шины фактически теряют сцепление с дорогой.
Майк Дафф, Автомобиль и водитель , 11 мая 2022 г.
Хотя подкачка является грубым способом маскировки данных, дифференциальные алгоритмы конфиденциальности могут быть настроены для точного удовлетворения требований конфиденциальности. New York Times , 21 апреля 2022 г.
В программе поощрения говорится, что больницы, которые обязуются постоянно предоставлять отчеты о пропускной способности, будут иметь право на дифференцированную скорректированную выплату, увеличенную на 0,25%.
Стефани Иннес, , Республика Аризона, , 12 апреля 2022 г.
А теперь, когда прибывают первые беженцы из Украины, мало где более ярко иллюстрирует дифференциал 9Получают лечение 0166 беженцев. Washington Post , 11 марта 2022 г.
Уровень избирательности приема также был связан с дифференциальным ростом объема заявлений.
Майкл Т. Нитцель, Forbes , 26 января 2022 г.
Таким образом, цифра 99 процентов не является репрезентативной для реального использования, поскольку минимальное измерение фильтрации маски N95 составляет 9.
New York Times , 21 апреля 2022 г.
В программе поощрения говорится, что больницы, которые обязуются постоянно предоставлять отчеты о пропускной способности, будут иметь право на дифференцированную скорректированную выплату, увеличенную на 0,25%.
Стефани Иннес, , Республика Аризона, , 12 апреля 2022 г.
А теперь, когда прибывают первые беженцы из Украины, мало где более ярко иллюстрирует дифференциал 9Получают лечение 0166 беженцев. Washington Post , 11 марта 2022 г.
Уровень избирательности приема также был связан с дифференциальным ростом объема заявлений.
Майкл Т. Нитцель, Forbes , 26 января 2022 г.
Таким образом, цифра 99 процентов не является репрезентативной для реального использования, поскольку минимальное измерение фильтрации маски N95 составляет 9. 5 процентов (что составляет перепад давления, посадку, утечку и т. д.).
Кори Гаскин, Ars Technica , 18 декабря 2021 г.
5 процентов (что составляет перепад давления, посадку, утечку и т. д.).
Кори Гаскин, Ars Technica , 18 декабря 2021 г. Крис Солари, 9 лет0165 Detroit Free Press , 16 февраля 2022 г.
Эта чудовищная мельница с шестиступенчатой автоматической коробкой передач Ford, соединенной с 9-дюймовым дифференциалом Strange Engineering , встроена в точную копию корпуса фастбэка Dynacorn Classic Bodies от Mustang 1967 года.
Роберт Росс, Robb Report , 20 декабря 2021 г.
Шесть разных бомбардиров привели «Иглз» к доминирующему голу 14:0 дифференциал в трех турнирных играх.
Кэм Керри, BostonGlobe.com , 15 ноября 2021 г.
Не потренировавшись с США, Букеру, Миддлтону и Холидей пришлось преодолевать долгий перелет и приспосабливаться к времени дифференциал для игры.
Дуэйн Рэнкин, , Республика Аризона, , 6 августа 2021 г.
Крис Солари, 9 лет0165 Detroit Free Press , 16 февраля 2022 г.
Эта чудовищная мельница с шестиступенчатой автоматической коробкой передач Ford, соединенной с 9-дюймовым дифференциалом Strange Engineering , встроена в точную копию корпуса фастбэка Dynacorn Classic Bodies от Mustang 1967 года.
Роберт Росс, Robb Report , 20 декабря 2021 г.
Шесть разных бомбардиров привели «Иглз» к доминирующему голу 14:0 дифференциал в трех турнирных играх.
Кэм Керри, BostonGlobe.com , 15 ноября 2021 г.
Не потренировавшись с США, Букеру, Миддлтону и Холидей пришлось преодолевать долгий перелет и приспосабливаться к времени дифференциал для игры.
Дуэйн Рэнкин, , Республика Аризона, , 6 августа 2021 г. Задний двигатель идентичен переднему блоку, но коробка передач добавляет электронный блокирующий механизм к 9.Дифференциал 0165 для обеспечения дополнительного сцепления при движении по бездорожью.
Сэм Абуэльсамид, Forbes , 20 мая 2021 г.
Нотр-Дам должен был закрыться со счетом 41-0, чтобы вернуться к этой точке дифференциал .
Том Нойе, The Indianapolis Star , 11 марта 2021 г.
Сохранение и улучшение этого числа может стать решающим фактором, если конференц-стол или «Щит болельщиков» сведутся к цели 9.0165 дифференциал .
Джулия По, orlandosentinel.com , 5 октября 2020 г.
Узнать больше
Задний двигатель идентичен переднему блоку, но коробка передач добавляет электронный блокирующий механизм к 9.Дифференциал 0165 для обеспечения дополнительного сцепления при движении по бездорожью.
Сэм Абуэльсамид, Forbes , 20 мая 2021 г.
Нотр-Дам должен был закрыться со счетом 41-0, чтобы вернуться к этой точке дифференциал .
Том Нойе, The Indianapolis Star , 11 марта 2021 г.
Сохранение и улучшение этого числа может стать решающим фактором, если конференц-стол или «Щит болельщиков» сведутся к цели 9.0165 дифференциал .
Джулия По, orlandosentinel.com , 5 октября 2020 г.
Узнать больше Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв. Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/дифференциал. По состоянию на 16 сентября 2022 г.
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/дифференциал. По состоянию на 16 сентября 2022 г. com: Энциклопедическая статья о дифференциал
com: Энциклопедическая статья о дифференциал 
 Например, скорость движущегося объекта можно интерпретировать как скорость изменения расстояния во времени. Если y = f(x) — функция, которая дифференцируется, то, согласно дифференциальному исчислению, используется обозначение f'(x) = dy/dx. Некоторые важные термины, связанные с дифференциальным исчислением, перечислены ниже:
Например, скорость движущегося объекта можно интерпретировать как скорость изменения расстояния во времени. Если y = f(x) — функция, которая дифференцируется, то, согласно дифференциальному исчислению, используется обозначение f'(x) = dy/dx. Некоторые важные термины, связанные с дифференциальным исчислением, перечислены ниже: Другими словами, значение зависимой переменной определяется независимой переменной.
Другими словами, значение зависимой переменной определяется независимой переменной. Производная функции f(x) представляется как f'(x), dy/dx, df/dx.
Производная функции f(x) представляется как f'(x), dy/dx, df/dx. ln .a , где a > 0, a ≠ 1
ln .a , где a > 0, a ≠ 1 Существуют два основных типа дифференциальных уравнений, а именно, обыкновенные дифференциальные уравнения и уравнения в частных производных. Обыкновенное дифференциальное уравнение — это уравнение, в котором есть только одна независимая переменная и уравнение содержит одну или несколько производных по этой переменной. Уравнение в частных производных состоит из одной или нескольких независимых переменных и их частных производных.
Существуют два основных типа дифференциальных уравнений, а именно, обыкновенные дифференциальные уравнения и уравнения в частных производных. Обыкновенное дифференциальное уравнение — это уравнение, в котором есть только одна независимая переменная и уравнение содержит одну или несколько производных по этой переменной. Уравнение в частных производных состоит из одной или нескольких независимых переменных и их частных производных. Правила дифференциального исчисления перечислены в таблице, приведенной ниже.
Правила дифференциального исчисления перечислены в таблице, приведенной ниже.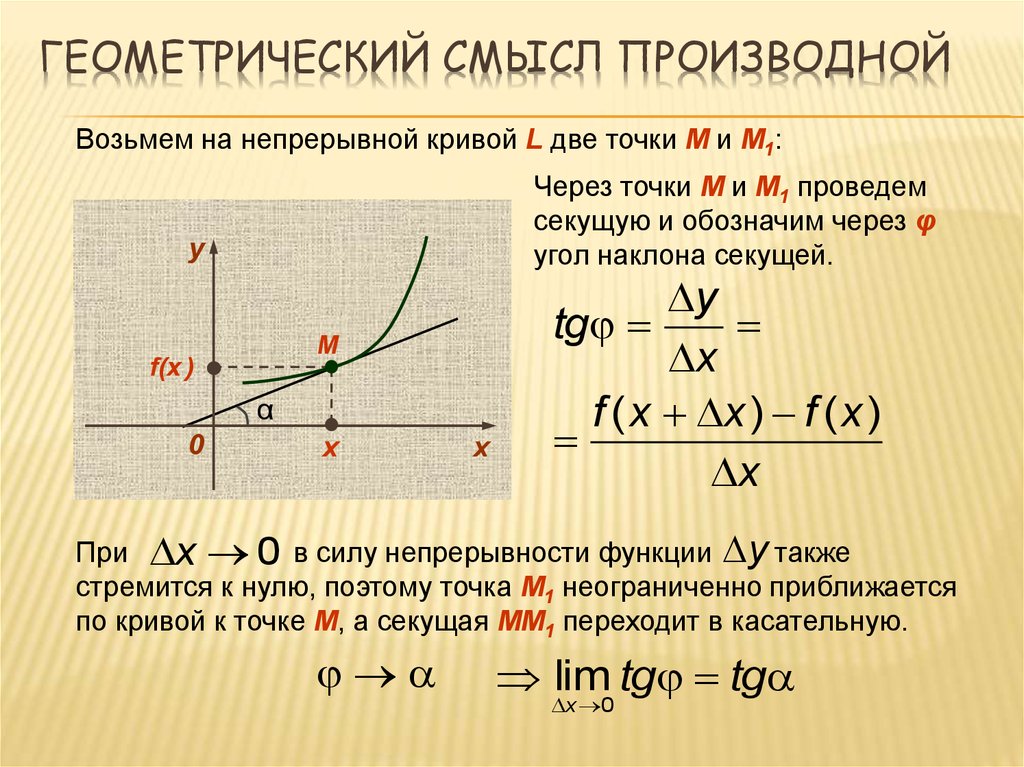 \ frac {\ mathrm {d} u} {\ mathrm {d} x} \) = f'[ г(х)]г'(х)
\ frac {\ mathrm {d} u} {\ mathrm {d} x} \) = f'[ г(х)]г'(х)



 Дифференциальное исчисление связано с нахождением скорости изменения функции, в то время как интегральное исчисление связано с нахождением площади под кривой.
Дифференциальное исчисление связано с нахождением скорости изменения функции, в то время как интегральное исчисление связано с нахождением площади под кривой. Термин «первый порядок» означает, что первый
появляется производная от $y$, но не производные более высокого порядка.
93/3+t+8/3$.
$\квадрат$
Термин «первый порядок» означает, что первый
появляется производная от $y$, но не производные более высокого порядка.
93/3+t+8/3$.
$\квадрат$ 2}$,
позволяя $A$ быть равным нулю.
$\квадрат$
2}$,
позволяя $A$ быть равным нулю.
$\квадрат$ 2-1$ имеет постоянные решения $y(t)=1$ и $y(t)=-1$.
2-1$ имеет постоянные решения $y(t)=1$ и $y(t)=-1$.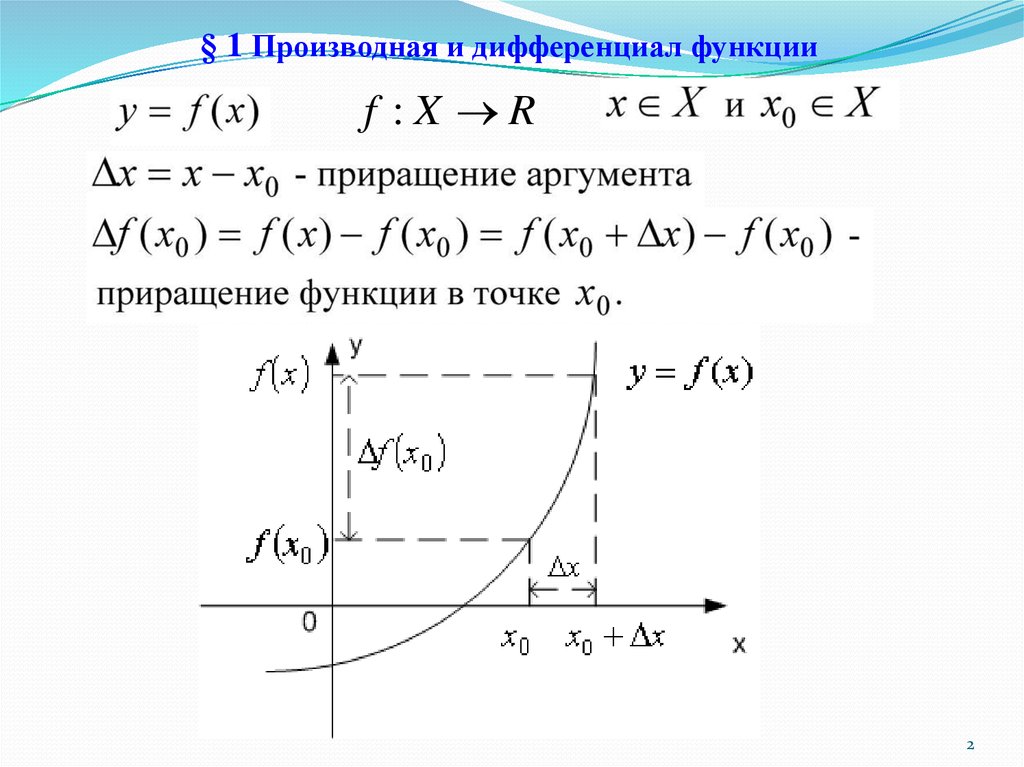 Пока это слишком
просто для моделирования большинства реальных популяций, в некоторых случаях это полезно
ограниченное время. Когда $k 9\circ$?
(отвечать)
Пока это слишком
просто для моделирования большинства реальных популяций, в некоторых случаях это полезно
ограниченное время. Когда $k 9\circ$?
(отвечать)