Как считать Объяснение с решенным Примером
Кубический корень — это любое число, умноженное само на себя три раза, чтобы получить куб. Совершенные кубы и кубические корни должны быть целыми числами и, следовательно, представляют собой целые числа, встречающиеся на числовой прямой. Куб изображается математически как любое число в третьей степени.
Кубический корень — это операция определения того, какое число при трехкратном умножении само на себя дает результат 25. Кубический корень числа — это коэффициент, который мы умножаем само на себя трижды, чтобы получить это число. Символом кубического корня является 3 кубический корень из, конец кубический корень . Нахождение кубического корня числа противоположно возведению числа в куб. 9{1\над{3}}\). В случае с числом 5, например, вопрос, каков результат после трехкратного умножения числа на само себя, приводит к ответу 125, или 5 x 5 x 5. Следовательно, кубический корень из 125 равен 5.
Это Можно получить кубический корень любого числа, но для целей этой статьи мы сосредоточимся только на числе 25.
Нахождение кубического корня — это процесс определения числа, которое при трехкратном умножении на само себя дает значение 25.
Как вычислить значение кубического корня из 25?
Существует два-три метода вычисления кубического корня любого числа без калькулятора. Это метод Галлея, метод деления и метод Ньютона-Рафсона. Давайте рассмотрим каждый метод по очереди, чтобы увидеть, как мы можем определить кубический корень из 25.
Кубический корень из 25 по методу Галлея
В численном анализе метод Галлея представляет собой алгоритм поиска корня, используемый для функций одной действительной переменной. с непрерывной второй производной. Он назван в честь Эдмонда Галлея, человека, который его создал. Он итеративно генерирует серию корневых приближений; их скорость сходимости к корню кубическая. 93 + 25))}= 2,55\)
\({\ подразумевает}\sqrt[3]{25} ≈ 2,829\)
Таким образом, кубический корень из 25 приблизительно равен 2,829.
Кубический корень из 25 методом деления
Этот метод аналогичен методу деления в длину, но вместо кратных делителей мы используем куб.
3=19.99\приблизительно25\)
Кубический корень из 25 по методу Ньютона Рафсона
Ньютона Рафсона — это итеративный метод для нахождения квадратного или кубического корня любого числа. Метод Ньютона-Рафсона (также известный как метод Ньютона) — это способ быстро найти хорошее приближение для корня вещественнозначной функции f(x) = 0. Он использует идею о том, что непрерывную и дифференцируемую функцию можно аппроксимировать. касательной к ней прямой. Алгоритм метода Ньютона-Рафсона следующий.
- Запишем задачу как функцию от x.
- Находим уравнение для его производной.
- Мы предполагаем возможное решение. Это решение называется \(x_0\).
- Далее применим формулу: \(x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}\), где x = (0, 1, 2, 3….)
- Мы останавливаемся, когда ответ двух итерационных шагов схож для некоторого выбранного количества значащих цифр.
Вот как мы можем использовать метод Ньютона Рафсона, чтобы найти кубический корень из 25.
92}\)
\(x_4 = 2,924\)
На этом можно остановиться. Ответ двух последовательных итераций одинаков. Таким образом, x = 2,924 — это кубический корень из 25.
Является ли кубический корень из 25 иррациональным?
Вещественное число, которое не может быть представлено в виде прямой дроби, называется иррациональным числом. Его нельзя описать с помощью соотношения. К настоящему времени мы знаем, что кубический корень 25 равен 2,924. Таким образом, 25 не является совершенным кубом. Не каждое число образует идеальный куб. Эти цифры иррациональны по своей природе. Однако кубический корень из 25 иррационален, потому что 2,924 не целое число.
Итог
Кубический корень из 25 равен 2,571. Таким образом, 25 не является совершенным кубом. Есть несколько способов узнать кубический корень из несовершенного кубического числа. Мы можем найти его с помощью метода Галлея, метода деления или метода Ньютона-Рафсона.
Решенные примеры на кубический корень из 25
Вот несколько решенных примеров на кубический корень из 25.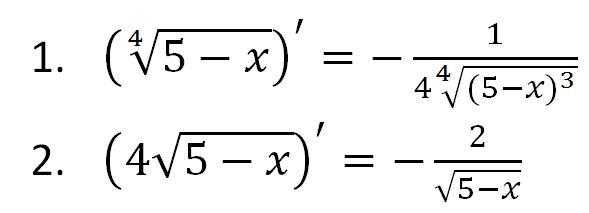
Решенный пример 1: Найдите кубический корень каждого из следующих чисел методом простой факторизации:
(i) 10648
(ii) 512
Решение:
(i)10648
\(\sqrt[3]{10648}=\sqrt[3]{2\times2\times2\times11\times11 \times11}\)
= 2 x 11
= 22
(ii) 27000
\(\sqrt[3]{27000}=\sqrt[3]{2\times2\times2\times3\times3\ times3\times5\times5\times5}\)
= 2 x 3 x 5
= 30
Пример 2: Если кубический корень из 25 равен 2,924, найдите кубический корень из 25000000.
{2}=292,4\).Надеюсь, эта статья о кубическом корне из 25 была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Кубический корень из 25. Часто задаваемые вопросы
В.1 Что такое кубический корень из 25?
Ответ 1 Кубический корень из 25 равен 2,924.
Q.