Решение квадратных уравнений через производные / Хабр
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого.
Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Нет.
Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль».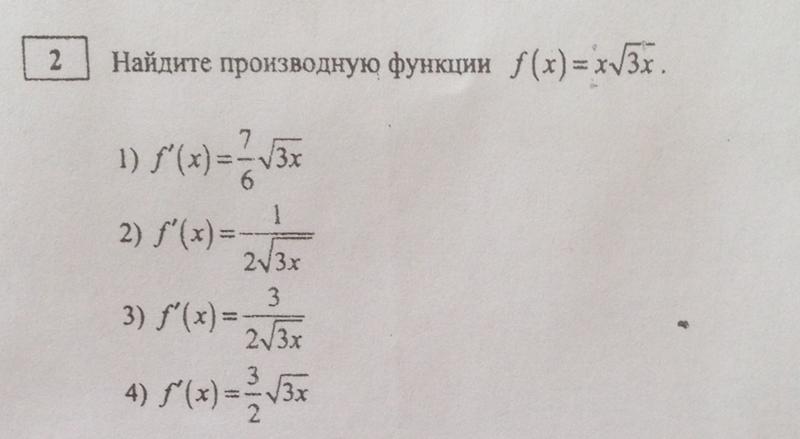
Иными словами, нам от положения необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
, также как и
Тогда, подставив все известные величины, получим:
Поделим все на :
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Размер национальных собраний: классический вывод закона кубического корня концептуально ошибочен
Введение
Можно ли оценить «оптимальный» размер национального собрания страны методами, аналогичными физическим исследованиям? Вопрос своевременный: в США бушуют дебаты о недостаточном представительстве на федеральном уровне и уровне штатов.
С другой стороны, недавно были предприняты инициативы по сокращению числа представителей в национальных парламентах многих стран, включая Францию, Венгрию, Ирландию, Японию, Мексику, Нидерланды, Португалию, Румынию и Великобританию. А Италия только что вышла из референдума по этому вопросу.
Классическим эталоном является работа Таагепера 1972 года [1], который ввел известную формулу кубического корня для связи A , числа членов парламента, и P o , населения:
A=aPo1/3,(1)
, где a — константа.
Позднее были представлены альтернативные подходы [2–5]. В частности, Ориоль и Гэри-Бобо [2] вывели закон квадратного корня, а затем эмпирически получили показатель степени 0,4 из последних данных для 100 стран. И основы закона кубического корня подверглись критике: в частности, Джейкобс и Отджес [6] поставили под сомнение причинно-следственную последовательность, которая якобы приводит к нему.
Соотношение между размерами A и P o следует рассматривать в более общем контексте [7–9]. Действительно, масштабные степенные отношения с населением были эмпирически и/или формально выведены для других величин, таких как число кандидатов на выборах [7, 8], производство патентов, личный доход и длина электрического кабеля [9]. Общее представление состоит в том, что « подобно крупномасштабным физическим термодинамическим системам, большие группы взаимодействующих людей могут проявлять универсальные статистические свойства»9.0008» [7]. Конечно, в наши задачи здесь не входит оспаривать это представление, которое подтверждается множеством фактов и привело к важному вкладу в понимание коллективных человеческих явлений. Наша цель состоит в том, чтобы показать, что в конкретном случае отношения кубического корня для членов парламента и населения вывод Ref. [1] был ошибочным.
Кроме того, законы масштабирования кубического корня имеют альтернативные математические объяснения [10] по отношению к [1] и были известны еще (по крайней мере) 1909 [11].
Таким образом, наша задача классического вывода Ref. [1] не обязательно означает, что сам закон неверен.
Метод
Работа Таагепера [1] по мнению многих экспертов остается вехой, известна широкой публике и часто используется в политических дебатах. Например, это рекламировалось в СМИ как «научная» поддержка одной из сторон на недавнем итальянском референдуме [4]. Таким образом, мы решили непосредственно взглянуть на его происхождение с точки зрения физика и неожиданно обнаружили, что оригинальная работа [1] затрагивает четыре критические проблемы:
(1) Закон кубического корня не был получен из его данных, и соответствующая подгонка была произвольно принудительной.
(2) Теоретические шаги, которые использовались для получения уравнения. 1 неправильно оценил один из его ключевых факторов.
(3) В модели предполагалось, что каждый представитель тратит в среднем одинаковое время на общение внутри и вне парламента – произвольная гипотеза, имеющая нереалистичные последствия.
(4) Никакая оценка «оптимального» размера по степенному закону, в том числе и по кубическому корню, не может достичь значимой точности.
Что касается первой задачи, то в исходной статье [1] действительно упоминался степенной закон, более общий, чем уравнение. 1:
A=aPon.(2)
Однако неожиданно возражали против его использования для подгонки данных: « Фактическое наилучшее соответствие данных выражению формы A = aP o n … можно было бы разработать, но это был бы тупик… Более плодотворно искать правдоподобную теоретическую модель, которая соответствовала бы наблюдаемой общей тенденции ». Этот аргумент в корне ошибочен с точки зрения физика: он рассматривает только одну гипотезу, отказываясь от априори от , чтобы продемонстрировать его превосходство по отношению к другим.
Результаты
Мы проанализировали последствия приведенного выше аргумента, применив ту же процедуру подгонки, что и в Ref.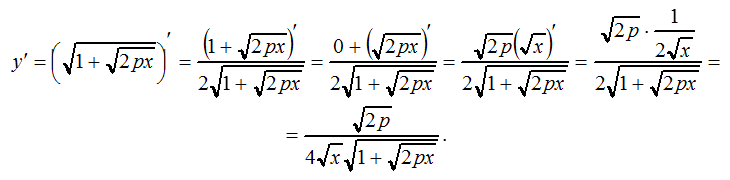
[1] к данным его Таблицы 1, т. е. методом наименьших квадратов логарифмов. Используя уравнение 2 вместо уравнения. 1, т. е. без ограничений (сплошная линия на рис. 1), получили:
A=0,10 Po0,45±0,03(3)
Показатель степени n = 0,45 на самом деле ближе к 0,5, закону квадратного корня, предложенному Ориолем и Гэри-Бобо [2], и к их эмпирическому значению 0,4 .
РИСУНОК. 1 . Логарифмический график исходных данных Таагепера [1]. Сплошная линия лучше всего соответствует уравнению. 3, тогда как пунктирная линия представляет собой (принудительное) соответствие закону кубического корня, приводящее к уравнению. 4.
Если заставить тот же набор данных соответствовать закону кубического корня, результат будет:
A=0,66 Po1/3; (4)
Соответствующая аппроксимация (рис. 1, пунктирная линия) статистически хуже: стандартное отклонение, 250, больше, чем для уравнения. 3, 209.
Чтобы представить вторую и третью проблемы, затрагивающие Ref. [1], мы должны рассмотреть ключевые шаги в выводе закона кубического корня. Короче говоря, время, затраченное на общение, считалось существенным фактором эффективности парламента. И это время было связано с количеством каналов связи.
Были рассмотрены два вида каналов: во-первых, каналы между каждым депутатом парламента и его/ее активным электоратом. Среднее число таких каналов на члена составляет:
CC≈kPo/A,(5)
Где kP o — доля населения, вовлеченная в политику.
Второй тип каналов связи соединяет различных членов собрания для обсуждения и реализации мер, определенных первым типом каналов. При общении между собой два члена сборки используют один и тот же канал, и в [1] утверждается, что общее количество каналов в этом случае:
CA=(1/2)A(A−1),(6)
Что, за исключением нереально малых сборок, может быть аппроксимировано как:
CA≈A2/2(7)
Каково соотношение между C C и C A ? Ссылка [1] просто предположил, что для максимальной эффективности C C = C A , что приводит к:
A=(2k)1/3Po1/3(8)
корневой закон уравнения.
1, где a = (2 k ) 1/3 .
Однако на эту логическую структуру влияют две концептуальные проблемы. Во-первых, уравнение 5 относится к каналам между одним членом собрания и соответствующим избирательным округом, тогда как уравнения. 6 и 7 дают количество межсборочных каналов для всех элементов. Для одного члена вместо уравнений. 6 и 7 необходимо использовать:
CA=(1/2)(A−1)≈A/2(9)
Что, если снова предположить, что C C = C A , приводит по:
A=(2k)1/2Po1/2(10)
Не кубический, а квадратный закон [2].
Чтобы лучше понять, почему уравнение. 9 является правильным и уравнения. 6 и 7 нет, представьте себе, что межсборочные «каналы связи» используются только для выступлений. Один член собрания делит с каждым спикером один канал, и общее количество его каналов соответствует количеству спикеров, т. е. представителей, а не его площади.
Это превращает закон кубического корня в закон квадратного корня.
Другой недостаток в приведенной выше логической структуре заключается в том, что нет абсолютно никаких доказательств, подтверждающих ее гипотезу о том, что C C = C A . Наоборот, это предположение вызывает проблемы. В оригинальной работе Ref. [1], это привело к уравнению. 8, и соответствующее принудительное наилучшее соответствие уравнения. 4 даст k ≈ 14%, что, надеюсь, слишком мало. И станет катастрофическими 0,3% при неограниченном наилучшем соответствии уравнения. 3.
Баланс между различными типами связи может меняться от страны к стране и со временем меняется. Например, современные средства связи могут уменьшить С С . Симметрично, эффективные переговорщики могут уменьшить C A . Таким образом, предположение априори , что C C = C A , является произвольным.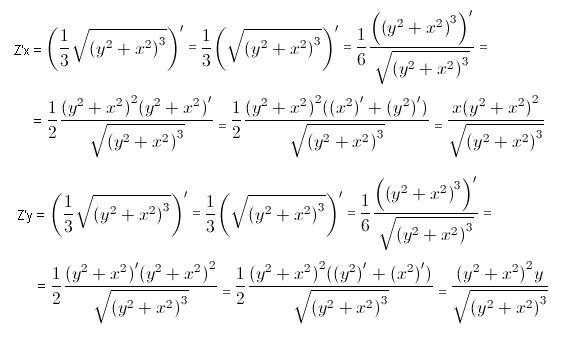
Предположим вместо этого, что C C / C A = x , уравнения. 8 и 10 становятся:
A=(2k/x)1/3Po1/3(11)
A=(2k/x)1/2Po1/2(12)
В обоих случаях коэффициент умножения равен комбинация k и x , которые нельзя отделить друг от друга путем наилучшего подбора данных. Возможно, можно было бы оценить 90 007 тыс. 90 008 из независимой информации, такой как грамотность, членство в партии и участие избирателей. Но оценить x чрезвычайно сложно из-за его многочисленных, конкурирующих и развивающихся причин и отсутствия данных.
Обсуждение
Трудности с вычислением x и k отрицательно сказываются на использовании степенного закона для определения «оптимального» размера национального собрания. И другие проблемы влияют на этот подход.
Обратите внимание, что Ref. [1] попытался связать население не с «оптимальными» размерами парламента, а с реальными размерами, используя данные для стран всех типов.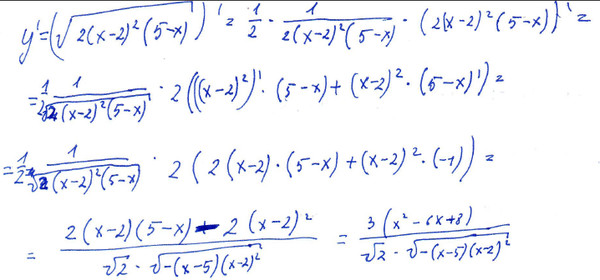
Из них многие, если не большинство, страдали от коррупции, неэффективной бюрократии и/или авторитарных режимов. Таким образом, они вряд ли могли привести к «оптимальным» значениям A .
Гипотетически можно попытаться извлечь «оптимальное» значение, используя подмножество «хороших» стран, возможно, с низкими индексами коррупции и бюрократической неэффективности. Однако даже фильтрация не могла решить четвертую проблему, затрагивающую Ref. [1]: точность. На самом деле, любая оценка Число со степенным законом очень чувствительно к показателю степени. Взяв производную уравнения 2 Получен:
(D A /D N ) = AP O N LN ( P O ) = A LN ( P 9008 O ), A LN ( P 9008 O ), A LN ( P 9008 O )
dA/A=1n(Po)dn
, так как P o большая, неопределенность d n , какой бы малой она ни была, умножается на большой коэффициент ln( P 2 o 900) большая относительная неопределенность d А / А .
Например, неопределенность d n ±0,03 из уравнения 3, с населением всего ≈617 000 человек, увеличило бы d A / A до ≈40%, что достаточно много, чтобы учесть большинство политических предпочтений.
Короче говоря, точная оценка «оптимального» размера национального собрания иллюзорна. И попытки ввести дополнительные факторы, кроме населения, не могут решить вышеуказанные проблемы.
В лучшем случае такой подход может выявить страны, которые сильно отклоняются от «средних», как Ref. [2] делали для Франции, США и Италии. Однако без фильтрации «среднее» будет для сочетания «хороших» и «плохих» стран, поэтому отклонение от него не обязательно будет отрицательным… и даже может быть положительным!
В заключение мы с удивлением обнаружили, что историческая и очень влиятельная работа Таагепера [1] использовала неверное уравнение для вывода своего знаменитого закона кубического корня и произвольно предполагала равное распределение времени между коммуникациями между ассамблеями и ассамблеями.
Неограниченное наилучшее соответствие исходных данных не поддерживает закон кубического корня и вместо этого будет способствовать степенному закону с показателем степени больше 1/3. Эти изъяны фатально подрывают основы закона кубического корня и дисквалифицируют — в том числе и по другим причинам — его популярное использование для оценки «оптимального» размера парламента для страны.
Заявление о доступности данных
В этом исследовании были проанализированы общедоступные наборы данных. Эти данные можно найти здесь: Ссылка 1 в статье.
Вклад авторов
Автор подтверждает, что является единственным автором этой работы и одобрил ее публикацию.
Финансирование
Работа, поддерживаемая в натуральной форме Федеральной политехнической школой Лозанны (EPFL).
Конфликт интересов
Автор заявляет, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Ссылки
1. Таагепера Р. Размер национальных собраний. Soc Sci Res (1972) 1: 385–401. Данные, извлеченные из этой статьи и используемые здесь, можно найти по адресу https://sciencehistory.epfl.ch/physics-and-sociology/
CrossRef Full Text | Google Scholar
2. Ориоль Э., Гэри-Бобо Р.Дж. Об оптимальном количестве представителей. Publ Choice (2012) 153: 419–445. doi:10.1007/s11127-011-9801-3
CrossRef Full Text | Академия Google
3. Ориоль Э., Гэри-Бобо Р.Дж. Чем больше, тем веселее? Выбор оптимального числа представителей в современных демократиях . Доступно по адресу: https://voxeu.org/optimal-number-representatives-democracy (2007 г.).
Google Scholar
4. De Sio L, Angelucci G. 945 sono troppi? 600 соно почи? Qual è il numero «ottimale» di parlamentari? . Доступно по адресу: https://cise.luiss.it/cise/2019/10/09/945-sono-troppi-600-sono-pochi-quale-e-il-numero-ottimale-di-parlamentari (2019 г.
).).
Google Scholar
5. Джейкобс К., Отжес С. Объяснение реформ сборочных размеров . Доступно по адресу: https://ecpr.eu/Filestore/PaperProposal/3bc100be-56fe-4efc-8d8c-a1f0b85e7f24.pdf (2014)
Google Scholar
6. Jacobs K, Otjes S. Объяснение размера сборок. Лонгитюдный анализ дизайна и реформы сборочных размеров в демократиях по всему миру. Elect Stud (2015) 40: 280–292. doi:10.1016/j.electstud.2015.10.001
Полнотекстовая перекрестная ссылка | Google Scholar
7. Мантовани М.С., Рибейро Х.В., Моро М.В., Пиколи С., Мендес Р.С. Законы масштабирования и универсальность в выборе кандидатов на выборах. Европейский физ. Письма (2011) 96:48001. doi:10.1209/0295-5075/96/48001
Полный текст CrossRef | Google Scholar
8. Мантовани М.С., Рибейро Х.В., Лензи Э.К., Пиколи С., Мендес Р.С. Участие в избирательном процессе: законы масштабирования и роль политических позиций. Phys Rev. E (2013) 88:024802.
doi:10.1103/PhysRevE.88.024802
Полнотекстовая перекрестная ссылка | Google Scholar
9. Bettencourt LMA, Lobo HD, Kühnert C, West GB. Рост, инновации, масштабирование и темп жизни в городах. Proc Natl Acad Sci Unit States Am (2007) 104: 7301–7306. doi:10.1073/pnas.0610172104
Полный текст CrossRef | Google Scholar
10. Кендалл М.Г., Стюарт А. Закон кубической пропорции в результатах выборов. Br J Sociol (1950) 1: 183–196. doi:10.2307/588113
CrossRef Полный текст | Академия Google
11. Гуджин Г., Грэм П.Дж. (2012). Места, голоса и пространственная организация выборов . Лондон, Великобритания: ECPR Press, глава 3.
Google Scholar
Interpolation (scipy.interpolate) — SciPy v1.10.1 Manual
Подпакет для объектов, используемых при интерполяции.
Как указано ниже, этот подпакет содержит сплайн-функции и классы,
1-D и многомерные (одномерные и многомерные)
классы интерполяции, полиномиальные интерполяторы Лагранжа и Тейлора и
обертки для FITPACK
и функции DFITPACK.
Одномерная интерполяция
| Интерполировать одномерную функцию. |
| Интерполяционный многочлен для набора точек |
| Интерполяционный многочлен для набора точек. |
| Удобная функция полиномиальной интерполяции. |
| Удобная функция полиномиальной интерполяции. |
| Удобная функция интерполяции pchip. |
| Кусочно-кубический интерполятор сопоставления значений и первых производных. |
| PCHIP Одномерная монотонная кубическая интерполяция. |
| Интерполятор Akima |
| Интерполятор данных кубического сплайна. |
| Кусочно-полиномиальный по коэффициентам и точкам останова |
| Кусочно-полиномиальный по коэффициентам и точкам останова. |
Многомерная интерполяция
Неструктурированные данные:
| Интерполировать неструктурированные данные D-D. |
| Кусочно-линейная интерполяция в измерениях N > 1. |
| Ближайший NDInterpolator(x, y). |
| CloughTocher2DInterpolator(точки, значения, tol=1e-6). |
| Интерполяция радиальной базисной функции (RBF) в N измерениях. |
| Класс для интерполяции радиальной базисной функции функций из N-D рассеянных данных в M-D область. |
| Устарело, начиная с версии 1.10.0. |
..])
..])Для данных по сетке:
| Многомерная интерполяция на регулярных или прямолинейных сетках. |
| Интерполяция на регулярной или прямолинейной сетке произвольных размеров. |
| Аппроксимация двумерным сплайном на прямоугольной сетке. |
См. также
scipy.ndimage.map_coordinates
Тензорные полиномы произведения:
| Полином кусочно-тензорного произведения |
Одномерные шлицы
| Одномерный сплайн в основе B-сплайна. |
| Вычислить (коэффициенты) интерполяционного B-сплайна. |
| Вычислить (коэффициенты) B-сплайна фитинга на основе LSQ (наименьший квадрат). |
| Вычислите (коэффициенты) функции сглаживания кубического сплайна, используя |
Функциональный интерфейс для процедур FITPACK:
| Найдите представление B-сплайна одномерной кривой. |
| Найдите представление B-сплайна N-D кривой. |
| Оценка B-сплайна или его производных. |
| |
| Найдите корни кубического B-сплайна. |
| Оценить все производные B-сплайна. |
| Вычисление сплайн-представления производной заданного сплайна |
| Вычислить сплайн для первообразной (интеграла) заданного сплайна. |
| Вставьте узлы в B-сплайн. |
.])
Объектно-ориентированный интерфейс FITPACK:
| Одномерный сглаживающий сплайн, соответствующий заданному набору точек данных. |
| Одномерный интерполирующий сплайн для заданного набора точек данных. |
| Одномерный сплайн с явными внутренними узлами. |
Двухмерные шлицы
Для данных по сетке:
| Аппроксимация двумерным сплайном на прямоугольной сетке. |
| Двумерная сплайновая аппроксимация на прямоугольной сетке на сфере. |
Для неструктурированных данных:
| Базовый класс для двумерных сплайнов. |
| Гладкая двумерная сплайновая аппроксимация. |
| Гладкая двумерная сплайновая аппроксимация в сферических координатах. |
| Взвешенная аппроксимация двумерным сплайном по методу наименьших квадратов. |
| Взвешенная аппроксимация двумерным сплайном по методу наименьших квадратов в сферических координатах. |
Низкоуровневый интерфейс для функций FITPACK:
| Найдите двумерное B-сплайновое представление поверхности. |
| Оценка двумерного B-сплайна и его производных. |
..])Дополнительные инструменты
| Возвращает интерполяционный многочлен Лагранжа. |
| Оцените полином Тейлора от f в точке x с помощью полиномиальной аппроксимации. |
| Возврат Паде-аппроксимация полинома как отношение двух полиномов. |
См. также
scipy.ndimage.map_coordinates , scipy.ndimage.spline_filter , scipy.signal.resample , scipy.signal.bspline , scipy.