Основные правила дифференцирования
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
(5)
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.
(6)
Правило 2. Если функции
и
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
(7)
т.е.
производная произведения двух функций
равна сумме произведений каждой из этих
функций на производную другой.
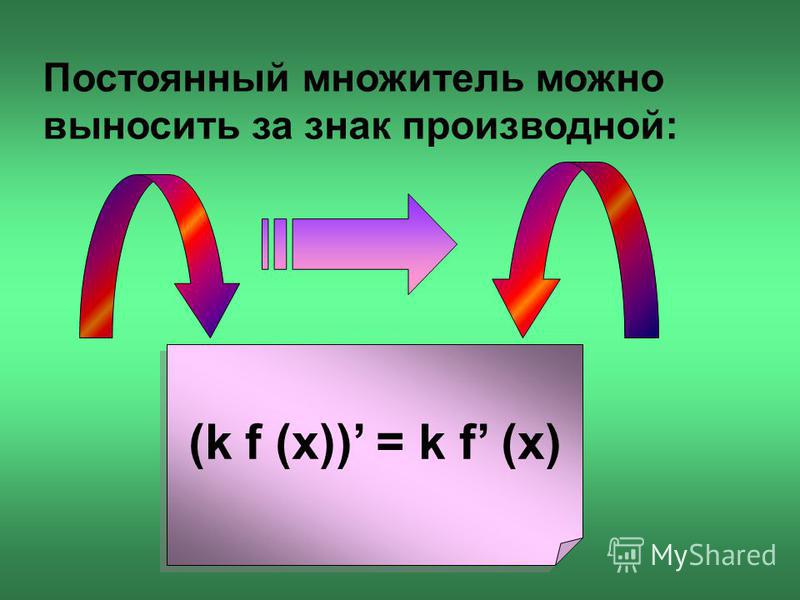
Следствие 1. Постоянный множитель можно выносить за знак производной:
(8)
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей имеем:
(9)
Правило 3. Если функции
и
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
(10)
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Пример 4. Найти производную функции
Решение. Применяя правила (5) и (8) и формулу (4) дифференцирования степенной функции получим
Пример
5.
Найти
производную функции
Решение. Применим правило (7) дифференцирования произведения, а затем найдём производные сомножителей так же, как в примере 4. Тогда получим
Пример 6. Найти производную функции
Решение. Применим правило (10) дифференцирования частного:
Затем, так же как и выше, вычислим производные в числителе. Имеем
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция Теперь
продифференцируем это выражение как
сложную функцию, имея ввиду, что y —
это функция от x. Отсюда видно, что искомая производная равна |
Пример 1 |
Вычислить производную функции . Решение. Применяем логарифмическое дифференцирование:
|
Пример 2 |
| Найти производную функции . Решение. Прологарифмируем обе части и затем продифференцируем.
|
Пример 3 |
Вычислить производную функции . Решение. Возьмем логарифм от обеих частей:
Теперь продифференцируем левую и правую части:
|
Пример 4 |
Продифференцировать . Решение. Сначала возьмем логарифм от обеих частей:
Дифференцируя левую и правую части соотношения, получаем
Следовательно, производная равна
|
3.6: Цепное правило — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2495
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Укажите цепное правило для композиции двух функций.
- Примените цепное правило вместе с степенным правилом.
- Правильно применяйте цепное правило и правило произведения/частного в сочетании, когда оба необходимы.
2+1}\ ). В этом разделе мы изучаем правило нахождения производной композиции двух или более функций. Получение цепного правила
Когда у нас есть функция, представляющая собой композицию двух или более функций, мы можем использовать все методы, которые мы уже изучили, чтобы дифференцировать ее. Однако использование всех этих методов для разбиения функции на более простые части, которые мы можем различать, может оказаться громоздким. Вместо этого мы используем цепное правило , которое гласит, что производная составной функции — это производная внешней функции, вычисляемой как внутренняя функция, умноженная на производную внутренней функции. 93)\).
Теперь, когда мы вывели частный случай цепного правила, мы сформулируем общий случай, а затем применим его в общей форме к другим составным функциям. Неформальное доказательство приведено в конце раздела.
Правило: Цепное правило
Пусть \(f\) и \(g\) — функции. Для всех \(x\) в области определения \(g\), для которых \(g\) дифференцируемо в \(x\) и \(f\) дифференцируемо в \(g(x)\), производная сложной функции
\[h(x)=(f∘g)(x)=f\big(g(x)\big) \nonumber \]
определяется как
\[h'(x)=f’\big(g(x)\big)\cdot g'(x).
\nonumber \]Альтернативно, если \(y\) является функцией \(u\), а \(u\) является функцией \(x\), то
\[\dfrac{dy} {dx}=\dfrac{dy}{du}⋅\dfrac{du}{dx}. \nonumber \]
Стратегия решения проблем: применение цепного правила
- Чтобы дифференцировать \(h(x)=f\big(g(x)\big)\), начнем с определения \(f(x) \) и \(g(x)\).
- Найдите \(f'(x)\) и оцените его в \(g(x)\), чтобы получить \(f’\big(g(x)\big)\).
- Найти \(g'(x).\)
- Напишите \(h'(x)=f’\big(g(x)\big)⋅g'(x).\)
Примечание : Применяя цепное правило к композиции из двух или более функций, имейте в виду, что мы работаем от внешней функции внутрь. Также полезно помнить, что производная от композиции двух функций может считаться состоящим из двух частей; производная композиции трех функций состоит из трех частей; и так далее. Также помните, что мы никогда не оцениваем производную по производной. 93\) в точке \(x=−2\).
- Подсказка
Используйте предыдущий пример в качестве руководства.
- Ответить
\(у=-48х-88\)
Комбинирование цепного правила с другими правилами
Теперь, когда мы можем комбинировать цепное правило и правило степени, мы рассмотрим, как комбинировать цепное правило с другими изученными нами правилами. В частности, мы можем использовать его с формулами для производных тригонометрических функций или с правилом произведения.
Пример \(\PageIndex{4}\): использование цепного правила для общей функции косинуса
Найдите производную \(h(x)=\cos\big(g(x)\big).\)
Решение
Подумайте о \(h(x)=\cos\big(g(x)\big)\) как \(f\big(g(x)\big)\), где \(f (х)=\cos х\). Поскольку \(f'(x)=-\sin x\), мы имеем \(f’\big(g(x)\big)=-\sin\big(g(x)\big)\). Затем делаем следующий расчет.
\[\begin{align*} h'(x)&=f’\big(g(x)\big)\cdot g'(x) & & \text{Применить правило цепочки.} \\[ 4 пт] 95+2x).\)
Упражнение \(\PageIndex{3}\)
Найдите производную \(h(x)=\sin(7x+2).
\)- Подсказка
Сначала примените цепное правило к \(h(x)=\sin\big(g(x)\big)\), а затем используйте \(g(x)=7x+2\).
- Ответить
\(h'(x)=7\cos(7x+2)\)
Здесь мы приводим список формул производных, которые можно получить, применяя цепное правило в сочетании с формулами производных тригонометрических функций. Их выводы аналогичны тем, которые использовались в приведенных выше примерах. Для удобства формулы также даны в обозначениях Лейбница, которые некоторым учащимся легче запомнить. (Мы обсудим цепное правило с использованием обозначений Лейбница в конце этого раздела.) Нет абсолютной необходимости запоминать их как отдельные формулы, поскольку все они являются приложениями цепного правила к ранее выученным формулам.
Использование цепного правила с тригонометрическими функциями
Для всех значений \(x\), для которых определена производная,
\(\dfrac{d}{dx}\Big(\sin(g( x))\Big)=\cos(g(x))\cdot g'(x)\) \(\dfrac{d}{dx}\Big(\sin u\Big)=\cos u\cdot\dfrac{du}{dx}\) \(\dfrac{d}{dx}\Big(\cos(g(x))\Big)=-\sin(g(x))\cdotg'(x)\) \(\dfrac{d}{dx}\Big(\cos u\Big)=-\sin u\cdot\dfrac{du}{dx}\) 92u\cdot\dfrac{du}{dx}\) \(\dfrac{d}{dx}\Big(\text{sec}(g(x))\Big)=\text{sec}(g(x))\tan(g(x)) \cdot g'(x)\) \(\dfrac{d}{dx}\Big(\text{sec}\,u\Big)=\text{sec}\,u\tan u\cdot\dfrac{du}{dx}\) \(\dfrac{d}{dx}\Big(\text{csc}(g(x))\Big)=-\text{csc}(g(x))\cot(g(x) )\cdot g'(x)\) \(\dfrac{d}{dx}\Big(\text{csc}\,u\Big)=-\text{csc}\,u\cot u \cdot\dfrac{du}{dx}. \ )Композиции трех или более функций
Теперь мы можем комбинировать цепное правило с другими правилами для дифференцирования функций, но когда мы дифференцируем состав трех или более функций, нам нужно применять цепное правило более одного раза. Если мы посмотрим на эту ситуацию в общих чертах, мы можем сгенерировать формулу, но нам не нужно ее запоминать, так как мы можем просто применить цепное правило несколько раз.
В общих чертах сначала пускаем
\[k(x)=h\Big(f\big(g(x)\big)\Big).\nonumber \]
Тогда, применяя цепное правило, мы получаем
\[k'( x)=\dfrac{d}{dx}\Big(h\big(f\big(g(x)\big)\big)\Big)=h’\Big(f\big(g(x)\ big)\Big)⋅\dfrac{d}{dx}\Big(f\big(g(x)\big)\Big).\nonumber \]
Снова применяя цепное правило, получаем
\[ k'(x)=h’\Big(f\big(g(x)\big)\Big)\cdot f’\big(g(x)\big)\cdot g'(x).\nonumber \ ]
Правило: цепное правило для композиции трех функций
Для всех значений \(х\), при которых функция дифференцируема, если
\(k(x)=h\Big(f\big(g(x)\big)\Big),\)
затем
\(k'(x)=h’\Big(f\ big(g(x)\big)\Big)\cdot f’\big(g(x)\big)\cdot g'(x).
\)Другими словами, мы применяем цепное правило дважды.
Обратите внимание, что производная от композиции трех функций состоит из трех частей. (Аналогичным образом производная композиции четырех функций состоит из четырех частей и т. д.) Кроме того, помните, , мы всегда можем работать снаружи внутрь, беря по одной производной за раз. 93)\)
Пример \(\PageIndex{9}\): Использование цепного правила в задаче о скорости
Частица движется вдоль координатной оси. Его положение в момент времени t определяется выражением \(s(t)=\sin(2t)+\cos(3t)\). Какова скорость частицы в момент времени \(t=\dfrac{π}{6}\)?
Решение
Чтобы найти \(v(t)\), скорость частицы в момент времени \(t\), мы должны продифференцировать \(s(t)\). Таким образом,
\[v(t)=s'(t)=2\cos(2t)−3\sin(3t).\nonumber \]
Доказательство цепного правила
На этом этапе мы представляем очень неформальное доказательство цепного правила.
Ради простоты мы игнорируем некоторые вопросы: например, мы предполагаем, что \(g(x)≠g(a)\) для \(x≠a\) в некотором открытом интервале, содержащем \(a\). Начнем с применения предельного определения производной к функции \(h(x)\), чтобы получить \(h'(a)\):\[h'(a)=\lim_{x→a} \dfrac{f\big(g(x)\big)−f\big(g(a)\big)}{x−a}. \nonumber \]
Переписывая, получаем
\[h'(a)=\lim_{x→a}\dfrac{f\big(g(x)\big)−f\big(g(a) \big)}{g(x)−g(a)}⋅\dfrac{g(x)−g(a)}{x−a}. \номер\]
Хотя ясно, что
\[\lim_{x→a}\dfrac{g(x)−g(a)}{x−a}=g'(a), \nonumber \]
it не очевидно, что
\[\lim_{x→a}\dfrac{f\big(g(x)\big)−f\big(g(a)\big)}{g(x)−g( а)}=f’\большой(г(а)\большой). \nonumber \]
Чтобы убедиться, что это так, вспомним сначала, что, поскольку \(g\) дифференцируема в \(a\), \(g\) также непрерывно в \(a.\). Таким образом,
\[\lim_{x→a}g(x)=g(a). \nonumber \]
Затем сделайте замену \(y=g(x)\) и \(b=g(a)\) и используйте замену переменных в пределе, чтобы получить
\[\lim_{x→a}\dfrac{f\big(g(x)\big)−f \big(g(a) \big)}{g(x)−g(a)}= \lim_{y→b}\dfrac{f(y)−f(b)}{y−b}=f'(b)=f’\big(g(a)\big).
\nonumber \]Наконец,
\[h'(a)=\lim_{x→a}\dfrac{f\big(g(x)\big)−f\big(g(a)\big )}{g(x)−g(a)}⋅\dfrac{g(x)−g(a)}{x−a}=f’\big(g(a)\big)\cdot g'( а). \nonumber \]
□
Пример \(\PageIndex{10}\): Использование цепного правила с функциональными значениями
Пусть \(h(x)=f\big(g(x)\big).\ ) Если \(g(1)=4,g'(1)=3\) и \(f'(4)=7\), найти \(h'(1).\)
Решение
Используйте цепное правило, затем подставьте.
\[ \begin{align*} h'(1)&=f’\big(g(1)\big)\cdot g'(1) & & \text{Применить правило цепочки.} \\[ 4pt]
&=f'(4)⋅3 & &\text{Подстановка}\; г(1)=4 \;\текст{и}\;г'(1)=3. \\[4pt]
&=7⋅3 & &\text{Подстановка}\; f'(4)=7. \\[4pt]
&=21 & &\text{Упростить.} \end{align*} \nonumber \]Упражнение \(\PageIndex{6}\)
Дано \(h(x)=f (г(х))\). Если \(g(2)=-3,g'(2)=4,\) и \(f'(-3)=7\), найди \(h'(2)\).
- Подсказка
Следуйте примеру \(\PageIndex{10}\).
- Ответить
28
Цепное правило с использованием обозначений Лейбница
Как и в случае с другими производными, которые мы видели, мы можем выразить цепное правило с помощью обозначений Лейбница. Это обозначение цепного правила широко используется в физических приложениях.
Для \(h(x)=f(g(x)),\) пусть \(u=g(x)\) и \(y=h(x)=f(u).\) Таким образом,
\[h'(x)=\dfrac{dy}{dx}\nonumber \]
\[f'(g(x))=f'(u)=\dfrac{dy}{du}\ nonumber \]
и
\[g'(x)=\dfrac{du}{dx}.\nonumber \]
Следовательно,
\[\dfrac{dy}{dx}=h'(x )=f’\big(g(x)\big)\cdot g'(x)=\dfrac{dy}{du}⋅\dfrac{du}{dx}.\nonumber \]
Правило: Цепное правило Используя обозначения Лейбница
Если \(y\) является функцией \(u\), а \(u\) является функцией \(x\), то
\[\dfrac{dy}{dx} =\dfrac{dy}{du}⋅\dfrac{du}{dx}. \номер\] 93).\)
Ключевые понятия
- Цепное правило позволяет различать композиции из двух или более функций. {n−1}\cdot g'(x)\)
Глоссарий
- Цепная линейка
- цепное правило определяет производную составной функции как производную от внешней функции, вычисленную как внутреннюю функцию, умноженную на производную от внутренней функции
Эта страница под названием 3.6: The Chain Rule распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- цепная линейка
- источник@https://openstax.
2+1}\ ). В этом разделе мы изучаем правило нахождения производной композиции двух или более функций. 
\nonumber \]
\)
\ )
\)
Ради простоты мы игнорируем некоторые вопросы: например, мы предполагаем, что \(g(x)≠g(a)\) для \(x≠a\) в некотором открытом интервале, содержащем \(a\). Начнем с применения предельного определения производной к функции \(h(x)\), чтобы получить \(h'(a)\):
\nonumber \]
{n−1}\cdot g'(x)\)