1.7. Производная сложной функции
Пример 6. Найти производную функции y = x2 + x −1 . 10x
Решение.
Воспользуемся свойствами (3), (4) и таблицей производных:
|
| 2 |
|
|
| ′ |
|
| 2 | ′ | x |
|
|
|
| 2 |
| x | ′ |
| |
|
| x | + x −1 |
|
|
|
| 10 −(x |
| + x −1) |
|
| |||||||||
y′= | = | (x + x −1) |
| (10 ) | = | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
| 10 | x |
|
|
| (10 | x | ) | 2 |
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| . | |||||
| (2x +1) 10x −(x2 + x −1) 10x ln10 |
|
|
|
|
|
|
|
| ||||||||||||
= | . |
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
| 102x |
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Пример 7. | y = | x 3 | +3 x | |||||||||||||||||||
|
|
| . | |||||||||||||||||||
|
|
| ||||||||||||||||||||
Решение.По формуле производной частного (4) | sin x | |||||||||||||||||||||
получим: | ||||||||||||||||||||||
| x | 3 | +3 | x ′ |
| 3 | +3 | x | ′ | (x | 3 | +3 | x |
|
|
| ′ |
|
| |||
y’= |
|
|
| = (x |
|
| ) sin x − |
|
| ) (sin x) | = |
| ||||||||||
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| ||||
| sin x |
|
|
|
|
|
| sin | x |
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
| = | (3×2 +3x ln 3) sin x −(x3 | +3x ) cos x | . |
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
| sin2 x |
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Теорема. Пусть функция u=u(x) имеет производную в точке х, а функция y=f(u) имеет производную в соответствующей точке u=u(x). Тогда сложная функция y=f(u(x)) имеет производную в точке х, которая находиться по формуле:
Тогда сложная функция y=f(u(x)) имеет производную в точке х, которая находиться по формуле:
|
| ′ | = | ′ | ′ | (5) |
|
| yx | f (u) u (x). | |||
Доказательство. |
|
|
|
| ||
По определению производной: |
|
|
|
| ||
′ | y | . |
|
|
|
|
f (u) = lim | u |
|
|
|
| |
u→0 |
|
|
|
|
| |
По теореме о связи предела и бесконечно малой функции имеем:
| y | = f | ′ | α = 0. |
|
| |||
| u | (u) +α, lim | ||
|
| u→0 |
| |
14 |
|
|
|
|
Умножив обе части полученного равенства на приращение u,
получим: | = f (u) | u +α u. | ||
y | ||||
| ′ |
|
|
|
Разделим все члены последнего равенства на приращение x : | ||||
y | ′ |
| u | u |
x | = f (u) |
| x +α | x . |
Функция u =u(x) |
| непрерывна в точке x по теореме о непре- | ||
рывности функции, имеющей производную, поэтому u → 0 при
x →0 и lim α = 0. По определению производной
x→0
u′(x)
у′x =
= lim y . Поэтому
x→0 x
lim | y | = lim( f | ′ | u | +α | u | ) = |
x | (u) | x | x | ||||
x→0 | x→0 |
|
|
|
= f ′(u) lim | u | + | lim α | lim | u | = f ′(u) u′( x). |
x→0 | x |
| x→0 | x→0 | x |
|
Пример 8. Найти производную сложной функции y=(x2+1)10.
Решение. Положим: u=x2+1. Тогда y=(x2+1)10=u10 .
Для нахождения производной применим формулу (5):
y′x = (u10 )′ u′ =10u9 u′ =10(x2 +1)9 2x.
Пример 9. Найти производную сложной функции y=sin3x.
Решение. Положим: u=3x. Тогда y=sin3x=sinu.
По формуле (5) получим:
y′x = (sin u)′ u′ = cosu u′ = cos3x 3 = 3cos3x.
Пример 10. Найти производную функции y=cos2x=(cosx)2.
Решение. Положим: u=cosx. Тогда y=(cosx)2=u2.
По формуле (5) производная сложной функции равна: y´x=(u2)´ ·u´=2u•u´=2cosx·(-sinx)=-2cosx·sinx.
Пример 11. Найти производную функции y=arctgex .
15
Решение. Положим: u=ex. Тогда y=arctgu. Производная сложной функции по формуле (5) равна:
y’= (arctgu)’ u’= |
| 1 | u’= | ex | . |
| +u2 | 1+e2x | |||
1 |
|
| |||
Пример 12. Найти производную функции y = ln x . Решение. Положим: u=lnх. Тогда y = u .
Производная сложной функции равна: |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
y’= ( u )’ u’= |
|
| 1 |
| u’= |
|
|
| 1 |
|
| 1 |
| = |
| 1 | . |
| ||||||||
2 |
| u | 2 | ln x |
|
| x | 2x |
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ln x |
| |||||||||||
Пример 13. Найти производную функции y=lnarcsinx. | ||||||||||||||||||||||||||
Решение. Положим: | u=arcsinx, тогда y=lnu. |
| ||||||||||||||||||||||||
Производная сложной функции равна: |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
y’ = (ln u)’ u’= | 1 | u’ | = |
|
| 1 |
|
|
|
| 1 |
|
| = |
|
|
| 1 |
| . | ||||||
|
|
|
|
|
|
|
| 1− x2 |
|
|
| 1− x2 arcsin x | ||||||||||||||
|
|
| u |
|
| arcsin x |
|
|
|
|
|
|
|
|
|
| ||||||||||
Пример 14. Найти производную функции y=tg2x. |
| |||||||||||||||||||||||||
Решение. Положим: | u=2x, тогда y=tgu. |
|
|
| ||||||||||||||||||||||
Производная сложной функции равна: |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
y’= (tgu)’ u’= | 1 |
| u’= |
|
|
| 1 |
| 2x | ln 2 = |
|
| 2x ln 2 | . |
| |||||||||||
cos2 u |
|
| cos2 | 2x | cos2 2x |
| ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
| Пример 15. Найти производную функции y =10 x . |
|
| ||||||||||||||||
| Решение. Положим: u= | x , тогда у= 10u . |
|
|
|
|
| |||||||||||||
|
|
| Производная сложной функции равна: |
|
| |||||||||||||||
| y’= (10u )’ u’=10u ln10 u’=10 x ln10 | 1 |
| = | 10 x ln10 . |
| ||||||||||||||
| 2 |
|
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| x |
|
| 2 x |
|
| |||
|
| Пример 16. Найти производную функции |
|
|
|
|
| |||||||||||||
|
|
| 1 | 1 |
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
| = (2 − x5 )− |
|
| . |
|
|
|
|
|
|
|
|
|
| |||
|
| y = |
| 3 |
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
| 3 2 − x5 |
|
|
|
|
|
|
|
|
|
|
| ||||||
| Решение. |
|
| |||||||||||||||||
|
|
| 4 |
|
|
|
|
| 4 |
|
|
|
|
|
|
| 4 |
| ||
y’= − | 1 | (2 − x5 )−3 | (2 − x5 )′ = − | 1 |
| (2 − x5 )− |
| (−5×4 )= |
| 5 | (2 − x5 )− |
| x4. | |||||||
| 3 | 3 | ||||||||||||||||||
3 |
| 3 | ||||||||||||||||||
|
|
| 3 |
|
|
|
|
|
|
|
|
|
| |||||||
Здесь u=2-x5.
16
|
|
|
| Пример 17. Найти производную функции y=tg35x=(tg5x)3. | ||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Решение. Производная сложной функции равна: |
| ||||||||||||||||||||||||||||||||||||||||||||||
y’ = 3(tg5x)2 (tg5x)′ = 3tg 2 | 5x |
|
| 1 |
|
| (5x)′ = 3tg 2 5x |
| 1 | 5 | = | |||||||||||||||||||||||||||||||||||||||
cos2 5x | cos2 5x | |||||||||||||||||||||||||||||||||||||||||||||||||
=15 |
| tg | 2 5x | = | 15 | sin2 |
| 5x | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
| cos2 5x | cos4 |
| 5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
| Пример 18. |
| 4 +sin2 x . | ||||||||||||||||||||||||||||||||||||||||||||
|
|
| Решение. Производная сложной функции равна: |
| ||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ′ |
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
y’= |
|
|
|
|
|
|
|
|
|
| (4 +sin2 | x) | = |
|
|
|
|
|
|
|
|
|
|
| 2sin x | (sin x)′ = |
| |||||||||||||||||||||||
2 4 +sin2 x |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
| 4 +sin2 x |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
= |
| 1 |
|
|
|
|
|
| sin x cos x = |
| sin x cos x | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
4 +sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 +sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
| Пример 19. |
| |||||||||||||||||||||||||||||||||||||||||||||
|
|
| Решение: | 1 |
|
|
|
|
| (arctgx2 )′ = |
|
| 1 |
|
|
|
|
| 1 |
| (x2 )′ |
|
|
|
|
|
| |||||||||||||||||||||||
|
|
|
| y’= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = |
|
|
|
| |||||||||||||||||||||||||
|
|
|
|
| arctgx2 |
| arctgx2 |
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1+(x2 )2 |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
|
|
| 1 |
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
| = |
|
|
|
|
|
|
| 2x = | arctgx2 (1+ x4 ). |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
| arctgx2 | 1+ x4 |
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||
|
|
|
| Пример 20. Найти производную функции |
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
| y=ln4tgx=(lntgx)4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
|
|
|
| Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
| 1 | 1 |
|
|
| |||||||||||||
y’= 4(ln tgx)3 (ln tgx)′ = 4(ln tgx)3 | (tgx)′ |
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||
|
| = 4ln3 tgx |
|
|
|
| = | |||||||||||||||||||||||||||||||||||||||||||
tgx | tgx | cos2 x | ||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
| 4ln3 tgx | = |
|
| 4ln3 tgx |
| , т. | tgx = |
| sin x | . |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||
| tgx | cos2 x | sin x cos x |
| cos x |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||
|
|
|
| Пример 21. |
| |||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
| ||||||
|
| y’= 2arcsin 3x ln 2 (arcsin 3x)’= 2arcsin 3x ln 2 |
|
|
|
| (3x)′ = |
| ||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1−(3x)2 |
|
|
|
|
|
| |||
|
| = 2. |
|
|
| 1 |
|
|
|
| 3 = | 3 2arcsin 3x ln 2 | . |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1−9×2 |
|
|
|
|
|
|
| 1−9×2 |
|
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 17 |
определение, как найти, примеры решений
Поиск производной математической функции называется дифференцированием. Найти производную от математической функции – частая задача, встречающаяся в высшей математике. Говорить можно по-разному: найти производную, вычислить производную, продифференцировать функцию, взять производную, но все это одни и те же понятия. Бывают, конечно, и сложные задания, в которых нахождение производной всего лишь один из компонентов задачи. На нашем сервисе сайт у вас есть возможность вычислить производную онлайн как от элементарных, так и от сложных функций, не имеющих аналитического решения. Производная онлайн на нашем сервисе может быть найдена практически от любой математической функции, даже самой сложной, которую вам не смогли решить другие сервисы. А полученный ответ всегда верный на 100% и исключает ошибки. Посмотреть, как происходит процесс нахождения производной на нашем сайте можно на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберите любую функцию из списка примеров, она автоматически подставится в поле функции, а затем нажмите кнопку «Решение».
Найти производную от математической функции – частая задача, встречающаяся в высшей математике. Говорить можно по-разному: найти производную, вычислить производную, продифференцировать функцию, взять производную, но все это одни и те же понятия. Бывают, конечно, и сложные задания, в которых нахождение производной всего лишь один из компонентов задачи. На нашем сервисе сайт у вас есть возможность вычислить производную онлайн как от элементарных, так и от сложных функций, не имеющих аналитического решения. Производная онлайн на нашем сервисе может быть найдена практически от любой математической функции, даже самой сложной, которую вам не смогли решить другие сервисы. А полученный ответ всегда верный на 100% и исключает ошибки. Посмотреть, как происходит процесс нахождения производной на нашем сайте можно на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберите любую функцию из списка примеров, она автоматически подставится в поле функции, а затем нажмите кнопку «Решение». Вы увидите пошаговое решение, ваша производная будет найдена аналогично. Преимущества решения производной онлайн. Даже если вы знаете, как находить производные, этот процесс может потребовать немало времени и сил. Сервис сайт призван избавить вас от утомительных и долгих вычислений, в которых к тому же вы можете допустить ошибку. Производная онлайн у нас вычисляется одним нажатием кнопки «Решение» после ввода заданной функции. Также сайт отлично подойдет тем, кто хочет проверить свои умения находить производную математической функции и убедиться в правильности самостоятельного решения или найти допущенную в нем ошибку. Для этого достаточно лишь сравнить свой ответ с результатом вычислений онлайн-сервиса. Если вы не хотите пользоваться таблицами производных, с которыми нахождение нужной функции забирает достаточно времени, то используйте наш сервис вместо таблиц производных, чтобы найти производную. Основные преимущества нашего сайта в сравнении с другими аналогичными сервисами состоят в том, что вычисление происходит у нас очень быстро (в среднем 5 секунд) и за него не нужно ничего платить, — сервис абсолютно бесплатный.
Вы увидите пошаговое решение, ваша производная будет найдена аналогично. Преимущества решения производной онлайн. Даже если вы знаете, как находить производные, этот процесс может потребовать немало времени и сил. Сервис сайт призван избавить вас от утомительных и долгих вычислений, в которых к тому же вы можете допустить ошибку. Производная онлайн у нас вычисляется одним нажатием кнопки «Решение» после ввода заданной функции. Также сайт отлично подойдет тем, кто хочет проверить свои умения находить производную математической функции и убедиться в правильности самостоятельного решения или найти допущенную в нем ошибку. Для этого достаточно лишь сравнить свой ответ с результатом вычислений онлайн-сервиса. Если вы не хотите пользоваться таблицами производных, с которыми нахождение нужной функции забирает достаточно времени, то используйте наш сервис вместо таблиц производных, чтобы найти производную. Основные преимущества нашего сайта в сравнении с другими аналогичными сервисами состоят в том, что вычисление происходит у нас очень быстро (в среднем 5 секунд) и за него не нужно ничего платить, — сервис абсолютно бесплатный. От вас не потребуется никаких регистраций, вводов e-mail или своих персональных данных. Все, что необходимо – ввести заданную функцию и нажать кнопку «Решение». Что такое производная. Производная функции – основное понятие в математике и математическом анализе. Обратный этому процессу – интегрирование, то есть нахождение функции по известной производной. Говоря проще, дифференцирование является действием над функцией, а производная – это уже результат такого действия. Для вычисления производной функции в определенной точке, аргумент x заменяется численным значением и вычисляется выражение. Обозначается производная штрихом в правом верхнем углу над функцией. Также штрих может быть и обозначением конкретной функции. Для нахождения производной элементарной функции вам понадобится знать таблицу производной или иметь ее всегда под рукой, что может быть не очень удобно, а также знать правила дифференцирования, поэтому рекомендуем пользоваться нашим сервисом, где вычисляется производная онлайн, достаточно только ввести функцию в предназначенное для этого поле.
От вас не потребуется никаких регистраций, вводов e-mail или своих персональных данных. Все, что необходимо – ввести заданную функцию и нажать кнопку «Решение». Что такое производная. Производная функции – основное понятие в математике и математическом анализе. Обратный этому процессу – интегрирование, то есть нахождение функции по известной производной. Говоря проще, дифференцирование является действием над функцией, а производная – это уже результат такого действия. Для вычисления производной функции в определенной точке, аргумент x заменяется численным значением и вычисляется выражение. Обозначается производная штрихом в правом верхнем углу над функцией. Также штрих может быть и обозначением конкретной функции. Для нахождения производной элементарной функции вам понадобится знать таблицу производной или иметь ее всегда под рукой, что может быть не очень удобно, а также знать правила дифференцирования, поэтому рекомендуем пользоваться нашим сервисом, где вычисляется производная онлайн, достаточно только ввести функцию в предназначенное для этого поле. Аргументом должна быть x переменная, так как дифференцирование совершается по нему. Если надо вычислить вторую производную, то можно продифференцировать полученный ответ. Как вычисляется производная онлайн. Уже давно созданы и можно легко встретить таблицы производных для элементарных функций, поэтому вычислить производную элементарной (простой) математической функции – довольно простое дело. Однако когда требуется найти производную сложной математической функции, то это уже не тривиальная задача и она потребует немало усилий и затрат времени. От бессмысленных и долгих расчетов вы можете избавиться, если воспользуетесь нашим онлайн сервисом. Благодаря ему производная будет вычислена за считанные секунды.
Аргументом должна быть x переменная, так как дифференцирование совершается по нему. Если надо вычислить вторую производную, то можно продифференцировать полученный ответ. Как вычисляется производная онлайн. Уже давно созданы и можно легко встретить таблицы производных для элементарных функций, поэтому вычислить производную элементарной (простой) математической функции – довольно простое дело. Однако когда требуется найти производную сложной математической функции, то это уже не тривиальная задача и она потребует немало усилий и затрат времени. От бессмысленных и долгих расчетов вы можете избавиться, если воспользуетесь нашим онлайн сервисом. Благодаря ему производная будет вычислена за считанные секунды.
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.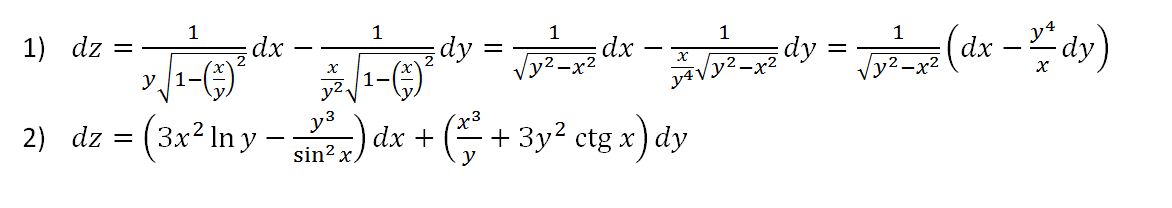
Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях.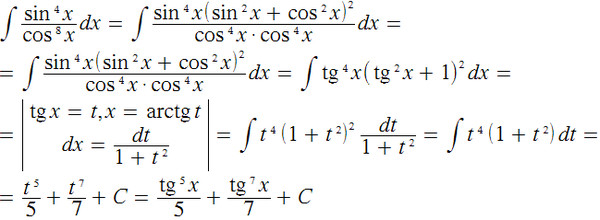 Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g» означает, что мы будем находить производную функции g.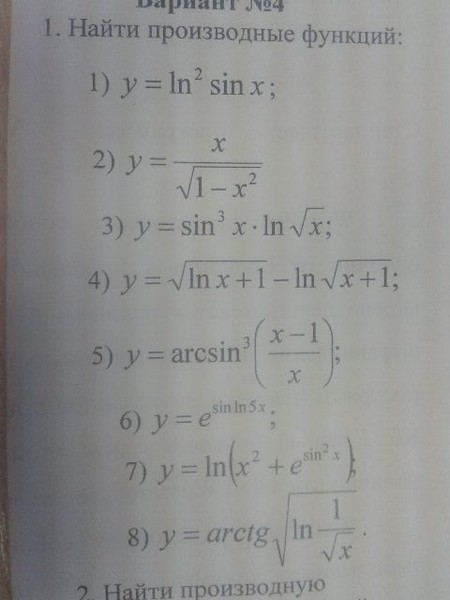
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- (sin x)»=cos x
- (cos x)»= –sin x
- (x n)»=n x n-1
- (e x)»=e x
- (ln x)»=1/x
- (a x)»=a x ln a
- (log a x)»=1/x ln a
- (tg x)»=1/cos 2 x
- (ctg x)»= – 1/sin 2 x
- (arcsin x)»= 1/√(1-x 2)
- (arccos x)»= — 1/√(1-x 2)
- (arctg x)»= 1/(1+x 2)
- (arcctg x)»= — 1/(1+x 2)
Пример 1. Найдите производную функции y=500.
Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).
Пример 2. Найдите производную функции y=x 100 .
Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x 100)»=100 x 99
Пример 3. Найдите производную функции y=5 x
Это показательная функция, вычислим ее производную по формуле 4.
Пример 4. Найдите производную функции y= log 4 x
Производную логарифма найдем по формуле 7.
(log 4 x)»=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С — константа.
1. Постоянный коэффициент можно выносить за знак производной
Пример 5. Найдите производную функции y= 6*x 8
Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.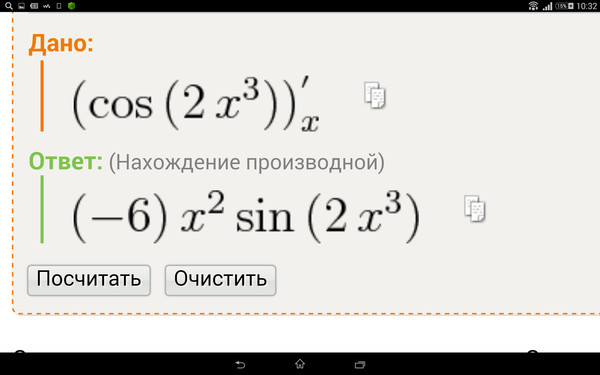
(6*x 8)» = 6*(x 8)»=6*8*x 7 =48* x 7
2. Производная суммы равна сумме производных
(f + g)»=f» + g»
Пример 6. Найдите производную функции y= x 100 +sin x
Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)»=100 x 99 и (sin x)»=cos x. Производная суммы будет равна сумме данных производных:
(x 100 +sin x)»= 100 x 99 +cos x
3. Производная разности равна разности производных
(f – g)»=f» – g»
Пример 7. Найдите производную функции y= x 100 – cos x
Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.
(x 100 – cos x)»= 100 x 99 + sin x
Пример 8. Найдите производную функции y=e x +tg x– x 2 .
В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:
(e x)»=e x , (tg x)»=1/cos 2 x, (x 2)»=2 x. Тогда производная исходной функции равна:
Тогда производная исходной функции равна:
(e x +tg x– x 2)»= e x +1/cos 2 x –2 x
4. Производная произведения
(f * g)»=f» * g + f * g»
Пример 9. Найдите производную функции y= cos x *e x
Для этого сначала найдем производного каждого множителя (cos x)»=–sin x и (e x)»=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.
(cos x* e x)»= e x cos x – e x *sin x
5. Производная частного
(f / g)»= f» * g – f * g»/ g 2
Пример 10. Найдите производную функции y= x 50 /sin x
Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)»=50 x 49 и (sin x)»= cos x. Подставив в формулу производной частного получим:
(x 50 /sin x)»= 50x 49 *sin x – x 50 *cos x/sin 2 x
Производная сложной функции
Сложная функция — это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:
(u (v))»=u»(v)*v»
Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) — сложная функция. Функцию u назовем внешней, а v — внутренней.
Пусть y= u(v(x)) — сложная функция. Функцию u назовем внешней, а v — внутренней.
Например:
y=sin (x 3) — сложная функция.
Тогда y=sin(t) — внешняя функция
t=x 3 — внутренняя.
Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.
(sin t)»=cos (t) — производная внешней функции (где t=x 3)
(x 3)»=3x 2 — производная внутренней функции
Тогда (sin (x 3))»= cos (x 3)* 3x 2 — производная сложной функции.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная от Sin3x – формула, доказательство, примеры
Производная от sin3x равна 3cos3x. Мы можем оценить дифференцирование sin3x, используя различные методы производных, такие как первый принцип производных и метод цепного правила. Мы знаем, что производная от sin(ax) равна a, умноженной на cos(ax), то есть d(sinax)/dx = a cos(ax), что определяется с помощью цепного правила производных. Подставив a = 3 в эту формулу, мы получим производную от sin3x как d(sin3x)/dx = 3 cos3x. 93x с использованием метода дифференцирования по цепному правилу. Мы также определим формулу производной sin3x, используя первый принцип и формулу производной куба грехов x, и решим некоторые примеры, связанные с концепцией, для лучшего понимания концепции.
Мы можем оценить дифференцирование sin3x, используя различные методы производных, такие как первый принцип производных и метод цепного правила. Мы знаем, что производная от sin(ax) равна a, умноженной на cos(ax), то есть d(sinax)/dx = a cos(ax), что определяется с помощью цепного правила производных. Подставив a = 3 в эту формулу, мы получим производную от sin3x как d(sin3x)/dx = 3 cos3x. 93x с использованием метода дифференцирования по цепному правилу. Мы также определим формулу производной sin3x, используя первый принцип и формулу производной куба грехов x, и решим некоторые примеры, связанные с концепцией, для лучшего понимания концепции.
| 1. | Что является производным от Sin3x? |
| 2. | Производная от формулы Sin3x |
| 3. | 93 раза?|
| 6. | Часто задаваемые вопросы о производной Sin3x |
Что является производным от Sin3x?
Производная sin3x в три раза больше cos3x, то есть d(sin3x)/dx = 3 cos3x. Дифференцирование sin3x — это процесс нахождения его производной, которую можно определить с помощью различных методов дифференцирования. Мы можем найти производную от sin3x, используя первый принцип производных, то есть определение пределов и метод дифференцирования по цепному правилу. В следующем разделе давайте рассмотрим формулу для производной от sin3x.
Дифференцирование sin3x — это процесс нахождения его производной, которую можно определить с помощью различных методов дифференцирования. Мы можем найти производную от sin3x, используя первый принцип производных, то есть определение пределов и метод дифференцирования по цепному правилу. В следующем разделе давайте рассмотрим формулу для производной от sin3x.
Производная от формулы Sin3x
Теперь формула для производной sin3x определяется как d(sin3x)/dx = 3 cos3x. Мы используем метод цепного правила, чтобы найти производную составных функций, а sin3x является составной функцией f(x) = sinx и g(x) = 3x, задаваемой туманом(x). На изображении ниже показана формула дифференцирования sin3x:
Производная от Sin3x по первому принципу
Теперь, когда мы знаем производную sin3x, в этом разделе мы оценим дифференцирование sin3x, используя первый принцип производных. Мы будем использовать различные формулы производных и пределы тригонометрии, чтобы доказать, что производная от sin3x равна 3 cos3x. Чтобы найти производную sin3x, мы берем предельное значение, когда x приближается к x + h. Чтобы упростить это, мы устанавливаем x = x + h и хотим взять предельное значение, когда h приближается к 0. Мы будем использовать следующие формулы:
Чтобы найти производную sin3x, мы берем предельное значение, когда x приближается к x + h. Чтобы упростить это, мы устанавливаем x = x + h и хотим взять предельное значение, когда h приближается к 0. Мы будем использовать следующие формулы:
- sin A — sin B = 2 cos ½ (A + B) sin ½ (A — B)
- lim x→0 (sinx)/x = 1
- d(f(x))/dx = lim h→0 [f(x+h) — f(x)]/h
Используя приведенные выше формулы, мы имеем
d(sin3x)/dx = lim h→0 [sin3(x+h) — sin3x]/h
= lim h→0 [sin (3x + 3h) — sin3x]/h
= lim h→0 {2 cos [(3x + 3h + 3x)/2] sin [(3x + 3h — 3x)/2]}/h — [Используя Грех А — Формула Греха Б]
= lim ч→0 {2 cos [(6x + 3h)/2] sin (3h/2)}/h
= lim ч→0 {2 cos [(6x + 3h)/2 ] × (3/2) lim h→0 sin (3h/2)}/(3h/2) — [Умножение и деление предела на 3/2]
= 2 cos (6x/2) × (3/2) × 1 [Используя формулу lim x→0 (sinx)/x = 1]
= 3 cos3x
Таким образом, мы доказали, что дифференцирование sin3x равно 3 cos3x по формуле Первый принцип дифференцирования.
Производная от Sin3x с использованием метода цепного правила
Мы используем метод цепного правила, чтобы найти производные составных функций. Мы знаем, что sin3x является композицией функций f(x) = sinx и g(x) = 3x и записывается как f(g(x)) = f(3x) = sin3x. Чтобы найти производную sin3x с помощью метода цепного правила, мы запишем ее как произведение производной sin3x по 3x и производной 3x по x.
d(sin3x)/dx = d(sin3x)/d(3x) × d(3x)/dx
= cos3x × 3 — [Поскольку производная sinx по x равна x] 93x равно 3 sin 2 x cosx.
☛ Похожие темы:
- Производное от Cosx
- Производная от 2x
- Производная Sin, обратная x
Часто задаваемые вопросы о производной Sin3x
Что такое производная Sin3x в исчислении?
Производная от sin3x равна 3 cos3x. Мы можем оценить эту производную, используя различные методы дифференцирования, такие как метод цепного правила. Производная функции дает скорость изменения функции по отношению к небольшому изменению переменной.
Мы можем оценить эту производную, используя различные методы дифференцирования, такие как метод цепного правила. Производная функции дает скорость изменения функции по отношению к небольшому изменению переменной.
Какова формула производной Sin3x?
Формула для производной от sin3x определяется как d(sin3x)/dx = 3 cos3x. Поскольку мы знаем, что производная от sin(ax) = a cos(ax) может быть вычислена с помощью цепного правила, поэтому, если мы подставим a = 3 в эту формулу, мы можем получить производную от sin3x.
Как найти производную Sin3x?
Производную от sin3x можно определить, используя первый принцип производных и метод цепного правила. Мы знаем, что используем цепное правило для производных сложных функций. Sin3x — это композиция двух функций sinx и 3x. 93x)/dx = 3 sin 3-1 x × d(sinx)/dx = 3 sin 2 x cosx.
Что такое вторая производная Sin3x?
Вторая производная sin3x равна -9 sin3x. Это можно определить, взяв производную от первой производной sin3x, то есть d 2 (sin3x)/dx 2 = d(3 cos3x)/dx = -9 sin3x.
Производная от sin x. Подход к исчислению
Подход
к
C A L C U L U S
Содержание | Главная
12
Производная sin x
Производная от cos x
Производное загара x
Производная от детской кроватки x
Производная сек x
Производная от csc x
ПРОИЗВОДНАЯ от sin x равна cos x . Чтобы доказать это, мы будем использовать следующее тождество:
.sin A − sin B = 2 cos ½( A + B ) sin ½( A − B ).
(Тема 20 Тригонометрии.)
Проблема 1. Используйте этот идентификатор, чтобы показать:
| грех ( х + ч ) — грех х | = |
Чтобы увидеть доказательство, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
| sin ( x + ч ) − sin x | = | 2 cos ½( x + h + x ) sin ½( х + ч — х ) |
| = | 2 cos ½(2 x + h ) sin ½ h | |
| = | ||
Прежде чем перейти к производной sin x , мы должны доказать лемму; которая является предварительной, вспомогательной теоремой, необходимой для доказательства основной теоремы. Эта лемма требует следующего тождества:
Задача 2. Показать, что тангенс θ, деленный на sin θ, равен .
| тангенс θ sin θ | = | 1 cos θ | . |
(См. Тему 20 Тригонометрии.)
| тангенс θ sin θ | = | тан θ · | 1 sin θ | = | sin θ cos θ | · | 1 sin θ | = | 1 cos θ |
Лемма, которую мы должны доказать, обсуждается в теме 14 тригонометрии. (Взгляните на него.) Вот он:
.
ЛЕММА. Если θ измеряется в радианах, то
Доказательство. Это невозможно доказать, применяя обычные теоремы о пределах (урок 2). Мы должны обратиться к геометрии и к значениям sin θ и радианам.
Пусть O будет центром единичной окружности, то есть окружности радиуса 1;
и пусть θ будет центральным углом первого квадранта BOA , измеренным в радианах.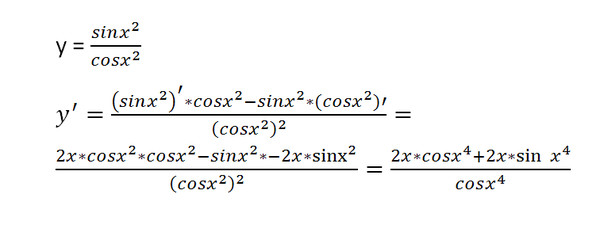
Тогда, поскольку длина дуги s = r θ, а r = 1, дуга BA равна θ. (Тема 14 Тригонометрии.)
Угол B’OA равен углу θ, что делает дугу AB’ равной дуге BA ;
провести прямую линию BB’ , разрезав AO на P ;
и проведите прямые линии BC, B’C , касающиеся окружности.
Затем
BB’ BAB’ BC + CB’ .
Теперь в этом единичном круге BP = PB’ = sin θ, (Тема 17 тригонометрии),
, так что BB’ = 2 sin θ;
| и до н.э. = CB’ = тангенс θ. (Для tan θ = | БК ОБ | = | БК 1 | = до н.э. .) |
Следовательно, приведенное выше неравенство принимает следующий вид:
2 sin θ
При делении каждого члена на 2 sin θ:
| 1 | θ sin θ | 1 cos θ | . |
(Задача 2.) И, взяв обратные значения, таким образом изменив смысл:
| 1 > | sin θ θ | > cos θ. |
(Урок 11 алгебры, теорема 5.)
При смене знаков смысл снова меняется:
| −1 | sin θ θ | −cos θ, |
(Урок 11 алгебры, теорема 4),
и если к каждому члену прибавить 1:
| 0 | 1 − | sin θ θ | 1 − cos θ. |
Теперь, когда θ становится очень близким к 0 (θ 0), cos θ становится очень близким к 1; поэтому 1 − cos θ становится очень близким к 0. Выражение в середине, будучи на меньше , чем 1 − cos θ, становится еще ближе к 0 (и слева ограничено 0), поэтому выражение в середине определенно приблизится к 0. Это означает:
Что мы и хотели доказать.
Учащийся должен иметь в виду, что «приближение» переменной к 0 или любому пределу (определение 2.1) не означает, что переменная когда-либо равна этому пределу.
Производная sin x
| д дх | грех х | = cos x |
Чтобы доказать это, применим определение производной (урок 5). Сначала вычислим коэффициент разности.
| = | , Проблема 1, | ||
| = | , при делении числителя и знаменателя на 2, | ||
| = | |||
Теперь возьмем предел как ч 0. Но предел произведения равен произведению пределов. (Урок 2.) Множитель справа имеет вид sin θ/θ. Следовательно, согласно лемме, при h 0 его предел равен 1. Следовательно,
(Урок 2.) Множитель справа имеет вид sin θ/θ. Следовательно, согласно лемме, при h 0 его предел равен 1. Следовательно,
| д дх | грех х | = cos x . |
Мы установили формулу.
Производная от cos x
| д дх | потому что х | = −sin x |
Чтобы установить это, мы будем использовать следующее тождество:
| потому что х = грех ( | № 2 | − x ). |
Функция любого угла равна кофункции своего дополнения.
(Тема 3 тригонометрии).
Следовательно, при применении цепного правила:
Мы установили формулу.
Производное загара x
| д дх | тан x = сек 2 x |
| Теперь загар x = | sin x cos x | . | (Тема 20 тригонометрии.) |
Следовательно, согласно правилу частных:
| д дх | желтовато-коричневый x | = | д дх | sin x cos x | = | COS x · COS x — SIN x (-SIN x ) COS 2 x | 5 ||
| = | cos 2 x + sin 2 x cos 2 x | |||||||
| = | 1 cos 2 x | |||||||
| = | сек 2 x . | |||||||
Мы установили формулу.
Задача 3. Производная кроватки x . Докажите:
| д дх | детская кроватка x = −csc 2 x |
| д дх | детская кроватка x | = | д дх | cos x sin x | ||||
| = | sin x (−sin x ) − cos x · cos x sin 2 x | |||||||
| = | −(sin 2 x + cos 2 x ) sin 2 x | |||||||
| = | − | 1 sin 2 x | ||||||
| = | −csc 2 x . | |||||||
Производная сек x
| д дх | с x | = сек x коричневый x |
| С сек x = | 1 cos x | = | (cos x ) −1 | , |
затем при использовании цепного правила и общего правила мощности:
909:06 Мы установили формулу.Задача 4. Производная csc x . Докажите:
| д дх | csc x | = | −csc x детская кроватка x |
| д дх | csc x | = | д дх | 1 sin x | = | |||
| = | ||||||||
| = | ||||||||
| = | ||||||||
| = | ||||||||
Пример. Вычислить производную от sin x 2 .
Вычислить производную от sin x 2 .
Решение . При применении цепного правила
| д дх | sin топор 2 | = | cos ax 2 · | д дх | топор 2 | = | cos ax 2 · | 2 топор | = | 2 топор cos топор 2 . |
Задача 5. Вычислите эти производные.
| а) | д дх | sin 5 x | = | 5 cos 5 x |
| б) | д дх | ½ sin 2 x | = | sin x cos x |
| в) | д дх | 2 cos 3 x | = | −6 sin 3 x |
| г) | д дх | x потому что x | = | cos x − x sin x |
| д) | д дх | sin 2 x cos x | = | 2 cos 2 x cos x − sin 2 x sin x |
| е) | д дх | желтовато-коричневый (3 x ) 2 | = | 18 x с 2 (3 x ) 2 |
| ж) | д дх | 2 кроватки | x 2 | = | – КСК 2 | x 2 |
| з) | д дх | с 4 x | = | 4 с 4 x желтовато-коричневый 4 x |
| i) | д дх | a csc bx | = | − ab csc bx детская кроватка bx |
| к) | = |
Задача 6.


 Найти производную функции
Найти производную функции



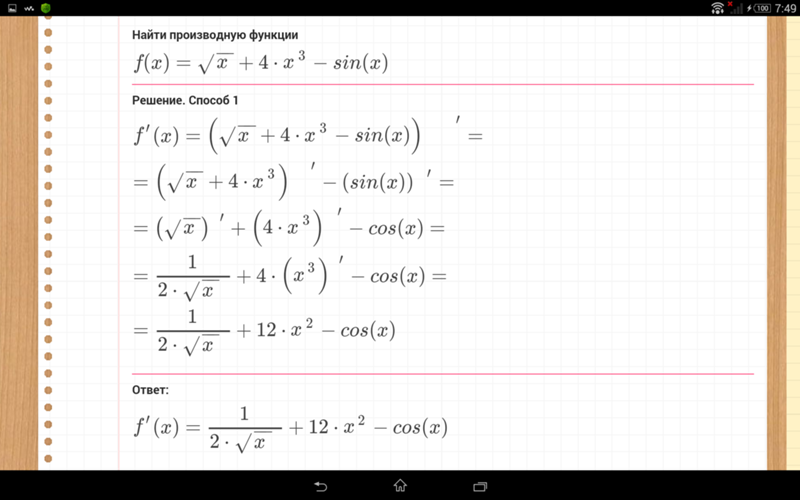

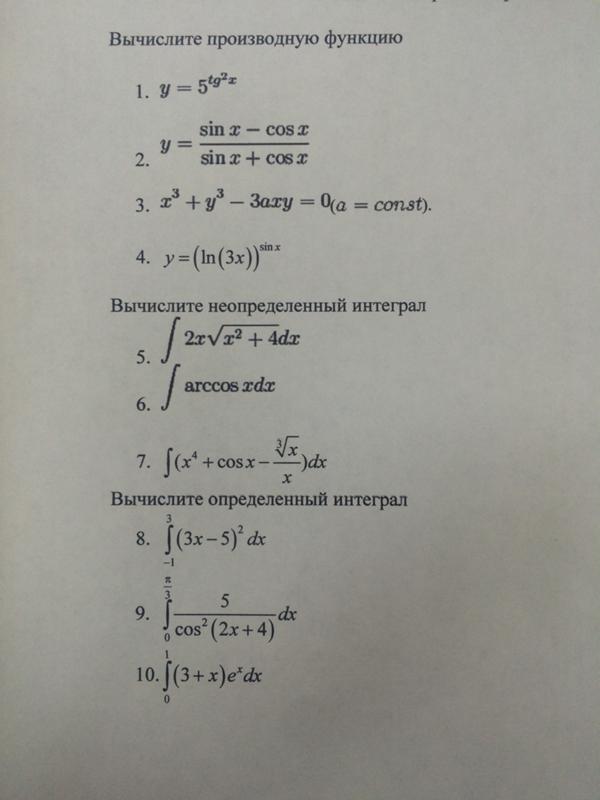
 Производная сложной функции равна:
Производная сложной функции равна:
 Найти производную функции y =
Найти производную функции y =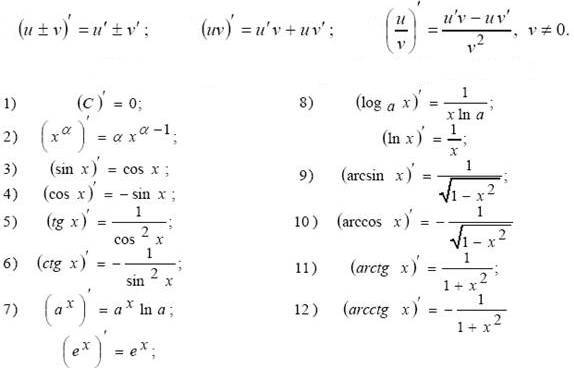
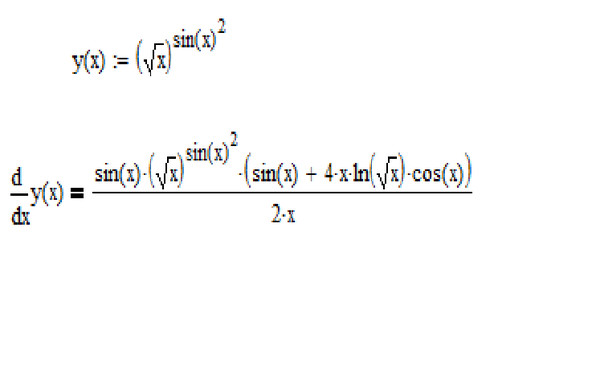 Найти производную функции y=lnarctgx2.
Найти производную функции y=lnarctgx2.

 к.
к. Найти производную функции y=2arcsin3x.
Найти производную функции y=2arcsin3x. arcsin 3x ln 2
arcsin 3x ln 2