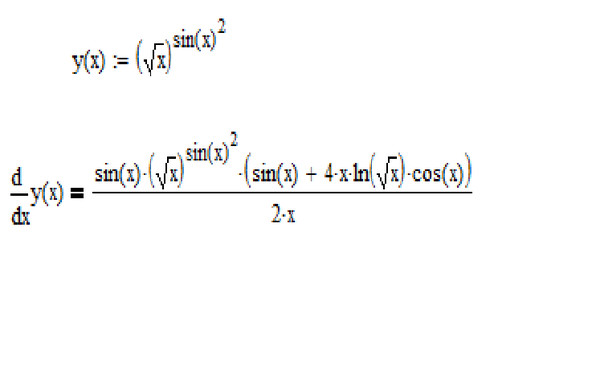Производная функции квадрата синуса равна синусу 2x, sin(2x) . Мы можем найти эту производную, используя цепное правило и производные фундаментальных тригонометрических функций.
В этой статье мы научимся вычислять производную сложной функции синус в квадрате. Мы увидим доказательство, графическое сравнение квадрата синуса x и его производной, а также несколько примеров.
ВЫЧИСЛЕНИЕ
Относится к …
Обучение получению функции квадрата синуса.
См. доказательство
Содержание
ВЫЧИСЛЕНИЕ
Актуально для …
Обучение вычислению функции квадрата синуса.
См. доказательство
Доказательство производной функции квадрата синуса с использованием цепного правила
Если вам это нужно, рекомендуем просмотреть формулу цепного правила в качестве предварительного условия для этой темы, перейдя по этой ссылке: Цепное правило производных.
Точно так же вы можете посетить эту другую ссылку для доказательства производной функции синуса: Производная синуса, sin(x). 92)}$
Отбросив путаницу, первое — это «целая тригонометрическая функция», возведенная в степень двойки, а вторая — тригонометрическая функция «переменной, возведенной в степень двойки».
Поскольку это составная функция, формула цепного правила используется для нахождения формулы производной функции квадрата синуса, при условии, что вы уже освоили формулу цепного правила и производную функции синуса.
Предположим, нас попросили получить производную от 92$
$latex f'(u) = 2u$
Вывод внутренней функции g(x) с использованием формулы производной тригонометрической функции sine через x , мы имеем
$latex g (x) = \sin{(x)}$
$latex g'(x) = \cos{(x)}$
Алгебраически умножая производную внешней функции $latex f'(u)$ на производную внутренней функции $latex g'(x)$ имеем
$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$
$latex \frac{dy}{ dx} = (2u) \cdot (\cos{(x)})$ 9{2}{(x)}$ имеет домен
$latex (-\infty,\infty)$ или всех действительных чисел
и существует в диапазоне
$latex [0,1]$
, тогда как производная $latex f'(x) = \sin{(2x)}$ имеет домен
$latex (-\infty,\infty)$ или всех действительных чисел
и существует в диапазон
$latex [-1,1]$
Примеры
В следующих примерах мы научимся получать составные синусоидальные квадратичные функции.
92(x) с доказательством и графиками
Производная греха (2х): формула, доказательство, примеры, решение
Найдите производную греха (2х), а также формулу синуса в тригонометрии и как доказать производную греха 2х.
от Алана Уокера — Опубликовано на 10 ноября 2022 г.
Знакомство с производной от sin(2x)
Производные находят широкое применение практически во всех областях техники и науки. Производную от sin2x можно вычислить, следуя правилам дифференцирования. Или мы можем напрямую найти производную от sin (2x), применив первый принцип дифференцирования.
В этой статье вы узнаете, что такое производная от sin (2x) и как дифференцировать sin2x, используя различные подходы.
Какая производная от sin2x?
Дифференцирование sin2x по переменной cx равно 2cos(2x). Обозначается d/dx(sin(2x)). Это скорость изменения тригонометрической функции sin(2x). В треугольнике дифференциал sin2x равен отношению противолежащего катета к гипотенузе.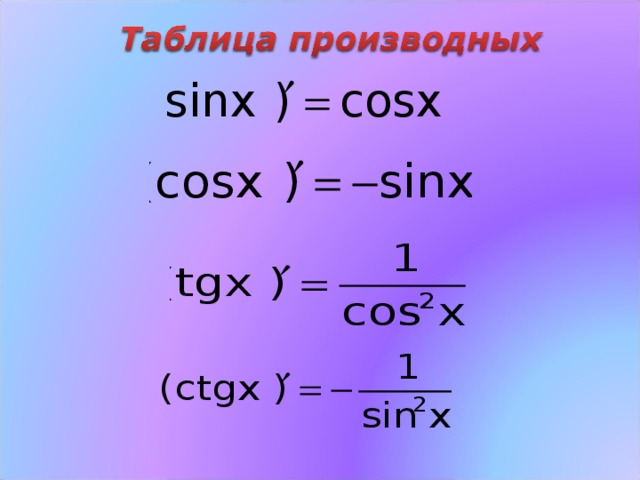
Пишется как;
sin x = противолежащая сторона/гипотенуза
Производная формулы sin(2x)
Формула sin квадрат x равна отрицательному значению функции косинуса, т.е.
d/dx (sin(2x)) = 2cos (2x)
Как доказать производную sin2x?
Существует множество способов получения производных sin (2x). Следовательно, мы можем доказать производную sin (2x), используя;
Первый принцип
Цепное правило
Частное правило
Sin 2x производная по первому принципу
Производная функции по первому принципу относится к нахождению общего выражения для наклона кривой с помощью алгебры. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна,
f(x)=lim f(x+h)-f(x)/h
Доказательство производной sin(2x) первым Principle
Чтобы доказать производную от sin (2x), используя первый принцип, замените f(x) на sin (2x) или вы можете заменить его на sin x, чтобы вычислить производную от sin x.
f′(x)=lim h➜0 f(x+h)-f(x)/h
f(x) = lim sin 2(x+h) — sin (2x)/h
Следовательно,
f(x) = lim [sin 2(x+h) — sin (2x)]/h
Теперь по тригонометрической формуле sin A cos B + cos A sin B = sin (A + B)
f(x) = lim [sin 2x cos 2h + cos 2x sin 2h — sin 2x]/h
f(x) = lim [- sin 2x(1 — cos 2h) + cos 2x sin 2h]/h
Теперь, используя формула половинного угла, 1- cos 2h = 2 sin 2 (h), приведенное выше уравнение записывается как:
f(x) = (-sin 2x) { lim [(2 sin 2 (h))]/h} + (cos 2x) {lim (sin 2h)/2h}
f(x) =( -sin 2x) [lim (sin(h))/(h). lim sin (h)] + (cos 2x) {lim (sin 2h)/2h}
Как мы знаем,
Lim (sin 2x/2x) = 2, получаем
f(x) = 0+cos2x (2)
Следовательно,
f(x) = 2cos (2x)
Производная sin 2x по цепному правилу
Производная sin (2x) может быть вычислена по цепному правилу, поскольку функция косинуса может быть записана как совмещение двух функций.
Цепное правило производных определяется как;
dy/dx = dy/du x du/dx
Доказательство дифференцирования sin2x по цепному правилу
Чтобы доказать производную sin 2x по цепному правилу, предположим, что sin(2x) можно записать как комбинацию двух функций . Используя это, найдем производную от sin(2x)
y = sin u, где u = 2x
Используя цепное правило,
y = cos u.du/dx
и
du/dx = 2
Теперь, используя значение u.
y = 2cos (2x)
Таким образом, мы получили формулу производной sin (2x) по цепному правилу.
Производная от sin(2x) с использованием правила отношения
Поскольку функция синуса представляет собой отношение противоположной гипотенузы треугольника. Следовательно, производная от sin 2x также может быть вычислена с помощью правила отношения. Частное правило определяется как;
d/dx (f/g) = f(x). g(x) -g(x).f(x) /{g(x)} 2
Доказательство производной sin(2x) по правилу частных
Чтобы доказать производную sin(2x), мы можно записать,
f(x) = sin (2x) = 1/ cosec (2x) =u/v
Предположим, что u = 1 и v = cosec (2x).
Теперь по правилу частных
f(x) = (vu — uv)/v 2
f'(x) = [cosec (2x) d/dx(1) + 1. d/dx(cosec ( 2x))] / (cosec 2x) 2
= [cosec x (0) — 1(-2cosec 2x cot 2x)] / cosec 2 2x
= (2cosec (2x).cot (2x) ) / cosec 2 2x
= 2cos (2x)
Следовательно, мы получили производную от sin (2x), используя правило дифференцирования.
Как найти производную sin(2x) с помощью калькулятора?
Самый простой способ вычислить производную sin (2x) — использовать онлайн-инструмент. Для этого вы можете воспользоваться нашим калькулятором производных. Здесь мы предлагаем вам пошаговый способ расчета производных с помощью этого инструмента.
Запишите функцию как sin(2x) в поле ввода функции. На этом шаге вам нужно указать входное значение в виде функции, так как вам нужно вычислить производную от sin(2x).
Теперь выберите переменную, по которой вы хотите дифференцировать sin(2x).
