404 Cтраница не найдена
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
В одном городе любая улица соединяет либо две различные площади, либо площадь тупиком, либо два тупика. с любой площади выходит ровно пять улиц. всего в городе 49 улиц. какое наименьшее количество
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
На пишите пожалуйста решение
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз
Найдите значение выражение 4\25+15\4 Напишите решение пожалуйста срочно надо
Пользуйтесь нашим приложением
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Таблица производных
Таблица производных| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
Степень х.
Экспоненциальный/логарифмический
Тригонометрический
Обратный тригонометрический
Гиперболический
Те, у кого гиперссылки имеют доказательства. 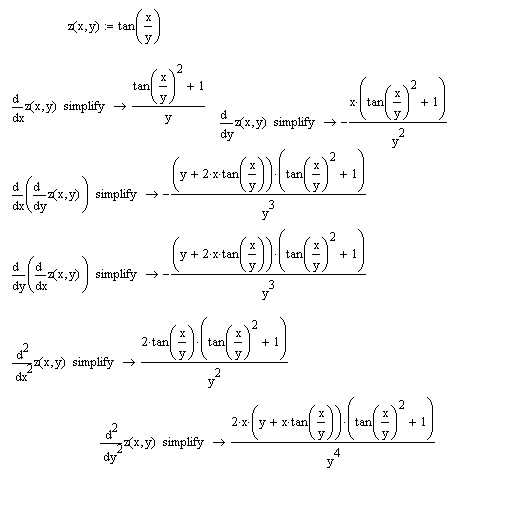 | |||||||||||||||||||||||||||||||||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
Как найти производную от y tan x, используя математику первого класса CBSE
Ответ
Проверено
167,4 тыс.+ просмотров
Подсказка: Здесь в этом вопросе мы рассматриваем данную функцию как y, и мы собираемся продифференцировать заданную функцию по x. Функция является тригонометрической функцией, поэтому для дифференцирования функции мы используем стандартные формулы тригонометрии, а затем упрощаем.
Полное пошаговое решение:
В математике производная функции действительной переменной измеряет чувствительность к изменению значения функции по отношению к изменению ее аргумента. Производные являются основным инструментом исчисления.
Теперь здесь, в этом вопросе, мы должны найти производную данной функции, используя первый принцип. Производная по первому принципу относится к использованию алгебры для нахождения общего выражения для наклона кривой. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна \[f'(x) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(x + h) — f (х)}}{ч}\]
здесь \[f(x) = \tan (x)\] и \[f(x + h) = \tan (x + h)\], и мы знаем, что отношение касательной тригонометрии можно записать как \[\ tan (x) = \dfrac{{\sin (x)}}{{\cos (x)}}\], поэтому сначала упростим \[f(x + h) — f(x)\]. Таким образом, мы имеем
\[ \Rightarrow f(x + h) — f(x) = \tan (x + h) — \tan (x)\]
Отношение тангенса тригонометрии записывается в виде тригонометрии синуса и косинуса соотношение.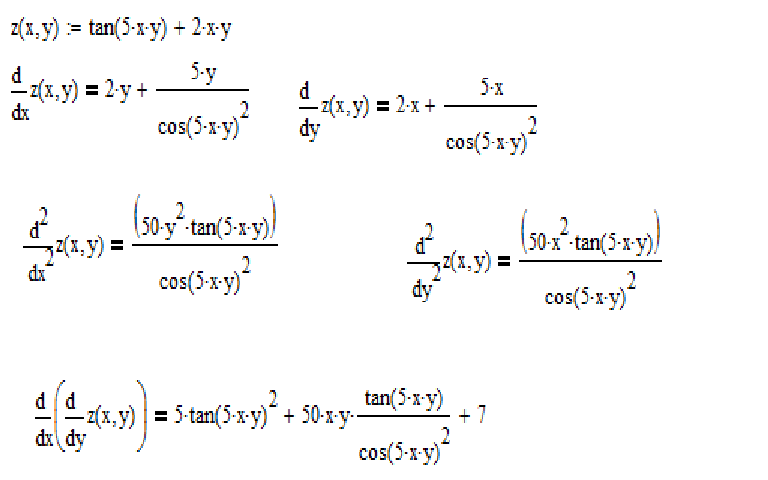
\[ \Rightarrow f (x + h) — f (x) = \ dfrac {{\ sin (x + h)}} {{\ cos (x + h)}} — \ dfrac {{\ sin (x) )}}{{\cos (х)}}\]
Используйте формулы тригонометрии, и он определяется как \[\sin (A + B) = \sin A\cos B + \cos A\sin B\] и \[\cos (A + B) = \cos A\ cos B — \sin A\sin B\]
\[ \Rightarrow f(x + h) — f(x) = \dfrac{{\sin (x).\cos (h) + \sin (h). \cos (x)}}{{\cos(x).\cos(h) — \sin(x).\sin(h)}} — \dfrac{{\sin(x)}}{{\cos (x)}}\]
Принимая LCM, мы получаем
\[ \Rightarrow f(x + h) — f(x) = \dfrac{{\cos (x)\left( {\sin(x). \cos (h) + \sin (h).\cos (x)} \right) — \left( {\cos (x).\cos (h) — \sin (x).\sin (h)} \right)\sin (x)}}{{\cos (x)\left( {\cos(x).\cos(h) — \sin(x).\sin(h)}\right)}} \] 92}x\]
Примечание: Дифференцирование определяется как производная функции по независимой переменной. Здесь зависимая переменная — это у, а независимая переменная — это х. Если функция должна дифференцироваться с использованием первого принципа, мы используем формулу, и она определяется как \[f'(x) = \mathop {\lim}\limits_{h \to 0} = \dfrac{{f(x + h) — f(x)}}{h}\] , Используя формулы предела и тригонометрии, мы можем получить результат
Недавно обновленные страницы
Вычислите изменение энтропии, связанное с конверсией.


 12.16
12.16