Производная от умножения двух чисел
Содержание статьи
1. Теорема о производной произведения функций
2. Примеры вычислений
Теорема о производной произведения функций
Нахождение производной функции называют дифференцированием. Чтобы научиться находить производные, необходимо знать правила дифференцирования. Они связаны с арифметическими действиями, а именно включают в себя правила производных от суммы функций, произведения двух функций и отношения двух функций. В этой статье рассмотрим, как находить производные от умножения двух чисел.
Производная от умножения двух чисел находится по следующему правилу дифференцирования: $(u\cdot v)’ = u’v + uv’$. Словесно это правило объясняется в теореме о производной произведения функций.
Теорема 1
Если в т. $x$ функции $f(x)$ и $g(x)$ имеются производные, то в точке $x$ произведение этих функций имеет производную, которая равна сумме произведений одной из данных функций и производной другой.
$(f(x)g(x))’=f(x)g(‘(x)+f'(x)g(x). $
$
Для упрощения этой записи в правиле о произведении вместо $f(x)$ используется $u$, а вместо $g(x)$ — $v$.
Приведём доказательство.
Положим $y=f(x)g(x)$.
$y+\Delta y=(f(x)+\Delta f(x))(g(x)+\Delta g(x)).$
$\Delta y=(f(x)+\Delta f(x))(g(x)+\Delta g(x))-f(x)g(x)=f(x)g(x)+f(x)\Delta g(x)+\Delta f(x)g(x)+\Delta f(x)\Delta g(x)=f(x)\Delta g(x)+g(x)\Delta f(x)+\Delta f(x)\Delta g(x).$
$\frac{\Delta y}{\Delta x}=\frac{f(x)\Delta g(x)}{\Delta x}+\frac{\Delta f(x)g(x)}{\Delta x}+\frac{\Delta f(x)\Delta g(x)}{\Delta x}.$
$\lim\limits_{x\to 0} \frac{\Delta y}{\Delta x}=f(x)\lim\limits_{x\to 0}\frac{\Delta g(x)}{\Delta x}+g(x)\lim\limits_{x\to 0}\frac{\Delta f(x)}{\Delta x}+\lim\limits_{x\to 0}\frac{\Delta f(x)}{\Delta x}\lim\limits_{x\to 0}\Delta g(x)=f(x)g'(x)+g(x)f'(x)+f'(x)\cdot 0.$
Формула доказана.
Теорема распространяется на произведение любого количества дифференцируемых функций. Для примера запишем правило для трёх множителей, используя упрощённую запись:
$(u\cdot v\cdot w)’=uvw’+uv’w+u’vw.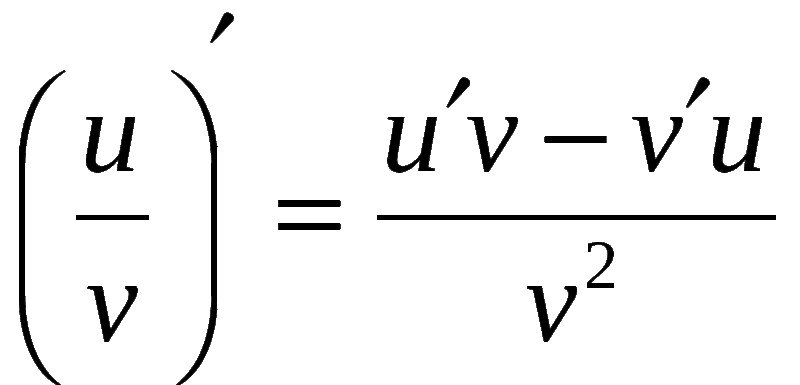
Таким образом, мы рассмотрели теорему о производной произведения функций и решили несколько примеров.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 17.04.2022
Производная произведения и частного функции
- Формулы производной произведения и частного функции
- Найти производную произведения функций самостоятельно, а затем посмотреть решение
- Производная суммы частных
- Найти производную частного функции самостоятельно, а затем посмотреть решение
- Продолжаем решать задачи вместе
Формула производной произведения функции имеет вид .
Формула производной частного функции имеет вид .
Однако было бы наивно надеяться, что на контрольной или экзамене Вам обязательно
попадётся пример на нахождение производной такого частного:
,
где легко подставить простенькое выражение в формулу и выдать правильное решение.
В реальных задачах требуется найти производную таких произведений и частных, в которые вкрались тригонометрические выражения и логарифмы, не говоря уже о множителях (константах), и вообще о том, что может содержать произведение или частное функции. Поэтому примеры нахождения производной произведения и частного функций вынесены в эту отдельную статью.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 1.Найти производную функции
.
Решение. От нас требуется найти производную произведения функций. Прежде всего вынесем множитель 2 за знак производной:
.
Теперь применяем формулу дифференцирования произведения:
Приводим слагаемые в скобках к общему знаменателю
:В числителе первого слагаемого можно заметить знакомое по школьной математике выражение двойного угла:
Существует также известное из школьной математики тождество:
.
Подставляем его в наш промежуточный результат и получаем:
.
Производная данного произведения найдена.
Пример 2.Найти производную функции
.
Пример 3.Найти производную функции
.
Посмотреть правильные решения примеров 2, 3.
- Пригодится: тригонометрические тождества для преобразования выражений
Пример 4.Найти производную функции
Решение. Перед нами сумма частных. Следовательно, каждое слагаемое будет дифференцировано как частное. Применяем правило дифференцирования частного, не забывая, чему равны производные числа(константы) и самой переменной
Пример 5.Найти производную функции
Шаг 1. Применим правило дифференцирования частного:
Шаг 2. Находим производную произведения в числителе:
Шаг 3. Находим производную суммы:
Находим производную суммы:
Шаг 4. Находим производную функции:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на x:
Нет времени вникать в решение? Можно заказать работу!
Пример 6.Найти производную функции
.
Пример 7.Найти производную функции
.
Посмотреть правильные решения примеров 6, 7
.- Пригодится: тригонометрические тождества для преобразования выражений
Пример 8.Найти производную функции
Шаг 1. Применим правило дифференцирования произведения:
Шаг 2. Найдём производную частного, помня, что производная константы равна нулю, а корень из константы является также константой:
Шаг 3. Находим производную арктангенса (формула 12 в таблице производных):
Искомая производная:
Проверить решение именно Вашей задачи можно на калькуляторе производных.
Пример 9.Найти производную функции
Шаг 1. Применим правило дифференцирования частного:
Шаг 2. Дифференцируем по правилам для произведения и показательной функции (формула 17 в таблице производных):
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :
Вновь настоятельно рекомендуем изучить производную сложной функции.
| Назад | Листать | Вперёд>>> |
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Поделиться с друзьями
Весь блок «Производная»
- Что такое производная
- Найти производную
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
Производная произведения и частного
{\prime }}=1\cdot \left( \sqrt[3]{x}-1 \right)+x\frac{1}{3\sqrt[3]{x}}= \\& =\sqrt[3]{x}-1+\sqrt[3]{x}\cdot \frac{1}{3}=\frac{4}{3}\sqrt[3]{x}-1 \\\end{align}\]Ответ найден.
Зачем раскладывать производные на множители?
Только что мы использовали несколько очень важных математических фактов, которые сами по себе не имеют отношения к производным, однако без их знания все дальнейшее изучение этой темы просто не имеет смысла.
Во-первых, решая самую первую задачу и, уже избавившись от всех знаков производных, мы зачем-то начали раскладывать это выражение на множители.
Во-вторых, решая следующую задачу, мы несколько раз переходили от корня к степени с рациональным показателем и обратно, при этом используя формулу 8-9-го класса, которую стоило бы повторить отдельно.
По поводу разложения на множители ― зачем вообще нужны все эти дополнительные усилия и преобразования? На самом деле, если в задаче просто сказано «найти производную функции», то эти дополнительные действия не требуются. Однако в реальных задачах, которые ждут вас на всевозможных экзаменах и зачетах, просто найти производную зачастую недостаточно. Дело в том, что производная является лишь инструментом, с помощью которой можно узнать, например, возрастание или убывание функции, а для этого требуется решать уравнение, раскладывать его на множители. И вот здесь этот прием будет очень уместен. Да и вообще, с функцией, разложенной на множители, гораздо удобней и приятней работать в дальнейшем, если требуются какие-то преобразования. Поэтому правило № 1: если производную можно разложить на множители, именно так и стоит поступать. И сразу правило № 2 (по сути, это материал 8-9-го класса): если в задаче встречается корень n-ной степени, причем, корень явно больше двух, то этот корень можно заменить обычной степенью с рациональным показателем, причем в показателе появится дробь, где n― та самая степень ― окажется в знаменателе этой дроби.
Однако в реальных задачах, которые ждут вас на всевозможных экзаменах и зачетах, просто найти производную зачастую недостаточно. Дело в том, что производная является лишь инструментом, с помощью которой можно узнать, например, возрастание или убывание функции, а для этого требуется решать уравнение, раскладывать его на множители. И вот здесь этот прием будет очень уместен. Да и вообще, с функцией, разложенной на множители, гораздо удобней и приятней работать в дальнейшем, если требуются какие-то преобразования. Поэтому правило № 1: если производную можно разложить на множители, именно так и стоит поступать. И сразу правило № 2 (по сути, это материал 8-9-го класса): если в задаче встречается корень n-ной степени, причем, корень явно больше двух, то этот корень можно заменить обычной степенью с рациональным показателем, причем в показателе появится дробь, где n― та самая степень ― окажется в знаменателе этой дроби.
Разумеется, если под корнем присутствует какая-то степень (в нашем случае это степень k), то она никуда не девается, а просто оказывается в числителе этой самой степени. {2}}+4}\], читатель вправе ожидать графических выкладок, т. е., графиков, построений и т. д., но, ни в коем случае, не аналитических преобразований.
{2}}+4}\], читатель вправе ожидать графических выкладок, т. е., графиков, построений и т. д., но, ни в коем случае, не аналитических преобразований.
Еще хотел бы обратить ваше внимание на одну особенность оформления задач, которые мы сегодня рассматриваем. Многие ученики считают, что я привожу слишком подробные выкладки, и многие из них можно было бы пропустить или просто решить в уме. Однако именно такая подробная запись позволит вам избавится от обидных ошибок и значительно увеличит процент правильно решенных задач, например, в случае самостоятельной подготовки к контрольным или экзаменам. Поэтому если вы еще неуверенны в своих силах, если вы только начинаете изучать данную тему, не спешите ― подробно расписывайте каждый шаг, выписывайте каждый множитель, каждый штрих, и очень скоро вы научитесь решать такие примеры лучше, чем многие школьные учителя. Надеюсь, это понятно. Давайте посчитаем еще несколько примеров.
Несколько интересных задач
На этот раз, как мы видим, в составе вычисляемых производных присутствует тригонометрия. {\prime }}$ можно рассматривать и как производную частного, и как производную степенной функции. При этом если все вычисления выполнены верно, то ответ всегда получится одним и тем же. Во-вторых, при вычислении производных, содержащих и переменную, и константу, принципиально важным является то, где находится переменная ― в числителе или в знаменателе. В первом случае, когда переменная находится в числителе, мы получаем простую линейную функцию, которая элементарно считается. А в случае, если переменная стоит в знаменателе, то мы получаем более сложное выражение с сопутствующими выкладками, приведенными ранее.
{\prime }}$ можно рассматривать и как производную частного, и как производную степенной функции. При этом если все вычисления выполнены верно, то ответ всегда получится одним и тем же. Во-вторых, при вычислении производных, содержащих и переменную, и константу, принципиально важным является то, где находится переменная ― в числителе или в знаменателе. В первом случае, когда переменная находится в числителе, мы получаем простую линейную функцию, которая элементарно считается. А в случае, если переменная стоит в знаменателе, то мы получаем более сложное выражение с сопутствующими выкладками, приведенными ранее.
На этом урок можно считать законченным, поэтому если вам что-то непонятно по производным частного или произведения, да и вообще, если у вас есть любые вопросы по этой теме, не стесняйтесь ― заходите на мой сайт, пишите, звоните, и я обязательно постараюсь вам помочь.
Сами по себе производные ― тема отнюдь не сложная, но очень объемная, и то, что мы сейчас изучаем, будет использоваться в будущем при решении более сложных задач. Именно поэтому все недопонимания, связанные с вычислениями производных частного или произведения, лучше выявить немедленно, прямо сейчас. Не когда они представляют собой огромный снежный ком недопонимания, а когда представляют собой маленький теннисный шарик, с которым легко разобраться.
Именно поэтому все недопонимания, связанные с вычислениями производных частного или произведения, лучше выявить немедленно, прямо сейчас. Не когда они представляют собой огромный снежный ком недопонимания, а когда представляют собой маленький теннисный шарик, с которым легко разобраться.
Смотрите также:
- Вводный урок по вычислению производных степенной функции
- Простое определение производной функции
- Основное тригонометрическое тождество
- Как быстро извлекать квадратные корни
- Проценты в задачах на наибольшее-наименьшее значение используем пропорции
- Сложная задача B14: работа трех исполнителей
по какой формуле вычисляется, вывод, примеры решения
Содержание:
- Что такое производная произведения двух функций
- Вывод формулы производной от умножения двух чисел с доказательством
- Примеры решения задач
Содержание
- Что такое производная произведения двух функций
- Вывод формулы производной от умножения двух чисел с доказательством
- Примеры решения задач
Что такое производная произведения двух функций
Производная произведения равна произведению производной первого множителя на второй множитель плюс произведение первого множителя на производную второго множителя: \((uv)’=u’v+uv’\)
В данном случае существует важное условие. Ни при каких обстоятельствах производная произведения функций не равна произведению производных каждого множителя.
Ни при каких обстоятельствах производная произведения функций не равна произведению производных каждого множителя.
Вывод формулы производной от умножения двух чисел с доказательством
В процессе доказательства теоремы следует рассмотреть функцию \(h(x)\), которую можно записать, как произведение двух других функций:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(h(x)=f(x)\cdot g(x)\)
Необходимо выполнить вычисления производной рассматриваемой функции, руководствуясь общим алгоритмом. Предположим, что \triangle x является некоторым приращением аргумента. В таком случае, приращение функции \(h(x)\) имеет вид:
\(\triangle h=h(x+\triangle x)-h(x)=(f(x+\triangle x)\cdot g(x+\triangle x))-(f(x)\cdot g(x))\)
Приращения каждого множителя:
\(\triangle f=f(x+\triangle x)-f(x)\Rightarrow f(x+\triangle x)=\triangle f+f(x)\)
\(\triangle g=g(x+\triangle x)-g(x)\Rightarrow g(x+\triangle x)=\triangle g+g(x)\)
Выполним подстановку:
\(\triangle h=(\triangle f+f(x))\cdot (\triangle g+g(x))-f(x)\cdot g(x)=\\ =\triangle f\cdot \triangle g+\triangle f\cdot g(x)+f(x)\cdot \triangle g+f(x)\cdot g(x)-f(x)\cdot g(x)=\\ =\triangle f\cdot \triangle g+\triangle f\cdot g(x)+f(x)\cdot \triangle g\)
Далее можно найти производную:
\(h'(x)=\lim_{\triangle x\rightarrow 0}\frac{\triangle h}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle f\cdot \triangle g+\triangle f\cdot g(x)+f(x)\cdot\triangle g}{\triangle x}=\\ =\lim_{\triangle x\rightarrow 0}\left(\frac{\triangle f}{\triangle x}\cdot\frac{\triangle g}{\triangle x}\right)+\lim_{\triangle x\rightarrow 0}\frac{\triangle f}{\triangle x}\cdot g(x)+f(x)\cdot\lim_{\triangle x\rightarrow 0}\frac{\triangle g}{\triangle x}=\\ =f'(x)\cdot g'(x)\cdot 0+f'(x)\cdot g(x)+f(x)\cdot g'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\)
Таким образом, производная произведения двух функций равна сумме двух слагаемых: производная первой функции на вторую плюс первая функция на производную второй:
\(\left(f(x)\cdot g(x)\right)’=f'(x)\cdot g(x)+f(x)\cdot g'(x)\)
Следствие
Пусть\( u, \, v, \, w, \, \)z являются функциями от независимой переменной \( x. \)
\)
Тогда:
\(\bigl( u \, v \, w \bigr)’ = u’ v \, w + u \, v’ w + u \, v \, w’\)
\(\bigl( u \, v \, w \, z \bigr)’ = u’ v \, w \, z + u \, v’ w \, z + u \, v \, w’ z + u \, v \, w \, z’\)
Представим доказательства первой формулы. В первую очередь следует применить формулу производной произведения для функций \(u\) и \(v \)\, \(w\), а затем — для функций \(v \) и \(w\):
\(\bigl( u \, v \, w \bigr)’ = \bigl( u \cdot (v \, w) \bigr)’ = u’ \cdot (v \, w) + u \cdot (v \, w)’ = u’ \, v \, w + u \cdot (v’ \, w + v \, w’) = u’ v \, w + u \, v’ w + u \, v \, w’\)
Аналогичным способом можно доказать подобные формулы.
Примеры решения задач
Задача 1
Задача
Требуется найти производную произведения двух функций:
\(y = x\ln x\)
Решение:
В первую очередь можно рассчитать производные от каждого из множителей. В случае с множителем x производная будет равна:
\((x)’=1\)
Производная второй функции \(\ln x \) определяется с помощью формулы для логарифма и составляет:
\((\ln x)’ = \frac{1}{x}\)
Используя формулу производной произведения можно получить решение задачи:
\(y’=(x\ln x)’=(x)’\ln x + x(\ln x)’=\ln x + x\cdot \frac{1}{x} = \ln x + 1\)
Ответ: \(y’=\ln x + 1\)
Задача 2
Задача
Необходимо найти производную функции:
\(y = x^2e^{3x}\)
Решение:
Производная первой функции равна:
\((x^2)’=2x\)
Производная второй функции равна:
\((e^{3x})’=e^{3x}\cdot (3x)’=e^{3x} \cdot 3 = 3e^{3x}\)
С помощью теоремы о производной произведения двух функций можно записать следующее решение:
\(y’=(x^2e^{3x})’=(x^2)’e^{3x}+x^2(e^{3x})’=2xe^{3x}+3x^2e^{3x}\)
Далее следует вынести экспоненты за скобки, чтобы упростить запись ответа:
\(y’=(3x^2+2x)e^{3x}\)
Ответ: \(y’=(3x^2+2x)e^{3x}\)
Задача 3
Задача
Нужно найти производную:
\(y(x) = x \sin x\)
Решение:
С помощью правила дифференцирования произведения двух функций запишем:
\(( u v )’ = u’ v + u v’\)
\(y’ = (x \sin x)’ = (x)’ \sin x + x (\sin x)’\)
По информации из таблицы производных можно найти:
\((x^a)’ = a x^{a-1}\)
\((\sin x)’ = \cos x»\)
Таким образом:
\((x)’ = \left(x^1 \right)’ = 1 \cdot x^{1-1} = x^0 = 1\)
В результате, получим:
\(y’ = (x)’ \sin x + x (\sin x)’ = 1 \cdot \sin x + x \cos x\)
Ответ: \( y'(x) = \sin x + x \cos x\)
Задача 4
Задача
Требуется определить производную функции от переменной \(x\) :
\(y(x) = e^x \left( x^2 — 2x + 2 \right)\)
Решение:
Используя формулу производной произведения двух функций, можно записать:
\(( u v )’ = u’ v + u v’\)
\(y’ = \left( e^x \left( x^2 — 2x + 2 \right) \right)’ = \left( e^x \right)’ \left( x^2 — 2x + 2 \right) + e^x \left( x^2 — 2x + 2 \right)’\)
С помощью формулы производной суммы и разности функций, следует записать уравнения:
\(( u \pm v \pm w )’ = u’ \pm v’ \pm w’\)
\(\left( x^2 — 2x + 2 \right)’ = \left( x^2 \right)’ — ( 2x )’ + ( 2 )’\)
Применив правила дифференцирования постоянных, получим:
\((C)’ = 0\)
\((Cu)’ = C u’\)
\(( 2x )’ = 2 (x)’\)
\(( 2 )’ = 0\)
По таблице производных необходимо определить, что:
\(\left( e^x \right)’ = e^x\)
\(\left(x^a \right)’ = a x^{a-1}\)
Таким образом:
\(\left(x^2 \right)’ = 2 x^{2-1} = 2 x^1 = 2 x\)
\((x)’ = \left(x^1 \right)’ = 1 \cdot x^{1-1} = x^0 = 1\)
\(\left( x^2 — 2x + 2 \right)’ = \left( x^2 \right)’ — 2( x )’ + ( 2 )’ = 2x — 2 + 0\)
В таком случае:
\(y’ = \left( e^x \right)’ \left( x^2 — 2x + 2 \right) + e^x \left( x^2 — 2x + 2 \right)’ = e^x \left( x^2 — 2x + 2 \right) + e^x \left( 2x — 2 \right) = x^2 e^x — 2x e^x + 2 e^x + 2x e^x — 2 e^x = x^2 e^x\)
Ответ: \( y'(x) = x^2 e^x\)
Задача 5
Задача
Необходимо найти производную функции:
\(y(x) = e^x (\sin x — \cos x)\)
Решение: С помощью последовательного применения правил дифференцирования решим задачу:
\(\left( e^x \right)’ = e^x\)
\(( \sin x )’ = \cos x\)
\(( \cos x )’ = — \sin x\)
\((\sin x — \cos x)’ = ( \sin x )’ — ( \cos x )’ = \cos x + \sin x\)
\(y’ = \left( e^x (\sin x — \cos x) \right)’ = \left( e^x \right)’ (\sin x — \cos x) + e^x (\sin x — \cos x)’ = e^x (\sin x — \cos x) + e^x (\cos x + \sin x) = 2 e^x \sin x\)
Ответ: \(y’ = 2 e^x \sin x\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок. 2
2
Производная функции. Мини-курс. 11 видео уроков. — Math
Производная функции. Мини-курс. 11 видео уроков.
Алгебра 10, 11 класс. Высшая математика. Математический анализ. Что такое предел функции? Базовое понятие и определение предела функции. Как посчитать предел? Вычислить предел функции. Предел функции в точке. Найти предел функции. Неопределенность в математике. Что называют неопределенностью? Что избавиться от неопределенности? Неопределенность (0/0) — как ее раскрыть? Способы раскрытия неопределенности. Что такое лимит. Лимит функции. Как вычислить лимит функции. Что значит «стрелочка» в лимитах (пределах). Сопряженные множители. Как домножить на сопряженные множители. Как избавиться от иррациональности при раскрытии неопределенности? Как разложить многочлен на множители, чтобы избавиться от иррациональности и посчитать предел? Теория. Определение предела функции: Предел (лимит) это значение к которому стремится функция, когда х стремится к х0. Примеры с решением. Задания с объяснением.
Примеры с решением. Задания с объяснением.
- Пример 1: Вычислить предел функции.
- Пример 2: Вычислить предел функции, раскрыв неопределенность (0/0) разложением числителя и знаменателя на множители.
- Пример 3: Вычислить предел функции, раскрыв неопределенность (0/0) умножением на сопряженный множитель.
- Пример 4: Вычислить предел функции, раскрыв неопределенность (0/0) преобразовав выражение.
Алгебра 10, 11 класс. Высшая математика. Математический анализ. Определение производной. Физический и геометрический смысл производной. Приращение аргумента. Приращение функции. Нахождение производной функции, используя определение производной. Примеры с решениями.
- Пример 1: Найти приращение функции.
- Пример 2: Найти производную функции, используя ее определение.
В классическом дифференциальном исчислении производная чаще всего определяется через понятие предела, однако исторически теория пределов появилась позже дифференциального исчисления. Исторически производная вводилась кинематически (как скорость) или геометрически (определяясь по сути наклоном касательной, в разных конкретных формулировках). Производной функции у = f(х) в точке х называется предел отношения приращения функции в точке x0 к приращению аргумента, когда приращение аргумента стремится к нулю (можно обозначить у’ или f'(х)). Операция нахождения производной называется дифференцированием.
Исторически производная вводилась кинематически (как скорость) или геометрически (определяясь по сути наклоном касательной, в разных конкретных формулировках). Производной функции у = f(х) в точке х называется предел отношения приращения функции в точке x0 к приращению аргумента, когда приращение аргумента стремится к нулю (можно обозначить у’ или f'(х)). Операция нахождения производной называется дифференцированием.
Урок 2. Производная элементарной степенной функции.
Как брать производную от икс в степени n. Таблица производных. Производная элементарной степенной функции. Как правильно преобразовать функцию прежде чем брать производную. Свойства степени. Алгебра 10, 11 класс. Примеры с решением. Задания с объяснением.
Урок 3.
 Производная суммы. Правила дифференцирования.
Производная суммы. Правила дифференцирования.Алгебра 10, 11 класс. Высшая математика. Математический анализ. Производная суммы. Правила дифференцирования. Примеры с решениями.
- Пример 1: Найти производную функции.
- Пример 2: Найти производную функции в точке.
Урок 4. Производная произведения. Производная частного. Правила дифференцирования.
Алгебра 10, 11 класс. Высшая математика. Математический анализ. Производная функции. Производная произведения. Производная частного. Правила дифференцирования.
Урок 5. Производная сложной степенной функции. Найти производную в точке х0.
Сложная функция. Какая функция называется сложной? Производная сложной функции. Правила дифференцирования. Производная сложной степенной функции. Найти производную функции в точке х0. Алгебра 10, 11 класс. Примеры с решением. Задания с объяснением.
Найти производную функции в точке х0. Алгебра 10, 11 класс. Примеры с решением. Задания с объяснением.
- Пример 1: Найти производную функции.
- Пример 2: Найти производную функции в точке.
Урок 6. Производные тригонометрических функций.
Высшая математика. Математический анализ. Правила дифференцирования. Производная. Производная тригонометрических функций. Производная синуса, производная косинуса, производная тангенса, производная котангенса. Алгебра 10, 11 класс. Производная суммы, производная частного, производная произведения. Производная элементарных функций. Тригонометрия. Примеры с решением.
- Пример 1: Найти производную суммы тригонометрических функций.
- Пример 2: Найти производную произведения тригонометрических функций.
- Пример 3: Найти производную частного тригонометрических функций.
Урок 7. Производная сложной тригонометрической функции.
Правила дифференцирования. Производная. Производная сложных тригонометрических функций. Какая функция называется сложной? Производная сложной функции. Производная синуса, производная косинуса, производная тангенса, производная котангенса. Алгебра 10, 11 класс. Производная суммы, производная частного, производная произведения. Производная элементарных функций. Тригонометрия. Примеры с решением.
- Пример 1: Найти производную сложной тригонометрической функции.
- Пример 2: Найти производную косинуса трех икс под корнем.
- Пример 3: Найти производную произведения.
- Пример 4: Найти производную тангенса в квадрате.
- Пример 5: Найти производную частного.
Урок 8. Производные сложных тригонометрических функций в точке.
Производные сложных тригонометрических функций в точке.
Правила дифференцирования. Производная. Производная сложных тригонометрических функций. Какая функция называется сложной?Производная сложной функции. Производная сложной тригонометрической функции в точке. Производная синуса, производная косинуса, производная тангенса, производная котангенса. Алгебра 10, 11 класс. Производная суммы, производная частного, производная произведения. Производная элементарных функций. Тригонометрия. Примеры с решением.
- Пример 1: Найти производную сложной тригонометрической функции.
- Пример 2: Найти производную тангенса икс квадрат.
- Пример 3: Найти производную произведения.
- Пример 4: Найти производную тангенса в квадрате.
- Пример 5: Найти косинус икс куб и косинус куб икс.
Урок 9. Производная показательной функции. Правила нахождения производных.
Правила нахождения производных.
Производная показательной и сложной показательной функции. Алгебра 10, 11 класс. Какая функция называется показательной? Формулы для нахождения производной показательной функции. Что такое натуральный логарифм? Какой логарифм называется натуральным. Чему равно число е. Что является аргументом показательной функции. Правила нахождения производных. Правило суммы, произведения и частного для производных. Формулы для производных. Как взять производную показательной функции. Примеры с решением.
- Пример 1: Найти производную показательной функции с экспонентой в основании.
- Пример 2: Найти производную сложной показательной функции.
- Пример 3: Производная произведения с показательной функцией.
- Пример 4: Производная частного с показательной функцией.
- Пример 4: Производная показательной функции с тангенсом.
- Пример 5: Производная показательной функции у которой синус в основании.
- Пример 6: Производная синуса у которого аргумент показательная функция.

Урок 10. Производная логарифма. Производная логарифмической функции.
Производная логарифмической функции. Производная сложной логарифмической функции. Производная частного. Производная произведения. Натуральный логарифм, десятичный логарифм. Производная логарифма. Число е. Производная натурального логарифма. Производная ln. Производная lg. Производная десятичного логарифма. Алгебра 10, 11 класс. Математический анализ. Мат анализ. Матан. Правила дифференцирования. Примеры с решением. Производная сложной функции. Производная от логарифма в степени. Производная ln в степени. Производная лн. Производная лг. Производная логарифма функции. Производная сложного логарифма. Производная логарифма сложной функции. Производная функция натурального логарифма. Сложная производная натурального логарифма. Производная логарифма примеры. Производная натурального логарифма сложной функции. Производная логарифм х. Производная натурального логарифма примеры. Производная логарифма формула. Производная натурального логарифма в степени. Производная от логарифма. Найти производную. Найти производную функции. Найти производную логарифма.
Производная логарифм х. Производная натурального логарифма примеры. Производная логарифма формула. Производная натурального логарифма в степени. Производная от логарифма. Найти производную. Найти производную функции. Найти производную логарифма.
Полезные материалы:
Комбинаторика, теория вероятностей и математическая статистика. Базовый курс.
- Информация о материале
- Автор: Math
- Категория: Высшая математика
- Вперед
Добавить комментарий
Композиция функций
«Композиция функций» — это применение одной функции к результатам другой:
Результат f() передается через g()
Записывается: (g º f)(x)
Что означает: g(f(x))
Пример:
f(x) = 2x+3 и g(x) = x 2 «x» просто заполнитель . Чтобы избежать путаницы, назовем это просто «ввод»:
Чтобы избежать путаницы, назовем это просто «ввод»:
f(ввод) = 2(ввод)+3
g(вход) = (вход) 2
Начнем:
(g º f)(x) = g(f(x))
Сначала применим f, затем применим g к что результат:
(g º f)(x) = (2x+3) 2
Что, если мы поменяем порядок f и g?
(f º g)(x) = f(g(x))
Сначала мы применяем g, затем применяем f к этому результату:
(f º g)(x) = 2x 2 + 3
Получаем другой результат!
Когда мы меняем порядок, результат редко бывает таким же.
Будьте осторожны, какая функция стоит первой.
Символ
Символом композиции является маленький кружок:
(g º f)(x)
Это , а не закрашенная точка: (g · f)(x), так как это означает умножить .
Составлено с самим собой
Мы можем даже составить функцию с самим собой!
Пример:
f(x) = 2x+3
(f º f)(x) = f(f(x))
Сначала мы применяем f, затем применяем f к этому результату:
(f º f)(x) = 2(2x+3)+3 = 4x + 9
Мы должны сделать это без красивой диаграммы:
(f º f)(x)= f(f(x) )
= f(2x+3)
= 2(2x+3)+3
= 4x + 9
Доменов
До сих пор это было легко, но теперь мы должны рассмотреть Доменов функции.
Домен – это набор всех значений , которые входят в функцию.
Функция должна работать для всех значений, которые мы ей даем, поэтому зависит от нас, , чтобы убедиться, что мы правильно определили домен!
Пример: домен для √x (квадратный корень из x)
Мы не можем получить квадратный корень из отрицательного числа (если только мы не используем мнимые числа, но мы ими не являемся), поэтому мы должны исключить отрицательные числа:
Домен √x состоит из всех неотрицательных действительных чисел
В числовой строке это выглядит так:
Используя нотацию конструктора множеств, записывается:
{ x | x ≥ 0}
Или, используя интервальную запись, это:
[0,+∞)
Важно правильно указать Домен, иначе мы получим плохие результаты!
Домен составной функции
Мы должны получить оба домена правильно (составная функция и первая используемая функция).
При выполнении, например, (g º f)(x) = g(f(x)):
- Убедитесь, что мы правильно получили домен для f(x) ,
- Затем также убедитесь, что g(x) получает правильный домен
Пример:
f(x) = √x и g(x) = x 2Домен f(x) = √x состоит из неотрицательных вещественных чисел
Домен
3 из
g(x) = x 2 все действительные числаСоставная функция:
(g º f)(x) = g(f(x))
= (√x) 2
= x
Теперь «x» обычно имеет домен всех действительных чисел …
… но поскольку это составная функция , мы должны также рассмотрим f(x) ,
Итак, все домены состоят из неотрицательных действительных чисел
Почему оба домена?
Ну представь функции машины… первая проплавляет пламенем дырку (только для металла), вторая просверливает дырку побольше (работает по дереву или металлу):
То, что мы видим в конце, это просверленное отверстие, и мы можем подумать, что «это должно подойти для дерева или металла ». Но если мы подложим дрова в g º f, то первая функция f разожжет огонь и все сожжет! |
Итак, важно то, что происходит «внутри машины».
Разложение функции
Мы можем пойти другим путем и разбить функцию в состав других функций.
Пример:
(x+1/x) 2Эту функцию можно составить из следующих двух функций:
f(x) = x + 1/x
g(x) = x 2
И получаем:
(g º f)(x) = g(f(x))
= g(x + 1/x)
= (x + 1/x) 2
Это может быть полезно, если исходная функция слишком сложна для работы.
Резюме
- «Композиция функций» — это применение одной функции к результатам другой.
- (g º f)(x) = g(f(x)) , сначала применить f(), затем применить g()
- Мы также должны учитывать домен первой функции
- Некоторые функции можно разложить на две (или более) более простые функции.

Частные производные
Частная производная — это производная, в которой некоторые переменные остаются постоянными. Как в этом примере:
Пример: функция для поверхности, которая зависит от двух переменных
x и y
Когда мы находим наклон в направлении x (при фиксированном y ), мы нашли частную производную.
Или мы можем найти наклон в направлении y (при фиксированном x ).
Давайте сначала подумаем о функции одной переменной (x):
f(x) = x 2
Мы можем найти его производную, используя степенное правило:
f’(x) = 2x
А как насчет функции двух переменных (x и y):
f(x, y) = x 2 + y 3
Мы можем найти его частичную производную по x , если рассматривать y как константу (представьте, что y — число вроде 7 или что-то в этом роде):
f’ х = 2х + 0 = 2х
Объяснение:
- производная от x 2 (относительно x) равно 2x
- мы рассматриваем y как константу , поэтому y 3 также является константой (представьте, что y=7, тогда 7 3 =343 также является константой), а производная константы равна 0
Чтобы найти частную производную по y , мы рассматриваем x как константу :
f’ у = 0 + 3у 2 = 3у 2
Объяснение:
- мы теперь рассматриваем x как константу , поэтому x 2 также является константой, а производная константы равна 0
- производная от y 3 (по y) равна 3y 2
Вот и все. Просто не забудьте рассматривать все остальные переменные, как если бы они были константами .
Просто не забудьте рассматривать все остальные переменные, как если бы они были константами .
Удержание переменной константы
Итак, на что похоже «удержание переменной константой»?
Пример: объем цилиндра равен V = π r
2 hМы можем записать это в многомерной форме как
f(r, h) = π r 2 h
2 3
0 Для частной производной по r мы считаем h постоянным , а r изменяется:
f’ r = π (2r) h = 2πrh
(производная r
1 2 по 8 2 к r равно 2r, а π и h — константы) Там написано «при изменении только радиуса (минимально), объем изменится на 2πrh»
Это как если бы мы добавили скин с окружностью окружности (2πr) и высотой h.
Для частичной производной по отношению к H мы держим R постоянную :
F ‘ H = π r 2 (1) = πr 2
(πr 2
(πr 2
(πr 2
(πr 2
3 (1). 2 являются константами, а производная от h по h равна 1)
2 являются константами, а производная от h по h равна 1) В нем говорится: «Поскольку меняется только высота (минимально), объем изменяется на πr 2 »
Это похоже на то, как если бы мы добавили самый тонкий диск сверху с площадью круга πr 2 .
Давайте посмотрим на другой пример.
Пример: площадь поверхности квадратной призмы.
Поверхность включает верхнюю и нижнюю части площадью x 2 каждая и 4 стороны площадью xy каждая:
f(x, y) = 2x 2 + 4xy
f’ x = 4x + 4y
f’ y = 0 + 4x = 4x
Три или более переменных
У нас может быть 3 или более переменных. Просто найдите частную производную каждой переменной по очереди, рассматривая все остальные переменные как константы .
Пример: Объем куба с вырезанной из него квадратной призмой.
f(x, y, z) = z 3 − x 2 y
f’ x = 0 − 2xy = −2xy
f’ y = 0 − x 2 = −x 2
f’ z = 3z 2 − 0 = 3z 912 8 2 Когда есть много x и y, это может сбить с толку, поэтому умственный трюк состоит в том, чтобы заменить «константы» переменные буквами, такими как «c» или «k», которые выглядят как константы. У него везде есть x и y! Итак, давайте попробуем трюк с заменой букв. Относительно x мы можем заменить «y» на «k»: f(x, y) = k 3 sin(x) + x 2 tan(k) f’ x = k 3 cos(x) + 2x tan(k) Но не забудьте вернуть его обратно! f’ x = y 3 cos(x) + 2x tan(y) Аналогично по отношению к y мы превращаем «x» в «k»: f(x, y) = y 3 sin(k) + k 2 tan(y) f’ y = 3y 2 sin(k) + k 2 с 2 (у) f’ у = 3у 2 sin(x) + x 2 с 2 (у) , так как это небольшая дополнительная работа. Обозначение : мы использовали f’ x для обозначения «частной производной по x», но еще одно очень распространенное обозначение — использовать забавную обратную d (∂), например: ∂f ∂x = 2x То же, что и: f’ x = 2x ∂ называется «дел» или «ди» или «кудрявый ди» Итак ∂f ∂x можно сказать «del f del x» f(x, y, z) = x 4 − 3xyz ∂f ∂x = 4x 3 − 3yz ∂f ∂y = −3xz ∂f ∂z = −3xy Вы можете предпочесть это обозначение, оно определенно выглядит круто. Правило произведения в исчислении — это метод нахождения производной или дифференцирования функции, заданной в виде произведения двух дифференцируемых функций. Это означает, что мы можем применить правило произведения или правило Лейбница, чтобы найти производную функции вида: f(x)·g(x), такую, что и f(x), и g(x) являются дифференцируемыми. Правило произведения напрямую следует концепции пределов и производных при дифференцировании. Давайте разберемся с формулой правила произведения, ее доказательством на решенных примерах подробно в следующих разделах.
Пример: f(x, y) = y
3 sin(x) + x 2 tan(y) Пример: найдите частные производные числа
f(x, y, z) = x 4 − 3xyz , используя обозначение «curly dee»
Правило произведения — формула, доказательство, определение, примеры
1. Что такое правило продукта? 2. Формула правила продукта 3. Вывод формулы правила продукта 4. Правило продукта для продукта с более чем двумя функциями 5. 
Как применить правило произведения при дифференциации? 6. Часто задаваемые вопросы о правиле продукта Что такое правило продукта?
Правило произведения в исчислении — это метод, используемый для нахождения производной любой функции, заданной в виде произведения, полученного путем умножения любых двух дифференцируемых функций. Правило произведения словами гласит, что производная произведения двух дифференцируемых функций равна сумме произведения второй функции с дифференцированием первой функции и произведения первой функции с дифференцированием второй функции. Это означает, что если нам дана функция вида: f(x)·g(x), мы можем найти производную этой функции, используя производную правила произведения как,
\(\frac{d}{dx}\) f(x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
Формула правила продукта
Мы можем вычислить производную или вычислить дифференцирование произведения двух функций, используя формулу правила произведения в исчислении. Формула правила произведения имеет следующий вид:
Формула правила произведения имеет следующий вид:
\(\frac{d}{dx}\) f(x) = \(\frac{d}{dx}\) {u(x)·v(x)} = [v(x) × u'(x) + u(x) × v'(x)]
где,
- f(x) = Произведение дифференцируемых функций u(x) и v(x)
- u(x), v(x) = дифференцируемые функции
- u'(x) = производная функции u(x)
- v'(x) = производная функции v(x)
Вывод формулы правила продукта
В предыдущем разделе мы узнали о формуле произведения для нахождения производных произведения двух дифференцируемых функций. Для любых двух функций правило произведения может быть указано в обозначениях Лагранжа как
(u v)’ = u’·v + u·v’
или в обозначениях Лейбница как
\(\dfrac {d}{dx}\) (u·v) = \(\dfrac {du}{dx}\)·v + u·\(\dfrac {dv}{ dx}\)
Давайте посмотрим здесь на доказательство формулы правила произведения. Существуют различные методы доказательства формулы правила произведения, представленной как
- Используя первый принцип
- Использование цепной линейки
Доказательство формулы правила произведения с использованием первого принципа
Чтобы доказать формулу правила произведения с использованием определения производной или пределов, пусть функция h(x) = f(x)·g(x), такая что f(x) и g (x) дифференцируемы в точке x.
⇒ h ‘(x) = \(\ mathop {\ lim } \ limit_ {Δx \ to 0} \) [h (x + Δx) — h (x)] / Δx
= \(\ mathop { \lim }\limits_{Δx \to 0}\) \(\frac{f(x+Δx)g(x+Δx) — f(x)g(x)}{Δx}\)
= \( \ mathop {\ lim} \ limit_ {Δx \ to 0} \) \(\ frac {f (x + Δx) g (x + Δx) — f (x) g (x + Δx) + f (x) г (x+Δx) — f(x)g(x)}{Δx}\)
= \( \mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) — f(x)]g(x+Δx) + f(x)[g(x+Δx) — g(x)]}{Δx}\)
= \( \mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) — f(x)]g(x+Δx)}{Δx} + \mathop {\lim}\limits_{Δx \to 0} \frac{f( х)[g(x+∆x) — g(x)]}{∆x}\)
= \( (\ mathop {\ lim } \ limit_ {Δx \ to 0} \ frac {[f (x + Δx) — f (x)]} {Δx}) ( \ mathop {\ lim } \ limit_ {Δx \to 0} g(x+Δx))+ (\mathop {\lim }\limits_{Δx\to 0}f(x)) (\mathop {\lim}\limits_{Δx\to 0} \ frac{[g(x+Δx) — g(x)]}{Δx})\)
= \(g(x)\mathop {\lim}\limits_{Δx\to 0} \frac{[f (x + Δx) — f (x)]} {Δx} + f (x) \ mathop {\ lim} \ limit_ {Δx \ to 0} \ frac {[g (x + Δx) — g (x)] }{Δx}\)
∵ \(\ mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) — f(x)]}{Δx}\) = f’ (x) и \(\ mathop {\lim }\limits_{Δx \to 0}\frac{[g(x+Δx) — g(x)]}{Δx}\) = g'(x)
⇒ \(\frac{d}{dx}\) f(x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
Значит, доказано.
Доказательство формулы правила произведения с использованием цепного правила
Мы можем вывести формулу правила произведения в исчислении, используя формулу цепного правила, рассматривая правило произведения как частный случай цепного правила. Пусть f(x) — дифференцируемая функция такая, что h(x) = f(x)·g(x).
\(\frac{d}{dx}\) (f·g) = [δ(fg)/δf][df/dx] + [δ(fg)/δg][dg/dx] = g( df/dx) + f(dg/dx)
Следовательно, доказано.
Правило продукта для продукта с более чем двумя функциями
Правило произведения можно обобщить на произведения более двух факторов с использованием одной и той же формулы правила произведения. Например, для трех функций u(x), v(x) и w(x), произведение которых задано как u(x)v(x)w(x), мы имеем
\( \frac{d (uvw)}{dx}=\frac{du}{dx}vw+u\frac {dv}{dx}w+uv\frac {dw}{dx}{\frac {d(uvw)}{dx} } = {\ frac {du} {dx}} vw + u {\ frac {dv} {dx}} w + uv {\ frac {dw} {dx}} \)
Как применить правило произведения при дифференциации?
Чтобы найти производную функции вида h(x) = f(x)g(x), обе функции f(x) и g(x) должны быть дифференцируемыми функциями. Мы можем применить следующие шаги, чтобы найти вывод дифференцируемой функции h (x) = f (x) g (x), используя правило произведения.
Мы можем применить следующие шаги, чтобы найти вывод дифференцируемой функции h (x) = f (x) g (x), используя правило произведения.
- Шаг 1: Запишите значения f(x) и g(x).
- Шаг 2: Найдите значения f'(x) и g'(x) и примените формулу правила произведения, заданную как: h'(x) = \(\frac{d}{dx}\) f (x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
Давайте посмотрим на следующий пример, приведенный ниже, чтобы лучше понять правило произведения.
Пример: Найдите f'(x) для следующей функции f(x), используя правило произведения: f(x) = x·log x.
Решение:
Здесь f(x) = x·log x
u(x) = x
v(x) = log x
⇒u'(x) = 1
⇒v'(x) = 1/x
⇒f'(x) = [v(x)u'(x) + u(x)v'(x)]
⇒ f'(x) = [log x•1 + x•(1/x)]
⇒ f'(x) = log x + 1
Ответ: Производная от x log x с использованием правила произведения равна log x + 1.
Пример 1. Найдите производную от x · cos(x), используя формулу правила произведения. Решение: Пусть f(x) = cos x и g(x) = x. ⇒ f'(x) = -sin x ⇒[f(x)g(x)]’ = [g(x)f'(x) + f(x)g'(x)] Ответ: производная от x cos x по правилу произведения равна (- x sin x + cos x). Пример 2. Дифференцируйте x 2 log x, используя формулу правила произведения. Решение: Пусть f(x) = log x и g(x) = x 2 . ⇒ f'(x) = (1/x) ⇒[f(x)g(x)]’ = [g(x)f'(x) + f(x)g'(x)] Ответ: производная от x 2 log x с использованием правила произведения равна (x + 2x log x). Пример 3: Применение правила произведения для дифференцирования (1 — 2x)·sin x. Решение: Пусть f(x) = (1-2x), g(x) = sin x ⇒g'(x) = cos x ⇒[f(x)g(x)]’ = [g(x)f'(x) + f(x)g'(x)] Ответ: производная от (1 — 2x)·sin x с использованием правила произведения равна — 2 sin x + cos х — 2х потому что х. перейти к слайдуперейти к слайдуперейти к слайду Разбивайте сложные концепции с помощью простых визуальных средств. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайду Примеры правила продукта
⇒g'(x) = 1
⇒[f(x)g(x)]’ = [(x•(-sinx) + cosx•(1)]
⇒[f(x)g(x)]’ = — x sin x + cos x
⇒g'(x) = 2x
⇒[f(x)g(x)]’ = [(x 2 •(1/x) + log x•(2x)]
⇒[f(x)g(x)]’ = x + 2x log x
⇒f'(x) = -2
⇒[f(x)g(x)]’ = [(sin x•(-2) + (1 — 2x)•(cosx)]
⇒[f(x)g(x)]’ = — 2 sin x + cos x — 2x cos x Практические вопросы по правилу продукта
Часто задаваемые вопросы о правиле продукта
Что такое правило произведения дифференцирования в исчислении?
Правило произведения — это одно из правил производных, которое мы используем для нахождения производной функций вида P(x) = f(x)·g(x). Производная функции P(x) обозначается через P'(x). Если производная функции P(x) существует, то говорят, что P(x) дифференцируема, т. е. дифференцируемыми функциями являются те функции, производные которых существуют. Функция P(x) дифференцируема в точке x = a, если существует следующий предел.
Производная функции P(x) обозначается через P'(x). Если производная функции P(x) существует, то говорят, что P(x) дифференцируема, т. е. дифференцируемыми функциями являются те функции, производные которых существуют. Функция P(x) дифференцируема в точке x = a, если существует следующий предел.
\(P'(x) = \mathop {\lim }\limits_{h \to 0} \frac{P(a+h)-P(a)}{h}\)
Как найти производную Используете правило продукта?
Производные произведения двух дифференцируемых функций можно вычислить в исчислении с использованием правила произведения. Нам нужно применить формулу правила произведения для дифференцирования функции вида f(x) = u(x)v(x). Формула правила произведения имеет вид
.
f'(x) = [u(x)v(x)]’ = [u'(x) × v(x) + u(x) × v'(x)]
где f'(x), u'(x) и v'(x) — производные функций f(x), v(x) и u(x).
Что такое формула правила продукта?
Формула производной правила произведения — это правило дифференциального исчисления, которое мы используем для нахождения производной произведения двух или более функций. Предположим, что две функции, u(x) и v(x), дифференцируемы, тогда можно применить правило произведения, чтобы найти (d/dx)[u(x)v(x)] as,
Предположим, что две функции, u(x) и v(x), дифференцируемы, тогда можно применить правило произведения, чтобы найти (d/dx)[u(x)v(x)] as,
f'(x) = [u(x)v(x)]’ = [u'(x) × v(x) + u(x) × v'(x)]
Как вывести формулу для правила произведения?
Формула правила продукта может быть получена с использованием различных методов. Они даны как,
- Использование производных и предельных свойств или первого принципа
- Использование цепной линейки
Нажмите здесь, чтобы ознакомиться с подробным доказательством формулы продукта.
Как использовать правило продукта в дифференциации?
Правило произведения можно использовать для нахождения дифференцирования функции f(x) вида u(x)v(x). Производная этой функции с использованием правила произведения может быть задана как f'(x) = [u(x)v(x)]’ = [u'(x) × v(x) + u(x) × v'( x)]
Как вывести правило произведения, используя определение пределов и производных?
Доказательство правила произведения может быть дано с использованием определения и свойств пределов и производных. Для функции f(x) = u(x)·v(x) производная f'(x) может быть задана как
Для функции f(x) = u(x)·v(x) производная f'(x) может быть задана как
⇒ h'(x) = \(\ mathop {\lim }\limits_{ Δx \to 0}\) [h(x + Δx) — h(x)]/Δx
= \(\mathop {\lim}\limits_{Δx\to 0}\) \(\frac{f( x+Δx)g(x+Δx) — f(x)g(x)}{Δx}\)
= \(\mathop {\lim}\limits_{Δx\to 0}\) \(\frac {f(x+∆x)g(x+∆x) — f(x)g(x+∆x) + f(x)g(x+∆x) — f(x)g(x)}{∆x}\)
= \( \mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) — f(x)]g(x+Δx) + f(x)[g(x +∆x) — g(x)]}{∆x}\)
= \( \ mathop {\ lim } \ limit_ {Δx \ to 0} \ frac {[f (x + Δx) — f (x)] g (x + Δx)} {Δx} + \ mathop {\ lim }\limits_{Δx \to 0} \frac{f(x)[g(x+Δx) — g(x)]}{Δx}\)
= \( (\ mathop {\lim }\limits_ {Δx \to 0} \frac{[f(x+Δx) — f(x)]}{Δx})( \mathop {\lim }\limits_{Δx\to 0} g(x+Δx))+ (\ mathop {\ lim } \ limit_ {Δx \ to 0} f (x)) (\ mathop {\ lim } \ limits_ {Δx \ to 0} \ frac {[g (x + Δx) — g (x) ]}{Δx})\)
= \( г (х) \ mathop {\ lim } \ limit_ {Δx \ to 0} \ frac {[f (x + Δx) — f (x)]} {Δx } + f (x) \ mathop {\ lim} \ limit_ {Δx \ to 0} \ frac {[g (x + Δx) — g (x)]} {Δx} \)
∵ \(\ mathop {\lim }\limits_{Δx \to 0} \frac{[f(x+Δx) — f(x)]}{Δx}\) = f'(x) и \( \ mathop {\ lim } \ limit_ {Δx \ to 0} \ frac {[g (x + Δx) — g (x)]} {Δx} \) = g ‘(x)
⇒ \ (\ frac { d}{dx}\) f(x)·g(x) = [g(x) × f'(x) + f(x) × g'(x)]
Каковы применения формулы производной правила произведения ? Приведите примеры.

Мы можем применить правило произведения, чтобы найти дифференцирование функции вида u(x)v(x). Например, для функции f(x) = x 2 sin x мы можем найти производную как f'(x) = sin x·2x + x 2 ·cos х.
Как найти производную произведения более чем двух функций с помощью правила произведения?
Формулу дифференцирования произведений более чем двух функций можно обобщить, используя ту же формулу правила произведения. Например, для трех функций u(x), v(x) и w(x), произведение которых задано как u(x)v(x)w(x), мы имеем
\( \frac{d (uvw)}{dx}=\frac{du}{dx}vw+u\frac {dv}{dx}w+uv\frac {dw}{dx}{\frac {d(uvw)}{dx} } = {\ frac {du} {dx}} vw + u {\ frac {dv} {dx}} w + uv {\ frac {dw} {dx}} \) 92}\).
Загрузить БЕСПЛАТНЫЕ учебные материалы
Расчетный лист
Правила произведения, мощности и цепи – BetterExplained
Нагромождение правил для получения деривативов никогда по-настоящему не щелкало для меня. Правило сложения, правило произведения, правило частного — как они сочетаются друг с другом? Что мы вообще пытаемся сделать ?
Вот мой взгляд на производные:
- У нас есть система для анализа, наша функция f
- Производная f’ (также известная как df/dx) представляет собой пошаговое поведение
- Оказывается, f является частью большей системы (h = f + g)
- Используя поведение частей, можем ли мы понять поведение целого?
Да. У каждой детали есть «точка зрения» на то, сколько изменений она внесла. Объедините каждую точку зрения, чтобы получить общее поведение. Каждое производное правило является примером слияния различных точек зрения.
У каждой детали есть «точка зрения» на то, сколько изменений она внесла. Объедините каждую точку зрения, чтобы получить общее поведение. Каждое производное правило является примером слияния различных точек зрения.
А почему бы нам сразу всю систему не проанализировать? По той же причине вы не съедите гамбургер за один раз: маленькие кусочки легче уложить в голове. 92″ и сует вам в лицо график. Действительно ли это помогает нашей интуиции?
Не для меня. Графики сжимают ввод и вывод в одну кривую и скрывают механизм, который превращает одно в другое. Но производные правила о машинах, так что давайте посмотрим!
Я визуализирую функцию как процесс «ввод (x) => f => вывод (y)». компьютер наведения (начало серии ютуб).
Машина вычисляет такие функции, как сложение и умножение с помощью шестеренок — вы можете увидеть, как разворачивается механика!
Думайте о функции f как о машине с входным рычагом «x» и выходным рычагом «y». 2 составляет около 2. Производная оценивала, как далеко сдвинется выходной рычаг (совершенное, бесконечно маленькое качание сместит 2 единицы; мы сдвинули 2,01).
2 составляет около 2. Производная оценивала, как далеко сдвинется выходной рычаг (совершенное, бесконечно маленькое качание сместит 2 единицы; мы сдвинули 2,01).
Ключ к пониманию производных правил:
- Настройка системы
- Покачивайте каждую часть системы отдельно, чтобы увидеть, как далеко перемещается вывод
- Объединить результаты
Общее покачивание представляет собой сумму покачиваний каждой части.
Сложение и вычитание
Время для нашей первой системы:
Что произойдет, если вход (x) изменится?
В моей голове я думаю: «Функция h принимает один вход. Она подает тот же вход на f и g и добавляет выходные рычаги. f и g качаются независимо друг от друга и даже не знают друг о друге!»
Функция f знает, что внесет некоторое покачивание (df), g знает, что внесет некоторое покачивание (dg), и мы, блуждающие надзиратели, которыми мы являемся, знаем, что их индивидуальное ежеминутное поведение суммируется:
Опять же, давайте опишем каждую «точку зрения»:
- Общая система имеет поведение dh
- С точки зрения f, он вносит вклад df в целое [он не знает о g]
- С точки зрения g, он вносит вклад в dg в целом [он не знает о f]
Каждое изменение в системе связано с изменением какой-либо ее части (f и g). Если мы добавим вклад каждой возможной переменной, мы описали всю систему.
Если мы добавим вклад каждой возможной переменной, мы описали всю систему.
df vs df/dx
Иногда мы используем df, иногда df/dx — что дает? (На какое-то время это меня смутило)
- df — это общее понятие «как бы сильно f не изменилось»
- df/dx — это специфическое понятие «как бы сильно ни изменилось f с точки зрения того, насколько сильно изменилось x»
Общий «df» помогает нам увидеть общее поведение.
Аналогия: представьте, что вы едете по пересеченной местности и хотите измерить топливную эффективность своего автомобиля. Вы измеряете пройденное расстояние, проверяете свой бак, чтобы узнать, сколько бензина вы использовали, и, наконец, выполняете деление, чтобы вычислить «миль на галлон». Вы измеряли расстояние и бензин отдельно — вы не прыгали в бензобак, чтобы узнать расход на ходу!
В исчислении иногда мы хотим думать о фактическом изменении, а не об отношении. Работа на уровне «df» дает нам пространство для размышлений о том, как функция в целом покачивается. мы можем , в конечном итоге , уменьшите масштаб с точки зрения конкретного ввода.
мы можем , в конечном итоге , уменьшите масштаб с точки зрения конкретного ввода.
И мы сделаем это сейчас. Приведенное выше правило сложения может быть записано на основе «на dx» как:
Умножение (правило произведения)
Следующая головоломка: предположим, что наша система умножает части «f» и «g». Как она себя ведет?
Хм, хитрость — части взаимодействуют более тесно, но стратегия та же самая: посмотреть, как каждая часть вносит свой вклад со своей точки зрения, и объединить их:
- общее изменение h = вклад f (с точки зрения f) + вклад g (с точки зрения g)
Посмотрите на эту диаграмму:
Что происходит?
- У нас есть наша система: f и g умножаются, что дает h (площадь прямоугольника)
- Ввод «x» изменяется на dx off на расстоянии. f изменяется на некоторую величину df (думайте об абсолютном изменении, а не о скорости!). Точно так же g изменяется на собственную величину dg.
 Поскольку f и g изменились, площадь прямоугольника тоже изменилась.
Поскольку f и g изменились, площадь прямоугольника тоже изменилась. - Как изменилась площадь с точки зрения f? Ну, f знает, что он изменился с помощью df, но понятия не имеет, что случилось с g. С точки зрения f, он единственный, кто переместился и добавит часть площади = df * g .
- Аналогично, g не знает, как изменилось f, но знает, что добавит часть площади «dg * f»
Общее изменение в системе (dh) равно двум срезам площади:
Теперь, как и в нашем примере с количеством миль на галлон, мы «делим на dx», чтобы записать это с точки зрения того, насколько изменилось x:
(Кроме того: разделить на dx? Инженеры будут кивать, математики хмуриться. Технически df/dx — это не дробь: это полная операция взятия производной (с пределом и всем прочим). Но с точки зрения бесконечно малого , интуитивно, мы «масштабируемся по dx». Я улыбаюсь.)
Ключ к правилу произведения: добавьте два «кусочка площади», по одному с каждой точки зрения.
Попался: Но нет ли эффекта от одновременного изменения f и g (df * dg)?
Ага. Однако эта область бесконечно мала * бесконечно мала («бесконечно мала 2-го порядка») и невидима на текущем уровне. Это сложная концепция, но (df * dg) / dx исчезает по сравнению с обычными производными, такими как df/dx. Мы независимо изменяем f и g и комбинируем результаты, игнорируя результаты их совместного движения.
Цепное правило: это не так уж и плохо
Предположим, что g зависит от f, которое зависит от x:
Цепное правило позволяет нам «приблизиться» к функции и посмотреть, как начальное изменение (x) может повлиять окончательный результат по линии (g).
Интерпретация 1: Преобразование ставок
Обычная интерпретация состоит в том, чтобы умножить скорости:
x wiggles f. Это создает скорость изменения df/dx, которая изменяет g на dg/df. Таким образом, все покачивание будет таким:
Это похоже на метод «фактор-метка» на уроке химии:
Если ваша скорость «миль в секунду» изменится, умножьте на коэффициент преобразования, чтобы получить новые «мили». в час». Второй не знает о часе напрямую — он проходит преобразование секунды => минуты.
в час». Второй не знает о часе напрямую — он проходит преобразование секунды => минуты.
Аналогично, g не знает непосредственно об x, только f. Функция g знает, что она должна масштабировать свои входные данные на dg/df, чтобы получить выходные данные. Начальная скорость (df/dx) изменяется по мере продвижения вверх по цепочке.
Интерпретация 2: Преобразование покачивания
Я предпочитаю видеть цепное правило на основе «на покачивание»:
- x покачивания на dx, поэтому
- f покачивается df, поэтому
- г покачивается от dg
Круто. Но как они на самом деле связаны? Ах да, производная! (Это выходное покачивание на входное покачивание):
Помните, что производная от f (df/dx) определяет масштаб начального колебания. И то же самое происходит с g:
Он будет масштабировать любое колебание, возникающее на его входном рычаге (f), на dg/df. Если мы запишем df wiggle через dx:
, мы получим другую версию цепного правила: dx запускает цепочку, что приводит к некоторому конечному результату dg. Если мы хотим окончательное колебание с точки зрения dx, разделите обе стороны на dx:
Если мы хотим окончательное колебание с точки зрения dx, разделите обе стороны на dx:
Цепное правило — это не просто сокращение единицы метки фактора — это распространение колебания, которое корректируется на каждом шаге. 92). Ввод был f, и он обрабатывает f как одно значение. Позже мы второпях перепишем f через x. Но g не имеет к этому никакого отношения — его не волнует, что f можно переписать в терминах более мелких частей.
Во многих примерах переменная «x» является «концом строки».
Вопросы задают df/dx, т.е. «Дайте мне изменения с точки зрения x». Теперь x может зависеть от чего-то более глубокого, но об этом не просят. Это все равно, что сказать: «Мне нужны мили в час. Меня не волнуют мили в минуту или мили в секунду. Просто дайте мне мили в час». df/dx означает «перестать смотреть на входные данные, как только вы доберетесь до x».
Почему мы умножаем производные по цепному правилу, а для остальных добавляем их?
Обычные правила примерно объединяют точки зрения для получения общей картины. Какое изменение видит f? Какие изменения видит g? Сложите их в общую сумму.
Какое изменение видит f? Какие изменения видит g? Сложите их в общую сумму.
Цепное правило заключается в том, чтобы углубиться в одну часть (например, f) и посмотреть, контролируется ли она другой переменной. Это как заглянуть внутрь часов и сказать: «Эй, минутная стрелка управляется секундной стрелкой!». Мы остаемся внутри той же части. 94 действительно х*х*х*х. Это умножение 4 «независимых» переменных. Каждый x ничего не знает о других, с тем же успехом это может быть x * u * v * w.
Теперь подумайте о точке зрения первого x:
- Меняется с x на x + dx
- Изменение общей функции равно [(x + dx) — x][u * v * w] = dx[u * v * w]
- Изменение на основе «dx» составляет [u * v * w]
Аналогично,
- С вашей точки зрения меняется на du. Он вносит вклад (du/dx)*[x * v * w] на основе «на dx» 94 имеет четыре одинаковые «точки зрения», которые совмещаются. Буйя!
Сделайте передышку
Я надеюсь, вы видите производную в новом свете: у нас есть система частей, мы вносим изменения и видим, как все это движется.
 Речь идет о объединении точек зрения: что каждая часть добавляет к целому?
Речь идет о объединении точек зрения: что каждая часть добавляет к целому?В следующей статье мы рассмотрим еще более мощные правила (экспоненты, частные и друзья). Счастливая математика.
Другие сообщения из этой серии
- Нежное введение в изучение исчисления
- Понимание исчисления с помощью метафоры банковского счета
- Доисторическое исчисление: открытие Пи
- Аналогия с исчислением: интегралы как умножение
- Исчисление: построение интуиции для производной
- Как понимать деривативы: произведение, мощность и правила цепочки
- Как понимать производные: правило частных, показатели степени и логарифмы
- Интуитивное введение в ограничения
- Интуиция для ряда Тейлора (аналогия ДНК)
- Зачем нужны пределы и бесконечно малые числа?
- Обучение исчислению: преодоление нашей искусственной потребности в точности
- Дружеский разговор о том, 0,999… = 1
- Аналогия: исчисление камеры
- Практика абстракции: графы исчисления
- Quick Insight: более простая арифметика с исчислением
- Как прибавить от 1 до 100 с помощью исчисления
- Интеграл Sin(x): Геометрическая интуиция
Правило произведения для трех и более функций — Krista King Math
Как расширить правило произведения с двух до трех функций
Правило произведения — это производное правило, которое позволяет нам взять производную функции, которая сама является произведением двух других функций.
 Правило произведения говорит нам, что производная уравнения типа
Правило произведения говорит нам, что производная уравнения типа???y=f(x)g(x)???
будет выглядеть так:
???\frac{dy}{dx}=f\prime(x)g(x)+f(x)g\prime(x)???
Но что делать, если наша функция является произведением более чем двух функций? В этой ситуации, если наша функция
???y=f(x)g(x)h(x)???
тогда производная выглядит так:
???\frac{dy}{dx}=f\prime(x)g(x)h(x)+f(x)g\prime(x)h( х)+f(x)g(x)h\prime(x)???
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Мы видим, что исходная функция была произведением трех функций, а ее производная была суммой трех произведений. Если бы наша функция была произведением четырех функций, производная была бы суммой четырех произведений.
Как видите, когда мы берем производную по правилу произведения, мы берем производную одной функции за раз, умножая на две другие исходные функции. Чтобы быть более конкретным, мы берем производную от ???f(x)??? и умножаем ее на ???g(x)??? и ???h(x)???, оставив эти два как есть.
 Затем мы добавляем к этому производную от ???g(x)???, умноженную на ???f(x)??? и ???ч(х)??? оставили как есть. Мы можем продолжить эту схему, взяв производную только от одной из функций и оставив остальные в покое, для такого количества функций, сколько было перемножено вместе в нашей исходной задаче.
Затем мы добавляем к этому производную от ???g(x)???, умноженную на ???f(x)??? и ???ч(х)??? оставили как есть. Мы можем продолжить эту схему, взяв производную только от одной из функций и оставив остальные в покое, для такого количества функций, сколько было перемножено вместе в нашей исходной задаче.Глядя на уравнение, которое является произведением четырех функций, например
???y=f(x)g(x)h(x)j(x)???
производная равна
???\frac{dy}{dx}=f\prime(x)g(x)h(x)j(x)+f(x)g\prime(x)h( х)j(x)+f(x)g(x)h\prime(x)j(x)+f(x)g(x)h(x)j\prime(x)???
Видеопример применения правила произведения производных к произведению трех функций
9{13}\справа)\cdot\Big[12\sin{4x}\cos{5x}??????+2\sin{4x}\cos{5x}???
???+x\sin{4x}\cos{5x}???
???-5x\sin{4x}\sin{5x}???
???+4x\cos{4x}\cos{5x}\Big]???
Получить доступ к полному курсу исчисления 1
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, правило произведения, правило произведения для производных, производные, правила производных, три функции, множество функций, правило произведения для трех функций
0 лайковИсчисление I. Правило произведения и частного
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-4: Произведение и частное Правило 93} — x} \вправо)\влево( {10 — 20x} \вправо)\)
Показать все решения Скрыть все решения
На данный момент не так много причин использовать правило произведения. Как мы отмечали в предыдущем разделе, все, что нам нужно сделать для любого из них, — это просто умножить произведение, а затем дифференцировать.
С учетом сказанного мы будем использовать правило продукта для них, чтобы мы могли увидеть пример или два. По мере добавления новых функций в наш репертуар и по мере усложнения функций правило произведения будет становиться все более полезным и во многих случаях необходимым. 92}} \right)\) Показать решение
Обратите внимание, что мы взяли производную этой функции в предыдущем разделе и не использовали правило произведения в этот момент. Однако здесь мы должны получить тот же результат, что и тогда.
Теперь давайте решим задачу здесь. 2}} \right)\] 92} + 40x — 10\конец{выравнивание*}\]
2}} \right)\] 92} + 40x — 10\конец{выравнивание*}\]
Так как это было легко сделать, мы пошли дальше и немного упростили результаты.
Давайте теперь поработаем пару примеров с правилом частных. В этом случае, в отличие от примеров с правилом произведения, для пары этих функций потребуется правило отношения, чтобы получить производную. Однако для последних двух мы можем избежать правила частного, если захотим, как мы увидим.
Пример 2. Продифференцируйте каждую из следующих функций. 96}}}{5}\)
Показать все решения Скрыть все решения
a \(\displaystyle W\left( z \right) = \frac{{3z + 9}}{{2 — z}}\) Показать решение
Здесь нечего делать, кроме как использовать частное правило. Вот работа для этой функции.
\[\begin{align*}W’\left( z \right) & = \frac{{3\left( {2 — z} \right) — \left( {3z + 9} \right)\left( { — 1} \right)}}{{{{\left( {2 — z} \right)}^2}}}\\ & = \frac{{15}}{{{{\left( {2 — z} \right)}^2}}}\end{align*}\] 96}}}\) Показать решение
Кажется странным, что это здесь, а не в первой части этого примера, учитывая, что он определенно кажется проще, чем любой из двух предыдущих. На самом деле это проще. Есть смысл сделать это здесь, а не сначала. В этом случае есть два способа вычислить эту производную. Есть легкий путь и трудный путь, и в этом случае трудный путь является частным правилом. В этом смысл этого примера.
На самом деле это проще. Есть смысл сделать это здесь, а не сначала. В этом случае есть два способа вычислить эту производную. Есть легкий путь и трудный путь, и в этом случае трудный путь является частным правилом. В этом смысл этого примера.
Давайте воспользуемся правилом частных и посмотрим, что у нас получится. 97}}}\]
Итак, это был «тяжелый» путь. Ну что там было сложного? Ну на самом деле это было не так уж сложно, просто есть более простой способ сделать это, вот и все. Однако, сказав это, распространенной ошибкой здесь является неправильное вычисление производной числителя (константы). По какой-то причине многие люди дают производную от числителя в таких задачах как 1 вместо 0! Кроме того, есть некоторое упрощение, которое необходимо сделать в такого рода задачах, если вы используете правило частного. 95}\]
Наконец, давайте не будем забывать о наших применениях производных.
Пример 3. Предположим, что количество воздуха в воздушном шаре в любой момент времени \(t\) определяется выражением
\[V\left( t \right) = \frac{{6\sqrt[3]{t}}}{{4t + 1}}\]
Предположим, что количество воздуха в воздушном шаре в любой момент времени \(t\) определяется выражением
\[V\left( t \right) = \frac{{6\sqrt[3]{t}}}{{4t + 1}}\]
Определите, наполняется ли шар воздухом или стравливается воздух в \(t = 8\).
Показать решение
Если шар наполняется воздухом, то его объем увеличивается, а если из него сливается воздух, то объем уменьшается. Другими словами, нам нужно получить производную, чтобы мы могли определить скорость изменения объема при \(t = 8\) 9\prime} = f’\,g\,h\,w + f\,g’\,h\,w + f\,g\,h’\,w + f\,g\,h\,w ‘\конец{выравнивание*}\]
Получение этих продуктов более чем двух функций на самом деле довольно просто. Например, давайте взглянем на правило продукта трех функций.
Во-первых, мы не думаем об этом как о произведении трех функций, а вместо правила произведения двух функций \(f\,g\) и \(h\), которое мы можем затем использовать произведение двух функций правило.




 Поскольку f и g изменились, площадь прямоугольника тоже изменилась.
Поскольку f и g изменились, площадь прямоугольника тоже изменилась. Речь идет о объединении точек зрения: что каждая часть добавляет к целому?
Речь идет о объединении точек зрения: что каждая часть добавляет к целому?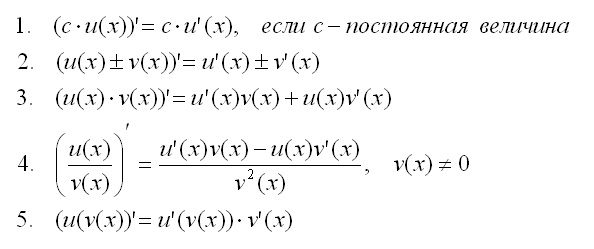 Правило произведения говорит нам, что производная уравнения типа
Правило произведения говорит нам, что производная уравнения типа Затем мы добавляем к этому производную от ???g(x)???, умноженную на ???f(x)??? и ???ч(х)??? оставили как есть. Мы можем продолжить эту схему, взяв производную только от одной из функций и оставив остальные в покое, для такого количества функций, сколько было перемножено вместе в нашей исходной задаче.
Затем мы добавляем к этому производную от ???g(x)???, умноженную на ???f(x)??? и ???ч(х)??? оставили как есть. Мы можем продолжить эту схему, взяв производную только от одной из функций и оставив остальные в покое, для такого количества функций, сколько было перемножено вместе в нашей исходной задаче.