Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
11.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Проведены четыре плоскости.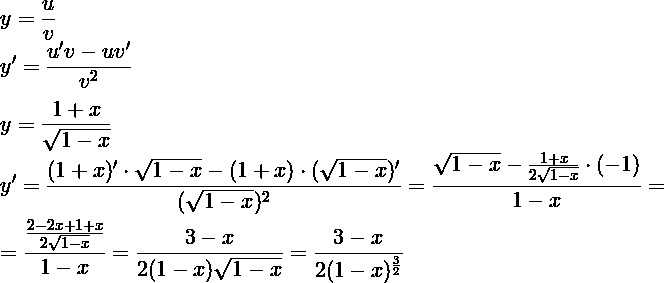
Коля, Дима и Саша собрали…
Через точку О,не лежащую между…
Клетки таблицы 4*7 раскрашены в черный и белый цвета. Пар соседних клеток разного цвета всего 26, пар соседних клеток черного цвета всего 9. Сколько соседних клеток белого цвета.
Решено
Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1
Пользуйтесь нашим приложением
Используйте определение предела, чтобы найти производную от $x+\sqrt x$
спросил
Изменено 7 лет, 11 месяцев назад
Просмотрено 7к раз
$\begingroup$
Функция $f(x) = x + \sqrt x$.
Как бы вы использовали предельное определение производной, чтобы найти производную этого уравнения?
- пределы
- производные
$\endgroup$
2
$\begingroup$
У нас есть
$$f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}$$
Пусть $$f(x) = x + \sqrt x$$
$$\begin{align}f'(x)&=\lim_{h\to0}\frac{(x+h + \sqrt {x+h})-(x + \sqrt x)}{h}\\ &=\lim_{h\to0}\frac{h + \sqrt {x+h} — \sqrt x}{h}\\ &=\lim_{h\to0}1+\frac{ \sqrt {x+h} — \sqrt x}{h}\\ &=\lim_{h\to0}1+\frac{\sqrt {x+h} — \sqrt x}{h}\frac{\sqrt {x+h} + \sqrt x}{\sqrt {x+ ч} + \sqrt х}\\ &=\lim_{h\to0}1+\frac{x+h — x}{h( \sqrt {x+h} + \sqrt x)}\\ &=\lim_{h\to0}1+\frac{h}{h( \sqrt {x+h}+ \sqrt x)}\\ &=\lim_{h\to0}1+\frac{1}{\sqrt {x+h} + \sqrt x}\\ &=1+\frac{1}{\sqrt {x} + \sqrt x}\\ f'(x)&=1+\frac{1}{2\sqrt {x}}\\ \end{выравнивание}$$
$\endgroup$
$\begingroup$
Подсказка
Вы знаете, что результат должен быть $f'(x) = 1 + \frac1{2\sqrt x}$, так что вы знаете, куда вы направляетесь.
Теперь просто поиграйте с определением
$$f'(x):= \lim_{h\to0} \frac{f(x+h)-f(x)}h = \lim_{h\to0} \frac{(x+h+\sqrt{ x+h}) — (x + \sqrt x)}h = \ldots$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью GoogleЗарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Найдите производную функции f(x) = x+ sqrt(X), используя определение производной
#производные #исчисление
Арианна А.
спросил 09/25/15Пожалуйста, помогите мне найти производную от f(x), используя определение производной
Подписаться І 2
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Уайатт Р. ответил 09/25/15
Репетитор
4.9 (68)
Специалист по предварительному проектированию/S.T.E.M
Об этом репетиторе ›
Об этом репетиторе ›
Lim h-> 0 Of f(x+h) — f(x)/h
Я собираюсь сначала упростить правую часть и применить ограничение в последнюю очередь.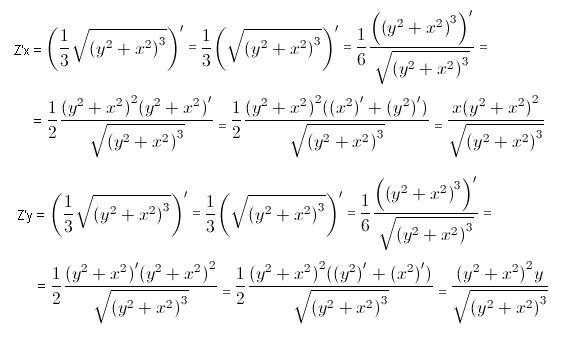
Кроме того, в некоторых учебниках вместо h используется Δx. Это не имеет значения.
Настройка формулы с использованием предоставленной функции дает:
x+h + sqrt(x+h) — (x + sqrt(x)/ h. примечание: весь числитель больше h
упрощение числителя
h + sqrt(x+h) — sqrt(x) /h Умножить на сопряженное число
h + sqrt(x+h) — sqrt(x)/h * sqrt(x+h) + sqrt(x)/sqrt(x+h) +sqrt(x)
=hsqrt(x+h)+hsqrt(x) + x + h+ sqrt(x(x+ h) — sqrt(x(x+h) — x/h(sqrt(x+h)+sqrt(x)
= hsqrt(x+h)+hsqrt(x)+h/h(sqrt(x+h)+sqrt(x)
умножьте h на числитель и сократите с h в знаменателе, чтобы получить
sqrt(x+h)+sqrt(x)+1/sqrt(x+h)+sqrt(x). Применить lim h-> 0
f'(x) = 1+2sqrt(x) /2sqrt(x) или
f'(x) = 1/2sqrt(x) + 1
Голосовать за 0 Понизить
Подробнее
Отчет
Дина Л.