Всё о 7 задаче ЕГЭ
6 задача ЕГЭ – на понимание производной функции. Задание проверяет знание связи между графиком функции и значением ее производной в различных точках, и наоборот – графиком производной и возрастанием/убыванием функции на интервалах и в точках.
Хотя это задание относится к сложному разделу (математический анализ), само по себе оно довольно простое. Решается в одно действие и знать нужно немного — для решения большинства задач хватит информации написанной на этих двух картинках:
Более подробно об этом теме – рассказано в этих видео:
Что такое производная | Наглядное объяснение на графиках
Разбор задач на поиск экстремумов, минимумов и максимумов
Геометрический смысл производной | Теория + разбор задач ЕГЭ
Задачи, которые были на экзамене за последние 10 лет
2011:
2012:
2013:
2014:
2015:
2016:
2017:
2018:
2019:
2020:
2021:
В открытом банке есть и другие типы заданий (на первообразную, физический смысл производной и условия касания), но в вариантах реальных ЕГЭ я таких задачи не нашла. Хотя это и не значит, что в будущем на ЕГЭ такого никогда не будет, так что лучше разберитесь и в них тоже. Вот примеры таких задач:
Хотя это и не значит, что в будущем на ЕГЭ такого никогда не будет, так что лучше разберитесь и в них тоже. Вот примеры таких задач:
Процент выполнения
Сколько процентов пишущих экзамен решили задачу на производные в разные годы:
Сколько процентов из тех, кто решал экзамен в 2021 году, набрал в задаче хотя бы 1 балл:
Какой вывод можно сделать? Шестую задачу решает примерно 6 человек из 10 и это третья задача по потерянным баллам (в первой части). Для меня это несколько удивительно, потому что 6 задача не требует большого количества знаний и решается в одно действие. В чем же может быть причина таких результатов?
Типичные ошибки
1. Перепутать производную и функцию
Многие начинают в этой задаче отвечать так будто перед ними график функции и выбирают точки – \(x_1\), \(x_4\), \(x_7\), \(x_8\). Хотя правильные точки \(x_4\), \(x_5\), \(x_6\) и ответ \(3\).
Хотя правильные точки \(x_4\), \(x_5\), \(x_6\) и ответ \(3\).
Вот, что авторы ЕГЭ написали в Методических рекомендациях по итогам ЕГЭ об этой задаче: «Выполнение – около 69%. Типичные ошибки связаны в первую очередь с невнимательным чтением условия – почти 24% участников указали количество точек, в которых значение функции положительно, а еще около 2% участников пытались перечислить номера точек, в которых производная принимает положительные значения.»
2. Не ограничить график данным отрезком
Если забыть про отрезок, который указан в конце условия, то в ответ задаче \(3\). Если не забывать про отрезок, то ответ в задаче \(2\). Составители ЕГЭ пишут, что около \(31\)% экзаменуемых делают такую ошибку, а правильный ответ дают лишь \(43\)%. Поэтому Ященко, Семенов и Высоцкий советуют начинать решение задачи с отмечания данного отрезка в КИМе. Напомню, что вы МОЖЕТЕ рисовать на выданных вам бланках КИМ.
3. Неправильно вычислить тангенс или не учесть убывание/возрастание функции
Чтобы найти производную в точке, нужно вычислить тангенс угла наклона касательной с положительным направлением оси \(Ox\). На практике задача решается в 2 этапа:
1. Определить убывает касательная или возрастает и соответственно поставить знак минус или плюс.
2. Определить тангенс угла в треугольнике, в котором гипотенуза является частью касательной, а вершины треугольника совпадали с вершинами клеточек.
В этой задаче многие, во-первых, забывали про первый пункт, а во-вторых, путались в определении тангенса и вместо \(\frac{AC}{BC}\) считали \(\frac{BC}{AC}\).
МЕНЮ
|
ЗАЧЕМ НУЖНЫ ПРОИЗВОДНЫЕ
На первый взгляд производные нужны чтобы забивать головы и без того
перегруженных школьников, но это не так. Но это опять в среднем. А вдруг она просто в последний час сначала полчаса ехала медленно-медленно, а потом вдруг разогналась и стала ехать быстро-быстро? Да, может быть и так. 
Как мы видим, чем больше мы разобьем наш промежуток в 3 часа — тем точнее получим результат. Но нам не нужен результат «точнее» — нам нужен совершенно точный результат. Значит и разбивать время надо на бесконечное число частей. А сама часть — следовательно будет бесконечно маленькой. Если вы поняли все вышеизложенное — то вы поняли смысл производной. Производная — это быстрота изменения чего-либо. Например в нашем случае скорость — это быстрота изменения «проеханного расстояния» с течением времени. А может быть «быстрота изменения температуры с изменением долготы в сторону севера». Или «быстрота исчезания конфет из вазы на кухне».  В общем если есть что-то,
некая величина «Y», которая зависит от некоторой величины «X»,
то скорее всего, есть и производная которая записывается dy/dx.
И она как раз показывает — как изменяется величина y при бесконечно
малом изменении величины x — как у нас расстояние изменялось при
бесконечно малом изменении времени. В общем если есть что-то,
некая величина «Y», которая зависит от некоторой величины «X»,
то скорее всего, есть и производная которая записывается dy/dx.
И она как раз показывает — как изменяется величина y при бесконечно
малом изменении величины x — как у нас расстояние изменялось при
бесконечно малом изменении времени.
Назад
|
Все приемы и приемы
На этой странице вы найдете все, что вам нужно знать о решении производных. Моя цель на этой странице – сделать из вас машину для решения производных :-).
Я расположил приемы, которые вам необходимо изучить, в таком порядке, чтобы вам было легче их понять. Эту страницу можно использовать как карту, которая поможет вам в изучении деривативов, или вы можете использовать ее для обзора всех методов решения деривативов.
Готовы? Пошли…
Основные правила
Использование определения Самый простой способ расчета производных — использование определения.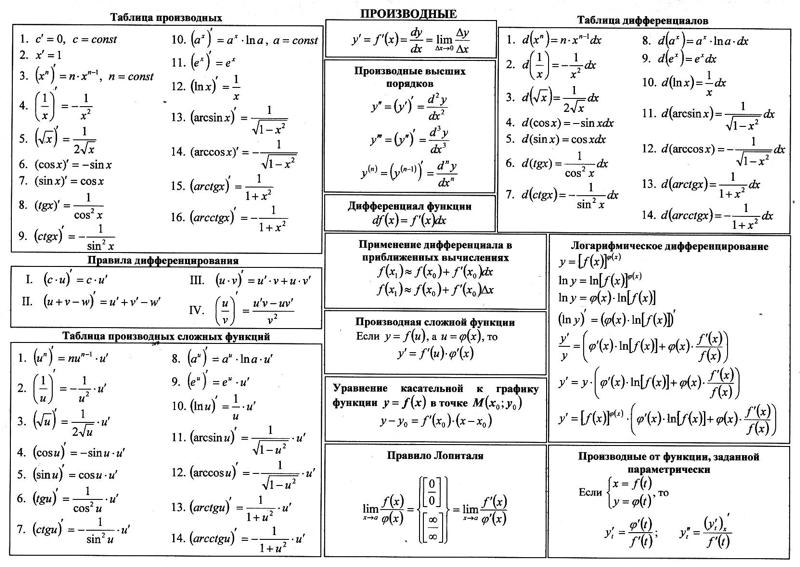 Это включает в себя расчет лимита. Вычислять производные таким образом — это искусство.
Это включает в себя расчет лимита. Вычислять производные таким образом — это искусство.
Как и в случае с любым другим навыком, вы совершенствуетесь только с практикой. Мы подробно говорим о том, как использовать определение на странице вычисления производной по определению.
Цепное правилоЦепное правило является наиболее важным правилом для получения деривативов. С его помощью вы сможете найти производную практически любой функции.
Чтобы узнать о цепном правиле, перейдите на эту страницу: Цепное правило.
Правило произведенияПравило произведения позволяет находить производные функций, которые являются произведениями других функций. Это очень полезный метод, и одна из немногих формул, которые вы должны запомнить в математическом анализе.
Чтобы узнать о правиле продукта, перейдите на эту страницу: Правило продукта.
Частное правило Частное правило — это частный случай правила произведения, поэтому вам не нужно запоминать другую формулу. Я покажу вам метод решения производных от частных с помощью правила произведения.
Я покажу вам метод решения производных от частных с помощью правила произведения.
Чтобы узнать об этом методе, перейдите на эту страницу: Правило частного.
Неявное дифференцированиеНеявное дифференцирование позволяет находить производные функций, выраженных забавным образом, которые мы называем неявными. Ключ в понимании цепного правила.
Чтобы узнать о неявной дифференциации, перейдите на эту страницу: Неявная дифференциация.
Основные формулы
Производная тригонометрических функцийЧтобы начать накапливать знания о производных, нам понадобятся некоторые формулы. Двумя основными являются производные тригонометрических функций sin(x) и cos(x). Сначала нам нужно найти эти две производные, используя определение.
Имея их в своем наборе инструментов, вы можете решать производные с использованием тригонометрических функций, используя другие инструменты, такие как цепное правило или правило произведения.
Чтобы узнать о производных тригонометрических функций, перейдите на эту страницу: Производные тригонометрических функций.
Производная экспоненциальной функцииДобавим еще одну функцию в список тех, от которых мы умеем брать производную. Это действительно полезно и красиво. Чтобы узнать о производной экспоненциальной функции, перейдите на эту страницу.
Производная логарифмовДобавим в наш список еще одну формулу, снова используя определение производной. Результат довольно удивительный.
Чтобы узнать о производной натурального логарифма, перейдите на эту страницу: Производная от ln(x).
Производная обратных триггерных функцийЗдесь мы узнаем о производной arcsin(x), arccos(x) и других. Эти формулы довольно сложно запомнить, поэтому полезно знать, как доказать их самому себе. Перейти на эту страницу: производная обратных триггерных функций.
Другие часто задаваемые формулы Есть некоторые формулы для производных, которые мне очень часто задают. Это:
Это:
- Производная от tan(x): не так хорошо известна, как производные от sin(x) и cos(x). Для его вычисления воспользуемся правилом отношения.
- Производная обратной функции: Как вообще найти производную обратной функции?
- Производная интеграла: вам нужно знать об интегралах, прежде чем увидеть это. Этот вопрос возникает всегда, и на этой странице мы неплохо развеиваем все сомнения.
И я думаю, что это суммирует основные методы решения производных. Если у вас есть какой-либо другой трюк или важный момент, который я, возможно, упустил, оставьте мне комментарий ниже, и мы сможем это обсудить.
Производные шести триггерных функций — Криста Кинг Математика
Шесть тригонометрических функций и их производные
Мы узнали об основных правилах производных, включая цепное правило, и теперь хотим обратить внимание на производные определенных видов функций.
В этом разделе мы рассмотрим производные тригонометрических функций, а позже мы рассмотрим производные экспоненциальных и логарифмических функций.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Тригонометрические производные
Существует шесть основных тригонометрических функций, и мы должны знать производную каждой из них.
Когда мы различаем триггерную функцию, мы всегда должны применять цепное правило. Например, в ???y=\sin{x}???, ???\sin??? и ???х??? , а не , перемноженные вместе. Вместо ???x??? является аргументом функции синуса. Для нас это означает, что аргумент всегда является «внутренней функцией», поэтому при дифференцировании нам всегда нужно умножать на производную от аргумента.
Для этих шести основных триггерных функций аргумент равен ???x???, а производная ???x??? равно ???1???, поэтому применяя цепное правило и умножая на ???1??? не меняет значения производной.
Но когда производная аргумента отличается от ???1???, то применение цепного правила, конечно же, окажет фактическое влияние на значение производной.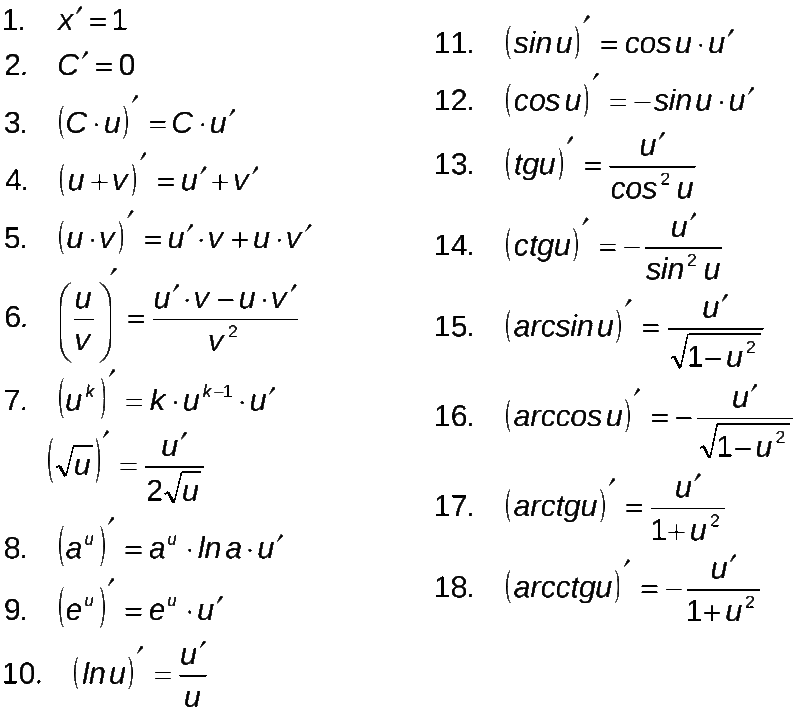

 Рассмотрим машину, которая
ездит по городу. Иногда стоит, иногда едет, иногда тормозит, иногда
разгоняется.
Рассмотрим машину, которая
ездит по городу. Иногда стоит, иногда едет, иногда тормозит, иногда
разгоняется.