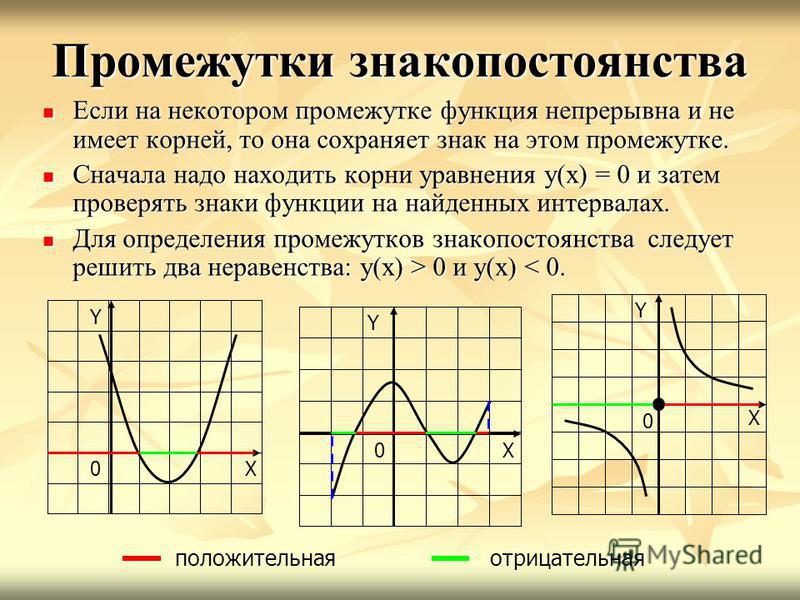
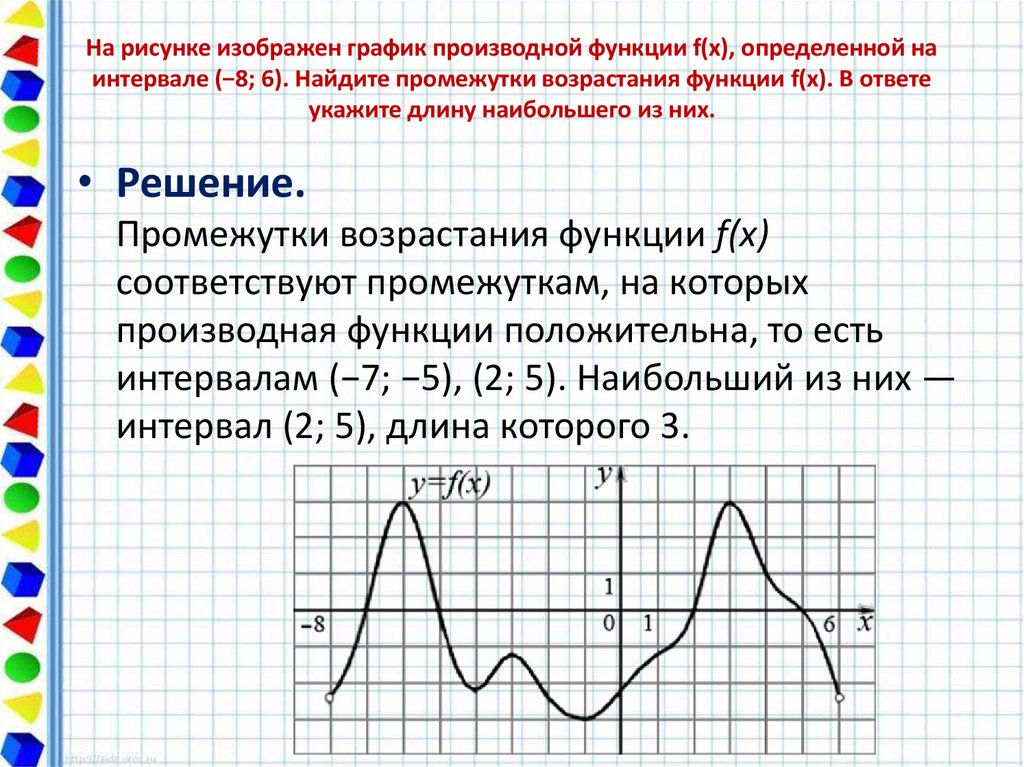
5.4. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.
Ответ: 4 5.5. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ: – 19 5.6. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ:
14
5.7. На рисунке изображен график
производной функции
,
определенной на интервале .
Найдите промежутки убывания функции
. В ответе укажите длину наибольшего из
них.
В ответе укажите длину наибольшего из
них.
Ответ: 6 5.8. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки убывания функции . В ответе укажите длину наибольшего из них.
Ответ: 3
5.9. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки убывания функции . В ответе укажите длину наибольшего из них.
Ответ: 3
5.10. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки убывания функции . В ответе укажите длину наибольшего из них.
Ответ: 4
5.
Ответ: 23
5.12. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки убывания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ: 1
5.13. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки убывания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ: – 18
6.1. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
Ответ: 0,75
6.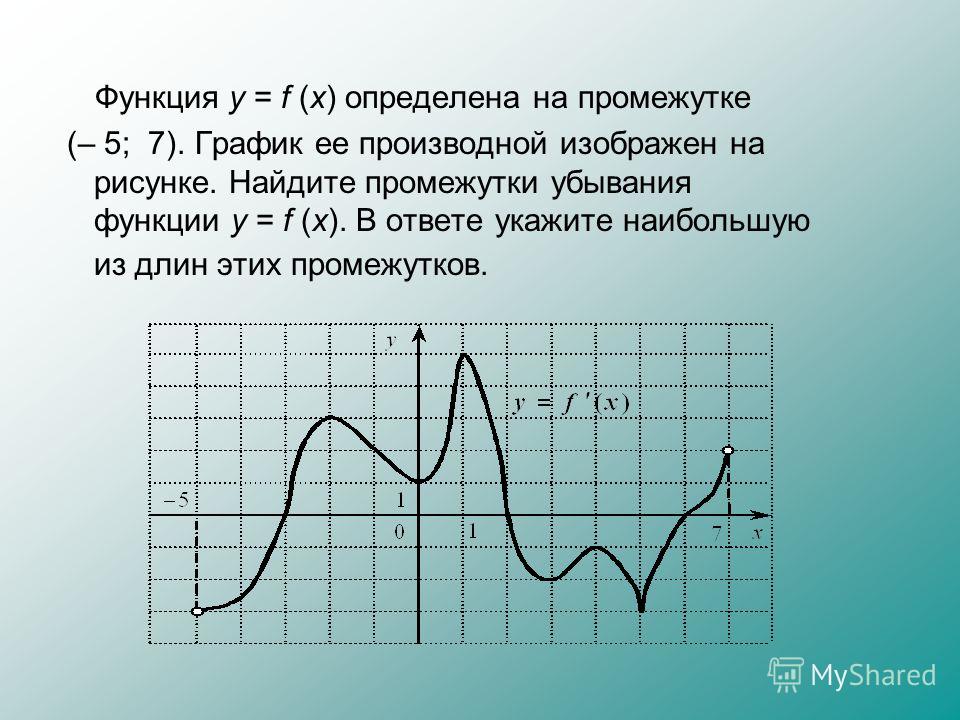 2.
На рисунке изображён график функции
и
касательная к нему в точке с абсциссой
.
Найдите значение производной функции
в
точке
.
2.
На рисунке изображён график функции
и
касательная к нему в точке с абсциссой
.
Найдите значение производной функции
в
точке
.
Ответ: 0,25
6.3. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
Ответ: 0,25
6.4. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
Ответ: 0,5
6.5. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
Ответ: – 0,25
6. 6.
На рисунке изображён график функции
и
касательная к нему в точке с абсциссой
.
Найдите значение производной функции
в
точке
.
6.
На рисунке изображён график функции
и
касательная к нему в точке с абсциссой
.
Найдите значение производной функции
в
точке
.
Ответ: – 0,25
6.7. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
Ответ: – 0,25
6.8. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
Ответ: – 0,5
7.1. Прямая является касательной к графику функции . Найдите абсциссу точки касания. Ответ: 0
7. 2.
Прямая параллельна
касательной к графику функции .
Найдите абсциссу точки касания.
Ответ: 0,5
2.
Прямая параллельна
касательной к графику функции .
Найдите абсциссу точки касания.
Ответ: 0,5
7.3. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания. Ответ: 4,5
7.4. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания. Ответ: – 0,5
14
Преобразование функции. Промежутки возрастания и убывания – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
С помощью операций преобразования графики некоторой функции \(y=f(x)\) можно превратить в график значительно более сложной функции без никаких вычислений. К операциям преобразования относятся:
- параллельный перенос осей координат;
- смена масштабов по осям координат;
- смена ориентации осей координат;
- преобразование абсолютных величин на графике.

| Преобразование | Описание | Рисунок |
|---|---|---|
\(y = f (x + c)\), c – число |
В случае \(c > 0\) график функции \(y = f (x)\) переносится влево на расстояние \(| c |\) |
|
|
В случае \(c < 0\) график функции \(y = f (x)\) переносится вправо на расстояние \(| c |\) |
||
|
\(y = f (x) + c\), c – число |
В случае \(c > 0\) график функции \(y = f (x)\) переносится вверх на расстояние \(| c |\) |
|
|
В случае \(c < 0\) график функции \(y = f (x)\) переносится вниз на расстояние \(| c |\) |
||
|
\(y = – f (x)\) |
График функции \(y = f (x)\) симметрично отражается относительно оси \(Ox\) |
|
|
\(y = f ( – x)\) |
График функции \(y = f (x)\) симметрично отражается относительно оси \(Oy\) |
|
|
\(y = f (kx)\), k – число |
В случае \(k > 1\) происходит сжатие графика функции \(y = f (x)\) в \(k\) раз к оси \(Oy\) |
|
|
В случае \(0 < k < 1\) происходит растяжение графика функции \(y = f (x)\) в \(\frac1{k}\) раз от оси \(Oy\) |
||
|
В случае \(– 1 < k <0\) происходит растяжение графика функции \(y = f (x)\) в \(\frac1{|k|}\) раз от оси \(Oy\) c последующим симметричным отражением графика относительно оси \(Oy\) |
||
|
В случае \(k < – 1\) происходит сжатие графика функции \(y = f (x) \ в \ | k |\) раз к оси \(Oy\) с последующим симметричным отражением графика относительно оси \(Oy\) |
||
|
\(y = k f (x)\), k – число |
В случае \(k > 1\) происходит растяжение графика функции \(y = f (x) \ в\ k\) раз от оси \(Ox\) |
|
|
В случае \(0 < k < 1\) происходит сжатие графика функции \(y = f (x) \ в \ \frac1{k}\) раз к оси \(Ox\) |
||
|
В случае \(– 1 < k < 0\) происходит сжатие графика функции \(y = f (x) \ в \ \frac1{|k|}\) раз к оси \(Ox\) с последующим симметричным отражением графика относительно оси \(Ox\) |
||
|
В случае \(k < – 1\) происходит растяжение графика функции \(y = f (x) \ в\ | k |\) раз от оси \(Ox\) с последующим симметричным отражением графика относительно оси \(Ox\) |
||
|
\(y = | f (x)|\) |
Часть графика функции \(y = f (x)\), расположенная в области \(y\ge0\), остается на месте. |
|
|
\(y = f (| x|)\) |
Ось \(Oy\) является осью симметрии графика функции \(y = f (| x|)\). Часть графика функции \(y = f (x)\), расположенная в области \(x\ge0\), остается на месте. Часть графика функции \(y = f (| x|)\), расположенная в области \(x < 0\), получается из части графика, расположенной в области \(x\ge 0\) при помощи симметричного отражения относительно оси \(Oy\) |
Функции, у которых имеет место убывание или возрастание на некотором числовом промежутке, называются монотонными функциями.
Возрастание функции. Функция называется возрастающей на интервале \([a;b]\), принадлежащем области определения функции, если большим значениям независимой переменной из этого интервала соответствуют большие значения функции, т. е. если \(x_2>x_1 \Rightarrow f(x_2)>f(x_1)\) для всех \(x_1\ и \ x_2\), принадлежащих интервалу.
е. если \(x_2>x_1 \Rightarrow f(x_2)>f(x_1)\) для всех \(x_1\ и \ x_2\), принадлежащих интервалу.
Убывание функции. Функция называется убывающей на интервале \([a;b]\), если большим значениям независимой переменной из этого интервала соответствуют меньшие значения функции, т. е. если \(x_2>x_1 \Rightarrow f(x_2)\) для всех \(x_1 \ и \ x_2\), принадлежащих интервалу.(x_1)\)
Теорема 1. Если во всех точках некоторого промежутка \(f'(x)=0\), то функция \(f(x)\) сохраняет в этом промежутке постоянное значение.
Этот промежуток может быть замкнутым или открытым, конечным или бесконечным.
Теорема 2 (достаточный признак возрастания). Если во всех точках некоторого промежутка \(f'(x)>0\), то функция \(f(x)\) возрастает в этом промежутке.
Теорема 3 (достаточный признак убывания). Если во всех точках некоторого промежутка \(f'(x)<0\), то \(f(x)\) убывает на этом промежутке.
Замечание. Условия теорем 2 и 3 не являются в полной мере необходимыми. Их можно несколько ослабить, а именно считать, что \(f'(x)\ge0\) или \(f'(x)\le0\), так как заключения теорем остаются справедливыми и тогда, когда производная обращается в нуль в конечном множестве точек.
Условия теорем 2 и 3 не являются в полной мере необходимыми. Их можно несколько ослабить, а именно считать, что \(f'(x)\ge0\) или \(f'(x)\le0\), так как заключения теорем остаются справедливыми и тогда, когда производная обращается в нуль в конечном множестве точек.
образование — функция интервалов возрастания и убывания по триггерной функции
спросил
Изменено 1 год, 10 месяцев назад
Просмотрено 280 раз
$\begingroup$
Мне трудно найти интервалы, где функция: 92 — 4x + 7 Cos[x] увеличивается и уменьшается с помощью mathematica. Я попытался использовать FindRoot , но это не слишком точно, потому что кривая имеет точки перегиба за пределами одних нулей.
Я сделал это до сих пор, что неправильно. Я пытаюсь найти, где он увеличивается и уменьшается на интервале $[-4,4]$
- образование
$\endgroup$
3
$\begingroup$
92 — 4x + 7 Cos[x] , вы можете найти все корни h' в интервале $[-4,4]$ с
Solve[h'[x] == 0 && -4 <= х <= 4, х]
Однако вы можете получить интервалы, в которых ч увеличивается и уменьшается непосредственно как неравенства с Уменьшить :
увеличение = Уменьшить[h'[x] > 0 && -4 <= x <= 4, x] уменьшение = уменьшение [h'[x] < 0 && -4 <= x <= 4, x]
Вы также можете обобщить за пределы интервала $[-4,4]$:
allincreasing = Уменьшить[h'[x] > 0, x] alldecreasing = Уменьшить[h'[x] < 0, x]
Если вам нужны числовые формы корней, просто введите N , например.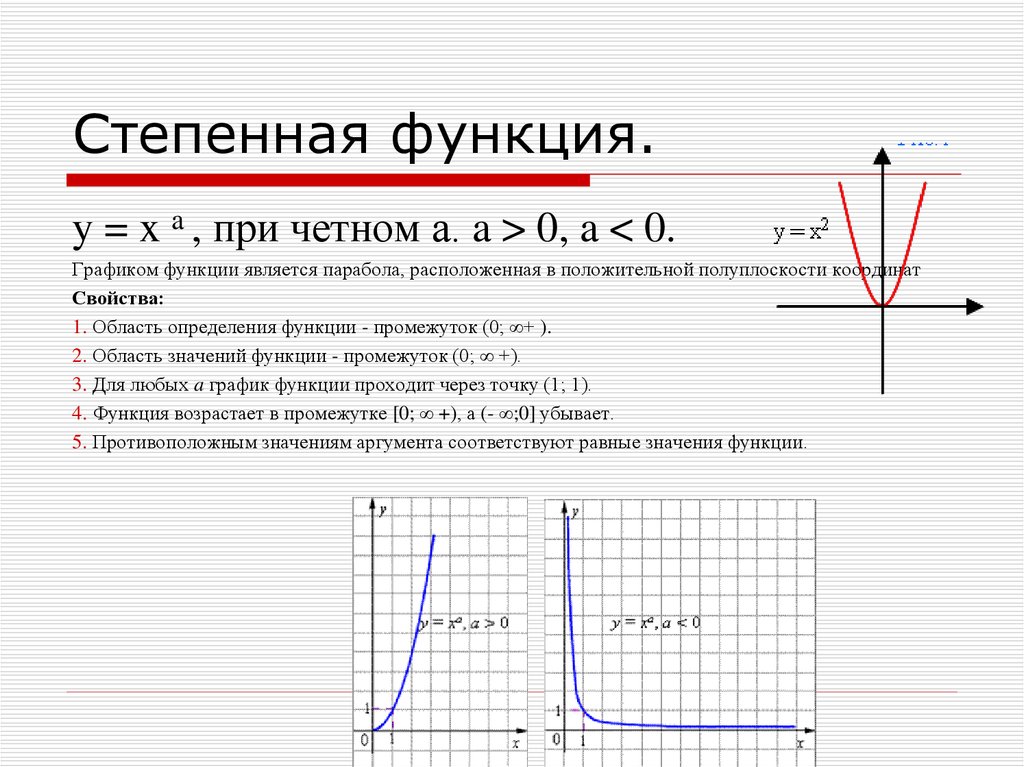
Н при увеличении .
$\endgroup$
3
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
открытых или закрытых интервалов? Это зависит – The Math Doctors
(Архивный вопрос недели)
Студенты обычно ожидают, что все учебники говорят об одном и том же (на самом деле, некоторые думают, что они могут спросить нас о «Теореме 6.2», и мы узнаем, что они говорят). о чем речь!). Реальность такова, что они могут даже давать противоречивые определения, в зависимости от точки зрения, с которой они подходят к теме. Здесь я хочу показать, как и почему они различаются, говоря об интервалах, на которых функция возрастает или убывает. Посмотрим, сможем ли мы разрешить «драку».
В этом углу… он должен быть открыт
Эта страница в нашем архиве фактически содержит два из трех ответов на вопрос в нашем архиве, причем второй является вызовом первому. Начнем с вопроса Бижана 2009 года, на который ответил доктор Минтер:
Конечные точки интервалов, где функция возрастает или убывает.Почему некоторые книги по математическому анализу включают концы при определении интервалов, в которых график функции возрастает или убывает при 3+12x\),
мы видим, что он увеличивается от -2 до +2. Но должны ли мы описать это как открытый интервал \(\left(-2,2\right)\) или как замкнутый интервал \(\left[-2,2\right] \)? Разные учебники дают разные ответы.
Доктор Минтер начал:
Вы задали отличный вопрос, и я согласен, что расхождения между различными учебниками вводят в заблуждение. Я полностью согласен с вашим утверждением, что интервалы должны быть открытыми (то есть не должны включать конечные точки). Позвольте мне попытаться дать исчерпывающее обоснование того, почему это должно быть. Мы используем производные, чтобы решить, является ли функция возрастающей и/или убывающей на заданном интервале. Интервалы, где производная положительна, предполагают, что функция возрастает на этом интервале, а интервалы, где производная отрицательна, предполагают, что функция на этом интервале убывает.
Далее он объясняет, что для того, чтобы производная была положительной в точке, она должна существовать там, поэтому функция должна быть определенной , возрастающей и дифференцируемой , в некотором интервале вокруг этой точки. Таким образом, он заключает:
Таким образом, чтобы функция возрастала (все эти концепции аналогичны и для убывающих интервалов), мы должны быть в состоянии показать, что функция больше для больших значений «x» и меньше для меньших значений «x» в небольшой окрестности вокруг каждой точки интервала. Конечная точка не может иметь оба этих свойства.Важно отметить, что и вопрос, и ответ исходят из перспективы исчисления и зависят от определения «возрастания» в терминах производной.
В том углу … его можно закрыть
Но это не только способ определить «возрастание на интервале»!
Еще в 1997 году доктор Джерри ответил на аналогичный вопрос, касающийся правил АП-исчисления:
Скобки или скобки? Мы обсуждали проблему на моем уроке Advanced Placement Calculus.Это касается функций возрастания/убывания, а также вогнутости вверх/вогнутости вниз. ... При выражении этих ответов в виде интервала, должен ли я использовать скобку, символизирующую, что конечная точка включена или скобка, символизирующая, что конечная точка не включена ?
Доктор Джерри ответил (частично):
В разных книгах, учителях и математиках используются немного разные определения возрастающих функций, но это не имеет большого значения, если одно из них последовательно. Предположим, что ваше определение возрастающей функции таково: f возрастает на интервале I, если для каждой пары точек p и q в I, если p < q, то f(p) < f(q) 92. Многие инструкторы, книги и даже экзамены AP часто не учитывают конечные точки. Если вы хотите быть сверхбезопасным, вы можете сделать вышеуказанный анализ. Это просто требует нескольких дополнительных шагов, обычно простых, помимо стандартного теста.Обратите внимание, что здесь вопрос и ответ все еще находятся в контексте исчисления, но доктор Джерри определяет «возрастание» без исчисления , а затем применяет теорему , которая связывает это определение с производной: Если производная положительна на интервале, затем функция возрастает на этом интервале.
Эта теорема ничего не говорит нам об интервалах, в которых производная иногда равна нулю, поэтому мы должны прибегнуть к определению, а не к теореме. И заключает, что его функция возрастает на полуинтервале \(\left[0,\infty\right)\).
Пожать друг другу руки и вступить в бой
Кажется, здесь есть разница во мнениях! Мы должны собрать их вместе и сравнить.
В 2014 году Кевин прочитал ответ доктора Минтера и задал ему вопрос:
Доктор Минтер привел аргумент, почему конечные точки *не* следует включать при определении интервалов, в которых функция возрастает или убывает. В вашем ответе подразумевается, что « увеличивается в точке » означает «имеет положительную производную в окрестности этой точки». Интересно, имеет ли смысл определять возрастание в точке. Меня также интересует другое определение, которое я придумал (которое, я признаю, не работает в определенном смысле). Мы можем определить 9(1/3) везде возрастает). Я также думаю о кусочных функциях со скачками; опять же, кажется, что мы должны быть в состоянии сказать, что они увеличиваются, даже если производная существует не везде.С этим вторым определением мне кажется, что если функция возрастает на (a, b) и непрерывна в точках a и b, то она гарантированно будет возрастать на [a, b]. Что вы думаете? Нужно ли нам по какой-то причине иметь определение «возрастания в точке»? Есть ли способ примирить эти два определения? Здесь, похоже, нет единого мнения. Это базовая концепция исчисления, и кажется, что есть два (очень убедительных) взгляда на нее, которые противоречат друг другу.
Это был очень проницательный вопрос. Как и предположил Кевин, здесь действительно две разные концепции. Концепция увеличения 90 112 на интервале 90 113 не требует вычислений и применима к недифференцируемым функциям. Концепция увеличения 90 112 в точке 90 113 требует исчисления, и часто авторы книг по исчислению действительно говорят об этом; В этом смысле доктор Минтер понял, что «возрастание на интервале» означает «возрастание в каждой точке интервала». [Доктор Фентон в неархивированном ответе 2007 года упомянул, что «увеличение в точке» можно определить как « f ( a ) больше любого f ( x ) для x слева от a , а f ( a ) меньше 3 f a .
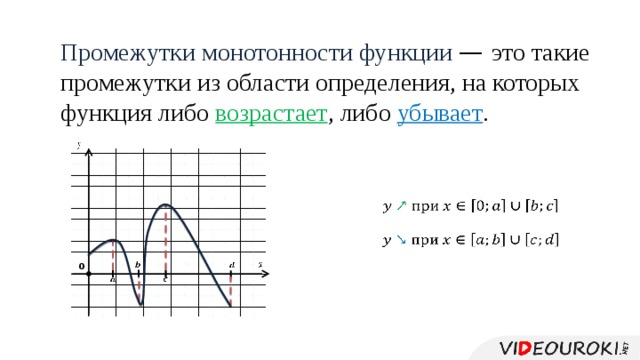
(1/3) равна растет повсюду, включая происхождение x = 0, несмотря на то, что производная на тот момент не определено. 9{3}\), увеличивается везде, хотя в начале координат оно (на мгновение) горизонтально:
Раздельное решение
Я также прокомментировал последний абзац Кевина о консенсусе:
На самом деле есть два разных понятия: концепция предварительного исчисления , применимая к любой функции; и концепция исчисления , применимая к дифференцируемым функциям. Я бы предпочел не путать их. Несмотря на то, что мы различаем равномерную и точечную непрерывность, эти понятия возрастания можно было бы лучше различать следующим образом: * Функция f равна увеличивается на интервале [0, 1], что означает, что при сравнении любых двух точек та, что справа, выше. * Функция f возрастает в раз в каждой точке интервала (0, 1), что означает, что производная везде положительна.Затем я процитировал разговор 2013 года, в котором поднималась эта тема, в котором я сослался на ответы доктора Минтера и доктора Джерри.
Вопрос там (в разгар долгой дискуссии с Аакаршем) еще больше усилил конфликт:
У меня есть y = f(x). На оси x расположены точки a, b и c. Когда х = а, у = 0; когда х = b, у = 4; когда х = с, у = 1. Я понимаю, что функция увеличивается на [a, b] . Я также понимаю, что функция уменьшается на [b, c] . Но почему буква б в скобках? Я знаю, что они указывают на закрытые интервалы; это не проблема. Если график увеличивается от точки a к точке b, то есть [a, b], но тогда график *ДОЛЖЕН* уменьшаться на (b, c]. Если увеличивается ДО "b", то уменьшается ОТ "b"... КРОМЕ "b"?Ого! Может ли функция возрастать и убывать в одной и той же точке? Если нет, то как бы вы решили, какой? (Обратите внимание, что Аакарша научили использовать закрытые интервалы, и он принял это.) Сначала я уточнил вопрос:
Я предполагаю, что вам дали такой график:Я думаю, вы спрашиваете, почему они включают конечные точки в интервалы. Это странно, потому что у нас были другие вопросы о том, почему конечные точки НИКОГДА не включаются в интервал увеличения или уменьшения! Разные тексты имеют разную политику в этом отношении.Как ваш текст ОПРЕДЕЛЯЕТ «возрастание на интервале»? Можете ли вы показать мне первый пример, который они приводят? См. эти страницы, которые подчеркивают эту изменчивость текстов: Скобки или скобки? http://mathforum.org/library/drmath/view/53566.html Конечные точки интервалов, где функция возрастает или уменьшение http://mathforum.org/library/drmath/view/73202.html Я склонен больше согласиться с первым из них, чем со вторым; но я думаю, что в предварительном исчислении было бы неплохо игнорировать эту деталь и либо всегда использовать открытые интервалы, либо всегда использовать закрытые интервалы. Это не очень важный вопрос; но ваше беспокойство о том, что функция не может возрастать и уменьшаться в одной и той же точке, склонит меня в сторону использования открытых интервалов, чтобы не сбить с толку таких студентов, как вы! На самом деле, однако, вы должны заметить, что ваше определение, вероятно, касается только увеличения или уменьшения В ИНТЕРВАЛЕ, а не В ТОЧКЕ. То есть они не говорят, что функция возрастает в точке b, а только говорят, что она возрастает в интервале [a, b].
Так не утверждается, что функция одновременно возрастает и убывает в точке b! Как только я увижу определение вашей книги, я смогу прояснить его.
Пока я продолжал писать Кевину,
Этот студент так и не ответил определением своего текста, поэтому я не смог обсудить с ним детали. Одной из таких деталей было бы различие между утверждением, что функция возрастает на интервале , и утверждением, что это максимальный интервал , в том смысле, что не существует содержащего интервала (открытого или закрытого), на котором она возрастает. . По моему опыту, в текстах многое остается невысказанным. Хотя эти упущенные детали могут упростить задачу для менее зрелого ученика, их стоит изучить с таким любопытным и способным человеком, как вы!Насколько я понимаю, когда учебник (особенно на уровне предварительного исчисления) запрашивает « интервал, на котором f возрастает», он не запрашивает какой-либо такой интервал, а наибольший .
В идеале это было бы так; но часто они будут полагаться на наш инстинкт, чтобы дать «лучший» ответ из возможных — точно так же, когда нас спрашивают, какой формы квадрат, мы не говорим «прямоугольник», а даем наиболее точный ответ, который подходит. Если они определили «возрастание», как я, то закрытый интервал является правильным ответом. Но есть место для разногласий, особенно среди студентов, которые мыслят более неформально.
В некоторых текстах, чтобы избежать путаницы с конечными точками, будет указано, что они запрашивают наибольший открытый интервал, на котором функция увеличивается. Я думаю, что это лучшее решение на этом уровне. На более высоком уровне, где важна точность определений, просто сформулируйте свое определение и действуйте в соответствии с ним.
Обработка различий
Случилось так, что за два месяца до того, как Кевин написал, кто-то еще написал о той же проблеме, предлагая добавить к ответу доктора Минтера некоторую информацию о причинах разных ответов.
Вопрос Кевина дал повод сделать именно это. В переписке с Кеном по поводу его предложения я сказал следующее:
Я согласен с вами по поводу разных определений. Это то, что я часто подчеркиваю в своих ответах; и это также объяснение того, что на нашем сайте есть ответы, которые не совпадают. Мне нравится отсылать «пациентов» к прошлым ответам, отчасти чтобы показать им, что на одну и ту же проблему можно смотреть с разных точек зрения. Я также признаю, что каждый ответ имеет свой собственный контекст, отвечая на вопрос конкретного учащегося либо в свете уровня этого учащегося, либо, возможно, в личном контексте этого доктора математики. Наша цель, как правило, не в том, чтобы дать всесторонний обзор темы, охватывающий все возможные варианты, а в том, чтобы показать разнообразие отдельных взаимодействий. Ни один ответ не будет охватывать все, что я хотел бы, чтобы он сделал (даже если это тот, который я написал сам пару лет назад). Поэтому я просто пишу еще один и ссылаюсь на старый(ые).


 Часть графика функции \(y = f (x)\), расположенная в области \(y < 0\), симметрично отражается относительно оси \(Ox\)
Часть графика функции \(y = f (x)\), расположенная в области \(y < 0\), симметрично отражается относительно оси \(Ox\) Почему некоторые книги по математическому анализу включают концы при определении интервалов, в которых график функции возрастает или убывает при 3+12x\),
Почему некоторые книги по математическому анализу включают концы при определении интервалов, в которых график функции возрастает или убывает при 3+12x\), 
 Это касается функций возрастания/убывания, а также вогнутости вверх/вогнутости вниз. ...
При выражении этих ответов в виде интервала, должен ли я использовать скобку, символизирующую, что конечная точка включена или скобка, символизирующая, что конечная точка не включена ?
Это касается функций возрастания/убывания, а также вогнутости вверх/вогнутости вниз. ...
При выражении этих ответов в виде интервала, должен ли я использовать скобку, символизирующую, что конечная точка включена или скобка, символизирующая, что конечная точка не включена ?  Эта теорема ничего не говорит нам об интервалах, в которых производная иногда равна нулю, поэтому мы должны прибегнуть к определению, а не к теореме. И заключает, что его функция возрастает на полуинтервале \(\left[0,\infty\right)\).
Эта теорема ничего не говорит нам об интервалах, в которых производная иногда равна нулю, поэтому мы должны прибегнуть к определению, а не к теореме. И заключает, что его функция возрастает на полуинтервале \(\left[0,\infty\right)\). С этим вторым определением мне кажется, что если функция возрастает на (a, b) и непрерывна в точках a и b, то она гарантированно будет возрастать на [a, b].
Что вы думаете? Нужно ли нам по какой-то причине иметь определение «возрастания в точке»? Есть ли способ примирить эти два определения?
Здесь, похоже, нет единого мнения. Это базовая концепция исчисления, и кажется, что есть два (очень убедительных) взгляда на нее, которые противоречат друг другу.
С этим вторым определением мне кажется, что если функция возрастает на (a, b) и непрерывна в точках a и b, то она гарантированно будет возрастать на [a, b].
Что вы думаете? Нужно ли нам по какой-то причине иметь определение «возрастания в точке»? Есть ли способ примирить эти два определения?
Здесь, похоже, нет единого мнения. Это базовая концепция исчисления, и кажется, что есть два (очень убедительных) взгляда на нее, которые противоречат друг другу.  (1/3) равна
растет повсюду, включая происхождение
x = 0, несмотря на то, что производная
на тот момент не определено. 9{3}\), увеличивается везде, хотя в начале координат оно (на мгновение) горизонтально:
(1/3) равна
растет повсюду, включая происхождение
x = 0, несмотря на то, что производная
на тот момент не определено. 9{3}\), увеличивается везде, хотя в начале координат оно (на мгновение) горизонтально: Вопрос там (в разгар долгой дискуссии с Аакаршем) еще больше усилил конфликт:
Вопрос там (в разгар долгой дискуссии с Аакаршем) еще больше усилил конфликт: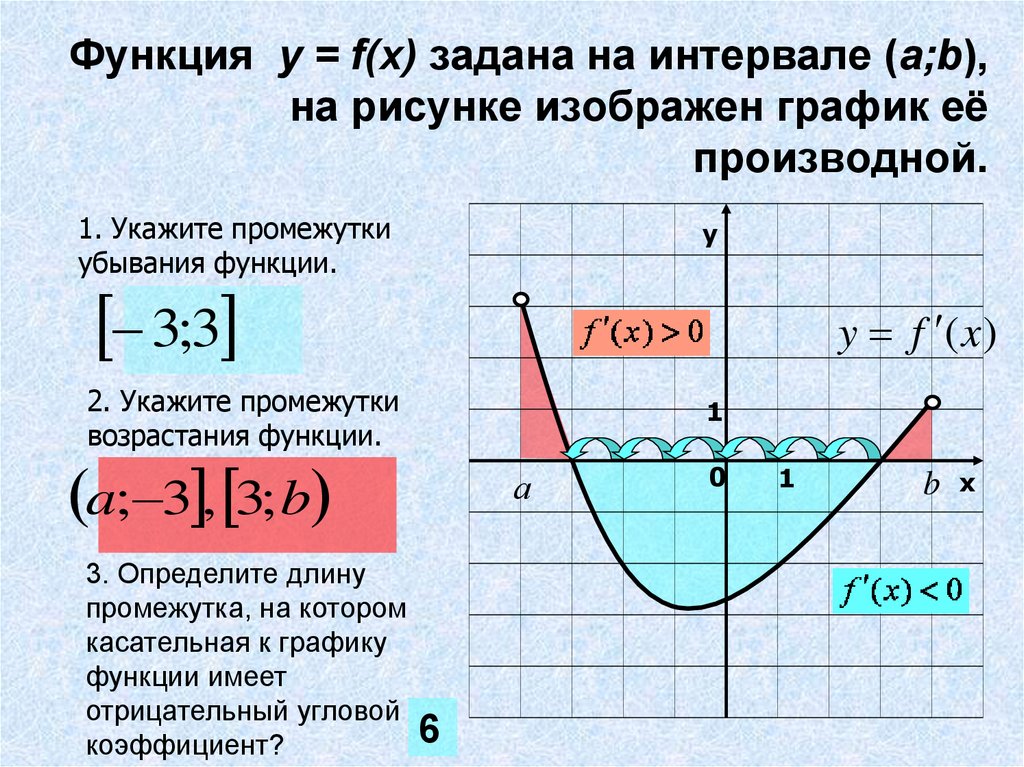 Как ваш текст ОПРЕДЕЛЯЕТ «возрастание на интервале»? Можете ли вы показать мне первый пример, который они приводят?
См. эти страницы, которые подчеркивают эту изменчивость текстов:
Скобки или скобки?
http://mathforum.org/library/drmath/view/53566.html
Конечные точки интервалов, где функция возрастает
или уменьшение
http://mathforum.org/library/drmath/view/73202.html
Я склонен больше согласиться с первым из них, чем со вторым; но я думаю, что в предварительном исчислении было бы неплохо игнорировать эту деталь и либо всегда использовать открытые интервалы, либо всегда использовать закрытые интервалы. Это не очень важный вопрос; но ваше беспокойство о том, что функция не может возрастать и уменьшаться в одной и той же точке, склонит меня в сторону использования открытых интервалов, чтобы не сбить с толку таких студентов, как вы!
На самом деле, однако, вы должны заметить, что ваше определение, вероятно, касается только увеличения или уменьшения В ИНТЕРВАЛЕ, а не В ТОЧКЕ. То есть они не говорят, что функция возрастает в точке b, а только говорят, что она возрастает в интервале [a, b].
Как ваш текст ОПРЕДЕЛЯЕТ «возрастание на интервале»? Можете ли вы показать мне первый пример, который они приводят?
См. эти страницы, которые подчеркивают эту изменчивость текстов:
Скобки или скобки?
http://mathforum.org/library/drmath/view/53566.html
Конечные точки интервалов, где функция возрастает
или уменьшение
http://mathforum.org/library/drmath/view/73202.html
Я склонен больше согласиться с первым из них, чем со вторым; но я думаю, что в предварительном исчислении было бы неплохо игнорировать эту деталь и либо всегда использовать открытые интервалы, либо всегда использовать закрытые интервалы. Это не очень важный вопрос; но ваше беспокойство о том, что функция не может возрастать и уменьшаться в одной и той же точке, склонит меня в сторону использования открытых интервалов, чтобы не сбить с толку таких студентов, как вы!
На самом деле, однако, вы должны заметить, что ваше определение, вероятно, касается только увеличения или уменьшения В ИНТЕРВАЛЕ, а не В ТОЧКЕ. То есть они не говорят, что функция возрастает в точке b, а только говорят, что она возрастает в интервале [a, b]. Так не утверждается, что функция одновременно возрастает и убывает в точке b!
Как только я увижу определение вашей книги, я смогу прояснить его.
Так не утверждается, что функция одновременно возрастает и убывает в точке b!
Как только я увижу определение вашей книги, я смогу прояснить его. 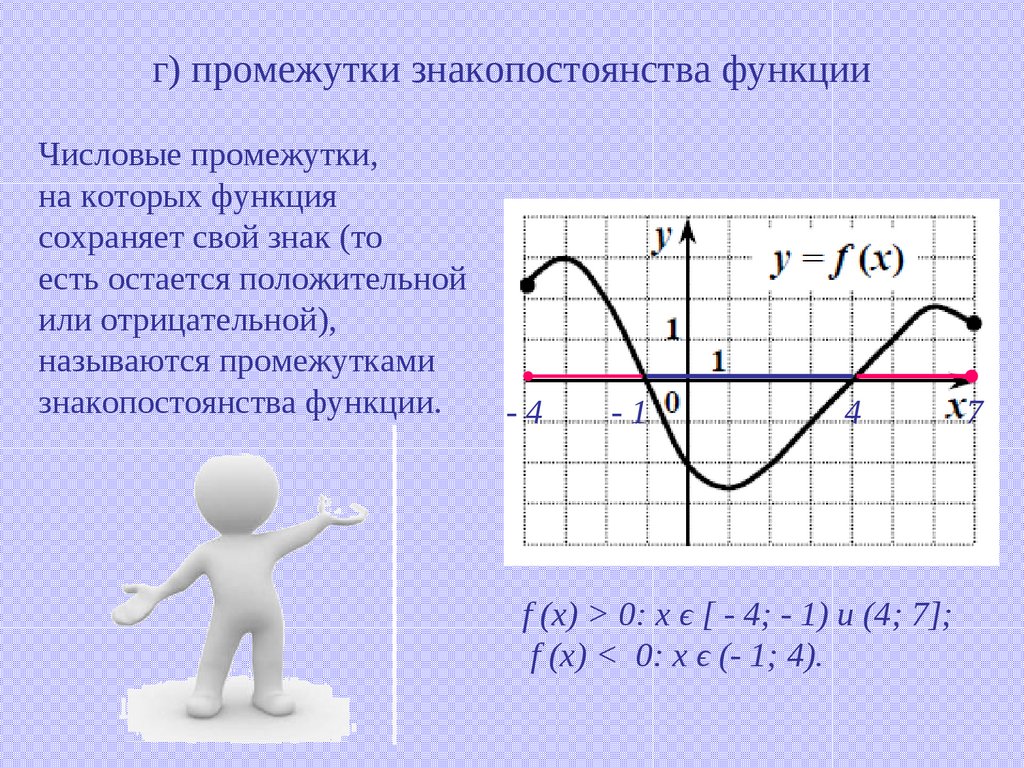 В идеале это было бы так; но часто они будут полагаться на наш инстинкт, чтобы дать «лучший» ответ из возможных — точно так же, когда нас спрашивают, какой формы квадрат, мы не говорим «прямоугольник», а даем наиболее точный ответ, который подходит. Если они определили «возрастание», как я, то закрытый интервал является правильным ответом. Но есть место для разногласий, особенно среди студентов, которые мыслят более неформально.
В идеале это было бы так; но часто они будут полагаться на наш инстинкт, чтобы дать «лучший» ответ из возможных — точно так же, когда нас спрашивают, какой формы квадрат, мы не говорим «прямоугольник», а даем наиболее точный ответ, который подходит. Если они определили «возрастание», как я, то закрытый интервал является правильным ответом. Но есть место для разногласий, особенно среди студентов, которые мыслят более неформально. Вопрос Кевина дал повод сделать именно это. В переписке с Кеном по поводу его предложения я сказал следующее:
Вопрос Кевина дал повод сделать именно это. В переписке с Кеном по поводу его предложения я сказал следующее: