Пропорцию как вычислить: 6 способов посчитать проценты от суммы с калькулятором и без

Содержание

§ Задачи на пропорции. Как решить пропорцию

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную

Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое
Чётные и нечётные функции

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Что есть лучшего? — Сравнив прошедшее, свести его с настоящим.

Козьма Прутков

на главную

Введите тему

Поддержать сайт

Пропорции Задачи на пропорции

Запомните!

По трём известным членам пропорции всегда можно найти её неизвестный (четвёртый) член.

Решить пропорцию — значит, найти все её члены. Решим пропорцию ниже
(найдём «x»).

Чтобы найти «x», используем основное свойство пропорции (правило «креста»).

Теперь мы готовы разбираться, как решать задачи на пропорции.

Часто задачи на пропорции тесно связаны с процентами. Свои знания о процентах, вы можете освежить в разделе «Проценты».

Разбор примера

Из лука сделано 50 выстрелов. 5 стрел пролетело мимо мишени. Определите процент попадания.

По традиции подчёркнем важные и числовые данные в задаче.

Обратите внимание, что нам нужно определить процент попаданий, а не процент пролетевших мимо стрел.

Поэтому вначале посчитаем, сколько стрел попало в цель. Сделать это не составит труда.

50 − 5 = 45 (стрел) — попало в цель.

Далее для решения задачи составим таблицу, куда занесём все данные. Запомните, что напротив 100% в таблице обычно пишется общее количество чего-либо. Неизвестные проценты обозначим буквой x.

	Стрелы	Проценты
Всего выпущено	50	100 %
Попало в цель	45	x %

Чтобы правильно записывать нужные данные в таблицу, запомните простое правило.

Запомните!

Одинаковые наименования нужно записывать друг под другом. Проценты записываем под процентами, килограммы под килограммами и т.д.

Теперь, используя таблицу, составим нужную пропорцию и решим её с помощью правила «креста».

Ответ: 90% — процент попадания в мишень.

Пропорции Задачи на пропорции

Задачи на пропорции, площади, теорема Пифагора

Когда мы с Вами производим расчет ремонта квартиры по количеству затрачиваемых материалов или по стоимости, то в любом случае, пользуемся математическими формулами. Полезно кое-что вспомнить из школьного курса, например, как рассчитать периметр или площадь комнаты, и как быть, если Вам предстоит ремонт круглого зала?

СОДЕРЖАНИЕ:

Как вычислить пропорцию
Как рассчитать площадь комнаты
- Прямоугольная комната
- Прямоугольная комната с кладовкой
- Круглый зал
Как определить расстояния через стены

Перейти к калькулятору

Давайте обозначим, с чем мы столкнемся в первую очередь, когда будем производить расчет ремонта квартиры.

Как вычислить пропорцию при подготовке цементных растворов

Это, пожалуй, самая распространенная математическая операция при ведении ремонтных работ. Когда нужно разводить водой сухую строительную смесь, будь-то цемент, ремсостав, штукатурка или шпаклевка (в статье Как шпаклевать стены в квартире наглядно демонстрируется эта необходимость), вычисление пропорции становится просто незаменимым:

Задача:

На 30 кг сухой смеси требуется 18 литров воды. Сколько воды нужно для разведения 4 кг сухой смеси?

Решение:

30 кг — 18 литров

4 кг — Х литров

Х=18*4/30=2,4 литра.

Ответ:

На 4 кг сухой смеси потребуется 2,4 литра воды.

Как рассчитать площадь комнаты

Комнаты бывают разные, но в основном — это прямоугольная комната, в которой может размещаться прямоугольная кладовка (очень типично для хрущевок).

Прямоугольная комната

Когда Вы покупаете паркет или кафель для своего будущего пола, то продавец обязательно спросит Вас, а на какую площадь Вам нужно? В этом случае Вы, естественно, должны уметь вычислять площадь своей комнаты или кухни. В подавляющем большинстве случаев все помещения имеют прямоугольную форму. Поэтому, если Вы возьмете рулетку и отмерите по длине комнаты: 5,5 метров, а по ширине 3,6 метров, то

Общая площадь=5,5*3,6 = 19,8 квадратных метров.

Прямоугольная комната с кладовкой

А если в прямоугольной комнате 19,8 квадратных метра стоит кладовка, которая отнимает часть площади, как рассчитать площадь помещения в этом случае? Тогда нужно замерить две стороны кладовки по длине и ширине, например это будет 70 см и 60 см (или 0,7 метра и 0,6 метра). Далее вычислить площадь кладовки: Площадь = 0,7*0,6=0,42 квадратных метра. А затем из общей площади комнаты вычесть площадь кладовки.

Общая площадь без кладовки = 19,8 — 0,42 = 19,38 квадратных метров.

Как видите, все достаточно просто.

Круглый зал

А если у Вас круглый зал? Тогда нужно встать в центр зала, отмерить расстояние от центра до стены, например это будет: 4 метра — это радиус Вашего зала. Площадь будет = 3,14*радиус*радиус.

Площадь круглого зала = 3,14*4*4 = 50,24 квадратных метров.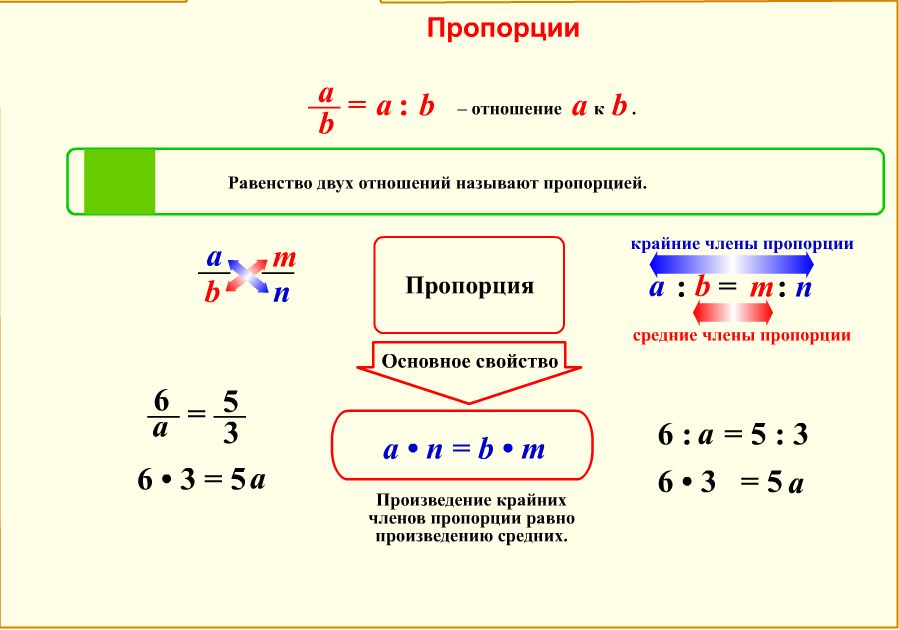

Как определить расстояния через стены

А вот еще один интересный пример, зачем нужна математика на практике. Есть мнение, что если на лестничной площадке или коридоре расположен электрощит, то ближайшая кровать в квартире не должна быть ближе чем 5 метров к этому электрощиту, иначе это считается вредным для здоровья.

На картинке, представленной ниже, родители ребенка озабочены установкой детской кроватки в детской комнате.

Как можно через стены определить 5 здесь метров или больше или меньше?

На помощь опять же приходит наша любимая математика, а конкретнее теорема Пифагора, которая гласит:

Квадрат гипотенузы равен сумме квадратов катетов

Что это нам дает? А вот что.

Перерисуем нашу картинку чуть-чуть по другому. Электорощит, детская кроватка и коридоры образуют четко выраженный прямоугольный треугольник, у которого есть 2 катета и одна гипотенуза:

Обозначим у этого треугольника стороны: А, В, С.

Стороны А и В можно легко померить рулеткой. Предположим, сторона А=50 см (0,5 метра), а сторона B=4 метра. Вот формула теоремы Пифагора, которую мы применим для расчета расстояния сквозь стены:

Подставляем данные в формулу и получаем:

C=4,03 метра.

Получается, что 4,03 < 5 метров, и детскую кроватку ставить у этой стены нежелательно! Таким образом, нужно сделать перепланировку комнаты.

На этом все. Сегодня мы узнали как при помощи применить школьную математику, когда необходимо выполнить расчет ремонта квартиры. Напишите, какие еще научные знания Вы применяли, когда делали ремонт.

Перейти к калькулятору по ремонту

Перейдите по ссылке на калькулятор для производства расчетов:

Калькулятор

Как вычислять соотношения и пропорции в математике

Обновлено 12 февраля 2020 г.

Кевин Бек

Понятие пропорции вам, вероятно, знакомо, но вы, возможно, не сможете написать для него строгое математическое определение. Например, вы можете признать, что 10-летний ребенок меньше взрослого человека нормального роста точно так же, как тот же взрослый меньше профессионального баскетболиста, хотя эти три размера различаются.

Точно так же вы, вероятно, знакомы с понятием соотношения . Например, если вы участвуете в спортивном соревновании и знаете, что соотношение фанатов-противников к дружественным болельщикам велико, вы можете быть склонны быть менее демонстративным, когда ваш любимый клуб забивает гол, чем если бы это соотношение было обратным.

В математике и статистике существует множество вопросов о пропорциях, процентах и соотношениях. К счастью, краткого объяснения основных понятий и нескольких примеров должно быть достаточно, чтобы сделать вас пропорционально лучшим учеником по математике.

Соотношения и пропорции

Соотношение — это дробь или два числа, выраженные в виде частного, например 3/4 или 179/2385. Но это особый вид дроби, который используется для сравнения связанных величин. Например, если в комнате 11 мальчиков и 13 девочек, соотношение мальчиков и девочек составляет 11 к 13, что может быть записано как 11/13 или 11:13.

Ratio в переводе с латинского означает «причина». Определение рационального числа — это число, которое может быть выражено в виде дроби; некоторые числа, такие как значение π в геометрии, иррациональны и не могут быть выражены таким образом, вместо этого они представляются бесконечным десятичным числом. Возможно, математики древности находили такое положение «неразумным».

Пропорция — это просто выражение, устанавливающее два равных друг другу отношения, используя разные абсолютные числа в дробях. Пропорции записываются как отношения, например, a/b = c/d или a:b = c:d.

Как решать пропорции

Для решения большинства простых задач на пропорции вам не нужна причудливая функция калькулятора пропорций. Например, предположим, что вы ходите в спортзал 17 раз за 30-дневный месяц. Каково соотношение дней в спортзале и дней без спортзала в этом месяце?

Ответ , а не (тренажерные дни/всего дней), так что не соблазняйтесь, думая, что ответ будет 17:30. Вместо этого вычтите дни в спортзале из общего числа дней, чтобы получить дни без спортзала, требуемую вторую часть вашего соотношения. Таким образом, ответ 17:13 (или 17/13).

Как вычислить пропорцию

Иногда без каких-либо вычислений очевидно, что два отношения пропорциональны друг другу. Если вы и ваша собака — единственные два животных в комнате, и вам говорят, что в соседнем спортзале 457 человек и 457 собак, то вы знаете, что соотношение людей и собак одинаково в обоих помещениях.

Но как быть с коэффициентами, которые не так просто сравнить с первого взгляда? Например, пропорционально ли 17/52 3/9? Если нет, то что больше?

Один из способов сделать это — вычислить десятичные числа каждой дроби и посмотреть, какая из них больше. Но если вы понимаете пропорции, вы можете вместо этого использовать перекрестное умножение, умножая противоположные знаменатели и числители:

(17/52) =?= (3/9)

(17)(9) = 153; (3)(52) = 156

Таким образом, отношения не совсем равны (3/9немного больше), а дроби непропорциональны.

Что такое константа пропорциональности?

Константа пропорциональности представляет собой постоянную разницу между коэффициентами пропорциональности. Если a пропорционально b, то в выражении a = kb k есть константа пропорциональности. Две переменные a и b называются обратно пропорциональными , если их произведение ab является константой для всех a и b, то есть когда a = C/b и b = C/a.

Пример: Количество любителей стрельбы из лука пропорционально количеству любителей бейсбола в данной кофейне. Сначала есть 6 любителей стрельбы из лука и 9 любителей бейсбола. Если число любителей бейсбола увеличится до 24, сколько должно быть любителей стрельбы из лука?

Найдите k, где a = kb, a = 6 и b = 9:
k = 6/9 = 2/3 = 0,667

Теперь решите уравнение a = (0,667)(24), чтобы получить 16 выстрелов из лука фанаты в уже более переполненном кафе.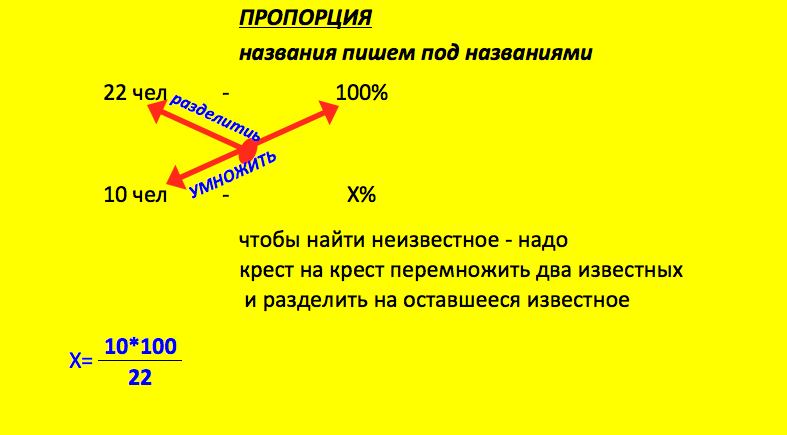

Как рассчитать процент как пропорцию в Excel

В этом руководстве мы обсудим как рассчитать проценты как пропорции в Excel .

В Excel вычислить процент просто. Это занимает всего несколько шагов и фокусируется на базовой арифметике.

В математике пропорция — это сравнение двух чисел. Так бывает, когда два отношения равны друг другу. Проще говоря, это доля или часть по сравнению или по отношению к целой группе или числу.

Процент является частью 100. Например, 50 из 0 из 100 или в процентном формате 50%. Итак, какова связь между процентом и пропорцией?

Во-первых, они оба относятся к части целого. Когда мы умножаем пропорцию на 100, мы получаем процент частей, которые были взяты из целого. Точно так же мы получаем пропорцию, умножая процент на целое.

Мы рассмотрим два способа расчета процентов как пропорций в Excel в зависимости от набора данных. Первый — это простое деление значения части или выборки на целое или общее значение. И второй использует СУММЕСЛИ функция.

Давайте рассмотрим сценарий, в котором вы должны вычислить процент как пропорцию в Excel.

Предположим, вы учитель, который хочет рассчитать процентную оценку результатов экзамена учащегося. Итак, вы хотите знать, каков процентный балл студента, набравшего 85 баллов из 100 на экзамене.

В этом примере вы можете получить процентное соотношение, разделив 85 на 100. Кроме того, вы можете быстро и легко выполнить эту задачу в Excel, особенно при работе с большими объемами данных.

Анатомия функции SUMIF

Синтаксис или способ писать функцию SUMIF следующим образом:

  = SUMIF (диапазон; возьмите каждый термин и поймите, что они означают:
  =  знак равенства - это то, как мы начинаем любое уравнение или функцию в Excel.
  СУММЕСЛИ()  — это наша функция  СУММЕСЛИ . Эта функция выполняет вычисление суммы диапазона на основе заданного условия.
  критерии  относятся к набору условий. Это может проверить, является ли значение больше, меньше или равно чему-то. В этом случае мы используем его для поиска конкретного продукта для расчета.
  sum_range  — необязательный аргумент. Это диапазон, в котором функция  СУММЕСЛИ  вычисляет сумму.
 Потрясающе! Давайте погрузимся в реальный пример расчета процента как пропорции в Excel.
  
  
 Реальный пример расчета процента как пропорции в Excel  Давайте посмотрим на наш образец данных. Например, мы хотим найти процент каждого заказанного продукта от общего количества заказанных продуктов.
  
 В этом случае у нас есть общее количество заказанных продуктов, что упрощает этот расчет. Формула для расчета процента как пропорции в Excel:  часть/всего = процент .
 По сути, нам нужно только разделить номер заказанного продукта на общее количество заказанных продуктов.
 Теперь давайте рассмотрим другую ситуацию. Например, мы хотим рассчитать процент как долю только определенных продуктов. В этом случае нам нужно знать только процент заказанных соков от общего количества заказанных продуктов.
  
 В этом случае мы будем использовать функцию  СУММЕСЛИ . Во-первых, нам нужно ввести критерии, которые в этом примере будут соком. Затем нам нужно выбрать ассортимент заказанной продукции. Наконец, разделите на общее количество заказанных товаров. И тада! Мы можем получить процент от заказанной продукции Juice.
 Вы можете сделать собственную копию приведенной выше электронной таблицы, используя ссылку, прикрепленную ниже.
  Сделайте копию примера электронной таблицы  
 Теперь давайте изучим пошаговый процесс выполнения этого расчета для применения в вашей работе.
  
  
 Как рассчитать процент в виде доли в Excel  В этом разделе обсуждаются шаги по вычислению процента в виде доли в Excel.
 1. Сначала введите знак равенства  = , чтобы начать расчет. Затем выберите ячейку, содержащую часть или пропорцию, которую вы хотите рассчитать. В данном случае мы выбираем  B2 . Наконец, разделите это на общее количество заказанных продуктов, которое находится в  B7 .
 Кроме того, мы вложим  B7 , чтобы превратить его в абсолютную ссылку на ячейку. Это блокирует его как наш знаменатель, когда мы перетаскиваем формулу вниз. Таким образом, вся формула будет   = B2/$B$7 9.0097  .
 2. Во-вторых, перетащите формулу с  B2  на весь столбец, чтобы применить ту же формулу.
 3. Далее нам нужно изменить результат с десятичного на процентный. Для этого перейдите в  Home  и щелкните раскрывающееся меню  Формат номера . Затем выберите  Percentage  .
 4. Если в процентах есть десятичные знаки, мы можем просто удалить это. Сначала выберите процентный столбец и щелкните правой кнопкой мыши. Затем нажмите на  Формат номера  .
 5. В окне  Числовой формат  перейдите в категорию  Процент . И измените  десятичных разряда  на ноль. Наконец, нажмите  OK , чтобы применить изменения.
 6. Теперь посчитаем процент только конкретных товаров. Во-первых, давайте создадим таблицу, в которую мы будем вводить результат. Укажите продукт, который вы используете, в данном случае это сок. Кроме того, мы будем использовать это как ссылку на ячейку.
 7. Далее введите ‘  =СУММЕСЛИ’  для запуска функции. Затем выберите диапазон, содержащий продукты  A11:A15  , и выберите ячейку, содержащую продукт, который вы ищете,  G10  . И это будет нашим критерием.
 Наконец, выберите диапазон, содержащий количество заказов ( B11:B15 ), и разделите все на общее количество заказанных продуктов. Таким образом, вся формула будет   =СУММЕСЛИ(A11:A15;G10;B11:B15)/$B$16   .
 8. Опять же, нам нужно изменить результат с десятичной точки на процентную. Поэтому щелкните правой кнопкой мыши десятичную дробь и выберите  Формат числа . Затем выберите категорию  Процент  и измените  Десятичные разряды  на ноль. Наконец, нажмите  OK , чтобы применить изменения.
 9. И тада! Мы успешно рассчитали процент как пропорцию в Excel.
  
 Отлично! Вот и все. Вы узнали, как рассчитать процент как пропорцию в Excel, используя основную формулу и  СУММЕСЛИ  функция. 
 Хотите узнать больше о возможностях Excel? Теперь вы можете использовать различные другие формулы Microsoft Excel, доступные для создания отличных рабочих листов, которые работают на вас. Не забудьте подписаться на нашу рассылку, чтобы первыми узнавать о последних руководствах и учебных пособиях от нас.
 Получайте от нас электронные письма о Google Таблицах. 
  Наша цель в этом году — создать множество содержательных и кратких руководств для таких пользователей Google Таблиц, как вы. Если вам понравился этот, вам понравится то, над чем мы работаем! Читатели получают ✨ ранний доступ ✨ к новому контенту.No related posts.