Проверка совместимости системы уравнений: Исследование систем линейных уравнений онлайн

Исследовать систему уравнений на совместимость.

Пример 1:

Исследуйте совместность системы линейных уравнений и в случае совместности найдите все её решения методом Гаусса.

Решение от преподавателя:

Исследуем эту систему по теореме Кронекера-Капелли. 
Выпишем расширенную и основную матрицы: 

2 1 -1 2 1 -1 2 1 3 0 1 3 x1 x2 x3

Здесь матрица А выделена жирным шрифтом.  
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. 
Умножим 1-ую строку на (-1). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой: 

0 -3 5 0 1 -1 2 1 3 0 1 3

Умножим 2-ую строку на (-3). Добавим 3-ую строку к 2-ой: 

0 -3 5 0 0 3 -5 0 3 0 1 3

Для удобства вычислений поменяем строки местами: 

0 -3 5 0 0 3 -5 0 3 0 1 3

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го. 

0 3 -5 0 3 0 1 3

Для удобства вычислений поменяем строки местами: 

0 3 -5 0 3 0 1 3

Определим ранг системы.  

0 3 -5 3 0 1

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно, rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной. 
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3 – свободные.  
Преобразуем матрицу, оставляя слева только базисный минор. 

0 3 0 5 3 0 3 -1

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид: 
3×2 = 5×3 
3×1 = 3 — x3 
Методом исключения неизвестных находим: 
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3, то есть нашли общее решение: 
x2 = 5/3×3 
x1 = 1 — 1/3×3 
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений.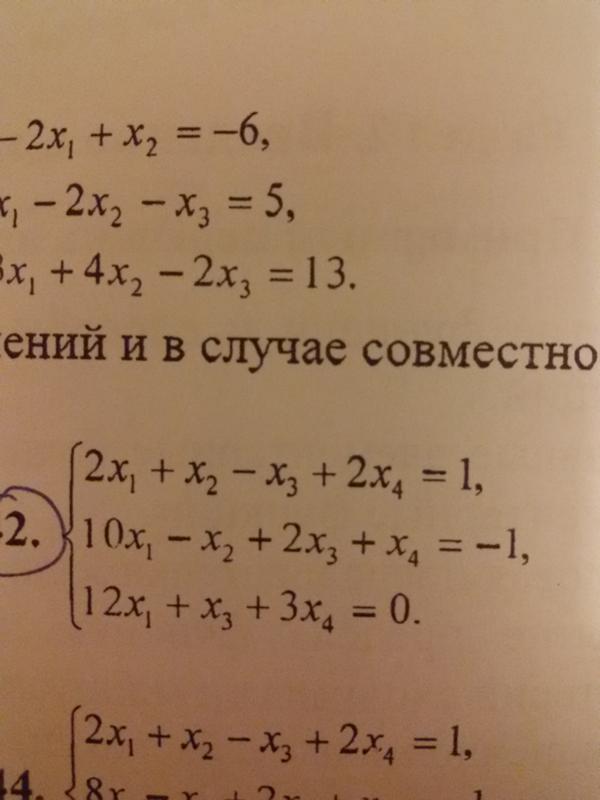 Система является неопределенной, т.к. имеет более одного решения. 

Пример 2:

Исследовать систему уравнений на совместность. В случае совместности найти общее решение методом Гаусса.

Решение от преподавателя:

Исследуем эту систему по теореме Кронекера-Капелли. 
Выпишем расширенную и основную матрицы: 

6 -2 -1 0 4 0 2 2 1 0 6 0 1 1 4 6 -4 -3 -1 4 x1 x2 x3 x4

Здесь матрица А выделена жирным шрифтом.  
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. 
Для удобства вычислений поменяем строки местами: 

0 2 2 1 0 6 -2 -1 0 4 6 0 1 1 4 6 -4 -3 -1 4

Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой: 

0 2 2 1 0 0 2 2 1 0 6 0 1 1 4 6 -4 -3 -1 4

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например, 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го. 

0 2 2 1 0 6 0 1 1 4 6 -4 -3 -1 4

Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой: 

0 2 2 1 0 0 -4 -4 -2 0 6 -4 -3 -1 4

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например, 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го. 

0 -4 -4 -2 0 6 -4 -3 -1 4

Определим ранг основной системы.

0 -4 -4 -2 6 -4 -3 -1

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля. Ранг этой системы равен rangA=2. 
Определим ранг расширенной системы. 

0 -4 -4 -2 0 6 -4 -3 -1 4

Ранг этой системы равен rangB=2. 
rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной. 
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃,x₄ – свободные.  
Преобразуем матрицу, оставляя слева только базисный минор. 

0 -4 0 4 2 6 -4 4 3 1

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид: 
— 4x₂ = 4x₃ + 2x₄ 
6x₁ — 4x₂ = 4 + 3x₃ + x₄ 
получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃,x₄, то есть нашли общее решение: 
x₂ = — x₃ — ¹/₂x₄ 
x₁ = ²/₃ — ¹/₆x₃ — ¹/₆x₄ 
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения. 

Работа вам нужна срочно. Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

• 22423 авторов готовы помочь тебе.
• 2402 онлайн

Условие совместности СЛАУ. Теорема Кронекера-Капелли

Установить, совместна ли система линейных уравнений, с помощью теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.

Теорема Кронекера-Капелли о совместности системы. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу её расширенной матрицы, то есть чтобы .

Здесь матрица A (матрица системы) — это матрица, составленная из коэффициентов при неизвестных:

В свою очередь матрица В (расширенная матрица) — это матрица, полученная присоединением к матрице системы столбца из свободных членов:

Ранги этих матриц связаны неравенством , при этом ранг матрицы

В может быть лишь на одну единицу больше ранга матрицы A.

Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.

• Если ранг матрицы равен числу неизвестных (), то система имеет единственное решение.
• Если ранг матрицы системы меньше числа неизвестных (), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.

Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть , то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен

m, так как ранг матрицы не может быть больше числа её строчек.

В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:

1) отыскать в матрице системы A ранга отличный от нуля минор порядка, равного рангу матрицы системы, то есть ранга r;

2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор ;

3) члены с коэффициентами, не входящими в , перенести в правую часть, а затем, придавая неизвестным, находящимся в правой части, произвольные значения, определить по формулам Крамера оставшиеся

r неизвестных из системы r уравнений с отличным от нуля определителем .

Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.

Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор

отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному придаём произвольное значение .

Оставшиеся неизвестные определяются из системы

Решая последнюю систему по формулам Крамера или иным способом, находим

,

,

.

Присоединяя сюда , получаем все решения данной системы линейных уравнений.

Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.

Решение. Вычисляем ранг матрицы этой системы:

.

Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:

.

Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:

Решая последнюю систему по формулам Крамера, находим

,

,

.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Системы линейных уравнений

Всё по теме «Системы уравнений и неравенств»

Решение систем линейных уравнений методом подстановки и методом сложения

Решение систем линейных уравнений методом Крамера

Решение систем линейных уравнений методом Гаусса

Решение систем линейных уравнений матричным методом (обратной матрицы)

Системы линейных неравенств и выпуклые множества точек

Начало темы «Линейная алгебра»

Определители

Матрицы

Поделиться с друзьями

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

• Биомедицинские и биологические науки.
• Бизнес и экономика
• Химия и материаловедение.
• Информатика. и общ.
• Науки о Земле и окружающей среде.
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные науки. и гуманитарные науки

Журналы по тематике  

• Биомедицина и науки о жизни
• Бизнес и экономика
• Химия и материаловедение
• Информатика и связь
• Науки о Земле и окружающей среде
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные и гуманитарные науки

Публикация у нас

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Публикуйте у нас  

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Недавно опубликованные статьи

Недавно опубликованные статьи

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Бесплатные информационные бюллетени SCIRP

Copyright © 2006-2023 Scientific Research Publishing Inc. Все права защищены.

Вершина

Система линейных уравнений и обращение матриц

Система линейных уравнений и обращение матриц

Этот учебный объект JavaScript E-labs предназначен для решения систем линейных уравнений до трех уравнений с тремя неизвестными. Это также позволяет нам найти обратную матрицу.

Другие учебные объекты JavaScript для принятия решений из этой серии относятся к различным областям применения в разделе МЕНЮ на этой странице.

Профессор Хоссейн Аршам    

---

При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab , а не клавиши со стрелками или клавиши ввода.

Инструкции и приложения:

1. Имена неизвестных переменных: X1, X2, X3,.. и X10, в зависимости от того, есть ли у вас одно уравнение, два уравнения или три уравнения с одной неизвестной, двумя неизвестными или тремя неизвестными переменными соответственно.
2. Начиная с левого верхнего угла, замените столько нулей в матрице данных коэффициентами неизвестных переменных в уравнениях вместе с их правыми значениями, сколько необходимо. Матрица коэффициентов должна представлять собой квадратную матрицу, расположенную в верхнем левом углу матрицы данных, поэтому не оставляйте пустых строк между ними.
3. JavaScript основан на операциях строки Gauss-Jordan (GJ). Требование для операций GJ состоит в том, что первый элемент в матрице коэффициентов должен быть ненулевым. Поэтому сначала введите коэффициент всех уравнений, имеющих ненулевой коэффициент X1; затем введите все остальные уравнения. То есть любое уравнение с нулевыми коэффициентами для X1 должно стоять в конце таблицы ввода данных.

   Численный пример 1. Рассмотрим следующую систему уравнений:

   Х2 + Х3 = 5
   3X1 + X3 = 6
   -Х1 + Х2 = 1
   

   Матрица коэффициентов переменных:

   0    1    1
   3    0    1
   -1    1    0
   

   Первая запись первого столбца равна нулю, хотя в нем всегда есть хотя бы один ненулевой элемент. Следовательно, мы должны перестроить систему уравнений таким образом, чтобы любое уравнение с нулевым коэффициентом X1 оказалось среди последнего набора уравнений. То есть, рассматривая эквивалентную систему уравнений:

   3X1 + X3 = 6
   -Х1 + Х2 = 1
   Х2 + Х3 = 5
   

   Решите эту эквивалентную систему уравнений, введя ее коэффициент и значения RHS в таблицу ввода данных, затем нажмите кнопку «Рассчитать». Выходом является решение: X1 = 1, X2 = 2 и X3 = 3, что можно проверить подстановками.

4. Нахождение обратной матрицы с помощью системы уравнений: Чтобы найти обратную квадратную матрицу размера n, решите n систем уравнений с единичным вектором в правой части. Следующий числовой пример иллюстрирует этот процесс:

   Численный пример 2. Предположим, мы хотим найти обратную (A ^-1 ) следующую матрицу (если она существует) A:

   		2	1
   А	=
   		1	-1

   В общем найти А ^-1 , столбец за столбцом, решить n систем уравнений, имеющих матрицу коэффициентов A, но с n различными векторами идентичности в качестве их правых значений.

   Для этого числового примера мы должны решить следующие две системы уравнений:

   2Х1 + Х1 = 1
   Х1 — Х2 = 0

   и

   2Х1 + Х1 = 0
   Х1 — Х2 = 1

   Обратите внимание, что коэффициенты переменных X1 и X2 являются матрицей A в обеих системах уравнений, однако RHS являются двумя единичными векторами в n = 2-мерном пространстве.

   Решения первой и второй систем уравнений в соответствии с вышеуказанной инструкцией дают первый и второй столбцы матрицы A ^-1 .

   Чтобы найти первый столбец A ^-1 , решите:

   2Х1 + Х1 = 1
   Х1 — Х2 = 0

   Это дает X1 = 1/3, X2 = 1/3. Чтобы найти второй столбец A ^-1 , решите:

   2Х1 + Х1 = 0
   Х1 — Х2 = 1

   Это дает X1 = 1/3, X2 = -2/3. Следовательно, A ^-1 p является

   		1/3	1/3
   А -1	=
   		1/3	-2/3

5. Примечание: Матрица, имеющая обратную, называется неособый или обратимый. Матрица называется вырожденной, если она не имеет обратной. Например, следующая матрица является сингулярной:

   1    6    4
   2    4   -1
   -1    2    5
   

   Поэтому при применении описанной выше процедуры обращения матрицы, если матрица вырожденная, то по крайней мере из систем уравнений не имеет решения.

6. Для редактирования ваших данных, включая добавление/изменение/удаление, вам не нужно нажимать на кнопку «очистить», а заново вводить свои данные заново. Вы можете просто добавить, изменить число на другое в той же ячейке или удалить число из ячейки, установив его значение равным нулю. После редактирования нажмите кнопку «Рассчитать».

   Это полезно, например. найти обратную матрицу A _10×10 , где мы должны изменить только значения RHS.

   Для расширенного редактирования или использования JavaScript для нового набора данных используйте кнопку «Очистить».

---

X1	Х2	X3	X4	Х5	Х6	Х7	Х8	Х9	x 10	RHS
Раствор Есть:
Х1	Х2	Х3	Х4	Х5	Х6	Х7	X8	Х9	Х10

 

---

Для получения технических сведений вернуться к:
Темы линейной алгебры

---

Пожалуйста, отправьте ваши комментарии по адресу:
Профессор Хоссейн Аршам

---

МЕНЮ

Инструменты принятия решений в экономике и финансах Классификация инвентаризации ABC Авторегрессионный временной ряд Бета и ковариационные вычисления Двумерные дискретные распределения Анализ безубыточности и прогнозирование Категории вероятностных и статистических инструментов Обнаружение тренда и автокреляции Определение выбросов Прогнозирование сглаживанием Модели управления запасами Решатели линейной оптимизации для загрузки Линейная оптимизация с чувствительностью Денежная математика: анализ сложных процентов Алгебра матриц и цепи Маркова Оценка среднего и дисперсии Измерение точности прогноза Другие полиномиальные регрессии Оптимальный возраст для замены Параметрическая система линейных уравнений Показатели эффективности для портфелей График временного ряда Прогнозы по регрессии Оценка доли Квадратичная регрессия Регрессионное моделирование Сезонный индекс Инвентаризационный анализ за один период Суммируйте свои данные Система уравнений и обращение матриц Испытание на случайные колебания Тест на сезонность Тест для стационарных временных рядов Статистика временных рядов Вероятностное моделирование Байесовский вывод для среднего Пересмотренная вероятность Байеса Двумерные дискретные распределения Сравнение двух случайных величин Принятие решений в условиях неопределенности Определение полезной функции Принятие рискованных решений Измерьте качество вашего решения Полиномиальные распределения Игры с нулевой суммой для двух человек

Статистика Ковариационный анализ Дисперсионный анализ для сжатых наборов данных Дисперсионный анализ для зависимых групп населения ANOVA: проверка средств Байесовский статистический вывод Статистика двумерной выборки Хи-квадрат Тест на родство Совместимость нескольких счетчиков Доверительные интервалы для двух совокупностей Описательная статистика Определение выбросов Эмпирическая функция распределения Равенство многовариантности Оценки с уверенностью Согласие для дискретных переменных Тестирование идентичных популяций Номера индексов с приложениями Тест К-С на равенство двух совокупностей Тест Лиллифорса для экспоненциального Множественные регрессии Процент: оценка и тестирование Тест парной пропорции Полиномиальные регрессии Объединение средних и отклонений P-значения для популярных дистрибутивов Квадратичная регрессия Определение объема выборки Пересмотр среднего значения и дисперсии Рассеянная диаграмма и выбросы Простая линейная регрессия Субъективная оценка оценок Субъективность при проверке гипотез Проверка нескольких коэффициентов корреляции Испытание на однородность совокупности Тест на нормальность Испытание на равномерное распределение Тестирование процесса Пуассона Тест на случайность Проверка нескольких пропорций Проверка среднего значения Тестирование медиан Проверка коэффициента корреляции Тестирование двух популяций Проверка дисперсии Тест «до и после» Другие средства Двухфакторный дисперсионный анализ Двухфакторный дисперсионный анализ с повторениями

---

Заявление об авторских правах.

No related posts.