Перпендикулярные прямые — определение, признаки, доказательства
Скорее всего, вы смогли бы отыскать три варианта:
Прямые параллельны друг другу;
Прямые совпадают, накладываются друг на друга;
Прямые пересекаются.
И были бы абсолютно правы! Интересно, что в пункте № 3 скрывается один интересный случай, который мы рассмотрим подробнее сегодня, а именно: прямые могут быть перпендикулярны друг другу.
Что это означает? Рассмотрим определение перпендикулярных прямых.
Основные определения
Перпендикулярные прямые — это прямые, которые пересекаются друг с другом под углом 90 градусов. Обозначение перпендикулярных прямых: а ┴ b.
Угол, равный 90 градусам, в математике называют прямым и помечают на чертеже квадратиком.
Еще один интересный факт из мира геометрии: если при пересечении двух прямых один из образовавшихся углов равен 90°, то и все остальные углы — прямые, а их сумма будет равна 360°.
Перпендикулярные отрезки — это отрезки, лежащие на перпендикулярных прямых.
Чтобы называться перпендикулярными, отрезкам не обязательно пересекаться самим. Достаточно, чтобы угол между прямыми, на которых они лежат, был равен 90°.
В качестве задачки со звездочкой давайте вспомним, в каких фигурах могут встречаться перпендикулярные отрезки (стороны)? Наверняка вы сразу назовете квадрат и прямоугольник, но также подходит прямоугольный треугольник и даже прямоугольная трапеция — с ней вы познакомитесь на уроках геометрии в 8-м классе.
Также перпендикулярно к стороне могут располагаться различные элементы внутри фигуры. Попробуйте расположить перпендикулярно друг другу диаметр и радиус окружности, две хорды, биссектрису угла треугольника (кстати, последнее задание получится выполнить только в случае, если проводить биссектрису угла к основанию равнобедренного треугольника).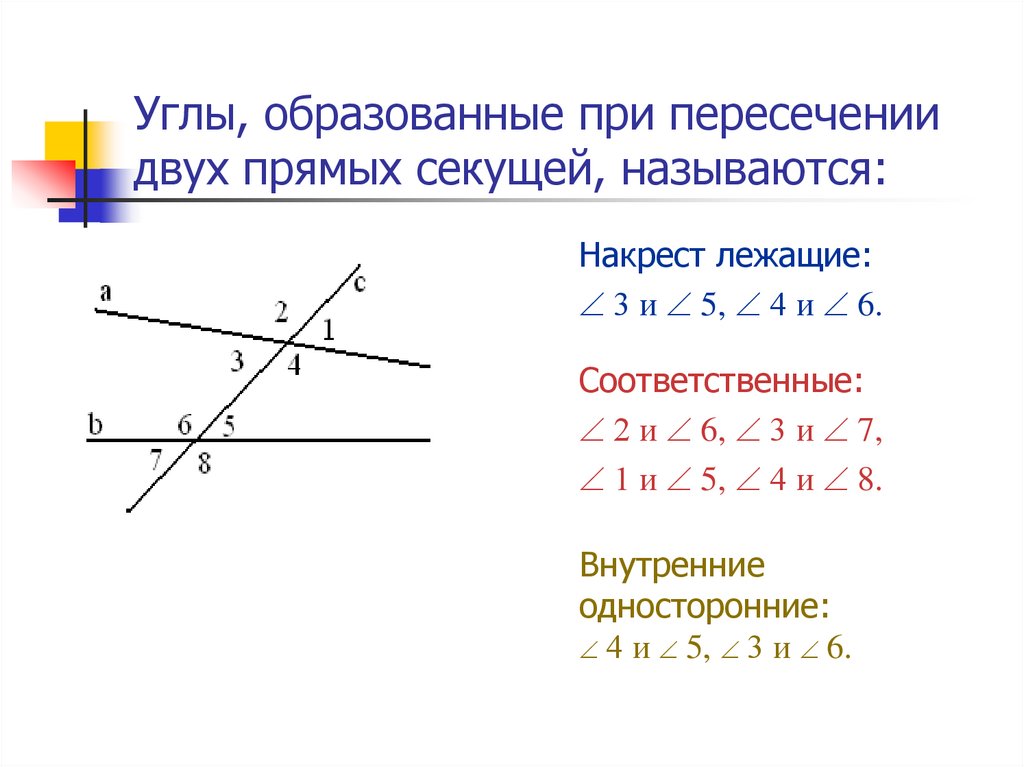
Как мы видим, прямые очень часто пересекаются под углом 90 градусов. Можно сказать, это своего рода обычное, будничное поведение прямых. Прямые углы окружают нас повсюду: в комнате, на оживленных улицах города, в бассейне и даже в любимой книге.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Способы построения перпендикулярных прямых
Но как можно построить перпендикулярные прямые? Что для этого может понадобиться? Давайте разберем все доступные нам способы.
Самый легкий — воспользоваться транспортиром. Построим прямую а и точку А, не лежащую на этой прямой. Совместим значение 90 градусов с точкой таким образом, чтобы нижняя часть транспортира в виде линейки полностью совпала с прямой, и сделаем засечку в отверстии транспортира. Соединим точку А с поставленной засечкой до пересечения с прямой.
Но что делать, если транспортир благополучно забыт дома и у нас есть только линейка и угольник? Внимательно рассмотрите рисунок и попрактикуйтесь в построении дома.
Теорема о перпендикулярных прямых и ее доказательство
Теорема о перпендикулярных прямых
Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.
«Кто это вообще придумал?», — можете возразить вы. «Почему мы должны этому верить? Вдруг все иначе, а нас обманывают». Если это так, то ваши опасения — показатель пытливости ума!
Что такое теорема? Это утверждение, нуждающееся в доказательстве. Это означает, что его не принимает на веру никто: ни вы, ни учитель, ни самый великий ученый. Есть много способов доказательства теорем, один из которых — метод от противного. Используя его, мы будто соглашаемся с противоположным заявлением и рассуждаем, что из этого последует.
Например, попробуем доказать утверждение «осенью грачи улетают на юг» методом от противного. Предположим, что грачи остаются зимовать в наших городах. Тогда мы должны видеть их осенью и зимой повсеместно, а в небе не должно быть видно признаков масштабного перелета. Так ли это на самом деле? Конечно же, нет.
Предположим, что грачи остаются зимовать в наших городах. Тогда мы должны видеть их осенью и зимой повсеместно, а в небе не должно быть видно признаков масштабного перелета. Так ли это на самом деле? Конечно же, нет.
Теперь с помощью этого метода попробуем доказать теорему о перпендикулярных прямых.
Предположим, что теорема ложна, а значит, через точку, лежащую на прямой, можно провести несколько перпендикулярных прямых.
Проверим гипотезу:
Возьмем линейку и проведем прямую а, отметив на ней точки С и D.
Далее построим перпендикулярную прямую из точки С. Угол КСD равен 90°.
Отрезок КС находится на прямой, перпендикулярной а.

Предположим, что есть еще одна прямая, перпендикулярная а. Проведем ее через точку С и отметим на ней точку L.
Тогда угол LCD равен 90° и угол КСD равен 90°.
Пункт номер 5 невозможен: от отрезка CD можно отложить только один прямой угол в данной плоскости.
А значит, через точку С можно провести только одну прямую, перпендикулярную прямой а.
Что и требовалось доказать: вы — молодцы!
Свойства перпендикулярных прямых
Перпендикулярные прямые обладают свойствами, которые можно использовать при решении геометрических задач.
Две прямые, перпендикулярные к третьей, не пересекаются
Конечно же, это свойство хорошо просматривается при построении. Но как мы уже выяснили, математики — народ сомневающийся, поэтому попробуем обосновать, почему это так.
Предположим, что прямые АА1 и ВВ1 все же пересекутся в точке К. Что бы это значило? Что мы совершили невероятное и опровергли теорему о перпендикулярных прямых! Ведь тогда получается, что через точку К проходит несколько перпендикулярных прямых, которые в свою очередь пересекают прямую а под углом 90 градусов! Как было сказано выше, это невозможно, а значит и прямые АА1
и ВВ1 не пересекаются.
Перпендикуляр, проведенный из точки к прямой, называется расстоянием от прямой до этой точки
Интересно, что такое расстояние является кратчайшим.
Представьте, что вам необходимо проложить путь от вас до огромного торгового центра, состоящего из множества магазинчиков. Вам не важно, в какой из них заглянуть, вы просто хотите потратить на дорогу как можно меньше времени. Какой путь вы выберете?
Конечно же, путь номер 2! Но есть ли этому научное объяснение?
Треугольник АВС прямоугольный, АВ и ВС— катеты, АС — гипотенуза. Согласно соответствию углов и сторон, в треугольнике наибольшая сторона лежит напротив наибольшего угла. Таким углом является прямой угол 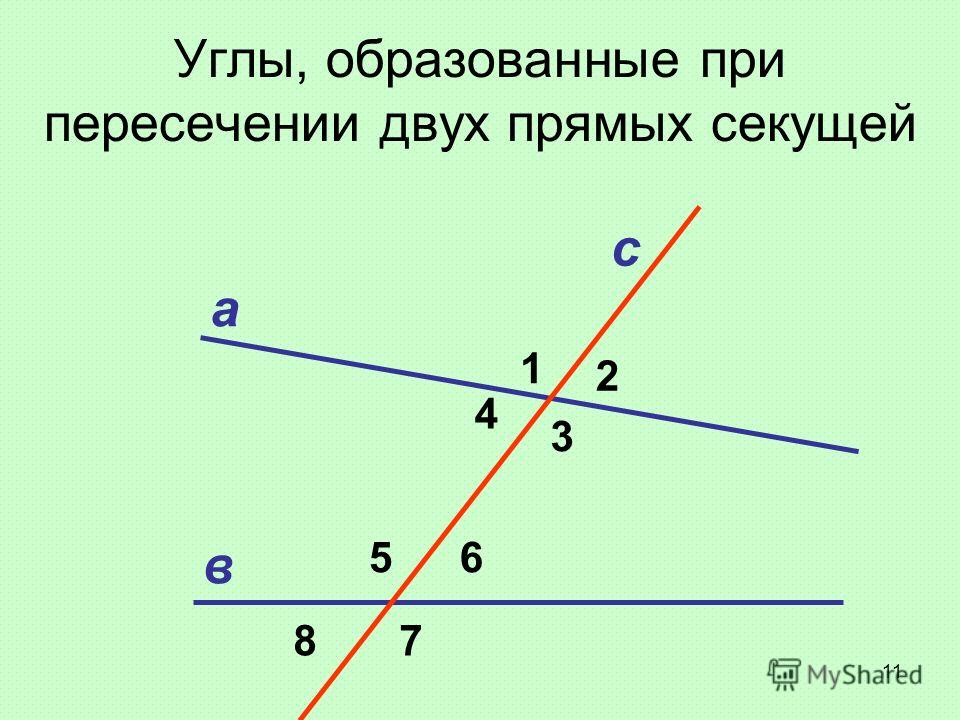 Под каким бы углом мы ни расположили гипотенузу, она всегда будет больше остальных сторон.
Под каким бы углом мы ни расположили гипотенузу, она всегда будет больше остальных сторон.
В задачах по геометрии часто просят найти расстояние между различными элементами: между двумя точками, между точкой и прямой, между двумя прямыми. Теперь вы знаете, что под расстоянием подразумевают перпендикуляр! Благодаря этому знанию вы избежите множества ошибок, ведь между двумя элементами можно провести бесконечное множество прямых (и кривых), но только один вариант будет верным.
Кстати, перпендикуляр, проведенный из вершины угла фигуры на прямую, содержащую противоположную сторону, известен под именем высота. С высотами связано множество теорем и свойств, которые вы будете изучать немного позже. В качестве интриги оставим вам пример того, где находится точка пересечения высот в треугольниках разного типа. Заметили что-то необычное?
Применение знания о перпендикулярных прямых
Напоследок ответим на вопрос, который мог возникнуть у некоторых из вас: «А как в древности люди решали вопрос с построением перпендикулярных прямых, прямых углов в частности? Были ли у них приспособления для этого?»
Построение прямых углов было важным умением даже в древности, так как от этого зависела крепость и устойчивость возведенных стен зданий, мостов, механизмов для строительства. Один лишний градус — и целый город мог оказаться в опасности из-за обрушившегося дворца или башни.
Один лишний градус — и целый город мог оказаться в опасности из-за обрушившегося дворца или башни.
Древние зодчие поняли, что возлагать все надежды на четырехугольники не стоит, потому что квадраты и прямоугольники легко превращаются в параллелограммы, меняя величину углов и оставляя неизменными длины сторон. Стоит только немного потянуть за «ушки» квадрата, как он начинает беспощадно ломать прямые углы, а ведь в условиях строительства многое может пойти не так и искривить конструкцию: ветер, изменение температуры, неточность мастера.
Хорошо, что есть более стабильная фигура — треугольник. Все дело в соотношении его сторон и углов, а еще в невозможности создать несколько треугольников из сторон заданной длины. Если у вас есть отрезки длиной 6, 8 и 10 сантиметров, из них можно составить только один треугольник. В случае, если одна сторона растянется под действием нагрузки или сожмется из-за понижения температуры — треугольник просто перестанет существовать.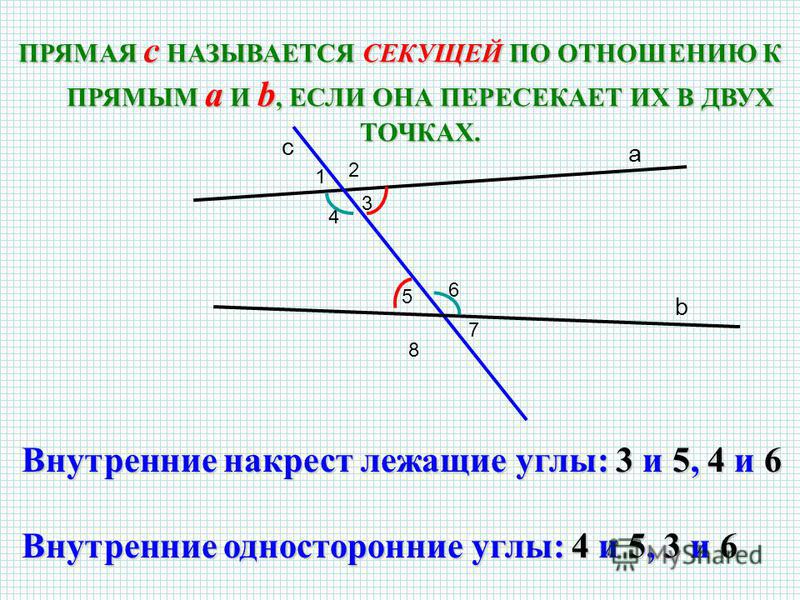
С этой точки зрения прямоугольные треугольники — лучшие друзья архитекторов, которые хотят строить ровные и красивые здания. Зодчие Древнего Египта использовали шнур или веревку, на которых через равные расстояния были завязаны 12 узлов. Строители натягивали такой шнур, создавая прямоугольный треугольник со сторонами 3, 4 и 5 единиц. Такой метод получения угла, равного 90 градусам, был сверхточным, а по сторонам-катетам-шнурам можно было выкладывать кирпичи или камни.
Удивлены? Еще больше поразительных фактов и, самое главное, помощь в понимании алгебры и геометрии вы получите на курсах профильной математики в онлайн-школе Skysmart. Секреты древних архитекторов, бытовые задачки и подготовка к экзаменам — все на удобной платформе с опытными учителями. Ждем вас!
Угол между пересекающимися прямыми: определение, примеры нахождения
Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.
В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.
Что такое угол между пересекающимися прямыми
Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.
Определение 1Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.
Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.
Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).
Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).
Взгляните на рисунок:
Перейдем к формулированию основного определения.
Определение 2Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые.
Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, то угол между ними в любом случае будет равен 90 градусам.
Как найти угол между пересекающимися прямыми на плоскости
Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.
Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.
Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.
Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.
У нас есть прямоугольная (декартова) система координат Oxy, в которой заданы две прямые. Обозначим их буквами a и b. Прямые при этом можно описать с помощью каких-либо уравнений. Исходные прямые имеют точку пересечения M. Как определить искомый угол (обозначим его α) между этими прямыми?
Начнем с формулировки основного принципа нахождения угла в заданных условиях.
Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор.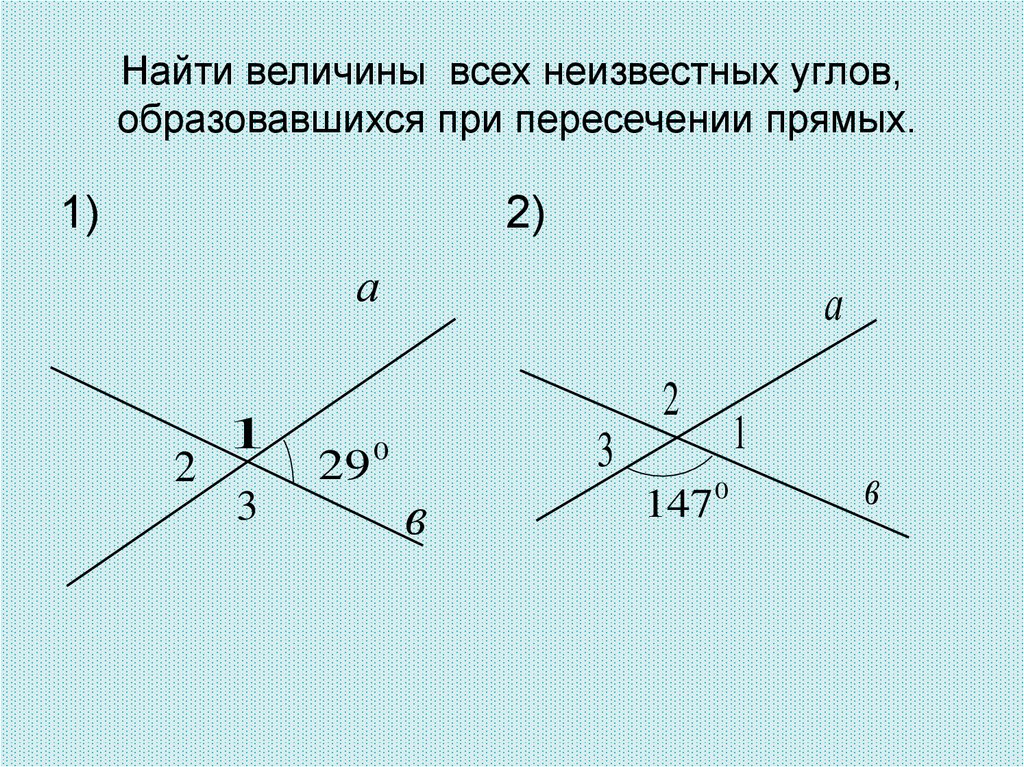 Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.
Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.
Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:
- угла между направляющими векторами;
- угла между нормальными векторами;
- угла между нормальным вектором одной прямой и направляющим вектором другой.
Теперь рассмотрим каждый способ отдельно.
1. Допустим, что у нас есть прямая a с направляющим вектором a→=(ax, ay) и прямая b с направляющим вектором b→(bx, by). Теперь отложим два вектора a→ и b→ от точки пересечения. После этого мы увидим, что они будут располагаться каждый на своей прямой. Тогда у нас есть четыре варианта их взаимного расположения. См. иллюстрацию:
Если угол между двумя векторами не является тупым, то он и будет нужным нам углом между пересекающимися прямыми a и b. Если же он тупой, то искомый угол будет равен углу, смежному с углом a→, b→^.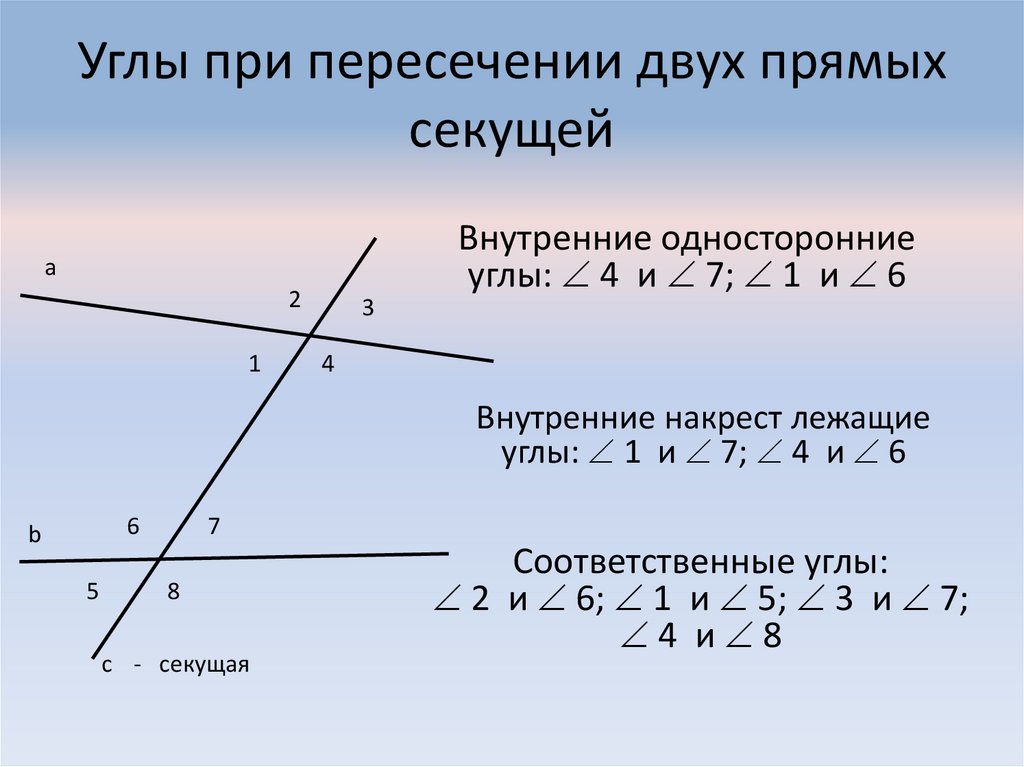 a→·b→=ax·bx+ay·byax2+ay2·bx2+by2
a→·b→=ax·bx+ay·byax2+ay2·bx2+by2
Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:
cos α=ax·bx+ay·byax2+ay2·bx2+by2=ax·bx+ay·byax2+ay2·bx2+by2
Тогда сам угол можно найти по следующей формуле:
α=arccosax·bx+ay+byax2+ay2·bx2+by2
Здесь a→=(ax, ay) и b→=(bx, by) – это направляющие векторы заданных прямых.
Приведем пример решения задачи.
Пример 1В прямоугольной системе координат на плоскости заданы две пересекающиеся прямые a и b. Их можно описать параметрическими уравнениями x=1+4·λy=2+λλ∈R и x5=y-6-3. Вычислите угол между этими прямыми.
Решение
У нас в условии есть параметрическое уравнение, значит, для этой прямой мы сразу можем записать координаты ее направляющего вектора. Для этого нам нужно взять значения коэффициентов при параметре, т.е. прямая x=1+4·λy=2+λλ∈R будет иметь направляющий вектор a→=(4, 1).
Вторая прямая описана с помощью канонического уравнения x5=y-6-3. Здесь координаты мы можем взять из знаменателей.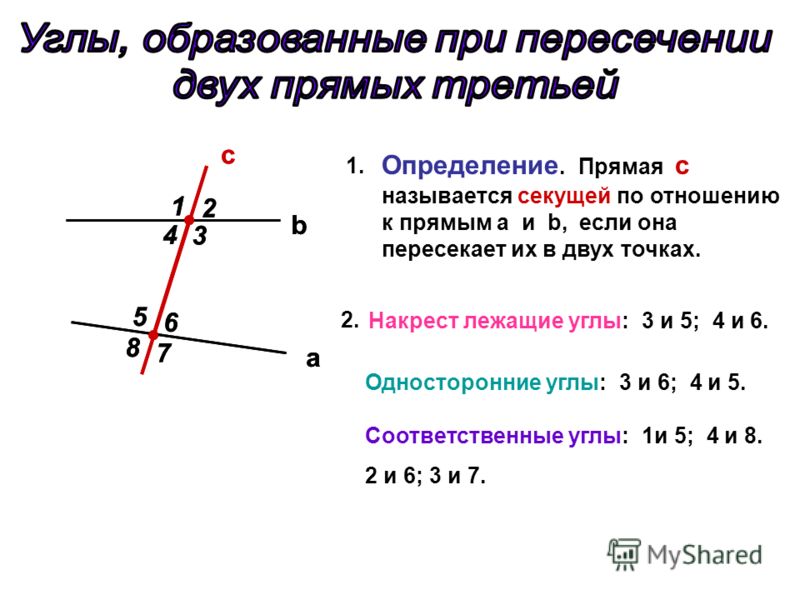 =ax·nbx+ay·nbyax2+ay2·nbx2+nby2
=ax·nbx+ay·nbyax2+ay2·nbx2+nby2
Нахождение самого угла:
α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2
Здесь a→ является направляющим вектором первой прямой, а nb→ – нормальным вектором второй.
Пример 3Две пересекающиеся прямые заданы уравнениями x-5=y-63 и x+4y-17=0. Найдите угол пересечения.
Решение
Берем координаты направляющего и нормального вектора из заданных уравнений. Получается a→=(-5, 3) и n→b=(1, 4). Берем формулу α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2 и считаем:
α=arcsin=-5·1+3·4(-5)2+32·12+42=arcsin7234
Обратите внимание, что мы взяли уравнения из предыдущей задачи и получили точно такой же результат, но другим способом.
Ответ: α=arcsin 7234
Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.
У нас есть прямая a, которая задана в прямоугольной системе координат с помощью уравнения y=k1·x+b1, и прямая b, заданная как y=k2·x+b2. Это уравнения прямых с угловым коэффициентом. Чтобы найти угол пересечения, используем формулу:
Это уравнения прямых с угловым коэффициентом. Чтобы найти угол пересечения, используем формулу:
α=arccosk1·k2+1k12+1·k22+1, гдеk1 и k2 являются угловыми коэффициентами заданных прямых. Для получения этой записи были использованы формулы определения угла через координаты нормальных векторов.
Пример 4Есть две пересекающиеся на плоскости прямые, заданные уравнениями y=-35x+6 и y=-14x+174. Вычислите величину угла пересечения.
Решение
Угловые коэффициенты наших прямых равны k1=-35 и k2=-14. Добавим их в формулу α=arccosk1·k2+1k12+1·k22+1 и подсчитаем:
α=arccos-35·-14+1-352+1·-142+1=arccos23203424·1716=arccos23234
Ответ: α=arccos23234
В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать. =a→, k→a→·k→=1·0-3·0-2·112+(-3)2+(-2)2·02+02+12=28=12
=a→, k→a→·k→=1·0-3·0-2·112+(-3)2+(-2)2·02+02+12=28=12
В итоге мы получили, что нужный нам угол будет равен arccos12=45°.
Ответ: cos α=12, α=45°.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Что такое перпендикулярные линии? Определение, свойства, примеры
Что такое перпендикуляр?Две отдельные линии, пересекающиеся друг с другом под углом 90° или под прямым углом, называются перпендикулярными линиями.
Пример :
Здесь AB перпендикулярна XY, потому что AB и XY пересекаются под углом 90°.
Непример:
| Две прямые параллельны и не пересекают друг друга. Они никогда не могут быть перпендикулярны друг другу. | Две линии пересекаются под острым углом. Значит, они не перпендикулярны. | Линии не пересекаются друг с другом под прямым углом. |
Рекомендуемые рабочие листы:
Перпендикулярный символ
Перпендикулярные линии представлены символом « ⊥ ».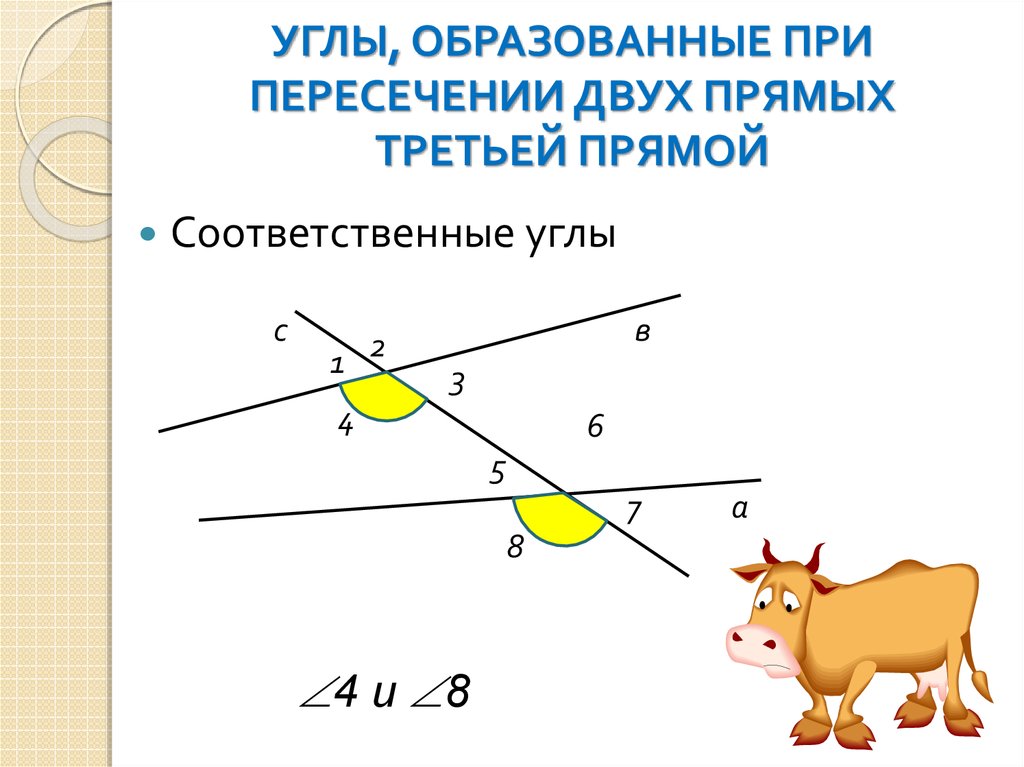 Допустим, м и н две прямые, пересекающиеся друг с другом под углом 90°, тогда они перпендикулярны друг другу и изображаются как м ⊥ n . Точка пересечения перпендикулярных прямых называется основанием перпендикуляра.
Допустим, м и н две прямые, пересекающиеся друг с другом под углом 90°, тогда они перпендикулярны друг другу и изображаются как м ⊥ n . Точка пересечения перпендикулярных прямых называется основанием перпендикуляра.
Свойства перпендикулярных линий
- Эти линии всегда пересекаются под прямым углом.
- Если две прямые перпендикулярны одной прямой, то они параллельны друг другу и никогда не пересекутся.
- Смежные стороны квадрата и прямоугольника всегда перпендикулярны друг другу.
- Стороны прямоугольного треугольника, заключающего прямой угол, перпендикулярны друг другу.
Примеры из жизни
В реальной жизни мы можем наблюдать много перпендикулярных линий.
Некоторые примеры: стороны установленного квадрата, стрелки часов в определенное время дня, углы доски, окно и символ Красного Креста.
Различие между перпендикулярными и параллельными прямыми
| Перпендикулярные прямые | Параллельные прямые | угол 0°. | Параллельные линии — это линии, которые всегда находятся на одинаковом расстоянии друг от друга. Параллельные прямые никогда не пересекаются. |
| Для обозначения перпендикулярной линии используется символ «⊥». | Для обозначения параллельной линии используется символ «||». |
| Пример: Угол открытки | Пример: Железнодорожные пути |
| Угол линейки0022 |
Построение перпендикулярных линий
Мы можем провести перпендикулярные прямые к заданной прямой двумя способами.
- Использование транспортира
- Использование компаса
Проведение перпендикулярной линии с помощью транспортира
Шаг 1: Пусть м — заданная линия, а A — заданная точка на ней.
Шаг 2: Поместите транспортир на линию м так, чтобы его базовая линия совпадала с м , а его центр приходится на A.
Шаг 3: Отметьте точку B против отметки 90 градусов на транспортире.
Шаг 4: Проведите линию n , проходящую через точки A и B.
Затем линию м ⊥ линию n в точке A.
Проведение перпендикулярной линии в заданной точке линии с помощью циркуля
Шаг 1: Поместите острие компаса в заданную точку A. Возьмите соответствующий радиус и нарисуйте дугу по обе стороны от заданной точки.
Шаг 2: Растяните компас шире. Поместите кончик компаса на новые точки и сделайте небольшую дугу над заданной линией. Две новые дуги пересекутся.
Шаг 3: Используйте линейку, чтобы соединить заданную точку A и точку B, где пересекаются дуги.
Решенные примеры на перпендикуляре
Пример 1. Укажите, являются ли данный набор прямых перпендикулярными или параллельными.
(а) | (б) |
| (C) | (D) |
Решение:
- .

- Перпендикулярные линии
- Перпендикулярные линии
- Параллельные линии
Пример 2: Напишите отношение между сегментами линии, обозначенными стрелкой в каждой фигуре.
(A)(B)(C)(D)Решение:
- AB ⊥ AE
- ПК || СР
- ПК || НМ
- ПБ ⊥ Н.Э.
Пример 3: Диагонали ромба перпендикулярны друг другу. Сколько прямых углов образовано при пересечении?
Решение:
Поскольку прямые AC и BD пересекаются под углом 90 градусов, в точке их пересечения имеется 4 прямых угла.
∠AED = ∠DEC = ∠CEB = ∠BEA = 90 градусов
Пример 4. Назовите некоторые двумерные фигуры с перпендикулярными линиями.
Решение:
Прямоугольник Прямоугольный Треугольник КвадратПрактические задачи
1
Определите пару перпендикулярных отрезков заданной формы.

AG и AB
FE и ED
FE и CD
CB и AB
Правильный ответ: FE и ED
FE и ED являются перпендикулярными отрезками.
2
Каждый объект имеет выделенную пару линий. Какой из выделенных парой линий этого объекта не показывает перпендикулярных линий?
A
B
C
D
Правильный ответ: A
Свеча. Его выделенная пара линий показывает параллельные линии.
3
В какой момент стрелки часов будут перпендикулярны друг другу?
12 часов
6 часов
3 часа
5 часов
Правильный ответ: 3 часа
В 3 часа стрелки часов находятся под углом 90 градусов к друг с другом. Значит, они перпендикулярны друг другу.
4
Сколько прямых перпендикулярно прямой CD на данном рисунке?
1
2
3
4
Правильный ответ: 3
Линия PQ, линия RS и линия TU перпендикулярны CD. Итак, на данном рисунке перпендикулярны прямой CD 3 прямые.
Итак, на данном рисунке перпендикулярны прямой CD 3 прямые.
Часто задаваемые вопросы
Что такое перпендикулярные линии?
Перпендикулярные линии — это линии, которые пересекаются друг с другом под углом 90 градусов.
Должны ли пересекаться перпендикулярные линии?
Эти линии всегда пересекаются под прямым углом.
Что такое перпендикуляр?
Перпендикулярный символ ⊥. Он используется между двумя линиями, чтобы показать, что они перпендикулярны друг другу.
В чем разница между перпендикулярными линиями и параллельными линиями?
Перпендикулярные прямые пересекаются под прямым углом (90°), а параллельные прямые параллельны друг другу и никогда не пересекаются.
Все ли пересекающиеся прямые всегда перпендикулярны?
Нет, не все пересекающиеся прямые перпендикулярны друг другу. Они могут пересекаться под разными углами, кроме 90 градусов.
Углы и треугольники
| Биссектрисы и перпендикуляры Две прямые перпендикулярны , если они пересекают друг друга, образуя два угла 90 ° . А линия делит отрезок пополам, если он делит отрезок на два равных отрезка. Длина каждого из новых отрезков называется «эквидистантной». Биссектриса — это прямая, которая пересекает отрезок с образованием двух углов 90 ° и делит этот отрезок на два равных отрезка. |
Две или более прямых, пересекающихся в одной точке, называются пересекающимися прямыми .
Две линии, которые пересекаются и образуют прямые углы, называются перпендикулярными линиями . Символ ⊥ используется для обозначения перпендикулярных линий.
Две линии, лежащие в одной плоскости и никогда не пересекающиеся, называются параллельными линиями. Параллельные линии всегда остаются на одном и том же расстоянии друг от друга. Символ // используется для обозначения параллельных линий. Третья линия называется поперечной линией. Когда эта линия возникает, создается несколько углов. Вы можете использовать эти углы, чтобы найти измерения других углов.
Углы, образованные пересекающимися линиями
При пересечении прямых образуются несколько типов углов. Знакомство с этими углами очень поможет вашему пониманию геометрии. Во-первых, некоторые термины, которые принесут пользу вашему обучению.
Знакомство с этими углами очень поможет вашему пониманию геометрии. Во-первых, некоторые термины, которые принесут пользу вашему обучению.
Смежные углы — Два угла являются смежными, если они имеют общую сторону и общую вершину (угловую точку) и не пересекаются. На приведенной ниже диаграмме (дополнительные углы) угол 70 и угол 110 смежны друг с другом, потому что они имеют общую сторону.
Прямые углы — Прямой угол образует «прямую линию» и равен 180 градусам.
В восьмом классе мы сосредоточимся на двух из этих угловых образований:
1) Дополнительные углы – это пары углов, сумма которых составляет 180 градусов. Если вы соедините два дополнительных уголка вместе, вы можете провести прямую линию через верхнюю часть двух углов. По сути, два угла вместе образуют полукруг. Дополнительные углы не ограничены соседними линиями, как на диаграмме справа. Ими могут быть любые два угла, сумма которых равна 180 градусам. |
2) Противоположные углы это углы, прямо противоположные друг другу, когда две прямые пересекаются на плоскости. Они конгруэнтны, что означает, что их измерение угла равно. |
Углы, образованные параллельными прямыми, пересеченными секущей
Когда даны две параллельные линии (см. рисунок справа), есть две основные области: внутренняя и внешняя. |
Когда две параллельные прямые пересекаются третьей линией, третья линия называется
поперечной . Две специальные пары углов образованы в этой конструкции
В примере справа восемь углов образуются, когда параллельные прямые m и n пересекаются поперечной линией, t. У фигуры 4 угла снаружи (углы 1,2,7,8) и 4 угла внутри фигуры (3,4,5,6).
|
Альтернативные внешние углы (см. |
|
| Углы в треугольнике В треугольнике три внутренних угла всегда дают в сумме 180°: A + B + C = 180° |
Доказательство
И вы можете легко видеть, что A + C + B делает 90 003 полных оборота от одной стороны прямой линии до другой, или 180° (дополнительные углы) |
Типы треугольников
Существует 3 специальных названия треугольников, которые говорят, сколько сторон (или углов) равны. Может быть 3, 2 или нет равных сторон/углов.
1) Равнобедренные треугольники имеют 3 равные длины сторон и 3 равных угла (всегда 60°). См. схему справа. |
|
|
Углы четырехугольника |
| Сравнение треугольников и четырехугольников Как было обнаружено ранее, сумма внутренних углов любого треугольника составляет 180 ° . |
Как насчет многоугольников с более чем четырьмя сторонами? |




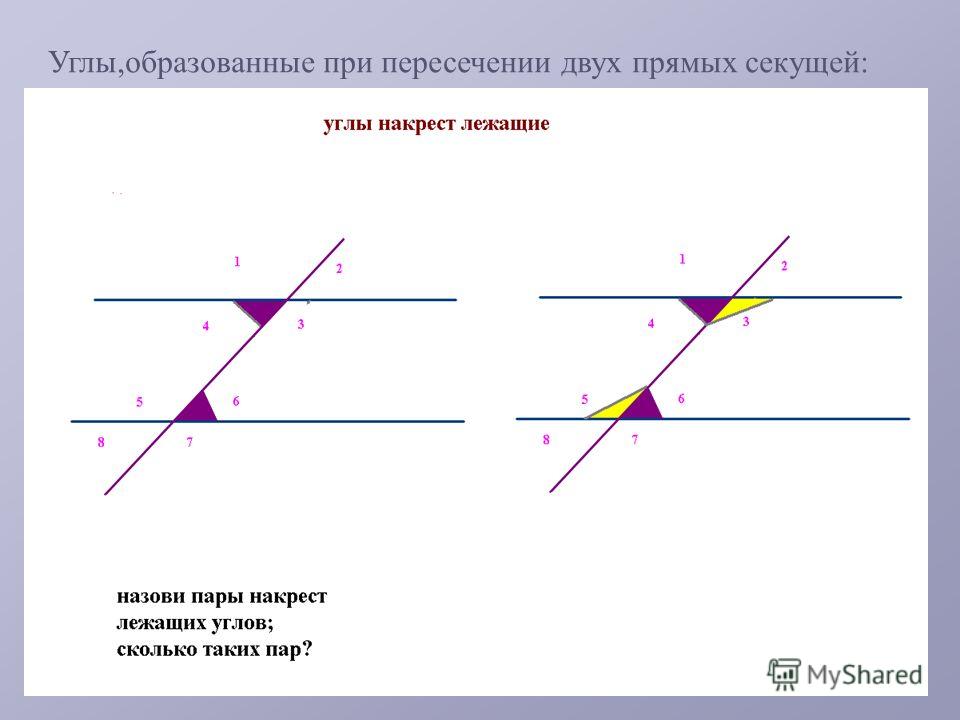
 справа) – это два угла, находящиеся снаружи параллельных прямых и на противоположных (альтернативных) сторонах поперечной. Альтернативные внешние углы несмежны и равны.
справа) – это два угла, находящиеся снаружи параллельных прямых и на противоположных (альтернативных) сторонах поперечной. Альтернативные внешние углы несмежны и равны. Итак:
Итак:
 (90°+45°+45°=180°)
(90°+45°+45°=180°) 