Qr разложение матрицы пример: QR-разложение матрицы онлайн

chisl_meth / Лаб 6 QR-алгоритм, метод итераций / QR-алгоритм

QR-разложение

Для нахождения собственных значений матрицы, используя QR-алгоритм, необходимо предварительно использовать QR-разложение, которое представляет собой разложение матрицы в виде , где Q – ортогональная матрица; R – верхнетреугольная матрица. Существует ряд методов для реализации QR-разложения: процесс Грама – Шмидта; преобразование Хаусхолдера; вращение Гивенса.

Процесс Грама – Шмидта

Рассмотрим процесс Грама – Шмидта для некоторой матрицы . Определим проекцию

,

тогда

Матрицы Q и R будем формировать следующим образом:

Матрицу R можно найти и другим путем. Преобразуем выражение следующим образом: . Произведение есть единичная матрица. Отсюда следует, что зная матрицу Q, мы можем определить матрицу R

.

Преобразование Хаусхолдера

Идея преобразования Хаусхолдера – осуществить ряд преобразований, которые позволят сделать нулевыми элементы столбцов ниже главной диагонали. Пусть имеется матрица:

.

Возьмем первый столбец и вычислим с его помощью вектор

,

который мы используем для построения матрицы Хаусхолдера:

.

Если умножить матрицу на исходную , то в первом столбце полученной матрицы ниже главной диагонали будут нули. Запишем минор матрицы :

и проделаем для этой матрицы операции записанные выше, т. е. , тогда

, ,

и т. д.

Матрицы разложения могут быть получены как

, .

Пример

.

Запишем первый столбец матрицы , тогда

,

Матрица будет иметь вид

Используя второй столбец минора , строим вектор и

,

Произведение матрицы на дает матрицу , у которой элементы ниже главной диагонали будут равны нулю.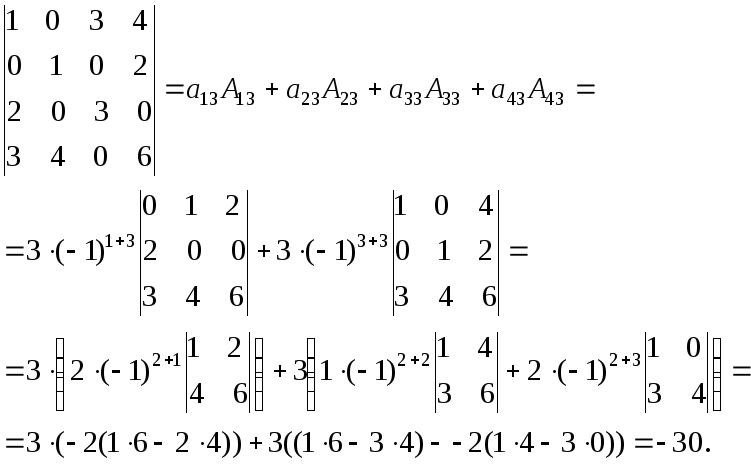 Это и есть искомая матрица R:

,

а матрица Q примет вид

.

QR-алгоритм

Теперь мы можем осуществить QR-разложение матрицы одним из приведенных способов. Тогда для последовательности матриц и запишем процесс, который представляет собой QR-алгоритм.

1. Задаем и .

2. Вычисляем , затем находим QR-разложение как .

3. Определяем и представляем в виде и т. д.

…

m. Находим , после чего записываем

На некотором шаге m матрица становится треугольной или почти треугольной, поэтому ее собственные числа будут находиться на главной диагонали. Чем больше

m, тем ближе собственные числа матрицы к собственным числам матрицы A.

Пример. Используя QR-алгоритм, вычислить собственные числа матрицы

.

Шаг 1.

Шаг 2.

Шаг 3.

…

Шаг 12.

Приближенные значения собственных чисел находятся на главной диагонали и равны

8.3.4. QR-разложение MathCAD 12 руководство

• Системы линейных уравнений
• 8.1. Хорошо обусловленные системы с квадратной матрицей
  • 8.1.1. Вычислительный блок Given / Find
  • 8.1.2. Функция lsolve
• 8.2. Произвольные системы линейных уравнений
  • 8.2.1. Переопределенные системы
  • 8.2.2. Недоопределенные системы
  • 8.2.3. Вырожденные и плохо обусловленные системы
• 8.3. Матричные разложения
  • 8.3.1. СЛАУ с треугольной матрицей
  • 8.3.2. Разложение Холецкого
  • 8.3.3. LU-разложение
  • 8.3.4. QR-разложение
  • 8.3.5. SVD-(сингулярное) разложение
• 8.4. Собственные векторы и собственные значения матриц

Среди матричных разложений особую роль играют ортогональные преобразования, обладающие свойством сохранения нормы вектора. Напомним из курса линейной алгебры, что матрица Q называется ортогональной, если Q^TQ=I, где I — единичная матрица. Свойство сохранения нормы вектора при ортогональных преобразованиях, т. е. |Qx|=|x|, дает рецепт поиска псевдорешения вырожденных СЛАУ, а именно, замену исходной задачи минимизации невязки с «плохой» матрицей |Аx-b| задачей |Q^T(Ax-b)|, в которой матрица уже будет «хорошей» благодаря специальному построению матрицы Q. Таким образом, ортогональные разложения используются при решении любых систем (в том числе с прямоугольной матрицей А, причем как переопределенных, так и недоопределенных).

Одним из важнейших вариантов ортогональных разложений некоторой матрицы А является QR-разложение вида A=QR, где Q — ортогональная матрица, а R — верхняя треугольная матрица:

•  qr (A) — QR-разложение:

•  А — вектор или матрица любого размера.

Результатом действия функции qr (А) является матрица, составленная из матриц Q и R соответственно (подобно рассмотренному в предыдущем разделе LU-разложению). Выделить матрицы QR-разложения несложно при помощи встроенной функции выделения подматрицы submatrix (листинг 8.22).

Листинг 8.22. QR-разложение сингулярной матрицы

Если бы исходная СЛАУ Aх=b не была вырожденной, то можно было сразу записать: Q

TQ-Rx=Q^Tb, откуда следует (благодаря ортогональности матрицы Q): Rx=Q^Tb. Так как матрица к — треугольная, решение данной системы получается по формулам прямого хода. Если использовать нашу пользовательскую функцию решения треугольной системы (см. разд. 8.3. Т), то результат исходной СЛАУ запишется в виде одной строки кода: trg(R,Q^Tb) (соответствующий пример решения невырожденной СЛАУ вы найдете на компакт-диске).

Обратимся теперь к проблеме решения СЛАУ с сингулярной квадратной NxN или прямоугольной NxM матрицей А. Если ее ранг равен k (он может быть меньше N и м, как в листинге 8.22, где N=M=S, a k=2), то получающаяся треугольная матрица R имеет следующую структуру:

где R1 — верхняя треугольная матрица, a R2 — просто некоторая матрица, а нули обозначают, в общем случае, нулевые матрицы соответствующих размеров.

Если система вырожденная, то она имеет бесконечное множество псевдорешений (векторов, минимизирующих норму невязки). При помощи QR-разложения можно сразу выписать одно из них (правда, не обладающее минимальной нормой). В нашем примере последняя строка матрицы R содержит одни нули, поэтому последняя компонента вектора псевдорешения х может быть абсолютно любой. Если положить х2=0, то остальные компоненты х определятся из треугольной СЛАУ R1x=Q^Tb, как это проиллюстрировано листингом 8.23.

Листинг 8.23. Поиск одного из псевдорешений вырожденной СЛАУ посредством QR-разложения (продолжение листинга 8.22 )

Для того чтобы выбрать из всего множества псевдорешений (минимизирующих невязку исходной СЛАУ) нормальное псевдорешение (т. е. обладающее минимальной нормой), необходимо решить соответствующую задачу минимизации (см. разд. 8.2.3). Если построено QR-разложение, сделать это намного легче. Если произвольную компоненту решения обозначить переменной у: х

2=у, то она определится из соответствующей задачи оптимизации (листинг 8. 24, 1—3 строки), а остальные составляющие самого решения х — из треугольной СЛАУ R1x=Q^Tb-R2y. В последней строке листинга выводится полученное нормальное псевдорешение, а также его норма и соответствующая норма невязки (которые полезно сравнить с результатом прошлого листинга). Вспомогательный рис. 8.13 помогает понять структуру минимизируемой функции из листинга 8.24.

Листинг 8.24. Нормальное псевдорешение вырожденной СЛАУ (продолжение листингов 8.22 и 8.23)

Рис. 8.13. Норма псевдорешения в зависимости от у (продолжение листинга 8.24)

Резюмируя практические аспекты применения QR-разложения, надо отметить, что алгоритмы решения СЛАУ на его основе практически одинаковы как для хорошо обусловленных, так и для сингулярных систем.

ПРИМЕЧАНИЕ

На прилагаемом к книге компакт-диске вы найдете дополнительные примеры построения QR-разложения как для квадратной, так и прямоугольной матрицы А.

Нравится

Твитнуть

Глава 24 Разложение QR | Матричная алгебра для ученых в области образования

Другим методом разложения является QR-разложение. Одним из преимуществ QR-разложения по сравнению с LU-разложением является то, что этот метод не требует, чтобы разложение выполнялось на квадратной матрице. QR-разложение приводит к разложению матрицы A (имеющей независимые столбцы) в произведение двух матриц, а именно Q и R : .

\[ \underset{m\times n}{\mathbf{A}} = \underset{m\times m}{\mathbf{Q}}~ \underset{m\times n}{\mathbf{R}} \]

, где Q — ортогональная матрица , ¹² и R — верхнетреугольная матрица.

24.1 Разложение QR с использованием R

Хотя существует способ вычисления матриц

Q и R вручную (например, с использованием процесса Грама-Шмидта), мы будем полагаться на вычисления. Чтобы выполнить QR-разложение в R, мы будем использовать функцию qr() , которая факторизует матрицу и возвращает список результатов, связанных с QR-разложением. Чтобы извлечь фактические Q и R матрицы из этого вывода, мы будем использовать функции qr.Q() и qr.R() соответственно.

 # Создать матрицу А
А = матрица (
  данные = с (5, -4, 1, 2),
  сейчас = 2
  )
# Выполняем QR-разложение
qr_разложение = qr(A)
# Просмотр матрицы Q
qr.Q(qr_decomp) 

 [1] [2]
[1,] -0,7809 0,6247
[2,] 0,6247 0,7809 

 # Просмотр матрицы R
qr.R(qr_decomp) 

 [1] [2]
[1,] -6,403 0,4685
[2,] 0,000 2,1864 

9-1 решить (qr.Q (qr_decomp))

 [1] [2]
[1,] -0,7809 0,6247
[2,] 0,6247 0,7809 

Мы также можем проверить, что произведение разложенных матриц равно A .

 # А = QR?
qr.Q(qr_decomp) %*% qr.R(qr_decomp) 

 [1] [2]
[1,] 5 1
[2,] -4 2 

24.2 Статистическое приложение: оценка коэффициентов регрессии с QR-разложением

Мы можем использовать две разложенные матрицы, Q и R , для вычисления элементов 93) colnames(X) <- c("Перехват", "x", "x2", "x3") # Создаем матрицу b б = матрица ( данные = с (1, 1, 1, 1), сейчас = 4 ) # Создать вектор значений y set. seed(1) y = X %*% b + rnorm(n, mean = 0, sd = 1)

Мы можем использовать QR-разложение, чтобы найти b .

 # Выполнение QR-декомпозиции
QR = qr(X)
# Находим b
обратное решение(qr.R(QR), t(qr.Q(QR)) %*% y) 

 [1]
[1,] 0,9038
[2,] 1,0066
[3,] 1.0000
[4,] 1.0000 

QR-разложение — это то, как {-1}\).↩︎

QR-факторизация | Реальная статистика с использованием Excel

Определение 1 : QR-факторизация (или QR-разложение ) квадратной матрицы A состоит из ортогональной матрицы Q и верхней треугольной матрицы R

, таких что 5 A R

= КР.

Свойство 1 (QR-факторизация) : Для любой n × n обратимой матрицы A мы можем построить QR-факторизацию.

Доказательство: пусть A ₁ , …, A _n представляют столбцы A . Поскольку A обратимо, мы знаем, что A ₁ , …, A _n  независимы и образуют основу для набора всех векторов-столбцов n  × 1. Следовательно, мы можем использовать процесс Грама-Шмидта для построения ортонормированного базиса Q ₁ , …, Q _n для множества всех n  × 1 векторов-столбцов. Пусть Q будет матрицей n × n , столбцами которой являются Q ₁ , …, Q _n . По свойству 4 ортогональных векторов и матриц Q является ортогональной матрицей, и поэтому по свойству 6 ортогональных векторов и матриц Q ^T Q = I .

Ищем матрицу R такую, что A = QR . Так как Q ^T Q = I, , то Q ^T A = Q ^T QR = R , отсюда заключаем, что R = Q ^T A и есть искомая матрица. Пусть R = [ r _ij ] и, следовательно, r _ij  = Q _i · A _j . Как мы видели в доказательстве теоремы 1 об ортогональных векторах и матрицах, каждое Q _i может быть выражено как линейная комбинация A ₁ , …, A _i , что означает, что r _ij  = 0 для i > j , что показывает, что R является верхней треугольной матрицей. Также легко показать по индукции, что r _ij > 0 для каждого i .

Наблюдение : Мы можем распространить свойство 1 на некоторые неквадратные матрицы. Доказательство аналогично, и Q и R построены одинаково.

Свойство 2 ( QR-факторизация ): Для любой m × n матрицы A с рангом ( A ) = n ≤ m , мы можем построить m × n ортонормированную матрицу Q и 6 n n верхняя треугольная матрица R такая, что A = QR .

Пример 1 : Найдите QR-факторизацию для матрицы A , которая сформирована из столбцов в примере 1 ортогональных векторов и матриц.

Как видно на рисунке 1 ортогональных векторов и матриц, A — это матрица 4 × 3. Формула дополнительного массива =ELIM(A4:E7) создает матрицу 4 × 3 только с одной нулевой строкой, показывающей, что rank( A ) = 3 (подробности см. в Приложениях Детерминанты и Линейные уравнения и Линейные независимые векторы). Поскольку rank( A ) = 3 ≤ 4, мы можем применить свойство 2.

Ортонормированная матрица Q вычисляется в примере 1 ортогональных векторов и матриц. Матрица R = Q ^T A  показана в диапазоне M4:O6 на рисунке 1 Ортогональные векторы и матрицы, рассчитанная с использованием формулы массива =МУМНОЖ(ТРАНСП(I4:K7),A4:C7). Обратите внимание, что R действительно является верхней треугольной матрицей.

Наблюдение : Вскоре мы покажем, как использовать QR-факторизацию для вычисления собственных значений и собственных векторов, и на самом деле мы покажем лучший способ получения такой QR-факторизации, которая менее подвержена ошибкам округления.

Сейчас мы покажем, как использовать QR-факторизацию, чтобы найти решение задачи AX = C , изучаемой в разделе «Определители и линейные уравнения». Прежде всего заметим, что поскольку A = QR и Q ортогональны, если AX = C , то C = AX = QRX и, следовательно, Q ^T C = Q ^T QRX = RX . Таким образом, RX = Q ^T C . Но поскольку R — это верхняя треугольная матрица, все диагональные элементы которой отличны от нуля (на самом деле они положительны), мы можем использовать обратную замену, чтобы найти решение для X . Фактически, если R = [ r _ij ], X = [ x _j ] и Q ^T C = [ b _i ], то мы будем иметь ряд уравнений вида (если смотреть снизу вверх):



2 9 первое уравнение можно использовать, чтобы найти значение x ₁ . Подставив это значение вместо x ₁ во второе уравнение, вы получите x ₂ . Продолжая таким образом, вы можете найти x _{n- 1} . Подстановка этих значений в последнее уравнение позволяет найти x _n .

Пример 2 : Решить следующую систему линейных уравнений с помощью QR-факторизации U10:X13 дает решение x = -0,34944, y = 0,176822 и z = 0,792727.

Рисунок 1. Решение AX = C с использованием QR-факторизации

Теперь мы покажем, как найти решение с помощью QR-факторизации. Сначала мы вычисляем Q ^T C (диапазон Z4:Z6) как =MMULT(ТРАНСП(I4:K7),X4:X7), используя значения для Q , показанные на рисунке 1 Ортогональных векторов и матриц. Затем мы вычисляем значения для X (диапазон AB4:AB6) с помощью обратной замены, используя формулы на рисунке 2.

Рисунок 2 – Формулы на рисунке 1

Определение 2 : Матрица Хаусхолдера A является квадратной матрицей, для которой существует вектор V такой, что I0 V ^{T 9 А = И – 2 ВВ Т .}

Свойство 3 : Матрица Хаусхолдера ортогональна

Доказательство: Пусть A будет матрицей Хаусхолдера. Сначала покажем, что A симметрично следующим образом:

Мы следующее показываем, что A ² = I , из которого следует, что AA ^T = A ² = I , что на определение, A. , , A. , A. A. . является ортогональным.

Наблюдение : В разделе «Ортогональные векторы и матрицы» показано, как сгенерировать QR-факторизацию для любой матрицы с использованием процедуры Грама-Шмидта. К сожалению, для практических целей эта процедура нестабильна в том смысле, что по мере ее применения на компьютере накапливаются ошибки округления, и поэтому, хотя теоретически получается корректная QR-факторизация, на практике результаты иногда могут быть неверными.

Теперь мы представляем процедуру построения QR-факторизации с использованием матриц Хаусхолдера, которая является более стабильной. Как и раньше, начнем со случая квадратной матрицы.

Свойство 4 : Каждая обратимая квадратная матрица A имеет QR-факторизацию. Кроме того, существует эффективный алгоритм для нахождения этой QR-факторизации.

Определить V _k = [ v _i ] по

v _I = 0 для I

Определите P _K = I — 2 V _K V _K V _K V _K ^{V _K V _K .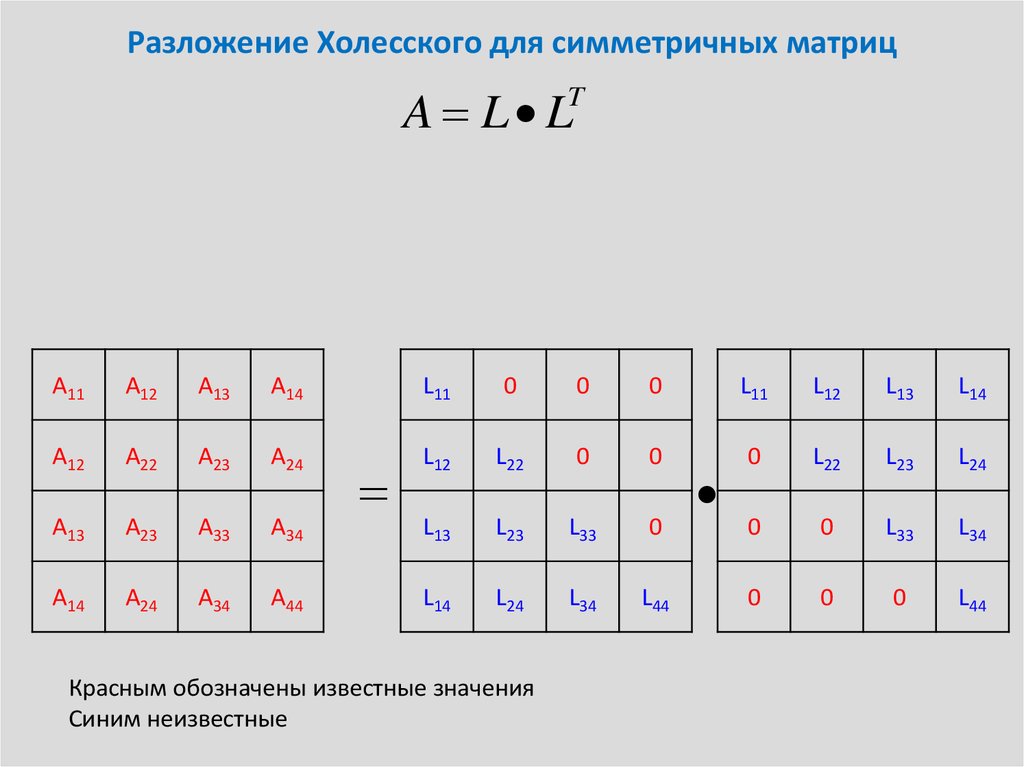 8 9. 8 9. 8 9.}

111118. P _k Q _{k -1} и R _k+1 = P _k R _k .

Теперь определите R = R _n и Q = Q _{n -1} ^Т .

Наблюдение : Свойство 4 сохраняется, даже если квадратная матрица A необратима. Доказательство требует небольшой модификации описанной выше процедуры.

Определение 3 : Процедура QR-факторизации для нахождения собственных значений/векторов квадратной матрицы выглядит следующим образом:

Пусть Q и R определены, как указано выше. Пусть А ₀ = А ,   Q ₀ = Q и R ₀ = R . Определить A _{k +1} = R _k Q _k . Since A _{k +1} is also invertible it has a QR decomposition A _{k +1} = Q _{k +1} R _{k +1} .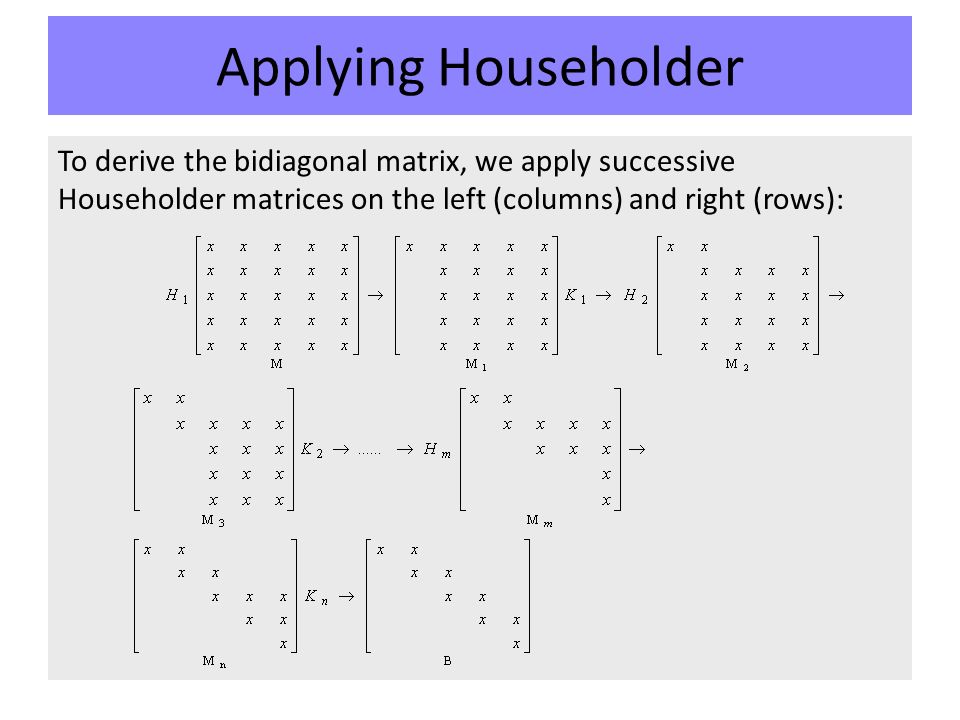

Свойство 5 : Если собственные значения A  различны и не равны нулю, тогда A _k сходится к верхней треугольной матрице с теми же собственными значениями, что и A . Если A симметрично, то A _k сходится к диагональной матрице с теми же собственными значениями, что и A .

Наблюдение : Поскольку собственные значения верхней треугольной матрицы находятся на диагонали, это означает, что для k достаточно больших собственных значений A  находятся на диагонали A _k .

Пример 3: Используйте метод QR-разложения, чтобы найти собственные значения

Начнем с нахождения Q и R .

Figure 3 – QR Factorization using a Householder matrix (step 1)

Thus

where A  = QR , R is an upper triangular matrix and Q ^T Q = я . Позвоните A ₀ = A , R ₀ = R и Q ₀ = Q , We Define A NEW 8 A = RQ Q Q QQ Q Q QQ Q QQ Q QQ QQ QQ Q QQ QQ Q . 1 = R ₀ Q ₀ ) и повторите процесс.

Рисунок 4 – QR-факторизация с использованием матрицы Хаусхолдера (шаг 2)

Результатом являются новые R и Q , which we now call R ₁ and Q ₁ such that A ₁ = Q ₁ R ₁ , R ₁ is an upper треугольная матрица и Q ₁ ^T Q ₁ = I . Как и прежде, теперь мы определяем новый A , то есть A ₂ = R ₁ Q ₁ и повторяем процесс. Мы продолжаем этот процесс, пока не получим A _k , что достаточно близко к тому, чтобы быть диагональной матрицей.

Теперь мы переходим к 9-й итерации, где A теперь сходятся к диагональной матрице:

Таким образом, собственные значения исходной матрицы A равны 4, 1 и 1.

Как только вы найдете собственное значение, вы можете использовать метод исключения Гаусса, чтобы найти соответствующие собственные векторы, поскольку они являются решениями однородного уравнения ( A – λI ) X = 0, что можно решить, как описано в определении 5 определителей и линейных уравнений. Единственная проблема с этим подходом заключается в том, что не все собственные значения матрицы различны (например, в примере 3). Исключение Гаусса может найти один такой собственный вектор, но не набор ортогональных собственных векторов (по одному для каждого экземпляра повторяющихся собственных векторов, как требуется в примере 3).

Лучше использовать тот факт, что соответствующие собственные векторы являются столбцами матрицы B = Q ₀ Q ₁ … Q _k (где k — итерация, где матрица 9015 k _{достаточно близка к диагонали 9015 k ). For Example 3 we define B 0 = Q 0 and B n +1 = B n Q n (shown as B′Q in K32 :M34 на рис. 4 и K214:M216 на рис. 5. Таким образом, мы заключаем, что собственные векторы, соответствующие 4, 1, 1, являются столбцами в матрице}

Поскольку описанный выше процесс сложен и утомителен для выполнения, проще и быстрее использовать следующие функции реальной статистики eigVAL, eigVECT и связанные с ними функции, как описано в Собственные значения и Собственные векторы.

Пример 4 : Используйте функцию eigVECTSym, чтобы найти собственные значения и собственные векторы для примера 3.

Выходные данные eigVECTSym(A6:C8) показаны на рисунке 6. eigVECTSym

, что является тем же результатом, который мы получили ранее.

Наблюдение : Мы можем распространить свойство 4 на некоторые неквадратные матрицы. Доказательство аналогично, и Q и R построены одинаково.

Свойство 6 (QR-факторизация) : Для любой m × n матрицы A с рангом ( A ) = n ≤ m , мы можем построить эффективным способом m1 × 6n ортонормированную матрица Q и верхнюю треугольную матрицу R n x n такую, что A = QR .

Поскольку описанный выше процесс сложен и утомителен для выполнения, проще и быстрее использовать следующие дополнительные функции для создания QR-факторизации матрицы.

Функции реальной статистики : Ресурсный пакет реальной статистики предоставляет следующие функции массива, где R1 — это диапазон м × n в Excel

QRFactorR (R1, prec ): выводит массив n × n R , для которого A = QR , где A — матрица в R1.

QRFactorQ (R1, prec ): выводит массив m × n R , для которого A = QR , где A — матрица в R1.

QRFactor (R1, prec ): выводит массив m+n × n . Первые м рядов вывода состоят из Q и следующие n строк вывода состоят из R , где A = QR и A — матрица в диапазоне R1.

prec можно использовать для указания того, что считается нулем в алгоритме, используемом для вычисления этих функций. Значение по умолчанию равно 0, но может быть приемлемо использовать какое-либо другое небольшое значение (например, 0,00001) как достаточно малое, чтобы его можно было считать равным нулю.

Обратите внимание, что для получения Q при выполнении свойства 6 вы также можете использовать тот факт, что Q = AR ^-1 , поэтому Q можно получить с помощью =MMULT(R1, MINVERSE(R2)), где R2 содержит формулу =QRFactorR(R1).

Пример 5 : Найдите QR-факторизацию матрицы в A4:D9 на рисунке 7.

, Диапазон F10:I15 содержит =QRFactorQ(A4,D9), хотя, поскольку R обратим, Q =AR ^-1 , и поэтому Q также можно получить, используя формулу рабочего листа =МУМНОЖ(A4,D9, МИНВЕРС(F4:I7)). Наконец, диапазон K4:N13 содержит формулу =QRFactorR(A4,D9).

Мы видим, что A = QR из формулы =МУМНОЖ(F10:I15,F4:I7) в диапазоне F18:I23. Из формулы =MMULT(TRANSPOSE(F10:I15),F10:I15) в диапазоне K18:N21 мы также видим, что Q ^T Q = I, , что демонстрирует частичную ортогональность, поскольку QQ ^T ≠ I.

Наблюдение : Свойство 6 выполняется независимо от ранга матрицы А есть.

Например, на рис. 8 показана QR-факторизация двух квадратных матриц 3 × 3 с рангом меньше 3.

для получения дополнительных примеров факторизации QR, включая различие между полной и сокращенной факторизацией QR и случая, когда количество строк в матрице меньше количества столбцов.

Функции реальной статистики : Как мы видели в примере 2, QR-факторизацию можно использовать для решения системы линейных уравнений. Описанный выше подход может быть расширен для инвертирования матрицы. Ресурсный пакет Real Statistics предоставляет следующие две функции для автоматизации этих процессов.

QRSolve (R1, R2) – предполагается, что R1 представляет собой диапазон м  ×  n диапазон, описывающий матрицу A , а R2 представляет собой диапазон м  × 1, описывающий вектор-столбец an C C C C0015 n  × 1 вектор-столбец X , содержащий решение AX = C

QRInverse (R1) = обратная матрица, описываемая диапазоном R1 (предполагается, что R1 является квадратной матрицей)

0 Наблюдение : Ссылаясь на рисунок 1, QRSolve(U4:W7, X4:X7) выведет результат, описанный в AB4:AB7.

Пример 6 : Найдите обратную матрицу в диапазоне W18:Y20 на рис.

No related posts.