Какие числа называются Иррациональные?
Определение иррациональных чисел
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры иррациональных чисел:
- π = 3,1415926…
- √2 = 1,41421356…
- e = 2,71828182…
- √8 = 2.828427…
- -√11= -3.31662…
Множество иррациональных чисел договорились обозначать латинской буквой I.
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Если натуральное число n не является точным квадратом, т.
Свойства иррациональных чисел
Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.
Свойства иррациональных чисел:
- результат суммы иррационального числа и рационального равен иррациональному числу;
- результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
- результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
- результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).
Определение рациональных чисел
А теперь наоборот: рассмотрим противоположное заданной теме определение.
Рациональное число
— это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.
Если число можно получить делением двух целых чисел — это число точно рациональное.Рациональные числа — это те, которые можно представить в виде:
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
- десятичная дробь 1,15 — это 115/100;
- десятичная дробь 0,2 — это 1/5;
- целое число 0 — это 0/1;
- целое число 6 — это 6/1;
- целое число 1 — это 1/1;
- бесконечная периодическая дробь 0,33333… — это 1/3;
- смешанное число это 25/10;
- отрицательная десятичная дробь -3,16 — это -316/100.
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Пусть а, b и c — любые рациональные числа.
Основные свойства действий с рациональными числами
|
Запутаться в числах — плевое дело, но только не в школе Skysmart. Ученикам помогают красочные персонажи интерактивной платформы и заботливые учителя.
Ученикам помогают красочные персонажи интерактивной платформы и заботливые учителя.
Приходите на бесплатный вводный урок математики вместе с ребенком: покажем, как у нас все устроено, порешаем задачки и вдохновим на учебу!
Иррациональные числа — урок. Алгебра, 8 класс.
Понятия рациональное число, иррациональное число произошли от латинского слова ratio — разум
(буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; так выражаются и в реальной жизни: «его поступок рационален» — это значит, что он поступил разумно; «так поступать нерационально» — обозначает, что так поступать неразумно).
Иррациональным числом называют действительное число, которое не является рациональным (его нельзя записать обыкновенной дробью). Иррациональное число — только бесконечная непериодическая дробь.
Если натуральное число \(n\) не является точным квадратом, т. е. n≠k2, где k∈ℚ, то n является иррациональным числом.
е. n≠k2, где k∈ℚ, то n является иррациональным числом.
Пример:
5=2,23606798…11=3,31662479…
Число π≈ \(3,141592…\) также является иррациональным. Это доказал в \(1766\) году немецкий математик И. Ламберт. Интересно, что для этого числа была взята буква греческого алфавита «пи», так как с этой буквы начинается греческое слово периферия — окружность.
Итак,
1. в результате всякого арифметического действия над рациональными числами (помимо деления на \(0\)) получаем рациональное число.
2. Любое арифметическое действие над иррациональными числами может привести в итоге к рациональному или к иррациональному числу.
3. Если в арифметическом действии принимают участие рациональное и иррациональное числа, то в итоге будет иррациональное число (исключение — умножение и деление на \(0\)).
4. Т. к. в результате действий по извлечению корней (квадратного и кубического) из неотрицательного числа получается иррациональное число, определились, что иррациональным выражением считают любое алгебраическое выражение, где есть действие по извлечению квадратного и кубического корня из переменной.
Калькулятор определения рационального и иррационального числа онлайн
Используемые нами числа подразделяются на различные множества: натуральные, целые, рациональные, комплексные или действительные. Существует также особый пласт бесконечных непериодических чисел, которые составляют иррациональное множество. Определить категорию выбранного числа можно при помощи онлайн-калькулятора.
Рациональные числа
К множеству рациональных относятся числа, которые можно представить в замкнутом виде, то есть в виде обыкновенной дроби. Такие дроби в числителе содержат целые числа, а в знаменателе — натуральные. К множеству натуральных относятся числа, которые мы используем при счете, к примеру, 1, 5 или 120. Целые числа — это расширенное множество натуральных, к которым добавляется нуль, а также отрицательные элементы, например, -5 или -120. Следовательно, рациональное множество содержит нуль, отрицательные и положительные числа.
Целые числа — это расширенное множество натуральных, к которым добавляется нуль, а также отрицательные элементы, например, -5 или -120. Следовательно, рациональное множество содержит нуль, отрицательные и положительные числа.
Также любое рациональное число можно представить в виде бесконечной периодической десятичной дроби. К примеру, 0,6666… является рациональным, так как представляется в замкнутом виде в форме дроби 2/3, а также является бесконечным и периодичным. Число 0,25 легко записать в виде 1/4, а бесконечность и периодичность легко выразить при помощи нулей — 0,2500000…
Таким образом, любая обыкновенная дробь — рациональное число. Любое число, представленное в замкнутом виде, также рациональное. Однако существует целый спектр чисел, которые невозможно представить в виде дробного соотношения или периодической десятичной дроби.
Иррациональные числа
Иррациональное число — это элемент иррационального множества, которое невозможно представить в виде дроби m/n, где m – целое число, а n – натуральное. Об иррациональности некоторых чисел знали с давних времен: античные геометры определили проблему несоизмеримости стороны квадрата и его диагонали, что соответствует иррациональности корня из 2. Кроме того, древние ученые впервые встретились с проблемой подсчета иррационального числа Пи, которое определяется как соотношение длины окружности к ее диаметру.
Об иррациональности некоторых чисел знали с давних времен: античные геометры определили проблему несоизмеримости стороны квадрата и его диагонали, что соответствует иррациональности корня из 2. Кроме того, древние ученые впервые встретились с проблемой подсчета иррационального числа Пи, которое определяется как соотношение длины окружности к ее диаметру.
На протяжении веков предпринимались попытки представить Пи в замкнутом виде, например как 22/7 или 355/113, однако с течением времени математики определяли Пи все точнее и точнее. Сегодня при помощи мощных компьютеров найдено число Пи с точностью 10 триллионов цифр после запятой. Представить Пи в виде соотношения целых чисел или периодичной десятичной дроби невозможно.
К данному множеству относятся следующие элементы:
- корни неквадратных чисел, например, корни из 2, 3, 5 или 7;
- число Пи и выражение типа pix;
- экспоненциальные выражения типа ex;
- натуральные логарифмы для любых положительных чисел больше 1.

Также к иррациональному множеству относятся различные математические константы, такие как золотое и серебряное сечение, экспонента, постоянная Эйлера — Маскерони или постоянная Апери.
Свойства чисел
Арифметические операции с иррациональными числами могут приводить к разным результатам. Так, действия с рациональными и иррациональными числами всегда приводит к образованию новой иррациональности. Однако арифметические операции с двумя иррациональными элементами могут заканчиваться образованием рациональной дроби.
Например, числа 0,3003000300003 и 0,033033303333 иррациональны. Первое образуется по принципу, что после каждой тройки количество нулей постоянно увеличивается. Второе формируется по принципу увеличения количества троек после каждого нуля. Эти числа невозможно представить в виде обыкновенных дробей по отдельности, однако, если сложить их мы получим следующий результат:
0,3003000300003 + 0,033033303333 = 0,3333333333 = 1/3.
В сухом остатке бесконечная периодичная дробь, которую легко выразить в замкнутом виде.
Наш калькулятор позволяет определить тип числа, которое вы можете выразить в виде обыкновенной дроби или корня любой степени из произвольного числа. Программа мгновенно определит множество, к которому относится выбранный элемент. Давайте попробуем на практике.
Примеры использования калькулятора
Определим рациональность нескольких чисел. Калькулятор предлагает нам задать число в виде правильной дроби, которое по определению является рациональным числом. Поэтому определять иррациональность при помощи калькулятора целесообразно только для чисел, выраженных в виде корняn-ной степени. Определим рациональность для следующих выражений:
- квадратный корень из 2 — 1,414, иррациональное;
- кубический корень 27 — 3, рациональное;
- корень пятой степени из 147 — 2,713, иррациональное.
Очевидно, что в некоторых случаях корни могут быть рациональными, что верно для квадратных и кубических чисел.
Заключение
Математические объекты разделяются на разные классы. В повседневной жизни мы оперируем натуральными числами, то есть целыми и положительными числами, которые используем при счете. Рациональные числа используются при измерениях, а иррациональные практически не находят распространения в быту — область их применения лежит в высокой науке. При помощи нашего онлайн-калькулятора вы можете проверить принадлежность любого числа к определенному множеству.
В повседневной жизни мы оперируем натуральными числами, то есть целыми и положительными числами, которые используем при счете. Рациональные числа используются при измерениях, а иррациональные практически не находят распространения в быту — область их применения лежит в высокой науке. При помощи нашего онлайн-калькулятора вы можете проверить принадлежность любого числа к определенному множеству.
1.3.1. Иррациональные числа
Глава 1. Арифметика
1.3.
1.3.1.
Оказывается, что для нужд самой математики как, впрочем, и для практики, уже введённых рациональных чисел не хватает. Исторически числа, отличные по своей природе от рациональных, впервые появились уже при желании вычислить диагональ квадрата по его стороне.
| 1 |
| Рисунок 1.3.1.1 |
Покажем, что длина такой диагонали не может быть выражена рациональным числом. Рассмотрим квадрат со стороной, равной 1. Пусть длина его диагонали равна d. Тогда, по теореме Пифагора, имеем:
то есть
Предположим, что d – рациональное число. Тогда существуют такие числа
что
и дробь
несократима. Получаем:
Из этого равенства следует, что, так как правая его часть делится на 2, то и его левая часть делится на 2. Значит и число m делится на 2. Другими словами существует такое целое число
что m = 2k. Но тогда
Однако из последнего равенства аналогично следует, что число n делится на 2. Последнее обстоятельство приводит к противоречию, так как числа m и n не могут быть одновременно чётными (по предположению, дробь
несократима). Значит, не существует такого рационального числа, которое бы выражало длину диагонали квадрата.
Из нашего примера следует, что такие числа существуют: длина диагонали квадрата со стороной 1 является именно таким числом. Аналогично можно доказать, что не существует рационального числа, квадрат которого равен 5, 7, 10, то есть числа являются иррациональными. Теперь вспомним, что любое рациональное число может быть представлено в виде периодической десятичной дроби и наоборот, любая десятичная периодическая дробь может быть представлена в виде рационального числа.
Любое иррациональное число можно записать в виде бесконечной непериодической дроби, и любая непериодическая дробь является иррациональным числом. |
Каждому действительному числу отвечает точка на координатной прямой, и наоборот, каждая точка на координатной прямой соответствует действительному числу. Действительно, для любой точки координатной прямой достаточно найти расстояние до неё от начала координат, а потом поставить перед этим числом знак плюс (+), если точка располагается правее начала координат, и знак минус (–) – если левее.
Изученные множества чисел обозначаются следующим образом:
Множество целых чисел содержится во множестве рациональных чисел которое, в свою очередь, является частью всего множества действительных чисел Эти отношения можно записать кратко в виде ,
Совершенно аналогично десятичным дробям вводятся правила действия над действительными числами.
Сложение. Сумма двух действительных чисел одного знака есть число того же знака. Модуль такой суммы равен сумме модулей слагаемых.
Пример 1Вычислить (+2) + (+3).
|
(+2) + (+3) = (+5). Ответ. –5. |
Сумма двух действительных чисел разных знаков имеет тот же знак, что и большее по модулю слагаемое. Модуль суммы равен разности модулей большего и меньшего слагаемых.
Модуль суммы равен разности модулей большего и меньшего слагаемых.
|
(+2) + (–3) = (–1). Ответ. –1. |
Вычитание. Чтобы вычесть из одного действительного числа другое действительное число, нужно к уменьшаемому прибавить число, противоположное вычитаемому.
Пример 3Вычислить (+2) – (–3).
|
(+2) – (–3) = 2 + 3 = 5. Ответ. +5. |
Умножение и деление. Произведение (частное) двух действительных чисел одного знака есть число положительное. Произведение (частное) двух действительных чисел разных знаков есть число отрицательное. Модуль произведения (частного) двух действительных чисел равен произведению (частному) модулей этих чисел.
Модуль произведения (частного) двух действительных чисел равен произведению (частному) модулей этих чисел.
Вычислить (+2) ∙ (–3).
| Ответ. –6. |
Арифметические операции над действительными числами обладают следующими свойствами (основные законы алгебры).
- a + b = b + a (переместительный закон сложения).
- (a + b) + c = a + (b + c) (сочетательный закон сложения).
- a + 0 = a (свойство нуля).
- a + (–a) = 0 (свойство противоположного числа).
- ab = ba (переместительный закон умножения).
- ab(c) = a(bc) (сочетательный закон).
- a(b + c) = ab + ac (распределительный закон умножения относительно сложения).
- a · 1 = a (основное свойство единицы).
-
(существование обратного числа).

Сравнение действительных чисел производится совершенно аналогично сравнению рациональных чисел. А именно, говорят, что действительное число a больше другого действительного числа b, и обозначают этот факт так: a > b, если разность (a – b) – положительное действительное число. Говорят, что действительное число a меньше другого действительного числа b, и обозначают этот факт так: a < b, если разность (a – b) – отрицательное действительное число. На действительные числа совершенно аналогично переносятся понятия отношений ≤ и ≥. При этом числовые неравенства обладают следующими свойствами:
- Если a > b, то b < a.
- Если a > b и b > c, то a > c (свойство транзитивности).
- Если a > b, то a + c > b + c.
- Если a > b и c > 0, то ac > bc.
- Если a > b и c < 0, то ac < bc.
- Если a > b и c > d, то a + c > b + d.
- Если a, b, c, d > 0, причём a > b и c > d, то ac > bd.

- Если a > b и c < d, то a – c > b – d.
- Если то
- Если то для любого натурального числа n справедливо неравенство
Кратко:
Иррациональное число — Квадратный Корень
Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби , где — целые числа, . Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Множество иррациональных чисел обычно обозначается заглавной латинской буквой в полужирном начертании без заливки. Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.
Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.
О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .
Свойства
- Всякое вещественное число может быть записано в виде бесконечной десятичной дроби, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
- Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
- Каждое вещественное трансцендентное число является иррациональным.
- Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
- Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.

- Порядок на множестве иррациональных чисел изоморфен порядку на множестве вещественных трансцендентных чисел.
- Множество иррациональных чисел несчётно, является множеством второй категории.[1]
Примеры
Иррациональными являются:
Примеры доказательства иррациональности
Корень из 2
Допустим противное: рационален, то есть представляется в виде несократимой дроби , где — целое число, а — натуральное число. Возведём предполагаемое равенство в квадрат:
- .
Отсюда следует, что чётно, значит, чётно и . Пускай , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Двоичный логарифм числа 3
Допустим противное: рационален, то есть представляется в виде дроби , где и — целые числа. Поскольку , и могут быть выбраны положительными. Тогда
Тогда
Но чётно, а нечётно. Получаем противоречие.
eСм. раздел «Доказательство иррациональности» в статье «e».
История
Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.
Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу,
который нашёл это доказательство, изучая длины сторон пентаграммы. Во
времена пифагорейцев считалось, что существует единая единица длины,
достаточно малая и неделимая, которая целое число раз входит в любой
отрезок. Однако Гиппас обосновал, что не существует единой единицы
длины, поскольку предположение о её существовании приводит к
противоречию. Он показал, что если гипотенуза равнобедренного
прямоугольного треугольника содержит целое число единичных отрезков, то
это число должно быть одновременно и четным, и нечетным.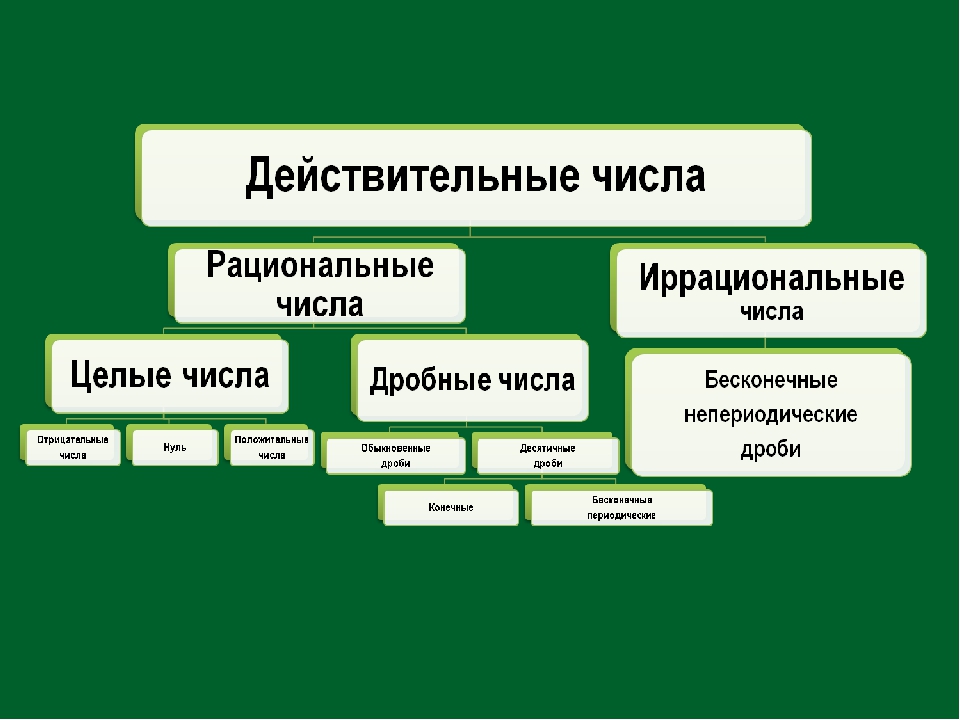 Доказательство
выглядело следующим образом:
Доказательство
выглядело следующим образом:
- Отношение длины гипотенузы к длине катета равнобедренного прямоугольного треугольника может быть выражено как a:b, где a и b выбраны наименьшими из возможных.
- По теореме Пифагора: a² = 2b².
- Так как a² четное, a должно быть четным (так как квадрат нечетного числа был бы нечетным).
- Поскольку a:b несократима, b обязано быть нечетным.
- Так как a четное, обозначим a = 2y.
- Тогда a² = 4y² = 2b².
- b² = 2y², следовательно b² четное, тогда и b четно.
- Однако было доказано, что b нечетное. Противоречие.
Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного
уважения. Существует легенда, что Гиппас совершил открытие, находясь в
морском походе, и был выброшен за борт другими пифагорейцами «за
создание элемента вселенной, который отрицает доктрину, что все сущности
во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную
проблему, разрушив лежавшее в основе всей теории предположение, что
числа и геометрические объекты едины и неразделимы.
Открытие Гиппаса поставило перед пифагорейской математикой серьёзную
проблему, разрушив лежавшее в основе всей теории предположение, что
числа и геометрические объекты едины и неразделимы.
Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе — на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.
Позже Евдокс Книдский
(410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию
пропорций, которая принимала во внимание как рациональные, так и
иррациональные отношения. Это послужило основанием для понимания
фундаментальной сути иррациональных чисел. Величина стала считаться не
числом, но обозначением сущностей, таких как отрезки прямых, углы,
площади, объёмы, промежутки времени — сущностей, которые могут меняться
непрерывно (в современном понимании этого слова). Величины были
противопоставлены числам, которые могут меняться лишь «прыжками» от
одного числа к соседнему, например, с 4 на 5. Числа составляются из
наименьшей неделимой величины, в то время как величины можно уменьшать
бесконечно.
Это послужило основанием для понимания
фундаментальной сути иррациональных чисел. Величина стала считаться не
числом, но обозначением сущностей, таких как отрезки прямых, углы,
площади, объёмы, промежутки времени — сущностей, которые могут меняться
непрерывно (в современном понимании этого слова). Величины были
противопоставлены числам, которые могут меняться лишь «прыжками» от
одного числа к соседнему, например, с 4 на 5. Числа составляются из
наименьшей неделимой величины, в то время как величины можно уменьшать
бесконечно.
Поскольку никакое количественное значение не сопоставлялось величине,
Евдокс смог охватить и соизмеримые, и несоизмеримые величины при
определении дроби как отношения двух величин, и пропорции как равенства
двух дробей. Убрав из уравнений количественные значения (числа), он
избежал ловушки, состоящей в необходимости назвать иррациональную
величину числом. Теория Евдокса позволила греческим математикам
совершить невероятный прогресс в геометрии, предоставив им необходимое
логическое обоснование для работы с несоизмеримыми величинами. «Книга 10
Элементов» Евклида посвящена классификации иррациональных величин.
«Книга 10
Элементов» Евклида посвящена классификации иррациональных величин.
Средние века
Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.
Арабские математики соединили древнегреческие понятия «числа» и
«величины» в единую, более общую идею вещественных чисел. Они критически
относились к представлениям Евклида об отношениях, в противовес ей они
развили теорию отношений произвольных величин и расширили понятие числа
до отношений непрерывных величин. В своих комментариях на Книгу 10
Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.)
исследовал и классифицировал квадратичные иррациональные числа (числа
вида) и более общие кубические иррациональные числа. Он дал определение
рациональным и иррациональным величинам, которые он и называл
иррациональными числами. Он легко оперировал этими объектами, но
рассуждал как об обособленных объектах, например:
Он дал определение
рациональным и иррациональным величинам, которые он и называл
иррациональными числами. Он легко оперировал этими объектами, но
рассуждал как об обособленных объектах, например:
| Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 — не являющихся квадратами. |
В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:
результат сложения
иррациональной величины и рациональной, результат вычитания рациональной
величины из иррациональной, результат вычитания иррациональной величины
из рациональной. |
Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:
Пусть единична величина
содержится в данной величине один или несколько раз, тогда эта [данная]
величина соответствует целому числу… Каждая величина, которая составляет
половину, или треть, или четверть единичной величины, или, сравненная с
единичной величиной составляет три пятых от нее, это рациональная
величина. И в целом, всякая величина, которая относится к единичной как
одно число к другому, является рациональной. Если же величина не может
быть представлена как несколько или часть (l/n), или несколько частей
(m/n) единичной длины, она иррациональная, то есть невыразимая иначе как
с помощью корней. И в целом, всякая величина, которая относится к единичной как
одно число к другому, является рациональной. Если же величина не может
быть представлена как несколько или часть (l/n), или несколько частей
(m/n) единичной длины, она иррациональная, то есть невыразимая иначе как
с помощью корней. |
Многие из этих идей были позже переняты европейскими математиками
после перевода на латынь арабских текстов в XII веке. Аль Хассар,
арабский математик из Магриба, специализировавшийся на исламских законах
о наследстве, в XII веке ввел современную символьную математическую
нотацию для дробей, разделив числитель и знаменатель горизонтальной
чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В
течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской
школы астрономии и математики исследовали бесконечные ряды, сходящиеся к
некоторым иррациональным числам, например, к π, а также показали
иррациональность некоторых тригонометрических функций. Джестадева привел
эти результаты в книге Йуктибхаза.
Джестадева привел
эти результаты в книге Йуктибхаза.
Наше время
В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер
(1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и
чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные
(доказав при этом существование трансцендентных чисел), тем самым
переосмыслив работы Евклида по классификации иррациональных чисел. По
этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ
начал рассмотрения, схожие с Гейне, именно 1872 год принято считать
годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои
теории при помощи бесконечных рядов, в то время как Дедекинд работал с
(ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.
Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.
В 1761 году Ламберт показал, что π не может быть рационально, а также что eⁿ иррационально при любом ненулевом рациональном n.
Хотя доказательство Ламберта можно назвать незавершённым, принято
считать его достаточно строгим, особенно учитывая время его написания.
Лежандр в 1794 году, после введения функции Бесселя-Клиффорда, показал,
что π² иррационально, откуда иррациональность π следует тривиально (рациональное число в квадрате дало бы рациональное). Существование трансцендентных чисел было доказано Лиувиллем
в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование,
используя другой метод, и обосновал, что любой интервал вещественного
ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.
Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.
Рациональные и иррациональные числа
Ранее мы уже показали, что $1\frac25$ — близко к $\sqrt2$. Если бы оно точно равнялось $\sqrt2$, задача была бы решена. Тогда соотношение — $\frac{1\frac25}{1}$, которое можно превратить в соотношение целых чисел $\frac75$, умножив верхнюю и нижнюю части дроби на 5, и было бы искомой величиной.
Но, к сожалению, $1\frac25$ не является точной величиной $\sqrt2$. Более точный ответ $1\frac{41}{100}$, дает нам соотношение $\frac{141}{100}$. Еще большей точности мы достигаем, когда приравниваем $\sqrt2$ к $1\frac{207}{500}$. В этом случае соотношение в целых числах будет равно $\frac{707}{500}$. Но и $1\frac{207}{500}$ не является точным значением корня квадратного из 2. Греческие математики потратили массу времени и сил, чтобы вычислить точное значение $\sqrt2$, но это им так и не удалось. Они не смогли представить соотношение $\frac{\sqrt2}{1}$ в виде соотношения целых чисел.
Но и $1\frac{207}{500}$ не является точным значением корня квадратного из 2. Греческие математики потратили массу времени и сил, чтобы вычислить точное значение $\sqrt2$, но это им так и не удалось. Они не смогли представить соотношение $\frac{\sqrt2}{1}$ в виде соотношения целых чисел.
Наконец, великий греческий математик Евклид доказал, что, как бы ни увеличивалась точность подсчетов, получить точное значение $\sqrt2$ невозможно. Не существует такой дроби, которая, будучи возведена в квадрат, даст в результате 2. Говорят, что первым к этому заключению пришел Пифагор, но этот необъяснимый факт настолько поразил ученого, что он поклялся сам и взял со своих учеников клятву хранить это открытие в тайне. Однако, возможно, эти сведения не соответствуют действительности.
Но если число $\frac{\sqrt2}{1}$ не может быть представлено в виде соотношения целых чисел, то и никакая дробь, содержащая $\sqrt2$, например $\frac{\sqrt2}{2}$ или $\frac{4}{\sqrt2}$ также не может быть представлена в виде соотношения целых чисел, поскольку все такие дроби могут быть преобразованы в $\frac{\sqrt2}{1}$, умноженное на какое нибудь число. Так $\frac{\sqrt2}{2}=\frac{\sqrt2}{1} \times \frac12$. Или $\frac{\sqrt2}{1} \times 2=2\frac{\sqrt2}{1}$, что можно преобразовать, умножив верхнюю и нижнюю части на $\sqrt2$, и получить $\frac{4}{\sqrt2}$. (Не следует забывать, что независимо от того, что представляет собой число $\sqrt2$, если мы умножим его на $\sqrt2$, то получим 2.)
Так $\frac{\sqrt2}{2}=\frac{\sqrt2}{1} \times \frac12$. Или $\frac{\sqrt2}{1} \times 2=2\frac{\sqrt2}{1}$, что можно преобразовать, умножив верхнюю и нижнюю части на $\sqrt2$, и получить $\frac{4}{\sqrt2}$. (Не следует забывать, что независимо от того, что представляет собой число $\sqrt2$, если мы умножим его на $\sqrt2$, то получим 2.)
Поскольку число $\sqrt2$ нельзя представить в виде соотношения целых чисел, оно получило название иррационального числа. С другой стороны, все числа, которые можно представить в виде соотношения целых чисел, называются рациональными.
Рациональными являются все целые и дробные числа, как положительные, так и отрицательные.
Как оказалось, большинство квадратных корней являются иррациональными числами. Рациональные квадратные корни есть только у чисел, входящих в ряд квадратных чисел. Эти числа называются также идеальными квадратами. Рациональными числами являются также дроби, составленные из этих идеальных квадратов. Например, $\sqrt{1\frac79}$ является рациональным числом, так как $\sqrt{1\frac79}=\frac{\sqrt16}{\sqrt9}=\frac43$ или $1\frac13$ ( 4 — это корень квадратный из 16, а 3 — корень квадратный из 9).
Например, $\sqrt{1\frac79}$ является рациональным числом, так как $\sqrt{1\frac79}=\frac{\sqrt16}{\sqrt9}=\frac43$ или $1\frac13$ ( 4 — это корень квадратный из 16, а 3 — корень квадратный из 9).
Материалы по теме:
Поделиться с друзьями:
Загрузка…Разница между рациональными и иррациональными числами
Математика — не что иное, как игра чисел. Число — это арифметическое значение, которое может быть цифрой, словом или символом, обозначающим количество, которое имеет много последствий, таких как подсчет, измерения, вычисления, маркировка и т. Д. Числа могут быть натуральными числами, целыми числами, целыми числами, действительными числами, сложными номера. Действительные числа далее делятся на рациональные числа и иррациональные числа. Рациональные числа — это числа, которые являются целыми и дробнымиС другой стороны, иррациональные числа — это числа, выражение которых в виде дроби невозможно. В этой статье мы собираемся обсудить различия между рациональными и иррациональными числами. Посмотри.
В этой статье мы собираемся обсудить различия между рациональными и иррациональными числами. Посмотри.
Сравнительная таблица
| Основа для сравнения | Рациональное число | Иррациональные числа |
|---|---|---|
| Имея в виду | Рациональные числа относятся к числу, которое может быть выражено в соотношении двух целых чисел. | Иррациональное число — это число, которое нельзя записать в виде отношения двух целых чисел. |
| Доля | Выражается в дроби, где знаменатель ≠ 0. | Не может быть выражено в долях. |
| Включает в себя | Совершенные квадраты | Surds |
| Десятичное расширение | Конечные или повторяющиеся десятичные дроби | Не конечные или не повторяющиеся десятичные дроби. |
Определение рациональных чисел
Термин «отношение» получен из слова «отношение», которое означает сравнение двух величин и выражается в простой дроби. Число называется рациональным, если оно может быть записано в виде дроби, такой как p / q, где и p (числитель), и q (знаменатель) являются целыми числами, а знаменатель — натуральное число (ненулевое число). Целые числа, дроби, включая смешанную дробь, повторяющиеся десятичные дроби, конечные десятичные дроби и т. Д., Являются рациональными числами.
Целые числа, дроби, включая смешанную дробь, повторяющиеся десятичные дроби, конечные десятичные дроби и т. Д., Являются рациональными числами.
Примеры рационального числа
- 1/9 — числитель и знаменатель являются целыми числами.
- 7 — Можно выразить как 7/1, где 7 — это целое число 7 и 1.
- √16 — поскольку квадратный корень может быть упрощен до 4, что является частным дроби 4/1
- 0, 5 — Может быть записано как 5/10 или 1/2, и все заканчивающиеся десятичные дроби являются рациональными.
- 0.3333333333 — Все повторяющиеся десятичные дроби рациональны.
Определение иррациональных чисел
Число называется иррациональным, когда его нельзя упростить до какой-либо доли целого числа (x) и натурального числа (y). Это также может быть понято как число, которое нерационально. Десятичное разложение иррационального числа не является ни конечным, ни повторяющимся. Он включает в себя дополнительные числа и специальные числа, такие как π («пи» — наиболее распространенное иррациональное число) и e. Surd — это несовершенный квадрат или куб, который нельзя уменьшить, чтобы удалить квадратный корень или кубический корень.
Surd — это несовершенный квадрат или куб, который нельзя уменьшить, чтобы удалить квадратный корень или кубический корень.
Примеры иррационального числа
- √2 — √2 не может быть упрощено, и поэтому оно нерационально.
- √7 / 5 — данное число является дробью, но это не единственный критерий, который следует называть рациональным числом. И числитель, и знаменатель должны быть целыми числами, а √7 не является целым числом. Следовательно, данное число нерационально.
- 3/0 — дробь с нулевым знаменателем, иррациональна.
- π — поскольку десятичное значение π никогда не заканчивается, никогда не повторяется и никогда не показывает какого-либо шаблона. Следовательно, значение pi не точно равно любой дроби. Число 22/7 является справедливым и приблизительным.
- 0.3131131113 — Десятичные дроби не заканчиваются и не повторяются. Поэтому его нельзя выразить как частное от дроби.
Ключевые различия между рациональными и иррациональными числами
Различие между рациональными и иррациональными числами может быть ясно показано на следующих основаниях
- Рациональное число определяется как число, которое может быть записано в соотношении двух целых чисел.
 Иррациональное число — это число, которое не может быть выражено в соотношении двух целых чисел.
Иррациональное число — это число, которое не может быть выражено в соотношении двух целых чисел. - В рациональных числах и числитель, и знаменатель являются целыми числами, где знаменатель не равен нулю. Пока иррациональное число нельзя записать дробью.
- Рациональное число включает числа, которые являются идеальными квадратами, такими как 9, 16, 25 и так далее. С другой стороны, иррациональное число включает в себя такие числа, как 2, 3, 5 и т. Д.
- Рациональное число включает только те десятичные дроби, которые являются конечными и повторяющимися. Наоборот, иррациональные числа включают те числа, десятичное разложение которых бесконечно, неповторяюще и не показывает паттерна.
Заключение
Изучив вышеприведенные пункты, совершенно ясно, что выражение рациональных чисел может быть возможным как в дробной, так и в десятичной форме. Напротив, иррациональное число может быть представлено только в десятичной форме, но не в виде дроби. Все целые числа являются рациональными числами, но все нецелые числа не являются иррациональными числами.
Определение рациональных и иррациональных чисел
Результаты обучения
- Определить рациональные числа из списка чисел
- Определите иррациональные числа из списка чисел
В этой главе мы позаботимся о том, чтобы ваши навыки твердо закрепились. Мы еще раз взглянем на типы чисел, с которыми работали во всех предыдущих главах. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа.И мы будем практиковаться в их использовании, как при решении уравнений и выполнении других процедур в алгебре.
Мы уже описали числа как счетные числа, целые числа и целые числа. Вы помните, в чем разница между этими типами чисел?
| счетные числа | [латекс] 1,2,3,4 \ точки [/ латекс] |
| целые числа | [латекс] 0,1,2,3,4 \ точки [/ латекс] |
| целые числа | [латекс] \ точки -3, -2, -1,0,1,2,3,4 \ точки [/ латекс] |
Рациональные числа
Какой тип чисел вы получите, если начнете со всех целых чисел, а затем включите все дроби? Числа, которые у вас будут, образуют набор рациональных чисел. Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональные числа
Рациональное число — это число, которое может быть записано в форме [латекс] \ frac {p} {q} [/ latex], где [latex] p [/ latex] и [latex] q [/ latex] — целые числа. и [латекс] q \ ne o [/ латекс].
Все дроби, как положительные, так и отрицательные, являются рациональными числами. Несколько примеров:
[латекс] \ frac {4} {5}, — \ frac {7} {8}, \ frac {13} {4}, \ text {and} — \ frac {20} {3} [/ latex]
Каждый числитель и каждый знаменатель — целое число.
Нам нужно посмотреть на все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы посмотрим на счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Целые числа являются рациональными числами? Чтобы решить, является ли целое число рациональным числом, мы пытаемся записать его как отношение двух целых чисел. Легкий способ сделать это — записать дробь со знаминателем один.
Легкий способ сделать это — записать дробь со знаминателем один.
[латекс] 3 = \ frac {3} {1} -8 = \ frac {-8} {1} 0 = \ frac {0} {1} [/ latex]
Поскольку любое целое число можно записать как отношение двух целых чисел, все целые числа являются рациональными числами.Помните, что все счетные числа и все целые числа также являются целыми числами, а значит, они тоже рациональны.
А как насчет десятичных знаков? Они рациональны? Давайте посмотрим на некоторые из них, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа — это рациональные числа. Целое число [латекс] -8 [/ латекс] может быть записано как десятичное [латекс] -8,0 [/ латекс]. Итак, очевидно, что некоторые десятичные дроби рациональны.
Подумайте о десятичном [латексе] 7.3 [/ латексе]. Можем ли мы записать это как отношение двух целых чисел? Потому что [латекс] 7.3 [/ latex] означает [latex] 7 \ frac {3} {10} [/ latex], мы можем записать это как неправильную дробь, [latex] \ frac {73} {10} [/ latex]. Итак, [latex] 7.3 [/ latex] — это соотношение целых чисел [latex] 73 [/ latex] и [latex] 10 [/ latex]. Это рациональное число.
Итак, [latex] 7.3 [/ latex] — это соотношение целых чисел [latex] 73 [/ latex] и [latex] 10 [/ latex]. Это рациональное число.
В общем, любое десятичное число, которое заканчивается рядом цифр, например [latex] 7.3 [/ latex] или [latex] -1.2684 [/ latex], является рациональным числом. Мы можем использовать разряд последней цифры в качестве знаменателя при записи десятичной дроби в виде дроби.
пример
Запишите каждое как отношение двух целых чисел:
1. [латекс] -15 [/ латекс]
2. [латекс] 6.81 [/ латекс]
3. [латекс] -3 \ frac {6} {7} [/ латекс]
Решение:
| 1. | |
| [латекс] -15 [/ латекс] | |
| Запишите целое число в виде дроби со знаминателем 1. | [латекс] \ frac {-15} {1} [/ латекс] |
| 2. | |
| [латекс] 6,81 [/ латекс] | |
Запишите десятичную дробь как смешанное число. | [латекс] 6 \ frac {81} {100} [/ латекс] |
| Затем преобразовать его в неправильную дробь. | [латекс] \ frac {681} {100} [/ латекс] |
| 3. | |
| [латекс] -3 \ frac {6} {7} [/ латекс] | |
| Преобразование смешанного числа в неправильную дробь. | [латекс] — \ frac {27} {7} [/ латекс] |
Давайте посмотрим на десятичную форму чисел, которые, как мы знаем, рациональны.Мы видели, что каждое целое число является рациональным числом, поскольку [latex] a = \ frac {a} {1} [/ latex] для любого целого числа, [latex] a [/ latex]. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.
Целое число [латекс] -2, -1,0,1,2,3 [/ латекс]
Десятичное [латекс] -2.0, -1.0,0.0,1.0,2.0,3.0 [/ latex]
Эти десятичные числа останавливаются.
Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму только что рассмотренных дробей.
Соотношение целых чисел [latex] \ frac {4} {5}, \ frac {7} {8}, \ frac {13} {4}, \ frac {20} {3} [/ latex]
Десятичные формы [латекс] 0.8, -0.875,3.25, -6.666 \ ldots, -6. \ Overline {66} [/ latex]
Эти десятичные дроби либо останавливаются, либо повторяются.
Что вам говорят эти примеры? Каждое рациональное число можно записать как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассматривали, выраженные как отношение целых чисел и десятичной дроби.
| Рациональные числа | ||
|---|---|---|
| Фракции | Целые числа | |
| Номер | [латекс] \ frac {4} {5}, — \ frac {7} {8}, \ frac {13} {4}, \ frac {-20} {3} [/ latex] | [латекс] -2,1,0,1,2,3 [/ латекс] |
| Коэффициент целого числа | [латекс] \ frac {4} {5}, \ frac {-7} {8}, \ frac {13} {4}, \ frac {-20} {3} [/ latex] | [латекс] \ frac {-2} {1}, \ frac {-1} {1}, \ frac {0} {1}, \ frac {1} {1}, \ frac {2} {1} , \ frac {3} {1} [/ latex] |
| Десятичное число | [латекс] 0. 8, -0,875,3,25, -6. \ Overline {6} [/ латекс] 8, -0,875,3,25, -6. \ Overline {6} [/ латекс] | [латекс] -2.0, -1.0,0.0,1.0,2.0,3.0 [/ латекс] |
Иррациональные числа
Есть ли десятичные дроби, которые не останавливаются и не повторяются? Да. Число [латекс] \ пи [/ латекс] (греческая буква пи, произносится как «пирог»), которое очень важно при описании кругов, имеет десятичную форму, которая не останавливается и не повторяется.
[latex] \ pi = \ text {3.141592654 …….} [/ Latex]
Точно так же десятичные представления квадратных корней чисел, которые не являются точными квадратами, никогда не прекращаются и никогда не повторяются.Например,
[latex] \ sqrt {5} = \ text {2.236067978… ..} [/ latex]
Десятичное число, которое не останавливается и не повторяется, не может быть записано как отношение целых чисел. Мы называем такое число иррациональным числом.
Иррациональное число
Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не останавливается и не повторяется.
Его десятичная форма не останавливается и не повторяется.
Давайте резюмируем метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа
- остановок или повторений, количество рациональное.
- не останавливается и не повторяется, цифра иррациональна.
пример
Определите каждое из следующего как рациональное или иррациональное:
1. [латекс] 0,58 \ overline {3} [/ латекс]
2. [латекс] 0,475 [/ латекс]
3. [латекс] 3,605551275 \ точки [/ латекс ]
Решение:
1. [latex] 0.58 \ overline {3} [/ latex]
Полоса над [latex] 3 [/ latex] указывает на то, что это повторяется.Следовательно, [латекс] 0,58 \ overline {3} [/ latex] является повторяющимся десятичным числом и, следовательно, является рациональным числом.
2. [latex] 0,475 [/ latex]
Эта десятичная дробь останавливается после [latex] 5 [/ latex], так что это рациональное число. {2} = 36 [/ латекс].{2} = 49 [/ latex], поэтому [latex] 44 [/ latex] не является идеальным квадратом.
{2} = 36 [/ латекс].{2} = 49 [/ latex], поэтому [latex] 44 [/ latex] не является идеальным квадратом.
Это означает, что [latex] \ sqrt {44} [/ latex] нерационально.
В следующем видео мы покажем больше примеров того, как определить, является ли число иррациональным или рациональным.
Рациональные и иррациональные числа | Алгебраические выражения
1.3 Рациональные и иррациональные числа (EMA4)
- Рациональное число
Рациональное число (\ (\ mathbb {Q} \)) — это любое число, которое можно записать как:
\ [\ frac {a} {b} \], где \ (a \) и \ (b \) — целые числа, а \ (b \ ne 0 \).
Все следующие числа являются рациональными числами:
\ [\ frac {10} {1} \; ; \; \ frac {21} {7} \; ; \; \ frac {-1} {- 3} \; ; \; \ frac {10} {20} \; ; \; \ frac {-3} {6} \] Мы видим, что все числители и все знаменатели целые.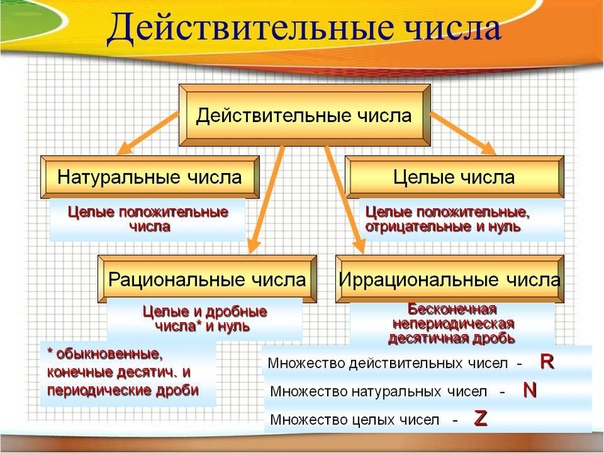
Это означает, что все целые числа являются рациональными числами, поскольку они могут быть записаны со знаменателем \ (\ text {1} \).
- Иррациональные числа
Иррациональные числа (\ (\ mathbb {Q} ‘\)) — это числа, которые нельзя записать в виде дроби с числителем и знаменателем в виде целых чисел.
Примеры иррациональных чисел:
\ [\ sqrt {2} \; ; \; \ sqrt {3} \; ; \; \ sqrt [3] {4} \; ; \; \Пи \; ; \; \ frac {1 + \ sqrt {5}} {2} \]Это не рациональные числа, потому что числитель или знаменатель не является целым числом.
Десятичные числа (EMA5)
Все целые числа и дроби с целыми числителями и ненулевым целым знаменателем являются рациональными числами. Помните, что когда знаменатель дроби равен нулю, дробь не определена.
Вы можете записать любое рациональное число в виде десятичного числа, но не все десятичные числа являются рациональными числами. Эти типы десятичных чисел являются рациональными числами:
Десятичные числа, которые заканчиваются (или заканчиваются).
 Например, дробь \ (\ frac {4} {10} \) может быть записана как \ (\ text {0,4} \).
Например, дробь \ (\ frac {4} {10} \) может быть записана как \ (\ text {0,4} \).Десятичные числа, состоящие из одной повторяющейся цифры. Например, дробь \ (\ frac {1} {3} \) может быть записана как \ (\ text {0,} \ dot {3} \) или \ (\ text {0,} \ overline {3} \).Обозначения точки и полосы эквивалентны и оба представляют собой повторяющиеся символы \ (\ text {3} \), то есть \ (\ text {0,} \ dot {3} = \ text {0,} \ overline {3} = \ text {0,333 …} \).
Десятичные числа, повторяющиеся из нескольких цифр. Например, дробь \ (\ frac {2} {11} \) также может быть записана как \ (\ text {0,} \ overline {18} \). Полоса представляет собой повторяющийся узор из \ (\ text {1} \) и \ (\ text {8} \), то есть \ (\ text {0,} \ overline {18} = \ text {0 , 181818…} \).
Вы можете увидеть точку вместо запятой, используемой для обозначения десятичного числа. Таким образом, число \ (\ text {0,4} \) также можно записать как 0,4
Таким образом, число \ (\ text {0,4} \) также можно записать как 0,4
Обозначение: Вы можете использовать точку или черту над повторяющимися цифрами, чтобы указать, что десятичная дробь является повторяющейся десятичной. Если полоса охватывает более одной цифры, то все числа под полосой повторяются.
Если вас просят определить, является ли число рациональным или иррациональным, сначала запишите число в десятичной форме.Если число заканчивается, то это рационально. Если так будет продолжаться вечно, ищите повторяющийся набор цифр. Если нет повторяющегося рисунка, то цифра иррациональна.
Когда вы записываете иррациональные числа в десятичной форме, вы можете продолжать записывать их для многих, многих десятичных знаков. Однако это неудобно и часто необходимо округлять.
Округление иррационального числа делает его рациональным числом, которое приближается к иррациональному числу.
Рабочий пример 1: Рациональные и иррациональные числа
Какие из следующих чисел не являются рациональными?
\ (\ pi = \ text {3,14159265358979323846264338327950288419716939937510 .
 ..} \)
..} \)\ (\ text {1,4} \)
\ (\ text {1,618033989…} \)
\ (\ text {100} \)
\ (\ text {1,7373737373 …} \)
\ (\ text {0,} \ overline {02} \)
Иррациональная, десятичная дробь не прерывается и не повторяется.
Рациональное, десятичное завершение.
Иррациональная, десятичная дробь не прерывается и не повторяется.
Рационально, все числа рациональны.

Рациональное десятичное число имеет повторяющийся образец.
Рациональное десятичное число имеет повторяющийся образец.
Преобразование конечных десятичных дробей в рациональные числа (EMA6)
Десятичное число состоит из целой и дробной части. Например, \ (\ text {10,589} \) имеет целую часть \ (\ text {10} \) и дробную часть \ (\ text {0,589} \), потому что \ (10 + \ text {0,589} = \ текст {10,589} \).
Каждая цифра после десятичной точки представляет собой дробь со знаменателем в возрастающей степени \ (\ text {10} \).
Например:
\ (\ text {0,1} \) равно \ (\ frac {1} {\ text {10}} \)
\ (\ text {0,01} \) равно \ (\ frac {1} {\ text {100}} \)
\ (\ text {0,001} \) равно \ (\ frac {1} {\ text {1 000}} \)
Это означает, что
\ begin {align *} \ text {10,589} & = 10 + \ frac {5} {10} + \ frac {8} {100} + \ frac {9} {\ text {1 000}} \\ & = \ frac {\ text {10 000}} {\ text {1 000}} + \ frac {\ text {500}} {\ text {1 000}} + \ frac {80} {\ text {1 000 }} + \ frac {9} {\ text {1 000}} \\ & = \ frac {\ text {10 589}} {\ text {1 000}} \ end {выровнять *}В следующих двух видеороликах объясняется, как преобразовать десятичные дроби в рациональные числа.
Часть 1
Видео: 2DBJ
Часть 2
Видео: 2DBK
Преобразование повторяющихся десятичных знаков в рациональные числа (EMA7)
Когда десятичная дробь является повторяющейся десятичной дробью, требуется немного больше работы, чтобы записать дробную часть десятичного числа в виде дроби.
Рабочий пример 2: Преобразование десятичных чисел в дроби
Запишите \ (\ text {0,} \ dot {3} \) в форме \ (\ frac {a} {b} \) (где \ (a \) и \ (b \) — целые числа).
Определите уравнение
\ [\ text {Let} x = \ text {0,33333 …} \]Умножить на \ (\ text {10} \) с обеих сторон
\ [10x = \ текст {3,33333 …} \]Вычтем первое уравнение из второго
\ [9x = 3 \]Упростить
\ [x = \ frac {3} {9} = \ frac {1} {3} \]Рабочий пример 3: Преобразование десятичных чисел в дроби
Запишите \ (\ text {5,} \ dot {4} \ dot {3} \ dot {2} \) в виде рациональной дроби.
Определите уравнение
\ [x = \ текст {5,432432432 …} \]Умножить на \ (\ text {1 000} \) с обеих сторон
\ [\ text {1 000} x = \ text {5 432,432432432 …} \]Вычтем первое уравнение из второго
\ [\ text {999} x = \ text {5 427} \]Упростить
\ [x = \ frac {\ text {5 427}} {\ text {999}} = \ frac {\ text {201}} {\ text {37}} = \ text {5} \ frac {\ text { 16}} {\ text {37}} \]В первом примере десятичное число было умножено на \ (\ text {10} \), а во втором примере десятичное число было умножено на \ (\ text {1 000} \).Это потому, что в первом примере повторялась только одна цифра (т.е. \ (\ text {3} \)), а во втором — три повторяющиеся цифры (т.е. \ (\ text {432} \)).
В общем, если у вас повторяется одна цифра, умножьте ее на \ (\ text {10} \). Если у вас повторяются две цифры, умножьте их на \ (\ text {100} \). Если у вас повторяются три цифры, умножьте их на \ (\ text {1 000} \) и так далее.
Не все десятичные числа можно записать как рациональные числа. Почему? Иррациональные десятичные числа, например \ (\ sqrt {2} = \ text {1,4142135…} \) нельзя записать с целым числителем и знаменателем, потому что они не имеют шаблона повторяющихся цифр и не завершаются.
Вы справитесь! Позвольте нам помочь вам учиться с умом для достижения ваших целей. Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки Упражнение 1.1Какое место на диаграмме занимает число \ (- \ frac {12} {3} \)?
Сначала упростите дробь: \ (- \ frac {12} {3} = -4 \)
\ (- \ text {4} \) является целым числом, поэтому оно попадает в набор \ (\ mathbb {Z} \).
В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?
- Каждое целое число — натуральное число.
- Каждое натуральное число — это целое число.
- В целых числах нет десятичных знаков.
Тщательно обдумайте каждый вариант:
- Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
- Натуральные числа — это \ (\ left \ {1; 2; 3; \ ldots \ right \} \), а целые числа — это \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \ ) (круг \ (\ mathbb {N} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является натуральным числом, оно должно быть целым числом. Это верно.
- Целые числа \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным.
Итак, верно только (ii).
Какое место на диаграмме занимает число \ (- \ frac {1} {2} \)?
\ (- \ frac {1} {2} \) находится в своей простейшей форме, поэтому его нет в \ (\ mathbb {N} \), \ (\ mathbb {N} _0 \) или \ (\ mathbb {Z} \).Он находится в пространстве между прямоугольником и \ (\ mathbb {Z} \).
В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?
- Каждое целое число — натуральное число.
- Каждое целое число является целым.
- В целых числах нет десятичных знаков.
Тщательно обдумайте каждый вариант:
- Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
- Целые числа \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \), а целые числа — \ (\ left \ {0 ; 1; 2; 3; \ ldots \ right \} \) (круг \ (\ mathbb {Z} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является целым это должно быть целое число. Это верно.
- Целые числа \ (\ left \ {0; 1; 2; 3; 4; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным .
Итак, верно только (ii).
\ (- \ sqrt {3} \)
\ (- \ sqrt {3} \) не имеет знака минус под квадратным корнем (минус находится вне корня) и не делится на ноль, поэтому он действительный.
\ (\ dfrac {0} {\ sqrt {2}} \)
\ (\ dfrac {0} {\ sqrt {2}} \) не имеет знака минус под квадратным корнем (минус находится вне корня) и не делится на ноль, поэтому он действительный.
\ (\ sqrt {-9} \)
\ (\ sqrt {-9} \) имеет знак минус под квадратным корнем, поэтому он не является действительным.
\ (\ dfrac {- \ sqrt {7}} {0} \)
\ (\ dfrac {- \ sqrt {7}} {0} \) имеет деление на ноль, поэтому не определено.
\ (- \ sqrt {-16} \)
\ (- \ sqrt {-16} \) имеет отрицательное число под квадратным корнем, поэтому оно не является действительным.
\ (\ sqrt {2} \)
\ (\ sqrt {2} \) не имеет минуса под квадратным корнем (минус находится вне корня), не делится на ноль, поэтому он действительный.
\ (- \ frac {1} {3} \) рационально. Дробь целых чисел — это рациональное число.
\ (\ text {0,651268962154862.7 \) является рациональным, целым, целым и натуральным числом. Его можно записать как целое число.
\ (\ пи + 3 \)
\ (\ pi \) иррационально. \ (\ text {3} \) рационально (это целое число). Любое рациональное число, добавленное к любому иррациональному числу, иррационально.
Следовательно, \ (\ pi + 3 \) иррационально.
\ (\ пи + \ текст {0,858408346} \)
\ (\ pi \) иррационально.\ (\ text {0,858408346} \) является рациональным (это конечная десятичная дробь). Любое рациональное число, добавленное к любому иррациональному числу, иррационально.
Следовательно, \ (\ pi + \ text {0,858408346} \) иррационально.
\ (\ frac {5} {6} \) рационально.
Поскольку \ (a \) — целое число, \ (\ frac {a} {3} \) рационально.
Поскольку \ (b \) — целое число, \ (\ frac {-2} {b} \) рационально.
Обратите внимание, что \ (b \) не может быть \ (\ text {0} \), так как это делает дробь неопределенной.
Поскольку \ (c \) иррационально, \ (\ frac {1} {c} \) иррационально.
\ (\ frac {a} {14} = \ frac {1} {14} \) рационально.
\ (\ frac {a} {14} = \ frac {-10} {14} \) рационально.
\ (\ frac {a} {14} = \ frac {\ sqrt {2}} {14} \) иррационально.
\ (\ frac {a} {14} = \ frac {\ text {2,1}} {14} \) рационально.
Проверить, какое из чисел входит в набор \ (\ left \ {1; 2; 3; 4; \ ldots \ right \} \). Следовательно, \ (\ text {7} \) и \ (\ text {11} \) — натуральные числа.
Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- \ sqrt {8} \;; \; \ text {3,3231089 …} \;; \; 3+ \ sqrt {2} \;; \; \ pi \) все иррациональны.
Любое число, являющееся квадратным корнем из отрицательного числа, не является действительным.Следовательно, нереально только \ (\ sqrt {-1} \).
Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- 3 \;; \; 0 \;; \; -8 \ frac {4} {5} \;; \; \ frac {22} {7} \; \; 7 \;; \; \ text {1,} \ overline {34} \; \; 9 \ frac {7} {10} \;; \; 11 \) — все рациональные числа.
Проверьте, какое из чисел входит в набор \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \).Следовательно, \ (- 3 \;; \; 7 \;; \; 11 \) — целые числа.
Любая дробь, разделенная на \ (\ text {0} \), не определена. Следовательно, только \ (\ frac {14} {0} \) не определено.
\ (\ текст {2,121314 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни на одном из номеров нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Нерационально, нет повторяющегося рисунка.
\ (\ текст {1,242244246 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни на одном из номеров нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Нерационально, нет повторяющегося рисунка.
\ (\ текст {3,324354 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни на одном из номеров нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Нерационально, нет повторяющегося рисунка.
\ (\ текст {3,3243} \ dot {5} \ dot {4} \)
\ (\ text {0,1} = \ frac {1} {10} \)
\ begin {align *} \ text {0,12} & = \ frac {1} {10} + \ frac {2} {100} \\ & = \ frac {10} {100} + \ frac {2} {100} \\ & = \ frac {12} {100} \\ & = \ frac {3} {25} \ end {выровнять *}
\ begin {align *} \ text {0,58} & = \ frac {5} {10} + \ frac {8} {100} \\ & = \ frac {50} {100} + \ frac {8} {100} \\ & = \ frac {58} {100} \\ & = \ frac {29} {50} \ end {выровнять *}
\ begin {align *} \ text {0,2589} & = \ frac {2} {10} + \ frac {5} {100} + \ frac {8} {\ text {1 000}} + \ frac {9} {\ text { 10 000}} \\ & = \ frac {\ text {2 000}} {\ text {10 000}} + \ frac {500} {\ text {10 000}} + \ frac {80} {\ text {10 000}} + \ гидроразрыв {9} {\ text {10 000}} \\ & = \ frac {\ text {2 589}} {\ text {10 000}} \ end {выровнять *}
Мы видим, что повторяется только цифра \ (\ text {1} \), и поэтому мы можем записать это как: \ (\ text {0,} \ dot {1} \).
\ (\ text {0,1212121212 …} \)
Существует повторяющийся шаблон \ (\ text {12} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {12} \)
\ (\ text {0,123123123123 …} \)
Существует повторяющийся шаблон \ (\ text {123} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {123} \)
\ (\ text {0,11414541454145 …} \)
Шаблон 4145 повторяется, поэтому мы можем записать это число как: \ (\ text {0,11} \ overline {4145} \).7 \ текст {00}} & = \ текст {2} \ текст {остаток} \ текст {4} \\ \ frac {\ text {7}} {\ text {33}} & = \ text {0,} \ text {2 121} \ ldots \\ & = \ текст {0,} \ точка {\ текст {2}} \ точка {\ текст {1}} \ end {выровнять *}
\ begin {align *} \ frac {2} {3} & = 2 \ left (\ frac {1} {3} \ right) \\ & = 2 (\ text {0,333333 …}) \\ & = \ текст {0,666666 …} \\ & = \ текст {0,} \ точка {6} \ end {выровнять *}
\ begin {align *} 1 \ frac {3} {11} & = 1 + 3 \ left (\ frac {1} {11} \ right) \\ & = 1 + 3 (\ text {0,0
\ begin {align *} 4 \ frac {5} {6} & = 4 + 5 \ left (\ frac {1} {6} \ right) \\ & = 4+ 5 (\ text {0,1666666 …}) \\ & = 4 + \ текст {0,833333 …} \\ & = \ текст {4,8} \ точка {3} \ end {выровнять *}
\ begin {align *} 2 \ frac {1} {9} & = 2 + \ text {0,1111111 …} \\ & = \ текст {2,} \ точка {1} \ end {выровнять *}
\ begin {align *} х & = \ текст {0,55555…} \ text {и} \\ 10x & = \ text {5,55555 …} \\ 10x — x & = (\ text {5,55555 …}) — (\ text {0,55555 …}) \\ \ text {9} x & = \ text {5} \\ \ поэтому x & = \ frac {5} {9} \ end {выровнять *}
\ begin {align *} 10x & = \ text {6,3333 …} \ text {и} \\ 100x & = \ текст {63,3333 …} \\ 100x — 10x & = (\ text {63,3333 …}) — (\ text {6,3333 …}) \\ \ text {99} x & = \ text {57} \\ \ поэтому x & = \ frac {57} {90} \ end {выровнять *}
\ (\ текст {0,} \ точка {4} \)
\ begin {align *} х & = \ текст {0,4444…} \ text {и} \\ \ text {10} x & = \ text {4,4444 …} \\ 10x — x & = (\ text {4,4444 …}) — (\ text {0,4444 …}) \\ \ text {9} x & = \ text {4} \\ \ поэтому x & = \ frac {\ text {4}} {\ text {9}} \ end {выровнять *}
\ (\ text {5,} \ overline {31} \)
\ begin {align *} х & = \ текст {5,313131 …} \ текст {и} \\ 100x & = \ text {531,313131 …} \\ 100x — x & = (\ text {531,313131…}) — (\ text {5,313131 …}) \\ \ text {99} x & = \ text {526} \\ \ поэтому x & = \ frac {526} {99} \ end {выровнять *}
\ (\ text {4,} \ overline {\ text {93}} \)
\ begin {align *} х & = \ текст {4,939393 …} \ текст {и} \\ 100x & = \ text {493,939393 …} \\ 100x — x & = (\ text {493,939393 …}) — (\ text {4,939393 …}) \\ \ text {99} x & = \ text {489} \\ \ поэтому x & = \ frac {\ text {163}} {\ text {33}} \ end {выровнять *}
\ (\ text {3,} \ overline {\ text {93}} \)
\ begin {align *} х & = \ текст {3,939393…} \ text {и} \\ 100x & = \ text {393,939393 …} \\ 100x — x & = (\ text {393,939393 …}) — (\ text {3,939393 …}) \\ \ text {99} x & = \ text {390} \\ \ поэтому x & = \ frac {\ text {130}} {\ text {33}} \ end {выровнять *}
Что такое иррациональные числа? Определения, свойства, примеры
Иррациональные числа — это те действительные числа, которые нельзя представить в виде отношения. Другими словами, те действительные числа, которые не являются рациональными числами, называются иррациональными числами.Гиппас, пифагорейский философ, открыл иррациональные числа в V веке до нашей эры. К сожалению, его теорию высмеяли и бросили в море. Но существуют иррациональные числа, давайте взглянем на эту страницу, чтобы лучше понять концепцию, и поверьте нам, вас не выбросят в море. Скорее, зная концепцию, вы также узнаете список иррациональных чисел, разницу между иррациональными и рациональными числами, а также то, являются ли иррациональные числа действительными числами.
Что такое иррациональные числа?
Иррациональные числа — это набор действительных чисел, которые нельзя выразить в виде дроби, p / q, где p и q — целые числа. Знаменатель q не равен нулю (q ≠ 0). Кроме того, десятичное разложение иррационального числа не заканчивается и не повторяется.
Иррациональные числа Определение: Иррациональные числа — это действительные числа, которые не могут быть представлены в виде простой дроби. Их нельзя выразить в форме отношения, например p / q, где p и q — целые числа, q 0.Противоречие рациональных чисел.
Общие примеры иррациональных чисел
Ниже приведены некоторые часто используемые иррациональные числа.
- ㄫ (пи) — иррациональное число. π = 3⋅14159265… Десятичное значение никогда не останавливается ни в какой точке. Поскольку значение ㄫ ближе к дроби 22/7, мы принимаем значение числа пи как 22/7 или 3,14 (Примечание: 22/7 — рациональное число.)
- √ 2 — иррациональное число.Рассмотрим прямоугольный равнобедренный треугольник с двумя равными сторонами AB и BC длиной 1 единицу. По теореме Пифагора гипотенуза AC будет равна √2. √2 = 1⋅414213⋅⋅⋅⋅
- Число Эйлера e — иррациональное число. е = 2⋅718281⋅⋅⋅⋅
- Золотое сечение, φ 1,61803398874989….
Свойства иррациональных чисел
Свойства иррациональных чисел помогают нам выбрать иррациональные числа из набора действительных чисел.Ниже приведены некоторые свойства иррациональных чисел:
- Иррациональные числа состоят из непрерывных и неповторяющихся десятичных знаков.
- Это только реальные числа.
- Когда складываются иррациональное и рациональное числа, результат или их сумма является только иррациональным числом. Для иррационального числа x и рационального числа y их результат x + y = иррациональное число.
- Когда любые иррациональные числа умножаются на любое ненулевое рациональное число, их произведение является иррациональным числом.Для иррационального числа x и рационального числа y их произведение xy = иррационально.
- Для любых двух иррациональных чисел их наименьшее общее кратное (НОК) может существовать, а может и не существовать.
- Сложение, вычитание, умножение и деление двух иррациональных чисел может быть или не быть рациональным числом.
Как определить иррациональное число?
Мы знаем, что иррациональные числа — это только действительные числа, которые нельзя выразить в форме p / q, где p и q — целые числа и q 0.Например, √ 5, √ 3 и т. Д. — иррациональные числа. С другой стороны, числа, которые могут быть представлены в форме p / q, такие, что p и q являются целыми числами, а q ≠ 0, являются рациональными числами.
Символ иррациональных чисел
Прежде чем узнать символ иррациональных чисел, обсудим символы, используемые для других типов чисел.
Действительные числа состоят как из рациональных, так и из иррациональных чисел. (R-Q) определяет, что иррациональные числа могут быть получены путем вычитания рациональных чисел (Q) из действительных чисел (R).Это также можно записать как (R \ Q). Символ = Q ‘.
Набор иррациональных чисел
Набор иррациональных чисел можно получить, написав несколько иррациональных чисел в скобках. Набор иррациональных чисел можно получить с помощью некоторых свойств.
- Все квадратные корни, не являющиеся полным квадратом, являются иррациональными числами. {√ 2 , √3 , √5 , √8}
- Число Эйлера, Золотое сечение и Пи — одни из самых известных иррациональных чисел. {e, ∅, ㄫ}
- Квадратный корень любого простого числа — иррациональное число.
Таблица иллюстрирует список некоторых иррациональных чисел .
| Иррациональное число | значение |
|---|---|
| π | 3,14159265 …. |
| e | 2,7182818 ….. |
| √2 | 1.414213562 … |
| √3 | 1.73205080 … |
| √5 | 2,23606797 …. |
| √7 | 2,64575131 …. |
| √11 | 3,31662479 … |
| √13 | 3,605551275 … |
| -√3 / 2 | -0,866025 …. |
| ∛47 | 3.60882608 |
Рациональные числа против иррациональных чисел
Любое число, которое определяется в виде дроби p / q или отношения , называется рациональным числом. Он может состоять из числителя (p) и знаменателя (q), где q не равно нулю. Рациональное число может быть целым или целым числом.
- 2/3 = 0,6666 = 0,67. Поскольку десятичное значение повторяется (повторяется). Итак, мы приблизили его к 0.67
- √4 = 2 и -2, где 2 и -2 — целые числа.
Таблица показывает разницу между рациональными и иррациональными числами.
| Рациональные числа | Иррациональные числа |
|---|---|
| Может быть выражено в виде дроби или отношения. | Не может быть выражено в виде дроби или отношения. |
| Все квадратные числа рациональны | Любой квадратный корень, не являющийся полным квадратом, является иррациональным |
Десятичное значение является либо завершающим, либо непрерывным повторением. Пример: 0,33333, 0,656565 .., 1,75 | Десятичное значение не повторяется и не прерывается в любой точке. Пример: π, √ 13, e |
Интересные факты об иррациональных числах
Есть несколько интересных фактов об иррациональных числах, которые заставляют нас глубоко понять, почему стоит за тем.
1. Случайное изобретение √2
Квадратный корень из 2 или √2 был первым изобретенным иррациональным числом при вычислении длины равнобедренного треугольника. Он использовал знаменитую формулу Пифагора a 2 = b 2 + c 2
AC 2 = AB 2 + BC 2 ⇒ AC 2 = 1 2 +1 2 ⇒ AC = √ 2
√2 находится между числами 1 и 2, так как значение равно 1.41421 … Итак, он обнаружил, что длина AC не может быть выражена в виде дробей или целых чисел.
2. Значение π
Значение π приблизительно равно 22 триллионам цифр без конца. Компьютеру потребовалось около 105 дней с 24 жесткими дисками, чтобы вычислить значение числа пи.
3. Изобретение числа Эйлера e
Число Эйлера впервые ввел Леонард Эйлер, — швейцарский математик в 1731 году.Это «е» также называется числом Нэпье , которое в основном используется в логарифме и тригонометрии.
Доказательство иррационального числа:
Давайте разберемся, как доказать, что данный несовершенный квадрат иррационален. Вот пошаговое доказательство того же.
Чтобы доказать: √2 — иррациональное число.
Предположим, √2 — рациональное число. Тогда по определению рациональных чисел можно записать, что
√2 = p / q … (1) где p и q — взаимно простые целые числа, а \ (q ≠ 0 \) (Копростые числа — это числа, общий делитель которых равен 1).2 \ end {align} \)
Это означает, что 2 также является простым делителем q 2 . Снова из теоремы, можно сказать, что 2 также является простым делителем q.
Согласно исходному предположению, p и q — простые числа, но полученный выше результат противоречит этому предположению, поскольку p и q имеют 2 в качестве общего простого множителя, кроме 1. Это противоречие возникло из-за неправильного предположения, что √2 рационально. .
Итак, √2 иррационально.
Статьи, связанные с иррациональными числами
Важные моменты
- Произведение любых двух иррациональных чисел может быть как рациональным, так и иррациональным.Пример (а): Умножаем √2 и π ⇒ 4,4428829 … иррациональное число. Пример (b): умножьте √2 и √2 ⇒ 2 — рациональное число.
- Множество иррациональных чисел не замыкается при умножении, в отличие от множества рациональных чисел.
- Сложение или умножение двух иррациональных чисел может быть рациональным; например, √2 × √2 = 2. Здесь √2 — иррациональное число. Если его умножить дважды, то полученный конечный продукт будет рациональным числом, т.е.e 2.
Часто задаваемые вопросы об иррациональных числах
Что такое иррациональные числа в математике?
Иррациональные числа — это набор действительных чисел, которые нельзя выразить в виде дробей или соотношений. Пример: π, √2, e, √5
Как определить иррациональное число?
За любое число, которое нерационально, считается иррациональным. Иррациональные числа можно записывать десятичными дробями, но не дробями. Кроме того, эти числа, как правило, содержат бесконечные неповторяющиеся цифры справа от десятичной дроби.
Что такое рациональные числа?
Все числа вида p / q, где p и q — целые числа, а q не равно 0, — рациональное число. Примеры рациональных чисел: 1/2, -3/4, 0,3 или 3/10.
В чем разница между рациональными и иррациональными числами?
Рациональные числа — это числа, которые являются завершающими или не завершающимися повторяющимися числами, тогда как иррациональные числа — это числа, которые не заканчиваются и не повторяются после определенного количества десятичных знаков.
2/3 — иррациональное число?
Нет, 2/3 — не иррациональное число. 2/3 = 0,666666 …. что является повторяющимся десятичным числом. Следовательно, 2/3 — рациональное число.
Что такое оконечные номера?
Завершающие числа — это десятичные дроби, которые заканчиваются после определенного количества десятичных знаков. Например, 1,5, 3,4, 0,25 и т. Д. Являются конечными числами. Все конечные числа являются рациональными числами, поскольку их легко записать в форме p / q.
Почему иррациональные числа называются сурдами?
Surd относится к выражению, которое включает квадратный корень, кубический корень или другие символы корня.Сурды используются для точного написания иррациональных чисел. Все сурды считаются иррациональными числами, но все иррациональные числа не могут считаться сурдами. Иррациональные числа, не являющиеся корнями алгебраических выражений, такие как π и e, не являются серыми.
Примеры уравнений с рациональными и иррациональными числами
И рациональные, и иррациональные числа можно назвать действительными числами, но когда дело доходит до их свойств, есть несколько отличий. Вы можете представить рациональное число в форме P / Q, где P и Q — целые числа, а Q 0.
Иррациональные числа нельзя записать простыми дробями. 2/3 — это пример рационального числа, тогда как √2 — иррациональное число.
Определения
Давайте начнем с определения каждого термина отдельно, затем мы сможем узнать больше о каждом и проработать несколько примеров.
Что такое рациональное число?
Любое число, выраженное в виде дроби с положительными, отрицательными числами и нулем, называется рациональным числом. Рациональные числа происходят от слова «соотношение».Другими словами, это соотношение двух целых чисел. Например, 3/2 — рациональное число, что означает деление 3 на другое целое число 2.
Что такое иррациональное число?
По сути, иррациональные числа могут быть записаны как десятичные дроби, но как отношение двух целых чисел. В иррациональных числах после десятичной точки обычно есть бесконечные неповторяющиеся цифры. Возьмем этот пример: √8 = 2,828.
Примеры рациональных и иррациональных чисел
Для Rational
- 0.5 можно записать как ½ или 5/10, а любое завершающее десятичное число является рациональным числом.
- √81 как квадратный корень можно упростить до 9, которое является частным от дроби 9/1
- Вы можете выразить 3 как 3/1, где 3 является частным целых чисел 3 и 1.
- 0,777777 — повторяющееся десятичное число и является рациональным числом.
- 1/5 — рациональное число, поскольку знаменатель и числитель являются целыми числами.
Для иррациональных
- √2 это число не может быть упрощено; следовательно, это иррациональное число.
- Π — это иррациональное число, имеющее значение 3,142…, которое является бесконечным и неповторяющимся числом. Следовательно, значение π не равно какой-либо дроби. Дробь 22/7 — это всего лишь оценка.
- 0,212112111… является иррациональным числом, которое не повторяется и не заканчивается, поэтому его нельзя выразить как частное от дроби.
- Хотя число в √7 / 5 дано как дробь, числитель и знаменатель должны быть целыми числами. Но поскольку √ 7 не является целым числом, указанное число иррационально.
- 5/0 иррационально. Любая дробь со знаменателем 0 иррациональна.
Свойства рациональных и иррациональных чисел
Это основные правила арифметики, выполняемые над рациональными и иррациональными числами
Правило 1: Результат суммы двух рациональных чисел также является рациональным
Правило 2: Произведение двух рациональных чисел является рациональным
Правило 3: результат суммы двух иррациональных чисел может быть рациональным или иррациональным
- Возьмем для примера: √2 + √2 = 2√2 иррационально
- , а 2 + 2√5 + (-2√5) = 2 результат является рациональным
Правило 4: Результат произведения двух иррациональных чисел может быть иррациональным или рациональным.
- Возьмем для примера: √2 * √3 = √6 иррационально
- , а √2 * √2 = √4 = 2 рациональных
Давайте теперь сосредоточимся на индивидуальных свойствах рациональных и иррациональных чисел.
Отличительные особенности рациональных чисел
- Сумма рациональных чисел всегда является рациональным числом. Например, если W и Z — два рациональных числа, сумма W и Z рациональна.
- Результат деления рационального числа на ненулевое число — рациональное число.Например, W ÷ Z = рациональное число.
- Произведение любых двух или трех рациональных чисел дает другое рациональное число. Например, если вы умножите W и Z, полученный ответ должен быть рациональным.
- Разница между двумя рациональными числами дает другое число. Например, если вы вычтете Z из W, вы получите рациональное число.
Поскольку результат суммы любых двух рациональных чисел является рациональным числом, рациональные числа всегда должны быть замкнутыми.Следовательно, рациональные числа одинаково закрыты для умножения, вычитания и деления, если делитель не равен нулю.
Как представить рациональные числа в виде десятичных знаков
Любое рациональное число можно выразить как завершающее десятичное или непрерывное десятичное число. Завершающий десятичный разделитель — это любое десятичное число, в котором после конечного числа десятичных знаков следующие за ним значения разряда равны 0. Например, 1/8 = 0,125.
Как видно из данного примера, деление точное.Такие частные называются завершающими десятичными знаками. В качестве альтернативы, рациональные числа также могут быть выражены как непрерывные десятичные дроби. Неограничивающая десятичная дробь — это те десятичные дроби, которые бесконечно продолжаются после десятичной точки.
Давайте посмотрим на эти примеры:
- 3/7 = 0,42857142
- 18/23 = 0,78260869
В двух приведенных выше примерах вы понимаете, что разделение никогда не заканчивается, независимо от того, как долго оно может продолжаться. Частные таких делений называются завершающими десятичными знаками.
В некоторых случаях непрерывная десятичная дробь может иметь цифру или набор чисел, которые непрерывно повторяются. Эти непрерывные десятичные дроби называются периодическими, повторяющимися или циркулирующими десятичными знаками. Набор повторяющихся цифр называется периодом повторяющейся десятичной дроби.
Примеры
4/9 = 0,44444444
11/30 = 0,36666666
Отличительные особенности иррациональных чисел
- Произведение иррациональных чисел может быть как рациональным, так и иррациональным.
- Результат произведения ненулевого рационального числа и иррационального числа всегда иррационально.
- Сумма иррациональных чисел может быть как рациональной, так и иррациональной.
- Сумма рационального и иррационального числа всегда иррациональна.
- Разница между двумя иррациональными числами может быть или не быть иррациональной.
- Сумма рационального и иррационального числа всегда иррациональна.
Значительные различия между рациональными и иррациональными числами
- Рациональное число может быть выражено как отношение двух чисел в (форме p / q), а иррациональное число — нет.
- Рациональное число включает числа, которые могут заканчиваться или повторяться, в то время как иррациональные числа не завершаются и не повторяются.
- Рациональное число имеет полные квадраты, такие как 4, 9, 16, 25 и т. Д., В то время как иррациональные числа имеют морщины, такие как √2, √3, √5, √7.
- Для рационального числа числитель и знаменатель являются целыми числами, знаменатель которых не равен нулю: 3/2 = 1,5, 3,6767, .
- Иррациональные числа нельзя записать дробью: √5, √11.
Часто задаваемые вопросы (FAQ)
Что такое рациональные и иррациональные числа?
Вы можете выразить рациональные числа в форме отношения (P / Q & Q ≠ 0), но для иррациональных чисел вы не можете выразить их в виде дроби.Тем не менее, оба они являются действительными числами, которые вы можете включить в числовую строку.
В чем существенная разница между рациональными и иррациональными числами?
Рациональные числа — это конечные и повторяющиеся десятичные дроби, а иррациональные числа — бесконечные и неповторяющиеся.
Пи — действительное число?
Пи (π) — иррациональное число, поэтому это действительное число. Значение (π) составляет 22/7 r 3,142…
Является ли 4 рациональным числом?
Да, это так, потому что оно удовлетворяет всем условиям рационального числа.Вы можете выразить это как отношение, если знаменатель не равен нулю.
Если вы представляете десятичное число чертой, оно рационально или иррационально? Десятичное число с полосой означает, что число после десятичной дроби повторяется, поэтому это рациональное число.
3.605551275… рационально или иррационально?
Многоточие (…) после 3.605551275 показывает, что число не завершается и не имеет повторяющегося шаблона. Так что это иррационально.
Заключение
Рациональные числа могут применяться для расчета скорости износа, колебаний, течения воды или скорости ветра.Приведенные выше примеры и объяснения позволяют любому легко отличить рациональное число от иррационального.
Оставьте первый комментарий ниже.
Что такое рациональное число? Определение и примеры
Вы слышали термин «рациональные числа»? Вам интересно: «Что такое рациональное число?» Если да, то вы попали в нужное место!
В этой статье мы обсудим определение рационального числа, дадим примеры рациональных чисел и дадим несколько советов и приемов, чтобы понять, является ли число рациональным или иррациональным.
Что такое рациональное число?
Чтобы понять, что такое рациональные числа, нам сначала нужно охватить некоторые основные математические определения:
- Целые числа — это целые числа (например, 1, 2, 3 и 4), а — их отрицательные аналоги (например, -1, -2, -3 и -4).
- Дроби — это числа, выраженные в виде отношений. Дробь — это часть целого.
- У дробей есть числители, — числа в верхней части дроби, которые показывают части, взятые из целого.
- У дробей также есть знаменатели, — числа внизу дроби, показывающие, сколько частей состоит в целом.
Хорошо! Теперь, когда мы знаем эти термины, давайте вернемся к нашему первоначальному вопросу.
Что такое рациональное число?
Рациональное число — это число, которое может быть выражено дробью , где числитель и знаменатель дроби являются целыми числами. Знаменатель рационального числа не может быть нулевым.
Рациональное число выражается уравнением
а / б, б ≠ 0
, где a и b — целые числа.
Это уравнение показывает, что все целые числа, конечные десятичные дроби и повторяющиеся десятичные дроби являются рациональными числами. Другими словами, большинство чисел — рациональные числа.
Вот подсказка: , если вы работаете с числом, состоящим из длинной строки с разными десятичными знаками, тогда ваше число иррационально! Если вы работаете с целым числом или числом с терминальными или повторяющимися десятичными знаками (например, 1.333333), значит ваш номер рациональный!
Примеры рациональных чисел
Теперь, когда мы знаем определение рационального числа, давайте воспользуемся этим определением, чтобы исследовать некоторые числа и посмотреть, являются ли они рациональными или нет.
Начнем с цифры 6.
Число 6 — целое число. Это тоже рациональное число. Почему?
Потому что 6 также можно выразить как 6/1.
При выражении 6 числитель и знаменатель являются целыми числами. Знаменатель не равен 0.
А как насчет числа -6?
-6 можно записать как -6/1. Или 6 / -1.
В любом случае -6 — рациональное число, потому что его можно выразить в виде дроби, где числитель и знаменатель являются целыми числами, а знаменатель не равен 0.
Что такое иррациональное число?
Противоположностью рациональных чисел являются иррациональные числа.
Проще говоря, иррациональные числа — это действительные числа, которые нельзя записать в виде простой дроби, такой как 6/1.
Возьмем π.
π — действительное число. Но это также иррациональное число, , потому что вы не можете записать π в виде простой дроби:
π = 3,1415926535897932384626433832795 (и подсчет)
Невозможно записать π в виде простой дроби, поэтому это иррационально.
То же самое и с √2.
√2 равно 1,4142135623730950 … (и т. Д.).
Вы не можете превратить √2 в простую дробь, поэтому это иррациональное число.
Известные иррациональные числа
Не существует известных рациональных чисел, потому что подавляющее большинство чисел являются рациональными. Есть несколько известных иррациональных чисел. Вот некоторые из них, которые вы могли видеть:
- e: Число e (число Эйлера) — еще одно известное иррациональное число. Люди также вычислили е с точностью до множества десятичных знаков без какого-либо изображения. Первые несколько цифр выглядят так: 2,71828182845353602874713527.
- π: Люди вычислили число Пи с точностью до квадриллиона десятичных знаков, но до сих пор нет никакой закономерности.Первые несколько цифр выглядят так: 3,1415926535897932384626433832795
- √: Многие квадратные корни, кубические корни и т. Д. Также являются иррациональными числами. Примеры:
- √3 = 1,7320508075688772935274463415059 (и т. Д.)
- √99 = 9.9498743710661995473447982100121 (и т. Д.)
Однако не все квадратные корни являются иррациональными числами! Если квадратный корень дает целое число (например, √4 или √9), значит, вы на самом деле работаете с рациональным числом!
Это не единственное, о чем нужно быть осторожным! Иногда умножение двух иррациональных чисел дает рациональное число.Например,
√2 * √2 = 2
2 — рациональное число.
Основные выводы
Рациональные числа — это числа, которые можно выразить простыми дробями.
Иррациональные числа — это числа, которые нельзя выразить простыми дробями.
Что дальше?
Хотите узнать о самых быстрых и простых способах конвертации между градусами Фаренгейта и Цельсия? Мы вас прикрыли! Ознакомьтесь с нашим руководством по лучшим способам преобразования Цельсия в градуса Фаренгейта (или наоборот).
Вы изучаете логарифмы и натуральные логарифмы на уроках математики? У нас есть руководство по всем правилам естественного ведения журнала , которые вам необходимо знать.
Знаете ли вы, что вода имеет особую плотность? Ознакомьтесь с нашим руководством, чтобы узнать , что такое плотность воды и как она может измениться.
Натуральные, целые, рациональные, иррациональные, действительные и другие числа
Натуральные числа
натуральное число (или , считая ) чисел — это 1,2,3,4,5 и т. Д.Есть бесконечно много натуральных чисел. Набор натуральных чисел, {1,2,3,4,5, …}, иногда для краткости пишут N .
Целые числа — натуральные числа вместе с 0.
(Примечание: некоторые учебники не согласны с этим и говорят, что натуральные числа включают 0.)
Сумма любые два натуральных числа также являются натуральными числами (например, 4 + 2000 = 2004), а произведение любых двух натуральных чисел натуральное число (4 × 2000 = 8000). Этот однако это неверно для вычитания и деления.
Целые числа
Целые числа — это набор действительных чисел, состоящий из натуральных чисел, их аддитивных обратных чисел и нуля.
{…, — 5, −4, −3, −2, −1,0,1,2,3,4,5, …}
Набор целых чисел иногда написано J или Z для краткости.
г. сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это не относится к делению … просто попробуйте 1 ÷ 2.
Рациональные числа
Рациональные числа те числа, которые можно выразить как отношение между два целых числа.Например, дроби 13 и −11118 являются рациональное число. Все целые числа входят в рациональные числа, поскольку любое целое число z можно записать как отношение z1.
Все десятичные дроби, которые заканчиваются, являются рациональными числами (с версии 8.27 можно записать как 827100.) Десятичные дроби которые после некоторой точки имеют повторяющийся узор, также являются рациональными: например,
0,0833333 …. = 112.
Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их сумма, разница, произведение и частное также являются рациональным числом (пока мы не делим на 0).
Иррациональные числа
Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби). В десятичной форме он никогда не заканчивается и не повторяется. В древние греки обнаружили, что не все числа рациональны; там — это уравнения, которые нельзя решить с помощью отношений целых чисел.
Первое такое уравнение для изучения было 2 = x2. Какие само число раз равно 2?
2 это около 1,414, поскольку 1,4142 = 1,999396, что близко к 2. Но вы никогда не попадете точно, возведя дробь в квадрат (или завершив десятичный).Квадратный корень из 2 — иррациональное число, то есть его десятичный эквивалент продолжается вечно, без повторяющегося шаблона:
2 = 1,41421356237309 …
Другой известный иррациональный числа золотое сечение , число с большим значение для биологии:
1 + 52 = 1,61803398874989 …
π (пи), отношение длины окружности к ее диаметру:
π = 3,14159265358979 …
и е, самое важное число в исчислении:
е = 2.71828182845904 …
Иррациональные числа можно далее разделить на алгебраических, чисел, которые являются решениями некоторого полиномиального уравнения (например, 2 и золотое сечение), и трансцендентных чисел , которые не являются решениями какого-либо полиномиального уравнения. π и e оба трансцендентны.
Реальные числа
Действительные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» в числовой строке.Существует бесконечно много действительных чисел, как и бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел на больше бесконечности.
«Меньший», или счетных бесконечности целых чисел и rationals иногда называют ℵ0 (alef-naught), и бесчисленное множество бесконечности реалов называется ℵ1 (алеф-он).
Есть еще «большие» бесконечности, но для этого вам следует взять курс теории множеств!
Комплексные числа
Комплексные числа — множество {a + bi | a и b — действительные числа}, где i — мнимая единица, −1.(нажмите здесь, чтобы подробнее о мнимых числах и операциях с комплексными числами).
Комплексные числа включают набор действительных чисел. Действительные числа в сложной системе записываются в виде a + 0i = a. реальное число.
Этот набор иногда записывается как C для краткости. Набор комплексных чисел важно, потому что для любого полинома p (x) с коэффициентами действительного числа все решения p (x) = 0 будут в C .
Beyond …
Есть и «побольше» наборы чисел, используемых математиками.Кватернионы , открытые Уильямом Х. Гамильтоном в 1845 году, образуют систему счисления с тремя разные мнимые единицы!
Рациональные и иррациональные числа — Surds — Higher — CCEA — GCSE Maths Revision — CCEA
Число считается рациональным, если его можно записать в виде дроби (одно целое число, деленное на другое целое число). Десятичная форма рационального числа имеет либо завершающую, либо повторяющуюся десятичную дробь. Примеры рациональных чисел: 17, -3 и 12.4. Другие примеры рациональных чисел: 5 ⁄ 4 = 1.25 (завершающая десятичная дробь) и 2 ⁄ 3 = \ (0. \ Dot {6} \) (повторяющаяся десятичная дробь).
Число иррационально, если его нельзя записать в виде дроби. Десятичная форма иррационального числа не прерывается и не повторяется. Примеры иррациональных чисел: \ (π \) = 3.14159 … и \ (\ sqrt {2} = 1.414213 \ dotsc \)
Surds
Surd — это выражение, которое включает квадратный корень, кубический корень или другой корень. символ. Сурды используются для точной записи иррациональных чисел — поскольку десятичные дроби иррациональных чисел не заканчиваются и не повторяются, они не могут быть записаны точно в десятичной форме.2 \) дает 2,9929 м 2 .
Ответ в форме surd дает нам возможность записать точный ответ, что полезно, если мы хотим использовать это значение в дальнейших вычислениях, чтобы минимизировать ошибки округления. Ответ в десятичной форме дает нам приблизительный ответ, который полезен, если мы хотим использовать ответ в практических целях, например, для рисования квадрата.

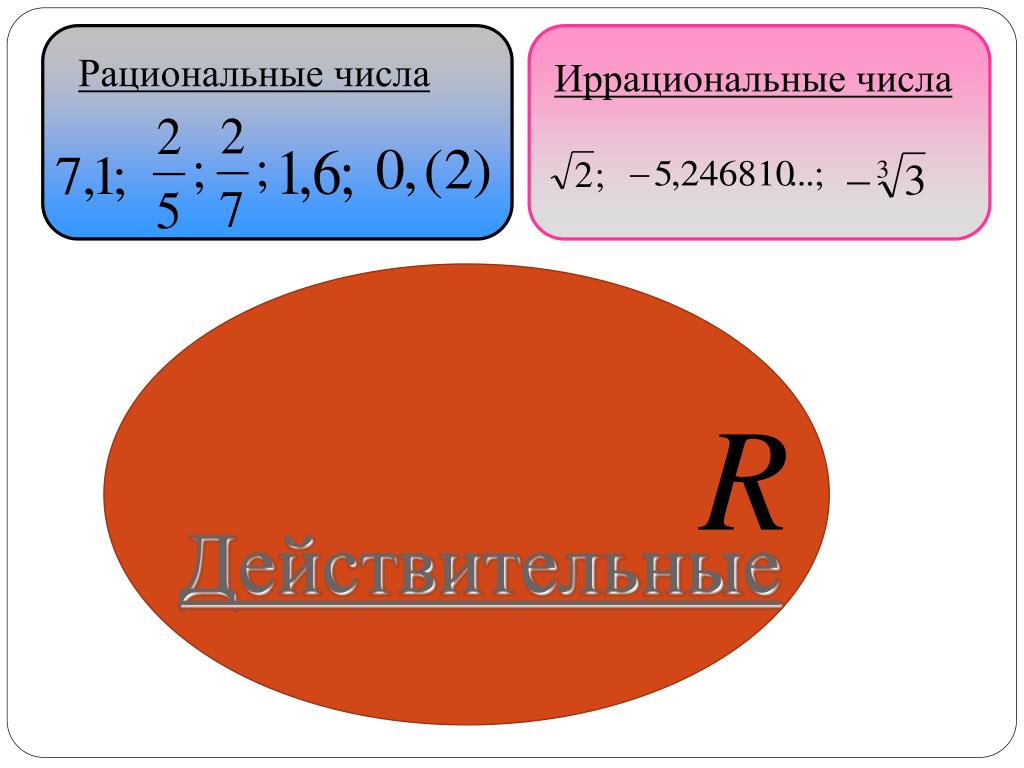


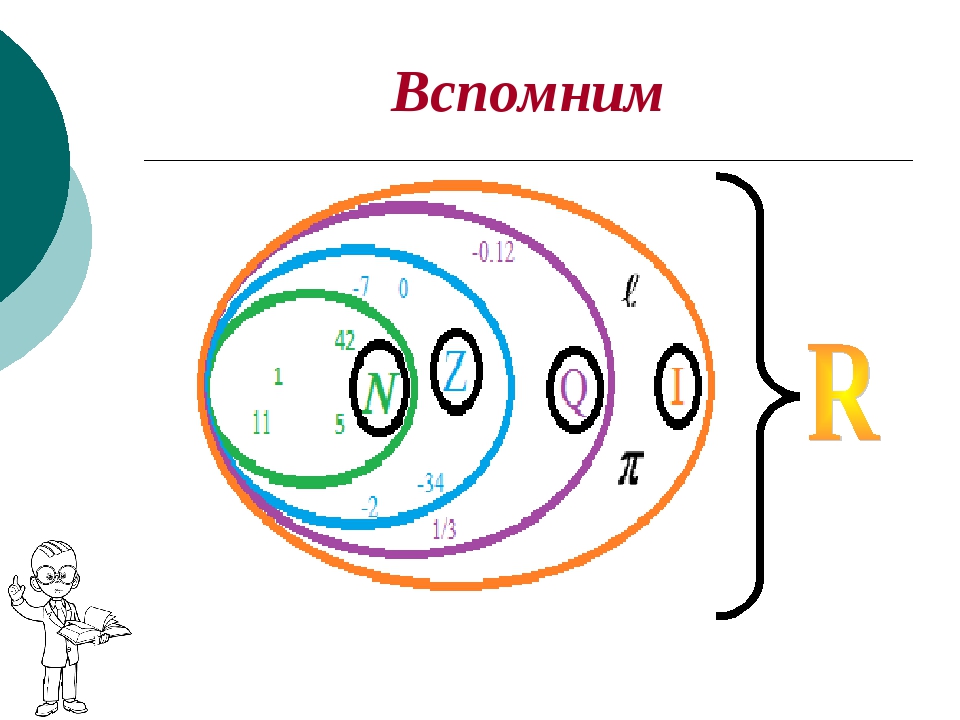
 Иррациональное число — это число, которое не может быть выражено в соотношении двух целых чисел.
Иррациональное число — это число, которое не может быть выражено в соотношении двух целых чисел.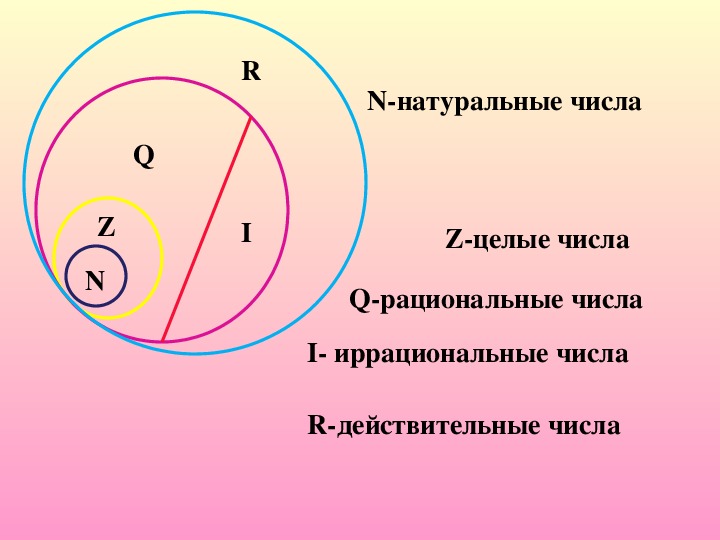 Например, дробь \ (\ frac {4} {10} \) может быть записана как \ (\ text {0,4} \).
Например, дробь \ (\ frac {4} {10} \) может быть записана как \ (\ text {0,4} \). ..} \)
..} \)