Рациональные иррациональные числа действительные натуральные: Какие числа называются действительными?

Тест: Действительные числа — Математика 8 класс

Тест: Действительные числа — Математика 8 класс

Английский язык

Астрономия

Белорусский язык

Биология

География

ИЗО

Информатика

История

Итальянский язык

Краеведение

Литература

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ

Русский язык

Технология

Физика

Физкультура

Химия

Черчение

Для учителей

Дошкольникам

VIP — доступ

• Предметы
»
• Математика
»
• 8 класс
»
• Действительные числа

Действительные числа

С помощью данного теста можно проверить знания учащихся по основным понятиям тем множества натуральных,целых, рациональных действительных чисел; контролировать формирование умений учащихся различать множества чисел.

Математика 8 класс | Автор: Карасева Лариса Михайловна | ID: 6377 | Дата: 3.

12.2015

Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться

Вопрос № 1

Числа, употребляемые при счете предметов, называются …

целыми
натуральными;
рациональными
иррациональными.

Вопрос № 2

Натуральные числа, числа им противоположные, и число нуль образуют множество …

натуральных чисел N
действительных чисел R
целых чисел Z
рациональных чисел Q.

Вопрос № 3

Числа, которые можно представить в виде дроби m/n, где m — целое, n — натуральное, образуют множество …

целых чисел Z

рациональных чисел Q
дробных чисел
натуральных чисел N

Вопрос № 4

Всякая бесконечная непериодическая десятичная дробь является … числом.

рациональным
целым
иррациональным
натуральным

Вопрос № 5

Множество действительных чисел R состоит из всех …

положительных и отрицательных чисел
рациональных и иррациональных чисел;
целых и дробных чисел

Вопрос № 6

Всякая бесконечная периодическая десятичная дробь является … числом.

рациональным
иррациональным
целым
натуральным

Вопрос № 7

Верно ли, что всякое натуральное число является целым?

да
нет

Вопрос № 8

Верно ли, что всякое рациональное число является целым?

да
нет

Вопрос № 9

Верно ли, что всякое иррациональное число является действительным?

да
нет

Вопрос № 10

Верно ли, что всякое целое число является действительным?

да
нет

Вопрос № 11

Верно ли, что всякое рациональное число является действительным?

да
нет

Показать ответы

Получение сертификата
о прохождении теста

Доступно только зарегистрированным пользователям

© TestEdu. ru 2013-2022

E-mail администратора: [email protected]

Представление чисел в памяти компьютера — Энциклопедия современных знаний

Основные виды чисел

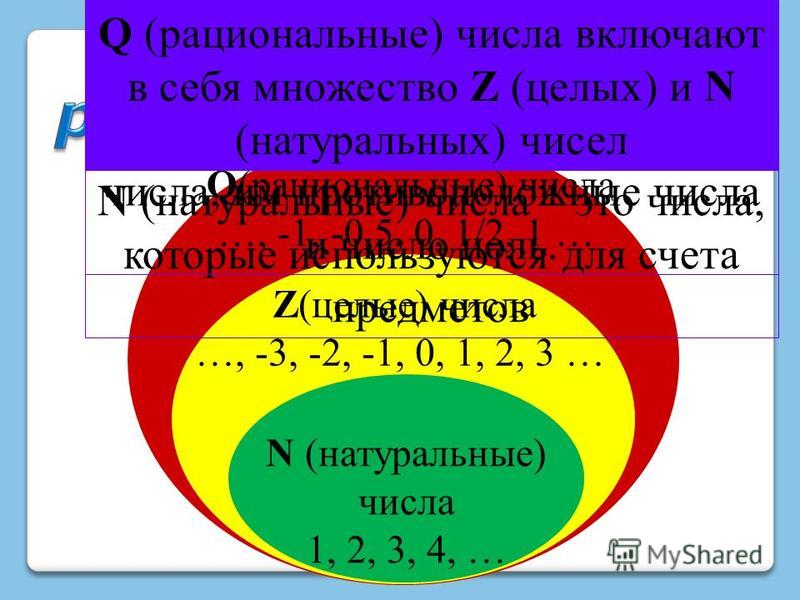
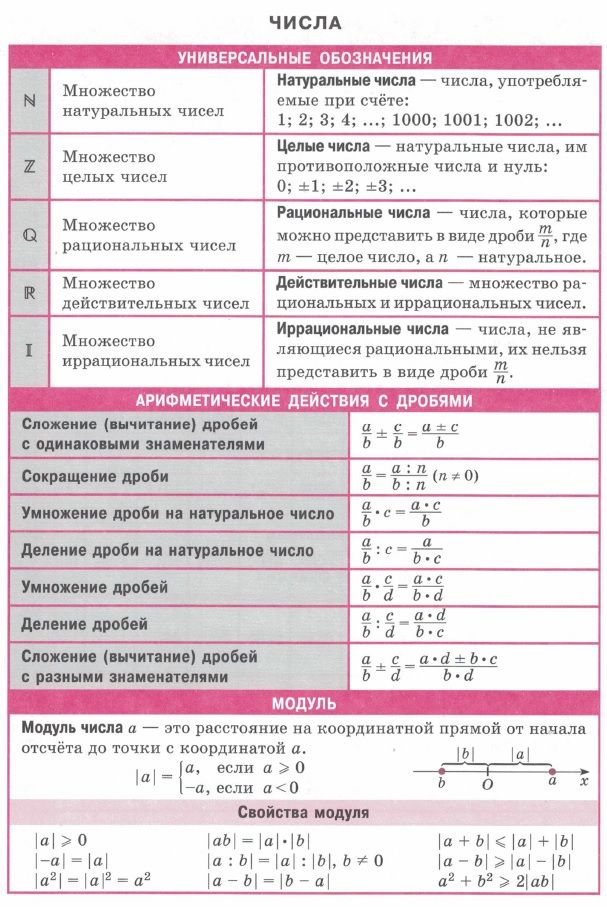
Натуральные числа, получаемые при естественном счёте; множество натуральных чисел обозначается . Т.е. (иногда к множеству натуральных чисел также относят ноль, то есть ). Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Натуральные числа коммутативны и ассоциативны относительно сложения и умножения, а умножение натуральных чисел дистрибутивно относительно сложения и вычитания.

Целые числа, получаемые объединением натуральных чисел с множеством отрицательных чисел и нулём, обозначаются . Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления).

Рациональные числа — числа, представленные в виде дроби m/n (n?0), где m — целое число, а n — натуральное число. Для рациональных чисел определены все четыре «классические» арифметические действия: сложение, вычитание, умножение и деление (кроме деления на ноль). Для обозначения рациональных чисел используется знак .

Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается . Его можно рассматривать как пополнение поля рациональных чисел при помощи нормы, являющейся обычной абсолютной величины. Кроме рациональных чисел, включает множество иррациональных чисел , не представимых в виде отношения целых. Кроме подразделения на рациональные и иррациональные, действительные числа также подразделяются на алгебраические и трансцендентные. При этом каждое трансцендентное число является иррациональным, каждое рациональное число — алгебраическим.

Комплексные числа , являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z = x + iy, где i — т. н. мнимая единица, для которой выполняется равенство i2 = ? 1. Комплексные числа используются при решении задач квантовой механики, гидродинамики, теории упругости и пр.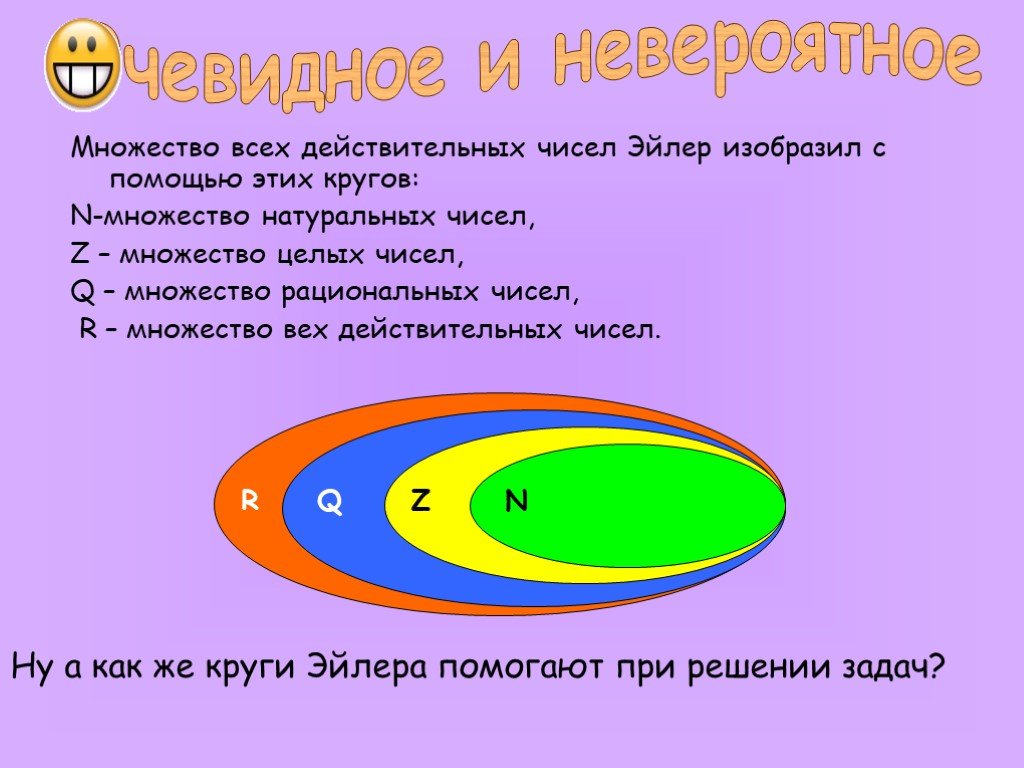

Для перечисленных множеств чисел справедливо следующее выражение:

Простые числа — натуральные числа, которые в качестве множителей имеют только себя и единицу. Ряд простых чисел имеет вид: Любое натуральное число N можно представить в виде произведения степеней простых чисел: 121968=24·32·50·71·112. Это свойство широко используется в практической криптографии.

Для перечисленных множеств чисел справедливо следующее выражение:

Обобщения чисел

Кватернионы представляющие собой разновидность гиперкомплексных чисел. Множество кватернионов обозначается . Кватернионы в отличие от комплексных чисел не коммутативны относительно умножения.

В свою очередь октавы , являющиеся расширением кватернионов, уже теряют свойство ассоциативности.

В отличие от октав, седенионы не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности.

Для этих множеств обобщённых чисел справедливо следующее выражение:

p-адические числа можно рассматривать как элементы поля, являющегося пополнением поля рациональных чисел при помощи т. н. p-адического нормирования, аналогично тому, как поле действительных чисел определяется как его пополнение при помощи обычной абсолютной величины.

Аде?ли определяются как бесконечные последовательности {a?,a2,a3,…ap…}, где a? — любое действительное число, а ap — p-адическое, причём все ap, кроме, может быть, конечного их числа, являются целыми p-адическими. Складываются и умножаются адели покомпонентно и образуют кольцо. Поле рациональных чисел вкладывается в это кольцо обычным образом r{r, r,…r,…}. Обратимые элементы этого кольца образуют группу и называются иде?лями.

Практически важным обобщением числовой системы является интервальная арифметика.

Представление чисел в памяти компьютера

Для представления натурального числа в памяти компьютера, оно обычно переводится в двоичную систему счисления. Для представления отрицательных чисел используется т. н. дополнительный код числа, который получается путём прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.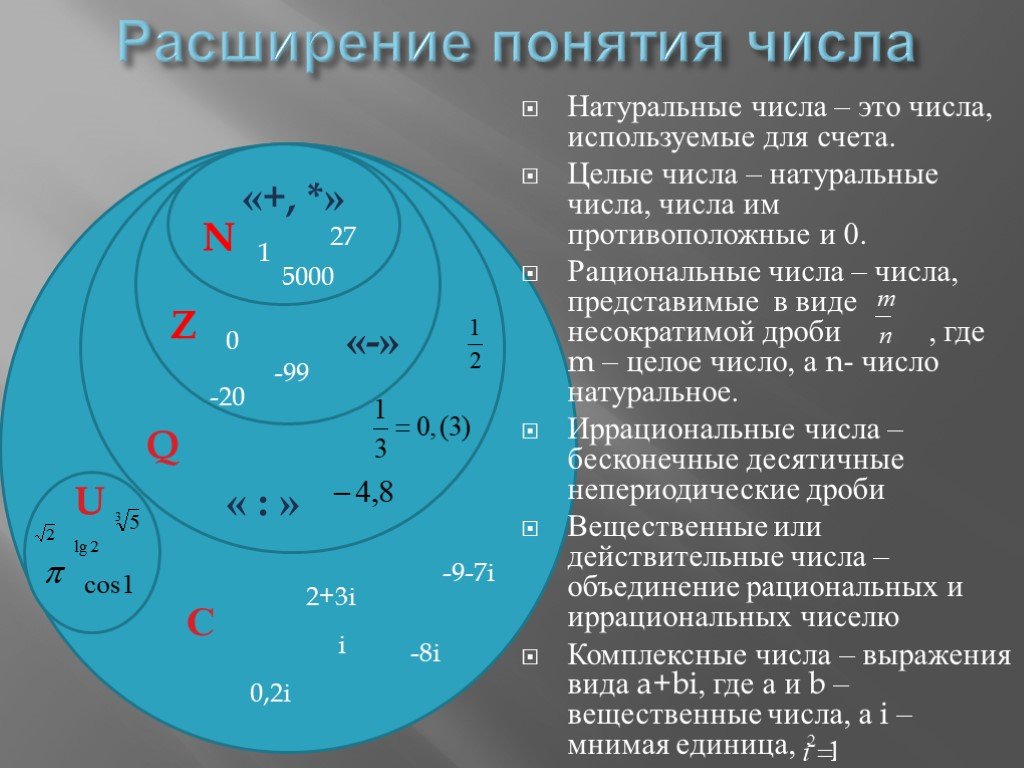

Представление действительных чисел в памяти компьютера имеет некоторые ограничения связанные с используемой системой счисления, а также ограниченностью объёма памяти, выделяемого под числа. Действительные числа обычно представляются в виде чисел с плавающей запятой. При этом лишь некоторые из действительных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями. В наиболее распространённом формате число с плавающей запятой представляется в виде последовательности битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа.

04 Представление чисел в компьютере

Похожие статьи.

• Формы представление чисел в эвм

• Структура пк: внешняя память компьютера, назначение, основные параметры.

• Память персонального компьютера.

• Представление звуковой информации в компьютере

Установите связь между наборами действительных чисел, рациональных, иррациональных, целых чисел, целых чисел и натуральных чисел, используя диаграммы Венна.

ЗА ПУБЛИКАЦИЯМИ-РЕАЛЬНЫЕ НОМЕРА-

2 видео

РЕКЛАМА

Ab Padhai каро бина объявления ке

Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

---

संबंधित वीडियो

Множества в математике Множества как натуральные числа; целое число; вещественное число)

1339104

Каждое рациональное число также целое число (б) а настоящий номер натуральное число         (г) целое число

3638963

Среди следующих утверждений утверждение с неправильно это Каждое натуральное число является целым числом. Каждое натуральное число является действительным числом. Каждое действительное число является рациональным числом. (d) Каждое целое является рациональным числом.

3639312

कारण सहित उत्तर दीजिए।
(я)
(ii)
(iii)
(iv)
(v)
(vi) प्रत्येक परिमेय संख्या एक पूर्ण संख्या है।

119412641

Текст Решение

Пересечение множества рациональных чисел и множества иррациональных чисел равно …………………

363432352

Верны или неверны следующие утверждения? Давать причины вашего ответа? Каждое целое число является натуральным числом Каждое целое является рациональным числом. Каждое рациональное число является целым числом. Каждое натуральное число является целым числом. Каждое целое число является целым числом Каждое рациональное число является целым числом

642567806

Введение | | Классификация системы счисления | | Натуральное число, | |Целое число || Целое число | |Реальное число | | Рациональное- Иррациональное число | |Комплексное число | | Мнимое число | | Prime-Composite Number

643446749

01:08:51

Верны или неверны следующие утверждения? Давать причины вашего ответа? Каждое целое число является натуральным числом Каждое целое является рациональным числом. Каждое рациональное число является целым числом. Каждое натуральное число является целым числом. Каждое целое число является целым числом Каждое рациональное число является целым числом

644851805

Натуральные числа|Целые числа|Целые числа|Дроби|Рациональные числа|OMR

645414374

Чистый = набор натуральных чисел.
Z = набор целых чисел.
Q = множество рациональных чисел.
Q = множество иррациональных чисел.
R = набор вещественных чисел.
Назовите четыре множества, в которых 12 является элементом.

646338039

Текст Решение

Нетто = множество натуральных чисел.
Z = набор целых чисел.
Q = множество рациональных чисел.
Q = множество иррациональных чисел.
R = набор вещественных чисел.
Назовите два набора, в которых √15 является элементом.

646338040

Text Solution

Net = множество натуральных чисел.
Z = набор целых чисел.
Q = множество рациональных чисел.
Q = множество иррациональных чисел.
R = набор вещественных чисел.
Элементом каких трех из приведенных выше наборов является 0?

646338041

Текст Решение

Net = множество натуральных чисел.
Z = набор целых чисел.
Q = множество рациональных чисел.
Q = множество иррациональных чисел.
R = набор вещественных чисел.
Элементом каких двух из приведенных выше наборов является 3+√10?

646338042

Текст Решение

Нетто = множество натуральных чисел.
Z = набор целых чисел.
Q = множество рациональных чисел.
Q = множество иррациональных чисел.
R = набор вещественных чисел.
Элементом каких трех из приведенных выше наборов является −6?

646338043

Текст Решение

Нетто = множество натуральных чисел.
Z = набор целых чисел.
Q = множество рациональных чисел.
Q = множество иррациональных чисел.
R = набор вещественных чисел.
В каком из двух наборов нет элемента 3/8?

646338044

Text Solution

ADVERTISEMENT

• BEYOND PUBLICATION-REAL NUMBERS-

• Establish the relation among the sets of Real numbers, Rational, Irrat. ..

  05:32

• The десятичное расширение 27/14 равно

  05:24

РЕКЛАМА

Объяснение урока: Реальные числа | Nagwa

В этом эксплейнере мы узнаем, как определять отношения между подмножествами действительных чисел и как представлять действительные числа в числовых рядах.‌

Напомним, что множество рациональных чисел ℚ — это множество всех частных целых чисел. Другими словами, он содержит все числа вида 𝑎𝑏, где 𝑎, 𝑏∈ℤ и 𝑏 отличен от нуля. Мы также видели, что существуют такие числа, как √2, которые не могут быть записывается как частное целых чисел; мы называем такие числа иррациональными числами. Поскольку это не рационально, оно должно быть элемент дополнения к ℚ∶ℚ. Мы называем это множеством иррациональных числа. Мы можем использовать этот набор для создания нового набора чисел, называемых действительными числами.

Определение: Вещественные числа и множество действительных чисел

Множество вещественных чисел, обозначаемое ℝ, задается формулой ℝ=ℚ∪ℚ. 

Вещественным числом является любой элемент множества ℝ; это включает в себя все числа, которые могут быть представлены на числовая линия, такая как целые числа, рациональные числа и иррациональные числа.

Чтобы изучить эту концепцию более подробно, давайте перейдем к первому примеру.

Пример 1. Нахождение объединения рациональных и иррациональных чисел

Что такое ℚ∪ℚ?

Ответ

Напомним, что ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ,𝑏≠0. Это известно как множество рациональных чисел; это множество всех частных целых чисел. Мы можем взять дополнение этого множества для представления всех числа, не являющиеся рациональными. Другими словами, ℚ — это набор всех чисел, которые нельзя представить как частное двух целых чисел. Мы называем их иррациональными числами.

Наконец, мы можем объединить эти множества, чтобы построить множество действительных чисел. У нас есть ℚ∪ℚ=ℝ.

В следующем примере мы рассмотрим, являются ли все нецелые числа рациональными.

Пример 2. Проверка утверждения о множестве целых чисел

Является ли каждое нецелое число рациональным?

Ответ

Напомним, что рациональное число — это число, которое можно записать как частное целых чисел, что эквивалентно утверждению, что он имеет либо завершающее десятичное расширение, либо повторяющееся десятичное расширение. Затем мы можем вспомнить, что такие числа, как 𝜋 не имеют повторяющегося или конечного десятичного разложения и, следовательно, не рациональны.

Этого достаточно, чтобы ответить на вопрос. Однако может быть полезно увидеть формальное доказательство этого факта. Предположим что √2 — рациональное число. Это означает, что √2=𝑎𝑏 для некоторого целые числа 𝑎 и 𝑏, где 𝑏 не равно нулю. Мы можем отметить, что √2 не является целым числом, так как не существует целого числа, квадрат которого равен 2. Если 𝑎 и 𝑏 имеют общие делители, мы можем отменить их, поэтому мы можем предположить, что их наибольший общий делитель равен 1. Теперь мы возвести в квадрат обе части уравнения, чтобы получить 2=𝑎𝑏.

Если умножить на 𝑏, получим 2𝑏=𝑎.

Левая часть уравнения четная, поэтому правая тоже должна быть четной. Тем не менее, 𝑎 целое число, поэтому 𝑎 должно быть четным. Допустим, 𝑎=2𝑘; подставив это в дает 2𝑏=(2𝑘),2𝑏=4𝑘𝑏=2𝑘.

Теперь правая часть уравнения четная, значит, левая тоже должна быть четной. Так как 𝑏 является целым числом, мы должны иметь, что 𝑏 четно. Но мы предположили, что 𝑎 и 𝑏 не имеют общих множителей. Это показывает, что наше исходное предположение о том, что √2 является рациональным числом не может быть правдой. Следовательно, √2 иррационально.

Следовательно, мы смогли показать, что утверждение о том, что каждое нецелое число является рациональным, неверно, поэтому ответ отрицательный.

Существует множество различных подмножеств действительных чисел: у нас есть иррациональные числа ℚ, рациональные числа ℚ, целые числа ℤ, натуральные числа ℕ и многое другое.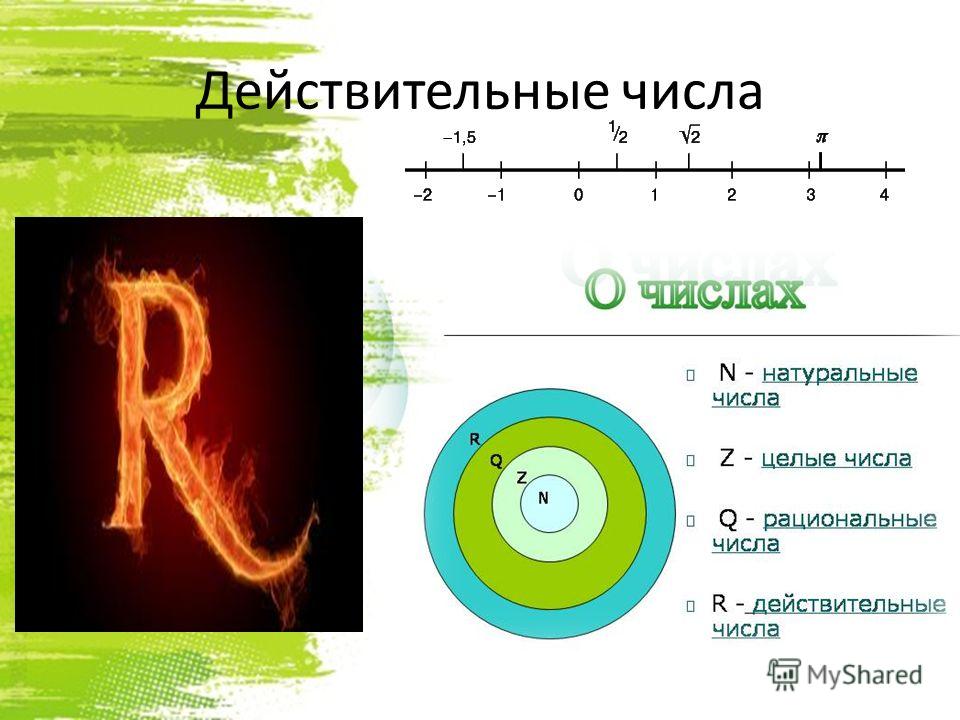 Часто нам нужно будет классифицировать заданные числа в каждом из этих наборов. Однако это может быть сложно, так как некоторые числа появляются в нескольких наборах. Например, 2 — это натуральное число, целое число и рациональное число.

Чтобы обойти эту проблему, мы можем рассмотреть диаграмму Венна, содержащую все эти множества. Наш самый внешний набор будет ℝ. Далее мы знаем, что ℝ=ℚ∪ℚ, и заметим, что нет числа, которое было бы одновременно рациональным и нерациональным. Итак, ℝ состоит из непересекающиеся множества ℚ и ℚ. Наконец, ℕ⊂ℤ⊂ℚ. Это дает нам следующую диаграмму Венна.

Теперь мы можем использовать это для классификации любого действительного числа. Например, мы уже показали, что 2∈ℕ, 2∈ℤ, 2∈ℚ и 2∈ℝ. Мы можем представлять это на диаграмме Венна, написав 2 внутри всех этих наборов следующим образом.

Теперь давайте рассмотрим пример использования диаграммы Венна для классификации списка заданных действительных чисел.

Пример 3. Размещение действительных чисел на диаграмме Венна

Для чисел √9, 7, 1,25, 13, −3, √2, √8 и √2, какие из следующие диаграммы Венна верны?

Ответ

Чтобы определить, какая из диаграмм Венна верна, сначала вспомним, что нам нужно записать каждое число внутри правильной подмножества. Если число обведено множеством, это указывает на то, что оно является членом множества.

Самый простой способ ответить на этот вопрос — исключить варианты. Мы можем сделать это, определив, какое подмножество каждого из данные числа являются членами и подмножества которых они не являются членами.

Начнем с того, что вспомним, что подразумевается под каждым набором. Мы пойдем от самого внутреннего подмножества наружу: √9,7,1.25,13,−3,√2,√8,√2.и

Во-первых, множество натуральных чисел ℕ — это множество счетных чисел; это дано ℕ={0,1,2,…}. Сразу видно, что 7∈ℕ. Мы можем Остановитесь здесь; однако 9является совершенным квадратом. Итак, √9=3. Следовательно, √9∈ℕ. Точно так же 8 — совершенный куб, поэтому √8=2. Следовательно, √8∈ℕ. Мы можем использовать это, чтобы исключить вариант C, так как он не включает √9∈ℕ и варианты D и E, поскольку они утверждают, что −3 — натуральное число.

Во-вторых, мы помним, что ℤ — это набор целых чисел, представляющий собой любое целое число, включая отрицательные. Мы видим, что −3∈ℤ. Однако остальные числа не являются целыми, поэтому мы переходим к следующее подмножество.

В-третьих, мы помним, что ℚ — это множество рациональных чисел: это множество всех частных целочисленные значения. Таким образом, 13∈ℚ. Мы также знаем, что любая десятичная дробь с конечным числом цифры — рациональное число. В частности, у нас есть 1,25=125100=54, поэтому 1,25 ℚ. Это позволяет нам исключить вариант Б, который утверждает, что это нерационально. числа.

Здесь можно остановиться; однако давайте проверим, что вариант А верен. Оставшиеся два числа, √2 и √2 нельзя записать как частное двух целых чисел. Чтобы увидеть Почему это так, вспомним сначала, что квадратный корень из неквадратного числа иррационален. Так как 2 не квадрат число √2 нерационально. Это означает, что он является элементом ℚ — множество иррациональных чисел. Мы также отмечаем, что ℝ=ℚ∪ℚ, поэтому √2∈ℝ. Точно так же мы можем вспомнить, что кубический корень несовершенного куба иррационален. Таким образом, √2∈ℚ и √2∈ℝ.

Это дает нам следующую диаграмму Венна.

Мы видим, что это точно соответствует варианту A.

Прежде чем мы перейдем к нашему следующему примеру, давайте посмотрим на классификацию чисел, заданных в разных формах, в правильные подмножества. действительных чисел. Мы можем сделать это, записав эти числа в таблицу с возможными подмножествами в виде столбцов.

Число	Натуральное число	Целое число	Рациональное число	Иррациональное число	Real Number
√−8
0.̇3
√9
√3
06

Первый шаг в классификации каждого из данных чисел состоит в том, чтобы вспомнить определения каждого из наборов:

• Множество натуральных чисел ℕ — это множество счетных чисел; это дано ℕ={0,1,2,…}.
• Набор целых чисел ℤ — это набор целых чисел, включая отрицательные: ℤ={…−3,−2,−1,0,1,2,3,…}.
• Множество рациональных чисел ℚ — это множество частных целых значений: ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ,𝑏≠0.
• Множество иррациональных чисел ℚ является дополнением множество рациональных чисел. Он включает в себя все числа, которые нельзя записать в виде частных целых чисел.
• Множество действительных чисел ℝ включает множества рациональных и иррациональных числа: ℝ=ℚ∪ℚ.

Тогда мы можем вспомнить, что все эти множества являются подмножествами действительных чисел. В частности, ℕ⊂ℤ⊂ℚ⊂ℝ.

Мы можем использовать это, чтобы упростить процесс заполнения таблицы.

Чтобы определить, в каком наборе находится каждое число, мы хотим упростить данное выражение для каждого числа.

Во-первых, заметим, что (−2)=−8, поэтому √−8=−2. Мы можем видеть, что это не является счетным числом; однако это целое число. Затем мы замечаем, что ℤ⊂ℚ⊂ℝ, так что это также рациональное и действительное число. Это не иррациональное число, так как оно рациональна; это дает нам следующее.

Number	Natural Number	Integer	Rational Number	Irrational Number	Real Number
√−8	×	✓	✓	×	✓

Во-вторых, отметим, что 0,̇3 — это десятичная дробь с повторяющимся десятичным расширением. В частности, мы можем отметить что это эквивалентно 13, так что это рациональное число. Это не счетное число и не целое число. Наконец, поскольку оно рационально, оно не является иррациональным и является действительным числом. Это дает нам следующие записи в таблице.

Number	Natural Number	Integer	Rational Number	Irrational Number	Real Number
0.̇3	×	×	✓	×	✓

В-третьих, мы хотим упростить выражение √9. Мы можем сделать это, заметив, что 3=9, поэтому √9=3. Это натуральное число, и, используя тот факт, что ℕ⊂ℤ⊂ℚ⊂ℝ, мы можем видеть, что это также целое, рациональное число и действительное число. Мы показали следующие записи.

Number	Natural Number	Integer	Rational Number	Irrational Number	Real Number
√9	✓	✓	✓	×	✓

Fourth , заметим, что 3 не является квадратным числом. Затем мы вспоминаем, что квадратный корень из неквадратного числа иррационален. Поскольку иррациональное число не может быть натуральным, целым или рациональным числом, а все иррациональные числа являются действительными числами, мы получаем следующие записи.

Number	Natural Number	Integer	Rational Number	Irrational Number	Real Number
√3	×	×	×	✓	✓

Finally , мы можем переписать 06 как 0. Это натуральное число, поэтому мы получаем следующие записи.

Число	Натуральное число	Целое число	Рациональное число	Irrational Number	Real Number
06	✓	✓	✓	×	✓

This gives us the following final table.

Number	Natural Number	Integer	Rational Number	Irrational Number	Real Number
√−8	×	✓	✓	×	✓
0. ̇3	×	×	✓	×	✓
√9	✓	✓	✓	×	✓
√3	×	×	×	✓	✓
06	✓	✓	✓	×	✓

In our next example, we will consider what happens when we складывать числа из разных подмножеств действительных чисел.

Пример 4. Понимание вещественных чисел

Если 𝑎∈ℤ, 𝑏∈ℝ и 𝑐∈ℚ, то 𝑎+𝑏+𝑐∈.

Ответ

Чтобы ответить на этот вопрос, давайте сначала попробуем некоторые возможные значения 𝑎, 𝑏 и 𝑐. Мы можем сделать это, вспомнив следующее:

• Множество целых чисел ℤ — это множество целых чисел, включая отрицательные: ℤ={…−3,−2,−1,0,1,2,3,…}.
• Множество рациональных чисел ℚ — это множество частных целых значений: ℚ=𝑎𝑏∶𝑎,𝑏∈ℤ,𝑏≠0.
• Множество иррациональных чисел ℚ является дополнением множества рациональных чисел. В него входят все числа, которые нельзя записать в виде частных целые числа, такие как √2.
• Множество действительных чисел ℝ включает множества рациональных и иррациональные числа: ℝ=ℚ∪ℚ.

Таким образом, мы могли бы иметь 𝑎=0, 𝑏=0 и 𝑐=0. Тогда у нас есть 𝑎+𝑏+𝑐=0+0+0=0. Однако мы хотим знать, что происходит в целом, поэтому давайте попробуем еще одна тройка значений.

Допустим, 𝑎=0, 𝑏=√2, ​​𝑐=0. Теперь у нас есть 𝑎+𝑏+𝑐=0+√2+0=√2. Отсюда мы видим, что сумма этих чисел иррациональна.

Мы можем использовать любое действительное значение 𝑏 наряду с 𝑎=0 и 𝑐=0, поэтому наш набор должен содержать все действительные значения. Следовательно, ответ ℝ.

В общем случае сумма чисел в некоторых подмножествах действительных чисел является замкнутой операцией.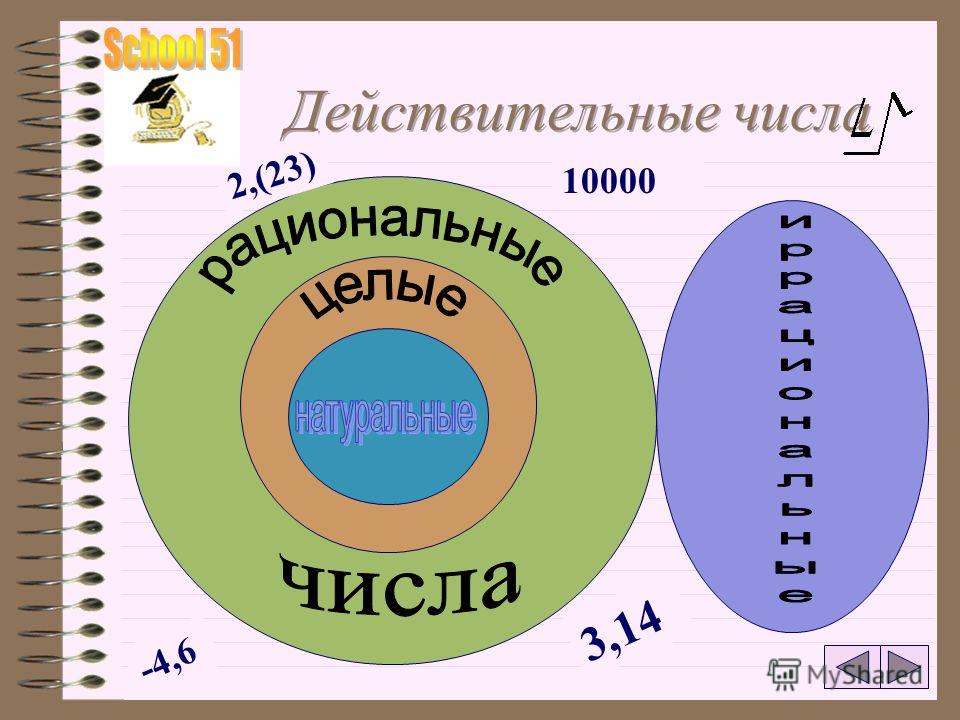 Например, сумма двух целых чисел всегда является целым числом, сумма двух рациональных чисел является рациональным числом, а сумма двух действительных чисел является действительным числом.

То же самое не верно для всех этих подмножеств ℝ. Например, √2 и −√2∈ℚ, но √2+−√2=0∉ℚ.

Это означает, что в общем случае нам нужно рассматривать 𝑎, 𝑏 и 𝑐 как элементы из ℝ, так как это самое большое подмножество, содержащее все три числа. Таким образом, суммируя три элементов ℝ дает нам действительное число.

Следовательно, ответ ℝ.

Есть еще один способ визуализации набора действительных чисел, и он включает использование числовой прямой. Для представления действительного числа на числовой прямой мы начинаем с точки, обозначающей ноль, а затем обозначаем правое направление как положительное, а левое — как отрицательное. Тогда мы говорим, что точка 𝐴 на числовой прямой представляет действительное число 𝑎, если ее смещение от 0 составляет 𝑎 единиц.

Например, мы можем представить некоторые действительные числа на числовой прямой, как показано на рисунке.

Мы говорим, что два действительных числа равны, если точки, представляющие их на числовой прямой, совпадают. Также стоит отметить что, поскольку эти точки основаны на смещении, мы можем определить смещение от точки 𝐴 к точке 𝐵 представляющие действительные числа 𝑎 и 𝑏 путем вычисления 𝑏−𝑎. Мы можем определить расстояние между точками, используя формулу |𝑏−𝑎|.

Пример 5. Размещение действительных чисел в числовой строке

Если точка 𝐴 на числовой прямой представляет √−27, а точка 𝐵 представляет собой √9, какой из следующих отрезков имеет большую длину?

1. 𝐴𝐶
2. 𝐶𝐵
3. 𝐴𝐵

Ответ

Мы можем начать с вычисления двух заданных выражений. Заметим, что −27=(−3), поэтому √−27=(−3)=−3.

Аналогично заметим, что 9=3, поэтому √9=√3=3. 

Мы можем использовать эти значения для обозначения 𝐴 и 𝐵 на числовой прямой.

В настоящее время существует множество различных способов определить, какой отрезок линии является самым длинным. На схеме мы видим, что 𝐴 и 𝐵 — самое большое расстояние друг от друга, поэтому 𝐴𝐵 должен быть самым длинным.

Также стоит вспомнить, как вообще найти длину отрезка между двумя точками на числовой прямой. Расстояние между значениями 𝑥 и 𝑦 на числовой прямой определяется выражением |𝑥−𝑦|. Это абсолютное значение смещения от точки 𝑋 указать 𝑌.

Если мы пометим значения, представленные 𝐴, 𝐵 и 𝐶, как 𝑎, 𝑏 и 𝑐 мы могли вычислить |𝑎−𝑏|, |𝑎−𝑐| и |𝑏−𝑐| определить длины отрезков.

Однако в данном случае это необязательно, так как мы видим, что 𝐴𝐵 является самым длинным сегментов линии, что является опцией C.

Давайте закончим повторением некоторых важных моментов из этого объяснения.