Электронный справочник по математике для школьников арифметика целые числа десятичная система счисления
| Справочник по математике | Арифметика | Арифметика целых чисел |
Содержание
| Натуральные (целые положительные) числа |
| Целые отрицательные числа |
| Целые числа |
| Десятичная система счисления |
Натуральные (целые положительные) числа
Числа
1 , 2 , 3 , …
называют натуральными или целыми положительными числами.
Множество натуральных чисел бесконечно. Множество натуральных чисел обозначают символом N.
Множество натуральных чисел обозначают символом N.
Число нуль, отрицательные и дробные числа не являются натуральными числами.
Целые отрицательные числа
Числа
– 1 , – 2 , – 3 , …
называют целыми отрицательными числами.
Множество целых отрицательных чисел бесконечно. Множество целых отрицательных чисел обозначают символом N– .
Целые числа
Множество целых чисел состоит из множества натуральных чисел, числа «нуль» и множества целых отрицательных чисел.
Множество целых чисел бесконечно. Множество целых чисел обозначают символом Z .
Множество целых чисел обозначают символом Z .
Десятичная система счисления
Системой счисления называют способ записи натуральных чисел при помощи символов, которые называют цифрами.
В обычной практической жизни используют десятичную система счисления. В этой системе числа записывают при помощи 10 цифр (арабских цифр):
0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .
Например, число, десятичная запись которого 361 , равно сумме трёх сотен, шести десятков и одной единицы:
В данном справочнике мы рассматриваем только десятичную систему счисления.
ЗАДАЧА. Сумма квадратов цифр положительного двузначного числа равна 13 . Если от этого числа отнять 9 , то получится число, записанное этими же цифрами, но в обратном порядке. Найдите это число.
Найдите это число.
РЕШЕНИЕ. Обозначив буквами x и y цифру десятков и цифру единиц искомого числа, соответственно, запишем это число в виде (черта сверху поставлена для того, чтобы отличить десятичную запись числа от произведения цифр x и y ). Тогда:
Число, записанное теми же цифрами, но в обратном порядке, имеет вид , причем
По условию задачи неизвестные x и y удовлетворяют системе уравнений
для решения которой преобразуем второе уравнение:
Далее получаем:
Теперь решим первое уравнение:
Поскольку число – 2 не является цифрой, то второй корень должен быть отброшен. Следовательно,
ОТВЕТ: Искомое число равно 32.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 7 из 13Следующая ⇒ В направлении возрастания и в направлении убывания.
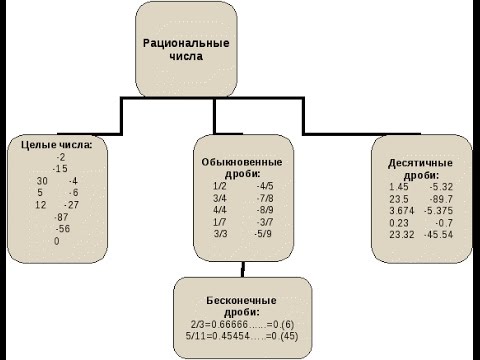
РАЦИОНАЛЬНЫЕ ЧИСЛА Что явилось главным мотивом для создания рациональных чисел? Главным мотивом для создания рациональных чисел была желание и необходимость создания числовых объектов характеризующих взаимоотношение части и целого. Что такое числовая обыкновенная дробь? Числитель? Знаменатель? Правильные, неправильные дроби – что это такое? Числовой обыкновенной дробью называется выражение , где m – любое целое число, а n –натуральное число. Число, стоящее над чертой называется числитель. Число, стоящее под чертой называется знаменатель. Дробь называется правильной если числитель меньше знаменателя и
Есть ли количественный смысл у числовой дроби? Да, есть. Положительная числовая дробь выражает количество частей (m) некоторого целого, поделенного на n равных частей. При таком понимании числовой дроби видим, что натуральные и целые числа также могут быть выражены при помощи числовой дроби знаменатель, которой равен единице.
73. Из какого материала и как была построена система рациональных чисел? Какие требования были выполнены при построении этой системы? Система рациональных чисел была построена из числовых обыкновенных дробей. Главным требованием при построении этой системы было продолжение операций и отношений, работающих на целых числах с сохранением их главных свойств, таким образом, чтобы операция деления была выполнима всегда.
Являются целые числа рациональными? Являются ли натуральные числа рациональными? Да, целые числа являются рациональными. Целые числа являются частью рациональных чисел.
Может ли число, представленное дробью быть целым? Натуральным? Может. Например, число -40/8 является целым числом -5. Точно таким образом число 40/8 является натуральным числом 5.
Каково главное или основное свойство дроби? Из чего оно следует? При определении рационального числа, представленного в виде числовой дроби, исходя из смысла числовой дроби постулируется, что все числовые дроби полученные из данной числовой дроби путем одновременного умножения числителя и знаменателя на одно и то же (любое) натуральное или целое число представляют то же самое рациональное число, что и исходная дробь. Исходя из этого формулируется ГЛАВНОЕ СВОЙСТВО ЧИСЛОВОЙ ДРОБИ: если числитель и знаменатель числовой дроби умножить или разделить (если это возможно) на одно и то же число, то рациональное число, которое представляет получившаяся дробь не изменится.
Сколькими способами рациональное число может быть представлено в виде дроби? Есть ли среди этих способов некий единственный, особый? Из основного свойства числовой обыкновенной дроби следует, что рациональное число может быть представлено в виде дроби бесконечным количеством способов. Однако, среди всех этих представлений есть случай, когда числитель и знаменатель нельзя разделить на одно и то же натуральное число. В этом случае дробь называется несократимой. Представление рационального числа в виде несократимой дроби единственно!!! Равенство двух дробей предпо-лагает, что одна из них сократима, так что две различные несократимые дроби не могут быть равны и значит представляют различные рациональные числа.
⇐ Предыдущая234567891011Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.) |
Типы действительных чисел — натуральные, целые, целые, рациональные и иррациональные числа
Система действительных чисел
- В математике числа классифицируются по типам в системе действительных чисел.

- Системы счисления могут быть подмножествами других систем счисления.
- Итак, число может иметь больше, чем 1 тип .
Чистый как грязь? ☺ Что ж, давайте узнаем больше, чтобы было понятнее!
Натуральные числа
Когда мы впервые научились считать, мы начали с 1, 2, 3, 4… и продолжали учиться, пока не дошли до миллионов и триллионов, верно? Эти счетные числа (1, 2, 3, 4, 5, 10, 100, 1000, 1 000 000…∞) называются натуральными числами.
Целые числа
Вы заметили, что чего-то не хватает в натуральных числах? Да, цифра 0! Хороший улов! Добавьте это к натуральным числам (0,1,2,3……∞), и вы получите целые числа!
- Итак, как видите, натуральные числа — это подмножество целых чисел.
- Кроме того, обратите внимание, что числа 1,2, 3… являются одновременно натуральными и целыми числами?
- 0 — это всего лишь целое число, а не натуральное число.

Целые числа
Целые числа включают все целые числа (0), а также отрицательные числа натуральных чисел: так (∞…, -4, -3, -2, -1, 0, 1, 2, 3,4 , …∞).
Итак, давайте еще раз посмотрим на шаблон –
- Все натуральные числа являются целыми числами и целыми числами
- Все целые числа являются целыми числами
- Отрицательные числа являются только целыми числами
Рациональные числа
Эти числа включают все вышеперечисленное (натуральные, целые, целые числа) ПЛЮС некоторые типы дробей/десятичных чисел .
Итак, что же делает дроби/десятичные дроби рациональными?
Дробь x/y, где числитель x – целое (…, -4, -3, -2, -1, 0, 1, 2, 3,4,…) , а знаменатель y – натуральное число ( 1, 2, 3,4) рационально.
Точно так же десятичная дробь, которая не повторяется (например, ¼ = 0,25, ¾ = 0,75), также является рациональной. Их также называют завершающими десятичными знаками.
Итак, рациональные числа могут выглядеть так:
(∞…,-4, -3,5, -3, -2¾, -2, -1½, -1, 0, 0,88, 1, 1¼, 2, 2,38, 3 , 3.91, 4, 4¼, …∞)
Иррациональные числа
Иррациональное число — это действительное число , которое нельзя записать в виде простой дроби . Другими словами, это десятичное число , которое никогда не заканчивается и не имеет повторяющегося шаблона 9.0011 .
- Десятичная дробь, которая постоянно повторяется, является хорошим примером этого.
- Самый известный пример иррационального числа — Π или пи .
- Π — отношение длины окружности к ее диаметру.
- Хотя его можно приблизить к 3,14159, фактическое значение Π начинается только с 3,14159. Последнее известное рекордное вычисление Π составляет до 2,7 ТРИЛЛИОНОВ цифр!
- Помните также, что это бесконечных цифр без повторяющегося шаблона .
Источник изображения: Википедия
- Что еще более важно — Π = 3,14159 нельзя выразить дробью!
- 22/7 — это приближение, которое мы используем для расчетов.

- Таким образом, Π не может быть выражено в виде дроби, десятичные цифры продолжают идти вечно и не повторяются в образце. Это делает его иррациональным числом!
- 22/7 — это приближение, которое мы используем для расчетов.
- Другим хорошим примером является √2 или квадратный корень из 2.
- Если вычислить его значение, оно приблизительно равно 1,41421356237309.50…
- Это также не может быть выражено в виде дроби, и поэтому иррационально
- Другие примеры — √3, √5, √7, √11 и т. д.…
- Автор
- Последние сообщения
Дивья Почимчерла
Как соучредитель STEAMism и TimeforAI, Дивья представляет собой творческую силу с миллионом идей, крутящихся в ее голове в любой момент. Она целеустремленная и любознательная — участвует во многих инициативах, в том числе в качестве волонтера-подростка в Детском музее Thinkery и волонтера Teen Court.. Она любит спорить, писать, учиться, общаться с другими и наставничество.
Последние сообщения от Дивья Почимчерла (посмотреть все)
элементарная теория множеств — Есть ли больше рациональных чисел, чем целых?
спросил
Изменено 1 год, 1 месяц назад
Просмотрено 28 тысяч раз
$\begingroup$
Мне сказали, что число рациональных чисел точно такое же, как и целых чисел.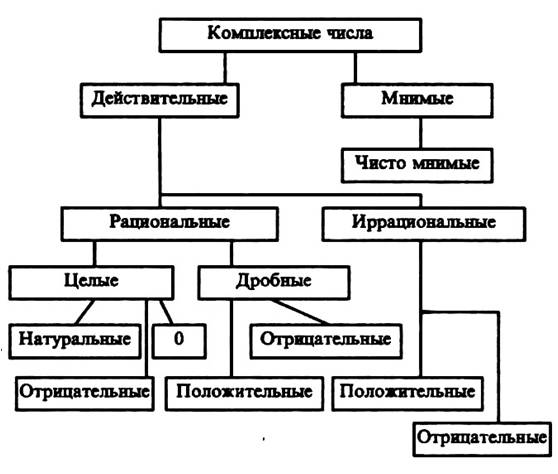 Множество рациональных чисел счетно бесконечно, поэтому каждое рациональное число может быть связано с положительным целым числом, поэтому существует такое же количество рациональных чисел, как и целых чисел. Я игнорировал проблемы, связанные со знаками, но с ними легко справиться.
Множество рациональных чисел счетно бесконечно, поэтому каждое рациональное число может быть связано с положительным целым числом, поэтому существует такое же количество рациональных чисел, как и целых чисел. Я игнорировал проблемы, связанные со знаками, но с ними легко справиться.
Чтобы подсчитать рациональные числа, рассмотрим наборы рациональных чисел, в которых знаменатель и числитель положительны, а их сумма равна некоторой константе. Если константа равна 2, это 1/1. Если константа равна 3, есть 1/2 и 2/1. Если константа равна 4, есть 1/3, 2/2 и 3/1. До сих пор мы отсчитывали 6 рациональностей, и если мы будем продолжать достаточно долго, мы в конечном итоге будем считать до любой конкретной рациональности, которую вы захотите упомянуть.
Проблема в том, что мне очень трудно это принять. У меня две причины. Во-первых, эта логика, по-видимому, предполагает, что бесконечность — это конечное число. Вы можете сосчитать и пронумеровать любое рациональное число, но вы не можете сосчитать все рациональные числа. Вы даже не можете сосчитать все положительные целые числа. Бесконечность — это код для «независимо от того, как далеко вы считаете, вы никогда не считаете достаточно». Если бы можно было считать до бесконечности, можно было бы считать на один шаг меньше и остановиться на счете бесконечность-1, который должен отличаться от бесконечности.
Вы даже не можете сосчитать все положительные целые числа. Бесконечность — это код для «независимо от того, как далеко вы считаете, вы никогда не считаете достаточно». Если бы можно было считать до бесконечности, можно было бы считать на один шаг меньше и остановиться на счете бесконечность-1, который должен отличаться от бесконечности.
Вторая причина заключается в том, что очень легко создавать альтернативные отображения. Между нулем и единицей бесконечно много рациональных чисел, между единицей и двумя бесконечно много рациональных чисел и так далее. Мне это кажется гораздо более разумным подходом, подразумевающим, что существует бесконечное число рациональных чисел для каждого целого числа.
Но даже в этом случае это всего лишь один из многих альтернативных способов отображения между диапазонами рациональных чисел и диапазонами целых чисел. Поскольку вы можете подсчитывать рациональные числа, вы также можете подсчитывать шаг на любую величину для каждого рационального числа.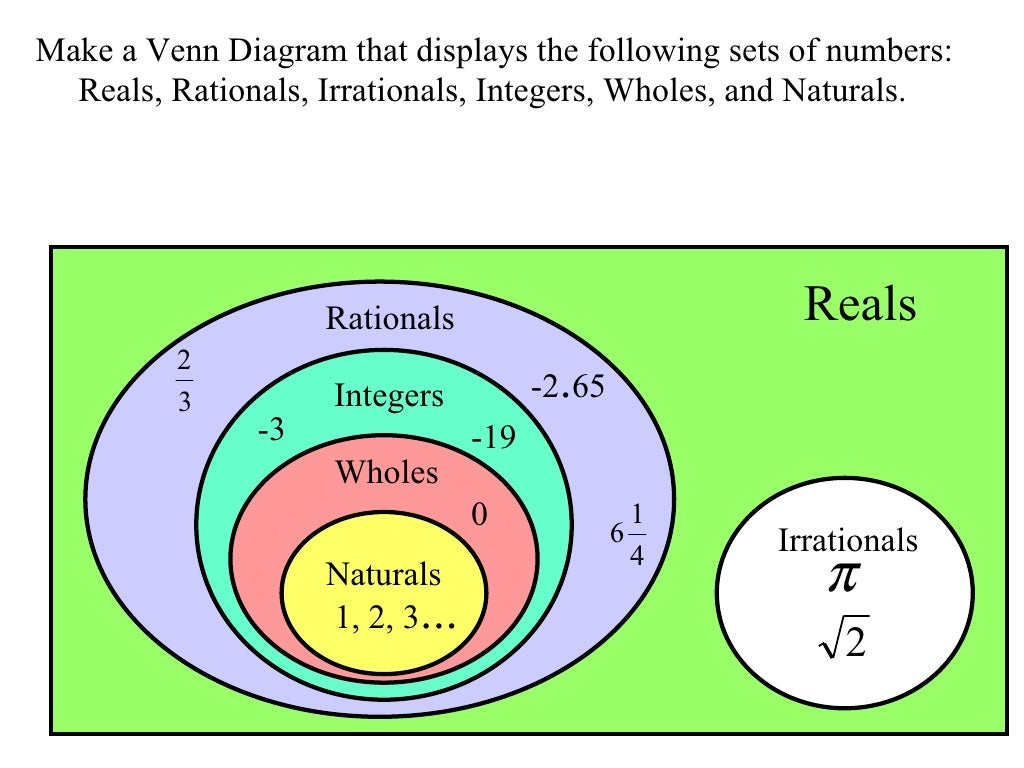 Вы можете использовать 1..10 для первого рационального и 11..20 для второго и т.д. Или 1..100 и 101..200 и т.д., или 1..1000 и 1001..2000 и т.д. Вы можете отобразить конечный диапазон целых чисел любого размера для каждого рационального числа таким образом, и, поскольку нет конечной верхней границы для количества шагов, вы можете утверждать, что для каждого рационального числа существует потенциально бесконечное число целых чисел.
Вы можете использовать 1..10 для первого рационального и 11..20 для второго и т.д. Или 1..100 и 101..200 и т.д., или 1..1000 и 1001..2000 и т.д. Вы можете отобразить конечный диапазон целых чисел любого размера для каждого рационального числа таким образом, и, поскольку нет конечной верхней границы для количества шагов, вы можете утверждать, что для каждого рационального числа существует потенциально бесконечное число целых чисел.
Итак… кто-нибудь может убедить меня, что на этот вопрос существует единственный однозначный правильный ответ? Есть ли рациональные числа больше, чем целые числа, или нет?
РЕДАКТИРОВАТЬ
Хотя я уже принял ответ, я просто добавлю дополнительный контекст.
Причина, по которой я сомневаюсь в этом, связана с кривой заполнения пространства Гильберта. Я нахожу это интересным из-за приложений к структурам данных многомерного индексирования в программном обеспечении. Однако я обнаружил утверждение Гильберта о том, что кривая Гильберта буквально заполняет многомерное пространство, которое трудно принять.
Как упоминалось в комментарии ниже, отрезок линии в один метр и отрезок линии в два метра можно рассматривать как наборы точек, но (согласно логике ответов ниже) эти два набора имеют одинаковый размер (мощность ). Тем не менее, мы не стали бы утверждать, что оба отрезка имеют одинаковый размер. Длины конечны и различны. Идя дальше этого, мы, конечно, не будем утверждать, что размер любого конечного отрезка прямой линии равен размеру квадрата один метр на один метр.
Рассуждение о кривой Гильберта теперь имеет смысл — множество точек на кривой равно множеству точек в пространстве, которое она заполняет. Раньше я слишком много думал об основах геометрии и не мог принять размер кривой равным размеру пространства. Однако это не основано на ложном аргументе о счете до бесконечности — это необходимое следствие альтернативной линии рассуждений. Эти две конструкции равны, потому что они обе представляют один и тот же набор точек. Из этого следует площадь/объем/и т. д. кривой.
кривой.
- теория элементарных множеств
- бесконечность
$\endgroup$
7
$\begingroup$
У математиков есть очень точные определения таких терминов, как «бесконечный» и «одинаковый размер». Единственный однозначный правильный ответ на этот вопрос заключается в том, что, используя стандартные математические определения, рациональные числа имеют «тот же размер», что и целые числа.
Во-первых, вот определения:
Определите «$0$» = пустое множество, «$1$» $= \{0\}$, «$2$» $= \{0,1\}$, «$3$» $= \{0, 1,2\}$ и т. д. Таким образом, число «n» на самом деле является множеством, состоящим из $n$ элементов.
Множество $A$ называется конечным тогда и только тогда, когда существует некоторое $n$ и функция $f:A\to n$, которая биективна.
Множество $A$ называется бесконечным тогда и только тогда, когда оно не конечно.
 (Обратите внимание, что это понятие ничего не говорит о том, что «счёт никогда не прекращается» или что-то в этом роде.)
(Обратите внимание, что это понятие ничего не говорит о том, что «счёт никогда не прекращается» или что-то в этом роде.)Говорят, что два множества $A$ и $B$ имеют «одинаковую длину», если существует функция $f:A\to B$, являющаяся биекцией. Обратите внимание, что мы НЕ требуем, чтобы ВСЕ функции были биекциями, просто чтобы была НЕКОТОРАЯ биекция.
Приняв эти определения, можно доказать, что рациональные и целые числа имеют одинаковый размер. Нужно просто найти конкретную биекцию между двумя множествами. Если вам не нравится то, что вы упомянули в своем посте, могу ли я предложить перечисление рациональных чисел Калкина-Уилфа?
Конечно, они дают биекцию между натуральными (без $0$) и рациональными числами, но если у вас есть такая биекция, легко построить биекцию из целых чисел в рациональные, составив с биекцией из целых чисел в положительные натуральные числа.
$\endgroup$
6
$\begingroup$
Возможно, этот ответ вас не очень удовлетворит, но я все равно попытаюсь объяснить.
Счетность. На самом деле мы не говорим о том, можно ли «сосчитать все рациональные числа», используя какой-то конечный процесс. Очевидно, что если существует бесконечное число элементов, вы не можете сосчитать их за конечное время, используя какой-либо разумный процесс. Вопрос в том, есть ли то же число рациональных чисел, что и положительные целые числа; это то, что означает, что множество является «счетным» — ибо существует взаимно-однозначных отображений положительных целых чисел в рассматриваемое множество. Вы описали такое отображение, и поэтому рациональные числа «счетны». (Вы можете не соглашаться с терминологией, но это не влияет на то, является ли концепция, которую она обозначает, последовательной.)
Альтернативные отображения. Вы, кажется, недовольны тем фактом, что, в отличие от случая конечного множества, вы можете определить инъекцию натуральных чисел в рациональные числа, которая не является сюръективной — что вы можете фактически определить более общую отношение , в котором каждое целое число связано с бесконечным числом рациональных чисел, но никакие два целых числа не связаны с одними и теми же рациональными числами. Что ж, в эту игру могут играть двое: вы можете определить отношение, в котором каждое рациональное число связано с бесконечным числом целых чисел, и никакие два рациональных числа не связаны с одними и теми же целыми числами! Просто определите отношение, согласно которому каждое положительное рациональное число a/b связано со всеми числами, которые делятся на 2 a , но не на 2 a+1 , и на 3 b , но не на 3 б+1 ; или, в более общем случае, соответственно 2 ка и 3 кб для любого положительного целого числа k. (Есть, как вы говорите, проблемы со знаками, но их можно сгладить.)
Что ж, в эту игру могут играть двое: вы можете определить отношение, в котором каждое рациональное число связано с бесконечным числом целых чисел, и никакие два рациональных числа не связаны с одними и теми же целыми числами! Просто определите отношение, согласно которому каждое положительное рациональное число a/b связано со всеми числами, которые делятся на 2 a , но не на 2 a+1 , и на 3 b , но не на 3 б+1 ; или, в более общем случае, соответственно 2 ка и 3 кб для любого положительного целого числа k. (Есть, как вы говорите, проблемы со знаками, но их можно сгладить.)
Вы можете пожаловаться, что отношение, которое я определил, не является «естественным». Возможно, вы имеете в виду тот факт, что целые числа представляют собой подмножеств рациональных чисел — на самом деле подгруппа, рассматривающая их обе как аддитивные группы — и что фактор-группа ℚ/ℤ бесконечна. Что ж, это определенно интересно, и это естественная структура, которая вызывает интерес. Но это больше, чем то, к чему пытается прийти проблема «простой кардинальности»: теория множеств интересуется размером независимо от структуры, и поэтому мы не ограничивайтесь картами, обладающими тем или иным видом «естественности». Конечно, если вы заинтересованы в отображениях, которые учитывают какую-то структуру, вы можете строить теории размера на основе этого: это то, что делается в теории меры (с мерой), линейной алгебре (с размерностью) и даже в теории групп. (с индексом). Поэтому, если вам не нравится кардинальность, как ее понимают теоретики множеств, вы можете рассмотреть более структурированные меры размера, которые кажутся вам более интересными!
Но это больше, чем то, к чему пытается прийти проблема «простой кардинальности»: теория множеств интересуется размером независимо от структуры, и поэтому мы не ограничивайтесь картами, обладающими тем или иным видом «естественности». Конечно, если вы заинтересованы в отображениях, которые учитывают какую-то структуру, вы можете строить теории размера на основе этого: это то, что делается в теории меры (с мерой), линейной алгебре (с размерностью) и даже в теории групп. (с индексом). Поэтому, если вам не нравится кардинальность, как ее понимают теоретики множеств, вы можете рассмотреть более структурированные меры размера, которые кажутся вам более интересными!
Непосредственные предшественники. Несколько не относящаяся к делу (но все же важная) жалоба, которую вы предъявляете, звучит так: » Если бы можно было считать до бесконечности, можно было бы считать на один шаг меньше и остановиться на счете «бесконечность-1», который должен отличаться от бесконечности.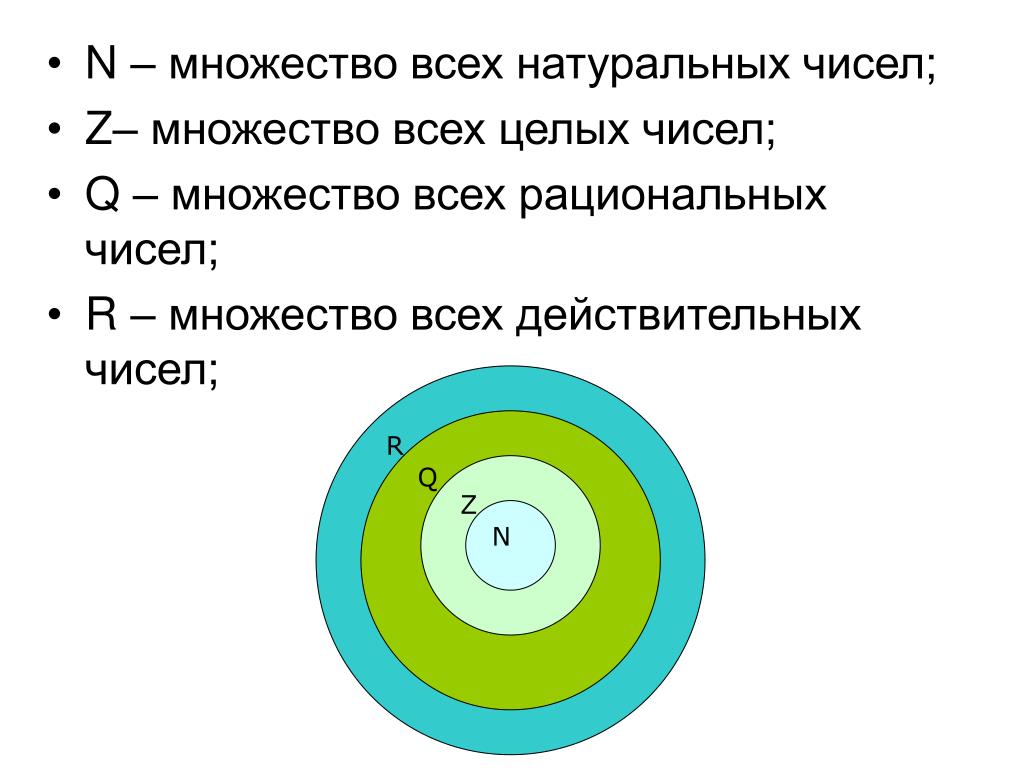 » Вопрос: почему вы обязательно сможете остановиться на «бесконечность минус один»? Это верно для конечных наборов, но не обязательно означает, что все, что верно для конечных наборов, верно и для бесконечных. (На самом деле, очевидно, что некоторые вещи обязательно потерпят неудачу.) — Это важно, если вы изучаете порядковые числа, которые в некотором роде отражают процесс подсчета (обозначение вещей как «первого», «второго», «третьего»). , и так далее), из-за понятия предельного ординала: первый «бесконечный» элемент правильного порядка не имеет непосредственных предшественников! Опять же, вы вправе сказать, что это концепции, в изучении которых вы лично не заинтересованы, но это не означает, что они обязательно непоследовательны.
» Вопрос: почему вы обязательно сможете остановиться на «бесконечность минус один»? Это верно для конечных наборов, но не обязательно означает, что все, что верно для конечных наборов, верно и для бесконечных. (На самом деле, очевидно, что некоторые вещи обязательно потерпят неудачу.) — Это важно, если вы изучаете порядковые числа, которые в некотором роде отражают процесс подсчета (обозначение вещей как «первого», «второго», «третьего»). , и так далее), из-за понятия предельного ординала: первый «бесконечный» элемент правильного порядка не имеет непосредственных предшественников! Опять же, вы вправе сказать, что это концепции, в изучении которых вы лично не заинтересованы, но это не означает, что они обязательно непоследовательны.
Подводя итог: теоретики множеств измеряют «размер множества», используя простое определение, которое не заботится о структуре и может противоречить вашей интуиции, если вы хотите взять структуру целых чисел (и рациональную числа) очень серьезно, а также хочу сохранить свои интуитивные представления о конечных множествах. У этого есть два решения: попытайтесь напрячь свою интуицию, чтобы приспособиться к идеям теоретиков множеств, или изучить другую область математики, которая вам кажется более интересной!
У этого есть два решения: попытайтесь напрячь свою интуицию, чтобы приспособиться к идеям теоретиков множеств, или изучить другую область математики, которая вам кажется более интересной!
$\endgroup$
3
$\begingroup$
В математике множество называется бесконечным , если его можно поставить в соответствие 1-1 с его собственным подмножеством, а конечным оно не бесконечно. (Я знаю, что представление бесконечного как примитивного и конечного как производного кажется безумием, но сделать это проще, поскольку в противном случае вы должны предположить, что целые числа существуют, прежде чем говорить, что множество конечно)
Что касается ваших замечаний:
— с помощью вашего метода (если вы не забудете отбросить дроби типа 4/6, что равно 2/3) вы на самом деле посчитали рациональных чисел, так как для каждого числа у вас есть функция, которая связывает его с натуральным числом . Это правда, что вы не можете сосчитать ВСЕ рациональные числа или все целые числа; но ведь и целую прямую линию провести нельзя, не так ли?
— с бесконечными наборами вы можете создавать бесконечные отображения, но вам просто нужно одно отображение 1-1, чтобы показать, что два набора равны.
Это правда, что вы не можете сосчитать ВСЕ рациональные числа или все целые числа; но ведь и целую прямую линию провести нельзя, не так ли?
— с бесконечными наборами вы можете создавать бесконечные отображения, но вам просто нужно одно отображение 1-1, чтобы показать, что два набора равны.
$\endgroup$
3
$\begingroup$
Мощность множества рациональных чисел такая же, как мощность целых чисел такая же, как мощность натуральных чисел.
Когда мы подсчитываем конечное множество элементов, мы строим однозначное отображение из набора на конечный начальный сегмент натуральных чисел. Если мы хотим знать, имеют ли два конечных множества одинаковую мощность (являются ли они равномощными), мы можем: 1) подсчитать оба множества и посмотреть, получим ли мы одно и то же число, или 2) попытаться построить однозначное отображение из одного установить на другой. Если мы можем построить карту, указанную в (2), то множества равномощны.
Если мы можем построить карту, указанную в (2), то множества равномощны.
Обобщая эту процедуру с конечных множеств на произвольные множества, мы получаем, что для любых двух множеств множества имеют одинаковую мощность (равнозначны), если существует биекция (однозначное отображение между множествами, лежащее на цель, а не просто в). В конечном случае, если существует однозначное отображение, являющееся биекцией, все однозначные отображения взаимно однозначны. Это не относится к бесконечным множествам, что является корнем вашего второго беспокойства.
Чтобы решить эту вторую проблему, рассмотрим отображение отрицательных целых чисел в положительные целые числа, которое отображает каждое отрицательное целое число в его абсолютное значение. Существование этой карты показывает, что эти два множества равномощны. Конечно, мы можем построить взаимно однозначное отображение из отрицательных целых чисел в положительные целые числа, которые находятся в, а не в. (Рассмотрите карту, которая переводит каждое отрицательное целое число в его произведение на -2.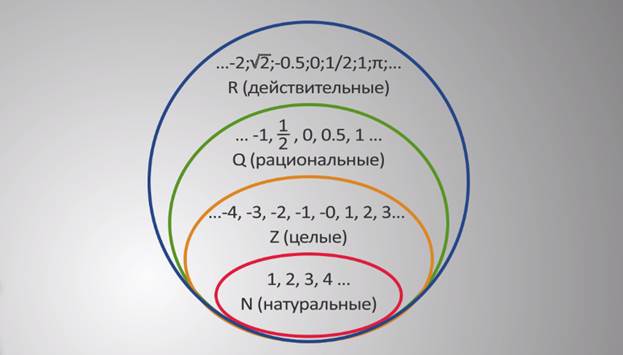 ) Но существование этих альтернативных карт не влияет на тот факт, что между множествами существует по крайней мере одна биекция, и это все, что требуется для тех множества равномощны.
) Но существование этих альтернативных карт не влияет на тот факт, что между множествами существует по крайней мере одна биекция, и это все, что требуется для тех множества равномощны.
Что касается вашего первого беспокойства, я не понимаю, почему вы думаете, что процедура предполагает, что «бесконечность — конечное число». Это включает в себя указание функции отображения из одного набора в другой, которая является один-один и на. Эта попытка, безусловно, может потерпеть неудачу, как показывает аргумент Кантора о диагонализации, согласно которому мощность множества всегда строго меньше, чем мощность его набора мощности. (Подходящим применением этой техники является хорошо известное доказательство того, что мощность вещественных чисел больше мощности натуральных чисел.)
$\endgroup$
2
$\begingroup$
Вы можете думать об этом по-другому. Рассмотрим набор действительных чисел от 0 до 1, а затем набор действительных чисел от 0 до 2.
Рассмотрим набор действительных чисел от 0 до 1, а затем набор действительных чисел от 0 до 2.
Интуитивно кажется, что набор действительных чисел от 0 до 2 вдвое больше, чем набор от 0 до 2. 1. Однако это не так, потому что оба множества имеют одинаковые мощность .
Рассмотрим функцию $f(x) = 2x$. Каждое вещественное число от 0 до 1 равно , биецируемому на вещественному числу от 0 до 2. Следовательно, множества имеют одинаковый размер.
$\endgroup$
1
$\begingroup$
Я приведу вам мой любимый аргумент для доказательства биекции между $\mathbb{Z}$ и $\mathbb{Q}$, и для меня этот аргумент действительно убедителен (по крайней мере, столь же убедителен, как и биекция между $\mathbb{N}$ и $\mathbb{Z}$). 9{a_4}\cdots,$$
то есть как (бесконечное) произведение простых степеней, показатели которых $(a_1,a_2,\ldots)$, все натуральных чисел равны $0$, за исключением конечного числа из них.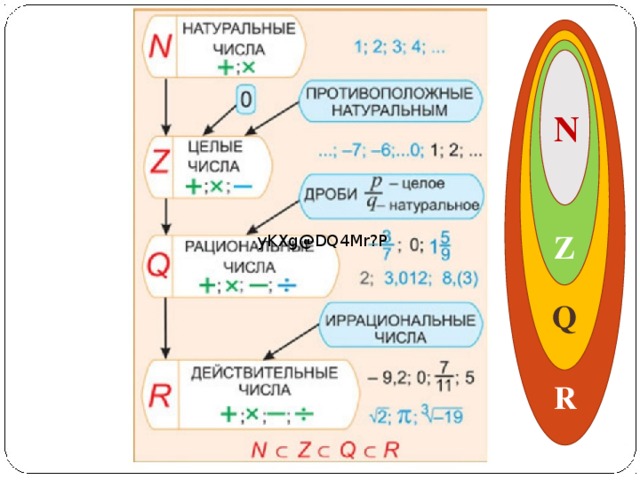



 Натуральные числа являясь частью целых чисел, также являются рациональными числами.
Натуральные числа являясь частью целых чисел, также являются рациональными числами.




 (Обратите внимание, что это понятие ничего не говорит о том, что «счёт никогда не прекращается» или что-то в этом роде.)
(Обратите внимание, что это понятие ничего не говорит о том, что «счёт никогда не прекращается» или что-то в этом роде.)