Радиус и диаметр окружности — Математика и Английский
Радиус это в математике
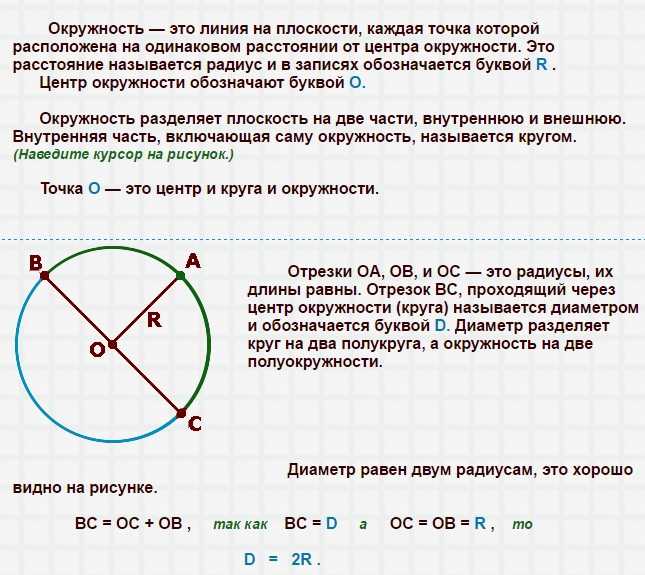
Окружность — это фигура в геометрии, которая состоит
Из множества точек, расположенных на одинаковом
Расстоянии от заданной точки (центра окружности).
Радиус Окружности — это отрезок, который соединяет
Центр окружности с какой-либо точкой окружности.Диаметр окружности — это отрезок, который соединяет
Две любые точки окружности, причем сам отрезок
Должен проходить через центр окружности
Eсли от центра окружности провести
Отрезки ко всем точкам окружности, то они будут иметь
Одинаковую длину, то есть равны. В математике
Такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
Равны между собой, имеют одинаковую длину.
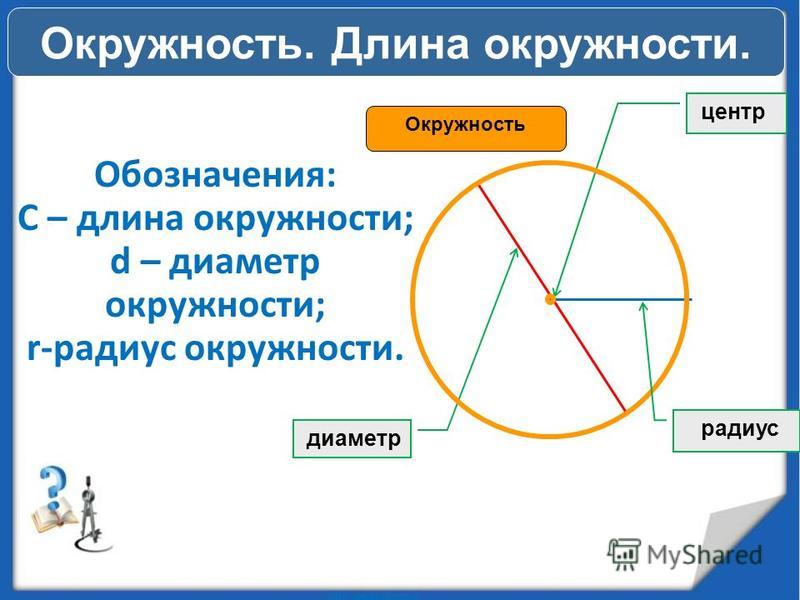
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, R или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
Радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
Получившееся число и будет радиусом.
Формула радиуса окружности через Диаметр:
Формула диаметра окружности через Радиус:
Также, окружность, может быть вписанной в фигуру, описанной
Около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура

Существует радиус вписанной окружности
И радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
Зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
Которая вписана в геометрическую фигуру.Радиус описанной окружности — это радиус окружности,
Которая описана около геометрической фигуры.
Радиус Окружности — это отрезок, который соединяет
Центр окружности с какой-либо точкой окружности. Диаметр окружности — это отрезок, который соединяет
Две любые точки окружности, причем сам отрезок
Должен проходить через центр окружности
Окружность — это фигура в геометрии, которая состоит
Из множества точек, расположенных на одинаковом
Расстоянии от заданной точки (центра окружности).
Формула радиуса окружности зависит от того находится фигура внутри окружности, или окружность находится около фигуры.
Colibrus. ru
27.04.2020 2:28:24
2020-04-27 02:28:24
Источники:
Https://colibrus. ru/radius-i-diametr-okruzhnosti/
Диаметр и радиус — что это такое? » /> » /> .keyword { color: red; }
Радиус это в математике
В жизни человек часто сталкивается с понятием окружность. Все едят с круглых тарелок, грызут круглые яблоки, катаются на велосипеде или ездят на транспорте с круглыми колесами и просто видят круглое солнце.
Понятия радиус и диаметр
Немногие задумываются, что на самом деле круг – очень сложная замкнутая фигура. Она состоит из главной точки (так называемый центр), а также из множества точек, которые идут от этого центра. Расстояние от центральной точки до окружности называют радиус. Чаще всего это понятие обозначается букой «R».
Если соединить две противоположные друг другу точки окружности и провести между ними линию, то она и будет диаметром. Диаметр обозначают символом «Ø». То есть радиус всегда будет равен половине диаметра.
Диаметр обозначают символом «Ø». То есть радиус всегда будет равен половине диаметра.
Как использовать эти понятия в жизни
Вообще с этими понятиями знакомы практически все, кто учил геометрию в школе. Взрослые тоже часто сталкиваются с ними, когда помогают детям делать домашнее задание или просто проверяют его.
Также эти понятия очень часто используются в черчении, к примеру, в архитектуре, когда планируется сделать круглое окно, арку или другую круглую деталь.
В ландшафте тоже не обойтись без радиуса и диаметра, ведь именно они позволят поделить круг на несколько частей, создав яркие цветочные композиции. Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами.
Во время конструирования одежды тоже часто встречаются понятия радиус и диаметр. Например, когда шьют шляпы, юбки или круглые накладные воротники.
Понятия диметр и радиус часто используются в программировании и создании сайтов. К примеру, многие создают программы для коррекции кругов (последние используются в разных сферах).
Важно обратить внимание, что понятия диаметр и радиус касаются не только круга. Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.
Другие понятия
Существует еще несколько понятий, которые могут пригодиться тем, кто работает с диаметром или радиусом:
- Дуга. Это кривая линия, которая является частью окружности. Ее измеряют в градусах. Сумма всех дуг составляет 360 градусов. Хорда. В отличие от кривой дуги это прямой отрезок, который соединяет две точки на окружности. Хорда отличается и диаметра – последний всегда равен двум радиусам и всегда проходит через центральную точку круга. Хорда же может быть длиннее или короче радиуса и никогда не проходит через центральную точку на круге.
 Сектор. Простыми словами, круг – это торт или пирог. Сектор же это треугольный кусок, который вырезается из этого пирога или торта. Касательная. Это линия, которая проходит рядом с кругом так, что соприкасается только с одной точкой на окружности.
Сектор. Простыми словами, круг – это торт или пирог. Сектор же это треугольный кусок, который вырезается из этого пирога или торта. Касательная. Это линия, которая проходит рядом с кругом так, что соприкасается только с одной точкой на окружности.Все перечисленные выше понятия пригодятся не только тем, кто учит геометрию, но и тем, кто имеет дело с кругами в других сферах. В математике существует несколько формул, которые помогут выяснить величину любого из описанных выше понятий по заданным параметрам.
Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами.
Premudrosty. ru
30.11.2017 0:22:49
2017-11-30 00:22:49
Источники:
Https://premudrosty. ru/diametr-i-radius-chto-eto-takoe. html
Радиус — это. Что такое Радиус? » /> » /> .keyword { color: red; }
Радиус это в математике
Ра́диус (лат. Radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка. Радиус составляет половину диаметра.
Радиус составляет половину диаметра.
Содержание
Свойства
- Радиус, проведённый в точку окружности, перпендикулярен окружности в этой точке. Радиус, перпендикулярныйхорде, делит её пополам.
Связанные определения
- в окружности — это угол, образованный двумя радиусами. кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Этимология
Слово «радиус» впервые встречается в 1569 г. у французского учёного П. Рамуса, несколько позже у Ф. Виета. Становится общепринятым лишь в конце XVII века. Происходит от лат. Radius , означающего «луч, спица колеса».
Обобщения
Радиусом множества, лежащего в метрическом пространстве с метрикой, называется величина \rho(x, y))/2″ width=»» height=»» />. Например, радиус N-размерного гиперкуба со стороной S равен
\sqrt.» width=»» height=»» />
См. также
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.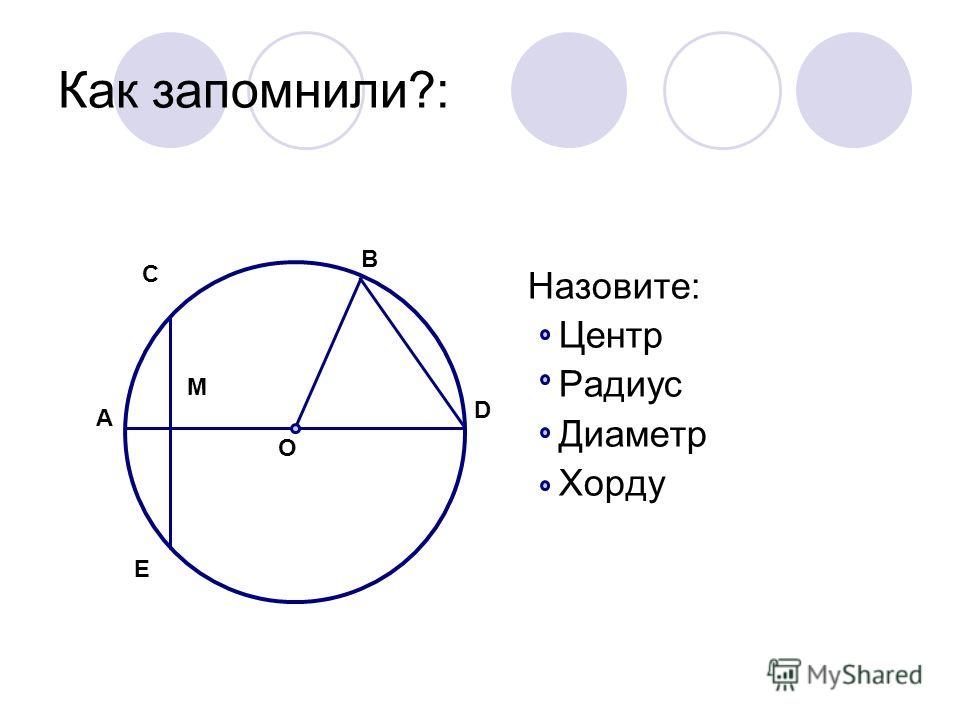
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.
Эта отметка установлена 14 мая 2011.
- Классическая геометрия Метрическая геометрия
Wikimedia Foundation. 2010 .
Полезное
Смотреть что такое «Радиус» в других словарях:
Радиус-FM — Страна Беларусь … Википедия
РАДИУС — (лат. radius луч). 1) полупоперечник круга; в кривых линиях и кривых поверхностях линия, проведенная от центра в окружности. 2) кость, лежащая рядом с локтевою и образующая с нею локтевую часть руки. Радиус вектор. Расстояние какой нибудь точки… … Словарь иностранных слов русского языка
РАДИУС — муж., лат. полупоперечник круга, полуось шара, луч, нога, которою круг очерчен; черта или мера от остья (средоточия, центра) до обода. Радиус вектор, полупоперечник долгокруга (эллипса). | Радиус, лучевая кость; она лежит рядом с локтевою и с нею … Толковый словарь Даля
РАДИУС — РАДИУС, радиуса, муж.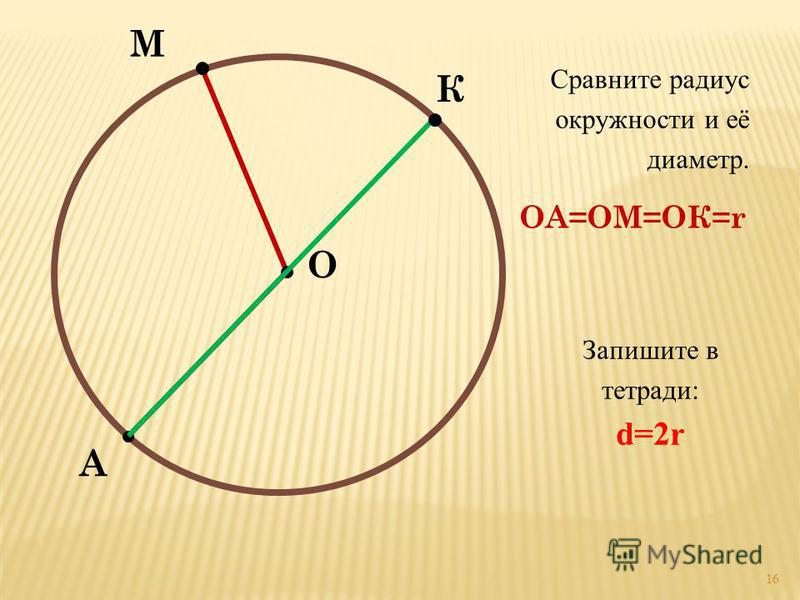 (лат. radius луч, спица). 1. Прямая, соединяющая точку центра с любой точкой окружности или поверхности шара (мат.). 2. перен. Величина охвата чего нибудь, сфера распространения чего нибудь (по отношению к какому нибудь… … Толковый словарь Ушакова
(лат. radius луч, спица). 1. Прямая, соединяющая точку центра с любой точкой окружности или поверхности шара (мат.). 2. перен. Величина охвата чего нибудь, сфера распространения чего нибудь (по отношению к какому нибудь… … Толковый словарь Ушакова
Радиус — закругленной части режущей кромки инструмента. [http://www. manual steel. ru/eng a. html] Тематики металлургия в целом EN nose radius … Справочник технического переводчика
РАДИУС — (лат. radius букв. спица колеса, луч), отрезок, соединяющий какую либо точку окружности или сферы с центром, а также длина этого отрезка … Большой Энциклопедический словарь
РАДИУС — РАДИУС, в геометрии расстояние или прямая от центра окружности или сферы к любой точке ОКРУЖНОСТИ или поверхности сферы … Научно-технический энциклопедический словарь
РАДИУС — РАДИУС, а, муж. 1. В математике: отрезок прямой, соединяющий центр шара или круга с любой точкой сферы или окружности, а также длина этого отрезка. 2. перен. Охват, область распространения чего н. Р. действия авиации. | прил. радиусный, ая, ое… … Толковый словарь Ожегова
2. перен. Охват, область распространения чего н. Р. действия авиации. | прил. радиусный, ая, ое… … Толковый словарь Ожегова
РАДИУС — (стар.) градшток (см.). Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
Радиус — сущ., кол во синонимов: 2 • критрадиус (1) • отрезок (12) Словарь синонимов ASIS. В. Н. Тришин. 2013 … Словарь синонимов
- Радиус, проведённый в точку окружности, перпендикулярен окружности в этой точке. Радиус, перпендикулярныйхорде, делит её пополам.
Содержание
- Радиус, проведённый в точку окружности, перпендикулярен окружности в этой точке. Радиус, перпендикулярныйхорде, делит её пополам.
- в окружности — это угол, образованный двумя радиусами. кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
\sqrt.» width=»» height=»» />
1 полупоперечник круга; в кривых линиях и кривых поверхностях линия, проведенная от центра в окружности.
Dic. academic. ru
27.07.2017 6:22:57
2017-07-27 06:22:57
Источники:
Https://dic. academic. ru/dic. nsf/ruwiki/6846
Что такое круг радиус периметр площадь. Как найти и чему будет равна длина окружности
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
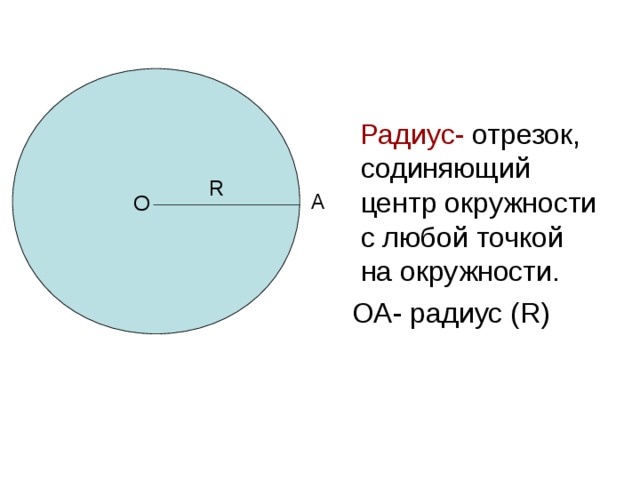
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром.
 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два .
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r .
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда.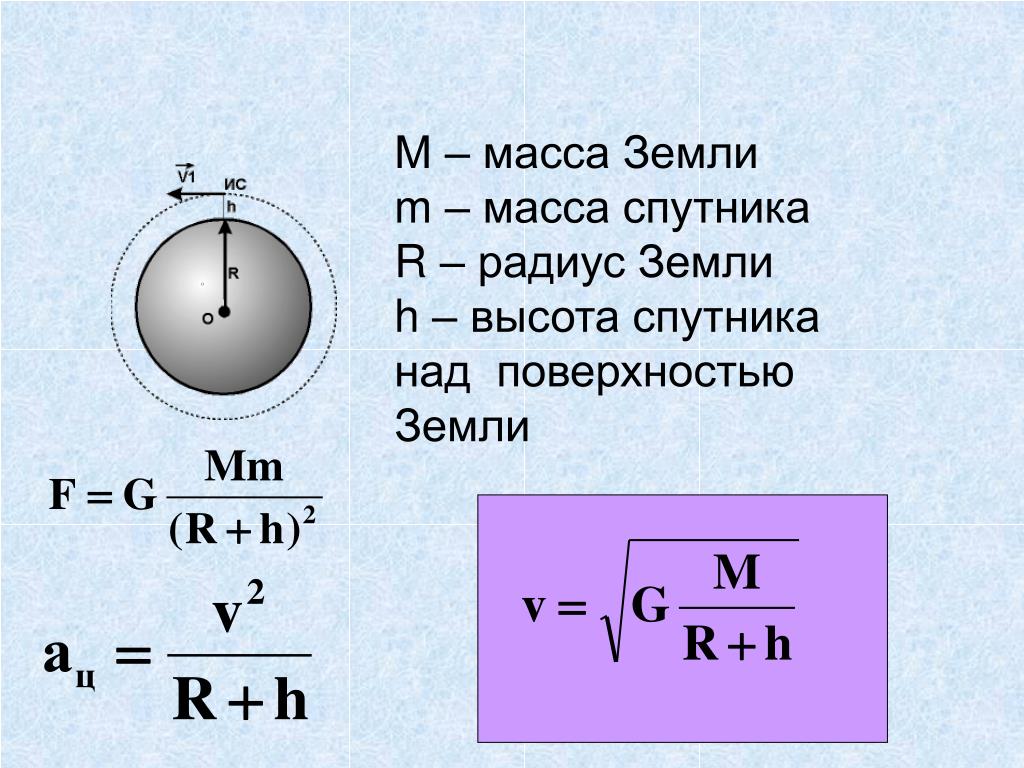 С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.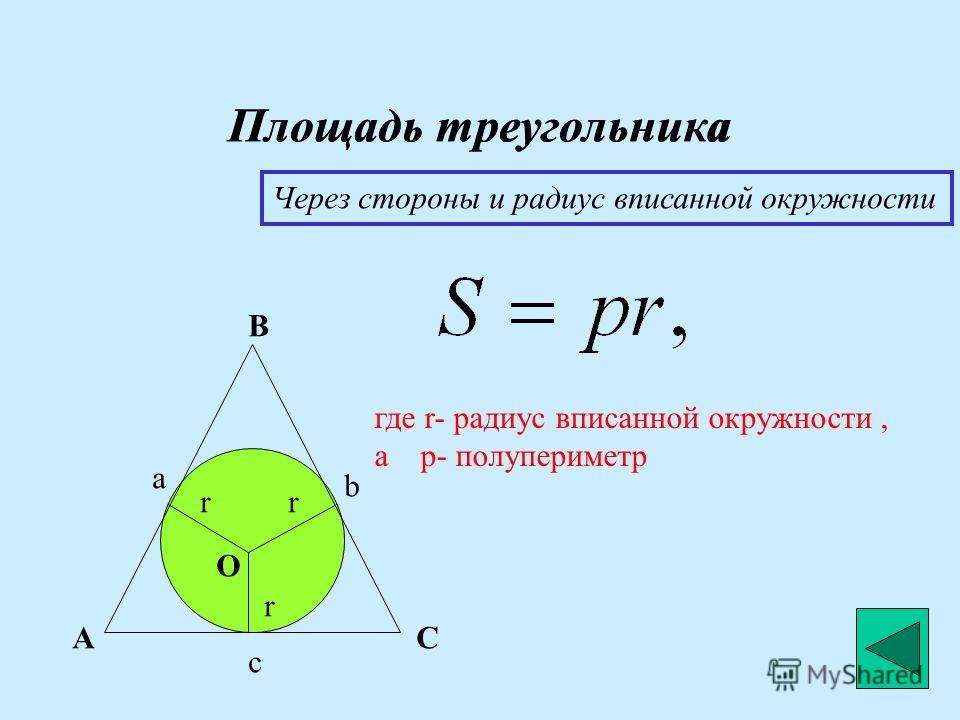
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него.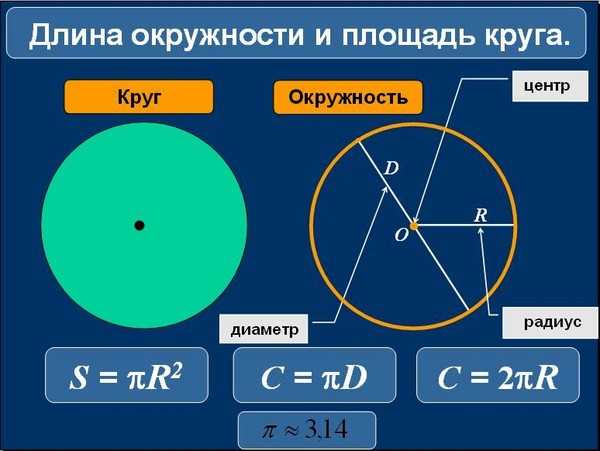 В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr. Рассмотрим применение формулы на примере простых задач:
Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр.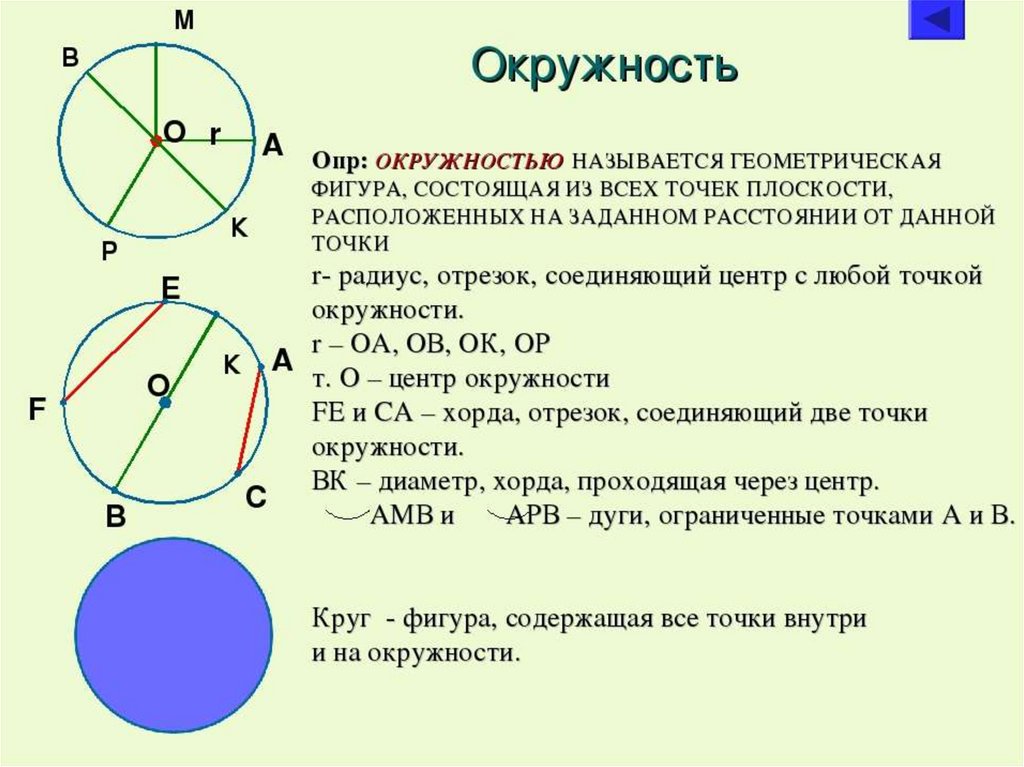 На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Радиус описанной и вписанной окружности: Формулы и примеры | Хай-тек
Краткое содержание:
- Что такое радиус
- Радиус и диаметр
- Примеры задач
- Формулы для радиуса описанной окружности
- Найти радиус описанной окружности треугольника по сторонам
- Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
- Найти радиус описанной окружности равнобедренного треугольника по сторонам
- Найти радиус описанной окружности прямоугольного треугольника по катетам
- Радиус описанной окружности трапеции по сторонам и диагонали
- Найти радиус описанной окружности около квадрата
- Радиус описанной окружности прямоугольника по сторонам
- Радиус описанной окружности правильного многоугольника
- Радиус описанной окружности правильного шестиугольника
- Формулы для радиуса вписанной окружности
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Радиус вписанной окружности в прямоугольный треугольник
- Радиус вписанной окружности в равнобочную трапецию
- Радиус вписанной окружности в квадрат
- Радиус вписанной окружности в ромб
- Радиус вписанной окружности в правильный многоугольник
- Радиус вписанной окружности в шестиугольник
- Примеры задач
- Обсуждение
Здравствуйте мои дорогие подписчики и гости сайта 9111.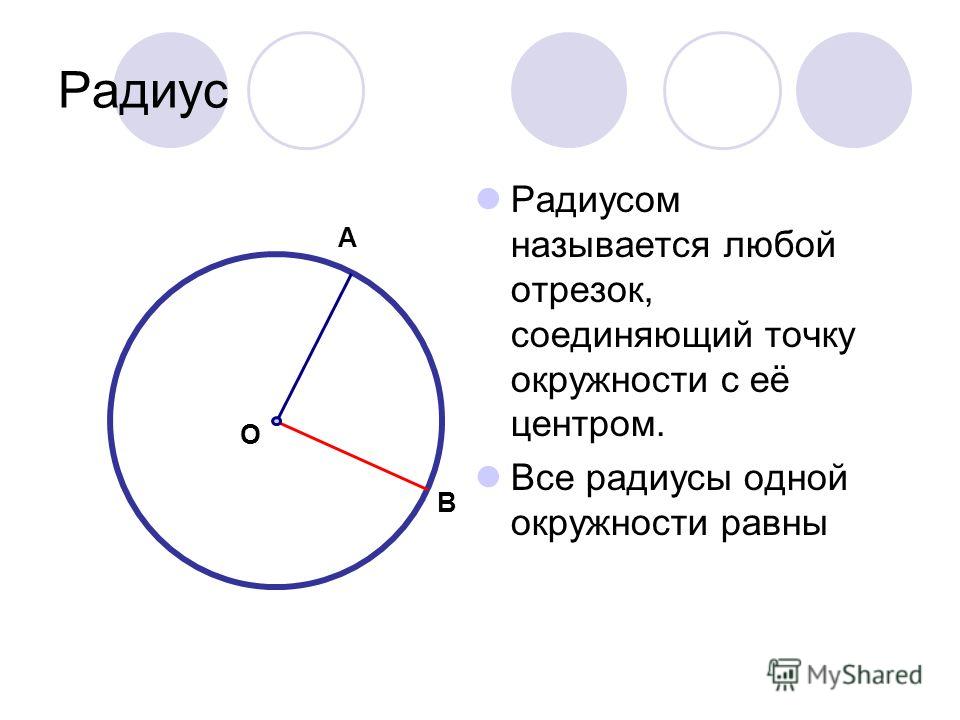 ru!
ru!
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
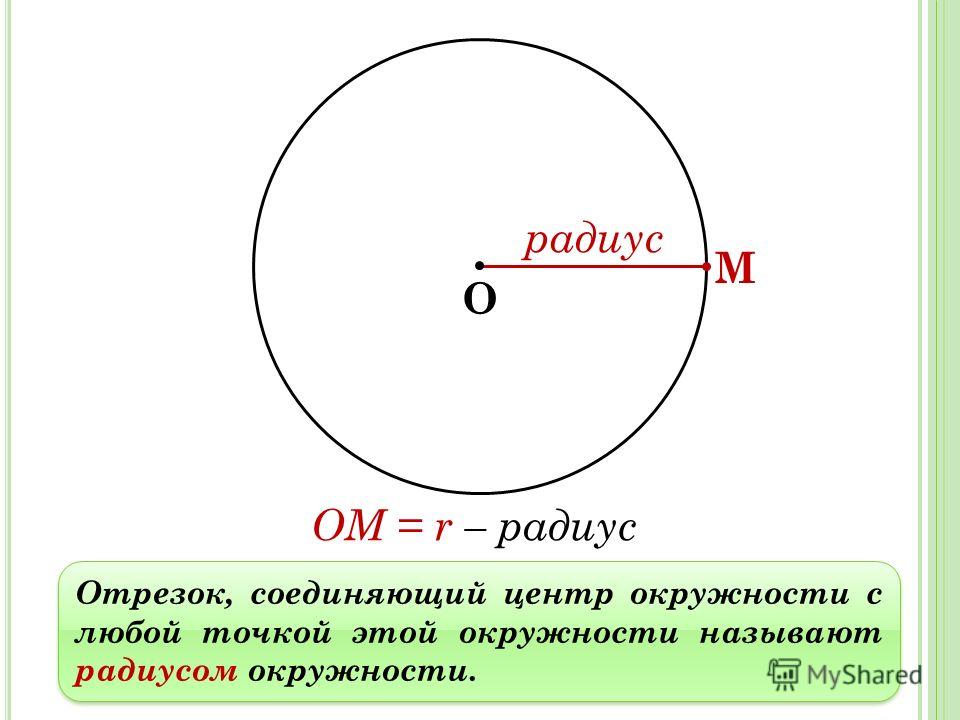
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически.
**************************************
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.

Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
А именно:
Длина диаметра равна удвоенной длине радиуса.
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2.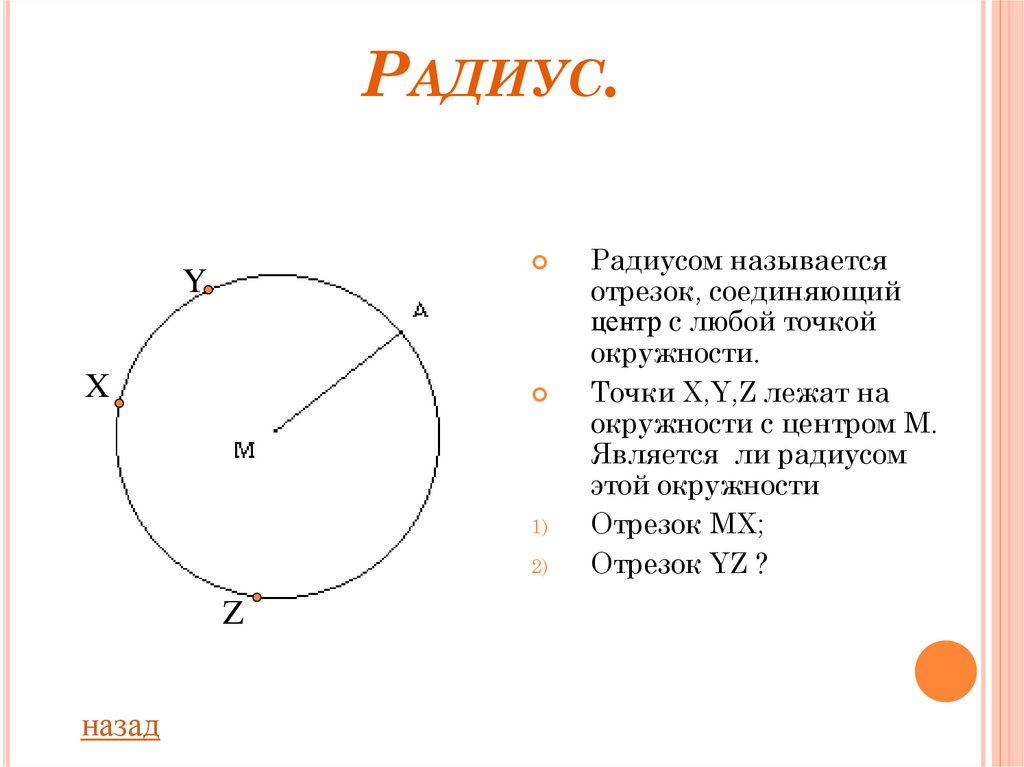
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Формулы для радиуса описанной окружности
Найти радиус описанной окружности треугольника по сторонам
Формула радиуса описанной окружности треугольника (R ) :
Найти радиус описанной окружности равностороннего треугольника по стороне или высоте
Формула радиуса описанной окружности равностороннего треугольника через его сторону:
Формула радиуса описанной окружности равностороннего треугольника через высоту:
Найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
Формула радиуса описанной окружности равнобедренного треугольника (R):
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.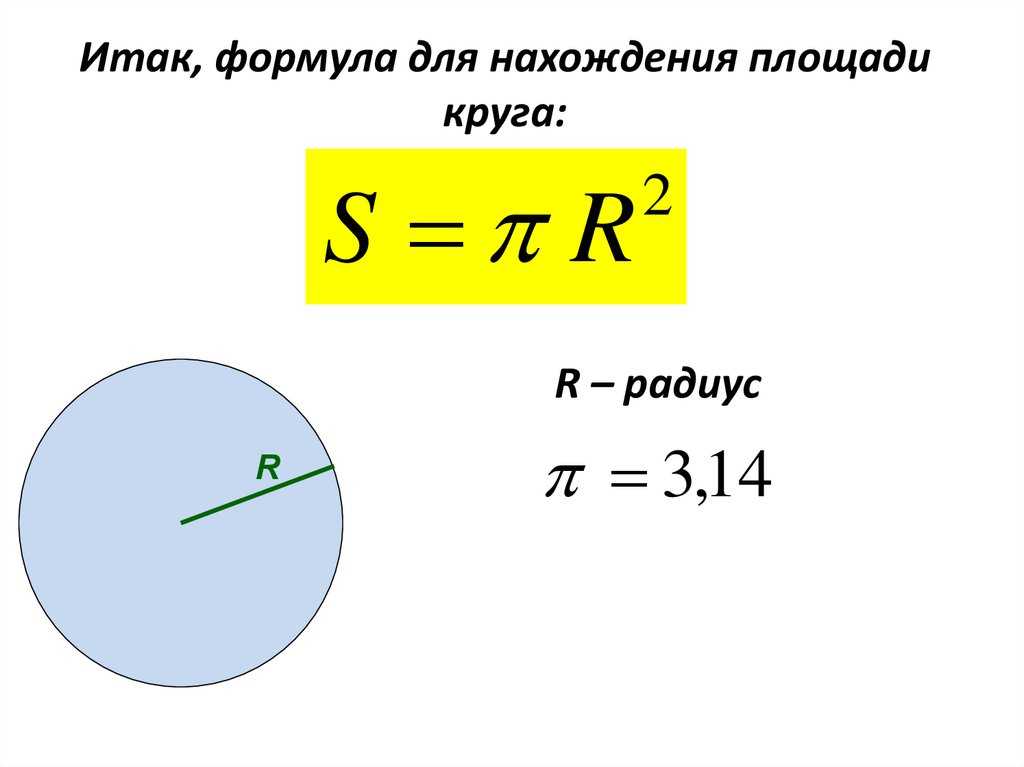
Формула радиуса описанной окружности прямоугольного треугольника (R):
Радиус описанной окружности трапеции по сторонам и диагонали
Формула радиуса описанной окружности равнобокой трапеции, (R)
Найти радиус описанной окружности около квадрата
Радиус описанной окружности квадрата равен половине его диагонали
Формула радиуса описанной окружности квадрата (R):
Радиус описанной окружности прямоугольника по сторонам
Радиус описанной окружности прямоугольника равен половине его диагонали
Формула радиуса описанной окружности прямоугольника (R):
Радиус описанной окружности правильного многоугольника
Формула радиуса описанной окружности правильного многоугольника, (R):
Радиус описанной окружности правильного шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
Формула радиуса вписанной окружности в треугольник (r):
Радиус вписанной окружности в равносторонний треугольник
Формула для радиуса вписанной окружности в равносторонний треугольник (r):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
Формулы радиуса вписанной окружности если известны: стороны и угол
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (r ) :
Радиус вписанной окружности в прямоугольный треугольник
Формула радиуса вписанной окружности в прямоугольный треугольник (r):
Радиус вписанной окружности в равнобочную трапецию
Формула радиуса вписанной окружности равнобочной трапеции (r):
Радиус вписанной окружности в квадрат
Формула радиуса вписанной окружности в квадрат (r):
Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
Формула радиуса вписанной окружности в ромб через диагонали (r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол (r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону (r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
Радиус вписанной окружности ромба, равен половине его высоты
Формула радиуса вписанной окружности в ромб (r ) :
Радиус вписанной окружности в правильный многоугольник
Формула радиуса вписанной окружности в правильный многоугольник, (r):
Радиус вписанной окружности в шестиугольник
Формула радиуса вписанной окружности в шестиугольник, (r):
Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:
Всем спасибо и приятного просмотра! Если понравилась публикация подписывайтесь и ставьте палец вверх!
Источники:
- https://KtoNaNovenkogo.
 ru/voprosy-i-otvety/radius-chto-ehto-takoe-kak-najti-radius-okruzhnosti-formula.html
ru/voprosy-i-otvety/radius-chto-ehto-takoe-kak-najti-radius-okruzhnosti-formula.html - https://MicroExcel.ru/radius-kruga/
- https://www-formula.ru/2011-09-24-00-42-22
- https://www-formula.ru/2011-09-24-00-40-48
- https://MicroExcel.ru/radius-vpisannogo-v-treugolnik-kruga/
Радиус Определение и значение | Dictionary.com
- Основные определения
- Викторина
- Связанный контент
- Примеры
- Британский
- Медицинский
- Научный
Уровень сложности этого слова.
[ rey-dee-uhs ]
/ ˈreɪ di əs /
Сохранить это слово!
См. синонимы для: radius / radii на сайте Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.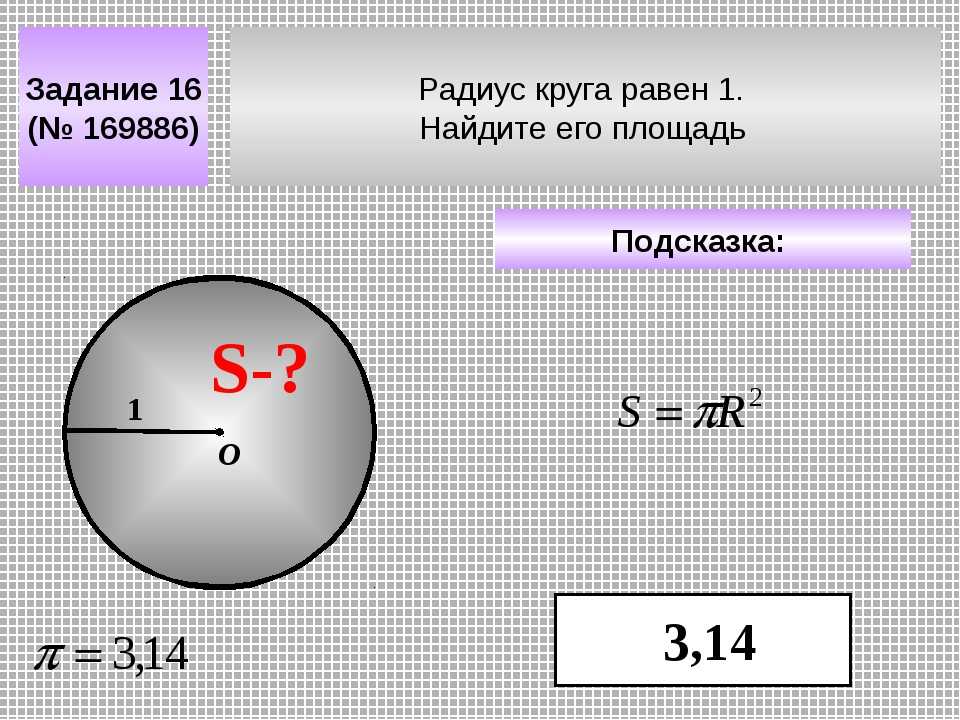
Определение радиуса
существительное во множественном числе ra·di·i [rey-dee-ahy], /ˈreɪ diˌaɪ/, ra·di·us·es.
прямая линия, идущая от центра круга или сферы к окружности или поверхности: Радиус круга равен половине диаметра.
длина такой линии.
любая радиальная или излучающая часть.
круглая территория, протяженность которой определяется длиной радиуса от данной или указанной центральной точки: каждый дом в радиусе 50 миль.
поле или диапазон действия или влияния.
степень возможной эксплуатации, перемещения и т. д., как при однократном запасе топлива: радиус полета самолета.
Анатомия. кость предплечья со стороны большого пальца. Сравните локтевую кость (определ. 1).
Зоология. соответствующая кость в передней конечности других позвоночных.
Машины стали редкими. ход эксцентрикового колеса или кулачка.
закругленный угол или кромка обработанного или литого куска металла.
Энтомология. одна из главных продольных жилок в передней части крыла насекомого.
одна из главных продольных жилок в передней части крыла насекомого.
ВИКТОРИНА
Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Должны ли вы пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Начало радиуса
1590–1600; <Латинское: посох, стержень, спица, луч, изначально, луч 1
СЛОВА, КОТОРЫЕ МОГУТ СПУТАТЬСЯ С радиусом
окружность, диаметр, радиус, касательнаяСлова рядом с радиусом
радий B, излучение радия, радий F, сульфат радия, радиевая терапия, радиус, радиус действия, радиус конвергенции, радиус кривизны, радиус вращения, радиус стержня
Dictionary.com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc. 2022
Слова, относящиеся к радиусу
амбита, граница, компас, пространство, расширение, экстент, интервал, предел, орбита, охват, досягаемость, полудиаметр, пространство, пролет , спица
Как использовать радиус в предложении
В этот момент решатели, такие как Тхань Нгуен, использовали тригонометрию для вычисления внутреннего радиуса кольца, которое оказалось равным R√3.

Можете ли вы разрезать квадрат… на большее количество квадратов?|Зак Висснер-Гросс|8 января 2021 г.|FiveThirtyEight
Команда Гринина не только нашла значение зарядового радиуса протона, согласующееся со значением, полученным в мюонных водорода, они вывели гораздо более точное значение постоянной Ридберга.
Прорыв в измерении строительных блоков природы — такие романтичные факты|Субодх Патил|8 января 2021 г.|Nautilus
Знай свой радиус Каждое смарт-устройство реализует свой радиус геозоны немного по-разному.
Геозона может повысить уровень вашего умного дома, если вы правильно его настроите|Whitson Gordon|4 января 2021 г.|Popular-Science
Через нашу сеть централизованно расположенных центров выполнения мы можем обслуживать клиентов в небольшом радиусе доставки .
Gorillas, стартап по доставке продуктов по требованию, штурмом взявший Берлин, привлек 44 миллиона долларов серии A|Стив О’Хир|11 декабря 2020 г.
 |TechCrunch
|TechCrunch
радиус заряда.
Физика несколько менее сломана, но все же не совсем верно|Джон Тиммер|2 декабря 2020|Ars Technica
Под «Интернетом» подразумевались люди в радиусе семи кубов от человека, который это написал Сообщение блога.
Возмущение по поводу челки Бейонсе Бетти Пейдж: почему СМИ должны перестать объективировать женщин|Фиби Робинсон|15 октября 2014|DAILY BEAST
Вскоре даже самые близкие зрители, прямо на краю моего пустого радиуса, повернулись и посмотрели на меня.
Почему американцы должны любить чемпионат мира|Шон Уилси|12 июня 2014|DAILY BEAST
Еще одно требование заключалось в том, что колумбийской национальной полиции не разрешалось находиться в радиусе 12 миль от его тюрьмы.
Частной тюрьмой Пабло Эскобара теперь управляют монахи для пожилых людей|Джефф Кампанья|7 июня 2014 г.|DAILY BEAST
В 2012 году FIS объявила о новом требовании, увеличивающем минимальный радиус поворота лыж GS на восемь метров.

Столкновение в Сочи, которое нельзя пропустить: Боде Миллер и Тед Лигети|Джейк Брайт|9 февраля 2014 г.|DAILY BEAST
Затем они были разбросаны по радиусу 300 миль, покрытым оврагами, ущельями и сосновыми лесами .
Зверства в Боснии, величайшая в мире судебно-медицинская головоломка|J.P. О’Мэлли|1 декабря 2013 г.|DAILY BEAST
И со своего насеста я мог заметить прохождение чего-то крупнее годовалого бизона в радиусе не менее шести миль.
Необработанное золото|Бертран В. Синклер
Некоторые из них, сильнее других, пускали корни в радиусе ста миль, другие — в нескольких лигах и не более.
Старые друзья самые лучшие|Джек Шарки
Генерал Штойбен, наблюдая за большим радиусом действия лагеря, пришел к выводу, что все силы Корнуоллиса были за рекой.
Священное наследие: жизнь Вирджинии|Дороти М. Торпи
В радиусе пяти миль много соседей; поезда в город — это еще не все, что можно было бы пожелать.

Дочери Данауса|Мона Кэрд
Очень плотный туман окутывал все вокруг, ограничивая обзор окружающих объектов радиусом около пятидесяти ярдов.
Известные приключения и побеги из тюрьмы во время гражданской войны|Разное
Определения радиуса в Британском словаре
радиус
/ (ˈreɪdɪəs) /
существительное во множественном числе -dii (-dɪˌaɪ) или -diuses
прямая линия, соединяющая центр круга или сферы с любой точкой на окружности или поверхность
длина этой линии, обычно обозначаемая символом r
расстояние от центра правильного многоугольника до вершины (длинный радиус) или перпендикулярное расстояние до стороны (короткий радиус)
анатомия внешняя и чуть короче двух костей предплечья человека, от локтя до запястья
соответствующая кость у других позвоночных
любая из жилок крыла насекомого
группа лучевых цветков, встречающихся у таких растений, как маргаритка модификатор) радиусный рычаг
боковое смещение кулачка или эксцентрикового колеса
круглая площадь, размер которой определяется длиной ее радиусаполиция останавливала каждый грузовик в радиусе четырех миль
эксплуатационный предел корабля, самолета и т. д.
д.
Происхождение слова для радиуса
C16: от латинского: стержень, луч, спица
Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Медицинские определения радиуса
радиуса
[ rā′dē-əs ]
сущ. пл. ra•di•us•es
Отрезок, соединяющий центр окружности с любой точкой на ее окружности.
Длинная, призматическая, слегка изогнутая кость, более короткая и толстая из двух костей предплечья, расположенная латеральнее локтевой кости.
Медицинский словарь Стедмана The American Heritage® Copyright © 2002, 2001, 1995, компания Houghton Mifflin. Опубликовано компанией Houghton Mifflin.
Научные определения радиуса
радиус
[ rā′dē-əs ]
Радиусы во множественном числе (rā′dē-ī′) радиусы
Отрезок линии, соединяющий центр круга или сферы с любой точкой на окружность круга или поверхность сферы. Это половина длины диаметра.
Это половина длины диаметра.
Более короткая и толстая из двух костей предплечья или нижней части передней ноги. Смотрите больше на скелете.
Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Круги: их определения и способы их рисования
EquationsExamples
Purplemath
Окружность — это геометрическая фигура, и в алгебре она малопригодна, поскольку уравнение окружности не является функцией. Но вам, возможно, придется работать с уравнениями окружности на уроках алгебры, возможно, в главе под названием «Коники» (по причинам).
В терминах «приматив» (то есть в физических и неалгебраических терминах) круг — это геометрическая фигура, образованная на песке палками и веревкой. Вы начинаете с того, что вбиваете одну из палочек в песок; эта палка представляет собой «центр» круга.
Содержание продолжается ниже. затем вы туго натягиваете петлю другой палкой и, удерживая эту вторую палку совершенно вертикально, протаскиваете ее по песку на дальней части петли веревки. Получившаяся фигура, нарисованная на песке, представляет собой круг.
Получившаяся фигура, нарисованная на песке, представляет собой круг.
В алгебраических терминах круг — это фигура, образованная набором (или «геометрическим местом») точек ( x , y ) на некотором фиксированном расстоянии r от некоторой фиксированной точки ( h , k ). Значение r называется «радиусом» окружности, а точка ( h , k ) называется «центром» окружности.
«Общее» уравнение окружности:
x 2 + y 2 + DX + EY + F = 0
Форма «Центр-радий»:
( x — H ) 2 +- ( +- +- +- +- +- +- +- +- ( +- +- +- +- +- +- + — ч ). K ) 2 = R 2
… где H и K поступают из центральной точки ( H , K и H , K ) и H , K ) и H и R и R и и R . исходит из значения радиуса r . Если центр находится в начале координат, то ( h , k ) = (0, 0), то уравнение упрощается до
исходит из значения радиуса r . Если центр находится в начале координат, то ( h , k ) = (0, 0), то уравнение упрощается до
Примечание: «Общая» форма может быть представлена в вашей книге с использованием других букв для коэффициентов, но форма «центр-радиус» будет использовать те же буквы, что и выше: Центр всегда обозначается как «( h , k )», а радиус всегда обозначается как « r «. В вашей книге также может упоминаться так называемая «стандартная» форма уравнения окружности. К сожалению, «стандартная форма» не имеет фиксированного значения, которое я смог определить, поэтому вам придется следить за тем, что подразумевается под этим термином в вашей книге.
Вы можете преобразовать форму уравнения окружности «центр-радиус» в «общую» форму путем умножения и упрощения; вы можете преобразовать в другом направлении, заполнив квадрат.
Форма уравнения окружности центр-радиус исходит непосредственно из формулы расстояния и определения окружности. Если центром окружности является точка ( h , k ), а радиус равен длине r , то каждая точка ( x , y ) на окружности расстояние r от точки ( h , k ). Подставив эту информацию в формулу расстояния (используя r для расстояния между точками и центром), мы получим:
Если центром окружности является точка ( h , k ), а радиус равен длине r , то каждая точка ( x , y ) на окружности расстояние r от точки ( h , k ). Подставив эту информацию в формулу расстояния (используя r для расстояния между точками и центром), мы получим:
Вам следует практиковаться, пока вы не сможете легко распознать эту формулу, потому что ожидается, что вы сможете считывать с него информацию.
- Определите центр и радиус окружности с помощью уравнения ( x − 2) 2 + y 2 = 5 2 и нарисуйте окружность.
Термин y 2 означает то же самое, что и ( y − 0) 2 , поэтому уравнение на самом деле имеет вид ( x − 2) 2 6 5 2 = 5 2 . Поскольку уравнение окружности теперь представлено в форме центр-радиус, я могу напрямую прочитать значения: центр должен находиться в точке ( h , k ) = (2, 0), а радиус должен быть равен r = 5.
Чтобы сделать набросок, я сначала нарисую точку для центра:
Затем карандашом набросаю маркеры, которые находятся на расстоянии пяти единиц от центра в каждом из четырех «легких» » направления:
Затем я начерчу изогнутые части между этими маркерами, переворачивая бумагу по ходу дела:
ответ сплошной темной линией:
Чтобы передать красивый рисунок, я сотру карандашные пометки с чернового варианта и скопирую значения центра и радиуса, которые я нашел ранее.
центр: ( ч , к ) = (2, 0)
радиус: r = 5
Подсказка: может быть очень полезно поворачивать бумагу, когда вы рисуете, чтобы в итоге получился круг, который выглядит довольно круглым.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении центра и радиуса круга (или пропустить виджет и перейти к следующей странице). Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/circle.htm
2стр. 3
Центр окружности – формула, определение, примеры
Окружность определяется как геометрическое место движущейся точки на плоскости, расстояние от которой до фиксированной точки на плоскости остается постоянным или фиксированным. Эта фиксированная точка называется центром окружности. Давайте узнаем больше о центре круга в этой статье.
| 1. | Определение центра окружности |
| 2. | Центр круга Формула |
| 3. | Как найти центр окружности? |
| 4. | Часто задаваемые вопросы о центре круга |
Определение центра окружности
Окружность — это двухмерная фигура, определяемая центром и радиусом. Мы можем нарисовать любой круг, если знаем центр круга и его радиус. Окружность может иметь бесконечное число радиусов. Центр окружности — это точка пересечения всех радиусов. Его также можно определить как середину диаметра круга. Обратите внимание на приведенный ниже рисунок, где O — центр круга, а OP — радиус.
Мы можем нарисовать любой круг, если знаем центр круга и его радиус. Окружность может иметь бесконечное число радиусов. Центр окружности — это точка пересечения всех радиусов. Его также можно определить как середину диаметра круга. Обратите внимание на приведенный ниже рисунок, где O — центр круга, а OP — радиус.
Центр круга Формула
Формула центра окружности также известна как общее уравнение окружности . В круге, если координаты центра равны (h,k), r — радиус, а (x,y) — любая точка на круге, то формула центра круга приведена ниже:
(x — h) 2 + (y — k) 2 = r 2
Это также известно как центр уравнения окружности. Мы будем использовать эту формулу в следующих разделах, чтобы найти центр окружности или уравнение окружности.
Как найти центр окружности?
Чтобы найти центр круга, мы выполним несколько простых шагов. Есть два случая, когда нас могут попросить найти центр круга:
- Когда дан круг и нам нужно найти его центр.

- Когда дано уравнение окружности и нам нужно найти координаты ее центра.
Когда дается круг
Когда нам дан круг и нам нужно найти его центральную точку, мы можем выполнить шаги, перечисленные ниже:
Шаг 1: Нарисуйте хорду PQ в круге и внимательно отметьте ее длину (которая составляет 4 дюйма). на рисунке ниже).
Шаг 2: Нарисуйте другую хорду MN, параллельную PQ, так, чтобы она была той же длины, что и PQ.
Шаг 3: Соедините точки P и N отрезком с помощью линейки.
Шаг 4: Соедините точки Q и M.
Шаг 5: Точка пересечения PN и QM является центром окружности.
Когда дано уравнение окружности
Если мы знаем уравнение окружности и нам нужно найти ее центр, то мы будем использовать следующие шаги. Давайте разберемся в этом с помощью примера.
Пример: Найдем координаты центра окружности с помощью уравнения x 2 + y 2 — 4x — 6y — 87 = 0
Решение: Шаги для нахождения координат центра окружности перечислены ниже:
- Шаг 1: Напишите данное уравнение в виде общего уравнения окружности: (x — h) 2 + (y — k) 2 = r 2 , путем сложения или вычитания чисел с обеих сторон.
Мы можем записать данное уравнение в виде x 2 — 4x + y 2 — 6y = 87. Добавьте 4 к обеим частям уравнения, чтобы получить идеальный квадрат x-2. Итак, мы получим, х 2 — 4x + 4 + y 2 — 6y = 87 + 4.
⇒ (x — 2) 2 + y 2 — 6y = 91
Прибавьте 9 к обеим сторонам квадрат у — 3
⇒ (х — 2) 2 + у 2 — 6у + 9 = 91 + 9
⇒ (х — 2) 2 + (у — 3) 2 = 2 . 100
⇒ (x — 2) 2 + (y — 3) 2 = 10 2
Это похоже на общее уравнение окружности.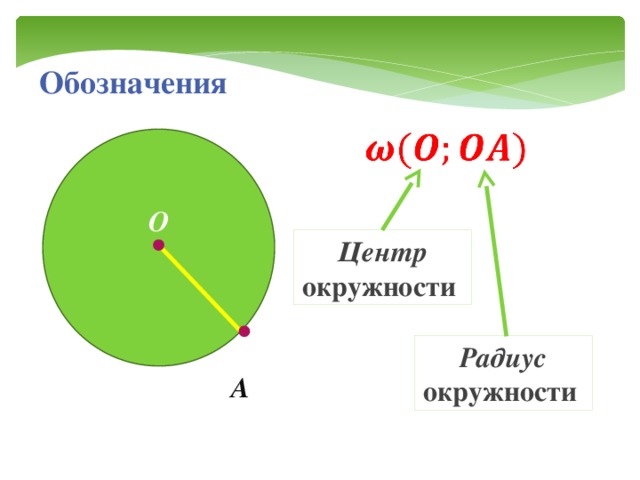
- Шаг 2: Сравните это уравнение с общим уравнением и определите значения h, k и r.
Если сравнить (x — 2) 2 + (y — 3) 2 = 10 2 с (x — h) 2 + (y — k) 2 = r 2 2 , мы можем определить, что h = 2, k = 3 и r = 10. Итак, мы получили координаты центра окружности, которые равны (h, k) = (2, 3).
Как найти центр окружности с двумя точками?
Если даны конечные точки диаметра окружности, то для нахождения координат центра используем формулу середины точки, так как центр является серединой диаметра окружности. Шаги, чтобы найти центр круга с двумя точками, приведены ниже:
- Шаг 1: Предположим, что координаты центра круга равны (h, k).
- Шаг 2: Используйте формулу средней точки, которая гласит, что если (h, k) — координаты середины отрезка с концами (x 1 , y 1 ) и (x 2 , y 2 ), тогда (h, k) = [(x 1 + x 2 ]/2, [y 1 + y 2 ]/2).

- Шаг 3: Упростите его и получите координаты центра круга.
Возьмем в качестве примера окружность, в которой конечные точки диаметра указаны как (-2, 4) и (6, 16). Тогда координаты его центра:
(h, k) = [(-2 + 6)/2, (4 + 16)/2]
(h, k) = (4/2, 20/ 2)
(h, k) = (2, 10)
Следовательно, координаты центра окружности с концами диаметра равны (2, 10).
☛ Статьи по теме
Проверьте эти интересные статьи, связанные с концепцией центра круга в геометрии.
- Круговые формулы
- Сектор круга
- Длина окружности
- Площадь круга
Часто задаваемые вопросы о центре круга
Что такое центр круга?
Центр круга — это точка, в которую мы помещаем кончик циркуля при рисовании круга. Это середина диаметра круга. В круге расстояние от центра до любой точки окружности всегда одинаково, что называется радиусом круга.
Каковы координаты центра окружности и длины радиуса?
Координаты центра окружности представляют собой расстояние центральной точки от оси x и оси y соответственно. Обычно он обозначается в виде (h, k), где h и k представляют координаты x и y соответственно. Длина радиуса обозначается через r. Координаты центра и радиуса связаны друг с другом в виде уравнения: (x — h) 2 + (у — к) 2 = г 2 .
Что такое центр окружности, представленной уравнением (x — 5)
2 + (y + 6) 2 = 42?Если сравнить данное уравнение с общим уравнением центра окружности: (x — h) 2 + (y — k) 2 = r 2 , то можно увидеть, что h = 5, k = -6, а r = √42. Итак, центр круга находится в точке (5, -6).
Как найти центр окружности?
Чтобы найти центр круга, мы можем провести внутри круга две параллельные хорды одинаковой длины. Затем соедините противоположные концы аккордов.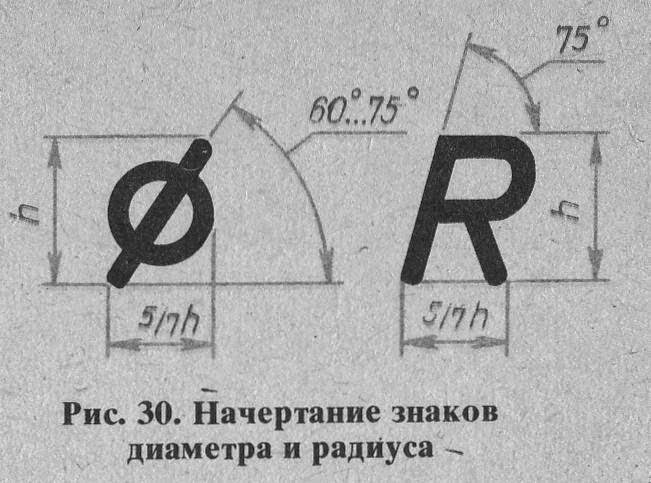

 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l. 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
 ru/voprosy-i-otvety/radius-chto-ehto-takoe-kak-najti-radius-okruzhnosti-formula.html
ru/voprosy-i-otvety/radius-chto-ehto-takoe-kak-najti-radius-okruzhnosti-formula.html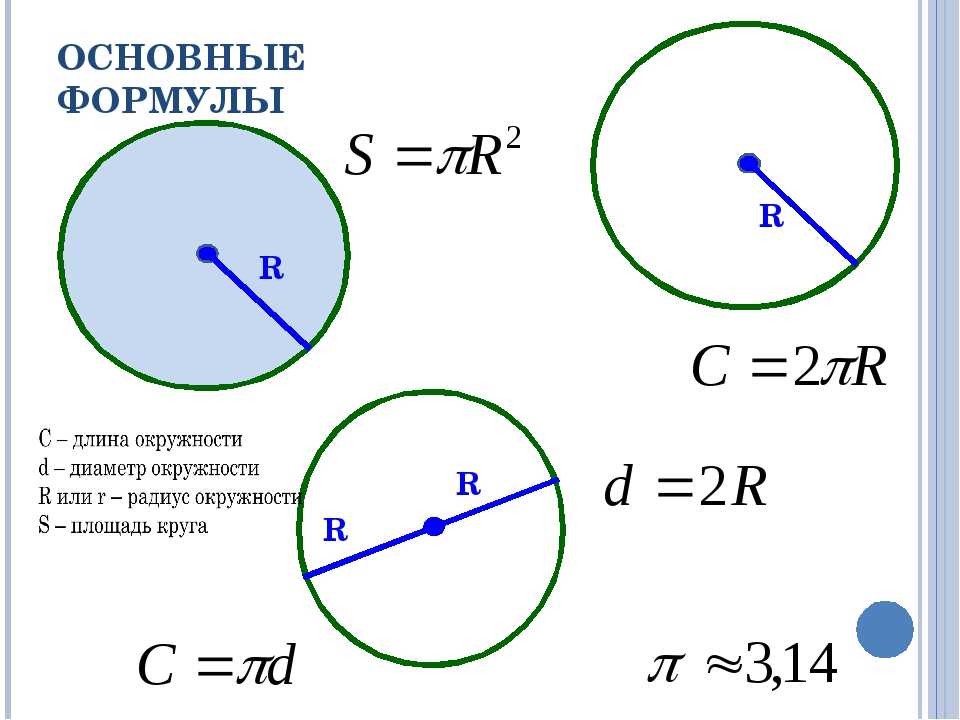
 |TechCrunch
|TechCrunch