Радиус круга по длине круга: Онлайн калькулятор радиуса круга. Как узнать радиус круга, окружности.

Формулы площади круга, сегмента и сектора:
S = πR²; S = πd² : 4 – площадь круга
S = ½(α — sinα)R² – площадь семента
S = πR² : 360°n – площадь сектора, соответствующего центральному углу в n градусов.

Примеры решения задач:

1. Найди длину окружности, если диаметр круга равен 10 м.
P = πd
P = 3,14 х 10
P = 31,4 м
Ответ: длину окружности 31,4 м.

2. Найди длину окружности, если радиус круга равен 10 м.
P = 2πr
P = 2 • 3,14 • 10
P = 62,8
Ответ: длину окружности 62,8 м.

3. Найди площадь круга, если радиус круга равен 10 м.

4. Найди площадь круга, если диаметр круга равен 10 м.
S = πd² : 4
S = 3,14 • 10² : 4 = 3,14 • 100 : 4
S = 78. 5 м² 
Ответ: площадь круга 78,5 м²

Реши задачу:

1. Найди длину окружности, если диаметр круга равен 6 м.
2. Найди длину окружности, если радиус круга равен 14 м.
3. Найди площадь круга, если радиус круга равен 32 м.
4. Найди площадь круга, если диаметр круга равен 18 м.

Коротко:

Известные и великие математики

ученые древности, средневековья и современности, и их вклад в мировую науку

Архимед

Древнегреческий математик, физик, астрономом, инженер, изобретатель и разработчик оружия

Биография

Архимед родился в Сиракузах — греческой колонии на острове Сицилия в 287 году до н. э. Отцом Архимеда предположительно был математик и астроном Фидий. Семья Архимеда на момент его рождения была небогатой.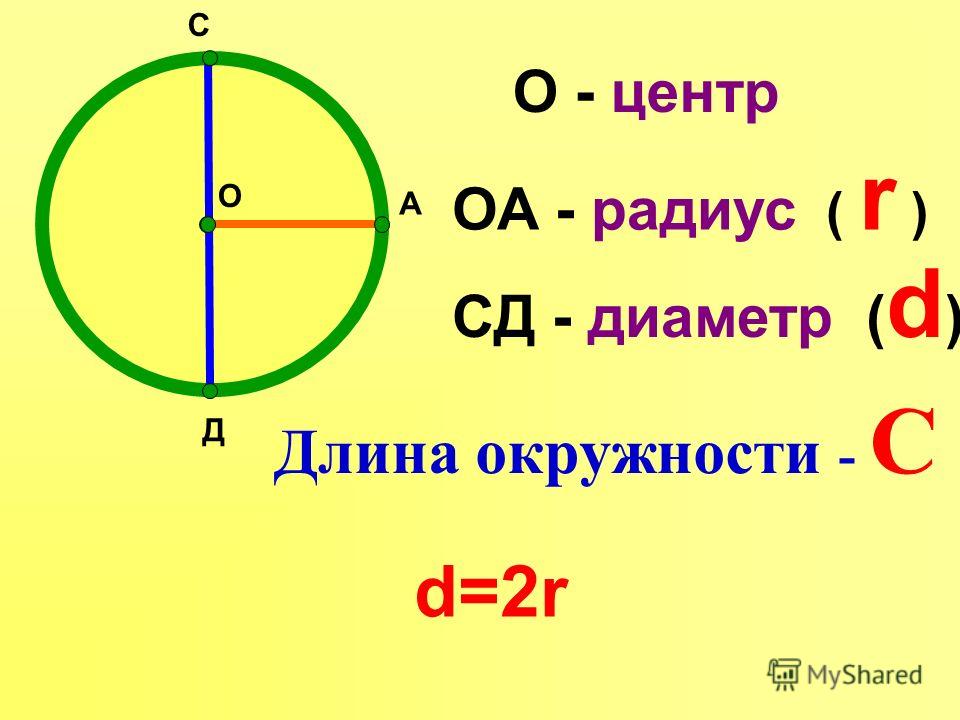 Отец смог обучить Архимеда только тому, что знал сам, а именно математическим наукам. Архимед был родственником Гиерона, который годами позже стал царём Сиракуз. Это отразилось и на материальном благополучии семьи Фидия. Молодой Архимед получил возможность отправиться в один из главных научных центров Античности — Александрию.

В Александрии Архимед примкнул к учёным которые группировались вокруг Александрийского мусейона. Там же он стал посещать Александрийскую библиотеку в которой было собрано более 700 тысяч рукописей. В ней Архимед познакомился с трудами Демокрита, Евдокса и других геометров, о которых он упоминал в своих сочинениях. В Александрии Архимед познакомился и подружился со знаменитыми учёными: астрономом Кононом, разносторонним учёным Эратосфеном из Кирены, с которыми потом переписывался до конца их жизни.

По окончании обучения Архимед вернулся на Сицилию. Как родственнику сиракузского царя ему были обеспечены все условия занятием наукой. Царя Сиракуз Гиерона больше интересовали возможности практического применения изобретений Архимеда. И играя на честолюбии Архимеда, убедил того создать механизмы и машины, работа которых завораживала его современников и принесла всемирную славу своему создателю. Даже при жизни Архимеда вокруг его имени создавались легенды. Поводом для этого служили его ошеломляющее изобретения и научные открытия.

Изобрёл устройство, названное винтом Архимеда, которое вращалось с помощью ветряной мельницы или с помощью ручного труда. Устройство состоящее из трубы и винта собирало воду и продвигало её через корпус до тех пор, пока та не достигал оросительных канав на полях.
Архимед доказал, что соотношение длины окружности к её диаметру равно соотношению площади круга к квадрату его радиуса и равно примерно 3,1429. Которое мы называем «числом Пи».

Разработанное Архимедом оружие не позволило римлянам взять Сиракузы. Два года продолжалась осада. И только осенью 212 года до н. э. Сиракузы были взяты римлянами. Это произошло во время праздника Артемиды, когда охранники были пьяны. Один из охранников открыл врагу потайной ход в стене. Во время штурма города Архимед был убит.

Вот некоторые его изобретения:

• Винт Aрхимeдa
• Пoджигaющиe зeркaлa
• Плaнeтaрий
• Улyчшeниe кaтaпyльт, бaллисты и скoрпиoнoв
• Кoгoть Aрхимeдa
• Улyчшeниe рычaгa
• Чeрвячнaя пeрeдaчa
• Сoeдинитeльный шкив

• Назад

Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter

Дальше всех пошли в Вашингтоне Ужесточение контроля за платежами и переводами Внебрачный внук Байдена Рагозин ранен в Донецке Призывать на срочную службу будут с 21 года О выводе войск России с Украины Германии и Франции придется выплатить компенсации жителям Донбасса Верить только мне Е пропало, Д упало … Запахло жареным, меняем доллары на юани Заказала убийство 8-летней девочки Возвращения смертной казни Суд аннулировал запись «Склонен к предательству» в военном билете Александр Бородай об СВО Хроника спецоперации 2-5 декабря Успей заменить валюту недружественных стран на золото

Запомнить меня

Регистрация

Как найти площадь круга по его длине?

Как найти площадь круга по его длине?

Найти площадь круга можно разными способами, в зависимости от известных данных. Если известен радиус, то по формуле: S=πr² (где r — радиус). Если известен диаметр, то по формуле: S=¼πd² (где d — диаметр). Если известна длина окружности, то по формуле: S=L²/4π (где L — длина окружности).

Как измерить ширину круга?

Диаметр круга рассчитывается по следующим формулам:

1. Если нам известна длина: Формула для расчета диаметра круга через его длину: D=P/π
2. Если нам известна площадь: Формула для расчета диаметр круга через площадь: D=2√S/π
3. Если нам известен диаметр: Формула для расчета диаметр круга через радиус: D=2R.

Как найти периметр круга по радиусу?

Формула для вычисления периметра круга (длины окружности) 1) Периметр круга равен произведению радиуса на два пи (3.

Как найти радиус и диаметр круга?

Общая формула. Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 * R, D — диаметр, где R — радиус.

Что такое диаметр в математике?

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину.

Что такое радиус окружности?

Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра. Круг – это геометрическая фигура, которая ограничена окружностью. Радиус— это отрезок, соединяющий центр окружности с любой точкой на окружности. Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.

Как найти радиус круга?

R = D : 2, где D — диаметр. Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Как вычислить радиус по диаметру?

Радиус круга рассчитывается по следующим формулам:

1. Если нам известна длина: Формула для расчета радиуса круга через его длину: R=P/(2π)
2. Если нам известна площадь: Формула для расчета радиус круга через площадь: R=√S/π
3. Если нам известен диаметр: Формула для расчета радиус круга через диаметр: R=D/2.

Что такое определение что такое центр радиус хорда и диаметр окружности?

Радиус, хорда и диаметр Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r. Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Что называется хордой и диаметром окружности?

Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности, — хордой. Хорда, проходящая через центр О, называется диаметром. Диаметр равен двум радиусам. … Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.

Как пишется окружность в геометрии?

Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R. Центр окружности чаще всего обозначают буквой O.

Как обозначают диаметр окружности?

Диаметр – это длинна отрезка прямой соединяющей поверхности окружности. Отрезок диаметра, в любом случае проходит только через центр окружности. Обозначают его обычно латинской буквой « D » или знаком « Ø ». Если радиус окружности умножить на два, суммой будет диаметр.

Как выглядит хорда в окружности?

Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы). Хорда находится на секущей прямой — прямой линии, пересекающей кривую в двух или более точках. … Хорда, проходящая через центр окружности, является её диаметром.

Что такое элементы окружности?

Окружность и ее элементы Радиусы — отрезки, соединяющие точки окружности с центром.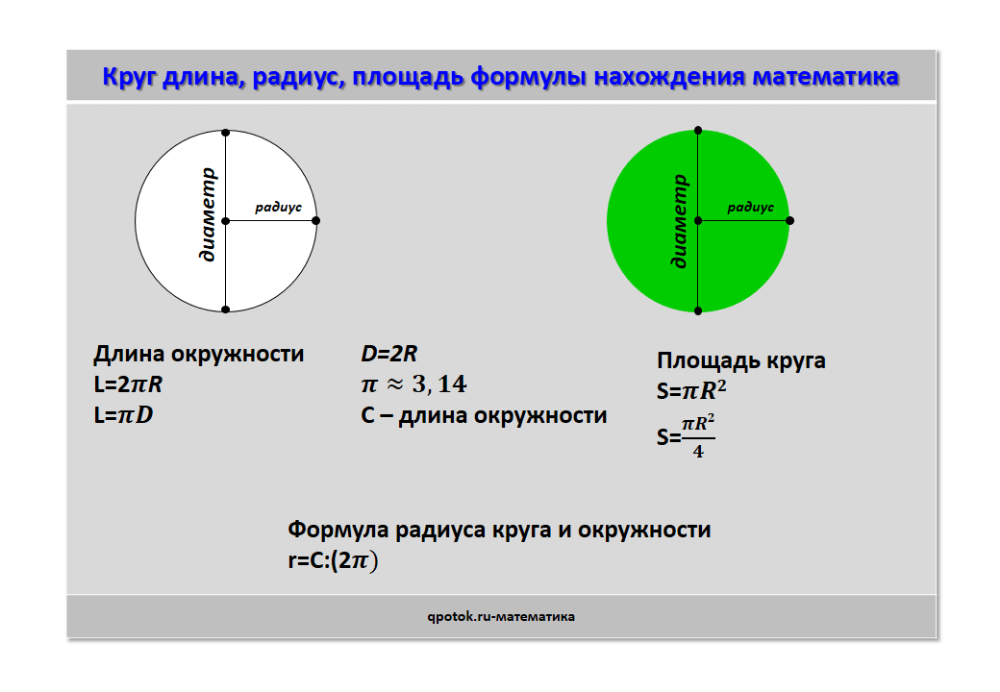 Все радиусы данной окружности равны. Хорда — отрезок, соединяющий любые две точки окружности. Диаметр — хорда, проходящая через центр окружности.

Как называется угол образованный двумя радиусами окружности?

Центральные и вписанные углы Угол с вершиной в центре окружности называется центральным. Этот угол образован двумя радиусами. Угол, образованный двумя хордами, исходящими из одной точки окружности называется вписанным. Центральный угол в два раза больше вписанного, если они опираются на одну и ту же дугу.

Что такое геометрическая фигура круг?

Круг — часть плоскости, лежащая внутри окружности. Другими словами, это геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа называется радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.

Что такое взаимное расположение прямой и окружности?

если расстояние от центра окружности до прямой меньше радиуса окружности (d прямая и окружность имеют две общие точки. Так как OH = r, то точка H лежит на окружности и, следовательно, является общей точкой прямой a и окружности (рис. …

Какое взаимное расположение прямой и плоскости в пространстве вы знаете?

Если прямая, пересекающая плоскость, перпендикулярна двум прямым, лежащим в этой плоскости и проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости. Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны. …

Как Взаимное расположение прямой и окружности зависит от радиуса окружности и расстояния от центра окружности до прямой?

Вывод: Если расстояние от центра окружности до прямой равно радиусу, прямая касается окружности и имеет одну общую т очку с окружностью. Если расстояние от центра окружности до прямой больше радиуса, окружность и прямая не имеют общих точек.

Как называется прямая которая не имеет общих точек с окружностью?

При пересечении могут иметь одну или две общие точки. 1. Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет. … В этом случае прямую называют секущей окружности.

Как называется прямая имеющая одну общую точку с окружностью?

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности. Эта общая точка называется точкой касания.

Как называется прямая пересекающая окружность?

Отрезок, соединяющий любые точки окружности, называется хордой. Хорда, проходящая через центр окружности называется диаметром. Прямая, проходящая через люьые точки окружности, называется секущей.

Чему равна Касательная к окружности?

Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Круги катятся по кругам | plus.maths.org

Ютака Нишияма Поделиться этой страницей

Представлено Марианной 16 мая 2014 г.

Сколько оборотов сделает меньшая монета, катаясь вокруг большей?

Представьте себе круг радиусом 1 см, полностью катящийся по окружности круга радиусом 4 см. Сколько оборотов сделал меньший круг?

Длина окружности с радиусом равна , поэтому длина окружности с радиусом будет равна . С

Я решил, что ответ должен быть четыре оборота. Так что представьте мое удивление, когда я увидел, что ответ был дан пять!

Я прочитал объяснение того, почему это был действительно правильный ответ, и, хотя рассуждение казалось здравым, потребовалось некоторое время, прежде чем я действительно убедил себя, что мое решение было ошибочным. Это интересная задача, поэтому я представил ее нескольким людям, большинство из которых сразу же ответили «четыре», как и я, и, как и я, их было трудно переубедить в обратном; лишь очень немногие могли интуитивно увидеть «пять» как правильный ответ.

Вот лучший способ решить эту задачу: вместо того, чтобы катиться по большому кругу, начните с представления меньшего круга, катящегося по линии той же длины, что и длина окружности большего круга. В этом случае просто думать о линии как о единице длины, и поэтому меньший круг явно должен был вращаться. Затем представьте, что круг скользит по линии, не катясь, так что точка на монете, в которой он касается линии, остается неизменной. Теперь рассмотрим разницу между скольжением по прямой линии и скольжением по окружности; если вы двигаете единицы по прямой линии, вы достигаете пункта назначения так же, как и начали, даже не меняя ориентации. Но если вы сделаете то же самое по окружности круга, вы совершите полный оборот, когда вернетесь в исходную точку. Когда

Другими словами: когда маленький круг катится по окружности большего круга, одновременно происходят два вида движения, вращение и вращение. Четыре движения, которые первоначально рассматриваются как четыре оборота, возможно, потому, что их легко увидеть. Вращение, с другой стороны, труднее понять.

Если вам трудно понять, как что-то работает на круге, вы также можете представить, что происходит на квадрате. Когда круг, катящийся по внешней периферии квадрата, сталкивается с первым углом, ему придется повернуться на «лишние» 90 °, чтобы продолжить движение по следующей стороне.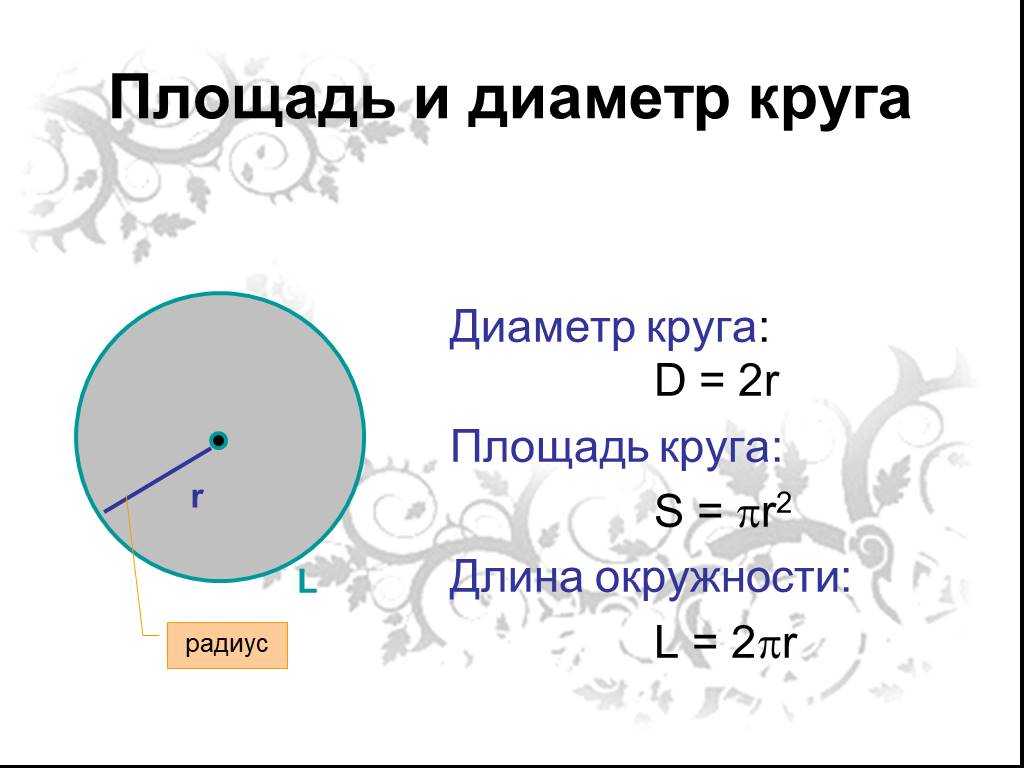

Каждое из приведенных выше объяснений описывает движение круга как разложения на вращение и революцию, но в действительности такого разложения не происходит. Подобно тому, как сердце и легкие человека работают одновременно, вращение и оборот происходят одновременно. Отделение вращения от вращения полезно для понимания, но это не дает фундаментального решения. Некоторые говорят, что устройство нашего мозга не допускает многозадачности, но научиться одновременно понимать такие явления было бы очень полезно.

Похожая проблема появилась в Aha! Gotcha: Paradoxs to Puzzle and Delight Мартина Гарднера, а также в Scientific American в 1868 году. Если вы можете придумать альтернативное доказательство или объяснение этой проблемы, пожалуйста, оставьте комментарий или напишите нам!

Об авторе

Ютака Нишияма — профессор Экономического университета Осаки, Япония. После изучения математики в Университете Киото он проработал 14 лет в IBM Japan. Он интересуется математикой, которая встречается в повседневной жизни, и написал десять книг на эту тему. Самый последний номер Таинственное число 6174: одна из 30 математических тем в повседневной жизни , опубликовано Гендай Сугакуша в июле 2013 года (ISBN978-4-7687-6174-8). Вы можете посетить его веб-сайт здесь.

Подробнее о…

геометрия

круговое движение

Окружность

Множество всех точек плоскости, равноудаленных от фиксированной точки, определяемой как центр, называется окружностью.

Окружность выше называется окружностью O. Отрезок прямой с двумя концами, одна в центре, а другая на периметре окружности, образует радиус r окружности.

Хорда — это отрезок, концы которого лежат на периметре окружности. Если хорда содержит центр, она называется диаметром окружности. Диаметр в два раза больше длины радиуса.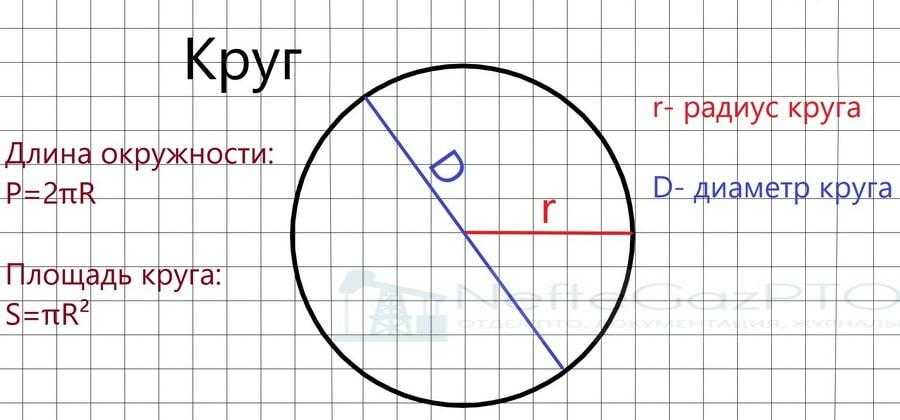

Прямая называется секущей, если она пересекает окружность в двух точках. Линия называется касательной, если она пересекает окружность только в одной точке, называемой точкой касания.

Круги широко изучаются в геометрии. Ниже приведены некоторые важные понятия, связанные с кругами.

Окружность

Длина окружности C аналогична периметру многоугольника в том смысле, что она является мерой расстояния по окружности.

Длина окружности приведенного выше круга может быть найдена по формуле

C = 2πr

, где r — радиус окружности. Также можно использовать формулу C = πd, где d — диаметр окружности. π — математическая константа, представляющая отношение длины окружности к ее диаметру. Он примерно равен 3,14.

Пример:

На рисунке ниже показана окружность A с радиусом AB = 4,4 и длиной окружности

C = 2π·4,4 = 27,6.

Отрезок линии под кругом представляет прямую длину его окружности.

Дуга окружности

Дуга окружности является частью окружности.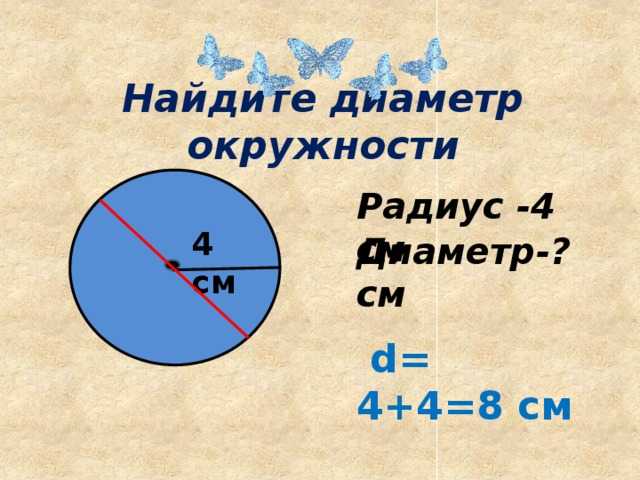

Дуга AB, обозначенная символически как , показана красным цветом для окружности O. Она называется малой дугой, поскольку охватывает менее половины окружности окружности. называется большой дугой, поскольку она охватывает более половины окружности окружности. Второстепенные дуги обычно называют с помощью двух точек, а большие дуги обычно называют с помощью трех.

Длина дуги — это часть длины окружности окружности. Его можно рассчитать по формуле

, где θ — центральный угол в градусах, опирающийся на дугу. Если угол задан в радианах, длину дуги можно найти, используя:

s = rθ

Для круга O ниже мера равна,

Площадь

Площадь круга – это плоская область, ограниченная окружность круга. Площадь измеряется в квадратных единицах длины, а окружность измеряется в единицах длины.

Область, заштрихованная серым цветом внутри круга O вверху, является его площадью. Формула площади:

A = πr ²

, где r — радиус окружности.