Параллельное и последовательное соединение резисторов (сопротивлений)
Содержание
- Отличия от последовательного и смешанного подключений
- Объединение резистивных радиокомпонентов
- Параллельное соединение резисторов онлайн калькулятор
- Как правильно рассчитать сопротивление
- Как рассчитать сложные схемы соединения резисторов
- Формула параллельного соединения резисторов
- Типы проводников
- Зависимость сопротивления
- Последовательное соединение резисторов.
Отличия от последовательного и смешанного подключений
Иные способы соединения понятны из показанных на картинке примеров. Без специальных вычислений понятно, что параллельное включение резисторов создает несколько путей прохождения тока. Следовательно, в отдельных цепях его сила будет меньше, по сравнению с контрольными точками на входе и выходе. Вместе с тем напряжение в отмеченных местах остается неизменным.
Последовательное соединение резисторов увеличивает общее электрическое сопротивление. Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.
Ток в этой цепи (по базовым принципам) не будет изменяться. Однако на каждом пассивном элементе можно будет обнаружить измерительным прибором соответствующее падение напряжения.
Смешанный вариант – это объединение представленных выше соединений. Различные комбинации используют для деления напряжения, решения других задач. Для упрощения расчетов суммируют последовательность соединенных сопротивлений в отдельных цепях:
Rобщ = R1 + R2 + … + Rn.
Вне зависимости от сложности схемы, на входе и выходе по первому закону Кирхгофа токи будут одинаковыми.
Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.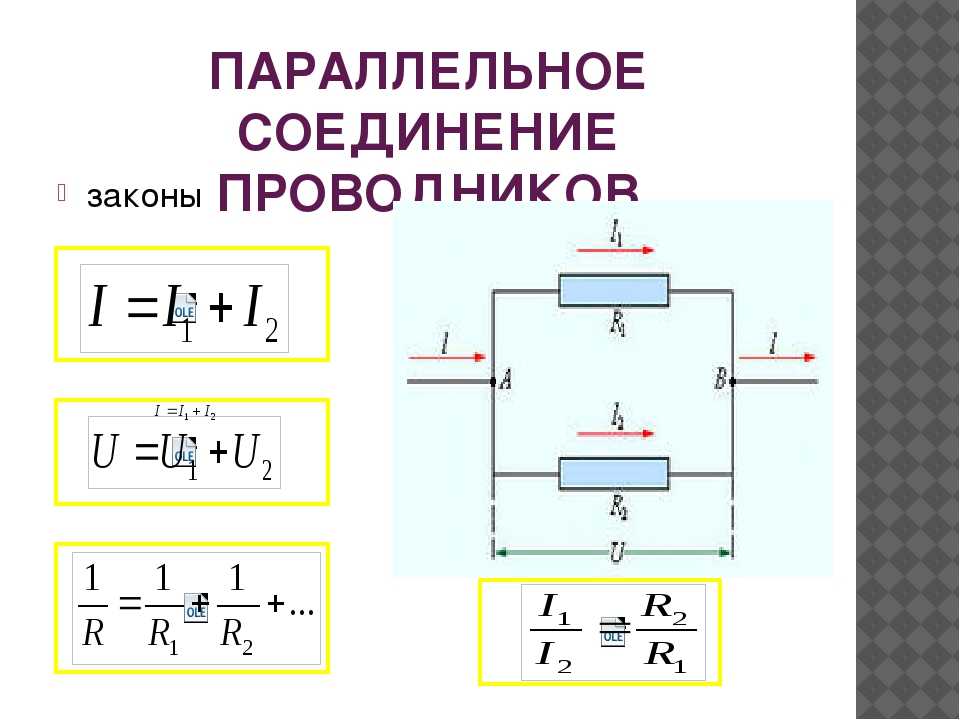
https://youtube.com/watch?v=jJX6IsRhnhs
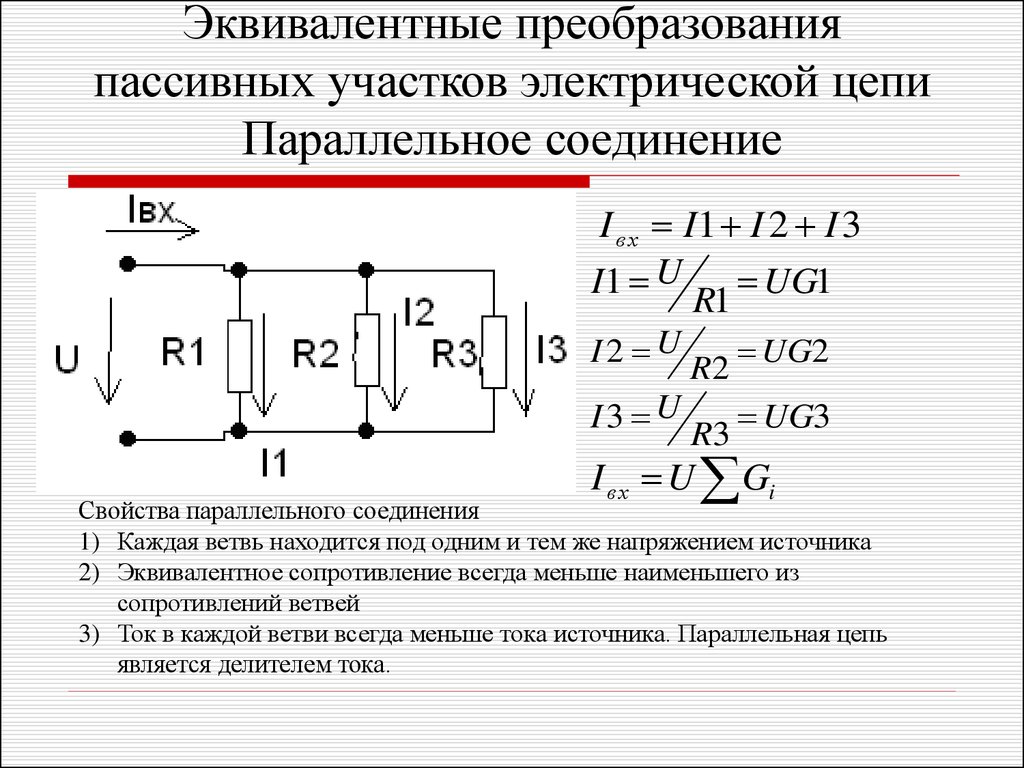
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
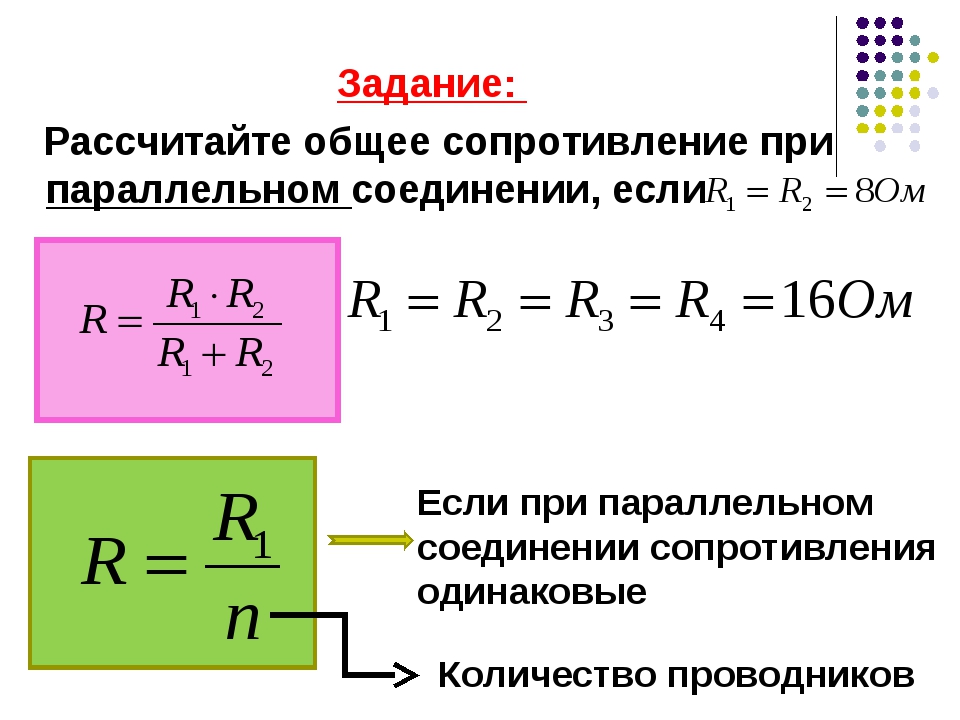
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов.
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Параллельное соединение резисторов онлайн калькулятор
Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться
Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:
Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.
Для этого вам необходимо:
- Указать в графе “количество резисторов” их число, в нашем примере их три;
- После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
- Далее нажмите кнопку “рассчитать” и в окошке “параллельное сопротивление в цепи” вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку “сбросить”, чтобы обнулить значение параллельно включенных элементов калькулятора.
Подключение магнитного пускателя через кнопочный пост видео
Для расчета суммарного сопротивления калькулятором используется такое соотношение:
- Rсум – суммарное сопротивление параллельно соединенных элементов
- R1 – сопротивление первого резистора;
- R2 – сопротивление второго резистора;
- R3 – сопротивление третьего резистора;
- Rn – сопротивление n-ого элемента.
Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:
Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:
Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.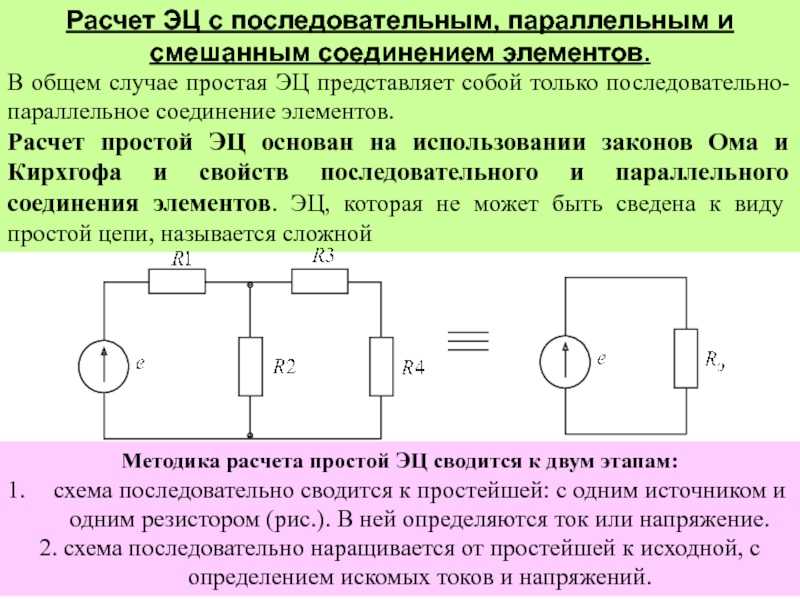
Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах
Онлайн калькулятор для расчета параллельного сопротивления позволит установить общее эквивалентное сопротивление в цепи R1 + R2 +Rn. Данный калькулятор можно смело назвать одним из самых простых и эффективных.
Литейная машина под давлением
Для получения результатов вам необходимо ввести:
- Количество резисторов.
- Указать мощность каждого резистора (Ом).
- Нажать кнопку «Расчитать».
В результате вы сможете получить точно сопротивление резисторов в сети
Калькулятор для расчета параллельного сопротивления позволит безошибочно все определить, а это очень важно, так как ручной расчет считается достаточно сложным и трудоемким процессом.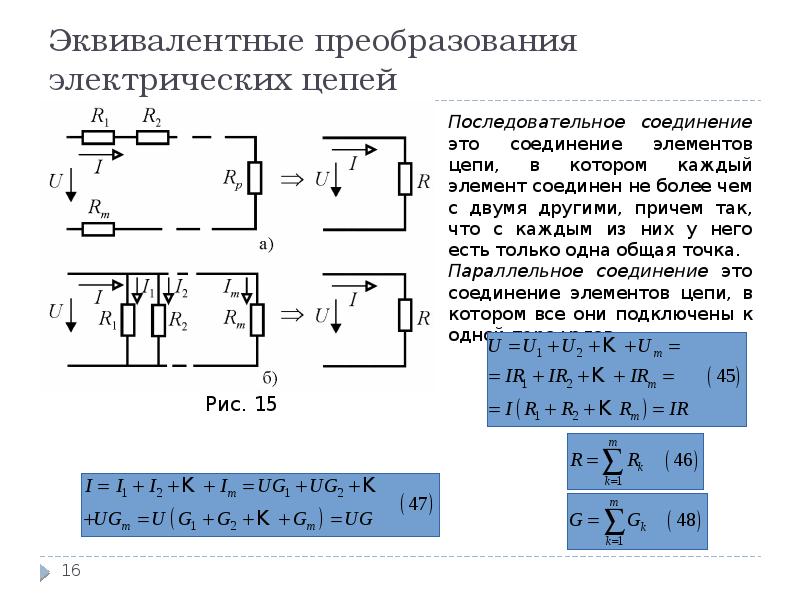
Для того чтобы определить общее эквивалентное сопротивление, можно воспользоваться точным и удобным калькулятором. Где, внеся данные по количеству резисторов, калькулятор произведет расчет в автоматическом режиме.
Данное соединение является одним из 2-ух видов, в данном случае оба вывода 1-го из резисторов соединяются с выводами 2-го резистора. В иных случаях их принято соединять параллельно или последовательно, чтобы можно было создать схемы сложного типа.
Многофункциональный станок своими руками чертежи
Для того чтобы найти ток, который протекает через определенный резистор, следует использовать формулу: Произведем расчеты согласно примеру Разрабатывается устройство, в котором есть необходимость использовать резистор, которое имеет сопротивление 8Ом. Исходя из того, что номинальный ряд согласно стандартным значениям таких резисторов не имеет, выходом будет использование
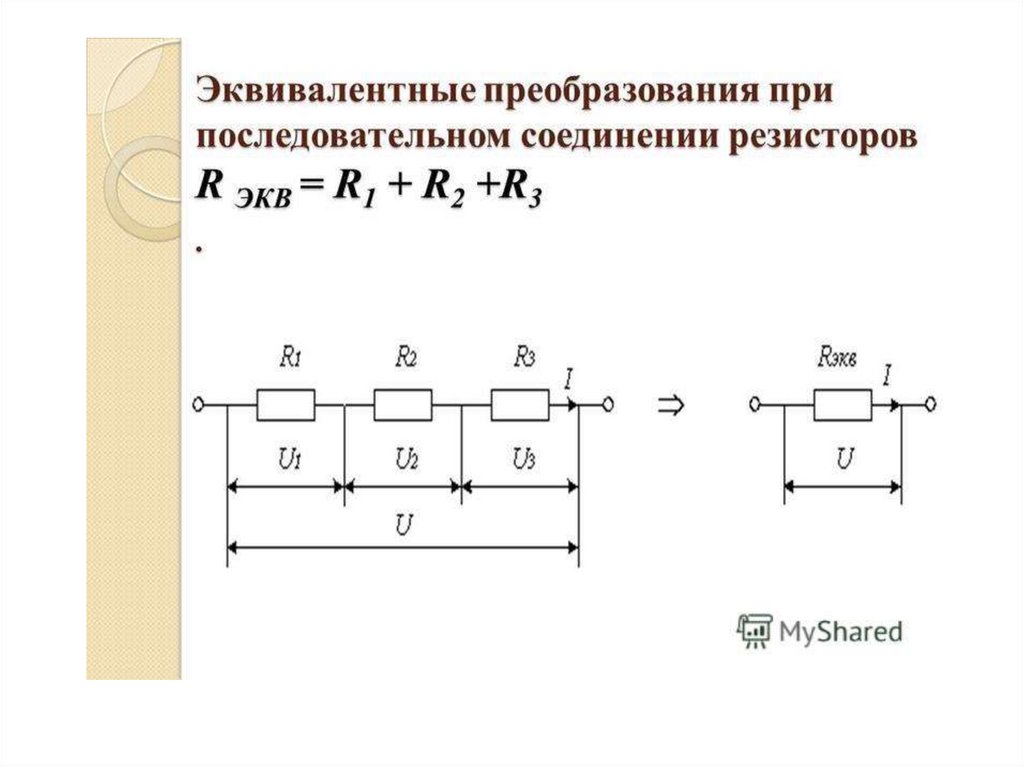
Для такого способа производятся следующие расчеты: Данная формула показывает, что в случае когда R1 = R2, R будет составлять ровно половину сопротивления 1-го из 2-ух резисторов. И если R=8Ом, то соответственно R1 и R2 = 2*8=16Ом.
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
Как правильно рассчитать сопротивление
Для выбора и установки элементов в цепь нужно заранее просчитать номинал и мощность составных частей.
Применяют для этого правило Ома для участка цепи, чтобы рассчитать сопротивление, выражение выглядит так:
R = U/I.
U — будет напряжением на выводах компонента.
I — показатель тока на участке цепи.
Это выражение используется для токов постоянного направления.
Если трудно самостоятельно рассчитать этот показатель, то существуют специальные онлайн-калькуляторы. Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Внимание! Если нет опыта в работе с электрикой, желательно не выполнять ремонт проводки самостоятельно, потому что при неправильной работе может случиться короткое замыкание, что чревато возникновением пожара. Также необходимо помнить, что при работе с проводкой нужно полностью обесточить сеть
Подключение для светодиодов
В заключении необходимо отметить, что подключать резисторы можно тремя способами: параллельно, последовательно и смешанно. Для тех, кто не имеет особых навыков работы с электрикой, рекомендуется выбирать последовательный метод соединения.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.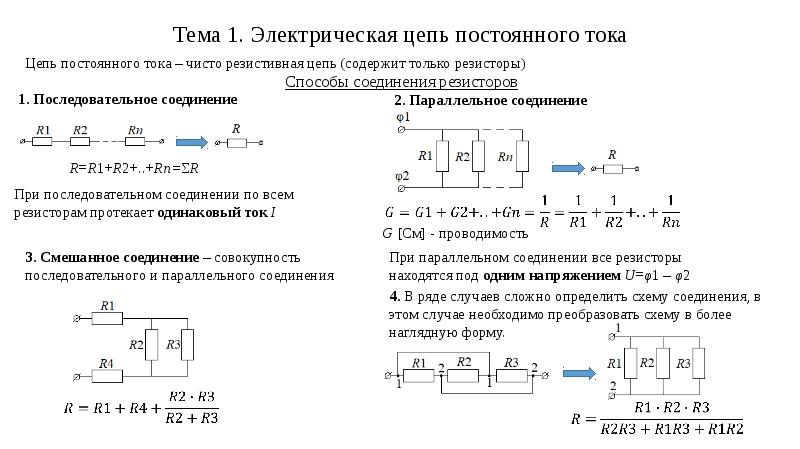
Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.

Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».
Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
RA = RAB RAC/(RAB+RAC+RDC).
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.
RAB=(RARB+RARC+RBRС)/RC
О разнице подключения звезда и треугольник читайте здесь.
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S.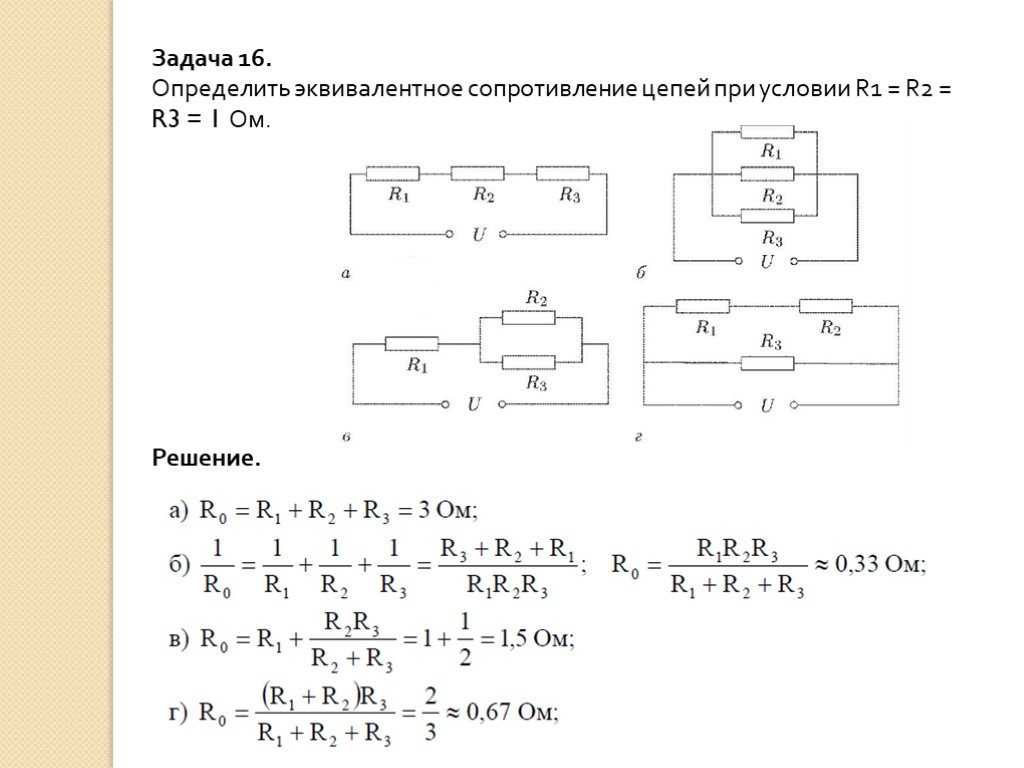 Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.
Последовательное соединение резисторов.
Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:
Например.При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.
При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.
Tags: автомат, ампер, бра, бросить, вид, выбор, дом, е, звезда, как, кт, магнит, мощность, напряжение, номинал, подключение, полоска, потенциал, правило, принцип, провод, проект, пуск, р, размер, расчет, резистор, ремонт, ряд, сад, свет, светодиод, сеть, система, соединение, соединение резистор, сопротивление, схема, тен, тип, ток, треугольник, ук, электричество, эффект
Простой расчет параллельного соединения резисторов — калькулятор
В статье подробно рассмотрим, как параллельно соединять резисторы и научимся легко считать сопротивление тока в электрической цепи и узнаем, для чего вообще нужно параллельное соединение резисторов.
Содержание
- 1 Понятие и определение
- 2 Что ещё нужно учитывать
- 3 Особенности включения
- 3.1 Отличия от иных вариантов подключения
- 4 Формула
- 4.1 Онлайн-калькулятор расчета параллельного соединения резисторов
- 5 Как выполняется расчёт
- 5.1 Пример №1
- 5.2 Пример расчёта №2
- 6 Ток в цепи параллельно соединенных резисторов
- 6.1 Сила тока
- 6.2 Мощность
- 6.3 Как найти сопротивление
- 7 Примеры применения при параллельном соединении
- 8 Видео
Понятие и определение
Параллельное соединение резисторов имеет некоторый принцип, согласно которому, выводы одного изделия подключены и работают с аналогичными выводами другого. Создаются подобные решения, чтобы специально формировать более трудные по своему составу и компоновке схемы.
Что ещё нужно учитывать
Параллельное соединение определяет принцип, согласно которому величина, установленная обратной общему показателю цепи, будет равна непосредственно сумме величин, обратных значению включённых проводников. Такая же ситуация будет отмечена при значительно большем количестве проводниковых элементов.
Такая же ситуация будет отмечена при значительно большем количестве проводниковых элементов.
Особенности включения
Параллельное соединение резисторов предусматривает, что показатель напряжения везде будет одинаковым, но ток фиксируется пропорциональным.
Отличия от иных вариантов подключения
В данной схеме, исключается подключение к источнику различных наименований реактивных компонентов. Исключаются проблемные процессы колебания, сопряжённые ранее с фиксируемыми циклами смены уровня получения энергии в контексте подачи нагрузки.
Формула
Формула, согласно которой проводится расчёт и составляется схема резисторов в параллельном соединении:
\[ 1/Rобщ=1/R1+1/R2 \]
\[ Rобщ=1/(1/R1+1/R2) \]
\[ Rобщ=(R1*R2)/(R1+R2) \]
Онлайн-калькулятор расчета параллельного соединения резисторов
Как выполняется расчёт
Проводя расчёт сопротивления для рассматриваемого соединения резисторов, нужно учесть факт, общий параметр всегда будет несколько ниже, нежели параметр наименьшего в приведённом сочетании.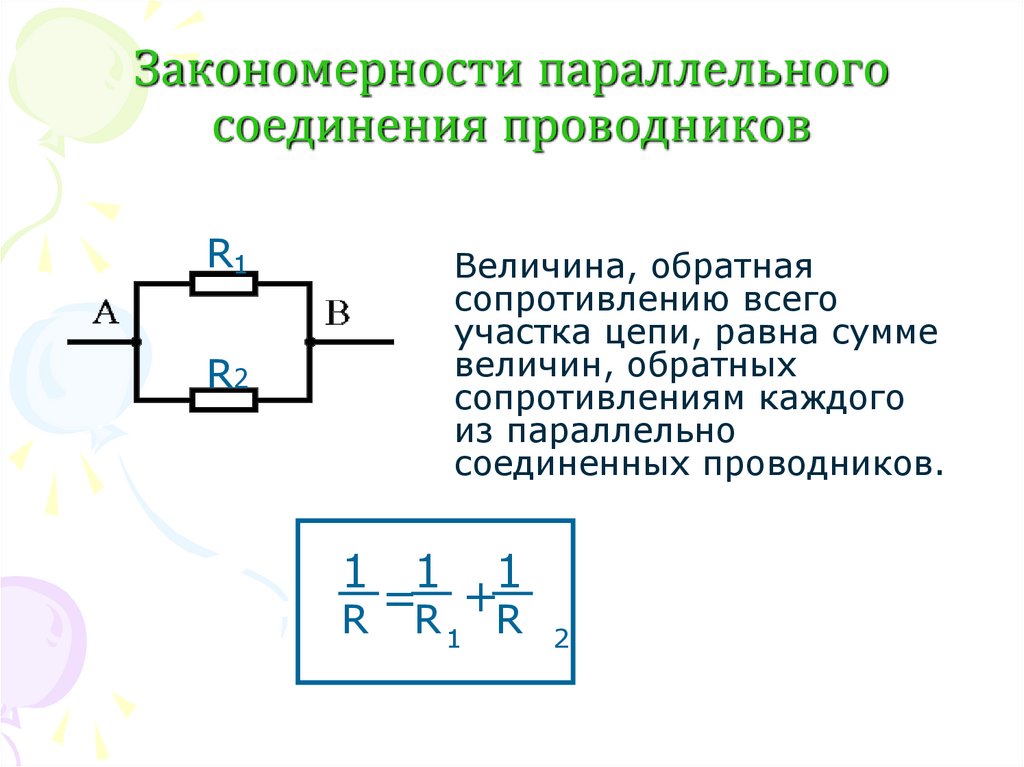
Пример №1
Потребуется включить резистор, имеющий сопротивление 8 Ом. Рассматривая номенклатуру изделий, отмечаем, резистор с подобным параметром в базовых наименованиях отсутствует. Необходимо использовать параллельную схему. В дальнейшем, расчёт выполняется:
\[ 1/R=1/R1+1/R2 \]
\[ 1/R=(R1+R2)/(R1*R2) \]
\[ R=(R1*R2)/(R1+R2) \]
В данном случае можно увидеть, что если оба значения равны между собой, то итог будет соответствовать половине одного из используемых двух резисторов. Если ставится задача подобрать сопротивление 8 Ом, то значение 2*8=16 Ом.
\[ R=(R1*R2)/(R1+R2)=(16*16)/(16+16)=8 \]
Таким образом, чтобы получить значение равное 8 Ом, соединяем два резистора по 16 Ом параллельно.
Пример расчёта №2
Есть три элемента: R1=200, R2=470, R=220
Общее значение выводится по формуле:
\[ 1/R=1/R1+1/R2/1/R3 \]
\[ 1/R=1/200+1/470+1/220=0,0117 \]
\[ R=1/0,0117=85,67 Ом \]
Данный метод без проблем актуален для выполнения расчёта практически любой численности включённых в конструкцию элементов.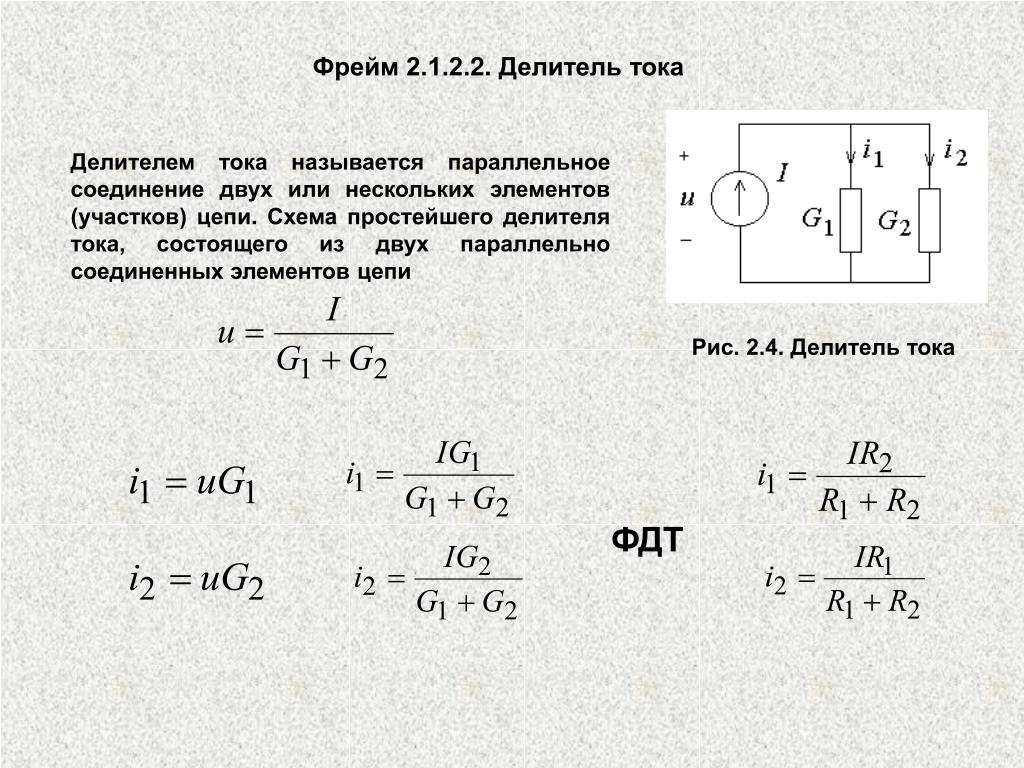
Ток в цепи параллельно соединенных резисторов
При параллельном соединении отмечается, что ток, приравнивается сумме из отдельных составляющих. Показатель в каждом ответвлении, не фиксируется идентичным значению в соседних ответвлениях. К отдельному резистору прикладывается идентичное напряжение.
Сила тока
Актуально выполнить расчёт для всех ветвей. Общий показатель силы тока составляет 8А, тогда предстоит распределить напряжения, показатель замеряется на отдельно рассмотренных участках.
\[ U12=I*Rэкв1=0,8*((2*4)/(2+4))=0,8*1,3=1,04 V \]
\[ I1=U12/R1=0,52 А \]
\[ I2=U12/R2=0,26 А \]
Корректность выполненных вычислений определяется:
\[ I=I1+I2=0,52+0,26≈0,8 А \]
Мощность
Для корректного выбора резисторов учитывается и мощность рассеивания. Данный показатель можно рассчитывать так:
\[ P=U*I \]
U — напряжение, В
I — сила тока, А
Показатель косвенным образом определяет некоторое количество энергии, она будет потребляться на выделение тепла.
Как найти сопротивление
Определение сопротивления выполняется по формулам:
\[ 1/G \]
\[ U/I \]
\[ U2/P \]
\[ P/I2 \]
Выбор параллельного подключения резисторов определяется с учётом входных параметров. Стоит только помнить о том, что показатель напряжения и уровень тока в отдельных ответвлениях идентичны.
Примеры применения при параллельном соединении
Конструктивно, каждый резистор рассчитан на некоторый рабочий диапазон температурного воздействия. Увеличение порога вызовет разрушение места пайки, соединения, самой детали, даже расположенных соседних блоков. Стоит помнить, что существуют одновременные соединения резисторов, приведённая компоновка способна нарушить функциональность и исправное состояние.
Благодаря использованию автоматических схем определения рабочих показателей можно переставлять резисторы, устанавливать в конкретном месте различные светодиоды, корректировать уровень сигнала на выходе.
Видео
youtube.com/embed/X7_lDtGzXTY?feature=oembed&wmode=opaque» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Калькулятор расчёта параллельного соединения резисторов — Строй Обзор
Содержание
- Вычислить сопротивление нескольких параллельно соединённых резисторов (до 10)
- Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединения
- Формула параллельного соединения резисторов
- Параллельное соединение резисторов — расчет
- Пример №1
- Пример расчета №2
- Как рассчитать сложные схемы соединения резисторов
- Ток, протекающий в цепи параллельно соединенных резисторах
- Параллельное соединение резисторов — онлайн калькулятор
- Подведем итог
Вычислить сопротивление нескольких параллельно соединённых резисторов (до 10)
Впишите любое количество любых номиналов в омах и кликните мышкой в таблице.
Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединения
Если нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R1 и R2.
Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).
Подбираем (меняем) нужный номинал из того что есть.
Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.
Замечания и предложения принимаются и приветствуются!
Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:
Параллельное соединение резисторов
Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.
Для этого вам необходимо:
- Указать в графе «количество резисторов» их число, в нашем примере их три;
- После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
- Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.
Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.
Для расчета суммарного сопротивления калькулятором используется такое соотношение:
- Rсум — суммарное сопротивление параллельно соединенных элементов
- R1 — сопротивление первого резистора;
- R2 — сопротивление второго резистора;
- R3 — сопротивление третьего резистора;
- Rn — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:
Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:
Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.
Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов — расчет
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Калькулятор параллельного резистора| Как рассчитать эквивалентное сопротивление в параллельной цепи?
Калькулятор параллельного резистора — это простой инструмент, который можно использовать для расчета эквивалентного сопротивления в параллельной цепи. Просто введите необходимую информацию в инструмент и нажмите кнопку расчета, чтобы мгновенно получить эквивалентное сопротивление.
Просто введите необходимую информацию в инструмент и нажмите кнопку расчета, чтобы мгновенно получить эквивалентное сопротивление.
Калькулятор параллельных резисторов: Рассчитайте эквивалентное сопротивление n резисторов в параллельной цепи с помощью нашего Калькулятора параллельных резисторов. Затем воспользуйтесь Калькулятором параллельного резистора, чтобы быстро и легко рассчитать эквивалентное сопротивление и отсутствующие значения сопротивления. В следующих разделах вы узнаете, что такое параллельное сопротивление, как его рассчитать, как узнать, находится ли цепь в параллельном комбинаторе, и как узнать, находится ли цепь в параллельном комбинаторе.
Если напряжение между резисторами одинаково, говорят, что цепь соединена параллельно. Ток распределяется по этим цепям, а затем объединяется, когда они встречаются в одном месте. Сопротивление измеряется в Омах. 1 Ом определяется как электрическое сопротивление между двумя точками, которое приводит к току в 1 Ампер при приложении к разности потенциалов в 1 вольт.
Формула расчета эквивалентного сопротивления в параллельной цепи следующая: 1/R = 1/R₁ + 1/R₂ +… + 1/R n
- Где R = эквивалентное параллельное сопротивление
- R₁, R₂,… R n — сопротивление отдельных резисторов, пронумерованных 1, 2, 3,…n
Для определения параллельного сопротивления выполните простые действия, описанные ниже. Ниже приведена последовательность, в которой они происходят
- Сначала найдите сопротивления отдельных резисторов.
- Затем для каждого резистора определите его обратное значение.
- Используя формулу 1/R = 1/R₁ + 1/R₂ +… + 1/R n , сложите все обратные величины отдельных резисторов.
- После подстановки известных чисел упростите уравнение, чтобы быстро получить сопоставимое значение сопротивления.
Резисторы, соединенные последовательно, эквивалентны одному резистору с сопротивлением, равным сумме каждого отдельного резистора. С другой стороны, параллельные резисторы создают эквивалентное сопротивление, которое всегда ниже, чем общее сопротивление каждого отдельного резистора. Это имеет смысл, если подумать: при подаче напряжения на резистор протекает определенное количество тока.
С другой стороны, параллельные резисторы создают эквивалентное сопротивление, которое всегда ниже, чем общее сопротивление каждого отдельного резистора. Это имеет смысл, если подумать: при подаче напряжения на резистор протекает определенное количество тока.
Вы эффективно установили новый путь для прохождения большего тока, когда последовательно подключаете второй резистор к первому. Общий ток, поступающий от источника питания, всегда будет несколько выше, чем ток, проходящий через один резистор, независимо от того, насколько велик второй резистор. Если общий ток больше, общее сопротивление также должно быть ниже.
Дополнительные концепции см. на сайте Physicscalculatorpro.com, чтобы получить быстрые ответы с помощью этого бесплатного инструмента.
Вопрос 1: В приведенной ниже схеме найдите ток I и ток, протекающий через каждый из резисторов.
Три резистора соединены последовательно и действуют как резистор с сопротивлением. Запрос дается как
1/R = 1/100 + 1/400 + 1/200
Умножить все члены на 400
400 R = 4 + 1 + 2
R = 400/7 Ом
основной ток I определяется по формуле;
I = 7/R = 7/(400 / 7) = 49/400 А
Теперь для определения тока, протекающего через каждый резистор, применим закон Ома.
I 1 = 7/100 А — ток, протекающий через резистор 100 Ом.
I 2 = 7 / 400 А — ток, протекающий через резистор 400 Ом.
I 2 = 7 / 200 А — ток, протекающий через резистор 200 Ом.
В качестве упражнения убедитесь, что сумма трех вышеуказанных токов равна току I = 49 / 400 A.
1. Как рассчитать параллельное сопротивление?
Для расчета полного сопротивления в параллельной цепи можно использовать следующую формулу: 1/R t = 1/R₁ + 1/R₂ + 1/R 3 +…. Ток продолжит течь во всех параллельных путях, если один из них разорван.
2. В чем разница между параллельным и последовательным?
Последовательная цепь имеет одинаковую величину тока, протекающего через все компоненты. С другой стороны, в параллельных цепях компоненты соединены параллельно, в результате чего цепь разделяет ток.
3. Что делает резисторы параллельными?
Если выводы двух резисторов подключены к одним и тем же двум узлам, они параллельны. Общее эквивалентное сопротивление меньше, чем у наименьшего параллельного резистора.
Общее эквивалентное сопротивление меньше, чем у наименьшего параллельного резистора.
4. Как делится ток в параллельных цепях?
Ток в параллельной цепи разделяется на несколько ветвей перед рекомбинацией и возвратом к источнику. Когда ток разделяется на две ветви, ток в каждой ветви равен току до разделения.
5. Какая лампочка в параллельной цепи перегорит первой?
В последовательной конфигурации лампочка с более высоким сопротивлением перегорает первой, поскольку она может выдерживать большее напряжение.
Расчет параллельного сопротивления — Pi My Life Up
В этом руководстве мы покажем вам, как рассчитать параллельное сопротивление, а также предоставим вам простой в использовании калькулятор параллельного сопротивления.
Параллельное сопротивление является полезной частью электроники, но его может быть трудно вычислить, когда вы начинаете иметь дело с более чем двумя резисторами.
Каждый резистор, который вы добавляете параллельно, уменьшает общее сопротивление. Такое поведение удобно, когда вам нужно определенное сопротивление, но у вас нет резистора, соответствующего требуемому значению.
Уменьшение сопротивления вызвано тем, что ток имеет больше путей прохождения. Каждый новый резистор, включенный параллельно, пропускает больший ток через цепь и, следовательно, уменьшает общее сопротивление, с которым сталкивается ваша цепь.
Например, в цепи с двумя параллельными резисторами одинакового номинала сопротивление уменьшится ровно вдвое. Математика немного отличается для разных сопротивлений и если у вас больше резисторов. Мы углубимся в это позже в руководстве.
Если вы хотите увеличить сопротивление цепи, а не уменьшить его, то вместо этого вы можете использовать последовательно соединенные резисторы.
Чтобы рассчитать общее сопротивление в цепи с параллельными резисторами, у нас есть удобный калькулятор, который значительно упрощает этот процесс.
Если вас смущают цвета на резисторе, обязательно ознакомьтесь с руководством по цветовой маркировке резистора, поскольку оно научит вас всему, что вам нужно знать.
Чтобы использовать наш калькулятор параллельного сопротивления, просто установите количество резисторов, для которых вы хотите рассчитать параллельное сопротивление. Затем введите значение для каждого резистора.
Общее сопротивление вашей параллельной цепи будет рассчитываться и обновляться по мере того, как вы устанавливаете значение каждого резистора.
Количество резисторов:
Резистор 1:
Резистор 2:
Расчет общего сопротивления при параллельном подключении
Если вы хотите научиться, вы можете рассчитать сопротивление параллельно подключенных резисторов вручную. Этот процесс немного утомителен и может быстро усложниться, если вы имеете дело с несколькими резисторами, включенными параллельно.
Существуют три различных уравнения, которые можно использовать для параллельного расчета общего сопротивления.
Суммарное сопротивление двух одинаковых резисторов
Первое уравнение следует использовать только в том случае, если у вас есть два параллельных резистора с одинаковым сопротивлением.
Если два резистора одного сопротивления включены параллельно, то общее сопротивление равно половине сопротивления одного резистора.
Пример использования уравнения
Для этого примера предположим, что у нас есть два резистора по 200 Ом , включенных параллельно, как показано на схеме ниже.
Зная, что параллельно подключены только два резистора и что они одного номинала, мы можем использовать наше уравнение.
Отметив значение R1 как 200 , мы можем заполнить уравнение, как показано ниже. Теперь используйте уравнение для расчета общего сопротивления ( Rt ).
Чтобы получить общее сопротивление, все, что нам нужно сделать сейчас, это разделить наше значение 200 Ом на 2 .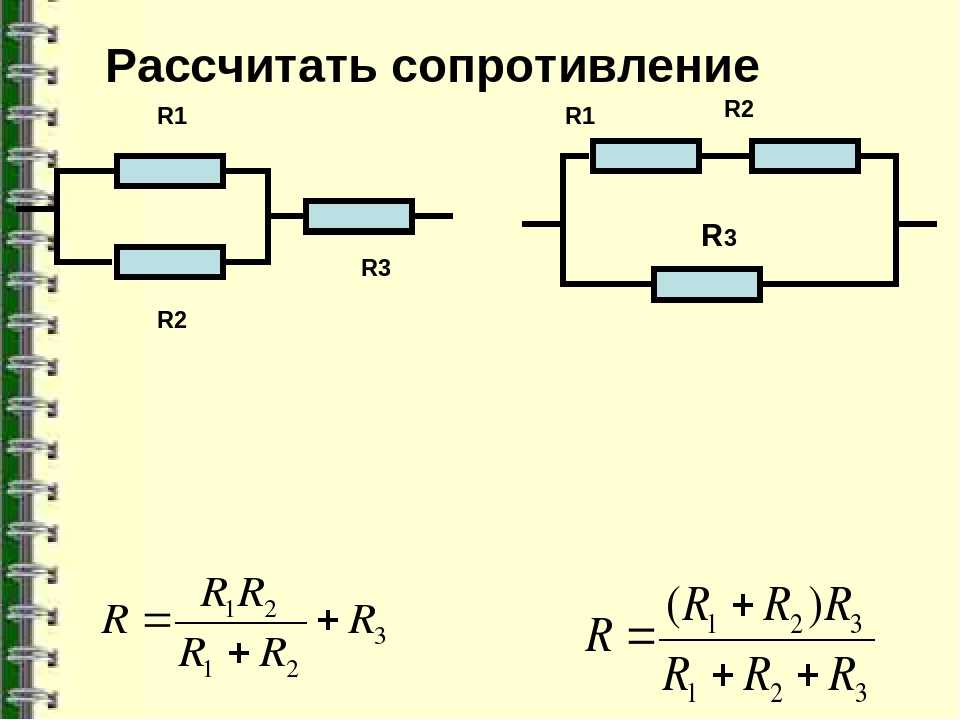
Ответ очень легко вычислить: 100 .
Теперь у вас должно быть представление о том, как справиться с простейшим сценарием двух параллельных резисторов одного номинала.
Суммарное сопротивление двух разных резисторов
Второе уравнение представляет собой упрощенную версию основного уравнения, которое мы будем использовать позже. Это уравнение используется, когда у вас есть два резистора с разным сопротивлением.
Есть несколько других процессов, которые необходимо выполнить для расчета сопротивления двух параллельных резисторов, но это не намного сложнее.
Пример использования уравнения
В этом примере мы будем предполагать, что у нас есть цепь с двумя параллельными резисторами разных номиналов.
В этой схеме у нас есть резистор 600 Ом и резистор 250 Ом , соединенные параллельно. Теперь мы хотим определить общее сопротивление, обеспечиваемое этими резисторами.
Для начала нам нужно заполнить наше уравнение, где R1 будет нашим резистором 600 Ом, а наше значение R2 будет 250 Ом резистор.
Теперь, когда уравнение заполнено, мы должны выполнить верхнее умножение и нижнее сложение, прежде чем продолжить.
Умножение 600 (R1) на 250 (R2) должно дать вам результат 150,000 . Добавление 600 (R1) к 250 (R2) должно дать вам ответ 850 .
Выработав оба значения, все, что нам нужно сделать, это разделить верхнее число на нижнее число. Сделав это, мы можем определить общее сопротивление двух резисторов, включенных параллельно.
Математика, которую вы должны выполнить в этом примере, равна 150 000 , деленная на 850 . Отсюда вы должны получить результат 176,47 . Будут лишние десятичные знаки, но мы округлим до ближайших двух.
Теперь у вас должно быть представление о том, как рассчитать общее сопротивление двух резисторов, включенных параллельно.
Далее мы покажем вам, как обращаться с тремя или более резисторами. Это уравнение представляет собой немного более сложный процесс, так как оно включает в себя много делений, что приводит к большим десятичным числам.
Это уравнение представляет собой немного более сложный процесс, так как оно включает в себя много делений, что приводит к большим десятичным числам.
Общее сопротивление нескольких резисторов
Третье и последнее уравнение, с которым мы будем иметь дело, это то, которое вы будете использовать для трех или более резисторов, включенных параллельно.
Уравнение довольно простое по своей сути и может быть легко расширено для работы с большим количеством резисторов.
Единственным недостатком этого уравнения является то, что оно занимает больше времени, чем больше резисторов вы добавляете.
Простым решением является использование параллельного калькулятора резисторов, который мы включили выше.
Пример использования уравнения
В этом примере мы покажем, как использовать более сложное уравнение параллельного резистора.
Для этого мы будем использовать несколько резисторов со значениями 100 Ом (R1) , 250 Ом (R2) , 200 Ом (R3) и 1 кОм (R4) .
Для начала нам нужно заполнить уравнение всеми нашими значениями.
Каждое из наших значений резисторов будет делителем 1 , и вы можете добавить в это уравнение столько резисторов, сколько вам нужно. В этом примере мы обрабатываем только четыре.
Наш следующий шаг — разделить 1 на каждое из значений резистора . Вы должны сохранить как можно больше десятичных знаков, поскольку точность влияет на окончательный расчет сопротивления.
Например, в нашем расчете мы делим 1 на 100 , что дает нам результат 0,01 .
После того, как вы закончили деление каждого набора значений, теперь нам нужно сложить каждое значение вместе.
Для нашего примера схемы это будет означать: 0,01 + 0,004 + 0,005 + 0,001 . К счастью для нас, это довольно плавно складывается и дает нам красивое круглое число 0,02 .
Далее мы должны переместить делитель из левой части уравнения в правую.
Этот ход будет означать, что наше вычисленное значение станет делителем 1 и должно выглядеть так, как показано ниже.
Наконец, разделите 1 на ваш делитель, и в нашем случае это будет 0,02 . Это уравнение рассчитает конечное общее сопротивление ваших резисторов, включенных параллельно.
Резюме
Надеюсь, теперь вы накопили достаточно знаний о том, как рассчитать общее сопротивление параллельных резисторов. Вы должны найти это удобным, если вы планируете делать какие-то проекты схем Raspberry Pi или любой другой проект электроники.
Если у вас есть какие-либо отзывы или вопросы относительно этого руководства, не стесняйтесь оставлять комментарии ниже.
Калькулятор параллельного резистора сериидля HP-67/97
Калькулятор параллельного резистора серии для HP-67/97 Музей калькуляторов HP
Эта программа защищена авторским правом © 1997 г. Джона Х. Мейера и используется здесь с разрешения.
Мейера и используется здесь с разрешения.
Эта программа поставляется без каких-либо заверений или гарантий. Таким образом, автор и Музей калькуляторов HP не несут ответственности и не несут ответственности, косвенной или иной, любого рода, возникающего в связи с использованием данного программного материала или любой его части.
| Калькулятор последовательных/параллельных резисторов | |||||
| Смена | Р всего | % ошибка | Число/десятилетие | ||
| Этикетка | R мин | R макс. | Серии | Параллельно | |
| Ключ | А | Б | С | Д | Е |
Обзор и инструкции
Эта программа находит два стандартных резистора, которые при последовательном или параллельном соединении дают наиболее близкое приближение к желаемому нестандартному значению сопротивления.
Два стандартных резистора могут быть соединены последовательно или параллельно, чтобы приблизиться к желаемому сопротивлению. Стандартные значения сопротивления рассчитываются по следующей формуле:
[10 (1/n) ] x
, где n = количество стандартных значений сопротивления за декаду, а x = целое число. Каждое последующее целое число приводит к следующему стандартному значению. 5% резисторов приходятся на 12 на декаду, таким образом, n=12. Значения прецизионных резисторов составляют 24 с точностью до декады, таким образом, n=24.
Для расчета наибольшего соответствия с использованием последовательного соединения используется следующий алгоритм: (R’ и R» — пробные сопротивления; R = желаемое сопротивление)
- R’ = [10 (1/n ) ] INT[log(R)/log (10 (1/n) )]
- Установить флаг 2
- R» = [10 (1/n) ] INT[log (R — R’)/log(10 (1/n) )]
- Если R» > R’, программа завершена.

- Ошибка вычисления = ABS [R- (R’+R»)]. Если это пока самая маленькая ошибка, сохраните R’ и R».
- Если установлен флаг 2, умножьте R» на 10 (1/n) , снимите флаг 2 и перейдите к шагу 5.
- Разделить R’ на 10 (1/n) . Перейти к шагу 2.
Если R» падает ниже минимального сопротивления (Rmin), Rmin заменяется на R». Программа аппроксимирует параллельное сопротивление, подставляя 1/R вместо R и обратное значение максимально допустимого (R max ) вместо R min .
Программа работает для конденсаторов и катушек индуктивности. Используйте параллельную программу для аппроксимации последовательной емкости и наоборот.
Для использования программы:
- Сторона загрузки 1 и сторона 2.
- Необязательно: Введите количество стандартных компонентов на декаду (по умолчанию — 24). Нажмите [f] [E].
- Установите отображение на единицу меньше, чем количество значащих цифр, указанное для стандартных компонентов (например, для 9,09 кОм установите [DSP] [2]).
 Также установите дисплей на ENG.
Также установите дисплей на ENG. - Введите минимальное стандартное значение (R min ). Нажмите А.
- Введите максимальное стандартное значение (R макс ). Нажмите Б.
- Введите требуемое сопротивление. Нажмите C, чтобы вычислить значения серии, или D, чтобы вычислить параллельные значения.
- Необязательно: Вычислите общее сопротивление по общему значению (нажмите [f] [A]).
- Необязательно: Вычислите % ошибки фактического сопротивления по сравнению с требуемым сопротивлением (нажмите [f] [B]).
- Дополнительно:
Возврат R мин. [RCL] [A]
Возврат R макс. [RCL] [B]
Возврат R (требуемое сопротивление) [RCL] [C]
Отзыв R 1 (первый стандартный резистор) [RCL] [D]
Отзыв R 2 (второй стандартный резистор) [RCL] [E]
Примечание. Описанные выше шаги 2–5 можно выполнять в любом порядке и в любое время. Чтобы вычислить новое приближение, просто повторите шаг 6.
Чтобы вычислить новое приближение, просто повторите шаг 6.
Программа
КОД СТРОКИ КЛАВИШИ НАЖАТИЯ КЛАВИШ (67) КОММЕНТАРИИ 001 31 25 00 Метка 0 [f] [LBL] [0] Вычислить R' и R'' 002 35 64 ABS [ч] [ABS] согласно 003 31 53 LOG [f] [LOG] формула на странице 1. 004 34 08 РКЛ8 [РКЛ] [8] 005 81 ÷ ÷ 006 31 83 INT [f] [INT] 007 34 09РКЛ9 [РКЛ] [9] 008 35 52 X⇔Y [ч] [X⇔Y] 009 35 63 Y x [h] [Y x ] 010 35 22 РТН [ч] [РТН] 011 32 25 15 Этикетка e [g] [LBL f] [e] 012 35 51 00 SF0 [ч] [SF] [0] Сохранить n 013 33 03 СТО3 [СТО] [3] 014 35 22 РТН [ч] [РТН] 015 31 25 11 Этикетка A [f] [LBL] [A] 016 33 11 STOA [STO] [A] Store R мин 017 35 22 РТН [ч] [РТН] 018 31 25 12 Этикетка B [f] [LBL] [B] 01933 12 STOB [STO] [B] Запомнить R max 020 35 22 РТН [ч] [РТН] 021 32 25 11 Этикетка a [г] [LBL f] [a] 022 35 23 ENG [h] [ENG] Вычислить R to 023 34 14 RCLD [RCL] [D] 024 35 71 01 Ф1? [ч] [Ф?] [1] 025 35 62 1/х [ч] [1/х] 026 34 15 RCLE [RCL] [E] 027 35 71 01 Ф1? [ч] [Ф?] [1] 028 35 62 1/х [ч] [1/х] 029 61 + + 030 35 71 01 Ф1? [ч] [Ф?] [1] 031 35 62 1/х [ч] [1/х] 032 35 22 РТН [ч] [РТН] 033 32 25 12 Метка b [g] [LBL f] [b] Вычисление % ошибки 034 34 13 RCLC [RCL] [C] 035 32 22 11 ГСБ [г] [ГСБ ф] [а] 036 32 82 % Изменение [г] [%CH] 037 31 23 ИСПРАВИТЬ [f] [ИСПРАВИТЬ] 038 35 22 РТН [ч] [РТН] 03931 25 14 Этикетка D [f] [LBL] [D] Параллельно прибл.040 35 62 1/х [ч] [1/х] 041 33 13 СТОЦ [СТО] [С] 042 35 51 01 SF1 [ч] [SF] [1] 043 34 12 РКЛБ [РКЛ] [Б] 044 35 62 1/х [ч] [1/х] 045 22 04 ГТО4 [ГТО] [4] 046 31 25 13 Этикетка C [f] [LBL] [C] Серия прибл. 047 33 13 СТОЦ [СТО] [С] 048 35 61 01 CF1 [ч] [CF] [1] 049 34 11 RCLA [RCL] [A] 050 31 25 04 Этикетка 4 [f] [LBL] [4] Установить n=24. Если флаг 051 33 04 STO4 [STO] [4] 0 установлен, установлен n 052 35 23 ENG [h] [ENG] соответствует пользователю 053 34 03 RCL3 [RCL] [3] предоставленный номер 054 02 2 2 значений 055 04 4 4 на декаду 056 35 71 00 Ф0? [ч] [Ф?] [0] 057 35 52 X⇔Y [ч] [X⇔Y] 058 35 62 1/х [ч] [1/х] 05932 53 10 x [g] [10 x ] Вычислить 10 (1/n) 060 33 09 СТО9 [СТО] [9] 061 31 53 LOG [f] [LOG] log[10 (1/n) ] 062 33 08 СТО8 [СТО] [8] 063 34 13 RCLC [RCL] [C] 064 33 07 STO7 [STO] [7] Ошибка инициализации=R 065 31 22 00 GSB0 [f] [GSB] [0] Вычислить R' 066 33 06 СТО6 [СТО] [6] 067 31 25 01 Этикетка 1 [f] [LBL] [1] 068 35 51 02 SF2 [ч] [SF] [2] 06934 13 RCLC [RCL] [C] 070 51 -- вычисление R'-R 071 31 22 00 GSB0 [f] [GSB] [0] Вычислить R'' 072 33 05 СТО5 [СТО] [5] 073 34 04 РКЛ4 [РКЛ] [4] 074 32 81 Х>Y? [g] [X>Y?] Если R''< R мин.






 Также установите дисплей на ENG.
Также установите дисплей на ENG.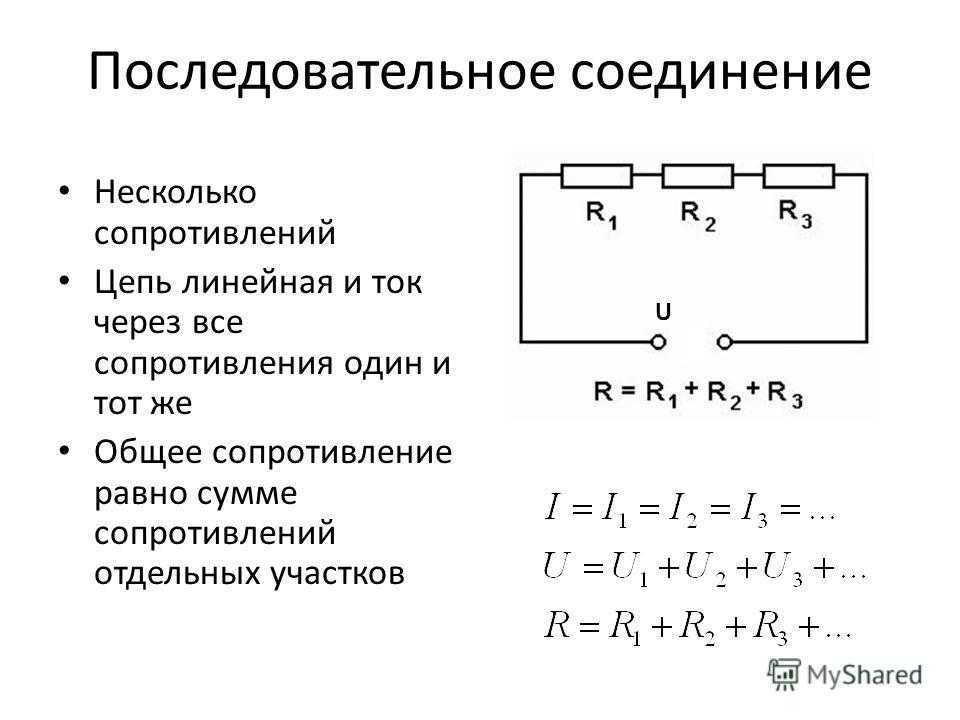 040 35 62 1/х [ч] [1/х]
041 33 13 СТОЦ [СТО] [С]
042 35 51 01 SF1 [ч] [SF] [1]
043 34 12 РКЛБ [РКЛ] [Б]
044 35 62 1/х [ч] [1/х]
045 22 04 ГТО4 [ГТО] [4]
046 31 25 13 Этикетка C [f] [LBL] [C] Серия прибл.
047 33 13 СТОЦ [СТО] [С]
048 35 61 01 CF1 [ч] [CF] [1]
049 34 11 RCLA [RCL] [A]
050 31 25 04 Этикетка 4 [f] [LBL] [4] Установить n=24. Если флаг
051 33 04 STO4 [STO] [4] 0 установлен, установлен n
052 35 23 ENG [h] [ENG] соответствует пользователю
053 34 03 RCL3 [RCL] [3] предоставленный номер
054 02 2 2 значений
055 04 4 4 на декаду
056 35 71 00 Ф0? [ч] [Ф?] [0]
057 35 52 X⇔Y [ч] [X⇔Y]
058 35 62 1/х [ч] [1/х]
05932 53 10 x [g] [10 x ] Вычислить 10 (1/n) 060 33 09 СТО9 [СТО] [9]
061 31 53 LOG [f] [LOG] log[10 (1/n) ]
062 33 08 СТО8 [СТО] [8]
063 34 13 RCLC [RCL] [C]
064 33 07 STO7 [STO] [7] Ошибка инициализации=R
065 31 22 00 GSB0 [f] [GSB] [0] Вычислить R'
066 33 06 СТО6 [СТО] [6]
067 31 25 01 Этикетка 1 [f] [LBL] [1]
068 35 51 02 SF2 [ч] [SF] [2]
06934 13 RCLC [RCL] [C]
070 51 -- вычисление R'-R
071 31 22 00 GSB0 [f] [GSB] [0] Вычислить R''
072 33 05 СТО5 [СТО] [5]
073 34 04 РКЛ4 [РКЛ] [4]
074 32 81 Х>Y? [g] [X>Y?] Если R''< R мин.
040 35 62 1/х [ч] [1/х]
041 33 13 СТОЦ [СТО] [С]
042 35 51 01 SF1 [ч] [SF] [1]
043 34 12 РКЛБ [РКЛ] [Б]
044 35 62 1/х [ч] [1/х]
045 22 04 ГТО4 [ГТО] [4]
046 31 25 13 Этикетка C [f] [LBL] [C] Серия прибл.
047 33 13 СТОЦ [СТО] [С]
048 35 61 01 CF1 [ч] [CF] [1]
049 34 11 RCLA [RCL] [A]
050 31 25 04 Этикетка 4 [f] [LBL] [4] Установить n=24. Если флаг
051 33 04 STO4 [STO] [4] 0 установлен, установлен n
052 35 23 ENG [h] [ENG] соответствует пользователю
053 34 03 RCL3 [RCL] [3] предоставленный номер
054 02 2 2 значений
055 04 4 4 на декаду
056 35 71 00 Ф0? [ч] [Ф?] [0]
057 35 52 X⇔Y [ч] [X⇔Y]
058 35 62 1/х [ч] [1/х]
05932 53 10 x [g] [10 x ] Вычислить 10 (1/n) 060 33 09 СТО9 [СТО] [9]
061 31 53 LOG [f] [LOG] log[10 (1/n) ]
062 33 08 СТО8 [СТО] [8]
063 34 13 RCLC [RCL] [C]
064 33 07 STO7 [STO] [7] Ошибка инициализации=R
065 31 22 00 GSB0 [f] [GSB] [0] Вычислить R'
066 33 06 СТО6 [СТО] [6]
067 31 25 01 Этикетка 1 [f] [LBL] [1]
068 35 51 02 SF2 [ч] [SF] [2]
06934 13 RCLC [RCL] [C]
070 51 -- вычисление R'-R
071 31 22 00 GSB0 [f] [GSB] [0] Вычислить R''
072 33 05 СТО5 [СТО] [5]
073 34 04 РКЛ4 [РКЛ] [4]
074 32 81 Х>Y? [g] [X>Y?] Если R''< R мин.