СТЬЮДЕНТ.РАСП (функция СТЬЮДЕНТ.РАСП)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel Web App Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
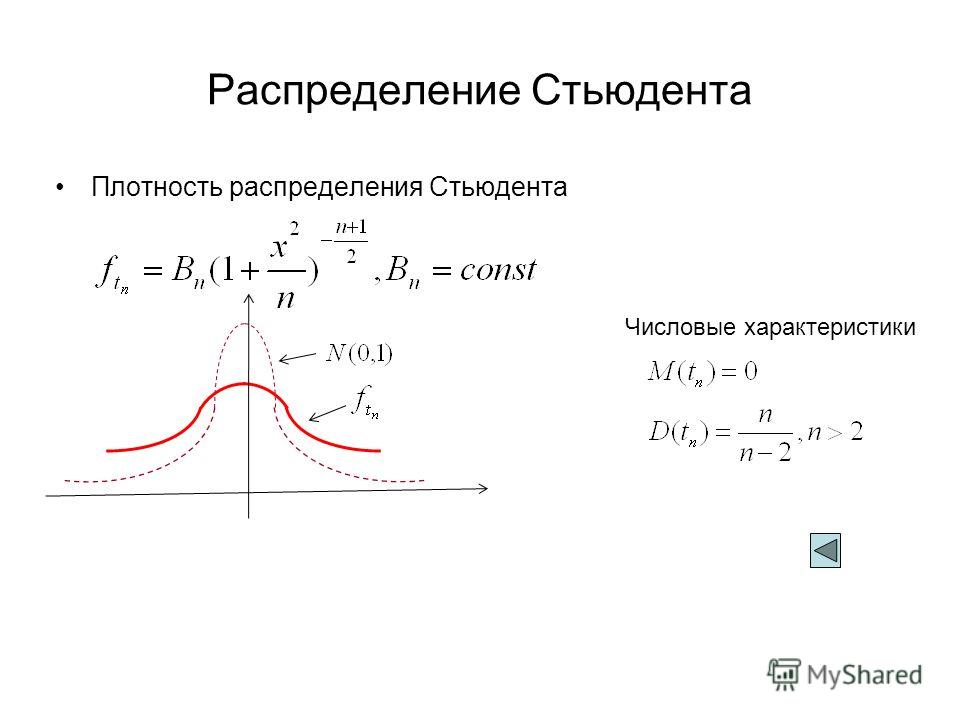
Возвращает левостороннее t-распределение Стьюдента. T-распределение используется для проверки гипотез при малом объеме выборки. Данную функцию можно использовать вместо таблицы критических значений t-распределения.
Синтаксис
СТЬЮДЕНТ.РАСП(x;степени_свободы;интегральная)
Аргументы функции СТЬЮДЕНТ.РАСП описаны ниже.
-
X Обязательный. Числовое значение, для которого требуется вычислить распределение.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция СТЬЮДЕНТ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
Степени_свободы Обязательный. Целое, указывающее число степеней свободы.
Замечания
-
Если какой-либо из аргументов не является числом, то Т.#VALUE! значение ошибки #ЗНАЧ!.
-
Если значение аргумента «степени_свободы» < 1, функция СТЬЮДЕНТ.
 РАСП возвращает значение ошибки. Значение «степени_свободы» не может быть меньше 1.
РАСП возвращает значение ошибки. Значение «степени_свободы» не может быть меньше 1.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=СТЬЮДЕНТ.РАСП(60;1;ИСТИНА) |
Левостороннее t-распределение СТЬЮДЕНТА для 60, возвращаемое как интегральная функция распределения с 1 степенью свободы. |
0,99469533 |
|
=СТЬЮДЕНТ.РАСП(8;3;ЛОЖЬ) |
Левостороннее t-распределение СТЬЮДЕНТА для 8, возвращаемое как весовая функция распределения с 3 степенями свободы. |
0,00073691 |
К началу страницы
tраспределение Стьюдента —
Теория
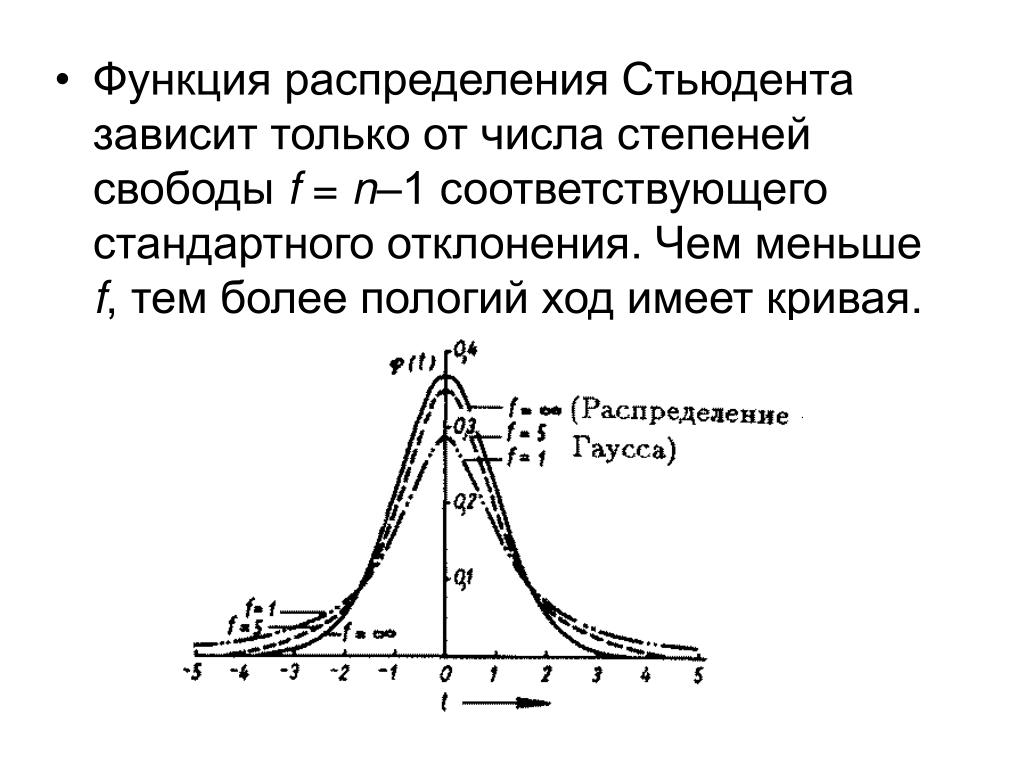
t-распределение Стьюдента – это непрерывное одномерное распределение с одним параметром – количеством степеней свободы. Форма распределения Стьюдента похожа на форму нормального распределения (чем больше число степеней свободы, тем ближе распределение к нормальному). Отличием является то, что хвосты распределения Стьюдента медленнее стремятся к нулю, чем хвосты нормального распределения.
Обычно распределение Стьюдента появляется в задачах, связанных с оценкой математического ожидания нормально распределенных случайных величин. Пусть X1 , …, Xn – независимые случайные величины, нормально распределенные с математическим ожиданием μ и дисперсией σ 2. Тогда мы можем получить следующие оценки для параметров μ и σ 2:
При этом оценка математического ожидания не равна в точности μ, а лишь колеблется вокруг этой величины. Разность истинного математического ожидания и рассчитанного на основе выборки, поделенная на масштабирующий коэффициент
имеет распределение, которое называется распределением Стьюдента с N степенями свободы. Есть и другие разделы статистики, в которых появляются случайные величины, распределенные по Стьюденту. Например, распределение Стьюдента используется при оценке значимости коэффициента корреляции Пирсона.
Чаще всего критерий Стьюдента применяется для проверки равенства средних значений в двух выборках.
Если X – случайная величина, то функция F(x) – интегральная функция распределения вероятностей, или просто функция распределения (иногда применяют термин кумулятивная функция распределения) случайной величины определяет вероятность P того, что случайная величина принимает значение, меньше x, т.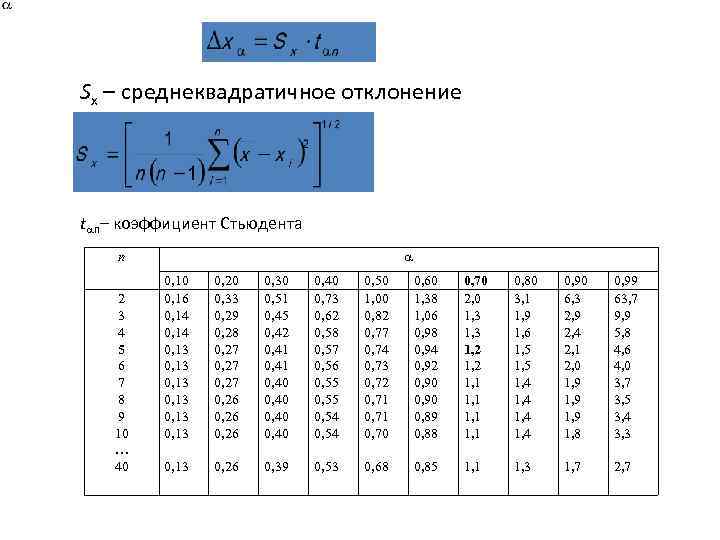
F(x) = P( X < x)
Функция распределения содержит всю информацию о случайной величине, поэтому изучение случайной величины заключается в исследовании ее функции распределения.
Функция распределения полностью характеризует случайную величину и является одной из форм закона распределения.
Из определения следует, что функция распределения любой случайной величины обладает следующими свойствами:
Свойства F(x):
1. Интегральная функция распределения принимает значения от 0 до 1.
2. F(x) – неубывающая функция, то есть F(x2) F(x1), если x2 > x1.
3. Вероятность того, что случайная величины X примет значение, заключенное в интервале (а, b) равна приращению интегральной функции распределения на этом интервале:
4. Если все значения непрерывной случайной величины принадлежат некоторому промежутку от a до b, то:
F(x) = 0, если x a, F(x) = 1, если x b
Функция распределения существует как для непрерывных, так и для дискретных случайных величин.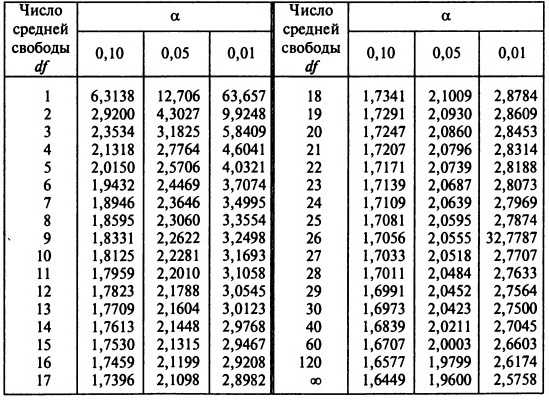
Дифференциальная функция (плотность распределения) – первая производная от интегральной ?(?)=??(?)?(?)
Свойства:
1.Функция не отрицательная величина.
2.Интегральная в бесконечных пределах, равен 1(площадь между кривой и осью абсцисс равна 1).
Распределение Стьюдента | Свойства, доказательства, упражнения
Марко Табога, доктор философии
Распределение Стьюдента — это непрерывное распределение вероятностей, которое часто встречается в статистике (например, в проверка гипотезы о среднем значении).
Он возникает, когда нормальная случайная величина делится на Хи-квадрат или Гамму. случайная переменная.
Содержание
Как возникает
- Стандартный чехол
Нестандартный корпус
Стандартное распределение Стьюдента
Определение
Отношение к Отношению к нормальной дисквиции
.
 значение
значениеОтклонение
Высшие моменты
Функция создания момента
Характеристическая функция
Функция распределения
СТУДЕНТ ТО В ОБЩЕЕ
- .
Характеристическая функция
Функция распределения
Подробнее
Конвергенция к нормальному распределению
Нецентральное распределение Т
Графики плотности
Сюжет 1- Изменение среднего
- . График 3 — Изменение степеней свободы
Решаемые упражнения
Упражнение 1
Упражнение 2
Упражнение 3
Ссылки
Как это возникает
Прежде чем вдаваться в подробности, мы даем обзор.
Стандартный кейс
Переменная имеет стандартное распределение Стьюдента с степеней свободы, если его можно записать в виде отношения
куда:
имеет стандартное нормальное распределение;
представляет собой случайную величину хи-квадрат с степени свободы;
а также независимы друг от друга.

Переменная хи-квадрат с степеней свободы, разделенных на имеет гамма-распределение (с параметрами а также ).
Как следствие, мы также можем видеть стандартное распределение Стьюдента с степени свободы как отношение
между стандартная нормальная переменная и квадратный корень гамма-переменной .
Нестандартный кейс
Переменная имеет нестандартное распределение Стьюдента , если оно может быть записывается как линейное преобразование стандартного один: где а также определяются по-прежнему.
Распределение характеризуется тремя параметрами:
Стандартное распределение Стьюдента
Начнем с частного случая стандартного распределения Стьюдента.
Сначала объяснив этот частный случай, изложение более общего случая значительно облегчается.
Определение
Стандартное распределение Стьюдента характеризуется следующим образом.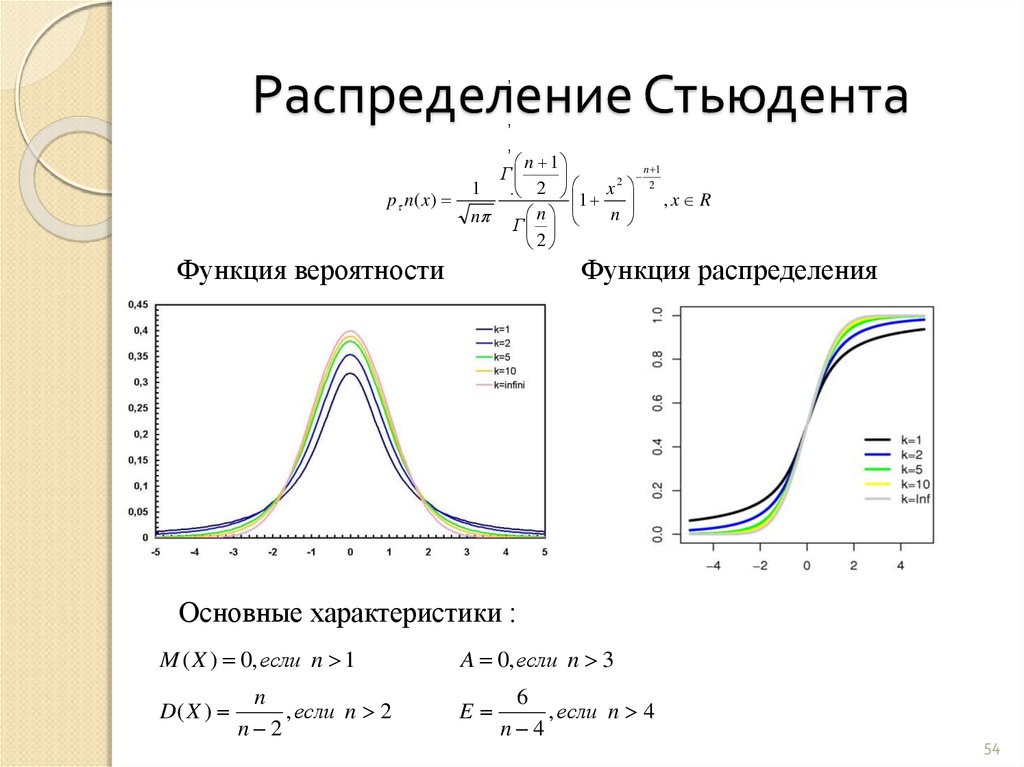
Определение Позволять быть непрерывным случайная переменная. Пусть это поддержка быть целым набор реальных числа:Пусть . Мы говорим, что имеет стандартный Распределение Стьюдента с градусов свободы тогда и только тогда, когда плотность вероятности функция это здесь это константа: и является бета-функцией.
Обычно число степеней свободы целое. (), но это также может быть реальным ().
Отношение к нормальному и гамма-распределению
Стандартную случайную величину Стьюдента t можно записать как обычную случайную переменная, дисперсия которой равна обратной величине гамма-случайной величины, как показывает следующее предложение.
Предложение Функция плотности вероятности можно написать как где:
— функция плотности вероятности нормального распределение со средним и дисперсия :
— функция плотности вероятности гамма-случайной величины с параметрами а также :где
Доказательство
Нам нужно доказать
что где и пусть
начнем с подынтегральной функции:
куда
а также
— функция плотности вероятности случайной величины, имеющей гамма
распределение с параметрами
а также
. Следовательно:
Следовательно:
Если — нормальная случайная величина с нулевым средним и дисперсией , условно , тогда мы можем думать о как отношениегде имеет стандартное нормальное распределение, имеет гамма-распределение и а также являются независимыми.
Ожидаемое значение
Ожидаемое значение стандартного t random Стьюдента переменная четко определена только для и это равно к
Доказательство
Из того, что плотность функция симметрична относительно : вышеуказанные интегралы конечны (и, следовательно, ожидаемое значение хорошо определено) только в том случае, если потому что и указанный выше предел конечен, только если .
Разница
Дисперсия стандартного t случайного числа Стьюдента переменная четко определена только для и это равно к
Доказательство
Его можно получить благодаря обычному
формула дисперсии
()
и интегральному представлению бета
Функция:От
приведенный выше вывод, должно быть ясно, что дисперсия хорошо определена
только тогда, когда
. В противном случае, если
,
приведенные выше несобственные интегралы не сходятся (и бета-функция не
четко определенные).
В противном случае, если
,
приведенные выше несобственные интегралы не сходятся (и бета-функция не
четко определенные).
Высшие моменты
-й момент стандартной случайной величины Стьюдента t четко определена только для и это равно до
Доказательство
Используя определение момента, мы получитьПоэтому, вычислить -й момент, а для проверки его существования и конечности нам нужно изучить следующий интеграл:От приведенного выше вывода, должно быть ясно, что -й момент четко определен только тогда, когда . В противном случае, если , вышеупомянутые несобственные интегралы не сходятся (интегралы включают бета функция, которая корректно определена и сходится только тогда, когда ее аргументы строго положительный — в этом случае только если ). Следовательно -й момент
Функция генерации момента
Стандартная случайная величина Стьюдента t
не обладает порождающим моментом
функция.
Доказательство
Когда случайная величина обладает производящей момент функцией, то -й момент существует и конечен для любого . Но мы доказали выше, что -й момент существует только для . Следовательно, не может иметь производящей момент функции.
Характеристическая функция
Не существует простого выражения для характеристической функции эталона Распределение Стьюдента. Его можно выразить в терминах Изменено Функция Бесселя второго рода (решение некоторого дифференциального уравнение, называемое модифицированным дифференциальным уравнением Бесселя).
Заинтересованный читатель может обратиться к Сутрадхару. (1986).
Функция распределения
Не существует простой формулы для
функция распределения
стандартной случайной величины Стьюдента t
поскольку
интегралне может
быть выражено через элементарные функции.
Поэтому обычно приходится прибегать к компьютерным алгоритмам для вычисления ценности .
Например, МАТЛАБ
команда: возвращает
значение функции распределения в точке х когда параметр степеней свободы равен n .
Распределение Стьюдента в целом
В то время как в предыдущем разделе мы ограничили наше внимание t Стьюдента распределения с нулевым средним и единичным масштабом, мы теперь имеем дело с общим случаем.
Определение
Распределение Стьюдента характеризуется следующим образом.
Определение
Позволять
быть непрерывной случайной величиной. Пусть его опорой будет вся совокупность реальных
числа:Пусть
,
а также
.
Мы говорим, что
имеет Распределение Стьюдента со средним значением
,
шкала
а также
градусов
свободы тогда и только тогда, когда его функция плотности вероятности
это здесь
это
константа: и
является бета-функцией.
Мы указываем, что имеет t-распределение со средним значением , масштабный параметр а также степени свободы к
Чтобы лучше понять распределение Стьюдента, вы можете взглянуть на его графики плотности.
Связь между стандартным и общим
Случайная величина имеет t-распределение с параметрами , а также если это линейное преобразование стандартного t Стьюдента случайная переменная.
Предложение Если , Тогда где случайная величина, имеющая стандарт т раздача.
Доказательство
С тех пор строго положительный, является строго возрастающей функцией . Поэтому мы можем использовать формулу для плотность функции непрерывного переменная:
Ожидаемое значение
Ожидаемое значение случайной величины Стьюдента t четко определена только для и это равно до
Доказательство
Является непосредственным следствием факта
что
(куда
имеет стандартное распределение t) и линейность ожидаемого
значение: как
мы видели выше,
четко определена только для
и, как следствие, также
четко определена только для
.
Разница
Дисперсия случайной величины Стьюдента t четко определена только для и это равно до
Доказательство
Его можно получить, используя формулу для дисперсия аффинных преобразований на (куда имеет стандартный т распределение): как мы видели выше, четко определена только для и, как следствие, также четко определена только для .
Функция генерации момента
Случайная величина Стьюдента t не обладает производящей момент функцией.
Доказательство
Это следствие того, что (куда имеет стандартное t-распределение) и того факта, что стандартное Случайная величина Стьюдента t не обладает производящей момент функцией (см. выше).
Характеристическая функция
Не существует простого выражения для характеристической функции Стьюдента.
t распределение (см. комментарии выше для стандартного случая).
Функция распределения
Как и в случае стандартного t-распределения (см. выше), простого формула для функции распределения случайной величины Стьюдента t .
Как следствие, обычно приходится прибегать к компьютерным алгоритмам для вычислить значения .
Большинство компьютерных программ предоставляют только подпрограммы для вычисления стандартная функция распределения t (обозначим ее через ).
В этих случаях нам нужно сделать преобразование, т.к.
следует:Для
например, МАТЛАБ
команда: возвращает
значение в точке x функции распределения
случайной величины Стьюдента t со средним значением mu , шкала сигма и n градусов
свобода.
Подробнее
В следующих разделах содержится более подробная информация о распределении t.
Сходимость к нормальному распределению
Распределение Стьюдента со средним
,
масштабный параметр
а также
степеней свободы сходится по распределению
к нормальному распределению со средним
и дисперсия
когда число степеней свободы
становится большим (сходится к бесконечности).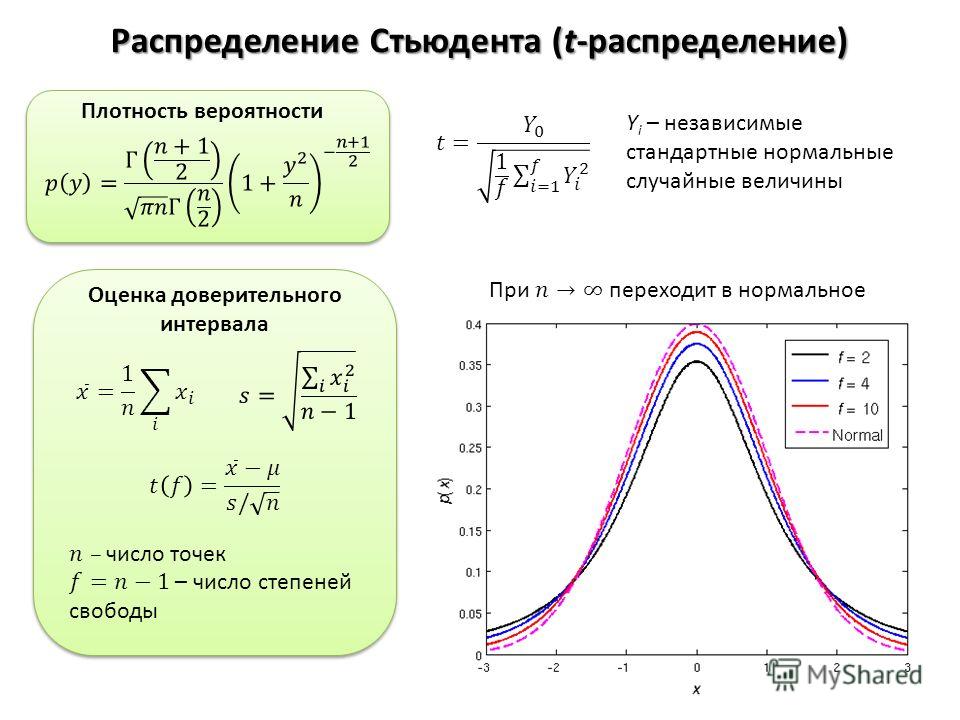
Доказательство
Как объяснялось ранее, если имеет t-распределение, его можно записать как где является стандартной нормальной случайной величиной, и представляет собой случайную величину хи-квадрат с степеней свободы, независимо от . Более того, как объяснялось в лекции о Распределение хи-квадрат, можно записать в виде суммы квадратов независимые стандартные нормальные случайные величины :Когда стремится к бесконечности, т. отношение сходится по вероятности , по закону больших чисел. Как следствие, по теорема Слуцкого, сходится по распределению к который является нормальной случайной величиной со средним значением и дисперсия .
Нецентральное распределение
Как обсуждалось выше, если
имеет стандартное нормальное распределение,
имеет гамма-распределение с параметрами
а также
а также
а также
независимы, то случайная величина
определенный
ашас
стандартное распределение Стьюдента с
степени свободы.
При тех же предположениях о а также , определить случайную величину в качестве следует: где является константой.
Переменная говорят, что у него есть нецентральный стандартный студенческий т дистрибутив с степени свободы и параметр нецентральности .
Мы не обсуждаем здесь детали этого распределения, но имейте в виду, что это распределение иногда используется в статистической теории (также в элементарной задачи) и что подпрограммы для вычисления его моментов и его распределения функцию можно найти в большинстве пакетов статистического программного обеспечения.
Графики плотности
В этом разделе показаны графики плотностей некоторых случайных величин, имеющих распределение.
Графики помогают нам понять, как форма распределения t меняется в зависимости от изменение его параметров.
График 1 — Изменение среднего
На следующем графике показаны две функции плотности вероятности Стьюдента t:
синяя линия — это PDF случайной величины Стьюдента t с параметрами , а также ;
оранжевая линия получается путем изменения параметров на , а также .

При изменении только среднего форма плотности не меняется, но плотность смещается вправо (меняется ее расположение).
График 2 — Изменение масштаба
В следующем сюжете:
синяя линия — это PDF случайной величины Стьюдента t с параметрами , а также ;
оранжевая линия получается путем изменения параметров на , а также .
Изменяя только параметр масштаба, от к , расположение графика не меняется (он остается в центре ), но форма графика меняется (плотность меньше в центре и больше плотности в хвостах).
График 3 — Изменение степеней свободы
В следующем сюжете:
синяя линия — это PDF случайной величины Стьюдента t с параметрами , а также ;
оранжевая линия получается путем изменения параметров на , а также .

Изменяя только число степеней свободы, от к , расположение графика не меняется (он остается в центре ) и его форма меняется незначительно (хвосты становятся тоньше).
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять быть нормальной случайной величиной со средним значением и дисперсия .
Позволять быть гамма-случайной величиной с параметрами а также , независим от .
Найдите распределение соотношение
Решение
Мы можем
написатьгде
имеет стандартное нормальное распределение и
имеет гамма-распределение с параметрами
а также
.
Следовательно
соотношение
стандартное распределение Стьюдента с
степени свободы и
имеет распределение Стьюдента со средним значением
,
шкала
а также
степени свободы.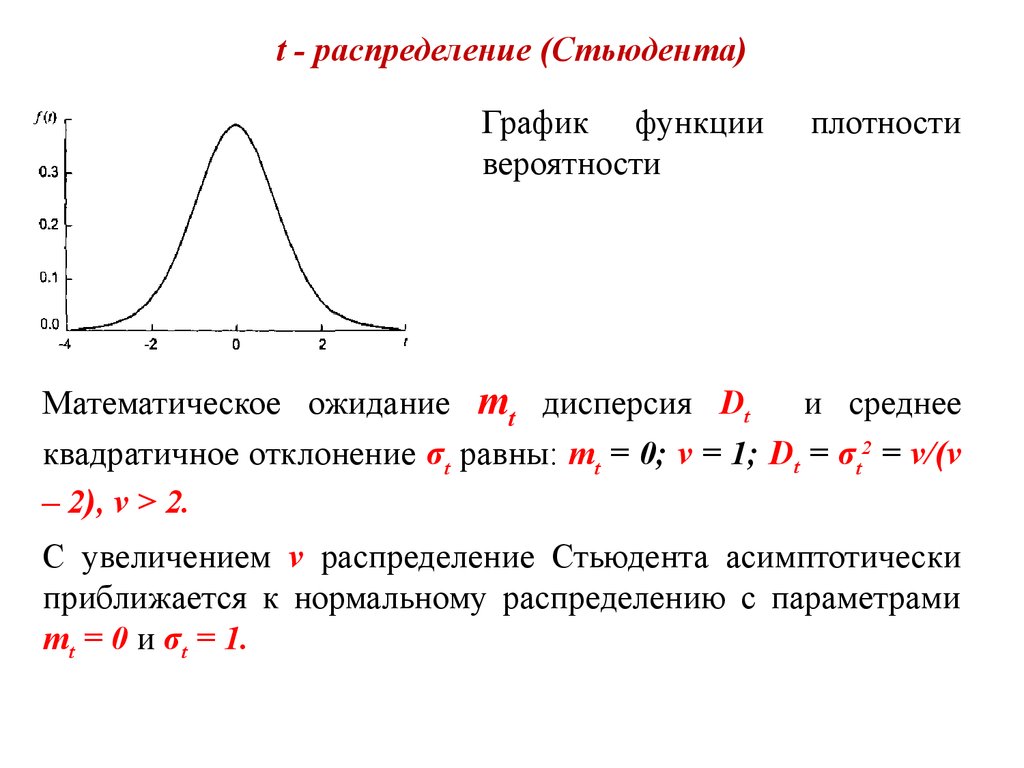
Упражнение 2
Позволять быть нормальной случайной величиной со средним значением и дисперсия .
Позволять быть гамма-случайной величиной с параметрами а также , независим от .
Найдите распределение случайного переменная
Решение
Мы можем написатьгде имеет стандартное нормальное распределение и имеет гамма-распределение с параметрами а также . Следовательно соотношение стандартное распределение Стьюдента с степени свободы.
Упражнение 3
Позволять быть случайной величиной Стьюдента со средним значением , шкала а также степени свободы.
Compute
Solution
Прежде всего, нам нужно написать вероятность с точки зрения функция распределения :Затем, выразим функцию распределения в терминах функции распределения стандартного t случайного числа Стьюдента переменная с степени свобода: так что:где различия можно вычислить с помощью компьютерного алгоритма, например, с помощью MATLAB команда
ткдф(0,6)-ткдф(-1/2,6)
Каталожные номера
Сутрадхар, Британская Колумбия (1986)
О характеристической функции
многомерного t-распределения Стьюдента, Canadian Journal of Statistics,
14, 329-337.
Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Распределение Стьюдента», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/probability-distributions/student-t-distribution.
т Распределение
|

 РАСП возвращает значение ошибки. Значение «степени_свободы» не может быть меньше 1.
РАСП возвращает значение ошибки. Значение «степени_свободы» не может быть меньше 1.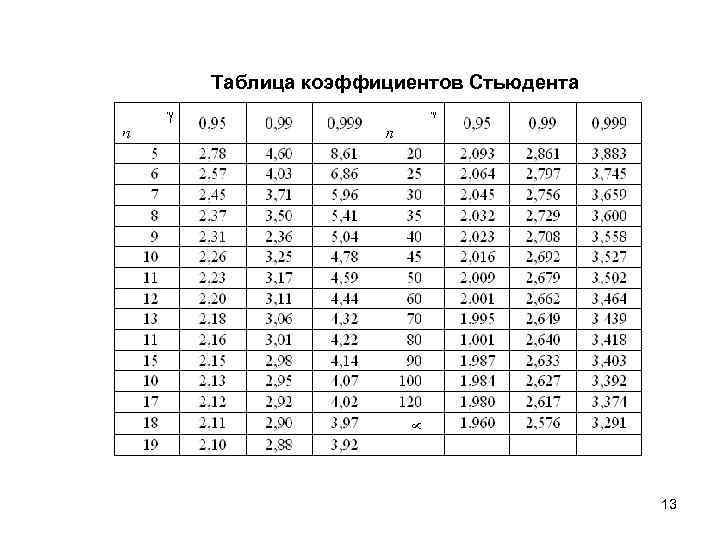
 значение
значение

 зависит от степеней свободы
зависит от степеней свободы Ты
выбрать значения N и вычислить выборочное среднее (M) и оценить
стандартная ошибка среднего (σ M )
с с М .
Какова вероятность того, что M окажется в пределах 1,96 с M от среднего значения генеральной совокупности (μ)? Это трудная проблема, потому что
есть два способа, в которых М может быть больше 1,96 s M из μ: (1) M случайно может быть либо очень высоким, либо очень
низкий и (2) s M может быть случайно
очень низкий. Интуитивно понятно, что вероятность
быть в пределах 1,96 стандартных ошибок среднего значения должно быть
меньше, чем в случае, когда известно стандартное отклонение
(и нельзя недооценивать). Но насколько меньше?
К счастью, способ решения этой проблемы был решен.
в начале 20 века У. С. Госсетом, определившим
распределение среднего деления на оценку
его стандартной ошибки.
Ты
выбрать значения N и вычислить выборочное среднее (M) и оценить
стандартная ошибка среднего (σ M )
с с М .
Какова вероятность того, что M окажется в пределах 1,96 с M от среднего значения генеральной совокупности (μ)? Это трудная проблема, потому что
есть два способа, в которых М может быть больше 1,96 s M из μ: (1) M случайно может быть либо очень высоким, либо очень
низкий и (2) s M может быть случайно
очень низкий. Интуитивно понятно, что вероятность
быть в пределах 1,96 стандартных ошибок среднего значения должно быть
меньше, чем в случае, когда известно стандартное отклонение
(и нельзя недооценивать). Но насколько меньше?
К счастью, способ решения этой проблемы был решен.
в начале 20 века У. С. Госсетом, определившим
распределение среднего деления на оценку
его стандартной ошибки.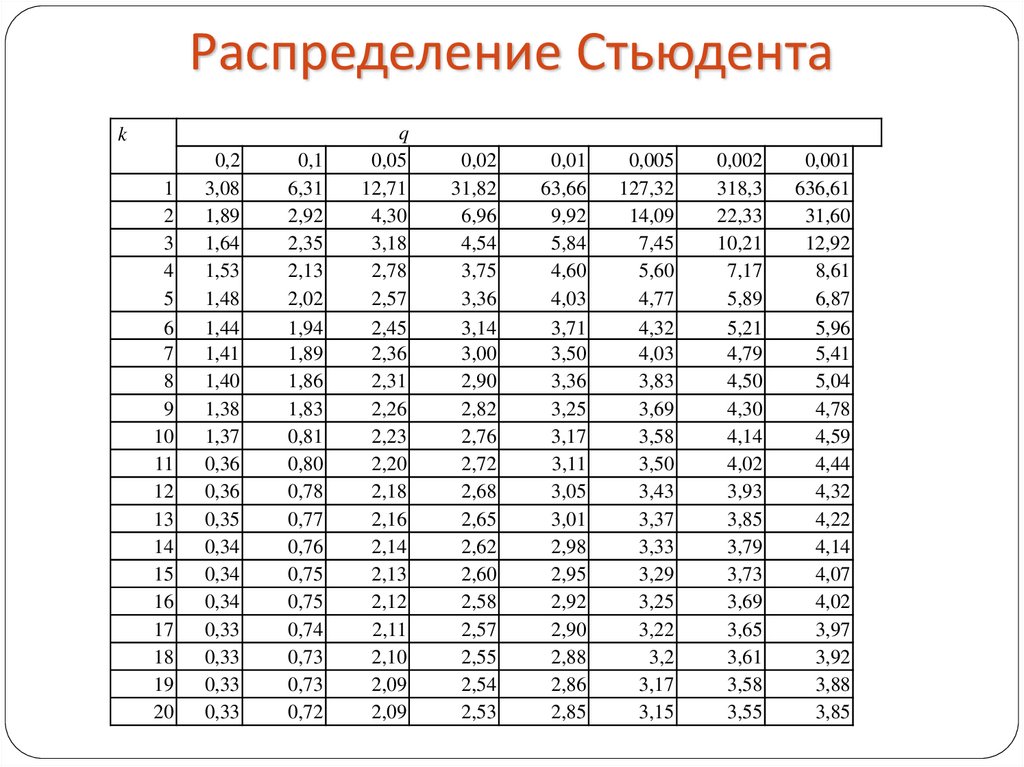 Это распределение называется Стьюдентом.
t распределение или иногда просто t
распределение. Госсет разработал t-распределение
и связанные статистические тесты во время работы на пивоварне
в Ирландии. По договору с пивоварней,
статью он опубликовал под псевдонимом «Студент». Что
вот почему t-тест называется «t-критерием Стьюдента».
Это распределение называется Стьюдентом.
t распределение или иногда просто t
распределение. Госсет разработал t-распределение
и связанные статистические тесты во время работы на пивоварне
в Ирландии. По договору с пивоварней,
статью он опубликовал под псевдонимом «Студент». Что
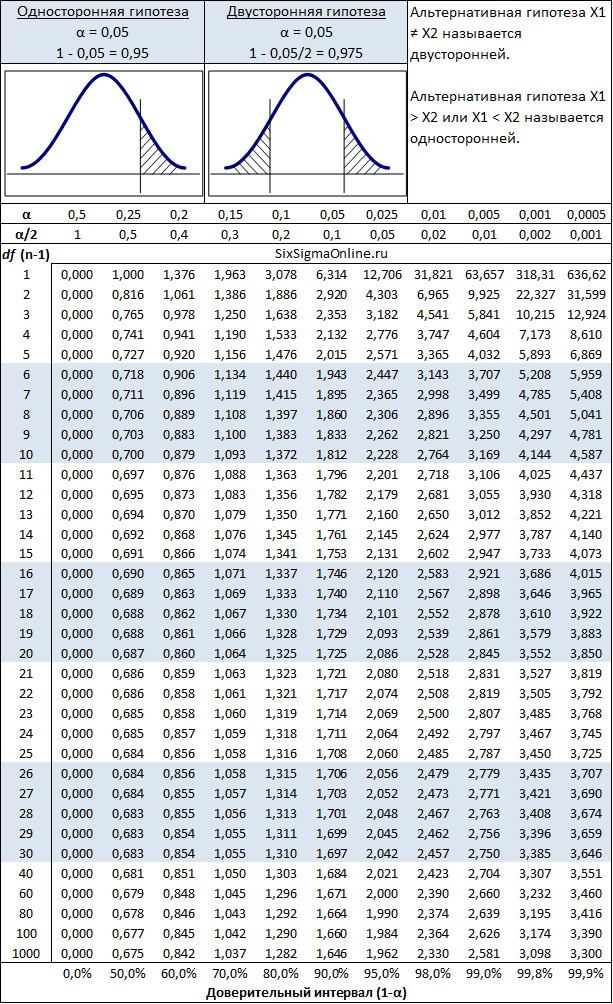
вот почему t-тест называется «t-критерием Стьюдента». Распределение t приближается к нормальному распределению по мере увеличения степеней свободы.
Распределение t приближается к нормальному распределению по мере увеличения степеней свободы.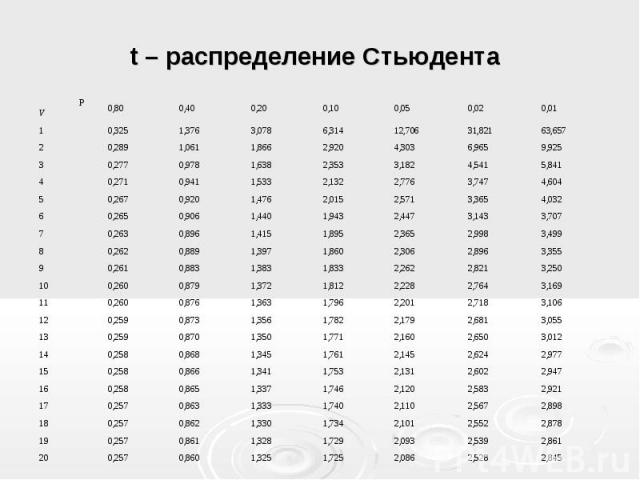 Уведомление
что при небольшом количестве степеней свободы значения t намного выше
чем соответствующие значения для нормального распределения и что
разница уменьшается по мере увеличения степеней свободы.
Значения в таблице 1 можно получить из «Найти
t для доверительного интервала».
Уведомление
что при небольшом количестве степеней свободы значения t намного выше
чем соответствующие значения для нормального распределения и что
разница уменьшается по мере увеличения степеней свободы.
Значения в таблице 1 можно получить из «Найти
t для доверительного интервала».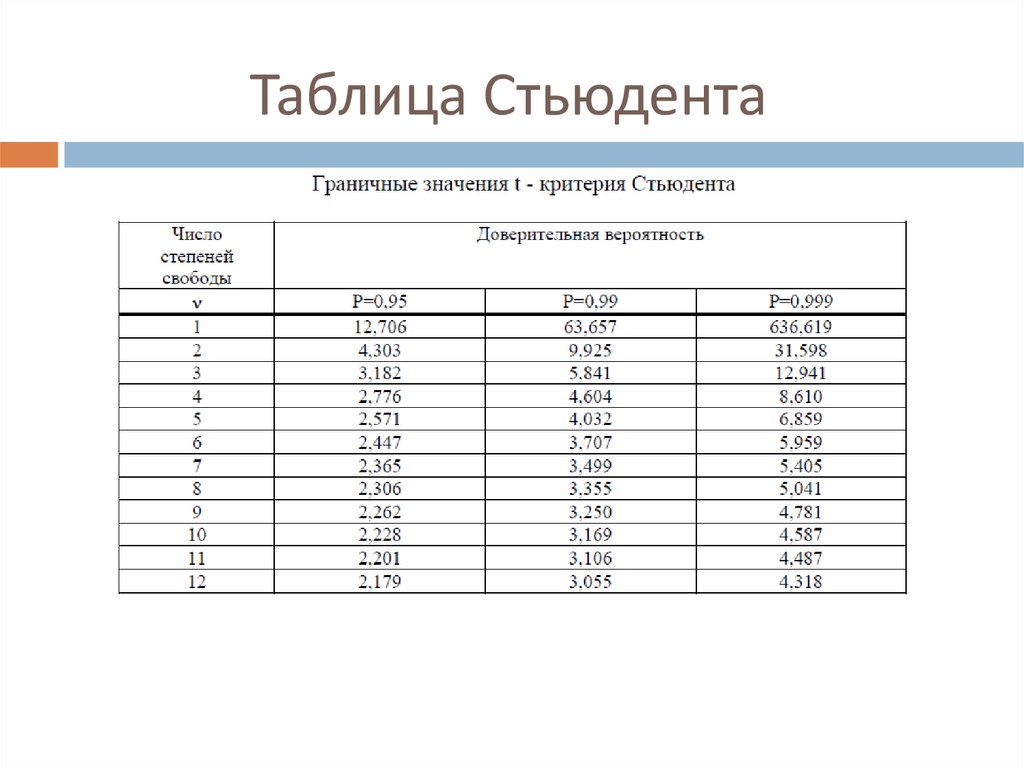 841
841 086
086 Из таблицы 1 вы
можно увидеть, что при 8 df вероятность равна 0,95 что среднее будет
находиться в пределах 2,306 с M от мк. Следовательно, вероятность того, что он будет находиться в пределах 1,96 с M от µ, ниже 0,95.
Из таблицы 1 вы
можно увидеть, что при 8 df вероятность равна 0,95 что среднее будет
находиться в пределах 2,306 с M от мк. Следовательно, вероятность того, что он будет находиться в пределах 1,96 с M от µ, ниже 0,95.