Рассчитать интеграл: Калькулятор Интегралов • По шагам!

Калькулятор Интегралов • По шагам!

Поддержка

Вам помог мой калькулятор? Расскажите своим друзьям об этом Калькуляторе и Вы тоже сможете мне помочь!

Наверху страницы введите функцию, которую Вы хотите проинтегрировать. Переменная интегрирования, пределы интегрирования и другие параметры могут быть изменены в разделе «Настройки«. Нажмите «=» чтобы запустить интегрирование/нахождение первообразной функции. Результат будет показан ниже на этой странице.

Как работает Калькулятор Интегралов

Для тех кому интересны технические подробности, в этой части рассказывается как устроен и работает Калькулятор Интегралов.

Сначала синтаксический анализатор (па́рсер) анализирует исходное математическое выражение. Он преобразует его в форму более удобную для компьютера, а именно в форму дерева (см. картинку ниже). В процессе такого преобразования, Интегральный Калькулятор должен соблюдать порядок операций с учетом их приоритета. Так же, как и то, что в математических выражениях знак умножения часто опускается, например, мы обычно пишем «5x» вместо «5*x». Калькулятор Интегралов должен уметь понимать такие случаи и сам добавлять знак умножения.

Па́рсер написан на JavaScript, и основывается на алгоритме сортировочной станции, поэтому может исполняться прямо в браузере. Это дает возможность генерировать удобочитаемое выражение на ходу, преобразуя получающееся дерево в код для LaTeX (Ла́тех). С помощью MathJax происходит генерация картинки и ее отображение в браузере.

По нажатию кнопки «=», Калькулятор Интегралов отправляет математическое выражение вместе с параметрами (переменной интегрирования и пределами интегрирования) на сервер, где оно анализируется еще раз. В этот раз выражение преобразуется в форму которая будет понятна системе компьютерной алгебры Maxima (Ма́ксима).

Ма́ксима вычисляет интеграл математической функции. Результат Ма́ксимы снова преобразуется в Ла́тех а затем показывается пользователю. Первообразная вычисляется с помощью алгоритма Ри́ша, который достаточно замысловат для понимания человеком. Именно поэтому задача показывать промежуточные шаги решения интегралов является такой сложной.

Для того чтобы всё-таки показать пошаговое решение, Калькулятор Интегралов использует такие же методы, которыми бы воспользовался человек. Алгоритм, который это осуществляет, разрабатывался в течении нескольких лет и был написан на собственном языке программирования Ма́ксимы. Программа содержит более чем 17000 строк кода. Если интегрируемое выражение совпадает по форме с уже известным, алгоритм применяет заранее определённые правила для решения интеграла (например, метод неопределённых коэффициентов для рациональных функций, тригонометрическую подстановку в интегралах с квадратным корнем из квадратичной функции или интегрирование по частям для продуктов определенных функций). Если же оно не совпадает с уже известным, тогда алгоритм пробует разные подстановки и преобразования пока интеграл не будет решен или пока не закончится отведённое для этого время или же пока не кончатся все возможные варианты. С одной стороны, у Калькулятора нет математической интуиции, которая бы очень помогла в поисках первообразной, но зато, с другой стороны, Калькулятор в состоянии перепробовать большое количество разных вариантов за очень короткое время. Такое пошаговое вычисление первообразной по правилам, зачастую, более компактно и элегантно чем вычисленное Ма́ксимой.

Еще один режим работы «Проверка  решения» должен решить сложную задачу по определению являются ли два математических выражения равными друг другу. Разница между выражениями вычисляется и упрощается с помощью Ма́ксимы настолько, насколько это возможно. К примеру, это может быть переписывание тригонометрических/гиперболических функций в их экспоненциальные формы. Если удается упростить разницу до нуля — задача выполнена. В противном случае, применяется вероятностный алгоритм, который вычисляет и сравнивает оба выражения в случайно выбранных местах. В случае с первообразной, вся процедура повторяется для каждой производной, т.к. первообразная может отличаться константой.

Интерактивные графики функций вычисляются в браузере и отрисовываются на Сanvas («Холст») из HTML5. Для каждой математической функции, которая должна быть отрисована, Калькулятор создает функцию JavaScript, которая затем вычисляется с шагом, необходимым для правильного отображения графика. Все сингулярности (например  полюса) функции обнаруживаются в процессе отрисовки и обрабатываются отдельно. Управление жестами для мобильных устройств сделано на основе hammer.js.

Если у Вас есть вопросы или пожелания, а так же идеи как улучшить Калькулятор Интегралов, пожалуйста пишите мне на e-mail.

Интегрирование тригонометрических функции

Для интегрирования рациональных функций вида R(sin x, cos x) применяют подстановку , которая называется универсальной тригонометрической подстановкой. Тогда . Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.

1. Если R(-sin(x),cosx) = -R(sin(x),cosx), то делают замену cos(x)=t и тогда sin(x)dx = -dt.
2. При R(sin(x),-cosx) = — R(sin(x),cosx), полагают sin(x)=t при этом cos(x)dx=dt
3. В случае R(-sin(x),-cosx) = R(sin(x),cosx) делают замену tg(x)=t, при которой x=arctg(t), , или замену ctg(x)=t, если это удобнее.

Интегрирование функций рационально зависящих от тригонометрических функций

1. Интегралы вида ∫sinn xdx, ∫cosnxdx, n>0
a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2sin2x=1-cos2x, 2cos2x=1+cos2x.
2. Интегралы вида ∫tgnxdx, ∫ctgnxdx, где n – целое.
Необходимо использовать формулы

3. Интегралы вида ∫sinⁿx·cos^mx dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x, если n — нечётное либо t=cos x, если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin2x=1-cos2x, 2cos2x=1+cos2x.
4. Интегралы вида
Если числа m и n одинаковой чётности, то используем подстановку t=tg x. Часто бывает удобным применить приём тригонометрической единицы.
5. ∫sin(nx)·cos(mx)dx, ∫cos(mx)·cos(nx)dx, ∫sin(mx)·sin(nx)dx

Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:

• sin α·cos β = ½(sin(α+β)+sin(α-β))
• cos α·cos β = ½(cos(α+β)+cos(α-β))
• sin α·sin β = ½(cos(α-β)-cos(α+β))

• Решение онлайн
• Видеоинструкция

С помощью данного онлайн-калькулятора можно вычислять интегралы по частям.

Решение сохраняется в формате Word.

Также рекомендуется ознакомиться с возможностью нахождения интегралов онлайн.

Примеры
1. Вычислить интеграл ∫cos4x·sin3xdx.
Делаем замену cos(x)=t. Тогда ∫cos⁴x·sin³xdx =
2. Вычислить интеграл .
Делая замену sin x=t, получаем

3. Найти интеграл .
Делаем замену tg(x)=t. Подставляя, получаем

Заметим, что замена ctg(x)=t здесь удобнее, так как тогда , и поэтому

Интегрирование выражений вида R(sinx, cosx)

Пример №1. Вычислить интегралы:

Решение.
а) Интегрирование выражений вида R(sinx, cosx), где R — рациональная функция от

sin x и cos x, преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t.
Тогда имеем

Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида ∫R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:

• Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx, то применяется подстановка cos x = t.
• Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx, то подстановка sin x = t.
• Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx, то подстановка tgx = t или ctg x = t.

В данном случае для нахождения интеграла
применим универсальную тригонометрическую подстановку tg(x/2) = t.
Тогда

=

или
Так как дробь правильная, то, представляем в виде суммы интегралов:


Возвращась к исходной переменной будем иметь

b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫R(sinx, cosx) dx имеет вид ∫sinmx·cosnxdx. В этом частном случае, если m нечетно, следует применить подстановку cos x = t. Если нечетно n, следует применить подстановку sin x = t. Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:

В данном случае

Интегральный калькулятор

• С шагами!

Поддержка

Пожертвование

Помог ли вам этот калькулятор? Тогда я был бы очень признателен за вашу поддержку. Вы можете сделать пожертвование через PayPal.

Выше введите функцию для интеграции. Переменная интегрирования , границы интегрирования и более могут быть изменены в « Options «. Щелкните « Go! «, чтобы начать вычисление интеграла/первообразной. Результат будет показан далее.

Как работает интегральный калькулятор

Для тех, кто имеет техническое образование, в следующем разделе объясняется, как работает интегральный калькулятор.

Сначала синтаксический анализатор анализирует математическую функцию. Он преобразует его в форму, более понятную компьютеру, а именно в дерево (см. рисунок ниже). При этом интегральный калькулятор должен соблюдать порядок операций. Особенностью математических выражений является то, что знак умножения иногда можно опустить, например, мы пишем «5x» вместо «5*x». Интегральный калькулятор должен обнаруживать эти случаи и вставлять знак умножения.

Парсер реализован на JavaScript, основан на алгоритме Shunting-yard и может работать прямо в браузере. Это позволяет быстро получать обратную связь при наборе текста путем преобразования дерева в код LaTeX. MathJax позаботится об отображении его в браузере.

Когда «Вперед!» После нажатия кнопки Калькулятор интегралов отправляет математическую функцию и настройки (переменную интегрирования и границы интегрирования) на сервер, где она снова анализируется. На этот раз функция преобразуется в форму, понятную системе компьютерной алгебры Maxima.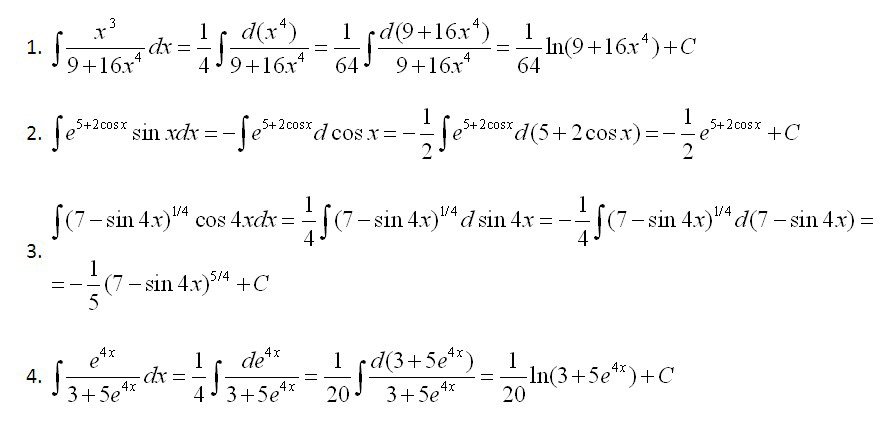

Maxima фактически вычисляет интеграл математической функции. Вывод Maxima снова преобразуется в LaTeX и затем предоставляется пользователю. Первообразная вычисляется с использованием алгоритма Риша, который трудно понять людям. Вот почему показать этапы вычисления интегралов очень сложно.

Чтобы показать шаги, калькулятор применяет те же методы интеграции, что и человек. Программа, которая это делает, разрабатывалась в течение нескольких лет и написана на собственном языке программирования Maxima. Он состоит из более чем 17000 строк кода. Когда подынтегральное выражение соответствует известной форме, оно применяет фиксированные правила для решения интеграла (например, разложение на частичные дроби для рациональных функций, тригонометрическая замена подынтегральных выражений, включающих квадратные корни квадратного многочлена, или интегрирование по частям для произведений определенных функций). . В противном случае он пробует различные подстановки и преобразования до тех пор, пока либо интеграл не будет решен, либо не истечет время, либо не останется ничего, что можно было бы попробовать.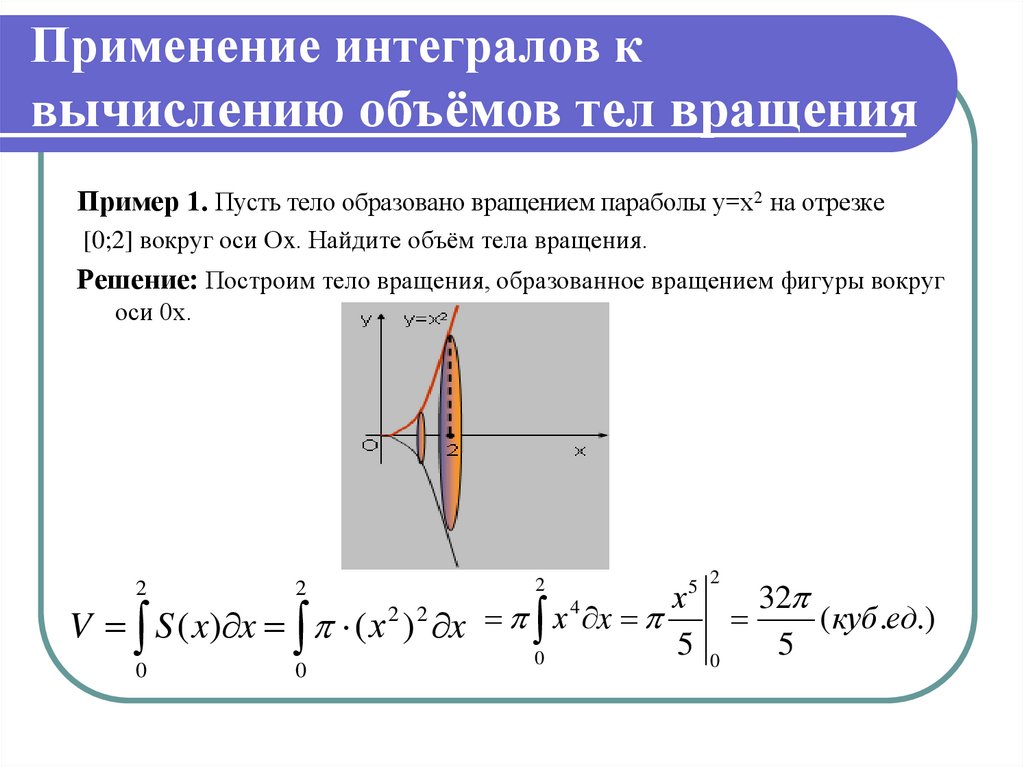 Калькулятору не хватает математической интуиции, которая очень полезна для нахождения первообразной, но, с другой стороны, он может перепробовать большое количество возможностей за короткое время. Пошаговые первообразные часто намного короче и элегантнее, чем найденные Максимой.

Функция «Проверить ответ» должна решить сложную задачу определения эквивалентности двух математических выражений. Их разница рассчитывается и максимально упрощается с помощью Maxima. Например, это включает в себя запись тригонометрических/гиперболических функций в их экспоненциальной форме. Если можно показать, что разность упрощается до нуля, то задача решена. В противном случае применяется вероятностный алгоритм, который оценивает и сравнивает обе функции в случайно выбранных местах. В случае первообразных вся процедура повторяется для каждой производной функции, поскольку первообразные могут отличаться на константу.

Графики интерактивных функций рассчитываются в браузере и отображаются в элементе холста (HTML5). Для каждой отображаемой функции калькулятор создает функцию JavaScript, которая затем вычисляется небольшими шагами, чтобы построить график. При построении графика особенности (например, полюса) обнаруживаются и обрабатываются особым образом. Управление жестами реализовано с помощью Hammer.js.

Если у вас есть какие-либо вопросы или идеи по улучшению интегрального калькулятора, не стесняйтесь писать мне по электронной почте.

Интегральный калькулятор: интеграция с Wolfram|Alpha

Ого! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

WolframAlpha

Решение интегралов с помощью Wolfram|Alpha

x sin

x2

dx

Математический ввод

Расчет и суммирование

• 3
• . тройные интегралы и несобственные интегралы. Калькулятор интегралов Wolfram|Alpha также показывает графики, альтернативные формы и другую важную информацию для улучшения вашей математической интуиции. 92 sin y dx dy, x=0 to 1, y=0 to pi

• Посмотреть другие примеры »

Доступ к средствам мгновенного обучения

Получите немедленную обратную связь и рекомендации с пошаговыми решениями для интегралов и Wolfram Генератор задач

Узнайте больше о:

• Пошаговые решения »
• Генератор задач Wolfram »

Что такое интегралы?

Интегрирование — важный инструмент в исчислении, который может дать первообразную или представить площадь под кривой.

Неопределенный интеграл от , обозначенный , определяется как первообразная от . Другими словами, производная от . Поскольку производная константы равна 0, неопределенные интегралы определяются только с точностью до произвольной константы. Например, поскольку производная от . Определенный интеграл от до , обозначаемый , определяется как площадь со знаком между и осью, от до .

Оба типа интегралов связаны между собой основной теоремой исчисления. Это утверждает, что если непрерывно на и является его непрерывным неопределенным интегралом, то . Это означает . Иногда требуется приближение к определенному интегралу. Обычный способ сделать это — поместить тонкие прямоугольники под кривую и сложить подписанные области вместе. Wolfram|Alpha может решать широкий спектр интегралов

Как Wolfram|Alpha вычисляет интегралы

Wolfram|Alpha вычисляет интегралы иначе, чем люди. Он вызывает функцию Integrate из Mathematica, которая представляет собой огромное количество математических и вычислительных исследований. Integrate не вычисляет интегралы так, как это делают люди. Вместо этого он использует мощные общие алгоритмы, которые часто включают очень сложную математику. Есть несколько подходов, которые он чаще всего использует. Один включает в себя разработку общей формы для интеграла, затем дифференцирование этой формы и решение уравнений для соответствия неопределенным символическим параметрам.