Рассчитывать параметры парной линейной регрессии можно если у нас есть: тест по экнометрики

тест по экнометрики

Тест

Парная регрессия и корреляция

1. Эконометрика — это:

а) наука, которая дает количественное выражение взаимосвязей в экономике;

б) учение о системе показателей, дающих представление об экономике;

в) различного рода цифровые данные.

2. Предметом эконометрики является:

а) сбор цифровых данных;

б) определение наблюдаемых в экономике количественных закономерностей;

в) изучение экономических законов.

3. Идентификация модели — это:

а) статистическое оценивание неизвестных параметров модели;

б) сбор необходимой статистической информации;

в) статистическая оценка параметров и модели в целом;

г) проверка точности модельных данных.

4. Выбор формы связи между переменными называется:

а) идентификацией;

б) идентифицируемостью;

в) верификацией;

г) спецификацией.

5. Нулевой называется гипотеза:

а) которая отклоняется;

б) подвергающаяся проверке;

в) которая содержит одно конкретное предположение.

6. Альтернативной называется гипотеза:

а) необходимая для проверки нулевой гипотезы;

б) которая отклоняется;

в) которая содержит несколько конкретных предположений.

7. Уровнем значимости называется:

а) совокупность значений критерия проверки, при которых нулевую гипотезу не отклоняют;

б) совокупность значений критерия проверки, при которых нулевую гипотезу отклоняют;

в) вероятность отвергнуть правильную нулевую гипотезу.

8. Наиболее наглядным видом выбора уравнения парной регрессии является:

а) аналитический;

б) графический;

в) экспериментальный (табличный).

9. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

а) не менее 5 наблюдений;

б) не менее 7 наблюдений;

в) не менее 10 наблюдений.

10. По выборке данных можно построить так называемое:

а) теоретическое уравнение регрессии;

б) эмпирическое уравнение регрессии;

в) любое уравнение регрессии.

11. Коэффициент линейного парного уравнения регрессии:

а) показывает среднее изменение результата с изменением фактора на одну единицу;

б) оценивает статистическую значимость уравнения регрессии;

в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

12. Суть коэффициента детерминации состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака у,

объясняемую регрессией, в общей дисперсии результативного признака;

в) характеризует долю дисперсии у, вызванную влиянием не учтенных в модели факторов.

13. На основании наблюдений за 50 семьями построено уравнение регрессии

ŷ = 284,56 + 0,672х, где у – потребление, х  доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

а) да;

б) нет;

в) ничего определенного сказать нельзя.

14. Суть метода наименьших квадратов состоит в:

а) минимизации суммы остаточных величин;

б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

15. Качество модели из относительных отклонений по каждому наблюдению оценивает:

а) коэффициент детерминации R;

б) F-критерий Фишера;

в) средняя ошибка аппроксимации .

16. Значимость уравнения регрессии в целом оценивает:

а) F-критерий Фишера;

б) t -критерий Стьюдента;

в) коэффициент детерминации R.

17. Классический метод к оцениванию параметров регрессии основан на:

а) методе наименьших квадратов;

б) методе максимального правдоподобия;

в) шаговом регрессионном анализе.

18. Остаточная сумма квадратов равна нулю:

а) когда правильно подобрана регрессионная модель;

б) когда между признаками существует точная функциональная связь;

в) никогда.

19. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) n — 1;

б) 1;

в) n —2.

20. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) n — 1;

б) 1;

в) n — 2.

21. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) n — 1;

б) 1;

в) n — 2.

22. Для оценки значимости коэффициентов регрессии рассчитывают:

a) F -критерий Фишера;

б) t -критерий Стьюдента;

в) коэффициент детерминации R.

23.

Какое уравнение регрессии нельзя свести к линейному виду:

а) = a + b ;

б) = a;

в) = a + b.

24. Какое из уравнений является степенным:

а) = a + b ;

б) = a;

в) = a + b.

25. Параметр b в степенной модели является:

а) коэффициентом детерминации;

б) коэффициентом эластичности;

в) коэффициентом корреляции.

26. Коэффициенткорреляции может принимать значения:

а) от -1 до 1;

б) от 0 до 1;

в) любые.

27. Для функции у = a + +

средний коэффициент эластичности имеет вид:

а) = ;

б) =  ;

в) =  .

28. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) y = a + b + ;

б) y = a + b + ;

в) y = a+ .

29. Если фактор не оказывает влияния на результат, то линия регрессии на графике:

а) параллельна оси Оу;

б) параллельна оси Ох;

в) является биссектрисой первой четверти декартовой системы координат.

30. Экспериментальный метод подбора вида уравнения регрессии основан на:

а) изучении поля корреляции;

б) сравнении величины остаточной дисперсии при разных моделях;

в) изучении природы связи признаков.

Тестовые задания для самопроверки (58)

1. Наиболее наглядным видом выбора уравнения парной регрессии является:

а) аналитический;

б) графический;

в) экспериментальный (табличный).

2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

а) не менее 5 наблюдений;

б) не менее 7 наблюдений;

в) не менее 10 наблюдений.

3. Суть метода наименьших квадратов состоит в:

а) минимизации суммы остаточных величин;

б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

4. Коэффициент линейного парного уравнения регрессии:

а) показывает среднее изменение результата с изменением фактора на одну единицу;

б) оценивает статистическую значимость уравнения регрессии;

в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

5. На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

а) да;

б) нет;

в) ничего определенного сказать нельзя.

6. Суть коэффициента детерминации состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;

в) характеризует долю дисперсии , вызванную влиянием не учтенных в модели факторов.

7. Качество модели из относительных отклонений по каждому наблюдению оценивает:

а) коэффициент детерминации ;

б) -критерий Фишера;

в) средняя ошибка аппроксимации .

8. Значимость уравнения регрессии в целом оценивает:

а) -критерий Фишера;

б) -критерий Стьюдента;

в) коэффициент детерминации .

9. Классический метод к оцениванию параметров регрессии основан на:

а) методе наименьших квадратов:

б) методе максимального правдоподобия:

в) шаговом регрессионном анализе.

10. Остаточная сумма квадратов равна нулю:

а) когда правильно подобрана регрессионная модель;

б) когда между признаками существует точная функциональная связь;

в) никогда.

11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;

б) ;

в) .

12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;

б) ;

в) .

13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;

б) ;

в) .

14. Для оценки значимости коэффициентов регрессии рассчитывают:

а) -критерий Фишера;

б) -критерий Стьюдента;

в) коэффициент детерминации .

15. Какое уравнение регрессии нельзя свести к линейному виду:

а) ;

б) :

в) .

16. Какое из уравнений является степенным:

а) ;

б) :

в) .

17. Параметр в степенной модели является:

а) коэффициентом детерминации;

б) коэффициентом эластичности;

в) коэффициентом корреляции.

18. Коэффициент корреляции может принимать значения:

а) от –1 до 1;

б) от 0 до 1;

в) любые.

19. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) ;

б) ;

в) .

Вопрос	1	2	3	4	5	6	7	8	9	10
Ответ	б	б	в	а	а	б	в	а	а	б
Вопрос	11	12	13	14	15	16	17	18	19
Ответ	б	в	а	б	в	б	б	а	в

Линейная регрессия

Линейная регрессия Вернуться к оглавлению

Обзор урока

• Линейная регрессия
• Метод наименьших квадратов
• Прогнозирование стандартных показателей
• Ошибки предсказания
• Домашнее задание

Последний урок мы ввели корреляцию и корреляцию коэффициенты Пирсона и Спирмена. В этом уроке мы придумаем уравнения линейной регрессии.

Линейная регрессия

Регрессия делает еще один шаг за пределы корреляции в определении связь между двумя переменными. Это создает уравнение так что значения могут быть предсказаны в пределах диапазона данных. Это известно как интерполяция . Выход за рамки наблюдений чреват опасностью и известен как экстраполяция . Тем не менее, делая это для определения федерального дефицита или необходимые уровни пенсионного финансирования, тем не менее, являются важными приложениями.

Поскольку речь идет о линейном корреляции и прогнозируемые значения должны быть как можно ближе к данные, уравнение называется наиболее подходящей линией или линия регрессии . Линия регрессии была названа в честь работы Гальтон сделал в генных характеристиках, которые вернулись (регрессировали) обратно к среднему значению. То есть у высоких родителей дети были ближе к средним.

Уклон является важным понятием, поэтому мы будем ознакомьтесь с некоторыми важными фактами здесь.

уклон = м = подъем/спуск = dy / dx = г / х =

Параллельные линии имеют одинаковый наклон.

Таким образом, если y = m x + b , то м — это уклон и b — это точка пересечения y (т. е. значение y , когда x = 0). Часто линейные уравнения записываются на стандартная форма с целыми коэффициентами (А х + В у = С). Такие отношения должны быть преобразованы в Форма пересечения наклона ( y = m x + b ) для удобного использования на графический калькулятор. Еще одна форма уравнения для линии называется формой точка-наклон . и выглядит следующим образом: г — г ₁ = м ( х — x ₁ ). Уклон м , как определено выше, x и y — наши переменные, а ( x ₁ , y ₁ ) — точка на прямой.

Специальные склоны

Важно понимать разницу между положительный , отрицательный , ноль и неопределенный наклон . Подводя итог, если наклон положительный, y увеличивается по мере увеличения x , и функция работает «в гору» (слева направо). Если наклон отрицательный, y уменьшается как x увеличивается, а функция работает по наклонной. Если наклон равен нулю, y не меняется, при этом постоянна — горизонтальная линия. Вертикальные линии проблематичны в том, что нет никаких изменений в x . Таким образом, наша формула не определена из-за деления по нулю. Некоторые назовут это состояние бесконечный наклон , но имейте в виду, что мы не можем сказать если это положительная или отрицательная бесконечность! Следовательно, довольно запутанный термин без уклона также широко используется для этой ситуации.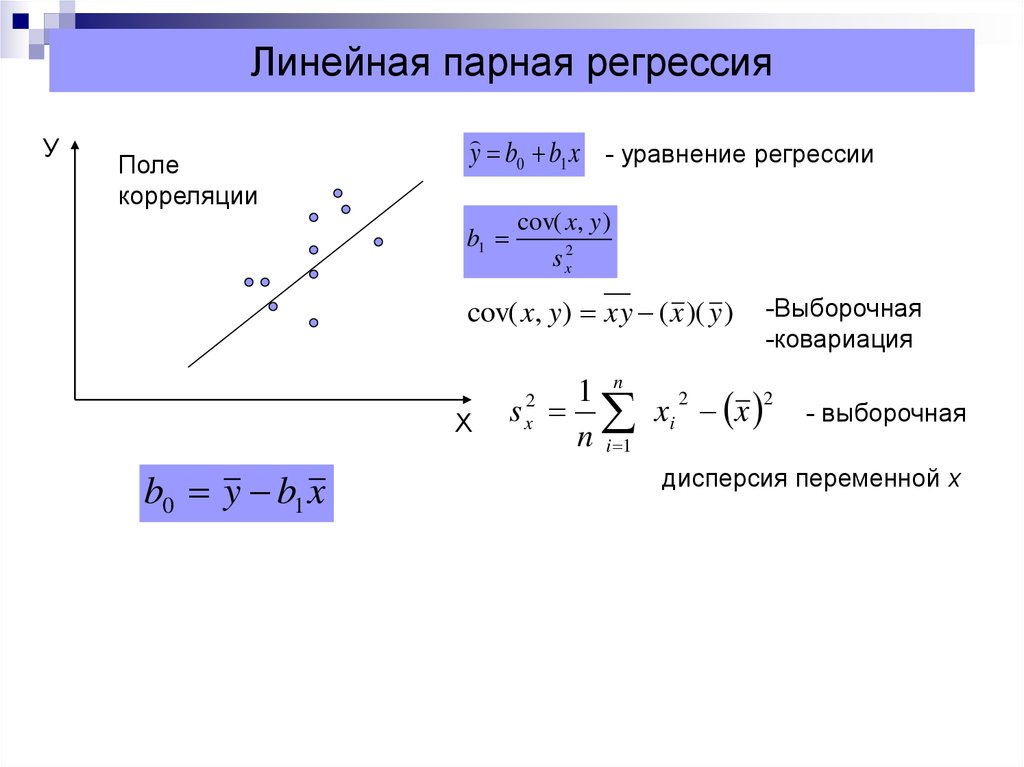

Уравнение прямой может быть выражено как у = м х + б или y = ax + b или даже y = a + bx . Как видим, линия регрессии имеет аналогичное уравнение. Существует множество причин для выбора одной формы уравнения над другой, и некоторые дисциплины имеют тенденцию выбирать одну для исключение другого. БЫТЬ ГИБКИМ как по порядку членов в уравнении, так и по символам используется для коэффициентов! С междисциплинарным характером многих исследований в наши дни, конфликт между различные обозначения должны быть сведены к минимуму.

у = Р 0 + Р 1 х где y , ß 0 и ß 1 представляет статистику населения. Если над переменной появляется колпачок, тогда они, вероятно, представляют выборочную статистику. Помните, что x наша независимая переменная как для строки, так и для данных.

y -пересечение линии регрессии равно ß ₀ и наклон ß ₁ . Следующие формулы дают y -перехват и наклон уравнения.

ß 0 = ( г )( х 2 ) — ( x )( xy )           n ( x 2 ) — (x) 2 6 ​​3 ß 1 = n ( xy ) — ( x ) ( Y ) N ( x 2 ) — ( x ) 2

) ²

) Обратите внимание, что знаменатели одинаковы, так что экономит расчеты. Также в калькуляторе будут значения для определенных порций. Другой способ записать уравнение — в форме точка-наклон. где центроид — это точка, которая всегда находится на прямой. Центроид представляет собой следующую упорядоченную пару: (среднее значение x , среднее значение y ).

Чтобы y -пересечение и наклон были точными, все промежуточные шаги должны быть удвоены столько значащих цифр (от шести до десяти?), сколько вы хотите в своем окончательном ответе (от трех до пяти?)!

Существуют определенные рекомендации для линий регрессии:

1. Используйте линии регрессии при наличии значительной корреляции для прогнозирования значений.
2. Не использовать, если нет значительной корреляции.
3. Оставайтесь в пределах диапазона данных. Не экстраполируйте!! Например, если данные от 10 до 60, не прогнозируйте значение для 400.
4. Не делать прогнозов для совокупности на основе линии регрессии другой совокупности.

Переменная y часто называется переменной критерия . и переменная x — переменная-предиктор . Наклон часто называют коэффициентом регрессии и перехват константы регрессии . Наклон также может быть компактно выражен как ß ₁ = r × с _у / с _x .

Обычно мы затем прогнозируем значения для y на основе значений x . Это еще не означает, что х вызвано х . Исследователю по-прежнему необходимо понять изучаемые переменные и контекст, в котором они работают прежде чем делать такую ​​интерпретацию. Конечно, простая алгебра также позволяет вычислить х значения для заданного значения y .

Пример: Напишите линию регрессии для следующих точек:

x	y
1	4
3	2
4	1
5	0
8	0

Решение 1: х = 21; у = 7; х ² = 115; у ² = 21; ху = 14
Таким образом, ß ₀ = [7·115 — 21·14] ÷ [5 · 115 — 21 ² ] = 511 ÷ 134 = 3,81 и ß ₁ = [5·14 — 21·7] ÷ [5 · 115 — 21 ² ] = -77 ÷ 134 = -0,575. Таким образом, линия регрессии для этого примера равна y = -0,575 x + 3,81.

Решение 2: На графическом калькуляторе TI-83+ введите данные в L ₁ и L ₂ и выполните LinReg(ax+b) L1, L2 ( STAT , CALC , 4) или LinReg(a+bx) L1, L2 ( STAT , CALC , 8). У вас должен получиться экран с
y = ax + b
a = -.5746…
b =3.8134…
7 r 0202 2 =.790…
r =.88888…
Если информация r отсутствует, выполните КАТАЛОГ ( 2nd 0 ) ДиагностикаВкл . ENTRY ( 2nd ENTER ) вернет команду на главный экран где другой ENTER выполнит его. Таким образом, мы видим, что около 79% вариаций и объясняется изменением x .

Между двумя линейными регрессиями нет математической разницы. формы LinReg(ax+b) и LinReg(a+bx) , только разные профессиональные группы предпочитают разные обозначения.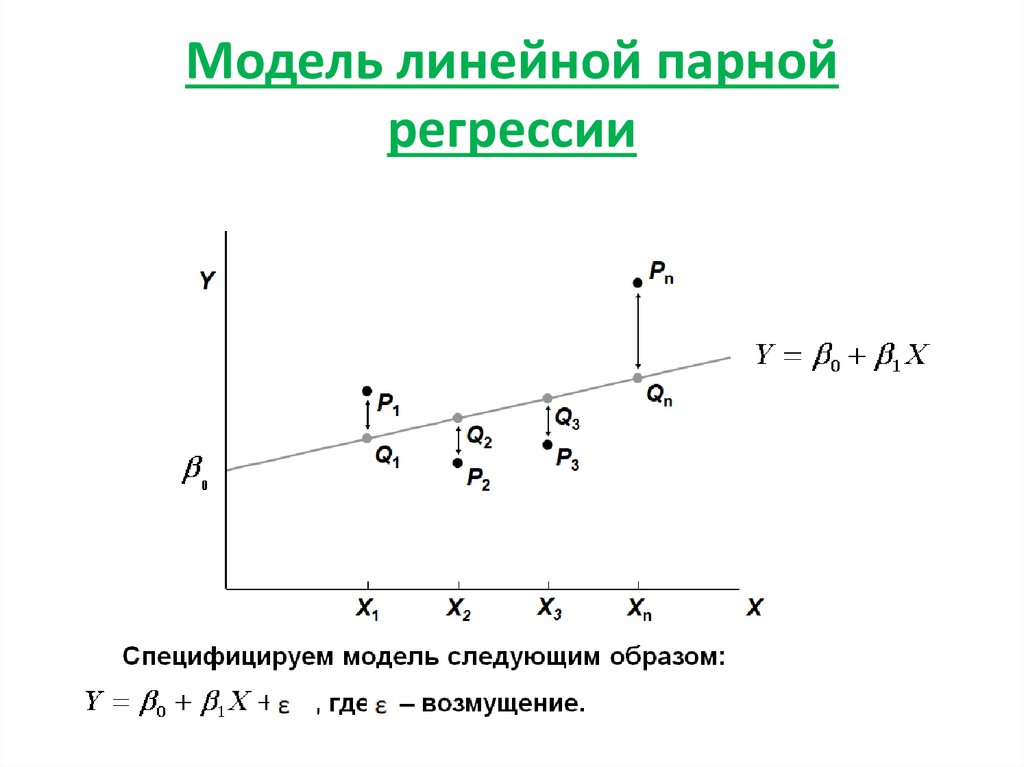 «Предпочитаемый», возможно, здесь слишком слабое слово. Производитель калькулятора включил обе формы, поскольку ни одна из них группа была готова пойти на компромисс и использовать другую.

Обратите внимание на наличие на вашем графическом калькуляторе TI-83+ нескольких других регрессионные функции также. Конкретно, квадратичный ( у = ах ² + бх + с ), кубический ( у = ах ³ + бх ² + сх + д ), квартика ( y = ax ⁴ + bx ³ + cx ² + dx + ), 7 экспоненциальный ( y = ab ^x ) и мощность или вариация ( y = x ^b ). Таким образом, простой способ найти квадратное число через три точки состоит в том, чтобы введите данные в пару списков, затем выполните квадратичную регрессию на списки.

Метод наименьших квадратов

Метод наименьших квадратов был впервые опубликован в 1806 году Лежандром. Однако Гаусс «сообщил обо всем Ольберсу в 1802 году».

Что такое свойство наименьших квадратов?
Сформируйте расстояние y — y ‘ между каждой точкой данных ( x , y ) и потенциальная линия регрессии y ‘ = m x + b . Каждое из этих различий известно как остаток . Возведите в квадрат эти остатки и просуммируйте их. Полученная сумма называется остаточной суммой квадратов или SS _res . Линия, которая лучше всего соответствует данным, имеет наименьшее возможное значение SS _res .

Этот ссылка на сайт имеет хороший красочный пример этих остатков, остаточных квадратов и остаточная сумма квадратов.

Пример: Найдите линию линейной регрессии через (3,1), (5,6), (7,8) методом грубой силы.
Решение:

x	Y	Y ‘	Y –‘	Y — Y ‘	Y — Y ‘	Y — Y 24	Y — ‘	Y — .
3	1	3 м + б	1 — 3 м — б
5	6	5 м + б	6 — 5 м — б
7	8	7 м + б	8 — 7 м — б

Используя тот факт, что ( A + B + C ) ² = А ² + В ² + С ² + 2 АВ + 2 АС + 2 ВС , мы можем быстро найти SS _res = 101 + 83 м ² + 3 б ² — 178 м — 30 б + 30 мб . Это выражение квадратично как по m , так и по b . Мы можем переписать его в обоих направлениях, а затем найти вершину для каждого из них. (что является минимумом, так как мы суммируем квадраты). Запомните вершину y = ax ² + bx + c is- b /2 a .

СС _рез = 3 б ² + (30 м — 30) б + (101 + 83 м ² — 178 м ).
СС _рез = 83 м ² + (30 б — 178) м + (101 + 3 б ² — 30 б 9003).
Из первого выражения находим b = (-30 m + 30)/6. Из второго выражения находим м = (-30 b + 178)/166. Эти выражения дают нам два уравнения с двумя неизвестными:
5 м + б = 5 и
83 м + 15 б = 89.
Их можно решить, чтобы получить м = 7/4 = 1,75 и b = -15/4 = -3,75. Вот как приведенные выше уравнения для ß ₀ и ß ₁ были получены из общего решения к двум общим уравнениям для SS _res .

Этот ссылка на сайт вызывает апплет Java, который позволяет добавить точку на график и посмотрите, какое влияние это оказывает на линию регрессии.

Этот ссылка на сайт вызывает апплет Java, который побуждает вас угадывать регрессию линия и коэффициент корреляции для набора данных.

Прогнозирование стандартных показателей

С помощью некоторой стандартной алгебры можно показать (Хинкл, стр. 129), что существует прямое (что означает, что перехват равен нулю) отношения между стандартными и баллами и стандартными x баллами, с коэффициентом корреляции наклон: z _y = r × z _x .

Ошибки прогнозирования

Хотя мы минимизируем сумму квадратов расстояний фактических х баллов из предсказанных х баллов ( х ‘), есть распределение этих расстояний или ошибок в предсказании что важно обсудить. Определим эти направленные (знаковые) расстояния (остатки) как е = ( у — и ‘), где y ‘ — наше прогнозируемое значение. Ясно, что как положительные, так и отрицательные значения встречаются со средним значением, равным нулю. Дисперсия может быть вычислена как

с 2 ух = е 2 /( н — 2).

Квадратный корень из этого значения является стандартным отклонением и известна как стандартная ошибка оценки . Альтернативная формула, полезная для больших выборок:

с yYx = s y sqrt(1- r 2 ) sqrt(( n — 1)/( n — 2)).

Когда выборки действительно велики, фактор, включающий отношения целых чисел чуть меньше n стремится к 1 и может быть опущено. Поскольку исключение фактора приведет к недооценке стандартной ошибки, его следует включать для небольших выборок. Большой против small несколько произвольно, с n = 30 произвольное полезное отсечение, выше которого нормальность гарантируется. В этом случае погрешность меньше 2%, когда n > 26 и менее 1%, когда n > 51. Однако оно составляет 10% или больше, когда n < 8!

Стандартная ошибка мала, когда корреляция высока. Это повышает точность предсказания.

Когда мы рассматриваем несколько дистрибутивов, часто предполагается, что их стандартные отклонения равны. Это свойство называется гомоскедастичность . Мы часто рассматриваем условное распределение или распределение всех y баллов с то же значение x . Если принять эти условные распределения все нормальны и гомоскедастичны, мы можем делать вероятностные утверждения о прогнозируемых результатах. Стандартное отклонение, которое мы используем, является стандартной ошибкой рассчитано выше.

ЗАДНЯЯ ЧАСТЬ	ДОМАШНЕЕ ЗАДАНИЕ	ДЕЯТЕЛЬНОСТЬ	ПРОДОЛЖИТЬ

---

• электронная почта: [email protected]
• голос/почта: 269 471-6629/ BCM&S Smith Hall 106; Университет Эндрюса; Берриен Спрингс,
• аудитория: 269 471-6646; Smith Hall 100/ ФАКС: 269 471-3713; МИ, 49104-0140
• домашний: 269 473-2572; 610 Н. Главная улица; Берриен Спрингс, Мичиган 49103-1013
• URL-адрес: http://www.andrews.edu/~calkins/math/edrm611/edrm06.htm
• Copyright © 1998-2005, Кит Г. Калкинс. Пересмотрено 19 июля 2005 г. или позднее.

Сравнение парных данных: регрессия или парный t-критерий?

Ваш t-критерий отвечает на вопрос, который вы хотите, а именно (вашими словами) «проверьте, дали ли два метода (в среднем) одинаковые результаты», и с этой стороны ваш анализ выглядит правильным. 2$ в регрессионном анализе по умолчанию — они не говорят нам ничего интересного об этой конкретной проблеме.

Чтобы фальсифицировать H0, мы должны сделать и защитить одно из следующих утверждений:

1. пересечение значительно отличается от 0.
2. наклон значительно отличается от 1.
3. комбинация наклона и точки пересечения значительно отличается от 1/0.

Утверждение № 1 можно (почти) прочитать из регрессионного диагноза: значения t и p предназначены для проверки гипотезы о том, что Intercept отличен от нуля. Но обратите внимание, что t-значение намного ниже, а p-значение намного выше, чем при прямом t-тесте. Фактически, мы должны понимать t-критерий одного коэффициента как контролирующий все другие переменные в моделях: в данном случае наклон. Это принципиально другой вопрос, чем тот, который мы изначально задали.

Утверждение #2 не может быть считано непосредственно из регрессионного диагноза, потому что по умолчанию он сравнивает наклон с 0, тогда как вы хотите сравнить его с наклоном 1, потому что именно такой наклон будет при нулевой гипотезе. Вы можете сделать это самостоятельно в качестве упражнения, вычтя единицу из подогнанного коэффициента наклона, разделив на указанную «Стандартную ошибку» для параметра наклона во втором столбце и применив t-тест к полученной t-статистике. Тем не менее, у нас все еще есть проблема смешивания как наклона, так и перехватов, и это не та «разница в средствах», которую вы ищете, поэтому я тоже не рекомендую это.

Для Утверждения №3 мы хотим сделать и то, и другое вместе. Мы можем сделать это с помощью ANOVA:

Во-первых, мы строим (несколько тривиальную) модель с принудительным наклоном 1 и точкой пересечения 0. На самом деле эта модель не имеет свободных параметров, но R счастлив построить объект класса lm для нас, чего мы хотим.

 null_model <- lm (методx ​​~ смещение (1 * метод) -1, данные = данные)
 

Затем вы можете сравнить это с моделью, которая вам подходит выше:

 anova(model, null_model)
 

Когда я делаю это для ваших данных, я получаю:

Таблица дисперсионного анализа

 Модель 1: methodx ~ methody
Модель 2: метод x ~ смещение (1 * метод) - 1
 Res.
No related posts.