Равны ли диагонали параллелограмма равны: В любом параллелограмме диагонали равны

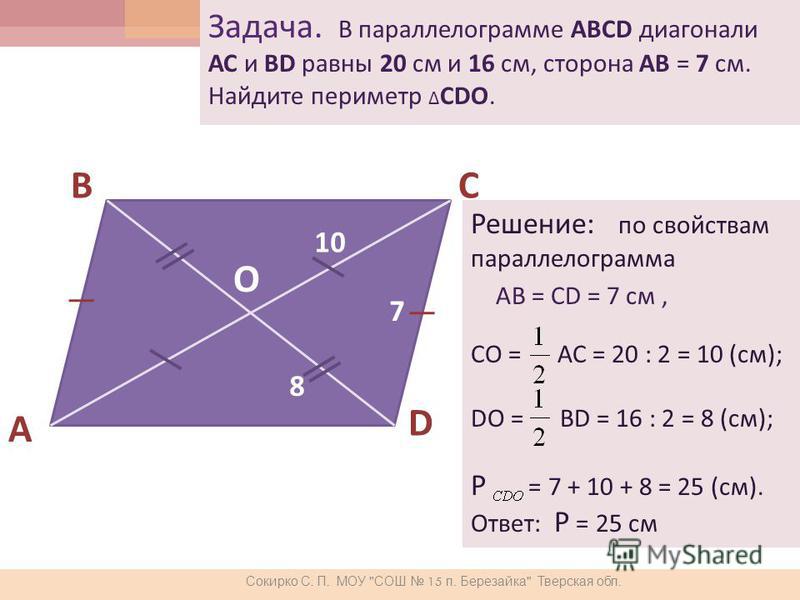
Диагонали параллелограмма равны? – Обзоры Вики

Противоположные углы параллелограмма равны по измерению. … Диагонали параллелограмм не одинаковой длины. Они делятся пополам друг с другом в точке пересечения с равными сторонами через точку пересечения.

Аналогично, как найти площадь параллелограмма? Формула для нахождения площади параллелограмма: Площадь = b * ч. Когда параллелограмм сидит горизонтально, буква b обозначает основание или сторону, которая лежит плоско на земле, а буква h обозначает высоту или расстояние между нижней и верхней сторонами.

Каково соотношение диагоналей параллелограмма? Диагонали делят друг друга пополам. Одна пара противоположных сторон параллельна и равна длине. Смежные углы являются дополнительными. Каждая диагональ делит четырехугольник на два равных треугольника.

Сколько диагоналей у параллелограмма? Обратите внимание на поведение две диагонали. В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. То есть каждая диагональ разрезает другую на две равные части.

Во-вторых Являются ли диагонали перпендикулярного параллелограмма? Если параллелограмм является ромбом, то его диагонали равны перпендикуляр. Если параллелограмм является ромбом, то каждая диагональ делит пополам пару противоположных углов.

Как найти площадь параллелограмма без площади и высоты?

Какая формула площади и периметра параллелограмма? Ответ: Площадь параллелограмма А находится по формуле. A = bh. Здесь b — длина одного основания, а h — высота. Далее, периметр параллелограмма равен сумме длин его четырех сторон.

Как найти углы параллелограмма с диагоналями?

Что такое диагональная формула? Формула для вычисления количества диагоналей n-стороннего многоугольника = п (п-3) / 2 где n — количество сторон многоугольника.

Как начертить параллелограмм с диагоналями?

Построить параллелограмм, если даны одна сторона и две диагонали.

1. Постройте отрезок AB длиной 7 см.
2. От точки A наметьте дугу радиусом 5 см.
3. От точки B наметьте дугу радиусом 4 см. …
4. Расширить АО и БО. …
5. Аналогичным образом нарисуйте дугу на расширенном луче ВО радиуса 4 см. …
6. Присоединяйтесь к AD, DC и BC.

Как найти пересечение диагоналей параллелограмма?

По теореме о диагоналях параллелограмма диагонали параллелограмма делят друг друга пополам. Итак, координаты перекрестка середины диагоналей — LN и — OM . Координаты пересечения диагоналей равны (7—2, 2). Вы можете проверить свой ответ, построив график ▱LMNO и нарисовав диагонали.

Как найти недостающий угол параллелограмма с диагоналями?

Делятся ли диагонали параллелограмма пополам? То есть, если обе пары противоположных сторон четырехугольника равны, то четырехугольник является параллелограммом. Теорема: Диагонали параллелограмма делят друг друга пополам.

Как доказать, что диагонали параллелограмма перпендикулярны? Докажите, что диагонали параллелограмма перпендикулярны тогда и только тогда, когда это ромб, т. е. все его стороны имеют одинаковую длину. (А + В) · (А – В) = А А – В В. Следовательно, (A + B) (A – B)=0 ⇔ A A = B B.

Как найти недостающую высоту параллелограмма?

Задачи по школьной математике.

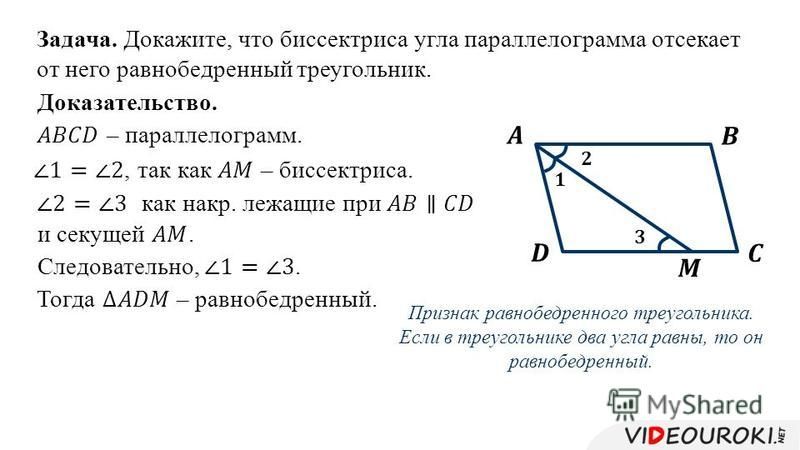Параллелограмм

Математика

1. Сторона параллелограмма втрое больше другой его стороны. Найдите стороны параллелограмма, если его периметр равен 24.

2. Сторона ромба равна 5, а меньшая диагональ равна 6. Найдите большую диагональ.
3. Найдите сторону ромба, если его диагонали равны 6 и 8.
4. Сторона ромба равна 17, а одна из диагоналей равна 30. Найдите длину второй диагонали.
5. Найдите тупой угол (в градусах) ромба, если высота, проведенная из его вершины, делит противоположную сторону пополам.
6. Диагональ ромба образует с его стороной угол 25^о. Найдите больший угол ромба.
7. Диагональ ромба равна его стороне. Найдите больший угол ромба.
8. Периметр ромба равен 24. Высота равна 3. Найдите тупой угол ромба.
9. В ромбе диагонали равны 10 и 15. Найдите площадь ромба.
10. Найдите сторону ромба, если его острый угол 30^о , а площадь равна 18.
11. Найдите сторону ромба, если его диагонали относятся как 3:4, а площадь равна 384.
12. Найдите большую сторону прямоугольника, площадь которого равна 400, а стороны относятся как 4 : 1.
13. Периметр прямоугольника равен 60. Одна сторона больше другой на 10. Найдите меньшую сторону прямоугольника.
14. В параллелограмме сторона АВ равна 6, диагонали равны 9 и 5, О — точка пересечения диагоналей. Чему равен периметр треугольника АОВ?
15. Сумма двух противоположных углов параллелограмма равна 94^о. Найдите больший угол параллелограмма.
16. Периметр параллелограмма равен 60. Найдите площадь параллелограмма, если его стороны относятся как 2 : 3, а острый угол равен 30^о.
17. Найдите площадь параллелограмма ABCD, если угол BAD равен 150^о, АВ равно 3 и AD равно 8.
18. Параллелограмм и прямоугольник имеют соответственно одинаковые стороны. Площадь параллелограмма в два раза меньше площади прямоугольника. Найдите тупой угол параллелограмма.
19. Найдите периметр параллелограмма, если его площадь равна 144, а высоты равны 8 и 12.
20. Диагонали параллелограмма равны 6 и 8, а угол между ними равен 30^о. Найдите площадь параллелограмма.
21. Площадь параллелограмма равна 120, а его высоты равны 8 и 12. Найдите периметр параллелограмма.
22. Стороны параллелограмма равны и . Найдите сумму квадратов длин диагоналей параллелограмма.
23. Стороны параллелограмма равны соответственно 6 и 16, а его тупой угол равен 120^о. Найдите длину меньшей диагонали параллелограмма.
24. Во сколько раз увеличится площадь квадрата, если его диагональ увеличить в 2 раза?
25. Во сколько раз увеличится площадь ромба, если каждую диагональ увеличить в 2 раза?
26. Во сколько раз изменится площадь прямоугольника, если каждую сторону увеличить в 3 раза?
27. Найдите сторону квадрата, равновеликого прямоугольнику со сторонами, равными 4 и 9.
28. Середины сторон квадрата соединены отрезками. Найдите отношение площади фигуры, образованной этими отрезками к площади квадрата.
29. Стороны квадрата ABCD разделены точками E, F, L и N в отношении 1:2 каждая. Найдите отношение площадей квадрата и четырехугольника EFLN.
30. Периметр прямоугольника равен 24. Внутри прямоугольника выбрана точка. Найдите сумму расстояний от этой точки до всех сторон прямоугольника.
31. В параллелограмме ABCD высота BE делит сторону AD в точке E пополам. Найдите сторону AB, если периметр параллелограмма равен 7, а периметр треугольника ABD равен 5.
32. Диагонали параллелограмма равны 17 и 19. Одна сторона равна 10. Найдите другую сторону.
33. В параллелограмме ABCD проведена высота BK. Найдите углы и стороны параллелограмма, если AK = 5, KD = 8 и угол ABK равен 30^о.
34. В параллелограмме боковая сторона равна 8 и острый угол при основании равен 30^о. Найдите проекции высоты, опущенной на основание, на основание и на боковую сторону.
35. Точки M и N — середины противолежащих сторон BC и AD параллелограмма ABCD. Докажите, что четырехуголь­ник AMCN — параллелограмм.
36. Биссектриса угла параллелограмма делит сторону па­раллелограмма на отрезки, равные a и b. Найдите стороны па­раллелограмма.

37. Высота параллелограмма, проведенная из вершины ту­пого угла, равна 2 и делит сторону параллелограмма пополам. Острый угол параллелограмма равен 30◦. Найдите диагональ, проведенную из вершины тупого угла, и углы, которые она об­разует со сторонами.

38. Диагонали  параллелограмма  ABCD  пересекаются  в точке O. Периметр параллелограмма равен 12, а разность пери­метров треугольников BOC и COD равна 2. Найдите стороны параллелограмма.

39. Сторона BC параллелограмма ABCD вдвое больше стороны AB. Биссектрисы углов A и B пересекают прямую CD в точках M и N, причем MN = 12. Найдите стороны паралле­лограмма.

40. Угол при вершине A ромба ABCD равен 20◦. Точки M и N — основания перпендикуляров, опущенных из вершины B на стороны AD и CD. Найдите углы треугольника BMN.

41. Докажите, что точки попарного пересечения биссек­трис всех четырех углов параллелограмма являются вершинами прямоугольника.

42. Докажите, что отрезок, соединяющий середины про­тивоположных сторон параллелограмма, проходит через его центр.

43. Найдите расстояние от центра ромба до его стороны, если острый угол ромба равен 30◦, а сторона равна 4.

44. На сторонах AB и CD прямоугольника ABCD взя­ты точки K и M так, что AKCM является ромбом. Диаго­наль AC составляет со стороной AB угол 30◦. Найдите сторону ромба, если наибольшая сторона прямоугольника ABCD рав­на 3.

45. Прямая имеет с параллелограммом ABCD единствен­ную общую точку B. Вершины A и C удалены от этой прямой на расстояния a и b соответственно. На какое расстояние удалена от этой прямой вершина D?
46. Угол при вершине A ромба ABCD равен 60◦. На сторо­нах AB и BC взяты соответственно точки M
    и N, причем AM = BN. Докажите, что треугольник DMN равносторонний.
47. Точка внутри параллелограмма соединена со всеми его вершинами. Докажите, что суммы площадей треугольников, прилежащих к противоположным сторонам параллелограмма, равны между собой.
48. На сторонах AB и AD параллелограмма ABCD взя­ты точки M и N так, что прямые MC и NC делят параллело­грамм на три равновеликие части. Найдите MN, если BD = d.
49. Пусть E и F — середины сторон BC и AD параллелограмма ABCD. Найдите площадь четырехугольника, образованного прямыми AE, ED, BF и FC, если известно, что площадь ABCD равна S.
50. Докажите, что середины сторон произвольного четырехугольника — вершины параллелограмма. Для каких четырехугольников этот параллелограмм является прямоугольником, для каких — ромбом, для каких — квадратом?

 

Метки задачи, параллелограмм. Смотреть запись.

плоскостная геометрия — Почему диагонали параллелограмма не равны?

$\begingroup$

Представьте себе параллелограмм и начертите его диагонали. Теперь площади двух треугольников на одном из оснований равны. Но по формуле Герона площади не равны. Так какое же этому объяснение.

• плоскостная геометрия

$\endgroup$

2

$\begingroup$

Ваши рассуждения немного туманны, но, похоже, вы думаете:

Вот два треугольника с одинаковыми $a$ и $b$, но разными $c$. Поскольку площадь можно вычислить из $a$, $b$ и $c$ по формуле Герона, разные $c$ приводят к разным площадям, поэтому площади треугольников не могут быть одинаковыми.

Но неверно, что разные $c$ обязательно ведут в разные области. Формула Герона $$ \sqrt{s(s-a)(s-b)(s-c)} \qquad\text{где}s=\frac{a+b+c}2$$ Увеличение $c$ при сохранении постоянных $a$ и $b$ приведет к увеличению $s$, и, следовательно, множители $s(s-a)(s-b)$ станут больше. Но множитель $s-c$ становится равным меньше на величину, которая может доминировать над увеличением трех других факторов — или, в соответствующих случаях, может точно компенсировать его!

В самом деле, установка $c$ либо в $a+b$, либо в $|a-b|$ сделает площадь $0$, а для некоторого $c$ между этими крайними точками треугольник будет иметь максимальную площадь, постоянно меняющуюся с $ с$. Каждая возможная площадь меньше, чем максимум создается двумя разными $c$, а именно одним выше и одним ниже $c$, что дает максимальную площадь.

$\endgroup$

$\begingroup$

Обратите внимание, хотя диагонали параллелограмма неравны по длине. вы должны рассматривать по одной диагонали за раз, которая является общей гипотенузой для обоих треугольников параллелограмма.

Таким образом, проводя за раз любую из двух неравных диагоналей параллелограмма, мы получаем два конгруэнтных треугольника, у которых все три соответствующие стороны равны по длине, и очевидно, что площади этих треугольников одинаковы по формуле Героя. Сумма площадей этих двух равных треугольников равна площади параллелограмма.

Предположим, что $AB=CD=a$ & $BC=AD=b$ две неравные стороны и $AC=d_1$ & $BD=d_2$ две неравные диагонали параллелограмма $ABCD$, тогда

$\ bullet$, проводя диагональ $AC=d_1$, получаем два конгруэнтных треугольника $\triangle ABC$ и $\triangle ACD$, каждый из которых имеет площадь $$=\sqrt{s(s-a)(s-b)(s-d_1)}$$, где $s=\frac{a+b+d_1}{2}$

$\bullet$ рисование диагонали $BD =d_2$, получаем два конгруэнтных треугольника $\треугольник ABD$ и $\треугольник BCD$, площадь каждого из которых $$=\sqrt{s(s-a)(s-b)(s-d_2)}$$, где $s=\frac{a+b+d_2}{2}$

$\endgroup$

$\begingroup$

Я только что сам столкнулся с этим вопросом, и после просмотра некоторых ответов в Интернете я не был удовлетворен ни одним из них, так как нашел их слишком сложными и не совсем понял суть. Итак, я опубликую свой вывод здесь:

Представьте себе параллелограмм с горизонтальными линиями AB и CD и вертикальными линиями AC и BD. Теперь представьте, что вы опускаете перпендикулярную линию из C на AB и другую перпендикулярную линию из B на CD. Вы увидите, что эти две перпендикулярные линии и горизонтальные линии параллелограмма образуют прямоугольник.

Диагональ CB параллелограмма также является одной из диагоналей этого прямоугольника, поскольку C и B являются двумя из четырех вершин, составляющих прямоугольник. Диагонали прямоугольника равны, поэтому диагональ, равная CB, будет определяться точками, в которых перпендикулярные линии, опущенные из B и C, пересекают горизонтальные линии параллелограмма и определяют две оставшиеся вершины прямоугольника.

Попробуйте нарисовать это, и вы увидите, что вторая диагональ параллелограмма, AD, явно не равна этому, а значит, и не равна диагонали CD.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Опишите свойства диагоналей параллелограмма.

Геометрия

Эшли М.

спросил 02.01.13

Как вы описываете свойства диагоналей параллелограмма.

Подписаться І 3

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Билл Ф. ответил 02.01.13

Репетитор

5 (1)

Опытный преподаватель и репетитор в Раунд-Рок, Техас

Смотрите таких репетиторов

Смотрите таких репетиторов

Добавление дополнительной информации о диагоналях в параллелограмме:

В параллелограмме диагонально-противоположные углы равны.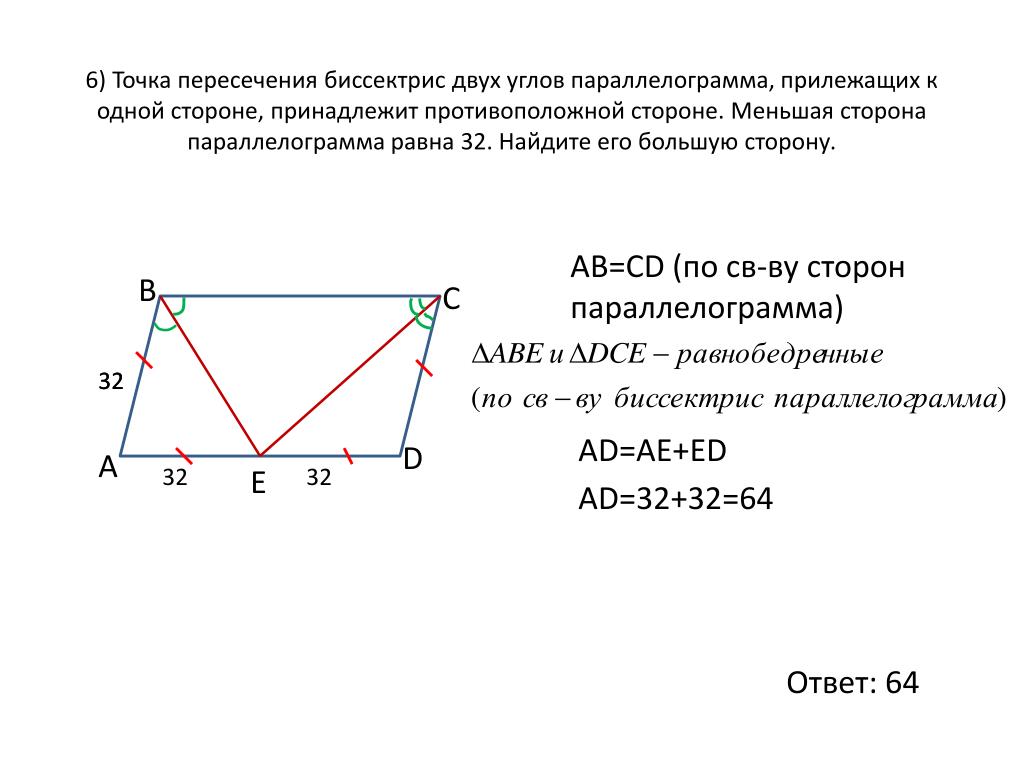 Начерченные диагонали, которые делят эти углы на два угла, в каждом углу создают противоположные равные углы:  внутренние угловые углы, образованные между диагональю и любой стороной, = углы, образованные на другом конце диагонали и противоположной эквивалентной стороне.

Диагонали образуют треугольники: в два раза больше треугольников, чем диагоналей. Эти треугольники конгруэнтны (равны по всем трем сторонам и трем углам), если один из них перевернуть или перевернуть и сравнить с треугольником, находящимся прямо напротив него.

Две диагонали делят друг друга пополам: пересекающаяся диагональ делит диагональ, которую пересекает, ровно пополам.

 

Голосовать за 0 Понизить

Подробнее

Отчет

Регина Г. ответил 02.01.13

Репетитор

5,0 (282)

Выпускник биотехнологии с опытом работы на дому, математикой и естественными науками

Об этом репетиторе ›

Об этом репетиторе ›

Противоположные стороны равны, противоположные углы равны, а соседние углы смежны.

Прочтите, если вам нужна дополнительная информация:

Если это настоящий параллелограмм, то оба набора противоположных сторон и углов должны быть равны. Если один набор не равен, линии не будут параллельны. Если вы продолжите линии через стороны, вы увидите сходство между точками пересечения с точки зрения углов. Используйте соломинки, палочки или веревки, чтобы поэкспериментировать с длинами сторон, чтобы получить что-то реальное, чтобы доказать это самому себе.

Редактировать:

Я неправильно понял вопрос. Я прошу прощения.

Билл прав. Если вы проведете линии через параллелограмм, от одного угла к его противоположному, то, соединив два других противоположных угла, вы создадите четыре треугольника, как вы это делаете, играя с рисунками квадратов.

Подобно тому, как вы можете идеально разрезать пирог, в итоге вы получите равные «ломтики». Однако в параллелограмме два ваших ломтика будут равны друг другу, а два других будут равны друг другу, если только все четыре стороны не равны по длине, как в квадрате или ромбе, где все «ломтики» будет то же самое.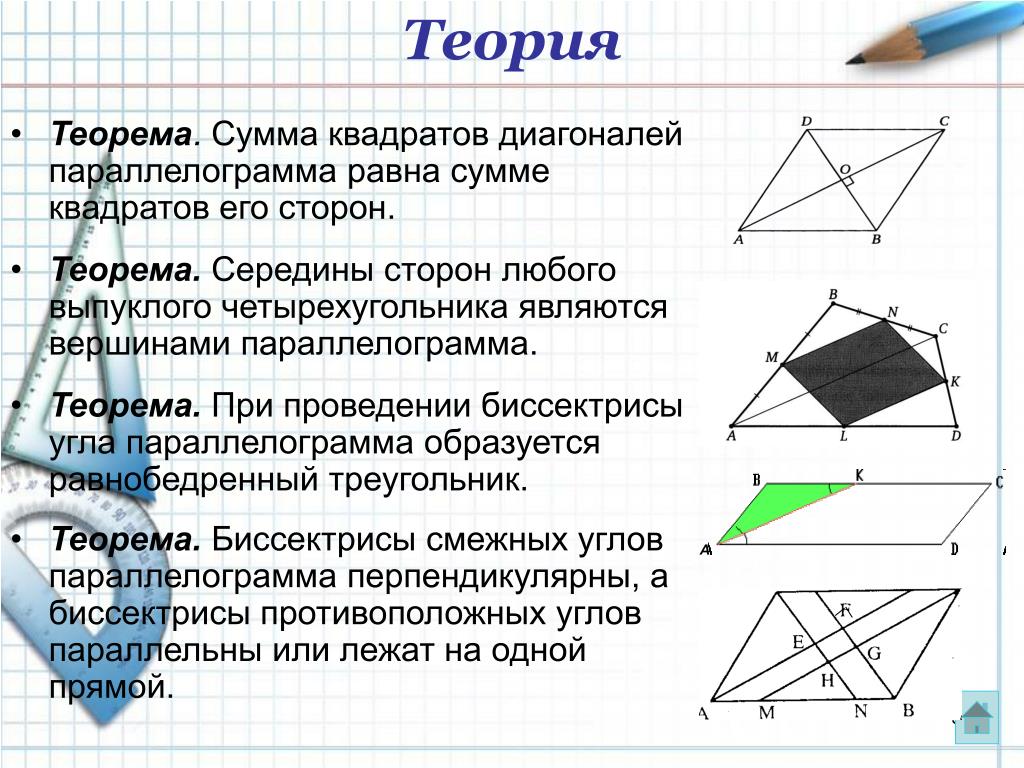

Кроме того, как заметил Билл, диагональные линии будут разделены ровно пополам друг другом.

Мне нравится рисовать их на миллиметровой бумаге с помощью линейки. Затем вы можете измерить свои линии и увидеть, что ваши диагонали делят друг друга пополам.

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн.