Разложение в ряд по степеням: Разложение функции в ряд Тейлора

Ряды (Математический анализ)

Ряды (Математический анализ)

Виленкин Н.Я., Куницкая Е.С., Мордкович А.Г. Ряды. Математический анализ. Учебное пособие для студентов-заочников III курса физико-математических факультетов педагогических институтов. — М.: Просвещение, 1982. — 160 с. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ, ФОРМУЛА И РЯД ТЕЙЛОРА § 1. ЧИСЛОВЫЕ РЯДЫ. СХОДИМОСТЬ И РАСХОДИМОСТЬ ЧИСЛОВОГО РЯДА 2. Сумма ряда. Сходящиеся и расходящиеся ряды. § 2. СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ 1. Необходимый признак сходимости ряда. Остаток ряда. § 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ И ИХ ОБЛАСТЬ СХОДИМОСТИ § 4. ФОРМУЛА ТЕЙЛОРА § 5. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА 1. а, где |x| 7. Разложение других элементарных функций. ЗАКЛЮЧЕНИЕ ГЛАВА II. ЧИСЛОВЫЕ РЯДЫ § 6. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 2. Признаки сходимости Даламбера и Коши. 3. Интегральный признак сходимости Коши. 4. Примеры исследования рядов на сходимость. § 7. СВОЙСТВА РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 1. Перестановка членов ряда с неотрицательными членами. 2. Группировка членов и умножение рядов с неотрицательными членами. § 8. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ 2. Абсолютно сходящиеся ряды. 3. Свойства абсолютно сходящихся рядов. 4. Свойства условно сходящихся рядов. § 9. ЧИСЛОВЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ ГЛАВА III. ФУНКЦИОНАЛЬНЫЕ РЯДЫ § 10. ОБЛАСТЬ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ РЯДОВ § 11. РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ 2. Чебышевское расстояние между функциями. 3. Равномерно сходящиеся функциональные последовательности. 4. Равномерно сходящиеся ряды. Признак Вейерштрасса. 5. Сохранение свойства непрерывности в случае равномерной сходимости. § 12. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ 1. Почленное интегрирование функциональных рядов. 2. Почленное дифференцирование функциональных рядов. § 13. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 1. Функции комплексного переменного. 2. Дифференцирование функций комплексного переменного. 3. Функциональные последовательности и ряды в комплексной области. ГЛАВА IV. СТЕПЕННЫЕ РЯДЫ § 14. КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА 2. Область сходимости степенного ряда. Круг и радиус сходимости. 3. Равномерная сходимость и непрерывность суммы степенного ряда. § 15. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ СТЕПЕННЫХ РЯДОВ 1. Интегрирование и дифференцирование степенных рядов в действительной области. 2. Почленное дифференцирование рядов в комплексной области. 3. Единственность разложения функции в степенной ряд. § 16. ПОКАЗАТЕЛЬНЫЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ 1. Показательная функция в комплексной области. 2. Тригонометрические функции в комплексной области. Формулы Эйлера. § 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ РЯДОВ 1. Вычисление значений функций и интегралов. 2. Вычисление пределов. 3. Метод последовательных приближений. ГЛАВА V. РЯДЫ ФУРЬЕ § 18. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ ФУНКЦИЙ 2. Скалярное произведение функций. 3. Ортонормированные системы функций. § 19. КОЭФФИЦИЕНТЫ ФУРЬЕ. РЯД ФУРЬЕ 2. Коэффициенты Фурье для тригонометрических систем функций. § 20. ЛЕММА РИМАНА 1. Кусочно гладкие функции. 2. Лемма Римана. § 21. ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ РЯДОВ ФУРЬЕ 1. Формула для частичных сумм ряда Фурье. 2. Сходимость разложения кусочно гладких функций в ряды Фурье. 3. Разложение функций, заданных на конечных промежутках, в ряд Фурье. 4. Разложение четных и нечетных функций в ряды Фурье. 5. Примеры разложения функций в ряды Фурье. Ответы к упражнениям

24.

4. Ряд Тейлора. Ряд Маклорена

Если функцияРазлагается в степенной ряд

В некоторой окрестности точки а, т. е. в интервале), то коэффициенты

Этого ряда определяются по формулам

(24.19)

Следовательно,

(24.20)

Ряд, стоящий в правой части формулы (24.20), называется рядом Тейлора для функции

Равенство (24.20) выполняется (ряд Тейлора сходится кВ интервале I, если остаток ряда Тейлора

Стремится к нулю при неограниченном возрастании и:

При всех х из интервала

Достаточное условие разложимости функции в ряд Тейлора. Если функция f(x) бесконечно дифференцируема в интервалеИ ее производные

Равномерно ограничены в этом интервале, т. е. существует такое положительное число С (не зависящее от), что

При всехИз, то верно равенство (24.20) во всем интервале

Формула (24.20) в частном случае приОпределяет разложение функции в ряд Маклорена:

(24.21)

.При разложении функций в степенные ряды часто используется формула

(24. 10) и разложения в ряд Маклорена следующих функций:

Пример 24.15. Разложить в ряд по степеням х функцию Воспользуемся разложением (24.10). В формулеЗапишемВместо

Таким образом, получено следующее разложение данной функции в степенной рад:

(24.22)

Этот ряд сходится при

Замечание. Формулу (24.22) можно получить и другим путем. Рад Является геометрическим рядом со знаменателем

; он сходится при, его сумма(получено по формуле

Пример 24.16. Разложить в ряд по степеням х функцию В формуле (24.22) вместо х запишем

Полученный ряд

Замечание. Этот пример можно решить и другим способом. Так как

То в соответствии с разложениями (24.10) и (24.22) по определению суммы степенных рядов (формула (24.13)) получаем

Пример 24.17. Разложить в ряд по степенямФункцию Преобразуем данную функцию следующим образом:

Введем новую переменнуюПолагаяВоспользуемся разложением

(24.10), записывая в немВместо

(1)

Или

Ряд (1) сходится приТ.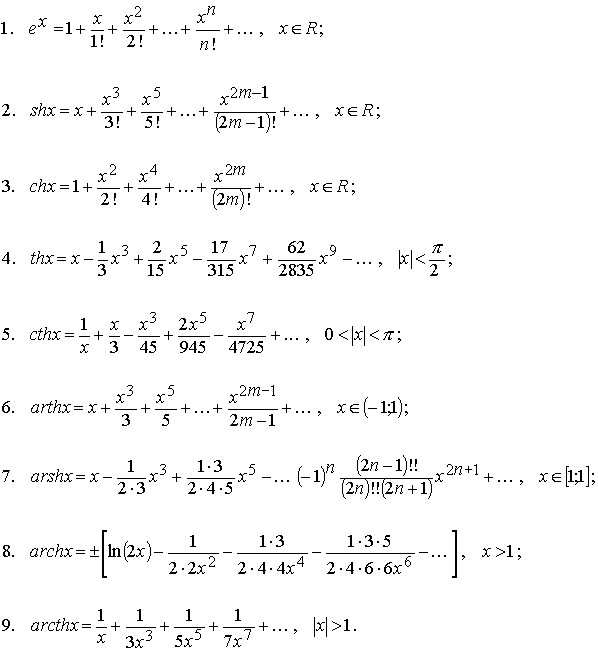 е. при, илиА ряд (2) сходит

Ся приИли при

Пример 24.18. Разложить в ряд по степенямФункцию  1 Разлагая данную функцию в сумму элементарных дробей, получаем   Так как

(3)

То по формуле (24.13) находим

Ряд (3) сходится при, ряд (4) сходится при, поэтому ряд (5) также

Сходится при, т. е. в интервале

Пример 24.19. Найти разложение в степенной ряд функции С помощью степенного ряда для Прежде всего напишем степенной ряд для функции, записывая в формуле (24.10)Вместо, получаем

Этот ряд сходится при, т. е. в интервале; следовательно, его можно

Интегрировать почленно по любому промежутку, содержащемуся в указанном интервале. Интегрируя ряд по промежутку, гдеНаходим

Поскольку, то

Этот ряд имеет радиус сходимости. На концах промежуткаРяд

Также сходится. В частности, приПолучаем ряд

< Предыдущая		Следующая >

4.

1: Введение в серию Power

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

91063

• Russell Herman
• University of North Carolina Wilmington 9{(n)}(0)}{n !} \номер\]

  Заметим, что ряды Маклорена являются частным случаем рядов Тейлора, для которых мы отмечаем, что ряды Маклорена являются частным случаем рядов Тейлора, для которых разложение составляет около \(x=0 .\) Типичный ряд Маклорена, который вы должны знать, приведены на рисунке \(\PageIndex{1}\).

  В следующем примере приведен простой пример построения ряда решения дифференциального уравнения.

  Рисунок \(\PageIndex{1}\): Распространенные расширения серии McLarin 9{x}-x-1 . \nonumber \]

  Это тот же результат, который мы получили ранее.

  ---

  Эта страница под названием 4.1: Введение в Power Series распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Расселом Херманом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

  1. Наверх
  • Была ли эта статья полезной?

  1. Тип изделия

     Раздел или Страница

     Автор

     Рассел Герман

     Лицензия

     CC BY-NC-SA

     Версия лицензии

     3,0

     Показать страницу TOC

     нет

  2. Теги

     1. силовая серия
     2. источник@http://people. uncw.edu/hermanr/mat361/ODEBook/index.htm

  Использование деления для нахождения представления степенного ряда — Криста Кинг Математика

  Замена полинома расширением его степенного ряда

  Иногда нам нужно использовать полиномиальное длинное деление, чтобы упростить дробь, но либо числитель, либо знаменатель не являются полиномами.

  В этом случае мы можем заменить не полином его разложением в степенной ряд, который будет полиномом.

  Привет! Я Криста.

  Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

  Самый простой способ сделать это для неполиномиальной функции — найти аналогичное известное разложение в степенной ряд, а затем изменить его, чтобы оно соответствовало неполиномиальной функции.

  Когда у нас будут полиномиальные выражения для числителя и знаменателя, мы будем выполнять полиномиальное деление в длину, пока не получим требуемое количество ненулевых членов.

  No related posts.