Разложение вектора по векторам онлайн калькулятор: Онлайн калькулятор. Разложение вектора по базису

Разложение многочлена на множители по модулю

УчебаМатематикаАлгебра

Калькулятор находит неразлагаемые множители полинома в конечном поле

Этот калькулятор находит все неразлагаемые множители многочлена одной переменной по модулю p, используя алгоритм Элвина Берлекампа. Описание алгоритма следует за калькулятором.

Разложение многочлена на множители методом Берлекампа

Коэффициенты полинома

Модуль

Входной многочлен

 

Решение

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Разложение многочлена на множители методом Берлекампа

Алгоритм представленный тут — это краткая компиляция алгоритма, описанного в Искусстве программирования Дональда Кнута ¹.

Входные данные

• u(x) — многочлен степени n, n>=2
• p — модуль, простое число

Подготовка

• Убедиться, что входной полином монический, если нет — разделить все коэффициенты на старший коэффициент u_n
• Проверить, что полином свободен от квадратов используя Разложение многочлена в конечном поле свободное от квадратов
• Для каждого свободного от квадратов множителя степени 2 и выше — прогнать следующий алгоритм

Алгоритм

• Найти матрицу Q (n * n ), где n — степень многочлена по следующему алгоритму:
  • Инициализировать вектор A (a₀, a₁ . .. a_n-1) = 1,0…0
  • Инициализировать первую строку матрицы Q (q_0,0, q_0,1 … q_0,n-1) = 0,0…0
  • Цикл по i = 1..n-1 выполнить:
    • Цикл по k = 1..n-1 выполнить:
      • Установить t = a_n-1
      • Цикл по j = n-1 .. 0 выполнить:
        • a_j=a _j-1-t*u_j, подразумевается, что a_-1 = 0
    • Установить значения строки i матрицы Q из вектора A
    • Вычесть 1 из элемента q_i,i матрицы Q
• Найти v^[1] … v^[r] линейно независимые векторы, такие что v^[1] Q = v^[2] Q = … v^[r] Q = (0,0…0)
  • Установить все элементы n-размерного вектора C в -1 : c₀ = c₁ = .. = c_{n-1 = -1}
  • Установить r = 0
  • Цикл по k = 0 … n-1 выполнить:
    • Цикл по j = 0 … n-1 выполнить:
      • Если q_k,j ≠ 0 и c_j<0
        • Установить a = q_k,j
        • Умножить столбец j матрицы Q на -1/a
        • Добавить к оставшимся столбцам (i ≠ j) столбец j умноженный на q_k,i
      • иначе (Если q_k,j=0 или c_j >= 0)
        • Установить r = r + 1
        • Установить каждый элемент i нового n-размерного вектора v
          [r] в одно из следующих значений:
          • a_k,s, если найден такой s-элемент вектора C, такой, что c_s = i
          • 1, если i = k
          • 0 — в противном случае
• Найти r множителей полинома u(x), используя векторы v^[2] . .. v^[r]
  • Найти все w_i = gcd(u(x),v^[2]-s) ≠ 1 для каждого s = 0 … p
  • Если количество w < r выполнить:
  • Цикл по j=3 … r до тех пор пока w < r
    • Заменить w_i множителями, найденными алгоритмом Евклида: gcd(v^[j]-s,w_i) ≠ 1 для каждого s = 0 … p

---

1. Д.Кнут Искусство программирования том 2, пар. 4.6.2 Факторизация полиномов ↩

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Модулярная арифметика
• • Факторизация полиномов
• • Факторизация полинома в конечном поле
• • Свободное от квадратов разложение многочлена в конечном поле
• • Выражения с многочленами
• • Раздел: Алгебра ( 46 калькуляторов )

 Алгебра Берлекамп Математика Многочлены модуль модулярная арифметика Полиномы Разложение многочлена факторизация

 PLANETCALC, Разложение многочлена на множители по модулю

Anton2020-11-03 14:19:37

‘; return ret; } }

4.

2. Разложение вектора по ортам. Модуль вектора

1⁰.Разложение вектора по ортам. Из прямоугольного параллелепипеда (рис. 4.1) следует:

.

Но ,,,, Следовательно,

(4.3)

Равенство (4.3) и есть формула разложения вектора по ортам координатных осей.

Таким образом, координатная запись вектора может быть осуществлена двумя способами:

2⁰.Модуль вектора. Векторявляется диагональю прямоугольного параллелепипеда (рис. 4.1). Квадрат длины диагонали равен сумме квадратов трех его измерений:

,

отсюда следует: , и наконец, получаем искомую формулу:

(4.4)

Модуль вектора равен корню квадратному из суммы квадратов его координат.

4.3. Линейные операции над векторами.

Сформулируем правила действийнад векторами в координатной форме.

.Координаты суммы (разности) векторов равны суммам (разностям) соответствующих координат этих векторов.

Пусть тогда

(4.5)

При умножении вектора на скаляр его координаты умножаются на этот скаляр.

Если и– скалярная величина, то

(4.6)

Покажем применение рассмотренного в этой главе материала к решению практической задачи.

Задача 4.1. Даны векторы:

Найти: координаты и модуль вектора

Решение.Используем координатную запись векторов и правила линейных операций над ними:

Модуль вектора вычислим по формуле (4.4):

Ответ.

4.4. Направляющие косинусы вектора

Определение 4.2. Направляющими косинусами ненулевого вектора называются косинусы углов, которые этот вектор образуют с осями координат (рис. 4.2)

.

Выразим координаты вектора через его модуль и углы:

С помощью данных равенств найдем выражения направляющих косинусов через координаты вектора и его модуль:

(4.7)

Вычислим сумму квадратов направляющих косинусов вектора :

Полученный результат в векторной алгебре сформулирован в виде следующего утверждения:

Сумма квадратов направляющих косинусов ненулевого вектора равна единице:

(4.8)

Задача 4.2.Определить направляющие косинусы вектора а также убедиться в справедливости тождества(4. 8).

Решение.1⁰. Определим координаты и модуль вектора:

2⁰. Вычислим направляющие косинусы вектора

3⁰. Проверим справедливость тождества (4.8):

Ответ.

4.5. Координаты точки в пространстве. Вычисление координат вектора и его модуля по координатам его начала и конца.

Введем понятие координат точки в пространстве через понятие радиус-вектора.

Определение 4.3. Радиус-вектором точки М называется вектор с началом в начале координат и концом в точке М, то есть вектор (рис. 4.3).

В качестве координат точки М примем координаты радиус-вектора.

Определение 4.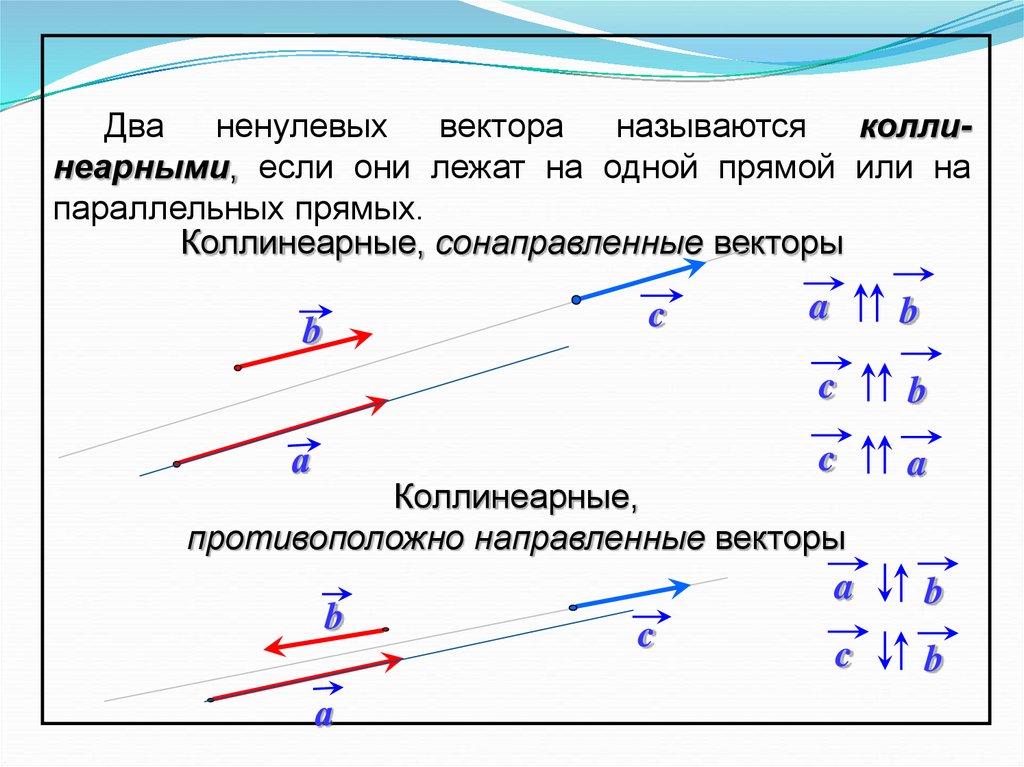 4.

Координатами точки в пространстве называются координаты ее радиус-вектора.

Координаты точки М (рис. 4.3) обозначаются символом:, или. Таким образом,

Поставим задачу:найти координаты и модуль вектора , если известны координаты его начала и конца: (рис. 4.4).

Решение.Проведем в точкиАиВ радиус-векторыи, выразим координаты векторачерез координаты векторови(см. определение 4.4), получим:

(4.9)

Координаты вектора равны соответствующим разностям координат конца и начала этого вектора.

Задача 4.3.Даны две точки: Найти координаты, разложение по ортам координатных осей, модуль и направляющие косинусы вектора

Решение.Для определения координат векторавоспользуемся формулой (4.9):

По формуле (4. 4) вычислим модуль вектора :

Найдем направляющие косинусы вектора :

Вычислим сумму квадратов направляющих косинусов:

Ответ.

Калькулятор угла векторной величины

Калькулятор векторной величины и угла находит величину и направление угла вектор из его компонентов или наоборот. Калькулятор можно использовать для вычисление модулей 2D и 3D векторов и углов направления.

Калькулятор векторной величины и угла:

ВХОДНЫЕ ПАРАМЕТРЫ
Векторная форма:		Компоненты вектора Величина и угол
Размер вектора:		2D-вектор 3D-вектор
КОМПОНЕНТЫ ВЕКТОРА
Вектор

ВЕЛИЧИНА И УГОЛ(Ы)
|А|	θ x (град)	θ y (град)	θ z (град)

Примечание. Используйте точку «.» как десятичный разделитель.

РЕЗУЛЬТАТЫ
Параметр	Символ	Значение	Блок
Векторные компоненты		—	—
		—
		—
Величина вектора A		—
Угол направления	θ х	—	градус
	θ у	—
	θ z	—

Векторный калькулятор

Заполните таблицу и нажмите кнопку «Создать график», чтобы использовать векторный калькулятор

величина

Угол (â °)

x

Y

Точечный продукт

B

A • B

C

B • C

D

C • D

8 B • C

D

C • D

8.

РЕКЛАМА

РЕКЛАМА

Содержание:

• Как пользоваться векторным калькулятором?
• Что такое вектор?
• Как найти компоненты вектора?
• Как добавить векторы?
• Как умножить два вектора с помощью скалярного произведения?

Дайте нам отзыв

✎

✉

Векторный калькулятор выполняет несколько вычислений с использованием до 10 векторов. Список его функций выглядит следующим образом:

1. При вводе величины и угла дает компоненты x и y вектора.
2. Когда вы вводите второй вектор, выполняется сложение двух векторов внизу.
3. Справа также показано скалярное произведение двух векторов.

Как пользоваться векторным калькулятором?

Чтобы найти угол и величину вектора с помощью этого калькулятора, выполните следующие действия.

Чтобы найти компоненты вектора: Введите величину и угол.

Чтобы найти сумму векторов и скалярное произведение: Введите величину и угол секундных векторов.

Что такое вектор?

Вектор определяется как:

 «Объект, имеющий величину и направление».

Вектор имеет две точки. Во-первых, это начальная точка, которая называется хвостом, а конечная точка называется головой.

Как найти компоненты вектора?

Компоненты вектора вычисляются с использованием величины и угла. Используемые формулы:

X-компонент = |F|cos????

Компонент Y = |F|sin????

Пример:

Найдите компоненты силы, модуль которой равен 20 Н и действует под углом 45 градусов.

Решение:

Шаг 1: Определите значения.

Величина = 20 N

Угол = 35 градусов

Шаг 2: Подставьте формулы.
X-компонент = |F|cos????

X-компонент = |20|cos35

X-компонент = 16,3830

Y-компонент = |F|sin????

Компонента Y = |20|sin45

Компонента Y = 14. 14

Как добавить векторы?

Одинаковые единицы суммируются. Вы должны добавить модуль единичного вектора i первого вектора в i Единичный вектор второго вектора и так далее.

Пример:

Добавьте следующие векторы.

6 i   7 j    1 k and 3 i   2 j    0 k

Solution:

   6 i   7 j    1 k  

+ 3 i   2 j    0 k

 ____________

   9 i   9 j    1 k

Как умножить два вектора с помощью скалярного произведения?

Скалярный продукт записывается в математической форме как

A . B = |A||B|cos????

Пример:  

Перемножить векторы A и B .

A = 9 i   3 j  2 k and B = 1 i   1 j    1 k  

The angle between the vectors составляет 20 градусов.

Решение:

Найдите величины A и B .

|А| = √ ((9) ² +(3) ² +(2) ² )

|А| = (81+9+4) ^½

|А| = 9,69

|В| = √ ((1) ² +(1) ² +(1) ² )

|B| = (1+1+1) ^½

|B| = 1,73

Теперь используйте это в формуле.

А . B = |9,69||1,73|cos 20

A.