Разложение в ряд Тейлора с примерами решения
Содержание:
- Понятие ряда Тейлора
- Степенная функция
- Примеры с решением
Понятие ряда Тейлора
Если функция определена в некоторой окрестности точки и имеет в точке производные всех порядков, то степенной ряд (1) называется рядом Тейлора функции в точке Пусть функция регулярна в точке т. е. представляется в некоторой окрестности точки хо сходящимся к этой функции степенным рядом
(2)
Тогда по теореме функция бесконечно дифференцируема в окрестности точки причем коэффициенты ряда (2) выражаются формулами (3) Таким образом, степенной ряд для функции регулярной в данной точке а, совпадает с рядом Тейлора функции в точке
Если известно, что функция бесконечно дифференцируема в точке (и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный для этой функции ряд Тейлора (1) сходится при к функции
Рассмотрим функцию
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Эта функция определена на откуда с помощью индукции легко показать, что где — многочлен степени Воспользуемся тем, что для любого к и докажем, что (4) Утверждение (4) верно при отхкуда, предположив, что формула (4) справедлива при находим
Таким образом, по индукции доказано равенство (4), и поэтому все коэффициенты ряда Тейлора (1) в точке для рассматриваемой функции равны нулю. Так как при то сумма ряда Тейлора не совпадает Иначе говоря, эту функцию нельзя представить рядом Тейлора, сходящимся к ней в окрестности точки
Так как при то сумма ряда Тейлора не совпадает Иначе говоря, эту функцию нельзя представить рядом Тейлора, сходящимся к ней в окрестности точки
Причина этого явления становится понятной, если функцию рассматривать в комплексной плоскости. В самом деле, функция не является непрерывной в точке так как Остаточный член формулы Тейлора. Пусть функция бесконечно дифференцируема в точке Тогда ей можно поставить в соответствие ряд (1). Обозначим и назовем остаточным членом формулы Тейлора для функции в точке Если существует то согласно определению сходимости ряда ряд (1) сходится к функции в точке т. е.
Возможно вам будут полезны данные страницы:
Найти частные производные |
Объём тела вращения |
Матричные уравнения: пример решения |
Метод Гаусса: пример решения |
Теорема 1.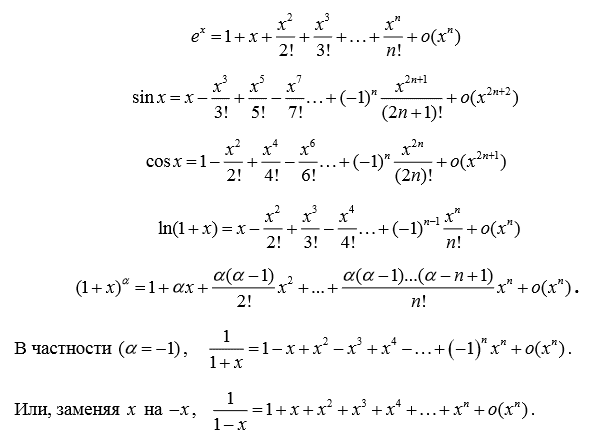 Если функции непрерывны на интервале где то для любого остаточный член формулы Тейлора для функции в точке можно представить: а) в интегральной форме б) в форме Лагранжа где принадлежит интервалу с концами О Формула (10) была доказана. Докажем формулу (9) методом индукции. В силу равенств (5) и (6) нужно показать, что
Если функции непрерывны на интервале где то для любого остаточный член формулы Тейлора для функции в точке можно представить: а) в интегральной форме б) в форме Лагранжа где принадлежит интервалу с концами О Формула (10) была доказана. Докажем формулу (9) методом индукции. В силу равенств (5) и (6) нужно показать, что
Воспользуемся равенством и преобразуем его жо левую часть с помощью формулы интегрирования по частям:
Таким образом, т. е. формула (11) верна при Предположим, что формула (11) является верной для номера т. е. Преобразуем интеграл в правой части формулы (12), применив формулу интегрирования по частям:
Отсюда следует, что равенство (12) можно записать в виде (11). Формула (9) доказана.
Теорема 2. Если функция и все ее производные ограничены в совокупности на интервале т. е. (13) то функция представляется сходящимся к ней в каждой точке интервала рядом Тейлора (8). О Пусть Тогда, используя формулу (10) и условие (13), получаем Так как для любого то из (14) следует, что выполняется условие (7), т.
Заметим, что коэффициенты -—разложения (15) для основных элементарных функций (показательной, гиперболических, тригонометрических и других. Показательная и гиперболические функции. Пусть Тогда для любого выполняются неравенства По теореме 2 ряд (15) для функции сходится к этой функции на интервале при любом т. е. радиус сходимости этого ряда Так как для функции выполняются равенства для любого гг, то по формуле (15) получаем разложение в ряд Маклорена показательной функции Используя разложение (16) и формулы находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса: Используя разложение (16) и формулы находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса: (18)
Радиус сходимости каждого из рядов (17), (18) б) Тригонометрические функции. Пусть Тогда По теореме 2 ряд (15) для функции сходится для любого т. е. радиус сходимости этого ряда Если для любого п, и по формуле (15) получаем разложение синуса в ряд Маклорена: Пусть Тогда для всех и для всех для всех По формуле (15) получаем
Пусть Тогда По теореме 2 ряд (15) для функции сходится для любого т. е. радиус сходимости этого ряда Если для любого п, и по формуле (15) получаем разложение синуса в ряд Маклорена: Пусть Тогда для всех и для всех для всех По формуле (15) получаем
Радиус сходимости каждого из рядов (19) и (20) в) Логарифмическая функция. Пусть Тогда откуда находим О Оценим остаточный член пользуясь формулой (9) при Преобразуем эту формулу, полагая Тогда и формула (9) примет вид Если то по формуле (23), используя равенство (21), получаем
Пусть Тогда справедливы неравенства так как Отсюда следует, что при любом выполняется неравенство Используя неравенство (27), из формулы (24) получаем следующую оценку остаточного члена: откуда следует, что Пусть Тогда так как Итак, если то остаточный член для функции стремится к нулю при т. е. ряд Маклорена сходится к Из формул (15) и (22) получаем разложение функции в ряд Маклорена радиус сходимости которого Формула (28) справедлива при и поэтому Заменяя в формуле (28) получаем
Степенная функция
Пусть Если — многочлен степени который можно записать по формуле бинома Ньютона в виде конечной суммы: Покажем, что если то функция представляется при каждом сходящимся к ней рядом Маклорена где
Так как то по формуле (23) получаем где Выберем число таким, чтобы выполнялось условие Тогда при всех справедливы неравенства
Используя неравенства (25) и (26), а также неравенство получаем
Из формулы (33) и оценок (34)-(36) следует неравенство (37) которое справедливо при всех и для каждого Так как при то Отметим важные частные случаи формулы В заключение заметим, что при разложении функций в ряд Тейлора обычно используют формулы (16)-(20), (28)-(30) и применяют такие приемы, как: представление данной функции в виде линейной комбинации функций, ряды Тейлора для которых известны; замена переменного; почленное дифференцирование и интегрирование ряда.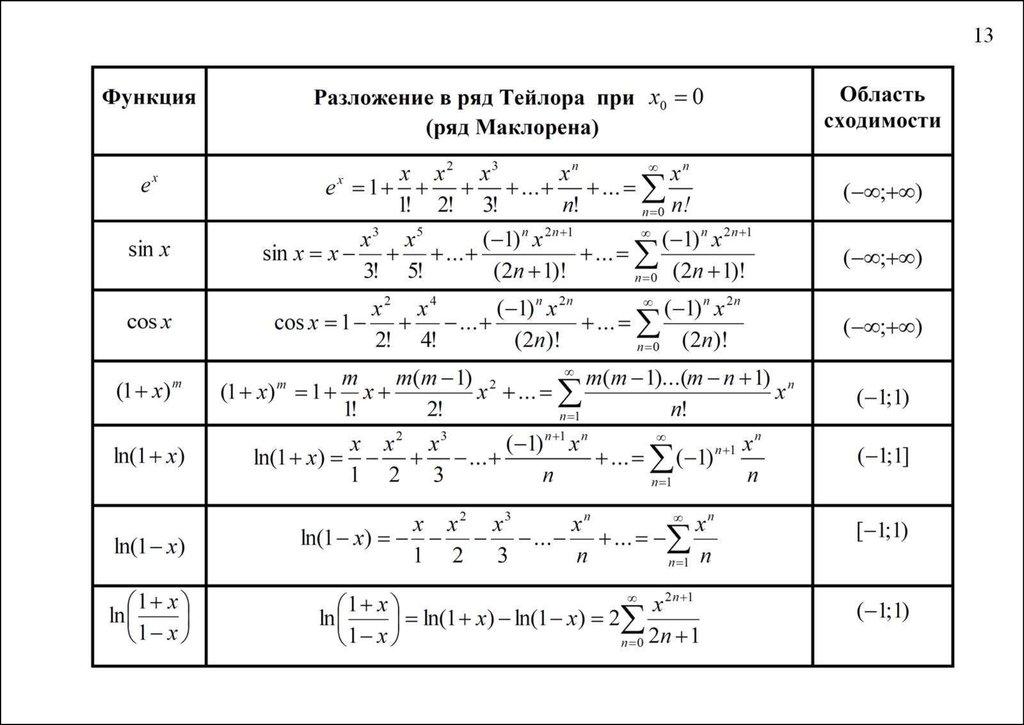
Примеры с решением
Пример 1.
Разложить в ряд Маклорена функцию и найти радиус сходимости ряда, если: Используя формулу (38), получаем ряд радиус сходимости которого б) Из равенства (30) следует, что
Следовательно,
Так как то’ при_ + 3 2(1 + |) 8(1-|) меняя формулы (38) и (39), получаем ряд
Пример 2.
Разложить в ряд Маклорена функции и найти радиусы сходимости рядов.
а) Почленно интегрируя ряд (40), получаем
б) Заменяя в формуле (41) получаем откуда следует, что
интегрируя ряд (41), получаем
Пример 3.
Разложить в ряд Тейлора в точке функцию Так как то, полагая получаем
Используя формулы (28) и (29), отсюда находим Следовательно,
Раздел недели: Плоские фигуры. | |||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Степенные ряды Тейлора, Маклорена (=Макларена) и периодический ряд Фурье. Разложение функций в ряды. / / Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Поделиться:
 Введите свой запрос: Введите свой запрос: | ||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||
A.5: Таблица разложений Тейлора
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 92253
- Джоэл Фельдман, Эндрю Рехницер и Элиз Йегер
- Университет Британской Колумбии 9n+\cdots\конец{выравнивание*}\]
Эта страница под названием A.
 5: Table of Taylor Expansions распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джоэлем Фельдманом, Эндрю Рехнитцером и Элиз Йегер посредством исходного контента, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
5: Table of Taylor Expansions распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джоэлем Фельдманом, Эндрю Рехнитцером и Элиз Йегер посредством исходного контента, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- CLP Учебники по математическому анализу
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://personal.
 math.ubc.ca/~CLP/CLP3
math.ubc.ca/~CLP/CLP3
- источник@https://personal.
Серия Taylor
Серия мощности категории 2 или категории 3 в x определяет функцию f путем установки
для любых x в интервале сходимости ряда.
Расширение серии Power на f ( x ) можно дифференцировать почленно, и результирующий ряд является допустимым представлением f ′( x ) в том же интервале:
Снова дифференцирование дает
и так далее. Замена
и вообще, подставляя x = 0 в степенном ряду вместо n -й производной от f , получаем
Они называются Коэффициенты Тейлора из f и результирующий степенной ряд
называется рядом Тейлора функции f .
Для данной функции f ее коэффициенты Тейлора могут быть вычислены по простой формуле, приведенной выше, и возникает вопрос, действительно ли ряд Тейлора f сходится к f ( x )? Если да, то есть если
для всех x в некоторой окрестности (интервал вокруг) 0, то говорят, что функция f является аналитической (в 0).
 [В более общем случае, если составить ряд Тейлора f относительно точки x = x 0 ,
[В более общем случае, если составить ряд Тейлора f относительно точки x = x 0 ,, и если этот ряд действительно сходится к f ( x ) для всех x в некоторой окрестности x 0 , то f называется аналитическим в точке x 0 .] Полиномы везде аналитичны, а рациональные функции (частные многочленов) аналитичны во всех точках, где знаменатель не равен нулю. Кроме того, известные трансцендентные (то есть неалгебраические) функции e х , sin х и cos х также везде аналитичны. Ряды Тейлора в таблице 1 встречаются так часто, что их стоит запомнить.
Для общего степенного ряда обычно невозможно выразить его в замкнутой форме через знакомые функции.
Пример 1 : Используйте Таблицу 1, чтобы найти разложение в ряд Тейлора для каждой из следующих функций:
а.

б.
в. В(1 + х )
д. e − x 2
и . х потому что х
ф. грех х потому что х
г. арктан x
а. Замена х на х 2 в разложении ряда Тейлора 1/(1 – x ) дает
с | х | < 1 эквивалентно | x 2 | < 1.
б. Дифференцирование 1/(1 – x ) дает 1/(1 – x ) 2 , поэтому дифференцирование разложения в ряд Тейлора 1/(1 – x ) почленно даст разложение в ряд 1 /(1 – x ) 2 :
с. Во-первых, замена x на − x в разложении ряда Тейлора 1/(1 – x ) дает разложение 1/(1 + x ):
Теперь, поскольку интегрирование 1/(1 + x ) дает In(1 + x ), интегрирование ряда Тейлора для 1/(1 + x ) почленно дает разложение для In(1 + x ), действительно для | х | < 1:
Техническое примечание: Интегрирование 1/(1 + x ) дает In (1 + x ) + c (где c — некоторая произвольная константа), поэтому, строго говоря, приведенное выше уравнение должно было быть записано как
Однако подстановка x = 0 в это уравнение показывает, что c = 0, поэтому приведенное выше разложение для In (1 + x ) действительно верно.


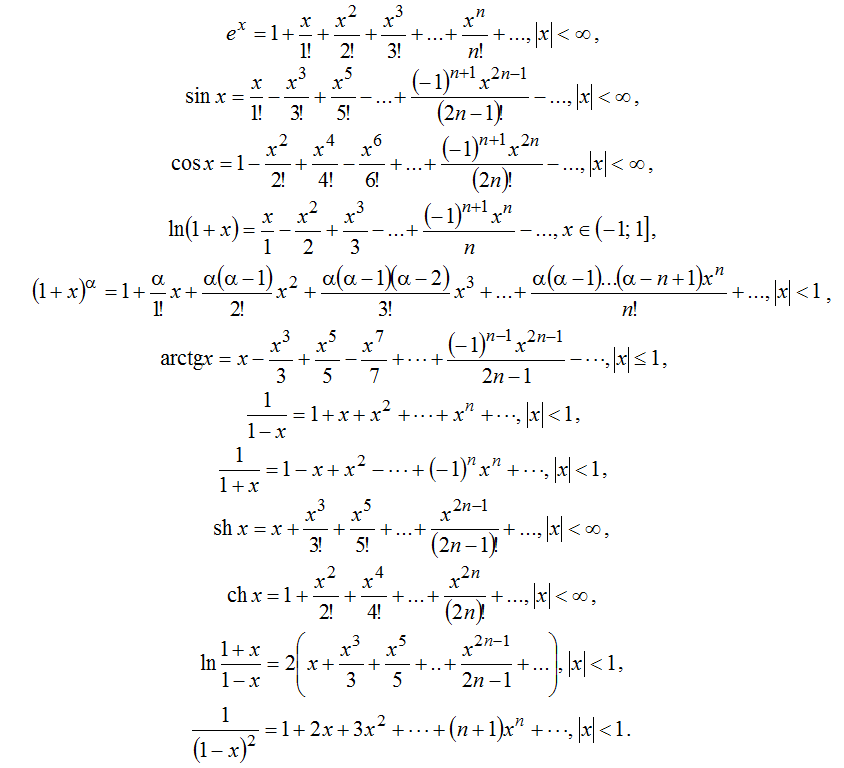 Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. Примеры некоторых распространенных разложений функций в ряды Тейлора в окрестностях точки 1.
Примеры некоторых распространенных разложений функций в ряды Тейлора в окрестностях точки 1.
 Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1
Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1
 5: Table of Taylor Expansions распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джоэлем Фельдманом, Эндрю Рехнитцером и Элиз Йегер посредством исходного контента, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
5: Table of Taylor Expansions распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джоэлем Фельдманом, Эндрю Рехнитцером и Элиз Йегер посредством исходного контента, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу. math.ubc.ca/~CLP/CLP3
math.ubc.ca/~CLP/CLP3 [В более общем случае, если составить ряд Тейлора f относительно точки x = x 0 ,
[В более общем случае, если составить ряд Тейлора f относительно точки x = x 0 ,
