Простые множители числа 23 — Calculatio
Калькулятор «Разложение чисел на простые множители»
Какие простые множители у числа 23?
Ответ: Простые множители числа 23: 23
Объяснение разложения числа 23 на простые множители
Разложение 23 на простые множители (факторизация) — это представление числа 23 как произведения простых чисел. Другими словами, необходимо выяснить, какие простые числа нужно перемножить, чтобы получилось число 23.
Так как число 23 является простым — его невозможно разложить на простые множители. 23 — это единственный простой множитель.
Минимальное простое число на которое можно разделить 23 без остатка — это 23. Следовательно, первый этап расчета будет выглядеть следующим образом:
23 ÷ 23 = 1
В итоге мы получили список всех простых множителей числа 23. Это: 23
Поделитесь текущим расчетом
Печать
https://calculat.
io/ru/number/prime-factors-of/23
<a href=»https://calculat.io/ru/number/prime-factors-of/23″>Простые множители числа 23 — Calculatio</a>
О калькуляторе «Разложение чисел на простые множители»
Данный калькулятор поможет разложить заданное число на простые множители. Например, Какие простые множители у числа 23? Выберите начальное число (например ’23’). После чего нажмите кнопку ‘Посчитать’.
Простые множители - это положительные целые числа, имеющие только два делителя - 1 и само себя.
Калькулятор «Разложение чисел на простые множители»
Таблица разложения чисел на простые множители
| Число | Простые множители |
|---|---|
| 8 | 23 |
| 9 | 32 |
| 10 | 2, 5 |
| 11 | 11 |
| 12 | 22 × 3 |
| 13 | 13 |
| 14 | 2, 7 |
| 15 | 3, 5 |
| 16 | 24 |
| 17 | 17 |
| 18 | 2 × 32 |
| 19 | 19 |
| 20 | 22 × 5 |
| 21 | 3, 7 |
| 22 | 2, 11 |
| 23 | 23 |
| 24 | 23 × 3 |
| 25 | 52 |
| 26 | 2, 13 |
| 27 | 33 |
| 28 | 22 × 7 |
| 29 | 29 |
| 30 | 2, 3, 5 |
| 31 | 31 |
| 32 | 25 |
| 33 | 3, 11 |
| 34 | 2, 17 |
| 35 | 5, 7 |
| 36 | 22 × 32 |
| 37 | 37 |
Алгебра (Ван дер Варден Б.
Л.) Алгебра (Ван дер Варден Б.Л.)
ОглавлениеПРЕДИСЛОВИЕ РЕДАКТОРАВВЕДЕНИЕ Глава первая. ЧИСЛА И МНОЖЕСТВА § 1. Множества § 2. Отображения. Мощности § 3. Натуральный ряд § 4. Конечные и счетные множества § 5. Разбиение на классы Глава вторая. ГРУППЫ § 6. Понятие группы § 7. Подгруппы § 8. Операции над комплексами. Смежные классы § 9. Изоморфизмы и автоморфизмы § 10. Гомоморфизмы, нормальные подгруппы и факторгруппы Глава третья. КОЛЬЦА, ТЕЛА И ПОЛЯ § 12. Гомоморфизмы и изоморфизмы § 13. Построение частных  Кольца многочленов§ 15. Идеалы. Кольца классов вычетов § 16. Делимость. Простые идеалы § 17. Евклидовы кольца и кольца главных идеалов § 18. Разложение на множители Глава четвертая. ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПРОСТРАНСТВА § 19. Векторные пространства § 20. Инвариантность размерности § 21. Двойственное векторное пространство § 22. Линейные уравнения над телом § 23. Линейные преобразования § 24. Тензоры § 25. Антисимметрические полилинейные формы и определители § 26. Тензорное произведение, свертка и след Глава пятая. ЦЕЛЫЕ РАЦИОНАЛЬНЫЕ ФУНКЦИИ § 27. Дифференцирование § 28. Корни § 29. Интерполяционные формулы § 30. Разложение на множители § 31. Признаки неразложимости § 32. Разложение на множители в конечное число шагов § 33. Симметрические функции § 34. Результант двух многочленов § 35. Результант как симметрическая функция корней § 36. Разложение рациональных функций на простейшие дроби Глава шестая.  n§ 53. Прямые произведения § 54. Групповые характеры § 55. Простота знакопеременной группы § 56. Транзитивность и примитивность Глава восьмая. ТЕОРИЯ ГАЛУА § 57. Группа Галуа § 58. Основная теорема теории Галуа § 59. Сопряженные группы, поля и элементы поля § 60. Поля деления круга § 61. Циклические поля и двучленные уравнения § 62. Решение уравнений в радикалах § 63. Общее уравнение n-й степени § 64. Уравнения второй, третьей и четвертой степеней § 65. Построения с помощью циркуля и линейки § 66. Вычисление группы Галуа. § 67. Нормальные базисы Глава девятая. УПОРЯДОЧЕННЫЕ И ВПОЛНЕ УПОРЯДОЧЕННЫЕ МНОЖЕСТВА § 68. Упорядоченные множества 70. Теорема Цермело § 71. Трансфинитная индукция Глава десятая. БЕСКОНЕЧНЫЕ РАСШИРЕНИЯ ПОЛЕЙ § 72. Алгебраически замкнутые поля § 73. Простые трансцендентные расширения § 74. Алгебраическая зависимость и алгебраическая независимость § 75.  Степень трансцендентности§ 76. Дифференцирование алгебраических функций Глава одиннадцатая. ВЕЩЕСТВЕННЫЕ ПОЛЯ § 77. Упорядоченные поля § 78. Определение вещественных чисел § 79. Корни вещественных функций § 80. Поле комплексных чисел § 81. Алгебраическая теория вещественных полей § 82. Теоремы существования для формально вещественных полей § 83. Суммы квадратов Глава двенадцатая. ЛИНЕЙНАЯ АЛГЕБРА § 84. Модули над произвольным кольцом § 85. Модули над евклидовыми кольцами. Инвариантные множители § 86. Основная теорема об абелевых группах § 87. Представления и модули представлений § 88. Нормальные формы матрицы над полем § 89. Элементарные делители и характеристическая функция § 90. Квадратичные и эрмитовы формы § 91. Антисимметрические билинейные формы Глава тринадцатая. АЛГЕБРЫ § 92. Прямые суммы и пересечения § 93. Примеры алгебр § 94. Произведения и скрещенные произведения § 95. Алгебры как группы с операторами.  Модули и представления§ 96. Малый и большой радикалы § 97. Звездное произведение § 98. Кольца с условием минимальности § 99. Двусторонние разложения и разложение центра § 100. Простые и примитивные кольца § 101. Кольцо эндоморфизмов прямой суммы § 102. Структурные теоремы о полупростых и простых кольцах § 103. Поведение алгебр при расширении основного поля Глава четырнадцатая. ТЕОРИЯ ПРЕДСТАВЛЕНИЙ ГРУПП И АЛГЕБР § 106. Представления центра § 107. Следы и характеры § 108. Представления конечных групп § 109. Групповые характеры § 110. Представления симметрических групп § 111. Полугруппы линейных преобразований § 112. Двойные модули и произведения алгебр § 113. Поля разложения простых алгебр § 114. Группа Брауэра. Системы факторов Глава пятнадцатая. ОБЩАЯ ТЕОРИЯ ИДЕАЛОВ КОММУТАТИВНЫХ КОЛЕЦ § 115. Нётеровы кольца § 116. Произведения и частные идеалов § 117. Простые идеалы и примарные идеалы § 118.  Общая теорема о разложении§ 119. Теорема единственности § 120. Изолированные компоненты и символические степени § 121. Теория взаимно простых идеалов § 122. Однократные идеалы § 123. Кольца частных § 124. Пересечение всех степеней идеала § 125. Длина примарного идеала. Цепи примерных идеалов в нётеровых кольцах Глава шестнадцатая. ТЕОРИЯ ИДЕАЛОВ В КОЛЬЦАХ МНОГОЧЛЕНОВ § 127. Универсальное поле § 128. Корни простого идеала § 129. Размерность § 130. Теорема Гильберта о корнях. Система результантов для однородных уравнений § 131. Примарные идеалы § 132. Основная теорема Нетера § 133. Сведение многомерных идеалов к нульмерным Глава семнадцатая. ЦЕЛЫЕ АЛГЕБРАИЧЕСКИЕ ЭЛЕМЕНТЫ § 134. Конечные R-модули § 135. Элементы, целые над кольцом § 136. Целые элементы в поле § 137. Аксиоматическое обоснование классической теории идеалов § 138. Обращение и дополнение полученных результатов § 139. Дробные идеалы § 140.  Теория идеалов в произвольных целозамкнутых целостных кольцахГлава восемнадцатая. НОРМИРОВАННЫЕ ПОЛЯ § 142. Пополнения § 143. Нормирования поля рациональных чисел § 145. Нормирование алгебраических расширений: общий случай § 146. Нормирования полей алгебраических чисел § 147. Нормирования поля рациональных функций § 148. Аппроксимационная теорема Глава девятнадцатая. АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ § 149. Разложения в ряды по степеням униформизирующих § 150. Дивизоры и их кратные § 151. Род g § 152. Векторы и ковекторы § 153. Дифференциалы. Теорема об индексе специальности § 154. Теорема Римана — Роха § 155. Сепарабельная порождаемость функциональных полей § 156. Дифференциалы и интегралы в классическом случае § 157. Доказательство теоремы о вычетах Глава двадцатая. ТОПОЛОГИЧЕСКАЯ АЛГЕБРА § 158. Понятие топологического пространства § 159.  Базисы окрестностей§ 160. Непрерывность. Пределы § 161. Аксиомы отделимости и счетности § 162. Топологические группы § 163. Окрестности единицы § 164. Подгруппы и факторгруппы § 165. Т-кольца и Т-тела § 166. Пополнение групп с помощью фундаментальных последовательностей § 167. Фильтры § 168. Пополнение группы с помощью фильтров Коши § 169. Топологические векторные пространства § 170. Пополнение колец § 171. Пополнение тел |
Объяснение урока: Факторизация простых чисел с показателями
В этом объяснении мы узнаем, как использовать различные стратегии для нахождения факторизации простых чисел с использованием показателей.
Вы уже должны понимать термины простое число, составное число, и фактор.
Определение: простые, составные и множители
- Факторы числа — это числа, которые мы перемножаем, чтобы получить
оригинальный номер.
Мы часто пишем множители парами.
Например, 6×1=6 и 2×3=6, поэтому 1, 2, 3 и 6 равны множители 6. Одна пара множителей для 6 — это 1 и 6, потому что их произведение равно 6; другой пара множителей 2 и 3. - Простое число — это целое число, имеющее ровно два делителя: 1 и само себя.
Например, 7 — простое число, потому что единственные делители 7 — это 1 и 7. - Составное число — это целое число, имеющее более двух делителей.
Например, 6 является составным числом, потому что оно имеет 4 делителя.
Мы часто пишем множители парами. Любое число можно записать как произведение некоторых его множителей. Полезный способ записи числа как произведение только простых чисел.
Определение: простая факторизация
Простая факторизация числа — это произведение простых чисел, которое равно исходному числу.
Например, 2×3×5 — простая факторизация
числа 30, потому что 2, 3 и 5 простые, а их произведение равно 30.
Пример 1. Нахождение простой факторизации малых чисел
Что из следующего является простой факторизацией числа 18?
- 18
- 2
- 2×9
- 2×3×3
- 3
Ответ
Чтобы проверить, какое произведение является простой факторизацией числа 18, мы должны проверить две вещи: что произведение равно 18 и что множители в произведение — все простые числа.
- Поскольку 18 не простое число, это неправильный ответ.
- Поскольку ни 2, ни 3 не равны 18, они неверны.
- Поскольку 9 не является простым числом, 2×9 не является простой факторизацией.
У нас осталось 2×3×3. И 2, и 3 простые, и произведение равно 18. Следовательно, это простая факторизация 18.
Разложение числа на простые множители может быть полезно, когда нам нужно найти наибольшую общую
делители или наименьшие общие кратные наборов чисел, но мы не будем здесь обсуждать, как это сделать.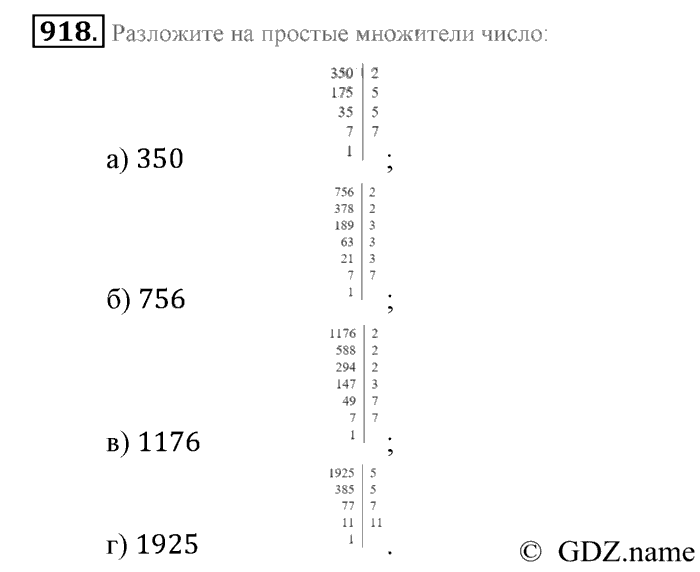
Вместо этого мы сосредоточимся на двух методах нахождения простой факторизации: факторных деревьях и методе деления.
по простым числам. Эти методы используют тот факт, что когда вы записываете число как
произведение его факторов, вы всегда можете обменять один из факторов на продукт, который
коэффициент равен.
Например, мы знаем, что 40=4×10. Но мы можем заменить 4 на 2×2 или заменить 10 на 2×5 в уравнение и произведение в правой части по-прежнему будут равны 40. Это дает нам возможность записывать числа как произведение все меньших и меньших множителей. Если мы продолжим наш пример для 40, мы получим 40=2×2×2×5, в этот момент мы не можем разбить ни один из факторов на меньшие числа, потому что все они простые.
Ключом к нахождению простых множителей является следующий результат.
Результат: Факторы числа
Если 𝑎 является множителем 𝑏, а 𝑏 является множитель 𝑐, то 𝑎 является множителем 𝑐.
Например, 6 является коэффициентом 12, а 2 и 3 являются коэффициентами 6, что означает, что 2 и 3
также множители 12.
Этот результат говорит нам, что мы можем работать с множителями нашего исходного числа (которые меньше и с ним легче иметь дело, чем с исходным числом) при поиске простых множителей.
Теперь мы увидим, как это помогает нам найти простую факторизацию числа, рисуя Факторные деревья.
Начните с числа 60. Найдите любую пару множителей 60 и запишите эти два числа на первый уровень дерева. Например, 60=6×10.
Затем выберите любое число в конце ветви и проверьте, является ли оно простым. Если да, то проверьте другой номер; если это не так, то снова факторизовать его. Например, 6 не простое, поэтому разложите 6 на 2×3 и запишите их на следующем уровень дерева.
Обратите внимание, что на любом этапе произведение чисел на концах ветвей равно равно начальному числу. Например, на предыдущем шаге множители на концах ветвей 2, 3 и 10, а 2×3×10=60.
Продолжайте разлагать составные числа на концах ветвей, пока не останется
только с простыми числами.
Если у вас есть только простые числа, вы нашли простую факторизацию номер. Запишите число как произведение этих факторов; мы можем использовать либо знак умножения или точка для представления умножения, поэтому, 60=2×3×2×560=2⋅3⋅2⋅5.или
Часто мы записываем простую факторизацию с факторами в порядке возрастания, поэтому 60=2×2×3×560=2⋅2⋅3⋅5или или с помощью показателей для группировки одинаковых факторов, 60=2×3×560=2⋅3⋅5.или
Мы суммируем метод рисования древовидной диаграммы ниже.
Как найти простую факторизацию с помощью дерева множителей
Шаг 1: Сначала найдите любую пару множителей для числа и запишите эти числа в первых двух ветвях.
Шаг 2: Для любого множителя, который не является простым, запишите его как произведение двух его множителей.
Шаг 3: Продолжайте, пока все ветви не оканчиваются простыми числами.
Шаг 4: Факторизация простых чисел представляет собой произведение всех простых чисел на концах ветвей древовидной диаграммы.
Хорошей практикой является записывать множители в простой факторизации в порядке возрастания и использовать показатели степени для упрощения выражения.
Примечание. Вы можете начать с любой пары множителей, и вы получите тот же набор простых множителей и ту же самую простую факторизацию. Единственное, что изменится, — это порядок, в котором вы найдете факторы.
Далее мы увидим, как использовать метод деления на простые числа. Этот метод иногда называют методом лестницы.
Чтобы найти простую факторизацию числа 60, начните с записи 60 на первом шаге. (если это поможет, вы можете думать о каждом шаге как о перевернутом делении). Затем запишите любой простой делитель 60 рядом с ним и частное под ним на новом шаге. Итак, мы можем выбрать 2 в качестве простого множителя 60, а затем записать частное в следующем шаг 60÷2=30.
На втором шаге мы должны учитывать коэффициенты 30 (которые также являются коэффициентами 60). В качестве простого множителя мы могли бы выбрать 2, 3 или 5.
Если мы выберем 3, то
частное для третьего шага равно 30÷3=10. Мы продолжаем
эти шаги, пока мы не получим частное 1. Это показывает нам, что нет никаких
больше простых множителей числа.
Как только мы получим частное 1, мы идентифицируем все простые множители числа 60; 60 это произведение простых множителей, записанных в левой части каждого шага. Следовательно, 60=2×3×5×2=2×3×5.
Подведем итоги метода деления на простые числа.
Как найти факторизацию простых чисел путем деления на простые числа
Шаг 1: Запишите число в верхнем шаге.
Шаг 2: Запишите простой множитель слева и разделите на этот простой множитель, чтобы получить частное в шаге ниже.
Шаг 3: Продолжайте находить простые множители и делить на них, пока не получите частное 1.
Шаг 4: Запишите число как произведение простых чисел в левой части.
Обратите внимание, что не имеет значения, какие простые множители вы выбираете на каждом шаге;
ответ всегда будет один.
Кроме того, вы можете записывать шаги в
метод в вертикальной линии вместо того, чтобы шагать вниз и вправо каждый раз.
Обратите внимание, что существует только одна простая факторизация числа. Неважно, какой метод вы выберете или какие факторы вы выберете на каждом этапе, в конце вы всегда будете получать один и тот же набор простых множителей.
Далее мы покажем, что эти методы можно использовать для нахождения простых факторизаций больших чисел.
Пример 2: Нахождение простой факторизации больших чисел
Найдите простую факторизацию числа 792.
Ответ
Существует несколько методов нахождения простой факторизации.
Метод 1 : Мы можем использовать метод деления на простые числа, чтобы найти каждый простой делитель один шаг за шагом.
Начните с нахождения простого делителя числа 792. Поскольку 792 четно, мы знаем, что 2 — это простой делитель. Итак, 792=2×396, и мы записываем это следующим образом.
Мы знаем, что все простые делители числа 396 будут также простыми делителями числа 792, поэтому следующий шаг — найти простой делитель числа 396 (например, 2) и разделить на него, продолжая находить простые множители результатов, пока не останется простых множителей.
В зависимости от простых множителей, выбранных на каждом шаге, конечный результат может выглядеть как следующее.
Как только мы получили результат 1, мы знаем, что больше нет простых множителей и что первичная факторизация 792 есть 2×2×2×3×3×11.
В зависимости от того, какую запись вы выберете для представления умножения, мы можно записать это, используя показатели степени, как 2×3×112⋅3⋅11.или
Метод 2 : В качестве альтернативы мы можем использовать факторные деревья для разложения числа на простые числа в несколько шагов.
Для этого начните с 792 в верхней части дерева и запишите пару множителей на первой
две ветви.
Затем для каждого числа в конце ветви разложите его дальше, если оно не простое.
Числа на концах ветвей, когда вы закончите, являются простыми факторы 792: 2×3×2×2×3×11 или, что то же самое, 2×3×11.
Наконец, обратите внимание, что если вы знаете простую факторизацию числа, вы можете найти все пары факторов, использующие ассоциативные и коммутативные свойства.
Например, мы можем использовать нашу простую факторизацию 792, чтобы найти множители 792.
Мы знаем, что 792=2×2×2×3×3×11. Если мы переставим эти факторы, используя свойство коммутативности, то мы знаем, что можем сгруппировать их и умножить в любом порядке на ассоциативное свойство. Следовательно, 792=(2×2×2)×(3×3×11)=8×33792=(2×11)×(2×2×3×3)=22×36, или
Таким образом, 8, 22 , 33 и 36 — все множители 792, и любой множитель 792, который больше единицы будет равно произведению ряда этих простых множителей.
Коэффициенты 18 | Определение, примеры, нахождение, положительное и отрицательное
Введение В математике мы часто сталкиваемся с проблемой решения задач, требующих делимости целых чисел и простого распознавания целых чисел, на которые число делится на целое число.
Такие числа называются множителями и основная цель данной статьи — определить, какие числа являются делителями 18, а какие нет, определить, могут ли множители целого числа, например для числа 18, быть дробными и отрицательными числами.
Множитель числа — это число, на которое данное число делится без остатка. Обычно, когда мы говорим о числовых факторах, мы говорим только о положительных целых факторах.
Например, делители 6 равны 1, 2, 3 и 6. Если 6 разделить на любое из чисел 1, 2, 3, 6, ответ будет целым числом:
6÷1=6
6÷2=3
63=2
66=1
Делителями числа являются любые числа, которые делятся на него точно, включая 1 и само число. Число 1 всегда является наименьшим целым делителем числа, само число всегда является наибольшим целым делителем числа. Таким образом, каждое число всегда имеет не менее двух делителей.
Если число имеет ровно два делителя, 1 и само число, то это число называется простым числом.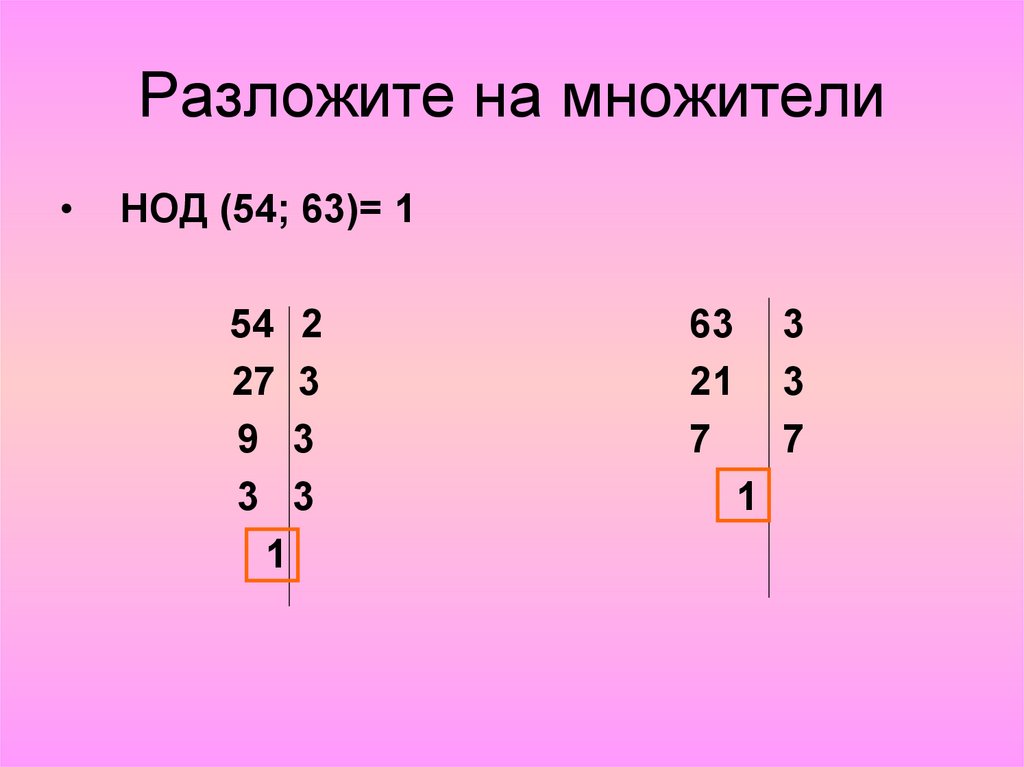
Число 1 не является простым числом. Наименьшим простым числом является число 2 (делится без остатка и на 1, и на 2). Чтобы определить, является число простым или нет, вы можете найти это число в таблице простых чисел.
Таблица простых чисел до 1000
ИНТЕРЕСНЫЙ ФАКТ: Два последовательных простых числа называются числами-близнецами или близнецами. Все близнецы от 2 до 1000 отмечены в таблице выше.
ПРИМЕР: Какие из следующих чисел являются простыми?
117, 191, 227, 319, 473, 502
РЕШЕНИЕ: Если вам нужно легко и быстро определить, является число простым или нет, воспользуйтесь таблицей простых чисел.
Ищем число 117 – есть числа 113 и 127, но нет числа 117. Значит, число 117 не является простым числом.
Найдите число 191 — это число есть в таблице, значит, это число — простое.
Среди чисел 227, 319, 473, 502 только число 227 находится в таблице простых чисел, поэтому только это число является простым числом.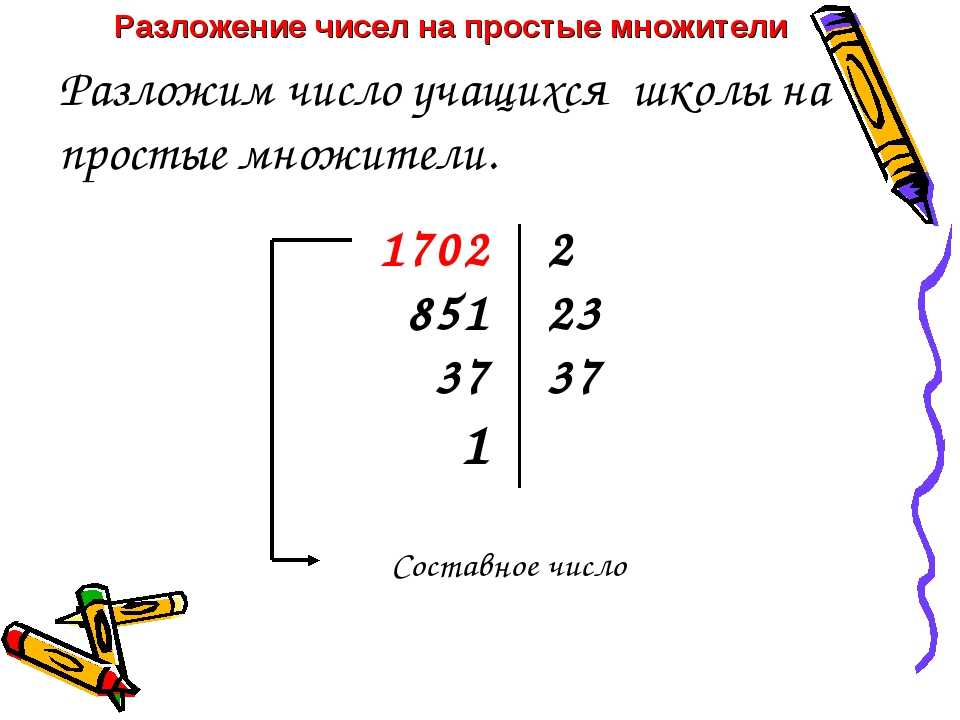
Кстати, вы можете легко утверждать, что число 502 не является простым числом — это число делится на 2 без остатка, поэтому оно четное число, а четное число больше 2 никогда не может быть простым числом.
Число, имеющее более двух делителей, называется составным числом.
Способы нахождения делителей числаСуществует три метода нахождения делителей числа:
- метод деления;
- метод умножения;
- метод простой факторизации.
МЕТОД ДЕЛЕНИЯ: метод деления состоит в том, чтобы найти все делители от 1 до самого числа, которые делят число без остатка.
МЕТОД УМНОЖЕНИЯ: метод умножения заключается в записи числа как произведения двух чисел различными возможными способами.
МЕТОД ПРОСТОЙ ФАКТОРИЗАЦИИ: метод простой факторизации состоит в том, чтобы представить составное число как произведение его простых множителей.
Метод деления для нахождения делителей 18 Поскольку числа 18 нет в таблице простых чисел, число 18 является составным числом, поэтому оно имеет более двух делителей.
Мы можем использовать деление, чтобы найти все положительные множители числа 18 (начнем с 1, затем сверим 2, 3, 4, 5, 6 и т. д. до 9 (число 9 равно половине 18) и само число 18):
18÷1=18
18÷2=9
18÷3=6
18÷4=4 р.2
18÷5=3 р.3
18÷6=3
18÷7=2 r.4
18÷8=2 r.2
18÷9=2
1818=1
Таким образом, 18 имеет всего 6 положительных факторов : 1, 2, 3, 6, 9 и 18.
Метод умножения для нахождения множителей 18Представьте число 18 как произведение двух чисел всеми возможными способами:
18 = 1 × 18
18 = 2 × 9
18 = 3 × 6
Все числа, которые используются в этих произведениях, являются делителями 18. Таким образом, положительные делители числа 18 равны 1, 2, 3, 6, 9и 18.
Метод простой факторизации для нахождения множителей числа 18 Основная факторизация — это способ представления числа как произведения его простых множителей.
Например,
18=6×3
не является простой факторизацией числа 18, поскольку число 6 не является простым числом.
Произведение
18=2×3×3
– это простая факторизация числа 18, поскольку числа 2 и 3 являются простыми числами.
Есть два возможных способа выразить число как произведение простых множителей:
- метод деления;
- метод факторного дерева.
ФАКТОРИЗАЦИЯ ПРОСТЫХ С ПОМОЩЬЮ МЕТОДА ДЕЛЕНИЯ
Метод деления можно использовать для нахождения простых множителей числа путем деления числа на простые числа. Чтобы найти простые множители числа с помощью метода деления, выполните следующие шаги:
ШАГ 1: Разделите число без остатка на наименьшее возможное простое число.
ШАГ 2: Разделите частное из шага 1 на наименьшее возможное простое число.
ШАГ 3: Повторяйте шаг 2, пока частное не станет равным 1.
ПОСЛЕДНИЙ ШАГ: Умножьте все простые множители, являющиеся делителями.
ПРИМЕР: Напишите разложение числа 18 на простые множители, используя метод деления.
РЕШЕНИЕ:
ШАГ 1. Наименьшее возможное простое число, на которое 18 делится без остатка, равно числу 2. Разделите 18 на 2:
18 ÷ 2=9
. частное 9 равно числу 3. Разделить 9на 3:
9 ÷ 3=3
ШАГ 3: Наименьшее возможное простое число, которое делит частное 3 без остатка, равно числу 3. Разделите 3 на 3:
3 ÷ 3=1
ПОСЛЕДНИЙ ШАГ: умножьте все простые множители, являющиеся делителями:
18=2×3×3
Вы можете переписать эту простую факторизацию в виде экспоненты:
18=2 x 3 2
ЗАМЕЧАНИЕ : Обычно этот процесс не описан так долго, но изображен в виде столбца, как показано ниже.
| 2 | 18 |
| 3 | 9 |
| 3 | 3 |
| 1 |
Prime factorization of 18=2x3x3
=2×3 2
ФАКТОРИЗАЦИЯ ПРОСТЫХ МЕТОДОВ С ИСПОЛЬЗОВАНИЕМ ДЕРЕВА ФАКТОРОВ
Дерево факторов – это специальная диаграмма, на которой мы рисуем множители числа, затем множители этих множителей и так далее, пока не получим только простые множители.
ПРИМЕР : Нарисуйте дерево множителей для числа 18.
РЕШЕНИЕ : Из таблицы умножения мы знаем, что 18=9×2. Таким образом,
Одно из этих чисел мы можем представить как произведение простых чисел:
9=3×3
Таким образом, итоговое дерево факторов равно
, а простая факторизация числа 18 равна 2×3×3 или 2×. 3 2 .
ЗАМЕЧАНИЕ : Вы можете начать с произвольных чисел, дающих 18 в произведении, но конечный продукт всегда должен быть таким же, как простая факторизация уникальный . Например, вы можете нарисовать следующие два дерева факторов для числа 18 и увидеть, что первичная факторизация для всех деревьев факторов одинакова. Это обеспечивается Фундаментальной теоремой арифметики, которая утверждает, что
каждое натуральное число, большее 1 , может быть записано как произведение простых чисел, и что с точностью до перестановки множителей это произведение единственно.
Чтобы найти простые множители числа с помощью метода факторного дерева, выполните следующие шаги:
ШАГ 1: Нарисуйте дерево множителей, начиная с произвольных чисел с произведением, равным заданному числу, и заканчивая только простыми числами.
ШАГ 2: Перемножьте все простые множители, встречающиеся в этом дереве множителей.
Метод нахождения множителей числа с помощью разложения числа на простые множители заключается в умножении произвольных комбинаций простых множителей.
ПРИМЕР : Разложение числа 18 на простые множители равно 2 x 3 2 . Запишите все положительные множители числа 18, используя метод простой факторизации.
РЕШЕНИЕ : Чтобы записать все множители и не потерять ни одного, воспользуйтесь следующим руководством по написанию комбинаций:
- сначала запишите все возможные степени первого простого множителя (начиная с показателя степени 0 и заканчивая максимально возможный показатель степени, определенный в простой факторизации числа):
2 0 =1, 2 1 =2
- затем выпишите все возможные степени второго простого множителя (начиная с показателя степени 0 и заканчивая максимально возможным показателем степени, определенным в простой факторизации числа):
3 0 =1, 3 1 =3, 3 2 =9
- and then all possible products of powers of both multipliers
2 1 x 3 1 =6 , 2 1 x 3 2 =18,
Таким образом, список всех 6 положительных множителей из 18, записанных в порядке возрастания, будет
1, 2, 3, 6, 9, 18
Обратите внимание, что только 2 и 3 являются простыми множителями числа 18.
Используя простую факторизацию числа, мы можем найти количество множителей этого числа. Для этого выполните следующие шаги:
ШАГ 1: Запишите простую факторизацию числа в форме экспоненты.
ШАГ 2: Добавьте единицу к каждому показателю степени.
ШАГ 3: Перемножьте все полученные числа. Это произведение обозначает количество множителей числа.
ПРИМЕР : Найдите количество множителей числа 18.
РЕШЕНИЕ : Из предыдущей темы разложение числа 18 на простые множители в экспоненциальной форме равно 2 x 3 2 .
Прибавьте 1 к каждому показателю степени:
1+1=2
2+1=3
и умножьте полученные суммы:
2×3=6
Следовательно, число множителей 18 равно 6.
Положительные пары множителей числа 18 Пара множителей числа представляет собой набор двух множителей, произведение которых дает это число.
Например, множители 5 и 6 образуют пару множителей 30, потому что
30=5×6
ПРИМЕР: Перечислите все пары множителей числа 18.
РЕШЕНИЕ: Начните с 1. Поскольку 18=1×18, поместите 1 в начало списка и 18 в конец списка. Множители 1 и 18 образуют первую пару множителей числа 18.
Теперь попробуйте 2. Поскольку 18=2×9, поместите 2 в начало списка (после 1) и 9 в конец списка (перед 18). . Множители 2 и 9 образуют вторую пару множителей числа 18.
Затем попробуйте 3. Поскольку 18=3×6, поместите 3 в начало списка (после 2) и 6 в конец списка (перед 9).). Факторы 3 и 6 образуют третью пару факторов 18.
| 1 | 2 | 3 | 6 | 18 | 18 | 7777777787878787878787878787878787878787878787878787878787 Итак, мы закончили!
Все эти пары состоят из положительных целых чисел.| -62 | -1 9 | -3 | -6 | -9 | -18 |
Здесь два числа, окрашенные в один цвет, образуют отрицательную пару множителей.
Кроме того, мы можем графически представить отрицательные пары факторов так же, как графическое представление положительных пар факторов.
Викторина- Какова сумма всех положительных множителей 18?
РЕШЕНИЕ : Число 18 имеет 6 положительных множителей: 1, 2, 3, 6, 9 и 18. Сумма этих множителей равна 1+2+3+6+9+18=39.
ОТВЕТ: 39
- Сколько пар множителей имеет число 18?
РЕШЕНИЕ : Число 18 имеет 3 пары положительных факторов:
(1, 18), (2, 9) и (3, 6)
и 3 пары положительных факторов:
(-1, -18),
Если длина и ширина прямоугольника — целые числа, сколько различных периметров может быть у этого прямоугольника? Каковы числовые значения этих периметров? РЕШЕНИЕ : Площадь прямоугольника можно найти, умножив ширину прямоугольника на его длину. Обратите внимание, что нас интересуют разные пары ширины и длины, то есть пара шириной 1 единица. и длиной 18 ед. задает тот же прямоугольник, что и пара шириной 18 единиц. и длиной 1 ед. Периметр прямоугольника равен удвоенной сумме его ширины и длины. Заполните следующую таблицу, чтобы найти периметр прямоугольника в каждом случае: ОТВЕТ: 3 разных периметра: 38 ед., 22 ед. и 18 ед. а) Число 18 — простое число. б) Число 18 составное. c) Число -9 является коэффициентом 18. d) Число 180 является коэффициентом 18, потому что 180⋅$\frac{1}{10}$=18. РЕШЕНИЕ : а) Число 18 находится между 17 и 19. Числа 17 и 19 находятся в таблице простых чисел, а число 18 не находится в таблице простых чисел. Это означает, что число 18 не является простым числом и утверждение а) неверно. б) Поскольку числа 18 нет в таблице простых чисел, это число является составным и утверждение б) верно. c) Глядя на отрицательные пары множителей, мы видим, что (-2, -9) является отрицательной парой множителей 18. Это означает, что число -9 является множителем 18 и утверждение c) верно. г) Число 180 не является делителем 18, так как равенство 180⋅110=18 содержит дробные числа, которые не могут быть делителями. Итак, утверждение г) неверно. ОТВЕТ : a) Неверно b) Верно c) Верно d) Неверно РЕШЕНИЕ: Согласно статье, простая факторизация числа 18 равна 2×3 2 . Тогда 18 2 = (2×3 2 ) 2 = 2 2 x 3 4 эти факторы. Чтобы найти количество множителей, прибавьте 1 к каждому показателю степени: 2+1=3 4+1=5 и полученные суммы умножить: 3 x 5=15 Следовательно, число множителей 18 2 равно 15. Теперь используем, алгоритм из примера в статье, чтобы найти все делители 18 2 . 2 0 =1, 2 1 =2, 2 2 =4 3 0 =1, 3 1 =3, 3 2 =9, 3 3 =27, 3 4 0 =831 909090 а затем все возможные произведения степеней обоих множителей 2 1 x3 1 = 6, 2 1 X3 2 = 18, 2 1 X3 3 = 54, 2 1 X345 4 Therefore, the list of all 15 positive множители 182=324, записанные в порядке возрастания, равны 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324 ОТВЕТ: 15 положительных факторов: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324 число (у него более двух делителей). Множители и кратные (для детей 8-10 лет) Рабочие листы (космическая тематика) Мы тратим много времени на изучение и сбор информации на этом сайте.
Если длина и ширина прямоугольника — целые числа, то возможны три варианта: Ширина Длина 1 ед. 18 шт. 2 шт. 9 шт. 3 шт. 6 шт. Ширина Длина Периметр 1 шт. 
18 шт. 2(1+18)=28 шт. 2 шт. 9 шт. 2(2+9)=22 ед. 3 шт. 6 шт. 2(3+6)=18 шт. 
x3 1 =12, 2 2 x3 2 =36, 2 2 x3 3 =108, 2 2 x3 4 =324
Умножение дробей на целые числа со словесными задачами (со знаменателем от 2 до 6) Рабочие листы по математике для 4-го класса
GCF: Наибольший общий множитель (на тему Дня святого Валентина) Рабочие листы по математике