| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Простые множители числа 24 — Calculatio
Калькулятор «Разложение чисел на простые множители»
Какие простые множители у числа 24?
Ответ: Простые множители числа 24: 2, 2, 2, 3
или
23 × 3
Объяснение разложения числа 24 на простые множители
Разложение 24 на простые множители (факторизация) — это представление числа 24 как произведения простых чисел. Другими словами, необходимо выяснить, какие простые числа нужно перемножить, чтобы получилось число 24.
Другими словами, необходимо выяснить, какие простые числа нужно перемножить, чтобы получилось число 24.
Так как число 24 является составным (не простым) мы можем разложить его на простые множители.
Для того, чтобы получить список простых множителей числа 24, необходимо итеративно делить число 24 на минимально возможное простое число пока в результате не получится 1 (единица).
Ниже полное описание шагов факторизации числа 24:
Минимальное простое число на которое можно разделить 24 без остатка — это 2. Следовательно, первый этап расчета будет выглядеть следующим образом:
24 ÷ 2 = 12
Теперь необходимо повторять аналогичные действия, пока в результате не останется 1:
12 ÷ 2 = 6
6 ÷ 2 = 3
3 ÷ 3 = 1
В итоге мы получили список всех простых множителей числа 24. Это: 2, 2, 2, 3
Можно упростить выражение и записать как: 23 × 3
Дерево простых множителей числа 24
Мы также можем визуализировать разложение числа 24 на простые множители в виде дерева факторизации:
Поделитесь текущим расчетом
Печать
https://calculat. io/ru/number/prime-factors-of/24
io/ru/number/prime-factors-of/24
<a href=»https://calculat.io/ru/number/prime-factors-of/24″>Простые множители числа 24 — Calculatio</a>
О калькуляторе «Разложение чисел на простые множители»
Данный калькулятор поможет разложить заданное число на простые множители. Например, он может помочь узнать какие простые множители у числа 24? Выберите начальное число (например ’24’). После чего нажмите кнопку ‘Посчитать’.
Простые множители - это положительные целые числа, имеющие только два делителя - 1 и само себя.
Калькулятор «Разложение чисел на простые множители»
Таблица разложения чисел на простые множители
| Число | Простые множители |
|---|---|
| 9 | 32 |
| 10 | 2, 5 |
| 11 | 11 |
| 12 | 22 × 3 |
| 13 | 13 |
| 14 | 2, 7 |
| 15 | 3, 5 |
| 16 | 24 |
| 17 | 17 |
| 18 | 2 × 32 |
| 19 | 19 |
| 20 | 22 × 5 |
| 21 | 3, 7 |
| 22 | 2, 11 |
| 23 | 23 |
| 24 | 23 × 3 |
| 25 | 52 |
| 26 | 2, 13 |
| 27 | 33 |
| 28 | 22 × 7 |
| 29 | 29 |
| 30 | 2, 3, 5 |
| 31 | 31 |
| 32 | 25 |
| 33 | 3, 11 |
| 34 | 2, 17 |
| 35 | 5, 7 |
| 36 | 22 × 32 |
| 37 | 37 |
| 38 | 2, 19 |
Коэффициенты 24 | Простая факторизация числа 24, Факторное дерево числа 24
Факторы числа 24 — это те числа, которые полностью делят 24, не оставляя остатка.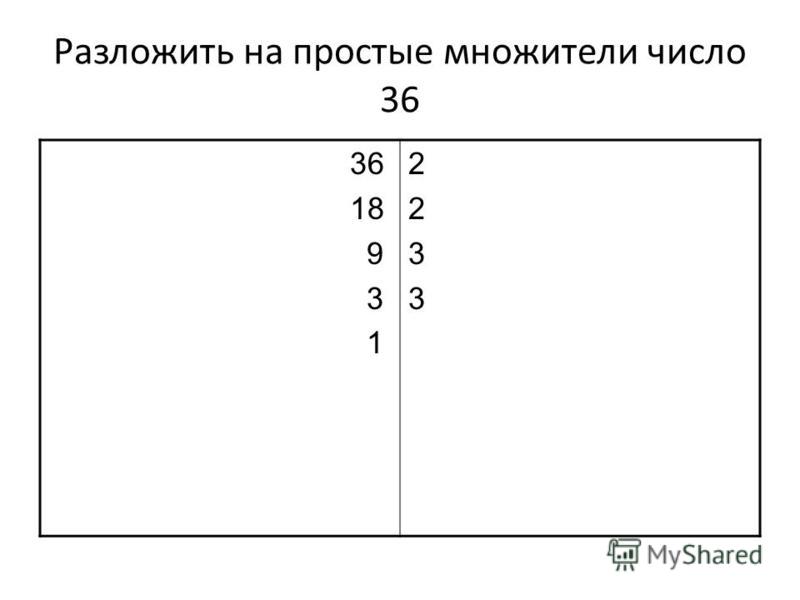 Есть 8 множителей из 24, среди которых 24 — самый большой множитель, а 2 и 3 — его простые множители. Простую факторизацию числа 24 можно выполнить, умножив все его простые множители так, чтобы произведение было равно 24. Давайте узнаем обо всех множителях 24, простой факторизации 24 и факторном дереве 24 в этой статье.
Есть 8 множителей из 24, среди которых 24 — самый большой множитель, а 2 и 3 — его простые множители. Простую факторизацию числа 24 можно выполнить, умножив все его простые множители так, чтобы произведение было равно 24. Давайте узнаем обо всех множителях 24, простой факторизации 24 и факторном дереве 24 в этой статье.
| 1. | Какие множители числа 24? |
| 2. | Разложение числа 24 на простые множители |
| 3. | Факторное дерево из 24 |
| 4. | Факторы 24 в парах |
| 5. | Часто задаваемые вопросы о факторах 24 |
Какие множители числа 24?
Делители 24 могут быть перечислены как 1, 2, 3, 4, 6, 8, 12 и 24. Согласно определению множителей, делители 24 — это те числа, которые делят 24 без остатка. Другими словами, мы можем сказать, что если умножить два числа и произведение равно 24, то числа являются делителями 24. Это означает, что 24 полностью делится на все эти числа. Помимо этого, 24 также имеет отрицательные факторы, которые могут быть перечислены как -1, -2, -3, -4, -6, -8, -12 и -24. Для отрицательных множителей нам нужно умножить отрицательный множитель на отрицательный множитель, например, (-6) × (-4) = 24,9.0007
Это означает, что 24 полностью делится на все эти числа. Помимо этого, 24 также имеет отрицательные факторы, которые могут быть перечислены как -1, -2, -3, -4, -6, -8, -12 и -24. Для отрицательных множителей нам нужно умножить отрицательный множитель на отрицательный множитель, например, (-6) × (-4) = 24,9.0007
Как найти делители числа 24?
Факторизация числа означает запись числа как произведения его множителей. Наиболее часто используемый метод нахождения множителей числа — метод умножения. Найдем множители числа 24 с помощью умножения.
Факторы 24 с использованием метода умножения
Давайте найдем множители 24 с помощью метода умножения, выполнив следующие шаги.
- Шаг 1: Чтобы найти множители 24 методом умножения, нам нужно проверить, какие пары чисел умножаются, чтобы получить 24. Итак, нам нужно разделить 24 на натуральные числа, начиная с 1 и продолжай до 9. Нам нужно записать те числа, которые полностью делят 24.

- Шаг 2: Числа, которые полностью делят 24, называются его делителями. Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Когда мы проверяем и перечисляем все числа до 9, мы автоматически получаем вместе с ним другой парный коэффициент. Например, начиная с 1, мы пишем 1 × 24 = 24, а 2 × 12 = 24 и так далее. Здесь (1, 24) образует первую пару, (2, 12) образует вторую пару, и список продолжается, как показано. Итак, когда мы записываем 1 как множитель 24, мы получаем другой множитель как 24; и поскольку мы пишем 2 как множитель 24, мы получаем 12 как другой множитель. Таким образом, мы получаем все факторы.
- Шаг 3 : После того, как список отмечен, мы получаем все делители числа 24, начиная с 1 вверх, вниз, а затем снова поднимаемся вверх до 24. Это дает нам полный список всех делителей числа 24 в виде показано на рисунке, приведенном выше.
Следовательно, делители числа 24 могут быть перечислены как 1, 2, 3, 4, 6, 8, 12 и 24. Теперь давайте узнаем о простой факторизации числа 24.
Теперь давайте узнаем о простой факторизации числа 24.
Прост-факторизация числа 24
Факторизация простых чисел — это способ представления числа в виде произведения его простых множителей. Простые делители числа — это те делители, которые являются простыми числами. Первичную факторизацию числа 24 можно выполнить, используя следующие шаги. Обратите внимание на приведенный ниже рисунок, чтобы понять простую факторизацию числа 24.
- Шаг 1: Первым шагом является деление числа 24 на его наименьший простой делитель. Мы знаем, что простой делитель — это простое число, являющееся делителем данного числа. Итак, с помощью правил делимости находим наименьший делитель заданного числа. Здесь мы получаем 2. Следовательно, 2 — наименьший простой делитель числа 24. Итак, 24 ÷ 2 = 12 .
- Шаг 2: Нам нужно многократно делить частное на 2, пока мы не получим число, которое больше не делится на 2. Итак, мы снова делим 12 на 2, что равно 12 ÷ 2 = 6
- Шаг 3: Разделите 6 еще раз на 2, чтобы получить 6 ÷ 2 = 3
- Шаг 4: Разделите частное на 3 еще раз, что равно 3 ÷ 3 = 1
- Шаг 5: Нам не нужно продолжать, так как мы получили 1 как наше частное.

- Шаг 6: Следовательно, разложение числа 24 на простые множители выражается как 2 × 2 × 2 × 3 = 2 3 × 3; где 2 и 3 — простые числа и простые множители числа 24.
Факторное дерево из 24
Мы также можем найти простые множители числа 24 с помощью дерева множителей. Факторное дерево 24 можно построить, разлагая 24 на множители, пока мы не достигнем его простых множителей. Эти факторы разделены и записаны в виде ветвей дерева. Окончательные множители обведены кружком и считаются простыми множителями числа 24. Давайте найдем простые множители числа 24, используя следующие шаги и дерево факторов, приведенное ниже.
- Шаг 1: Разделите 24 на два множителя. Возьмем 2 и 12.
- Шаг 2: Изучите эти множители, чтобы определить, являются ли они простыми или нет.
- Шаг 3: Поскольку 2 — простое число, мы обводим его кружком как один из простых множителей числа 24.
 Мы переходим к 12, составному числу, и далее разбиваем его на другие множители. Другими словами, мы повторяем процесс факторизации 12 и разбиения его на ветви, пока не достигнем простого числа.
Мы переходим к 12, составному числу, и далее разбиваем его на другие множители. Другими словами, мы повторяем процесс факторизации 12 и разбиения его на ветви, пока не достигнем простого числа. - Шаг 4: Здесь мы получаем 2 и 6. Итак, мы обводим 2, потому что это простое число, и разделяем 6 на 2 и 3. На этом этапе у нас остаются простые числа, 2 и 3. Мы обведите их, так как мы знаем, что они не могут быть факторизованы дальше. Это конец дерева факторов.
- Шаг 5: Следовательно, простые делители числа 24 = 2 × 2 × 2 × 3
Примечание: Следует отметить, что могут быть разные деревья множителей числа 24. Например, мы можем начать с разделения 24 на 4 и 6. Затем 4 можно разделить на 2 и 2, а 6 можно разделить на 2 и 3. Наконец, мы можем наблюдать те же самые простые множители, то есть 24 = 2 × 2 × 2 × 3
Коэффициенты 24 в парах
Делители числа 24 можно записывать парами. Это означает, что произведение парных множителей 24 всегда равно 24. Пары множителей 24 можно записать, как показано в таблице ниже:
Это означает, что произведение парных множителей 24 всегда равно 24. Пары множителей 24 можно записать, как показано в таблице ниже:
| Факторы | Коэффициенты положительной пары |
| 1 × 24 = 24 | 1, 24 |
| 2 × 12 = 24 | 2, 12 |
| 3 × 8 = 24 | 3, 8 |
| 4 × 6 = 24 | 4, 6 |
Возможны и отрицательные парные множители, потому что произведение двух отрицательных чисел также дает положительное число. Давайте посмотрим на множители отрицательной пары числа 24.
| Факторы | Коэффициенты отрицательной пары |
| -1 × -24 = 24 | -1, -24 |
| -2 × -12 = 24 | -2, -12 |
| -3 × -8 = 24 | -3, -8 |
| -4 × -6 = 24 | -4, -6 |
Следующие пункты объясняют некоторые особенности парных множителей числа 24.
- Парные множители числа 24 — это целые числа в парах, которые перемножаются для получения исходного числа, т. е. 24.
- Парные множители могут быть как положительными, так и отрицательными, но они не могут быть дробями или десятичными числами.
- Положительные парные множители числа 24 следующие: (1, 24), (2, 12), (3, 8) и (4, 6). Отрицательные парные множители числа 24: (-1, -24), (-2, -12), (-3, -8) и (-4, -6).
Важные примечания
- Только составные числа могут иметь более двух делителей. Поскольку 24 — составное число, оно имеет более двух делителей.
- Каждый множитель данного числа либо меньше, либо равен данному числу.
- Количество множителей заданного числа конечно. 24 имеет 8 делителей.
- Делители 24 — это те числа, которые делят 24 полностью, не оставляя остатка.
- 24 имеет всего 8 факторов: 1, 2, 3, 4, 6, 8, 12 и 24.
- Существует трюк, позволяющий вычислить общее количество делителей числа.
 Например, 24 = 2 × 2 × 2 × 3 = 2 3 × 3. Мы получаем простые факторизации 24 как 2 3 × 3. Просто прибавьте единицу (1) к показателям степени 3 и 1 по отдельности и умножьте их суммы. (3 + 1) × (1 + 1) = 4 × 2 = 8. Это означает, что 24 имеет всего 8 делителей.
Например, 24 = 2 × 2 × 2 × 3 = 2 3 × 3. Мы получаем простые факторизации 24 как 2 3 × 3. Просто прибавьте единицу (1) к показателям степени 3 и 1 по отдельности и умножьте их суммы. (3 + 1) × (1 + 1) = 4 × 2 = 8. Это означает, что 24 имеет всего 8 делителей.
Что нужно запомнить
Вспомним список множителей, отрицательных множителей и простых множителей числа 24. 12 и 24
☛ Связанные статьи
- Множители 224 — Множители 224 равны 1, 2, 4, 7, 8, 14, 16, 28, 32, 56, 112, 224
- Множители 243 — Множители 243 равны 1, 3, 9, 27, 81, 243
- Множители 245 — Множители 245 равны 1, 5, 7, 35, 49.
 , 245
, 245 - Множители 21 — Множители 21 равны 1, 3, 7, 21
- Множители 42 — Множители 42 равны 1, 2, 3, 6, 7, 14, 21, 42
- Коэффициенты 48 — Коэффициенты 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Примеры множителей числа 24
Пример 1: Запишите все положительные делители числа 24.
Решение:
Все положительные делители числа 24 равны 1, 2, 3, 4, 6, 8, 12 и 24.
- 24 Решение:
a.) Неверно, 6 является делителем 24, но 9 не является делителем 24.
b.) Верно, 2 и 3 являются простыми делителями числа 24.
Пример 3: Перечислите положительные и отрицательные парные множители числа 24.
Решение:
Положительные парные множители числа 24 следующие: (1, 24), (2, 12), (3, 8) и (4, 6). Отрицательные парные множители числа 24: (-1, -24), (-2, -12), (-3, -8) и (-4, -6).

перейти к слайдуперейти к слайдуперейти к слайду
Исследуйте удивительные способы узнать все о факторах!
Позвольте нашим лучшим преподавателям математики решить по шагам, которым вы следуете. Усвойте основную логику и никогда больше не боритесь с факторами.
Записаться на бесплатный пробный урок
Практические вопросы по факторам числа 24
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о факторах 24
Какие множители числа 24?
множителей числа 24 равны 1, 2, 3, 4, 6, 8, 12, 24, а его отрицательные множители равны -1, -2, -3, -4, -6, -8, -12, -24.
Каковы простые делители числа 24?
Простые делители числа 24 — это 2 и 3. Простые делители числа — это те делители, которые являются простыми числами. В этом случае, если мы разложим 24 на простые множители, мы получим 2 × 2 × 2 × 3 = 2 3 × 3, где 2 и 3 — простые числа и простые делители числа 24.
Каковы общие делители чисел 24 и 32?
Делители числа 24 могут быть перечислены как 1, 2, 3, 4, 6, 8, 12 и 24. Делители числа 32 могут быть перечислены как 1, 2, 4, 8, 16 и 32. Среди них , мы можем перечислить общие делители чисел 24 и 32 как 1, 2, 4 и 8. Теперь мы можем найти наибольший общий делитель (НОД) чисел 24 и 32, который равен 8.
Что такое наибольший общий делитель чисел 24 и 23?
Делители числа 24 равны 1, 2, 3, 4, 6, 8, 12, 24, а делители числа 23 равны 1, 23. Итак, мы видим, что числа 24 и 23 имеют только один общий делитель, равный 1. Следовательно, наибольший общий делитель (GCF) чисел 24 и 23 равен 1. Это также означает, что 24 и 23 взаимно просты.
Каковы общие делители чисел 24 и 21?
Делители числа 24 равны 1, 2, 3, 4, 6, 8, 12, 24, а числа числа 21 равны 1, 3, 7 и 21. Следовательно, (1, 3) являются общими делителями числа 24. и 21.
Какова сумма множителей числа 24?
Сумма всех множителей 24 может быть рассчитана путем сложения 1, 2, 3, 4, 6, 8, 12, 24, что равно 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы Factors
Factors of 24: Prime Factorization, Methods
Множители числа 24 — это, в основном, числа, на которые оно делится без остатка без остатка.
- Все множители: 1, 2, 3, 4, 6, 8, 12 и 24.
- Простые множители: 2, 3.
- Пары множителей:4, (1,22 2,12), (3,8), (4,6),(6,4),(8,3),(12,2) .
Факторизация простых чисел — это метод « выражения » или нахождения заданного числа как произведения простых чисел. Если число встречается более одного раза при простой факторизации, оно обычно выражается в экспоненциальной форме, чтобы сделать его более компактным.
Простая факторизация получается как : 2 × 2 × 2 × 3 = 2 3 × 3 .
Разложение числа 24 на простые множители методом обратного деления
Перевернутое деление — это один из методов, используемых для простой факторизации различных чисел.
В этом методе вы будете делить заданное «составное» число на несколько простых чисел (начиная с наименьшего) поровну, пока не получите простое число.
Он называется Upside-Down Division , потому что символ перевернут вверх ногами.
Здесь 24 – четное число. Таким образом, оно несомненно делится на 2 без остатка. Таким образом, 2 — его наименьший простой делитель 904:30 .
И получаем 24÷ 2 = 12. Теперь найдем простые множители полученного частного.
Повторяйте Шаг 1 и Шаг 2, пока мы не получим простое число как частное. Здесь 12 — это частное.
12÷ 2 = 6. Здесь 6 — частное. Теперь найдите простые делители числа 6.
6÷ 2= 3. Здесь 3 — простое число.
Итак, мы можем остановить процесс.
Таким образом, простая факторизация методом обратного деления получается: 2 × 2 × 2 × 3 = \(2^3 \times 3\).
Метод дерева факторов — это еще один способ получения простого разложения и всех факторов заданного числа.
Чтобы использовать этот метод для числа x ,
Сначала рассмотрим два множителя, скажем, a,b числа x, такие что a*b равно x и хотя бы один из них (a, b) является простым числом фактор говорят а.
Затем рассмотрим два делителя числа b, скажем, c, d, такие, что снова по крайней мере один из них является простым делителем. Этот процесс повторяется до тех пор, пока оба множителя не станут простыми, т. е. если мы получим оба множителя как простые на любом шаге, мы остановим процесс на этом.
Ниже приведено дерево множителей данного числа.
Здесь мы можем получить простую факторизацию 24 как 2 * 2 * 2 * 3, а два простых множителя равны 2, 3.
Сумма всех множителей искомого числа = (2 3 + 1 – 1)/(2 – 1) × (3 1 + 1 – 1)/(3 – 1) = 60
Каковы общие делители чисел 24 и 21?
Поскольку множители 24 равны 1, 2, 3, 4, 6, 8, 12, 24, а множители 21 равны 1, 3, 7, 21.



 Мы переходим к 12, составному числу, и далее разбиваем его на другие множители. Другими словами, мы повторяем процесс факторизации 12 и разбиения его на ветви, пока не достигнем простого числа.
Мы переходим к 12, составному числу, и далее разбиваем его на другие множители. Другими словами, мы повторяем процесс факторизации 12 и разбиения его на ветви, пока не достигнем простого числа. Например, 24 = 2 × 2 × 2 × 3 = 2 3 × 3. Мы получаем простые факторизации 24 как 2 3 × 3. Просто прибавьте единицу (1) к показателям степени 3 и 1 по отдельности и умножьте их суммы. (3 + 1) × (1 + 1) = 4 × 2 = 8. Это означает, что 24 имеет всего 8 делителей.
Например, 24 = 2 × 2 × 2 × 3 = 2 3 × 3. Мы получаем простые факторизации 24 как 2 3 × 3. Просто прибавьте единицу (1) к показателям степени 3 и 1 по отдельности и умножьте их суммы. (3 + 1) × (1 + 1) = 4 × 2 = 8. Это означает, что 24 имеет всего 8 делителей. , 245
, 245