| Сумма цифр | 24 |
| Произведение цифр | 768 |
| Произведение цифр (без учета ноля) | 768 |
| Все делители числа | 1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 32, 42, 48, 56, 64, 84, 96, 112, 128, 168, 192, 224, 336, 384, 448, 672, 896, 1344, 2688 |
| Наибольший делитель из ряда степеней двойки | 128 |
| Количество делителей | 32 |
| Сумма делителей | 8160 |
| Простое число? | Нет |
| Полупростое число? | Нет |
| Обратное число | 0. 0003720238095238095 |
| Римская запись | MMDCLXXXVIII |
| Индо-арабское написание | ٢٦٨٨ |
| Азбука морзе | ..— -…. —.. —.. |
| Факторизация | 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 * 7 |
| Двоичный вид | 101010000000 |
| Троичный вид | 10200120 |
| Восьмеричный вид | 5200 |
| Шестнадцатеричный вид (HEX) | A80 |
| Перевод из байтов | 2 килобайта 640 байтов |
| Цвет | RGB(0, 10, 128) или #000A80 |
| Наибольшая цифра в числе (возможное основание) | 8 (9) |
| Число Фибоначчи? | Нет |
| Нумерологическое значение | 6 семья, любовь, доброта, забота, переживания, обида, гармония, равновесие, баланс |
| Синус числа | -0. 9332339113479111 |
| Косинус числа | 0.35926935119806597 |
| Тангенс числа | -2.5975884339586126 |
| Натуральный логарифм | 7.89655270164304 |
| Десятичный логарифм | 3.4294292643817874 |
| Квадратный корень | 51. 84592558726288 |
| Кубический корень | 13.904106579545797 |
| Квадрат числа | |
| Перевод из секунд | 44 минуты 48 секунд |
| Дата по UNIX-времени | Thu, 01 Jan 1970 00:44:48 GMT |
| MD5 | b38e5ff5f816ac6e4169bce9314b2996 |
| SHA1 | 8eceef4ed8056e15bada60715b2cba3b2bbf724c |
| Base64 | MjY4OA== |
| QR-код числа 2688 |
Новости за 7 дней.
Сколько предметов домашнего обихода должно быть под рукой в ванной комнате? Их десятки. И что с ними делать? Как правило, они не отличаются выдающимся дизайном. Основой набора мебели для ванной комнаты Step стали популярные накладные раковины, устанавливаемые на столешницу, для которых предусмот….
Ассортимент гофрированных труб из нержавеющей стали торговой марки Stahlmann пополнился новыми диаметрами: 40А и 50А. Компания «Электросистемы и технологии» (входит в ГК «ССТ), официальный дистрибьютор бренда Stahlmann, по многочисленным просьбам клиентов расширила ассортимент гибких гофрированны….
Компания группы PORCELANOSA Grupo представляет свои новые коллекции напольного покрытия для наружного применения и самые инновационные технические решения для ванных комнат и систем гидроизоляции в официальных магазинах Испании и Португалии. Butech расширяет свой каталог продукции и технических реш….
В ассортименте EKF появилась эргономичная розетка для кухни со встраиваемой техникой.
Новинка c разъёмами типа РШ-ВШ позволяет удобно и эстетично подключить сразу два прибора – варочную панель и духовку.
Преимущества нового изделия:
привлекательная цена – можно сэкономить до 20 % бюджета;
ла….
Серия MPT включает четыре модели носимых видеорегистраторов Dahua со встроенными видеокамерами для ведения аудио- и видеозаписи непосредственно на месте события и формирования в случае происшествия доказательной базы. Эти мобильные устройства предназначены для использования в сфере обеспечения обще….
Одноабонентская вызывная панель IP-видеодомофона VTO2211G-WP обладает элегантным дизайном и тонкой легкой конструкцией. При этом она оснащена всем необходимым для быстрой установки и удобства эксплуатации. Помимо проводного интерфейса Ethernet, который также поддерживает подачу питания PoE, вызывн….
Стремительное развитие технологий и рост современных городов значительно влияют на наш образ жизни, дизайн и архитектуру.
В интерьерах стиль лофт лучше всего отражает урбанистический дух, предоставляя простор для творчества и самовыражения.
Новая коллекция мебели AQUATON ЛОФТ Урбан объединяет ос….
Решить проблему размещения на плоских кровлях дополнительного оборудования призваны два инновационных технических решения, разработанных Группой компаний fischer, мировым лидером в разработке и производстве современных крепежных изделий. Новые кровельные опоры — FFRB и FFRBH — призваны сделать эксп….
За изысканным интерьером всегда стоит качественный крепёж, который позволяет надёжно фиксировать полки, картины, люстры и другие аксессуары. Именно эту задачу решает серия пластиковых дюбелей с крюком EasyHook — новинка компании fischer, мирового лидера в сфере инновационных крепёжных решений. В с….
Качественная краска для деревянного пола – эффективное решение при реставрации старого или обустройстве нового напольного покрытия.
Правильно подобранный ЛКМ защитит дерево от истирания, исцарапывания, влаги, ультрафиолета, сохранит красивую фактуру дерева, придаст нужный оттенок, а также продлит с.
…
Представляем НОВИНКУ – клей SUPERFLEX K77 Белый для керамической плитки и керамогранита. SUPERFLEX K77 Белый – высокоэластичный плиточный клей на основе белого цемента для укладки любого типа плитки из керамогранита, клинкера, керамики и натурального камня, в том числе крупного формата. Свойства….
Динамики подавляющего большинства телевизоров хорошо справляются лишь с воспроизведением голосов дикторов новостей, а вот для музыки и спецэффектов в кино требуется более серьезное решение. Вот только большие колонки полноформатного домашнего кинотеатра — далеко не самый удобный и комфортный выход ….
Устройства ввода — это та часть компьютера, с которой мы напрямую контактируем каждый день. И именно от них часто зависит, насколько удобно нам будет работать, учиться или играть. Поэтому компания SVEN постоянно расширяет ассортимент компьютерных мышей и клавиатур, предлагая все новые решения. Ко….
Выбирайте паровую станцию, чтобы почувствовать себя обладателем профессиональной техники для домашнего использования.
По сравнению с классическими паровыми утюгами, паровая станция VT-2430 позволит Вам гладить белье в несколько раз быстрее и качественнее.
Отгладить костюм, брюки, платье, плащ или ….
Новый цвет — море сочетаний. За поисками этого оттенка мы отправились в Северную Европу. Нам нужен был серый, который вызывает ассоциацию с природой, а не бетонными джунглями. Глядя на пейзажи Исландии, мы поняли: «Вот он. Тот самый цвет». Спокойный, насыщенный, с теплым коричневым подтоном. ….
Компания dormakaba рада предложить Вам бесшумные решения для межкомнатных дверей — защёлки DORMA со смещённым магнитным ригелем серии 940-М WC и 940-М PZ. Товар на складе. Цвет исполнения торцевой планки замка: АВ – античная бронза и SN – матовый никель. Магнитные замки рекомендуются для установ….
Стилизованный рисунок натюрморта с кофе в обрамлении кофейных зернышек и сегменты с надписями на кофейную тематику чередуются с плитками, воспроизводящими фактуру шероховатого камня.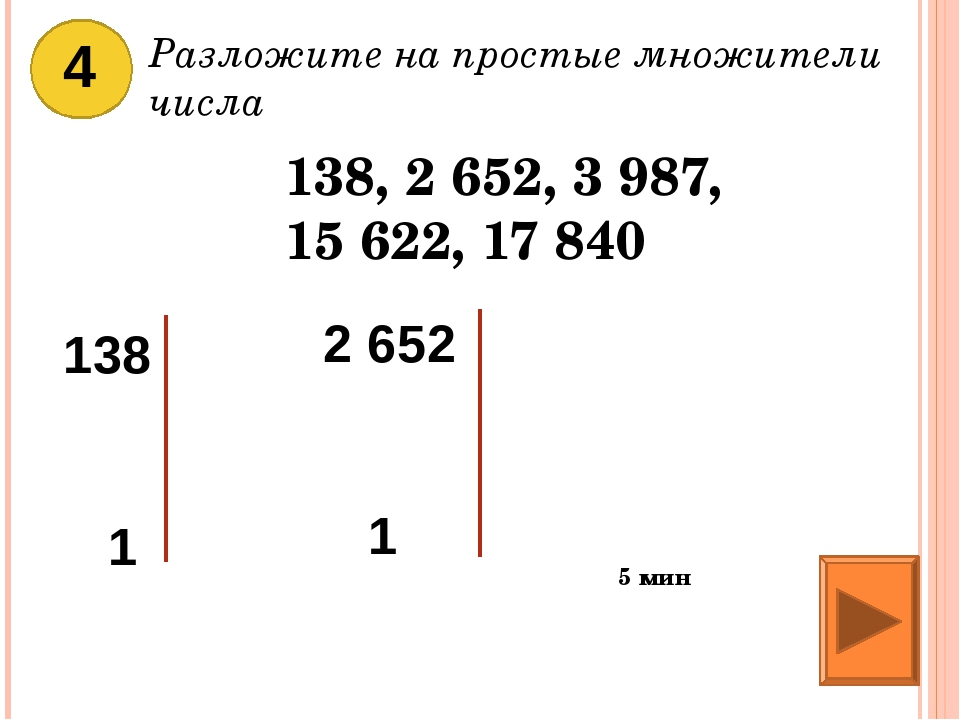
Баланс между акцентными и фоновыми элементами решен в пользу фона, что создает воздушность композиции, но при этом с….
Нежный узор из стилизованных полевых цветов. Плавными каллиграфическими росчерками он заполняет пространство, создавая легкий, вальсирующий ритм композиции. Отдельные элементы узора не объединены в сетку или колонны, традиционные для ритмики обойных принтов, а соединены в V-образные пересечения со….
Ветки, усыпанные некрупными цветами, застилают все полотно. Цельность композиции и наполненность пространства дизайна создают умиротворяющую обстановку и успокаивающий ритм. Тонкие веточки почти полностью укрыты цветами, присутствуют в узоре минимально. Переходы между элементами сглажены, отсутст….
Компактная вилка PPG16-42-201 с заземлением имеют разборную конструкцию и выполнена из ABS пластика и латунных токоведущих контактов.
Заземляющие стальные контакты, предусмотренные в конструкции, позволяют безопасно эксплуатировать электроприборы.
Применение:
Вилки разборные STEKKER серии PPG п….
Коробка «Express» 53800R теперь выпускаются в обновленном конструктиве. 8 герметичных вводов расположены по периметру коробки с максимальным размером вводов до 25 мм, а 2 дополнительных отверстия – на торцевой части коробки (их размер до 20 мм). Теперь есть возможность использовать c ответвительны….
Ассортимент шкафов из фибергласа пополнился новинками – в линейке появились цельнолитые навесные шкафы. Корпуса, изготовленные по этой технологии, имеют более высокую степень пыле- и влагозащиты и меньшую стоимость. При этом в новых моделях реализуются и все преимущества фибергласа: абсолютная кор….
Беспроводная технология LoRa – отличное решение для управления уличным освещением как для целых районов или дорог, так и для ограниченных участков – парковок ТЦ, дворов ЖК, парков и скверов.
Достаточно «защелкнуть» в светильник «умный» LoRa контроллер через стандартный NEMA разъем и освещение управ.
…
Ассортимент Werkel™ пополнился розетками с подсветкой в новых цветах: серебряный и слоновая кость. Кроме своей основной функции — питания электроприборов, розетка с помощью подсветки помогает обозначить себя в темное время суток. Подсветка создает равномерное рассеянное свечение, подходящее для ….
“Освещение придает пространству индивидуальный шарм. Важно, чтобы оно было отражением владельцев, подчеркивало многогранность дизайнерской идеи, даже в сдержанном и минималистичном интерьере.” — Добрый день! Меня зовут Заблодская Камилия, дизайнер студии «Time» с пятилетним опытом, и сегодня я под….
Идеально вписываются в любой интерьер и экономят средства на электроэнергии! ЭРА обновила ассортимент светодиодных ламп со штырьковым цоколем G4-G9, созданных для прямой замены предшественника – галогенной лампы. Капсульный светодиод мощностью 3-6 Вт излучает столько же света, сколько галогенная л….
К летнему сезону сформирован хороший товарных запас по силовым удлинителям ЭРА для дачных и строительных работ.
Второй квартал это самое горячее время для данной товарной группы, предлагаем обратить внимание на ассортимент.
Серия ЭРА RPx — удлинители на пластиковой катушке;
Серия ЭРА RMx — уд….
Компания ФОКУС представляет новый светильник ЖКХ 10, разработанный для освещения подъездов, лестничных площадок, коридоров и вспомогательных помещений. Благодаря степени защиты IP 65, обеспечивающей достаточную защиту от влаги и пыли, светильник так же можно размещать в помещениях с повышенной вл….
Компания представляет новую мебель для ванных комнат и спален, а также инновационную линейку кухонных гарнитуров, изготовленных из дерева и XTONE, для организации функциональных пространств. Компания Gamadecor делает выбор в пользу бесконечных и функциональных пространств за счет использования див….
Урок математики 5 класс Делимость натуральных чисел | План-конспект урока по математике (5 класс):
Урок Делимость натуральных чисел 5 класс
Цели урока: обобщить и систематизировать знания учащихся по теме «Делимость натуральных чисел», закрепить теоретические знания: определения делитель, кратное, простые и составные числа, свойства и признаки делимости, алгоритмы нахождения НОД и НОК,сформировать умения применять полученные теоретические знания для решения задач; развивать познавательный интерес, интеллектуальные и творческие способности учащихся; воспитывать целеустремленность и настойчивость в достижении цели.
Планируемые результаты: закрепление полученных знаний, формирование осознанных мотивов учения; развитие самосовершенствования, самовоспитания, самореализации, самоконтроля.пособ самоорганизации труда и самообразования.
Оборудование урока. мультимедиа проектор
Тип урока: обобщения и систематизации знаний
Ход урока
1. Организационный момент
2. Мотивация учебной деятельности
3. Актуализация опорных знаний
Повторение и закрепление теоретических знаний
Повторение определения: делитель, кратное, простые и составные числа, свойства и признаки делимости, алгоритмы нахождения НОД и НОК.
4. Закрепление изученного материала
Практикум решения упражнений
Найдите наибольший общий делитель чисел 18, 24, 36.
А) НОД (18, 24, 36) = 6;
В) НОД (18, 24, 36) = 5;
С) НОД (18, 24, 36) = 11;
Д) НОД (18, 24, 36) = 55.
Найдите наименьшее общее кратное чисел 12, 18, 50.
А) НОК (12, 18, 50) = 5;
В) НОК (12, 18, 50) = 300;
С) НОК (12, 18, 50) = 2;
Д) НОК (12, 18, 50) = 900.
Задача. Какое наибольшее количество команд, имеющих одинаковое количество мальчиков и одинаковое количество девочек, можно сформировать из 28 мальчиков и 12 девочек?
Задача. Длина шага Саши 40 см, а длина шага Вани 60 см. Через какое наименьшее расстояние их шаги будут совпадать? Сколько шагов при этом делает Саша?
Историческая справка (выступление учащихся)
Презентация о греческом математике, астрономе, географе и поэте – Эратосфене Киренском , алгоритме Евклида и его создателе
5. Проверка знаний и умений (взаимоконтроль). Самостоятельная работа
Контроль знаний и умений
1вариант
1 Какие из чисел 28; 24; 83; 378; 576; 892 делятся нацело:
1) на 2; 2) на 3.
2 Разложите число 1056 на простые множители.
3 Найдите наибольший общий делитель чисел:
24 и 42; 2) 128 и 192.
4 Найдите наименьшее общее кратное чисел:
1) 12 и 18; 2) 14 и 28; 3) 8 и 9.
5 Ребята на новогодней елке получили одинаковые подарки.
Во всех подарках вместе было 27 апельсинов и 45 яблок. Сколько ребят было на празднике?
2 вариант
1 Какие из чисел 28; 85; 108; 135; 240; 594 делятся нацело:
1) на 5; 2) на 9.
2 Разложите число 2688 на простые множители.
3 Найдите наибольший общий делитель чисел:
24 и 18; 2) 328 и 624.
4 Найдите наименьшее общее кратное чисел:
1) 12 и 16; 2) 15 и 30; 3) 4 и 15.
5 Ребята на новогодней елке получили одинаковые подарки. Во всех подарках вместе было 45 апельсинов и 72 яблок. Сколько ребят было на празднике?
6. Рефлексия деятельности на уроке.
Продолжи предложение:
- Сегодня я узнал…
- Было трудно…
- Я выполнял задания…
- Я понял, что…
7. Подведение итогов.
8. Домашнее задание. № 678, №698, придумать задачу.
Контрольная работа №7 по теме «НОД и НОК»математика 5 класс
Контрольная работа №7
Тема: « НОД и НОК»
ВАРИАНТ №1.
1.Какие из чисел 48; 378; 8480; 945; 932 делятся :
А) на 2
Б)на 3
В) на 4
Г)на 5
Д) на 6
е)На 10
Ж)на 15
2.Разложите 1056 на простые множители.
3.Найдите наибольший общий делитель чисел:
1) 24 и 42; 2) 14 и 28; 3) 8, 9 и 25
4.Найдите наименьшее общее кратное чисел:
1) 12 и 18; 2) 14 и 28; 3)8 и 9.
5.Тарас расставил свои модели самолетов поровну на 14 полках, а потом переставил их, тоже поровну, на 8 полок. Сколько моделей было у Тараса, если известно, что их у него больше, чем 100, и меньше, чем 120?
Контрольная работа №7
Тема: « НОД и НОК»
ВАРИАНТ №2.
1.Какие из чисел 24; 525; 8316; 480; 932 делятся :
А) на 2
Б)на 3
В) на 4
Г)на 5
Д) на 6
Е)на 10
Ж) на15
2.Разложите 2688 на простые множители.
3.Найдите наибольший общий делитель чисел:
1) 18 и 24; 2) 15 и 30; 3) 16, 27 и 5
4.Найдите наименьшее общее кратное чисел:
1) 12 и 16; 2) 15 и 30; 3)4 и 15.
5. Вася разложил собранные яблоки поровну в 12 пакетов, а потом переложил их, тоже поровну, в 16 пакетов. Сколько яблок было у Васи, если известно, что их у него больше, чем 80, и меньше, чем 110?
Разложение чисел на простые множители – калькулятор
Разложение числа на простые множители
Калькулятор выполняет разложение натуральных чисел на простые множители.
Калькулятор позволяет разложить одно, два, три или четыре числа на простые множители, а также найти их наибольший общий делитель и наименьшее общее кратное.
Разложение (факторизация) натуральных чисел на простые множители
Разложение на множители числа 100:100 = 2 * 2 * 5 * 5 = 22 * 52.
Разложение на множители числа 76:
76 = 2 * 2 * 19 = 22 * 19.
Разложение на множители числа 48:
48 = 2 * 2 * 2 * 2 * 3 = 24 * 3.
Разложение на множители числа 36:
36 = 2 * 2 * 3 * 3 = 22 * 32.
Разложение на множители числа 18:
18 = 2 * 3 * 3 = 2 * 32.
Разложение на множители числа 20:
20 = 2 * 2 * 5 = 22 * 5.
Разложение на простые множители числа 24:
24 = 2 * 2 * 2 * 3 = 23 * 3.
Разложение на простые множители числа 28:
28 = 2 * 2 * 7 = 22 * 7.
Разложение на простые множители числа 30:
30 = 2 * 3 * 5
Разложение на простые множители числа 32:
32 = 2 * 2 * 2 * 2 * 2 = 25.
Разложение на простые множители числа 36:
36 = 2 * 2 * 3 * 3 = 22 * 32.
Разложение на простые множители числа 40:
40 = 2 * 2 * 2 * 5 = 23 * 5.
Разложение на простые множители числа 42:
42 = 2 * 3 * 7
Разложение на простые множители числа 45:
45 = 3 * 3 * 5 = 32 * 5.
Разложение на простые множители числа 48:
48 = 2 * 2 * 2 * 2 * 3 = 24 * 3.
Разложение на простые множители числа 50:
50 = 2 * 5 * 5 = 2 * 52.
Разложение на простые множители числа 52:
52 = 2 * 2 * 13 = 22 * 13.
Разложение на простые множители числа 54:
54 = 2 * 3 * 3 * 3 = 2 * 33.
Разложение на простые множители числа 56:
56 = 2 * 2 * 2 * 7 = 23 * 7.
Разложение на простые множители числа 60:
60 = 2 * 2 * 3 * 5 = 22 * 3 * 5.
Как разложить на простые множители число 63:
63 = 3 * 3 * 7 = 32 * 7.
Как разложить на простые множители число 64:
64 = 2 * 2 * 2 * 2 * 2 * 2 = 26.
Как разложить на простые множители число 68:
68 = 2 * 2 * 17 = 22 * 17.
Как разложить на простые множители число 70:
70 = 2 * 5 * 7
Разложить на простые множители число 75:
75 = 3 * 5 * 5 75 = 3 * 52.
Разложить на простые множители число 78:
78 = 2 * 3 * 13
Разложить на простые множители число 80:
80 = 2 * 2 * 2 * 2 * 5 = 24 * 5.
Разложить на простые множители число 81:
81 = 3 * 3 * 3 * 3 81 = 34.
Разложить на простые множители число 84:
84 = 2 * 2 * 3 * 7 = 22 * 3 * 7.
Разложить на простые множители число 85:
85 = 5 * 17
Разложить на простые множители число 90:
90 = 2 * 3 * 3 * 5 = 2 * 32 * 5.
Разложить на простые множители число 96:
96 = 2 * 2 * 2 * 2 * 2 * 3 = 25 * 3.
Разложить на простые множители число 98:
98 = 2 * 7 * 7 = 2 * 72.
Разложить на простые множители число 99:
99 = 3 * 3 * 11 = 32 * 11.
|
39521910453Методическая разработка внеклассного мероприятия «Число и сила его значения» для 6 класса
При изучении математики, как в дошкольном, так и в школьном периоде большое внимание уделяется работа с числом, при решении различных задач. Школьники с разными развитием уровнями математических способностей всегда с интересом и увлеченностью решают задачи, если задача несет в себе познавательную информацию, связанную с историей чисел, их названий и суеверий народов мира.
Цель: Способствовать проявлению индивидуальных способностей учащихся и активизации их познавательной деятельности.
Задачи мероприятия:
1) обучающие: в увлекательной игровой форме повторить знания по математике 6 класса, способствовать развитию находчивости, смекалки, быстроты реакции;
2) развивающие: расширить кругозор обучающихся, интерес к математике;
3) воспитательные: формировать умения учащихся работать в группе.
Оборудование: презентация «Число и сила его значения»; текстовый вариант презентации для каждой команды; 4 таблицы с записанными числами от 1 до 30, записанными вразброс.
Участники мероприятия: 4 команды учащихся 6 класса
Введение
Ведущая: Здравствуйте. Сегодня проводится внеклассное мероприятие «Число и сила его значения», в котором принимают участие 4 команды учащихся 6 класса.
Представление жюри.
Не многие школьники скажут, что математика им нравится больше, чем другие школьные предметы. Другие скажут, что математику они любят за то, что им нравится решать интересные и трудные задачи, вычислять, работать с числами.
Число — это сложная, но очень интересная загадка. Числа сопровождают нас везде и всюду с самого дня рождения и во всех областях человеческой деятельности. Многие ли из нас знают, что означает число? У одних народов определенное число приносит удачу, у других беду.
Число появилось в глубокой древности. Древнегреческий математик и философ Пифагор утверждал, что «все вещи можно представить в виде чисел», что «числа правят миром». На основе цифр Пифагор создал науку предсказания — нумерологию, которую астрологи используют, при составлении гороскопов. Пифагор и его единомышленники считали, что числа несут добро, зло, счастье и несчастье. Эти суеверия дошли и до наших дней. Приведем несколько примеров.
Древние люди считали священными числа: 7(магическая семерка), 3 (святая троица), 13(чертова дюжина) и т. д. Число 7 в математике означает четвертое простое число, в науке — атомный номер азота, в христианстве — «мир создан за семь дней». В пословицах и словосочетаниях: «на седьмом небе»; «семь пятниц на неделе»; «семь раз отмерь — один раз отрежь». В мировой символике: Рим — город на семи холмах; Греция — «семь чудес света»; семь мудрецов, которых почитают и в наше время.
А число 13, как появилась легенда о несчастливом числе? В древности у китайцев, римлян и других народов за основу исчисления числа принимали число 12, оно как бы замыкало группу чисел.
Число 13 начинает новый цикл, тем самым нарушая равновесие, поэтому получило название несчастливого числа. В математике это шестое простое число; в науке — атомный номер алюминия; сумма квадратов двух простых чисел равна 13 (22+32 = 13). Во многих американских и европейских гостиницах нет 13 этажа и 13 номера. И есть суеверие, если это число выпадает на пятницу, день распятия Христа. Но число 13 считалось священным и благополучным у древних людей майя, древнем Китае.
В Японии, кроме числа 13, числа 4 и 9 тоже считаются несчастливыми. И все из — за того, что японское звучание слова четыре («ши») похоже на звучание слова «смерть» («си»), а число 9 по-японски звучит как «боль».
Помимо несчастливых чисел есть и счастливые, например, в Китае числа 8 и 9 относят благоприятным числам. Число 8 — число благоденствия; 9- символизирует полноту небес и земли. Благоприятной цифрой является также и цифра 7. Считается, что комбинации из чисел 7, 8, 9 приносят удачу их владельцу, стараются чтобы номер дома, квартиры или номер мобильного телефона включал эти числа.
В древности люди не могли применять числовые значения для предметов, применяя разные обозначения: один счет был для камней, другой для рыб и т. д. Но со временем люди научились отличать числовые понятия от конкретных вещей, что привело к тому, что числу стали приписывать магическое значение, представляясь в виде какого-то таинственного духа, который может приносить счастье или несчастье.
Многие суеверия в счастливые и несчастливые числа благополучно дожили до наших дней. Например: вера в счастливый билет. Билет, купленный за проезд в общественном транспорте, считается счастливым, если в шестизначном номере которого сумма первых трёх цифр совпадает с суммой трёх последних. Чтобы привлечь удачу нужно загадать желание и съесть его.
И в наши дни, многие взрослые подвержены к суевериям, чем дети. Большинство детей не знают, не слышали, не читали про числовые суеверия народов мира. И сегодня мы с помощью задач познакомимся с некоторыми числами.
Конкурс 1.
Разминка «быстрый счёт»
Вспомним дошкольные годы, где всех учили быстро считать. Приглашаем по одному участнику из каждой команды, которые хорошо умеют считать от 1 до 30. Нужно как можно быстрее показать числа от 1 до 30 (4 таблицы с числами от 1 до 30, записанными вразброс).
Конкурс 2. Блиц-опрос
- Первое простое число. (2)
- Самое маленькое трёхзначное число. (Сто)
- Что больше 2 см или 23 мм? (23 мм)
- Какую часть часа составляет 20 мин? ()
- Найти корень уравнения 6x = 1. (1)
- Простое число, которое стоит на четвертом месте? (7)
- Что больше — 10 или — 15? (– 10)
- Сколько секунд в часе? (3600)
Конкурс 3. Число исила его значения
1. «Пятница 13-ое не везде считается самым несчастливым днём календаря. В Греции и испаноязычных странах традиционно боятся выпадающего на 13-ое число вторника. А в Италии — пятницы, но другого числа, ведь этого числа итальянцы опасаются гораздо больше, чем 13. Возможное объяснение этому кроется ещё в могилах древних римлян, на которых были нередки надписи, перевод которых означает «Я жил» или «Моя жизнь кончена».
Задача: если сократить дробь на число, которого боятся итальянцы, то получится дробь . Найдите это число.
2. «Эти числа для многих подданных Английской Королевы означают, соответственно, «нет денег» и «срок истек». Это произошло оттого, что если в лондонском автобусе вставить электронную карту оплаты, то именно эти числа сообщат вам о нехватке денег или просрочке карты. Привыкнув к таким монологам бездушной машины, владельцы сотовых телефонов из столицы Великобритании стали использовать «автобусные» значения этих чисел в своих SMS-сообщениях, считая это не только более легким, но и более креативным способом общения».
Задача: решите уравнения 48-х=13 и 2х-2=20 вы найдете значение этих чисел, причем наибольший корень означает «нет денег», а наименьший корень «срок истек».
3. «Английский антрополог Роберт Данбар выявил взаимосвязь между размером новой коры больших полушарий головного мозга приматов и размером их стаи. На основании этих данных он определил оптимальный размер социальных связей для человека. Это же число находит подтверждение в самых разных исторических периодах и локациях: например, это оценочное число жителей неолитического поселения или размер базового подразделения римской армии. В 2010 году Данбар начал исследование социальной сети Facebook и пришёл к выводу, что его число действует и там: несмотря на то, что некоторые люди имеют в социальных сетях сотни и тысячи друзей, эффективно взаимодействовать средний человек способен с количеством контактов, которое не превышает это число».
Задача: найдите это число, вычислив наибольшее общее кратное чисел 3 и 50.
4. «Это название количественного числительного до 100 образуется не так, как другие. Объясняется это тем, что в древности условной единицей торговли меховыми шкурками была связка из такого числа штук, которое сегодня обозначается этим числительным. Ткань, в которую заворачивались эти шкурки, называлась именно этим числительным (от этого же корня происходит название одежды)».
Задача: Запишите название этого количественного числительного словом, если само это число составляет две трети часа.
5. Выделите целую часть дроби , и вы получите число, которое на тайском языке произносится как «ха». Какое число получится из фразы «Ха, ха, ха».
6. «А вот счастливым в Китае является наибольшее целое число выражения 9-х больше 0, но меньше 10, созвучное со словом «разбогатеть». Интересен еще и тот факт, что именно в Китае на аукционе «счастливых» мобильных номеров был продан за 1,1 млн. долларов номер 135 85 85 85 85, произношение которого созвучно с фразой «быть богатым, быть богатым, быть богатым, быть богатым».
7. «Одно и то же число может сулить несчастья в одной стране, тогда как в другой на это число надеются как на талисман удачи. Говоря о несчастливых числах, невольно вспоминаешь данное число. Многие люди не совершают важных сделок и покупок в этот день, например, некоторые французские авиакомпании исключили это число из нумерации рядов кресел в салоне. И такая оборонительная обстановка действует во многих странах Европы, а также в США».
Задача: вычислите корень уравнения 2х — 12=14 вы найдете это число.
8. «Подлинность купюры евро можно проверить по её серийному номеру, состоящему из буквы и одиннадцати цифр. Нужно заменить букву на её порядковый номер в латинском алфавите, сложить это число с остальными, затем складывать цифры результата, пока не получим одну цифру. Если эта цифра — 8, то купюра подлинная. Кстати, в долларе также зашифровано число 8. Если посчитать нумерологический код, то dollar = 8, а это самое денежное число: символ силы, мощи и энергии предпринимательства. Еще восьмерка символизирует бесконечность, способность к самовоспроизведению. Определите, какая из представленных купюр подлинная. Буква S в латинском алфавите имеет порядковый номер 19».
а) б)
№ | Конкурс | Критерии | 1 команда | 2 команда | 3 команда | 4 команда |
1 | Счет | 1 балл первому | ||||
2 | Блиц-опрос | По 1 баллу за ответ | ||||
3 | Числа, сотворившие чудеса | 3 балл за правильный и полный ответ | ||||
Итоги | ||||||
Подведение итогов. Награждение.
Ответы к конкурсу:
1. 17; 2. 11 и 35; 3. 150; 4. Сорок; 5. 555; 6. 8; 7.13; 8. а).
Литература:
- Учебник по математике, 6 класс Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд издательство: Мнемозина 2015 год., 214 стр.
- http://money-fact.livejournal.com/2688.html
- http://www.drozdovland.ru/index.php?action=add&id=1133&add&rod=244
4. У каждого народа свои несчастливые числа | Мир | ИноСМИ inosmi.ru/world/20130915/212973366.html
5. Интересные факты о цифрах и числах — Мир MS Excel
6. Влияние чисел на судьбу asosch2.narod.ru/tvorchestvo27.html
Основные термины (генерируются автоматически): число, простое число, задача, Греция, Китай, команда учащихся, корень уравнения, латинский алфавит, несчастливое число, порядковый номер.
Что такое факторизация числа 2688 на простые множители?
Почему разложение на простые множители 2,688 записывается как 2
7 x 3 1 x 7 1 ?Что такое факторизация на простые множители?
Факторизация на простые множители или Разложение на простые множители — это процесс определения, какие простые числа можно умножить вместе, чтобы получить исходное число.
Нахождение простых делителей 2,688
Чтобы найти простые множители, вы начинаете с деления числа на первое простое число, равное 2.Если здесь — это не остаток, то есть вы можете разделить поровну, тогда 2 — коэффициент числа. Продолжайте делить на 2, пока вы больше не сможете делить поровну. Запишите, на сколько двоек вы смогли равномерно разделить. Теперь попробуйте разделить на следующий простой множитель, равный 3. Цель состоит в том, чтобы получить частное, равное 1.
Если еще не имеет смысла, попробуем …
Вот несколько первых простых множителей: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29…
Начнем с деления 2,688 на 2
2,688 ÷ 2 = 1,344 — без остатка! 2 — это один из факторов!
1,344 ÷ 2 = 672 — Без остатка! 2 — это один из факторов!
672 ÷ 2 = 336 — без остатка! 2 — это один из факторов!
336 ÷ 2 = 168 — без остатка! 2 — это один из факторов!
168 ÷ 2 = 84 — без остатка! 2 — это один из факторов!
84 ÷ 2 = 42 — без остатка! 2 — это один из факторов!
42 ÷ 2 = 21 — без остатка! 2 — это один из факторов!
21 ÷ 2 = 10.5 — Есть остаток. Мы больше не можем делить на 2 поровну. Давайте попробуем следующее простое число
21 ÷ 3 = 7 — без остатка! 3 — один из факторов!
7 ÷ 3 = 2,3333 — есть остаток. Мы больше не можем делить на 3 поровну. Давайте попробуем следующее простое число
7 ÷ 5 = 1,4 — у него есть остаток. 5 не имеет значения.
7 ÷ 7 = 1 — без остатка! 7 — это один из факторов!
Оранжевые делители выше представляют собой простые делители числа 2,688. Если мы сложим все это вместе, мы получим множители 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 7 = 2,688.Его также можно записать в экспоненциальной форме как 2 7 x 3 1 x 7 1 .
Дерево факторов
Другой способ выполнить разложение на простые множители — использовать факторное дерево. Ниже представлено факторное дерево для числа 2,688.
Другие примеры простой факторизации
Попробуйте калькулятор коэффициентов
Факторы 2688 в парах (факторные пары для 2688)
Значит, вам нужно найти пары факторов для 2688, не так ли? Не бойся! В этом кратком руководстве мы опишем, что такое факторные пары 2688, как вы их находите, и перечислим их, чтобы вы могли доказать, что расчет работает.Давайте нырнем!
Что такое факторные пары?
Факторная пара — это комбинация двух факторов, которые можно умножить на 2688. В математических терминах число 2688 называется произведением, а два числа, которые можно умножить, чтобы получить равное, называются факторами.
Чтобы вычислить пары факторов для 2688, нам нужно сначала получить все факторы для 2688. Когда у вас есть список всех этих факторов, мы можем объединить их вместе, чтобы перечислить все пары факторов.
Полный список факторов для 2688: 1, 2, 3, 6, 7, 12, 21, 24, 42, 48, 84, 96, 128, 168, 192, 336, 384, 448, 672, 896, 1344. , и 2688.
Список факторных пар для 2688
Итак, теперь мы знаем все коэффициенты для 2688, и чтобы определить пары факторов, мы можем просмотреть этот список и найти все различные комбинации, которые можно использовать для умножения вместе, чтобы получить 2688.
Если факторов много, то вычисление всех пар факторов может занять некоторое время, но, к счастью, у нас есть мощность компьютеров, и мы можем автоматически рассчитать пары факторов 2688 для вас:
- 1 x 2688 = 2688
- 2 x 1344 = 2688
- 3 x 896 = 2688
- 6 x 448 = 2688
- 7 x 384 = 2688
- 12 x 224 = 2688
- 21 x 128 = 2688
- 24 x 112 = 2688
- 42 x 64 = 2688
- 48 x 56 = 2688
- 84 x 32 = 2688
- 96 x 28 = 2688
- 128 x 21 = 2688
- 168 x 16 = 2688
- 192 x 14 = 2688
- 336 x 8 = 2688
- 384 x 7 = 2688
- 448 x 6 = 2688
- 672 x 4 = 2688
- 896 x 3 = 2688
- 1344 x 2 = 2688
- 2688 х 1 = 2688
Итак, вот оно.Полное руководство по факторным парам 2688. Надеюсь, это поможет вам на уроке математики выучить (или научить) факторные пары таким образом, чтобы это было легко понять.
Не стесняйтесь попробовать калькулятор ниже, чтобы проверить другое число, или, если вам нравится, возьмите карандаш и бумагу и попробуйте сделать это вручную. Просто выбирайте небольшие числа! 😉
Цитируйте, ссылайтесь или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Факторы 2688 в парах». VisualFractions.com . По состоянию на 10 июня 2021 г. https://visualfractions.com/calculator/factor-pairs/factors-of-2688-in-pairs/.
«Факторы 2688 в парах». VisualFractions.com , https: // visualfractions.ru / калькулятор / пары факторов / факторы 2688 в парах /. По состоянию на 10 июня 2021 г.
Факторы 2688 в парах. VisualFractions.com. Получено с https://visualfractions.com/calculator/factor-pairs/factors-of-2688-in-pairs/.
Калькулятор факторных пар
Хотите найти пары факторов для другого числа? Введите свой номер ниже и нажмите рассчитать.
Расчет следующей факторной пары
Как найти множители 2688
Значит, вам нужно найти множители 2688, не так ли? В этом кратком руководстве мы опишем, что такое факторы 2688, как вы их находите, и перечислим пары факторов 2688, чтобы вы могли доказать, что расчет работает.Давайте нырнем!
Хотите быстро узнать или показать студентам, как найти множители 2688? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Факторы определения 2688
Когда мы говорим о множителях числа 2688, на самом деле мы имеем в виду все положительные и отрицательные целые числа (целые числа), которые можно равномерно разделить на 2688. Если бы вы взяли 2688 и разделили его на один из его множителей, Ответом будет еще один множитель 2688.
Давайте посмотрим, как найти все множители 2688 и перечислить их.
Как найти множители 2688
Мы только что сказали, что множитель — это число, которое можно разделить поровну на 2688. Таким образом, чтобы найти и перечислить все множители 2688, нужно пройти все числа до 2688 включительно и проверить, какие числа дают четное частное (что означает отсутствие десятичного разряда).
Выполнение этого вручную для больших чисел может занять много времени, но компьютерной программе это относительно легко сделать.Наш калькулятор рассчитал это за вас. Вот все множители 2688:
- 2688 ÷ 1 = 2688
- 2688 ÷ 2 = 1344
- 2688 ÷ 3 = 896
- 2688 ÷ 4 = 672
- 2688 ÷ 6 = 448
- 2688 ÷ 7 = 384
- 2688 ÷ 8 = 336
- 2688 ÷ 12 = 224
- 2688 ÷ 14 = 192
- 2688 ÷ 16 = 168
- 2688 ÷ 21 = 128
- 2688 ÷ 24 = 112
- 2688 ÷ 28 = 96
- 2688 ÷ 32 = 84
- 2688 ÷ 42 = 64
- 2688 ÷ 48 = 56
- 2688 ÷ 56 = 48
- 2688 ÷ 64 = 42
- 2688 ÷ 84 = 32
- 2688 ÷ 96 = 28
- 2688 ÷ 112 = 24
- 2688 ÷ 128 = 21
- 2688 ÷ 168 = 16
- 2688 ÷ 192 = 14
- 2688 ÷ 224 = 12
- 2688 ÷ 336 = 8
- 2688 ÷ 384 = 7
- 2688 ÷ 448 = 6
- 2688 ÷ 672 = 4
- 2688 ÷ 896 = 3
- 2688 ÷ 1344 = 2
- 2688 ÷ 2688 = 1
Все эти факторы можно использовать для деления 2688 на и получите целое число.Полный список положительных факторов для 2688:
1, 2, 3, 4, 6, 7, 8, 12, 14, 16, 21, 24, 28, 32, 42, 48, 56, 64, 84, 96, 112, 128, 168, 192, 224 , 336, 384, 448, 672, 896, 1344 и 2688
Отрицательные факторы 2688
Технически, в математике у вас также может быть отрицательный множитель 2688. Если вы хотите вычислить множители числа для домашнего задания или теста, чаще всего учитель или экзамен будут искать конкретно положительные числа.
Однако мы можем просто превратить положительные числа в отрицательные, и эти отрицательные числа также будут множителями 2688:
.-1, -2, -3, -4, -6, -7, -8, -12, -14, -16, -21, -24, -28, -32, -42, -48, — 56, -64, -84, -96, -112, -128, -168, -192, -224, -336, -384, -448, -672, -896, -1344 и -2688
Сколько существует факторов 2688?
Как видно из приведенных выше вычислений, всего 32 положительных фактора для 2688 и 32 отрицательных фактора для 2688, всего 64 фактора для числа 2688.
Есть 32 положительных множителя 2688 и 32 отрицательных множителя 2688. Какие отрицательные числа могут быть множителем 2688?
Факторные пары из 2688
Пара факторов — это комбинация двух факторов, которые можно умножить, чтобы получить 2688. Для 2688 все возможные пары факторов перечислены ниже:
- 1 x 2688 = 2688
- 2 x 1344 = 2688
- 3 x 896 = 2688
- 4 x 672 = 2688
- 6 x 448 = 2688
- 7 x 384 = 2688
- 8 x 336 = 2688
- 12 x 224 = 2688
- 14 x 192 = 2688
- 16 x 168 = 2688
- 21 x 128 = 2688
- 24 x 112 = 2688
- 28 x 96 = 2688
- 32 x 84 = 2688
- 42 x 64 = 2688
- 48 x 56 = 2688
Мы также написали руководство, в котором более подробно описаны пары факторов для 2688 на случай, если вам интересно!
Как и раньше, мы также можем перечислить все пары отрицательных факторов для 2688:
- -1 x -2688 = 2688
- -2 x -1344 = 2688
- -3 x -896 = 2688
- -4 x -672 = 2688
- -6 x -448 = 2688
- -7 x -384 = 2688
- -8 x -336 = 2688
- -12 x -224 = 2688
- -14 x -192 = 2688
- -16 x -168 = 2688
- -21 x -128 = 2688
- -24 x -112 = 2688
- -28 x -96 = 2688
- -32 x -84 = 2688
- -42 x -64 = 2688
- -48 x -56 = 2688
Примечание в отрицательные факторы пары, которые, поскольку мы умножаем минус на минус, получаем положительное число.
Итак, вот оно. Полное руководство по факторам 2688. Теперь у вас должны быть знания и навыки, чтобы вычислить свои собственные факторы и пары факторов для любого числа, которое вам нравится.
Не стесняйтесь попробовать калькулятор ниже, чтобы проверить другое число, или, если вам нравится, возьмите карандаш и бумагу и попробуйте сделать это вручную. Просто выбирайте небольшие числа!
Цитируйте, ссылайтесь или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Факторы 2688». VisualFractions.com . По состоянию на 10 июня 2021 г. https://visualfractions.com/calculator/factors/factors-of-2688/.
«Факторы 2688». VisualFractions.com , https://visualfractions.com/calculator/factors/factors-of-2688/. По состоянию на 10 июня 2021 г.
Факторы 2688. VisualFractions.com. Получено с https://visualfractions.com/calculator/factors/factors-of-2688/.
Калькулятор факторов
Хотите найти множитель для другого числа? Введите свой номер ниже и нажмите рассчитать.
Расчет следующего фактора
Факторы 2689
Множители 1365 — Найдите простые множители / множители 1365
Множители 1365 — это числа, которые при попарном умножении дают произведение 1365.Имеется 16 делителей числа 1365, из которых следующие являются его простыми множителями 3, 5, 7, 13. Сумма всех множителей числа 1365 составляет 2688.
Факторы 1365 представляют собой пары тех чисел, произведение которых дает 1365. Эти числа факторы — это либо простые числа, либо составные числа.
Чтобы найти множители 1365, нам нужно найти список чисел, которые делят 1365, не оставляя остатка.
Аналогичным образом мы можем найти и другие факторы. Следовательно, множители 1365 равны 1, 3, 5, 7, 13, 15, 21, 35, 39, 65, 91, 105, 195, 273, 455, 1365.
Число 1365 составное, поэтому оно состоит из простых делителей. Теперь давайте узнаем, как вычислить простые множители 1365. Первый шаг — разделить число 1365 на наименьший простой множитель, здесь он равен 3. Мы продолжаем делить, пока не получим ненулевой остаток.
Дальнейшее деление 455 на 3 дает ненулевой остаток. Итак, мы останавливаем процесс и продолжаем делить число 455 на следующий наименьший простой множитель. В конце концов, мы останавливаемся, если следующего основного фактора не существует или когда мы не можем дальше делиться.
Итак, разложение на простые множители числа 1365 можно записать как 3 1 × 5 1 × 7 1 × 13 1 , где 3, 5, 7, 13 — простые числа.
Парные множители 1365 — это пары чисел, которые при умножении дают произведение 1365. Попарно множители 1365:
ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, а) также является парным множителем этого числа.
Часто задаваемые вопросы по факторам 1365
Какие факторы у 1365?
Коэффициенты числа 1365: 1, 3, 5, 7, 13, 15, 21, 35, 39, 65, 91, 105, 195, 273, 455, 1365, а отрицательные факторы — -1, -3, -5. , -7, -13, -15, -21, -35, -39, -65, -91, -105, -195, -273, -455, -1365.
Какова сумма всех факторов числа 1365?
Сумма всех множителей 1365 = (3 1 + 1 — 1) / (3 — 1) × (5 1 + 1 — 1) / (5 — 1) × (7 1 + 1 — 1) / (7-1) × (13 1 + 1 -1) / (13-1) = 2688
Какие парные множители у 1365?
Парные множители числа 1365: (1, 1365), (3, 455), (5, 273), (7, 195), (13, 105), (15, 91), (21, 65), ( 35, 39).
Каков наибольший общий множитель 1365 и 1149?
Коэффициенты 1365 и 1149 равны 1, 3, 5, 7, 13, 15, 21, 35, 39, 65, 91, 105, 195, 273, 455, 1365 и 1, 3, 383, 1149 соответственно.
Общие множители 1365 и 1149 равны [1, 3].
Следовательно, GCF 1365 и 1149 составляет 3.
Сколько факторов числа 858 являются общими для факторов числа 1365?
Так как множители 1365 равны 1, 3, 5, 7, 13, 15, 21, 35, 39, 65, 91, 105, 195, 273, 455, 1365, а множители 858 — 1, 2, 3. , 6, 11, 13, 22, 26, 33, 39, 66, 78, 143, 286, 429, 858.
Следовательно, [1, 3, 13, 39] являются общими множителями 1365 и 858.
Корпус-Кристи Прайм — Дружественные поля и открытые карты
Это простое число, состоящее из 2688 цифр.Он также очень похож на колледж Корпус-Кристи в Кембридже. В верхнем левом углу закодированы мои инициалы JRH в кодировке ASCII. В правом нижнем углу указана моя дата рождения.
Меня вдохновило последнее видео Numberphile, в котором показано простое число из 1350 цифр, которое похоже на герб колледжа Тринити-Холл в Кембридже.
У меня есть несколько хороших открыток с этим номером. Если вы живете в Кембридже и хотели бы что-нибудь, пришлите мне электронное письмо.
Как это было сделано?
Я создал пиксельное искусство, которое немного похоже на Колледж, но немного сжато, поскольку пиксели квадратные, а символы — прямоугольники.
Затем я выбрал шрифт (Menlo) и подсчитал количество пикселей, используемых для каждой цифры. Я выбрал Menlo, потому что в нем очень тяжелые нули, которые, как мне казалось, могут пригодиться.
Затем я написал программу, которая генерировала «идеальное» число на основе этих двух частей информации. Затем я вручную внес две требуемые модификации (которые не были полностью нарциссическими — число должно заканчиваться нечетной цифрой, а числа, начинающиеся с 1, с большей вероятностью будут простыми).
Наконец, я произвел случайные колебания числа и проверил каждое с помощью критерия простоты Миллера-Рабина. В результате был составлен короткий список чисел, которые, скорее всего, были простыми. Я использовал фантастический инструмент Дарио Альперна, чтобы определить, действительно ли кто-то из них был первоклассным. Из 8 кандидатов, которых я создал за одну ночь, все они были первоклассными, поэтому я выбрал самого красивого, который вы видите выше.
Почему я был уверен, что это сработает?
Теорема о простых числах говорит нам, что существует примерно число меньше, чем.Так что примерно
2688-значные простые числа. Таким образом, примерно одно из каждых 6200 2688-значных чисел является простым. Я не смотрел на четные числа, так что это уменьшает их вдвое, так что все выглядит неплохо.
Я немного запустил свою программу и определил, что на моем оборудовании (MacBook Air с процессором 1,7 ГГц и 8 ГБ ОЗУ) моя программа может определить, являются ли около 30 2688-значных чисел простыми в минуту. Я подумал, что на поиск кандидата уйдет около 100 минут.На этот раз я немного переоценил: за ночь (9 часов) я проверил 25750 чисел и нашел 8 вероятных простых чисел. Это очень хорошо согласуется с расчетом конверта, приведенным выше.
Число
Не стесняйтесь проверить, проста ли она:
10010107777777777777707777777777777777777707777777777777777777771010010777777777777702077777777777777777702077777777777777777777100100077777777777777077777777777777777777077777777777777777777777777777777777777777050777777777777777777050777777777777777777777777777777777777777055107777777777777777015507777777777777777777777777777777777777705550777777777777777705550777777777777777777777777777777777777770000377777770077777773000077777777777777777777777777777777777770433307777770880777777033340777777777777777777777777777877777777700000777777100177777700000777777777777777777777787770777777777770997710550177777099
77777777077777777777777017777777777099
7105555017777099
77777771077777777777777047777777777099
7053003507177100007777777777407777777777777010777777778700080050051111115005008000777777777701077777777777701077777777771091100000011500099
777777701077777777777772477777777770000011150511116051110010077777777773277777777777777007777787777099301500115005 110051039
77777770077777777777777077877777771099300011110880111100039
77877777077777777777777047777777700000001111115005111112000000078777777407778777700070056011001105505911111111111110995055011001106500700070656065555005500555001111600511111100500550055556065605555555555555555555001508898880511100555555555555555550000005500000000000090
8880 90 0888888880111090111111105501111195111055011159951110908008008008111090599511105501115105501168008511030301118888888888111030301151206501158008011000011080080110535011188888888800000000550000001111105501111111111090
535011080080110000110800801105501108008010 11188888888881110000
018011055011080080210550110800801105550111000033000011105650110800801105501108008011055011080080110595034000000000999330595011080080110550110803331105501133333311093305555655555555555033 333331205501133300000055000000000000959999999999999095
00000000550000001111505505 111111111094
111211111111109411111150550511111111105501111111111092 000092 1111111055011112111110000111111211109508889888801110951111111000011111851110550111580950800880080111195198511105501115800511065011500081110920088888800111092800051105501150008311055011380801100550188888800111095500110808311055011380083110550113808011055555011008888880011055555011080831105601131105611130000110555550110088888800110555550110000311055011300111105555011111111055555011008888880011055555011111111055550111211110555501111111105555501100888888001105555501111111105500000000000055550000000000555550000088888800000555550000000000550120397
Нравится:
Нравится Загрузка…
Молекулярные роли и функции кольцевых РНК в эукариотических клетках
Darnell JE Jr (2013) Размышления об истории процессинга пре-мРНК и основные моменты современных знаний: единая картина. РНК 19: 443–460
CAS PubMed PubMed Central Статья Google Scholar
Hang J, Wan R, Yan C, Shi Y (2015) Структурная основа сплайсинга пре-мРНК. Наука 349: 1191–1198
CAS PubMed Статья Google Scholar
Aebi M, Hornig H, Padgett RA, Reiser J, Weissmann C (1986) Требования к последовательности для сплайсинга ядерной пре-мРНК высших эукариот. Ячейка 47: 555–565
CAS PubMed Статья Google Scholar
Beyer AL, Osheim YN (1988) Выбор сайта сплайсинга, скорость сплайсинга и альтернативный сплайсинг на возникающих транскриптах. Genes Dev 2: 754–765
CAS PubMed Статья Google Scholar
de la Mata M, Lafaille C, Kornblihtt AR (2010) Первый пришел, первый обслужил еще раз: факторы, влияющие на одно и то же альтернативное событие сплайсинга, по-разному влияют на относительные скорости удаления интронов. РНК 16: 904–912
PubMed PubMed Central Статья CAS Google Scholar
Puttaraju M, Been MD (1992) Группа I произвела перестановку последовательностей интрон-экзон (PIE) для получения кольцевых экзонов. Nucleic Acids Res 20: 5357–5364
CAS PubMed PubMed Central Статья Google Scholar
Jarrell KA (1993) Обратный сплайсинг интрона группы II. Proc Natl Acad Sci USA 90: 8624–8627
CAS PubMed PubMed Central Статья Google Scholar
Nigro JM, Cho KR, Fearon ER, Kern SE, Ruppert JM, Oliner JD, Kinzler KW, Vogelstein B (1991) Скремблированные экзоны. Ячейка 64: 607–613
CAS PubMed Статья Google Scholar
Cocquerelle C, Daubersies P, Majerus MA, Kerckaert JP, Bailleul B (1992) Сплайсинг с инвертированным порядком экзонов происходит проксимальнее больших интронов.EMBO J 11: 1095–1098
CAS PubMed PubMed Central Google Scholar
Кейпел Б., Суэйн А., Николис С., Хакер А., Уолтер М., Купман П., Гудфеллоу П., Ловелл-Бэдж Р. (1993) Циркулярные транскрипты гена Sry, определяющего семенники, в семенниках взрослых мышей. Ячейка 73: 1019–1030
CAS PubMed Статья Google Scholar
Schindewolf C, Braun S, Domdey H (1996) Создание кольцевого экзона in vitro из линейного транскрипта пре-мРНК.Nucleic Acids Res 24: 1260–1266
CAS PubMed PubMed Central Статья Google Scholar
Pasman Z, Been MD, Garcia-Blanco MA (1996) Циркуляризация экзонов в ядерных экстрактах млекопитающих. РНК 2: 603-610
CAS PubMed PubMed Central Google Scholar
Salzman J, Gawad C, Wang PL, Lacayo N, Brown PO (2012) Циркулярные РНК являются преобладающей изоформой транскрипта сотен генов человека в различных типах клеток.PLoS One 7: e30733
CAS PubMed PubMed Central Статья Google Scholar
Сабо Л., Зальцман Дж. (2016) Обнаружение кольцевых РНК: биоинформатические и экспериментальные проблемы. Nat Rev Genet 17: 679–692
CAS PubMed PubMed Central Статья Google Scholar
Vincent HA, Deutscher MP (2006) Распознавание и катализ субстрата экзорибонуклеазой РНКазой R.J Biol Chem 281: 29769–29775
CAS PubMed Статья Google Scholar
Popow J et al (2011) HSPC117 является важной субъединицей лигазного комплекса сплайсинга тРНК человека. Наука 331: 760–764
CAS PubMed Статья Google Scholar
Лу З., Филонов Г.С., Ното Дж. Дж., Шмидт С.А., Хаткевич Т.Л., Вен Й., Джаффри С.Р., Матера А.Г. (2015) Интроны тРНК многоклеточных животных генерируют стабильные кольцевые РНК in vivo.РНК 21: 1554–1565
CAS PubMed PubMed Central Статья Google Scholar
Nielsen H, Fiskaa T, Birgisdottir AB, Haugen P, Einvik C, Johansen S (2003) Способность образовывать полноразмерные интронные круги РНК является общим свойством интронов ядерной группы I. РНК 9: 1464–1475
CAS PubMed PubMed Central Статья Google Scholar
Li-Pook-Than J, Bonen L (2006) Множественные физические формы вырезанных интронных РНК группы II в митохондриях пшеницы. Нуклеиновые кислоты Res 34: 2782–2790
CAS PubMed PubMed Central Статья Google Scholar
Zaug AJ, Grabowski PJ, Cech TR (1983) Автокаталитическая циклизация вырезанной промежуточной последовательности РНК представляет собой реакцию отщепления-лигирования. Nature 301: 578–583
CAS PubMed Статья Google Scholar
Sullivan FX, Cech TR (1985) Обратимость циклизации промежуточной последовательности рРНК Tetrahymena: влияние на механизм выбора сайта сплайсинга. Ячейка 42: 639–648
CAS PubMed Статья Google Scholar
Hedberg A, Johansen SD (2013) Интроны ядерной группы I в процессе самосплайсинга и за его пределами. ДНК моба 4:17
CAS PubMed PubMed Central Статья Google Scholar
Chillon I, Molina-Sanchez MD, Fedorova O, Garcia-Rodriguez FM, Martinez-Abarca F, Toro N (2014) Характеристика in vitro эффективности сплайсинга и верности интрона группы II RmInt1 как средство контроля дисперсии его основной мобильный элемент. РНК 20: 2000–2010
CAS PubMed PubMed Central Статья Google Scholar
Андерсен К.Л., Бекерт Б., Маскида Б., Йохансен С.Д., Нильсен Х. (2016) Накопление стабильных полноразмерных кольцевых интронных РНК группы i во время теплового шока.Молекулы 21 (11): 1451–1468
Артикул CAS Google Scholar
Clement JQ, Qian L, Kaplinsky N, Wilkinson MF (1999) Стабильность и судьба сплайсированного интрона из клеток позвоночных. РНК 5: 206–220
CAS PubMed PubMed Central Статья Google Scholar
Jacquier A, Rosbash M (1986) Сплайсинг РНК и оборот интронов значительно уменьшаются из-за точки ветвления мутантных дрожжей.Proc Natl Acad Sci USA 83: 5835–5839
CAS PubMed PubMed Central Статья Google Scholar
Zhang Y et al (2013) Циркулярные интронные длинные некодирующие РНК. Mol Cell 51: 792–806
CAS PubMed Статья Google Scholar
Braun S, Domdey H, Wiebauer K (1996) Обратный сплайсинг прерывистого интрона пре-мРНК генерирует кольцевой экзон в ядерном экстракте клетки HeLa.Nucleic Acids Res 24: 4152–4157
CAS PubMed PubMed Central Статья Google Scholar
Szabo L et al (2015) Статистическое обнаружение сплайсинга показывает обогащение нейронов и тканеспецифическую индукцию кольцевой РНК во время внутриутробного развития человека. Геном Биол 16: 126
PubMed PubMed Central Статья CAS Google Scholar
Ashwal-Fluss R et al (2014) биогенез circRNA конкурирует со сплайсингом пре-мРНК. Mol Cell 56: 55–66
CAS PubMed Статья Google Scholar
Starke S, Jost I, Rossbach O, Schneider T, Schreiner S, Hung LH, Bindereif A (2015) Циркуляризация экзонов требует канонических сигналов сплайсинга. Cell Rep 10: 103–111
CAS PubMed Статья Google Scholar
Wang Y, Wang Z (2015) Эффективный обратный сплайсинг производит переводимые кольцевые мРНК. РНК 21: 172–179
PubMed PubMed Central Статья CAS Google Scholar
Памудурти Н.Р. и др. (2017) Трансляция CircRNAs. Mol Cell 66 (1): 9-21.e7
CAS PubMed PubMed Central Статья Google Scholar
Barrett SP, Wang PL, Salzman J (2015) Биогенез круговой РНК может протекать через экзон-содержащий предшественник лариата.Элиф 4: e07540
PubMed PubMed Central Статья CAS Google Scholar
Zhang Y, Xue W, Li X, Zhang J, Chen S, Zhang JL, Yang L, Chen LL (2016) Биогенез возникающих кольцевых РНК. Сотовый представитель 15: 611–624
CAS PubMed Статья Google Scholar
Kramer MC, Liang D, Tatomer DC, Gold B, March ZM, Cherry S, Wilusz JE (2015) Комбинаторный контроль экспрессии кольцевой РНК дрозофилы с помощью интронных повторов, hnRNP и белков SR.Genes Dev 29: 2168–2182
CAS PubMed PubMed Central Статья Google Scholar
Liang D, Wilusz JE (2014) Короткие интронные повторяющиеся последовательности облегчают производство кольцевой РНК. Genes Dev 28: 2233–2247
PubMed PubMed Central Статья CAS Google Scholar
Dubin RA, Kazmi MA, Ostrer H (1995) Инвертированные повторы необходимы для циркуляризации транскрипта Sry семенников мыши.Ген 167: 245–248
CAS PubMed Статья Google Scholar
Jeck WR, Sorrentino JA, Wang K, Slevin MK, Burd CE, Liu J, Marzluff WF, Sharpless NE (2013) Круглые РНК многочисленны, консервативны и связаны с повторами ALU. РНК 19: 141–157
CAS PubMed PubMed Central Статья Google Scholar
Zhang XO, Wang HB, Zhang Y, Lu X, Chen LL, Yang L (2014) Циркуляризация экзонов, опосредованная комплементарной последовательностью.Ячейка 159: 134–147
CAS PubMed Статья Google Scholar
Иванов А. и др. (2015) Анализ последовательностей интронов выявляет признаки биогенеза кольцевой РНК у животных. Cell Rep 10: 170–177
CAS PubMed Статья Google Scholar
de Koning AP, Gu W, Castoe TA, Batzer MA, Pollock DD (2011) Повторяющиеся элементы могут составлять более двух третей генома человека.PLoS Genet 7: e1002384
PubMed PubMed Central Статья CAS Google Scholar
Zheng Q et al (2016) Циркулярное профилирование РНК выявляет большое количество circHIPK3, который регулирует рост клеток за счет размораживания множества miRNA. Nat Commun 7: 11215
CAS PubMed PubMed Central Статья Google Scholar
Westholm JO et al (2014) Полногеномный анализ кольцевых РНК дрозофил показывает их структурные свойства и свойства последовательности, а также возрастное нейронное накопление.Cell Rep 9: 1966–1980
CAS PubMed PubMed Central Статья Google Scholar
Wang PL et al (2014) Циркулярная РНК экспрессируется через эукариотическое древо жизни. PLoS One 9: e
PubMed PubMed Central Статья CAS Google Scholar
Zaphiropoulos PG (1996) Циркулярные РНК из транскриптов гена цитохрома P450 2C24 крысы: корреляция с пропуском экзона.Proc Natl Acad Sci USA 93: 6536–6541
CAS PubMed PubMed Central Статья Google Scholar
Surono A, Takeshima Y, Wibawa T, Ikezawa M, Nonaka I, Matsuo M (1999) Циркулярные РНК дистрофина, состоящие из экзонов, которые были пропущены путем альтернативного сплайсинга. Hum Mol Genet 8: 493–500
CAS PubMed Статья Google Scholar
Burd CE, Jeck WR, Liu Y, Sanoff HK, Wang Z, Sharpless NE (2010) Экспрессия линейных и новых кольцевых форм некодирующей РНК, ассоциированной с INK4 / ARF, коррелирует с риском атеросклероза.PLoS Genet 6: e1001233
PubMed PubMed Central Статья CAS Google Scholar
Jeck WR, Sharpless NE (2014) Выявление и характеристика кольцевых РНК. Nat Biotechnol 32: 453–461
CAS PubMed PubMed Central Статья Google Scholar
Salzman J, Chen RE, Olsen MN, Wang PL, Brown PO (2013) Особенности клеточного типа экспрессии кольцевой РНК.PLoS Genet 9: e1003777
CAS PubMed PubMed Central Статья Google Scholar
Conn SJ et al (2015) Quaking РНК-связывающий белок регулирует образование circRNAs. Ячейка 160: 1125–1134
CAS PubMed Статья Google Scholar
Errichelli L et al (2017) FUS влияет на экспрессию кольцевой РНК в двигательных нейронах мышиных эмбриональных стволовых клеток.Nat Commun 8: 14741
CAS PubMed PubMed Central Статья Google Scholar
Wu JI, Reed RB, Grabowski PJ, Artzt K (2002) Функция сотрясения при миелинизации: регулирование альтернативного сплайсинга. Proc Natl Acad Sci USA 99: 4233–4238
CAS PubMed PubMed Central Статья Google Scholar
Hall MP, Nagel RJ, Fagg WS, Shiue L, Cline MS, Perriman RJ, Donohue JP, Ares M. Jr (2013) Quaking и PTB контролируют перекрывающиеся регуляторные сети сплайсинга во время дифференцировки мышечных клеток.РНК 19: 627–638
CAS PubMed PubMed Central Статья Google Scholar
Masuda A et al (2015) Позиционно-специфическое связывание FUS с формирующейся РНК регулирует длину мРНК. Genes Dev 29: 1045–1057
CAS PubMed PubMed Central Статья Google Scholar
Barash Y, Calarco JA, Gao W., Pan Q, Wang X, Shai O, Blencowe BJ, Frey BJ (2010) Расшифровка кода сращивания.Nature 465: 53–59
CAS PubMed Статья Google Scholar
Braunschweig U, Gueroussov S, Plocik AM, Graveley BR, Blencowe BJ (2013) Динамическая интеграция сплайсинга в пути регуляции генов. Ячейка 152: 1252–1269
CAS PubMed PubMed Central Статья Google Scholar
Li, X et al (2017) Скоординированный биогенез циркулярной РНК и функция NF90 / NF110 при вирусной инфекции.Mol Cell 67 (2): 214-227.e7
CAS PubMed Статья Google Scholar
Harashima A, Guettouche T, Barber GN (2010) Фосфорилирование белков NFAR дцРНК-зависимой протеинкиназой PKR представляет собой новый механизм регуляции трансляции и клеточной защиты. Genes Dev 24: 2640–2653
CAS PubMed PubMed Central Статья Google Scholar
Enuka Y, Lauriola M, Feldman ME, Sas-Chen A, Ulitsky I, Yarden Y (2016) Циркулярные РНК являются долгоживущими и обнаруживают только минимальные ранние изменения в ответ на фактор роста. Нуклеиновые кислоты Res 44: 1370–1383
CAS PubMed Статья Google Scholar
Schwanhausser B, Busse D, Li N, Dittmar G, Schuchhardt J, Wolf J, Chen W., Selbach M (2011) Глобальная количественная оценка контроля экспрессии генов млекопитающих. Nature 473: 337–342
PubMed Статья CAS Google Scholar
Hansen TB, Wiklund ED, Bramsen JB, Villadsen SB, Statham AL, Clark SJ, Kjems J (2011) miRNA-зависимое молчание гена, включающее Ago2-опосредованное расщепление кольцевой антисмысловой РНК. EMBO J 30: 4414–4422
CAS PubMed PubMed Central Статья Google Scholar
Schoenberg DR, Maquat LE (2012) Регулирование цитоплазматического распада мРНК. Nat Rev Genet 13: 246–259
CAS PubMed PubMed Central Статья Google Scholar
Kilchert C, Wittmann S, Vasiljeva L (2016) Регуляция и функции комплекса экзосом ядерной РНК. Nat Rev Mol Cell Biol 17: 227–239
CAS PubMed Статья Google Scholar
Schaeffer D, Tsanova B, Barbas A, Reis FP, Dastidar EG, Sanchez-Rotunno M, Arraiano CM, van Hoof A (2009) Экзосома содержит домены со специфической активностью эндорибонуклеазы, экзорибонуклеазы и цитоплазматической активности распада мРНК. Nat Struct Mol Biol 16: 56–62
CAS PubMed Статья Google Scholar
Wang X et al (2014) N6-метиладенозин-зависимая регуляция стабильности информационной РНК. Nature 505: 117–120
PubMed Статья CAS Google Scholar
Zhou C et al (2017) Идентификация и характеристика эпитранскриптомов кольцевой РНК m6A. bioRxiv
Huang H, Kawamata T, Horie T., Tsugawa H, Nakayama Y, Ohsumi Y, Fukusaki E (2015) Массовая деградация РНК в дрожжах в результате аутофагии, вызванной азотным голоданием.EMBO J 34: 154–168
CAS PubMed Статья Google Scholar
Lai CP, Kim EY, Badr CE, Weissleder R, Mempel TR, Tannous BA, Breakefield XO (2015) Визуализация и отслеживание доставки внеклеточных пузырьков опухоли и трансляции РНК с использованием мультиплексированных репортеров. Nat Commun 6: 7029
CAS PubMed PubMed Central Статья Google Scholar
Valadi H, Ekstrom K, Bossios A, Sjostrand M, Lee JJ, Lotvall JO (2007) Опосредованный экзосомами перенос мРНК и микроРНК — это новый механизм генетического обмена между клетками. Nat Cell Biol 9: 654–659
CAS PubMed Статья Google Scholar
Arroyo JD et al (2011) Комплексы Argonaute2 несут популяцию циркулирующих микроРНК независимо от пузырьков в плазме человека. Proc Natl Acad Sci USA 108: 5003–5008
CAS PubMed PubMed Central Статья Google Scholar
Zernecke A et al (2009) Доставка микроРНК-126 апоптозными тельцами индуцирует CXCL12-зависимую защиту сосудов. Научный сигнал 2: ra81
PubMed Статья Google Scholar
Lo Cicero A, Stahl PD, Raposo G (2015) Внеклеточные пузырьки перетасовывают межклеточные сообщения: хорошо или плохо. Curr Opin Cell Biol 35: 69–77
CAS PubMed Статья Google Scholar
Lasda E, Parker R (2016) Циркулярные РНК со-преципитируют с внеклеточными везикулами: возможный механизм клиренса circRNA. PLoS One 11: e0148407
PubMed PubMed Central Статья CAS Google Scholar
Ebbesen KK, Hansen TB, Kjems J (2016) Взгляд на биологию кольцевой РНК. RNA Biol, 1–11
Guo JU, Agarwal V, Guo H, Bartel DP (2014) Расширенная идентификация и характеристика кольцевых РНК млекопитающих.Genome Biol 15: 409
PubMed PubMed Central Статья CAS Google Scholar
Rybak-Wolf A et al (2015) Циркулярные РНК в мозге млекопитающих очень многочисленны, консервативны и динамически экспрессируются. Mol Cell 58: 870–885
CAS PubMed Статья Google Scholar
Рой С.К., Олсон С., Грейвли Б.Р., Замор П.Д., Мур М.Дж. (2015) Оценка связи между последовательностями РНК на больших расстояниях с помощью лигирования ДНК-ДНК с использованием шаблонов РНК.eLife 4: e03700
PubMed Central Google Scholar
Сахаркар М.К., Чоу В.Т., Кангуан П. (2004) Распределение экзонов и интронов в геноме человека. В Silico Biol 4: 387–393
CAS PubMed Google Scholar
Memczak S et al (2013) Циркулярные РНК представляют собой большой класс животных РНК с регуляторной активностью. Nature 495: 333–338
CAS PubMed Статья Google Scholar
Dang Y et al (2016) Отслеживание экспрессии кольцевых РНК в человеческих эмбрионах до имплантации. Геном Биол 17: 130
PubMed PubMed Central Статья CAS Google Scholar
Li Z et al (2015) Экзон-интронные кольцевые РНК регулируют транскрипцию в ядре. Nat Struct Mol Biol 22: 256–264
CAS PubMed Статья Google Scholar
Engreitz JM et al (2014) взаимодействия РНК-РНК делают возможным специфическое нацеливание некодирующих РНК на возникающие пре-мРНК и сайты хроматина. Ячейка 159: 188–199
CAS PubMed PubMed Central Статья Google Scholar
Kwek KY, Murphy S, Furger A, Thomas B, O’Gorman W, Kimura H, Proudfoot NJ, Akoulitchev A (2002) мяРНК U1 связывается с TFIIH и регулирует инициацию транскрипции. Nat Struct Biol 9: 800–805
CAS PubMed Google Scholar
Fong YW, Zhou Q (2001) Стимулирующий эффект факторов сплайсинга на удлинение транскрипции. Nature 414: 929–933
CAS PubMed Статья Google Scholar
Kaida D, Berg MG, Younis I, Kasim M, Singh LN, Wan L, Dreyfuss G (2010) U1 snRNP защищает пре-мРНК от преждевременного расщепления и полиаденилирования. Nature 468: 664–668
CAS PubMed PubMed Central Статья Google Scholar
Gardner EJ, Nizami ZF, Talbot CC Jr, Gall JG (2012) Стабильная интронная последовательность РНК (sisRNA), новый класс некодирующих РНК из ядра ооцита Xenopus tropicalis. Genes Dev 26: 2550–2559
CAS PubMed PubMed Central Статья Google Scholar
Talhouarne GJ, Gall JG (2014) Интронные РНК лариата в цитоплазме ооцитов Xenopus tropicalis . РНК 20: 1476–1487
CAS PubMed PubMed Central Статья Google Scholar
Pek JW, Osman I, Tay ML, Zheng RT (2015) Стабильные РНК с интронной последовательностью могут играть регулирующую роль в Drosophila melanogaster . J Cell Biol 211: 243–251
CAS PubMed PubMed Central Статья Google Scholar
Komarnitsky P, Cho EJ, Buratowski S (2000) Различные фосфорилированные формы РНК-полимеразы II и связанные с ними факторы процессинга мРНК во время транскрипции. Genes Dev 14: 2452–2460
CAS PubMed PubMed Central Статья Google Scholar
Koh W, Gonzalez V, Natarajan S, Carter R, Brown PO, Gawad C (2016) Динамический пропуск экзона ASXL1 и альтернативный круговой сплайсинг в одиночных клетках человека. PLoS One 11: e0164085
PubMed PubMed Central Статья CAS Google Scholar
Dar RD, Razooky BS, Singh A, Trimeloni TV, McCollum JM, Cox CD, Simpson ML, Weinberger LS (2012) Транскрипционная частота и размер пакета одинаково модулируются в геноме человека.Proc Natl Acad Sci USA 109: 17454–17459
CAS PubMed PubMed Central Статья Google Scholar
Elowitz MB, Levine AJ, Siggia ED, Swain PS (2002) Стохастическая экспрессия гена в одной клетке. Наука 297: 1183–1186
CAS PubMed Статья Google Scholar
Cai L, Dalal CK, Elowitz MB (2008) Частотно-модулированные всплески ядерной локализации координируют регуляцию генов.Nature 455: 485–490
CAS PubMed PubMed Central Статья Google Scholar
Deng Q, Ramskold D, Reinius B, Sandberg R (2014) Single-cell RNA-seq выявляет динамическую, случайную моноаллельную экспрессию гена в клетках млекопитающих. Наука 343: 193–196
CAS PubMed Статья Google Scholar
Shalek AK et al (2013) Одноклеточная транскриптомика выявляет бимодальность экспрессии и сплайсинга в иммунных клетках.Nature 498: 236–240
CAS PubMed PubMed Central Статья Google Scholar
de la Mata M et al (2003) Медленная РНК-полимераза II влияет на альтернативный сплайсинг in vivo. Mol Cell 12: 525–532
PubMed Статья Google Scholar
Caceres JF, Kornblihtt AR (2002) Альтернативный сплайсинг: множественные механизмы контроля и участие в заболеваниях человека.Тенденции Genet 18: 186–193
CAS PubMed Статья Google Scholar
Ip JY, Schmidt D, Pan Q, Ramani AK, Fraser AG, Odom DT, Blencowe BJ (2011) Глобальное влияние ингибирования элонгации РНК-полимеразы II на альтернативную регуляцию сплайсинга. Genome Res 21: 390–401
CAS PubMed PubMed Central Статья Google Scholar
Dujardin G, Lafaille C, de la Mata M, Marasco LE, Munoz MJ, Le Jossic-Corcos C, Corcos L, Kornblihtt AR (2014) Как медленное удлинение РНК-полимеразы II способствует альтернативному пропуску экзонов.Mol Cell 54: 683–690
CAS PubMed Статья Google Scholar
Fong N et al (2014) Сплайсинг пре-мРНК облегчается за счет оптимальной скорости элонгации РНК-полимеразы II. Genes Dev 28: 2663–2676
PubMed PubMed Central Статья Google Scholar
Carrillo Oesterreich F, Herzel L, Straube K, Hujer K, Howard J, Neugebauer KM (2016) Сплайсинг возникающей РНК совпадает с выходом интрона из РНК-полимеразы II.Ячейка 165: 372–381
CAS Статья Google Scholar
Suzuki H, Zuo Y, Wang J, Zhang MQ, Malhotra A, Mayeda A (2006) Характеристика расщепленного РНКазой R источника клеточной РНК, который состоит из лариатных и кольцевых РНК от сплайсинга пре-мРНК. Нуклеиновые кислоты Res 34: e63
PubMed PubMed Central Статья CAS Google Scholar
Lewis BP, Green RE, Brenner SE (2003) Доказательства широко распространенного сочетания альтернативного сплайсинга и нонсенс-опосредованного распада мРНК у людей.Proc Natl Acad Sci USA 100: 189–192
CAS PubMed Статья Google Scholar
Chedin F (2016) Возникающие связи: R-петли и формирование паттерна хроматина. Тенденции Genet 32: 828–838
CAS PubMed PubMed Central Статья Google Scholar
Sanz LA, Hartono SR, Lim YW, Steyaert S, Rajpurkar A, Ginno PA, Xu X, Chedin F (2016) Распространенные, динамические и консервативные структуры R-петли связаны со специфическими эпигеномными сигнатурами у млекопитающих.Mol Cell 63: 167–178
CAS PubMed PubMed Central Статья Google Scholar
Felipe-Abrio I, Lafuente-Barquero J, Garcia-Rubio ML, Aguilera A (2015) РНК-полимераза II способствует предотвращению опосредованных транскрипцией остановок репликационной вилки. EMBO J 34: 236–250
CAS PubMed Статья Google Scholar
Conn VM et al (2017) circRNA из SEPALLATA3 регулирует сплайсинг своей родственной мРНК посредством образования R-петли.Природные растения 3: 17053
CAS PubMed Статья Google Scholar
Shete S et al (2009) Полногеномное ассоциативное исследование идентифицирует пять локусов восприимчивости к глиоме. Нат Генет 41: 899–904
CAS PubMed PubMed Central Статья Google Scholar
Wrensch M et al (2009) Варианты в областях CDKN2B и RTEL1 связаны с предрасположенностью к глиомам высокой степени.Нат Генет 41: 905–908
CAS PubMed PubMed Central Статья Google Scholar
Bishop DT et al (2009) Полногеномное ассоциативное исследование идентифицирует три локуса, связанных с риском меланомы. Нат Генет 41: 920–925
CAS PubMed PubMed Central Статья Google Scholar
Cunnington MS, Santibanez Koref M, Mayosi BM, Burn J, Keavney B (2010) SNP хромосомы 9p21, ассоциированные с множественными фенотипами заболеваний, коррелируют с экспрессией anril.PLoS Genet 6: e1000899
PubMed PubMed Central Статья CAS Google Scholar
Nakaoka H et al (2016) Аллельный дисбаланс в регуляции ANRIL через взаимодействие хроматина в локусе риска эндометриоза 9p21. PLoS Genet 12: e1005893
PubMed PubMed Central Статья CAS Google Scholar
Holdt LM et al (2013) Элементы Alu в некодирующей РНК ANRIL на хромосоме 9p21 модулируют функции атерогенных клеток посредством трансрегуляции генных сетей.PLoS Genet 9: e1003588
CAS PubMed PubMed Central Статья Google Scholar
Holdt LM et al (2010) Экспрессия ANRIL связана с риском атеросклероза на хромосоме 9p21. Артериосклер Thromb Vasc Biol 30: 620–627
CAS PubMed Статья Google Scholar
Schunkert H et al (2011) Крупномасштабный ассоциативный анализ идентифицирует 13 новых локусов восприимчивости к ишемической болезни сердца.Нат Генет 43: 333–338
CAS PubMed PubMed Central Статья Google Scholar
Helgadottir A et al (2007) Распространенный вариант хромосомы 9p21 влияет на риск инфаркта миокарда. Наука 316: 1491–1493
CAS PubMed Статья Google Scholar
McPherson R et al (2007) Распространенный аллель хромосомы 9, связанный с ишемической болезнью сердца.Наука 316: 1488–1491
CAS PubMed PubMed Central Статья Google Scholar
Helgadottir A et al (2008) Такой же вариант последовательности на 9p21 ассоциируется с инфарктом миокарда, аневризмой брюшной аорты и внутричерепной аневризмой. Нат Генет 40: 217–224
CAS PubMed Статья Google Scholar
Yu W, Gius D, Onyango P, Muldoon-Jacobs K, Karp J, Feinberg AP, Cui H (2008) Эпигенетическое подавление гена-супрессора опухоли p15 его антисмысловой РНК.Nature 451: 202–206
CAS PubMed PubMed Central Статья Google Scholar
Kotake Y, Nakagawa T, Kitagawa K, Suzuki S, Liu N, Kitagawa M, Xiong Y (2011) Длинная некодирующая РНК ANRIL необходима для рекрутирования PRC2 в опухоль p15 (INK4B) и ее подавления. супрессорный ген. Онкоген 30: 1956–1962
CAS PubMed Статья Google Scholar
Yap KL et al (2010) Молекулярное взаимодействие некодирующей РНК ANRIL и метилированного гистона h4 лизина 27 с помощью polycomb CBX7 в подавлении транскрипции INK4a. Mol Cell 38: 662–674
CAS PubMed PubMed Central Статья Google Scholar
Holdt LM et al (2016) Циркулярная некодирующая РНК ANRIL модулирует созревание рибосомальной РНК и атеросклероз у людей. Nat Commun 7: 12429
CAS PubMed PubMed Central Статья Google Scholar
Abdelmohsen K et al (2017) Идентификация кольцевых РНК-мишеней HuR раскрывает подавление трансляции PABPN1 с помощью CircPABPN1. РНК Biol 14 (3): 361–369
PubMed PubMed Central Статья Google Scholar
Lebedeva S, Jens M, Theil K, Schwanhausser B, Selbach M, Landthaler M, Rajewsky N (2011) Транскриптомный анализ регуляторных взаимодействий РНК-связывающего белка HuR. Mol Cell 43: 340–352
CAS PubMed Статья Google Scholar
Hentze MW, Preiss T (2013) Циркулярные РНК: вариации загадки сплайсинга. EMBO J 32: 923–925
CAS PubMed PubMed Central Статья Google Scholar
Poliseno L, Salmena L, Zhang J, Carver B, Haveman WJ, Pandolfi PP (2010) Независимая от кодирования функция мРНК генов и псевдогенов регулирует биологию опухолей. Nature 465: 1033–1038
CAS PubMed PubMed Central Статья Google Scholar
Franco-Zorrilla JM et al (2007) Мимикрия мишеней обеспечивает новый механизм регуляции активности микроРНК. Нат Генет 39: 1033–1037
CAS PubMed Статья Google Scholar
Hansen TB, Jensen TI, Clausen BH, Bramsen JB, Finsen B, Damgaard CK, Kjems J (2013) Круги естественной РНК функционируют как эффективные губки для микроРНК. Nature 495: 384–388
CAS PubMed Статья Google Scholar
Hafner M et al (2010) Идентификация по всей транскриптоме РНК-связывающего белка и сайтов-мишеней микроРНК с помощью PAR-CLIP. Ячейка 141: 129–141
CAS PubMed PubMed Central Статья Google Scholar
You X et al (2015) Нервные кольцевые РНК происходят из синаптических генов и регулируются развитием и пластичностью. Nat Neurosci 18: 603–610
CAS PubMed PubMed Central Статья Google Scholar
Alhasan AA et al (2016) Обогащение циркулярной РНК в тромбоцитах является признаком деградации транскриптома. Кровь 127: e1 – e11
CAS PubMed PubMed Central Статья Google Scholar
Паули А., Вален Е., Шиер А.Ф. (2015) Идентификация (не) кодирующих РНК и малых пептидов: проблемы и возможности. BioEssays 37: 103–112
CAS PubMed Статья Google Scholar
Andrews SJ, Rothnagel JA (2014) Новые доказательства функциональных пептидов, кодируемых короткими открытыми рамками считывания. Нат Рев Генет 15: 193–204
CAS PubMed Статья Google Scholar
Kozak M (1986) Точечные мутации определяют последовательность, фланкирующую кодон инициатора AUG, который модулирует трансляцию эукариотическими рибосомами. Ячейка 44: 283–292
CAS PubMed Статья Google Scholar
Chen CY, Sarnow P (1995) Инициирование синтеза белка эукариотическим трансляционным аппаратом на кольцевых РНК. Наука 268: 415–417
CAS PubMed Статья Google Scholar
Bazzini AA et al (2014) Идентификация малых ORF у позвоночных с использованием рибосомного следа и эволюционной консервации. EMBO J 33: 981–993
CAS PubMed PubMed Central Статья Google Scholar
Li XF, Lytton J (1999) Циркулярный транскрипт экзона 2 натрий-кальциевого обменника. J Biol Chem 274: 8153–8160
CAS PubMed Статья Google Scholar
Legnini I et al (2017) Circ-ZNF609 представляет собой кольцевую РНК, которая может транслироваться и функционирует в миогенезе. Mol Cell 66 (1): 22-37.e9
CAS PubMed PubMed Central Статья Google Scholar
Zhou J, Wan J, Gao X, Zhang X, Jaffrey SR, Qian SB (2015) Dynamic m (6) Метилирование мРНК направляет трансляционный контроль ответа на тепловой шок. Nature 526: 591–594
CAS PubMed PubMed Central Статья Google Scholar
Meyer KD et al (2015) 5’UTR m (6) A способствует независимой от кэп трансляции. Ячейка 163: 999–1010
CAS PubMed PubMed Central Статья Google Scholar
Wang X et al (2015) N (6) -метиладенозин модулирует эффективность трансляции матричной РНК. Ячейка 161: 1388–1399
CAS PubMed PubMed Central Статья Google Scholar
Alarcon CR, Goodarzi H, Lee H, Liu X, Tavazoie S, Tavazoie SF (2015) HNRNPA2B1 является медиатором m (6) A-зависимых событий процессинга ядерной РНК. Ячейка 162: 1299–1308
CAS PubMed PubMed Central Статья Google Scholar
Xiao W et al (2016) Nuclear m (6) Считыватель YTHDC1 регулирует сплайсинг мРНК. Mol Cell 61: 507–519
CAS PubMed Статья Google Scholar
Abe N et al (2015) Трансляция кольцевой РНК в живых клетках человека. Научный представитель 5: 16435
CAS PubMed PubMed Central Статья Google Scholar
AbouHaidar MG, Venkataraman S, Golshani A, Liu B, Ahmad T (2014) Новое кодирование, трансляция и экспрессия генов реплицирующейся ковалентно замкнутой кольцевой РНК из 220 нуклеотидов.Proc Natl Acad Sci USA 111: 14542–14547
CAS PubMed PubMed Central Статья Google Scholar
Koh W et al (2014) Неинвазивный мониторинг in vivo тканеспецифической глобальной экспрессии генов у людей. Proc Natl Acad Sci USA 111: 7361–7366
CAS PubMed PubMed Central Статья Google Scholar
Lo YM et al (2007) Соотношение аллелей плацентарной РНК в плазме позволяет неинвазивным пренатальным обнаружением хромосомных анеуплоидий.Nat Med 13: 218–223
CAS PubMed Статья Google Scholar
Mitchell PS et al (2008) Циркулирующие микроРНК как стабильные маркеры крови для обнаружения рака. Proc Natl Acad Sci USA 105: 10513–10518
CAS PubMed PubMed Central Статья Google Scholar
Wan JC et al (2017) Жидкие биопсии достигли совершеннолетия: к внедрению циркулирующей опухолевой ДНК.Nat Rev Cancer 17: 223–238
CAS PubMed Статья Google Scholar
Ткач М., Тери С. (2016) Коммуникация посредством внеклеточных везикул: где мы находимся и куда нам нужно идти. Ячейка 164: 1226–1232
CAS PubMed Статья Google Scholar
Memczak S, Papavasileiou P, Peters O, Rajewsky N (2015) Идентификация и характеристика кольцевых РНК как нового класса предполагаемых биомаркеров в крови человека.PLoS One 10: e0141214
PubMed PubMed Central Статья CAS Google Scholar
Dou Y et al (2016) Циркулярные РНК подавляются в мутантных по KRAS раковых клетках толстой кишки и могут переноситься в экзосомы. Научный представитель 6: 37982
CAS PubMed PubMed Central Статья Google Scholar
Li Y et al (2015) Циркулярная РНК обогащена и стабильна в экзосомах: многообещающий биомаркер для диагностики рака.Cell Res 25: 981–984
CAS PubMed PubMed Central Статья Google Scholar
Umekage SU, Fujita T, Suzuki Y, Kikuchi Y (2012) Экспрессия кольцевой РНК in vivo методом перестановки интрон-экзон. В: Agbo EC (ed) Innovations in biotechnology, глава 4. InTech, Риека, Хорватия, стр. 75–90
Lo YM et al (1999) Количественный анализ внеклеточной ДНК вируса Эпштейна-Барра в плазме пациентов с раком носоглотки.Cancer Res 59: 1188–1191
CAS PubMed Google Scholar
Raposo G, Stoorvogel W (2013) Внеклеточные везикулы: экзосомы, микровезикулы и другие. J Cell Biol 200: 373–383
CAS PubMed PubMed Central Статья Google Scholar
Лотвалл Дж. И др. (2014) Минимальные экспериментальные требования для определения внеклеточных везикул и их функций: заявление о позиции Международного общества внеклеточных везикул.J Extracell Vesicles 3: 26913
PubMed Статья Google Scholar
Снайдер М.В., Кирчер М., Хилл А.Дж., Даза Р.М., Шендур Дж. (2016) Бесклеточная ДНК включает в себя нуклеосомный след in vivo, который сообщает о ее тканях происхождения. Ячейка 164: 57–68
CAS PubMed PubMed Central Статья Google Scholar
Vickers KC, Palmisano BT, Shoucri BM, Shamburek RD, Remaley AT (2011) МикроРНК транспортируются в плазме и доставляются в клетки-реципиенты липопротеинами высокой плотности.Nat Cell Biol 13: 423–433
CAS PubMed PubMed Central Статья Google Scholar
Skog J et al (2008) Микровезикулы глиобластомы транспортируют РНК и белки, которые способствуют росту опухоли и обеспечивают диагностические биомаркеры. Nat Cell Biol 10: 1470–1476
CAS PubMed PubMed Central Статья Google Scholar
Nikpay M et al (2015) Комплексный мета-анализ ишемической ассоциации по всему геному на основе 1000 геномов.Нат Генет 47: 1121–1130
CAS PubMed PubMed Central Статья Google Scholar
Consortium CAD et al (2013) Крупномасштабный ассоциативный анализ выявляет новые локусы риска для ишемической болезни сердца. Nat Genet 45: 25–33
Статья CAS Google Scholar
Broadbent HM et al (2008) Восприимчивость к ишемической болезни сердца и диабету кодируется отдельными, тесно связанными SNP в локусе ANRIL на хромосоме 9p.Hum Mol Genet 17: 806–814
CAS PubMed Статья Google Scholar
Яринова О. и др. (2009) Функциональный анализ локуса риска ИБС хромосомы 9p21.3. Артериосклер Thromb Vasc Biol 29: 1671–1677
CAS PubMed Статья Google Scholar
Liu Y et al (2009) Экспрессия транскрипта INK4 / ARF связана с вариантами хромосомы 9p21, связанными с атеросклерозом.PLoS One 4: e5027
PubMed PubMed Central Статья CAS Google Scholar
Zhou X et al (2016) Длинная некодирующая РНК ANRIL регулирует воспалительные реакции как новый компонент пути NF-kappaB. РНК Биол 13: 98–108
PubMed Статья Google Scholar
Vausort M et al (2016) Циркулярная РНК, связанная с инфарктом миокарда, прогнозирующая дисфункцию левого желудочка.J Am Coll Cardiol 68: 1247–1248
PubMed Статья Google Scholar
Wang K et al (2016) Кольцевая РНК защищает сердце от патологической гипертрофии и сердечной недостаточности, воздействуя на miR-223. Eur Heart J 37: 2602–2611
PubMed Статья Google Scholar
Boeckel JN et al (2015) Идентификация и характеристика регулируемой гипоксией эндотелиальной кольцевой РНК.Circ Res 117: 884–890
CAS PubMed Статья Google Scholar
Khan MA et al (2016) RBM20 регулирует продукцию кольцевой РНК из гена тайтина. Circ Res 119: 996–1003
CAS PubMed Google Scholar
Schafer S et al (2017) Варианты, усекающие титин, влияют на функцию сердца в когортах больных и в общей популяции. Нат Генет 49: 46–53
CAS PubMed Статья Google Scholar
Tan WL et al (2017) Картина круговой экспрессии РНК в сердце человека. Cardiovasc Res 113: 298–309
PubMed Google Scholar
Jakobi T, Czaja-Hasse LF, Reinhardt R, Dieterich C (2016) Профилирование и проверка репертуара круговой РНК в сердцах взрослых мышей. Genom Proteom Bioinform 14: 216–223
Статья Google Scholar
Zhao Z, Li X, Gao C, Jian D, Hao P, Rao L, Li M (2017) Циркулярная РНК периферической крови hsa_circ_0124644 может использоваться в качестве диагностического биомаркера ишемической болезни сердца.Научный представитель 7: 39918
CAS PubMed PubMed Central Статья Google Scholar
Zhao Z, Li X, Jian D, Hao P, Rao L, Li M (2017) Hsa_circ_0054633 в периферической крови может использоваться в качестве диагностического биомаркера преддиабета и сахарного диабета 2 типа. Acta Diabetol 54: 237–245
CAS PubMed Статья Google Scholar
Fan X, Weng X, Zhao Y, Chen W, Gan T, Xu D (2017) Циркулярные РНК при сердечно-сосудистых заболеваниях: обзор.Biomed Res Int 2017: 5135781
PubMed PubMed Central Google Scholar
Guarnerio J et al (2016) Онкогенная роль слитых циркулярных РНК, полученных из хромосомных транслокаций, связанных с раком. Ячейка 165: 289–302
CAS PubMed Статья Google Scholar
Грин Дж., Бэрд А.М., Брэди Л., Лим М., Грей С.Г., Макдермотт Р., Финн С.П. (2017) Циркулярные РНК: биогенез, функция и роль в заболеваниях человека.Фронт Mol Biosci 4:38
PubMed PubMed Central Статья Google Scholar
Meng S, Zhou H, Feng Z, Xu Z, Tang Y, Li P, Wu M (2017) CircRNA: функции и свойства нового потенциального биомаркера рака. Молочный рак 16:94
PubMed PubMed Central Статья Google Scholar
Ghosal S, Das S, Sen R, Basak P, Chakrabarti J (2013) Circ2Traits: обширная база данных круговой РНК, потенциально связанной с болезнью и признаками.Фронт Genet 4: 283
PubMed PubMed Central Статья CAS Google Scholar
Pan Q, Shai O, Lee LJ, Frey BJ, Blencowe BJ (2008) Глубокое исследование альтернативной сложности сплайсинга в человеческом транскриптоме с помощью высокопроизводительного секвенирования. Нат Генет 40: 1413–1415
CAS PubMed Статья Google Scholar
Aberg K, Saetre P, Jareborg N, Jazin E (2006) Human QKI, потенциальный регулятор экспрессии мРНК генов, связанных с олигодендроцитами человека, участвующих в шизофрении.Proc Natl Acad Sci USA 103: 7482–7487
PubMed PubMed Central Статья CAS Google Scholar
Batra R et al (2014) Потеря MBNL ведет к нарушению регулируемого в процессе развития альтернативного полиаденилирования при РНК-опосредованном заболевании. Mol Cell 56: 311–322
CAS PubMed PubMed Central Статья Google Scholar
Charizanis K et al (2012) «Muscleblind-like 2-опосредованный альтернативный сплайсинг в развивающемся мозге и нарушение регуляции при миотонической дистрофии».Нейрон 75: 437–450
CAS PubMed PubMed Central Статья Google Scholar
Scekic-Zahirovic J et al (2016) Токсическое усиление функции мутантного белка FUS имеет решающее значение для запуска клеточно-автономной потери двигательных нейронов. EMBO J 35: 1077–1097
CAS PubMed PubMed Central Статья Google Scholar
Ishigaki S et al (2017) Изменение соотношения изоформ тау, вызванное потерей функций FUS и SFPQ, приводит к FTLD-подобным фенотипам.Cell Rep 18: 1118–1131
CAS PubMed Статья Google Scholar
Larocque D, Galarneau A, Liu HN, Scott M, Almazan G, Richard S (2005) Защита мРНК p27 (Kip1) с помощью дрожащих РНК-связывающих белков способствует дифференцировке олигодендроцитов. Nat Neurosci 8: 27–33
CAS PubMed Статья Google Scholar
Irie K, Tsujimura K, Nakashima H, Nakashima K (2016) MicroRNA-214 способствует развитию дендритов, воздействуя на связанный с шизофренией ген дрожания (Qki).J Biol Chem 291: 13891–13904
CAS PubMed PubMed Central Статья Google Scholar
Licatalosi DD, Darnell RB (2006) Регулирование сплайсинга при неврологических заболеваниях. Нейрон 52: 93–101
CAS PubMed Статья Google Scholar
Vuong CK, Black DL, Zheng S (2016) Нейрогенетика альтернативного сплайсинга. Nat Rev Neurosci 17: 265–281
CAS PubMed PubMed Central Статья Google Scholar
Daguenet E, Dujardin G, Valcarcel J (2015) Патогенность дефектов сплайсинга: механистические представления о процессинге пре-мРНК обеспечивают новые терапевтические подходы. Представитель EMBO 16: 1640–1655
CAS PubMed PubMed Central Статья Google Scholar
Piwecka M et al (2017) Потеря кольцевого локуса РНК у млекопитающих вызывает дерегуляцию miRNA и влияет на функцию мозга. Наука 357 (6357). https://doi.org/10.1126/science.aam8526
Kwiatkowski TJ Jr и др. (2009) Мутации в гене FUS / TLS на хромосоме 16 вызывают семейный боковой амиотрофический склероз. Наука 323: 1205–1208
CAS PubMed Статья Google Scholar
Vance C et al (2009) Мутации в FUS, белке, обрабатывающем РНК, вызывают семейный боковой амиотрофический склероз типа 6. Science 323: 1208–1211
CAS PubMed PubMed Central Статья Google Scholar
Armakola M et al (2012) Ингибирование фермента, расщепляющего ветвления лариат РНК, подавляет токсичность TDP-43 в моделях болезни БАС. Нат Генет 44: 1302–1309
CAS PubMed PubMed Central Статья Google Scholar
Чжао Ю., Александров П.Н., Джабер В., Лукив В.Дж. (2016). Дефицит убиквитин-конъюгированного фермента UBE2A при болезни Альцгеймера (БА) связан с дефицитом естественной кольцевой губки miRNA-7 (circRNA; ciRS-7).Genes (Basel) 7
Floris G, Zhang L, Follesa P, Sun T (2017) Регулирующая роль циркулярных РНК и неврологические расстройства. Мол нейробиол 54: 5156–5165
CAS PubMed Статья Google Scholar
Chiu RW et al (2008) Неинвазивная пренатальная диагностика хромосомной анеуплоидии плода путем массового параллельного геномного секвенирования ДНК в материнской плазме. Proc Natl Acad Sci USA 105: 20458–20463
CAS PubMed PubMed Central Статья Google Scholar
Fan HC, Blumenfeld YJ, Chitkara U, Hudgins L, Quake SR (2008) Неинвазивная диагностика анеуплоидии плода путем секвенирования ДНК из материнской крови с помощью дробовика. Proc Natl Acad Sci USA 105: 16266–16271
CAS PubMed PubMed Central Статья Google Scholar
Fan HC, Gu W, Wang J, Blumenfeld YJ, El-Sayed YY, Quake SR (2012) Неинвазивное пренатальное измерение генома плода. Природа 487: 320–324
CAS PubMed PubMed Central Статья Google Scholar
Murtaza M et al (2013) Неинвазивный анализ приобретенной устойчивости к терапии рака путем секвенирования ДНК плазмы. Nature 497: 108–112
CAS PubMed Статья Google Scholar
Sun K et al (2015) Картирование ткани плазменной ДНК путем секвенирования метилирования всего генома для неинвазивных пренатальных оценок, оценок рака и трансплантации. Proc Natl Acad Sci USA 112: E5503 – E5512
CAS PubMed PubMed Central Статья Google Scholar
Guo S, Diep D, Plongthongkum N, Fung HL, Zhang K, Zhang K (2017) Идентификация блоков гаплотипа метилирования помогает в деконволюции образцов гетерогенной ткани и картировании опухолевой ткани происхождения из плазменной ДНК. Нат Генет 49: 635–642
CAS PubMed PubMed Central Статья Google Scholar
Melo SA et al (2015) Glypican-1 идентифицирует экзосомы рака и обнаруживает рак поджелудочной железы на ранней стадии. Nature 523: 177–182
CAS PubMed PubMed Central Статья Google Scholar
Hansen TB, Veno MT, Damgaard CK, Kjems J (2016) Сравнение инструментов предсказания кольцевой РНК. Нуклеиновые кислоты Res 44: e58
PubMed Статья Google Scholar
Geng HH, Li R, Su YM, Xiao J, Pan M, Cai XX, Ji XP (2016) Кольцевая РНК Cdr1as способствует инфаркту миокарда, опосредуя регуляцию экспрессии miR-7a его генов-мишеней. PLoS One 11: e0151753
PubMed PubMed Central Статья CAS Google Scholar
Tang CM et al (2017) CircRNA_000203 усиливает экспрессию генов, связанных с фиброзом, подавляя мишени miR-26b-5p, Col1a2 и CTGF в сердечных фибробластах. Научный журнал 7: 40342
PubMed PubMed Central Статья CAS Google Scholar
Zhou B, Yu JW (2017) Новая идентифицированная кольцевая РНК, circRNA_010567, способствует фиброзу миокарда посредством подавления miR-141 путем нацеливания на TGF-beta1. Biochem Biophys Res Commun 487: 769–775
CAS PubMed Статья Google Scholar
Bachmayr-Heyda A et al (2015) Корреляция количества циркулярной РНК с пролиферацией — на примере колоректального рака и рака яичников, идиопатического фиброза легких и нормальных тканей человека. Научный представитель 5: 8057
CAS PubMed PubMed Central Статья Google Scholar
Hsiao KY, Lin YC, Gupta SK, Chang N, Yen L, Sun HS, Tsai SJ (2017) Некодирующие эффекты кольцевой РНК CCDC66 способствуют росту и метастазированию рака толстой кишки.Cancer Res 77: 2339–2350
CAS PubMed Статья Google Scholar
Zhu M, Xu Y, Chen Y, Yan F (2017) Circular BANP, усиленная кольцевая РНК, которая модулирует пролиферацию клеток при колоректальном раке. Biomed Pharmacother 88: 138–144
CAS PubMed Статья Google Scholar
Weng W et al (2017) Циркулярная РНК ciRS-7-A — многообещающий прогностический биомаркер и потенциальная терапевтическая мишень при колоректальном раке.Clin Cancer Res 23 (14): 3918–3928
CAS PubMed Статья Google Scholar
Wang X et al (2015) Снижение экспрессии hsa_circ_001988 при колоректальном раке и его клиническое значение. Int J Clin Exp Pathol 8: 16020–16025
PubMed PubMed Central Google Scholar
Guo JN, Li J, Zhu CL, Feng WT, Shao JX, Wan L, Huang MD, He JD (2016) Комплексный профиль дифференциально экспрессируемых кольцевых РНК показывает, что hsa_circ_0000069 активируется и способствует пролиферации клеток, миграции и инвазия при колоректальном раке.Onco Targets Ther 9: 7451–7458
PubMed PubMed Central Статья Google Scholar
Xie H et al (2016) Новые роли circRNA_001569 в нацеливании на miR-145 в пролиферации и инвазии колоректального рака. Oncotarget 7: 26680–26691
PubMed PubMed Central Google Scholar
Guo W et al (2017) Полиморфизмы и паттерн экспрессии кольцевой РНК circ-ITCH вносят свой вклад в канцерогенез гепатоцеллюлярной карциномы.Oncotarget 8 (29): 48169–48177
PubMed PubMed Central Google Scholar
Wan L, Zhang L, Fan K, Cheng ZX, Sun QC, Wang JJ (2016) Circular RNA-ITCH подавляет пролиферацию рака легких посредством ингибирования пути Wnt / бета-катенин. Biomed Res Int 2016: 1579490
PubMed PubMed Central Google Scholar
Li F, Zhang L, Li W, Deng J, Zheng J, An M, Lu J, Zhou Y (2015) Циркулярная РНК ITCH оказывает ингибирующее действие на ESCC, подавляя путь Wnt / бета-катенин.Oncotarget 6: 6001–6013
PubMed PubMed Central Google Scholar
Huang G, Zhu H, Shi Y, Wu W, Cai H, Chen X (2015) cir-ITCH играет ингибирующую роль в колоректальном раке, регулируя путь Wnt / бета-катенин. PLoS One 10: e0131225
PubMed PubMed Central Статья CAS Google Scholar
Chen J et al (2017) Профиль циркулярной РНК идентифицирует circPVT1 как фактор пролиферации и прогностический маркер при раке желудка.Cancer Lett 388: 208–219
CAS PubMed Статья Google Scholar
Chen S, Li T, Zhao Q, Xiao B, Guo J (2017) Использование круговой РНК hsa_circ_0000190 в качестве нового биомаркера в диагностике рака желудка. Clin Chim Acta 466: 167–171
CAS PubMed Статья Google Scholar
Li WH et al (2017) Снижение экспрессии Hsa_circ_00001649 при раке желудка и его клиническое значение.Диск Марк 2017: 4587698
Google Scholar
Yao Z et al (2017) Ген ZKSCAN1 и родственная ему кольцевая РНК (circZKSCAN1) ингибируют рост, миграцию и инвазию клеток гепатоцеллюлярной карциномы, но с помощью различных сигнальных путей. Мол Онкол 11: 422–437
CAS PubMed PubMed Central Статья Google Scholar
Qin M et al (2016) Hsa_circ_0001649: кольцевая РНК и потенциальный новый биомаркер гепатоцеллюлярной карциномы.Биомарк рака 16: 161–169
CAS PubMed Статья Google Scholar
Shang X, Li G, Liu H, Li T, Liu J, Zhao Q, Wang C (2016) Комплексное кольцевое профилирование РНК показывает, что hsa_circ_0005075, новый биомаркер кольцевой РНК, участвует в развитии гепатоцеллюлярной карциномы. Медицина (Балтимор) 95: e3811
CAS Статья Google Scholar
Zheng J, Liu X, Xue Y, Gong W, Ma J, Xi Z, Que Z, Liu Y (2017) Кольцевая РНК TTBK2 способствует развитию злокачественности глиомы, регулируя путь miR-217 / HNF1beta / Derlin-1. J Hematol Oncol 10:52
PubMed PubMed Central Статья Google Scholar
Zhu J et al (2017) Дифференциальная экспрессия кольцевых РНК в мультиформной глиобластоме и ее корреляция с прогнозом. Transl Oncol 10: 271–279
PubMed PubMed Central Статья Google Scholar
Yang P, Qiu Z, Jiang Y, Dong L, Yang W, Gu C, Li G, Zhu Y (2016) Подавление кольцевой РНК cZNF292 подавляет образование трубок глиомы человека через сигнальный путь Wnt / бета-катенин. Oncotarget 7: 63449–63455
PubMed PubMed Central Google Scholar
Zhong Z, Lv M, Chen J (2016) Скрининг профилей дифференциальной циркулярной экспрессии РНК показывает регулирующую роль пути circTCF25-miR-103a-3p / miR-107-CDK6 в карциноме мочевого пузыря.Научный представитель 6: 30919
CAS PubMed PubMed Central Статья Google Scholar
Panda AC et al (2017) Идентификация связанных со старением кольцевых РНК (SAC-РНК) выявляет супрессор старения CircPVT1. Нуклеиновые кислоты Res 45: 4021-4035
CAS PubMed Статья Google Scholar
Li W, Zhong C, Jiao J, Li P, Cui B, Ji C, Ma D (2017) Характеристика hsa_circ_0004277 как нового биомаркера острого миелоидного лейкоза с помощью кругового профиля РНК и биоинформатического анализа.Int J Mol Sci 18: 597–598
PubMed Central Статья Google Scholar
Xia W et al (2016) Циркулярная РНК has_circ_0067934 активируется при плоскоклеточном раке пищевода и способствует пролиферации. Научный представитель 6: 35576
CAS PubMed PubMed Central Статья Google Scholar
Xuan L et al (2016) Circular RNA: новый биомаркер прогрессирующего рака гортани.Am J Transl Res 8: 932–939
PubMed PubMed Central Google Scholar
Наблюдения PN, HCP и CP
Ограничение химического состава фосфора в околозвездных оболочках, богатых углеродом и кислородом: наблюдения PN, HCP и CP
СПРАВОЧНИК
Арнетт, Д. 1996, Сверхновые и нуклеосинтез: Исследование истории материи от Большого взрыва до наших дней (Принстон: Princeton Univ. Press) Первая ссылка в статье | ОБЪЯВЛЕНИЯ Кокс, П., Лукас, Р., Хаггинс, П. Дж., Форвей, Т., Бачиллер, Р., Гильото, С., Майяр, Дж. П., & Омонт, А. 2000, A&A, 353, L25 Первое цитирование в статье | ОБЪЯВЛЕНИЯ Фукасаку, С., Хирахара, Ю., Масуда, А., Кавагути, К., Исикава, С., Кайфу, Н., и Ирвин, В. М. 1994, ApJ, 437, 410 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЯ Гелин, М., Чернихаро, Дж., Пауберт, Г., и Тернер, Б. Э. 1990, A&A, 230, L9 Первое цитирование в статье | ОБЪЯВЛЕНИЯ Гелин, М., Мюллер, С., Чернихаро, Дж., Аппони, А. Дж., Маккарти, М.К., Готтлиб, К. А., & Таддеус, П. 2000, A&A, 363, L9 Первое цитирование в статье | ОБЪЯВЛЕНИЯ Хайбергер, Дж. Л., Томсон, К. Дж., Янг, П. А., Арнетт, Д., и Зиурис, Л. М. 2003, ApJ, 593, 393 Первое цитирование в статье | IOPscience | ОБЪЯВЛЕНИЯ Кемпер, Ф., Старк, Р., Джасттанонт, К., де Котер, А., Тиленс, AGGM, Waters, LBFM, Cami, J., & Dijkstra, C. 2003, A&A, 407, 609 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЯ Lodders, K., & Fegley, B., Jr., 1999, в IAU Symp. 191, Asymptotic Giant Branch Stars, ed.Т. Ле Бертр, А. Лебр и К. Велькенс (Сан-Франциско: ASP), 279 Первое цитирование в статье | ОБЪЯВЛЕНИЯ Монье, Дж. Д., Тутхилл, П. Г., Лопес, Б., Крузалебес, П., Данчи, В. К., и Ханифф, К. А. 1999, ApJ, 512, 351 Первое цитирование в статье | IOPscience | ОБЪЯВЛЕНИЯ Мюллер, Х.С.П., Шлёдер, Ф., Штуцки, Дж., И Винневиссер, Г. 2005, J. Mol. Struct., 742, 215 Первое цитирование в статье | Crossref Пикетт, Х. М., Пойнтер, Р. Л., Коэн, Э. А., Делицкий, М. Л., Пирсон, Дж. К., и Мюллер, Х. С. П.1998, J. Quant. Spectrosc. Radiat. Перевод, 60, 883 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЯ Сопка, Р. Дж., Олофссон, Х., Йоханссон, Л. Э. Б., Нгуен-Кью-Рье, и Цукерман, Б. 1989, A&A, 210, 78 Первое цитирование в статье | ОБЪЯВЛЕНИЯ Тобола, Р., Клос, Дж., Лик, Ф., Халасински, Г., & Александр, М. Х. 2007, A&A, 468, 1123 Первое упоминание в статье | Crossref | ОБЪЯВЛЕНИЯ Тернер, Б. Э., Цуджи, Т., Балли, Дж., Гелин, М., и Черничаро, Дж. 1990, ApJ, 365, 569 Первое цитирование в статье | Crossref | ОБЪЯВЛЕНИЯ Янг, К.