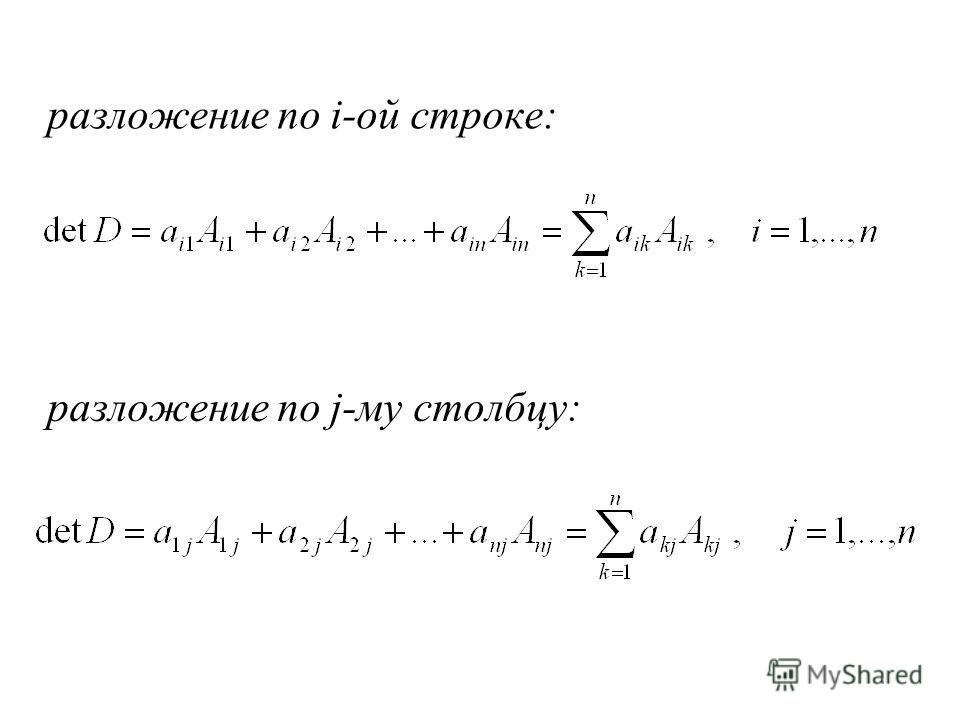Разложить определитель по строке онлайн: Нахождение определителя матрицы

Содержание

Вычислить определитель матрицы с примерами решения

Содержание:

Примеры с решением

Выбирается строка (или столбец) определителя, содержащие больше всего нулей. Используя свойство 6, зануляют в этой строке (или столбце) все элементы, кроме одного. После чего разлагают oт разделителя по этой строке (или столбцу). К полученному определителю применяют эту же схему.

Примеры с решением

Пример 1.

Вычислим определитель Мы видим, что все элементы отличны от нуля.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

В таком случае можно начать с любой строки или любого столбца. Например, с 1-го столбца. Наша цель — занулить все элементы, кроме одного, в 1-м столбце.

Прибавим 2-ю строку поэлементно к 4-й строке, а из 3-й строки вычтем поэлементно 1-ю строку, умноженную на 2:

Вынесем из последней строки общий множитель (2) за знак определителя

Мы получили в 1-м столбце два нуля. Также два нуля получены в 3-й строке. Прибавим 2-й столбец поэлементно к 4-му столбцу: Разложим определитель по 3-й строке: Вынесем из 1-й строки общий множитель (2) за знак определителя:

Возможно вам будут полезны данные страницы:

Матрица перехода
Действия над матрицами
Сложение матриц: примеры решения
Вычитание матриц: примеры решения

По одному нулю в 1-м столбце и 3-й строке. Вычтем из 2-й строки 1-ю строку, умноженную на 3:

Разложим определитель по 1-му столбцу:

Пример 2.

Вычислим определитель Основные методы вычисления определителей -го порядка. Метод понижения порядка определителя основан на следующем соотношении ( фиксировано):

где называется алгебраическим дополнением элемента и представляет собой (с точностью до знака ) определитель -го порядка, получающийся из исходного определителя вычеркиванием -й строки и -ro столбца, на пересечении которых стоит элемент .

Соотношение (4) называется разложением определителя по -й строке. Аналогично определяется разложение определителя по столбцу.

Прежде чем применять метод понижения порядка, полезно, используя основные свойства определителя, обратить в нуль все, кроме одного, элементы его некоторой строки (столбца).

Пример 3.

Вычислить определитель Из первой строки вычтем, а ко второй прибавим удвоенную третью. Полученный определитель разложим по первому столбцу. Имеем Далее опять обращаем в нуль все элементы первого столбца, кроме элемента в левом верхнем углу, и затем вычисляем определитель второго порядка:

Метод приведения к треугольному виду заключается в таком преобразовании определителя, когда все элементы, лежащие по одну сторону одной из его диагоналей, становятся равными нулю.

Пример 4.

Вычислить определитель

Вычитая первую строку из всех остальных, получаем

Метод рекуррентных соотношений позволяет выразить данный определитель, преобразуя и разлагая его по строке или столбцу, через определители того же вида, но более низкого порядка.

Полученное равенство называется рекуррентным соотношением.

Пример 5.

Вычислить определитель Вандермонда

Покажем, что при любом определитель Вандермонда равен произведению всевозможных разностей .Доказательство проведем по индукции, используя метод рекуррентных соотношений.

Действительно, при имеем

Пусть наше утверждение доказано для определителей Вандермонда порядка , т.е.

Преобразуем определитель следующим образом: из последней -й строки вычитаем -ю, умноженную на и, вообще, последовательно вычитаем из -Vi строки -ю, умноженную на . Получаем Разложим последний определитель по первому столбцу и вынесем из всех столбцов общие множители. Определитель принимает вид Получили рекуррентное соотношение. Используя предположение индукции, окончательно выводим:

1.2 Определители n-го порядка

Определитель n–го порядка состоит из n² элементов, записанных в n строк и в n столбцов , и имеет вид:

Элемент определителя а_i_j стоит в строке с номером i и в столбце с номером j. Индексы i и j могут принимать любые натуральные значения от 1 до n. Так, записав а_i₃(i=1,2,…,n), мы перечислим все элементы, стоящие в столбце с номером 3:

а₁₃, а₂₃, а₃₃,…,а_n₃. Элементы а_ij(при i=j) составляют главную диагональ определителя.

Вычисление определителя n-го порядка сводится к вычислению определителей третьего и второго порядка при помощи следующих свойств.

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами (не меняя порядка их номеров). Поэтому далее будем говорить о строках, подразумевая сказанное верным и для столбцов.

2. Если поменять местами две строки определителя, то он изменит свой знак.

3. Определитель с двумя одинаковыми (или пропорциональными) строками равен нулю.

4. Общий множитель всех элементов какой-либо его строки можно выносить за знак определителя.

5. Если все элементы какой-либо строки определителя равны нулю, то такой определитель равен нулю.

6. Определитель не изменится, если ко всем элементам какой-либо его строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Примеры.

№ 6. Вычислить определители:

а)

Здесь к элементам первого столбца прибавили элементы третьего столбца.

б)

К элементам первой строки прибавили элементы третьей.

в)

Этот определитель удобнее вычислять по правилу Сарруса, т.к. четыре из шести слагаемых равны нулю.

Вернемся к свойствам определителей. Но введем вначале понятия минора и алгебраического дополнения.

Если из данного определителя n-го порядка вычеркнем строку и столбец, на пересечении которых стоит элемент а_ij, то получим определитель (n-1)-го порядка, который называется минором элемента а_ij и обозначается М_ij_.Например, в определителе третьего порядка найдем минор М₂₁ элемента а₂₁. Для этого вычеркиваем вторую строку и первый столбец:

В определителе четвертого порядка можно записать 4х4=16 миноров, каждый из которых будет определителем третьего порядка.

Запишем миноры элементов а₃₂ и а₄₄, например, определителя четвертого порядка:

Алгебраическим дополнением элемента а_ij называется его минор, взятый со знаком (–1)ⁱ⁺^j, и обозначается А

ij.

Таким образом, А_ij=(–1)ⁱ⁺^jМ_ij.

Найдем, например, алгебраические дополнения элементов определителя .

Рассмотрим, наконец, свойство о разложении определителя по строке или столбцу.

7. Определитель равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.

Так, определитель третьего порядка, например, можно вычислить при помощи трех определителей второго порядка:

— разложение по элементам первой строки.

Следствие. Если все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению отличного от нуля элемента на его алгебраическое дополнение.

Поэтому, например,

№.7

В определителе третьего порядка мы к элементам первого столбца прибавили соответствующие элементы третьего, умноженные на 2.

Итак, с помощью свойств определителя можно разложить определитель любого порядка по строке или столбцу. Последовательно понижая порядок, вычислим определитель непосредственно, применив правило для вычисления определителя третьего или второго порядка.

Рассмотрим определители особого вида: диагональный и треугольный.

Диагональным определителем называется определитель, диагональные элементы которого отличны от нуля, а все остальные элементы равны нулю.

Треугольным определителем называется определитель, все элементы которого, расположенные ниже (или выше) главной диагонали, равны нулю.

№ 8 Вычислить диагональный определитель n-го порядка

Раскладывая определитель по элементам 1^го столбца, мы получили произведение Но определитель (n–1)-го порядка А₁₁ таким же образом представим в виде произведения и т. д.

Таким образом, диагональный определитель равен произведению элементов его главной диагонали.

Легко показать, что и треугольный определитель равен произведению элементов его главной диагонали:

№ 9 Вычислить определители:

2) т.к. в треугольном определителе один из элементов главной диагонали равен нулю.

Два рассмотренных в примере № 9 определителя мы свели к треугольной форме, получая в столбцах нули с помощью 6

го свойства определителей.

Покажем, как еще можно вычислить определитель, применяя изложенные свойства.

Опишем наши действия. В данном определителе привлекательна вторая строка, т.к. она уже содержит два нуля. Умножив все элементы 3-го столбца на 5, прибавим их к соответствующим элементам 1-го столбца. Полученный определитель равен произведению отличного от нуля элемента –1 на его алгебраическое дополнение А₂₃. Из первого столбца определителя 3-го порядка вынесем общий множитель 2 и получим нули во 2-м столбце, сложив 1-ю строку со второй, затем, сложив 3-ю строку со второй, умноженной на 5. Полученный определитель второго порядка можно упростить, сложив 2-ю строку с первой, умноженной на (-3). Затем из первой строки вынесем общий множитель 3.

Матрица

— Как расширить определители в степенном ряду?

Вы можете использовать мою функцию MatrixD из упрощения вопроса:

MatrixD[expr_, x__] := With[ {old = OptionValue[SystemOptions[], "DifferentiationOptions"->"ExcludedFunctions"]}, Внутренний`WithLocalSettings[ SetSystemOptions["DifferentiationOptions"->"ExcludedFunctions"->Join[old, {Det, Inverse, Tr}]]; Снять защиту[D]; (* обрабатывать список производных *) D[h:((Det|Tr|Inverse)[m_]), {z_, n_Integer}] := Nest[D[#, Replace[z, _List :> {z}]]&, h, n]; D[h:((Det|Tr|Inverse)[m_]), {z_List}] := D[h, #]& /@ z; D[h:((Det|Tr|Inverse)[m_]), z_, y___] := D[D[h, z], y]; (* определить производные для Det, Tr и Inverse *) D[Det[m_], z:Except[_List]] := Det[m] Tr[Inverse[m] .

Д[м,г]]; D[Tr[m_], z:Except[_List]] := Tr[D[m,z]]; D[Inverse[m_], z:Except[_List]] := -Inverse[m] . Д[м, г] . Обратный [м], D[выражение, х], SetSystemOptions["DifferentiationOptions"->"ExcludedFunctions"->old]; Очистить[D]; Защитить[D] ] ] 93\справа)$

Оценим несколько первых членов ряда, используя явный набор матриц:

 SeedRandom[2];
rules = Thread[{g0, g2, g4, g6, hd} -> RandomReal[1,{5,3,3}]]

{g0 -> {{0,72224, 0,109449, 0,470703}, {0,535582, 0,583178, 0,293942}, {0,165154, 0,601258, 0,754218}}, g2 -> {{0,771123, 0,778574, 0,0236104}, {0,922757, 0,992454, 0,350409}, {0,0450047, 0,501359, 0,633756}}, g4 -> {{0,642208, 0,389875, 0,664971}, {0,843882, 0,56904, 0,398212}, {0,238652, 0,673513, 0,419507}}, g6 -> {{0,587398, 0,00833523, 0,942441}, {0,771263, 0,147503, 0,964774}, {0,898747, 0,332963, 0,204548}}, hd -> {{0,839035, 0,250388, 0,238638}, {0,616616, 0,879303, 0,404504}, {0,402517, 0,516192, 0,292009}}}

И сравнение:

 N @СписокКоэффициентов[Серия[Кв. [Дет[г[х]]] /. правила, {х, 0, 3}], х]
коэфф /. правила //Развернуть

{0,507317, 0,663253, 0,436586, 0,0826776 + 0,572028 Log[x]}
{0,507317, 0,663253, 0,436586, 0,0826776 + 0,572028 Log[x]}

Бывший генеральный директор д-р Акрам Бутрос руководил MetroHealth через тюремный кризис, COVID-19: вот временная шкала Бутрос (слева) подчеркивает, что генеральный директор университетских больниц д-р Клифф Мегерян слушает дискуссию о несправедливости в отношении здоровья во время конференции Accelerating Health Equity 2022 года в центре Кливленда. Бутрос возглавил систему здравоохранения во время пандемии COVID-19пандемии и возглавил проект доступного жилья.

КЛИВЛЕНД, Огайо — Бывший генеральный директор MetroHealth доктор Акрам Бутрос, уволенный в понедельник, руководил системой здравоохранения в условиях расширения больничной системы, пандемии COVID-19 и кризиса в области здравоохранения в тюрьме округа Кайахога. Он также призвал больницы Кливленда заняться социальными детерминантами здоровья города.

Попечительский совет MetroHealth уволил Бутроса, руководившего системой больниц почти 10 лет, заявив, что он отдал себе более 1,9 доллара.миллионов несанкционированных бонусов. Бутрос сказал, что бонусы были санкционированы советом директоров.

Вот основные моменты пребывания Бутроса на посту:

Июнь 2013 г.: Бутрос был назначен президентом и генеральным директором MetroHealth. Родился в Каире, Египет, до приезда в Кливленд был терапевтом с 25-летним стажем успешного руководства больницами в академических медицинских центрах, общественных больницах и специализированных больницах.

2018-2019: Череда смертей в окружной тюрьме вызвала обеспокоенность по поводу медицинского обслуживания заключенных. MetroHealth в то время частично курировала здравоохранение заключенных и наняла Гэри Брэка, осведомителя, чьи публичные показания о кризисе побудили исполнительного директора округа Армонда Будиша силой заставить Бутроса уволить Брэка с работы.

2019: Началось строительство Glick Center, новой больничной башни, которая станет центральным элементом многолетнего трансформационного строительного проекта MetroHealth.

Апрель 2019 г.: Совет округа Кайахога единогласно одобрил трехлетнее соглашение с MetroHealth на сумму 42 миллиона долларов для надзора за всем медицинским обслуживанием в окружных тюрьмах.

Июнь 2019 г.: Бутрос призвал общественность к действиям по решению проблем со здоровьем в Кливленде, отметив, что последствия для здоровья связаны с социальными детерминантами здоровья. По адресу Эти проблемы, Бутрос сказал, что медицинское сообщество и местные лидеры должны «сосредоточиться на укреплении здоровья, а не на борьбе с болезнями».

2019: MetroHealth создала Институт H.O.P.E. (Здоровье, возможности, партнерство и расширение прав и возможностей), предоставляя пациентам и соседям свежие продукты, стабильное жилье, образование, профессиональную подготовку и другие услуги.

Март 2020 г.: В ответ на вспышку COVID-19 система здравоохранения начала тестирование на коронавирус, результаты которого готовы в течение двух часов.

Декабрь 2021 г.: Бутрос объявил, что намерен уйти в отставку в конце 2022 г.

Август 2022 г.: Открылся проект доступного жилья больничной системы Vía Sana в районе Кларк-Фултон в Кливленде. Это была первая инвестиция в размере 15 миллионов долларов в многофункциональный комплекс MetroHealth стоимостью 60 миллионов долларов рядом с 25-й Западной улицей, направленный на улучшение физического и экономического здоровья сообщества, прилегающего к его главному кампусу.

Сентябрь 2022: Айрика Стид из Чикаго была выбрана вместо Бутроса на посту следующего президента и генерального директора MetroHealth.

8 октября 2022 г.: Открыта больница поведенческого здоровья MetroHealth Cleveland Heights на 112 коек стоимостью 42 миллиона долларов. Ожидается, что он будет лечить около 5000 пациентов в год с такими состояниями, как биполярное расстройство, депрессия, наркомания, расстройства настроения и двойной диагноз, или с психическими заболеваниями и злоупотреблением психоактивными веществами.