Разложить в ряд фурье периодическую функцию: Ряд Фурье онлайн

Дифференциальное и интегральное исчисления для втузов, т.2

Дифференциальное и интегральное исчисления для втузов, т.2

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т. 2: Учебное пособие для втузов.—13-е изд.— М.: Наука, Главная редакция физико-математической литературы, 1985. — 560 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Второй том включает разделы: дифференциальные уравнения, кратные и криволинейные интегралы, интегралы по поверхности, ряды, уравнения математической физики, операционное исчисление, элементы теории вероятностей и математической статистики, матрицы. Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА XIII. (n) = f(x) § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 7. Вычисление площади поверхности § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14. Момент инерции и координаты центра масс тела § 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13. Степенные ряды. Интервал сходимости § 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 24. Ряды с комплексными членами § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4. Ряды Фурье для четных и нечетных функций § 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи § 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 7. Распространение тепла в неограниченном стержне § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7. Дифференцирование изображения § 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей 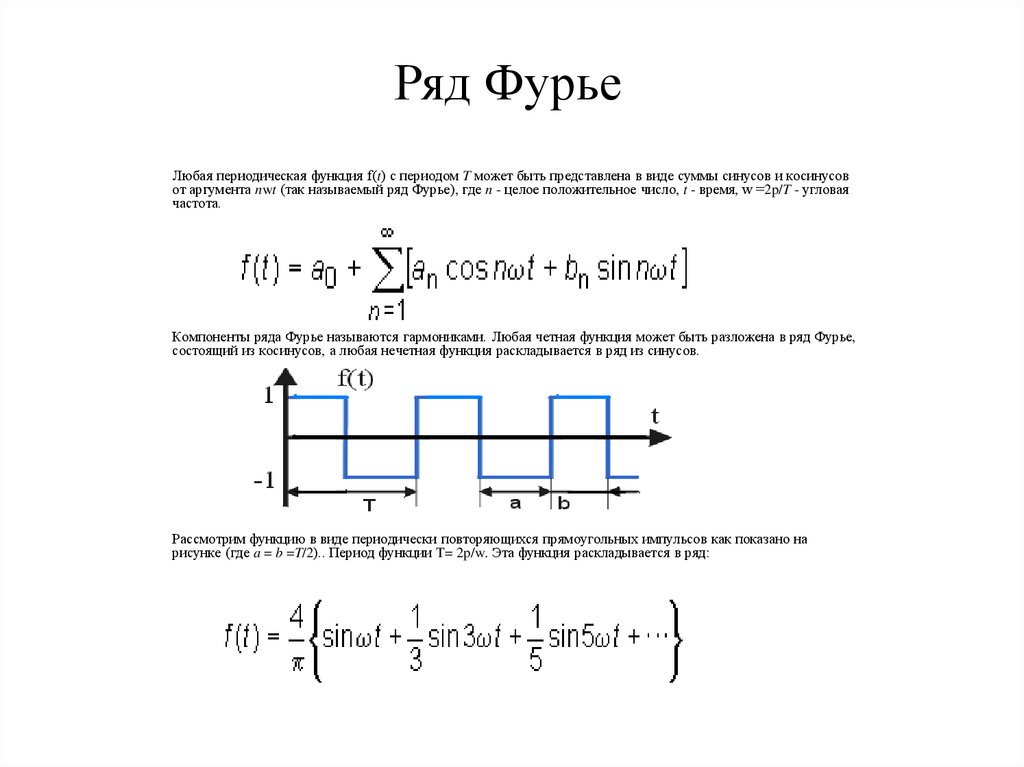§ 2. Классическое определение вероятности и непосредственный подсчет вероятностей § 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15. Нормальный закон распределения. Математическое ожидание нормального распределения § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 23. Двумерная случайная величина § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27. Задачи математической статистики. Статистический материал § 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому § 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ

XYZ — Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.

Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.   Вариант для печати.

Ряд Фурье периодических функций с периодом 2π. Четные и нечетные функции. Разложение в ряд Фурье по синусам. Ряд Фурье для произвольного интервала.

Ряд Фурье непериодических функций с периодом 2π. Разложение в ряд Фурье по косинусам. Ряд Фурье на полупериоде. Ряд Фурье на полупериоде для функций, заданных на интервале L≠2π.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=a_o+ a₁cosx+a₂cos2x+a₃cos3x+…+b₁sinx+b₂sin2x+b₃sin3x+…,

где a_o, a₁,a₂,…,b₁,b₂,.. — действительные константы, т.е.

(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

Коэффициенты a_o,a_n и b_n называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a₁cosx+b₁sinx) называется первой или основной гармоникой,

Другой способ записи ряда — использование соотношения acosx+bsinx=csin(x+α)

f(x)=a_o+c₁sin(x+α₁)+c₂sin(2x+α₂)+…+c_nsin(nx+α_n)

Где a_o — константа, с ₁=(a₁²+b₁²)^1/2 , с _n=(a_n²+b_n²)^1/2— амплитуды различных компонент, а фазовый угол равен a_n=arctg a_n/b_n.

Для ряда (1) член (a₁cosx+b₁sinx) или c₁sin(x+α₁) называется первой или основной гармоникой, (a₂cos2x+b₂sin2x) или c₂sin(2x+α₂) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций в ряд Фурье.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х² и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т. е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a_o и a_n

Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

Где коэффициенты ряда Фурье, 

Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.

Разложение по косинусам в диапазоне от 0 до L имеет вид

Как реализовать ряды Фурье в Python

Содержание

• Ряды Фурье (введение, определение, ключевые термины)
• Применение ряда Фурье
• Расширение ряда Фурье
• Реализация функций непрерывной волны с использованием Python

Ряд Фурье

Общая задача, когда дело доходит до математической физики и инженерной математики, заключается в преобразовании уравнений в систему координат, в которой выражения анализируются, распутываются и поддаются вычислениям и анализу. Инфраструктура для решения этой проблемы преобразования координат была введена Ж. Б. Жозефом Фурье в начале 18 века для исследования теории тепла, где он выдвинул концепцию ряда Фурье.

Ряд Фурье — это способ аппроксимации произвольной функции ( f(x) ) в виде бесконечной суммы синусов и косинусов с возрастающей частотой, которые обеспечивают ортогональную основу для пространства функций решения. Функции синуса и косинуса представлены как собственные функции уравнения теплопроводности. Предоставленные конкретные частоты представлены в виде собственных значений, которые выполняются в соответствии с геометрией с граничными условиями, определяющими амплитуды.

Вы столкнетесь с терминами Ряд Фурье и Преобразование Фурье часто. Разница между ними заключается в том, что ряд Фурье представляет собой разложение периодического сигнала в виде линейной комбинации синусов и косинусов, а преобразование Фурье — это процесс или функция, используемая для преобразования сигналов из временной области в частотную.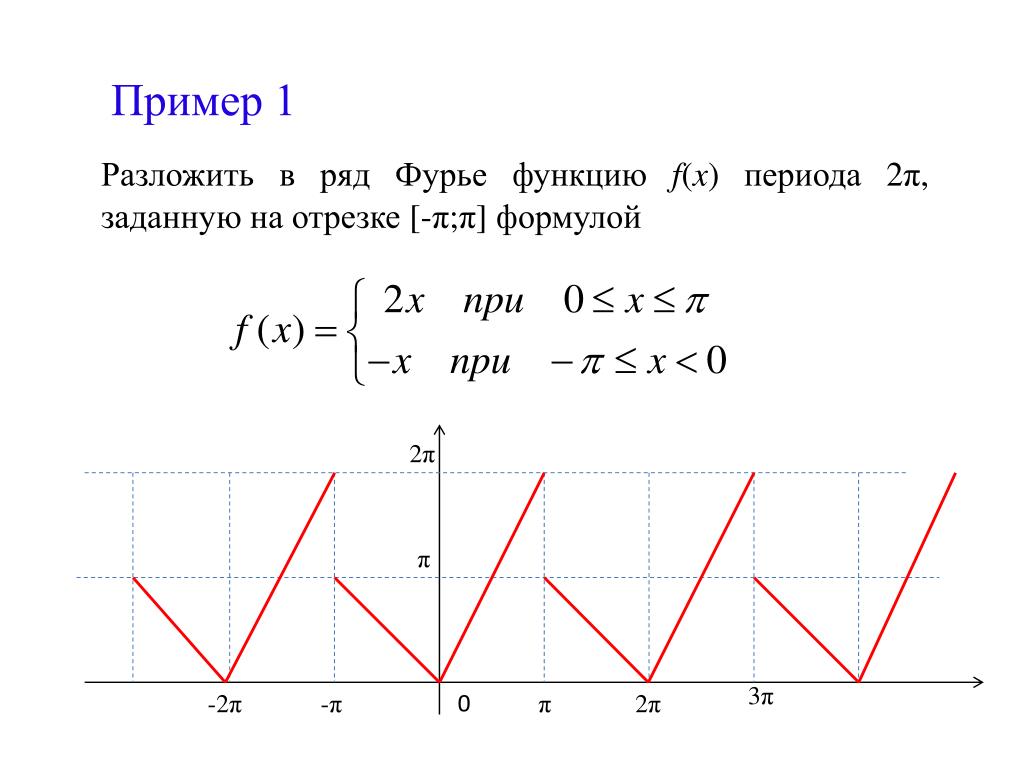

Чтобы наглядно понять, как работают ряды Фурье так, как мы их используем в сложных ситуациях, необходимо также понимать сложные темы уравнений теплопроводности, рядов Фурье, комплексных рядов Фурье, дискретного преобразования Фурье (ДПФ), быстрого преобразования Фурье (БПФ), квантовых вычислений. Преобразование Фурье, спектроскопия с преобразованием Фурье и т. Д. В этом кадре мы рассмотрим только основы, чтобы понять, что такое ряд Фурье и как он используется.

Применение рядов Фурье

1. Понятия гильбертовых пространств и теории операторов получают математическую основу с введением понятия рядов Фурье.
2. Это приводит к последовательной революции в развитии аналитической и вычислительной математики, анализа данных и числовой физики в инженерном масштабе.
3. Быстрое преобразование Фурье (БПФ) обеспечивает сжатие изображений и аудио в реальном времени, глобальные сети связи.

Таким образом, БПФ играет более существенную и заслуживающую внимания роль в формировании современного мира, чем любой алгоритм на сегодняшний день.

Расширение ряда Фурье

Функция ряда Фурье ( f(x)) может быть представлена ​​как периодическая функция. Любая функция периодична с периодом L, если она имеет один и тот же характер после интервала L вдоль оси X.

Аппроксимация функции в ряд Фурье

Это называется разложением функции в ряд Фурье. Где A0A_{0}A0​, AkA_{k}Ak​, BkB_{k}Bk​ называются Коэффициенты Фурье .

A0A_{0}A0 представляет площадь под функцией f(x) за один период времени ( 2*Pi ) и масштабируется по периоду времени, представляет собой среднее значение. AkA_{k}Ak​ и BkB_{k}Bk​ представляют собой функции, спроецированные на конкретный косинус и синусоиду.

Где, если

• f(x) четно, т. е. f(-x)=-f(x), тогда BkB_{k}Bk​s=0

• f(x) нечетно, т. е. f(-x)=f(x), тогда AkA_{k}Ak​s=0

Для нечетной функции с периодом 2L :

Для четной функции с периодом 2L :

Реализация непрерывных волновых функций в рядах Фурье с использованием Python:

3 90 Ряд Фурье состоит в том, чтобы иметь возможность нарисовать желаемый рисунок, складывая множество волн с различными колебаниями (или) гармоническими движениями, определяемыми периодическими функциями. Существуют базовые волны, которые можно реализовать и использовать для создания других волн. Основные волны:

• Прямоугольные волны
• Пилообразные волны
• Треугольные волны
• Полукруглые волны

В этом кадре мы сосредоточимся на квадратных волнах.

В Python мы можем использовать:

• Модуль SciPy.Signal — для доступа к встроенным кусочно-непрерывным функциям [квадрат, пилообразный и т. д.]
• Модуль SciPy.Integrate — используйте quad для интеграции.
• математический модуль — использовать math для математических функций [синус, косинус и т.д.]
• numPy module — для использования lambda для определения функций.

Код Python для генерации прямоугольной волны:

 импортировать numpy как np
импортировать matplotlib.pyplot как plt
из квадрата импорта scipy. signal
из scipy.integrate импортировать quad
from math import* //импорт всех функций из math
x=np.arange(-np.pi,np.pi,0.001) //ось x выбрана от –π до +π, значение
// 1 наименьший квадрат по оси x равен 0,001
y=square(x) // определение прямоугольной волновой функции 𝑦 = −1, 𝑓𝑜𝑟 − 𝜋 ≤ 𝑥 ≤ 0
//y= +1, 𝑓𝑜𝑟 0 ≤ 𝑥 ≤ 𝜋
//определить функцию
fc=лямбда x:square(x)*cos(i*x) //i: фиктивный индекс
fs = лямбда х: квадрат (х) * грех (я * х)
n=50 //максимальное значение I, без бесконечности, лучший результат с большим значением
An=[] // определение массива
Бн=[]
сумма=0
для я в диапазоне (n):
 an=quad(fc,-np.pi,np.pi)[0]*(1.0/np.pi)
 An.append(ан)
для я в диапазоне (n):
 bn=quad(fs,-np.pi,np.pi)[0]*(1.0/np.pi)
 Bn.append(bn) //помещение значения в массив Bn
для я в диапазоне (n):
 если я==0.0:
 сумма=сумма+An[i]/2
 еще:
 сумма=сумма+(An[i]*np.cos(i*x)+Bn[i]*np.sin(i*x))
plt.plot(x,сумма,'г')
plt.plot(x,y,'r--')
plt.title("ряд Фурье для прямоугольной волны")
plt.show()
 

График будет выглядеть как:

Пример: квадратная волна

𝒇 (𝒙) = {𝟎, −𝑳 ≤ ≤ 𝟎}

𝒇 (𝒙) = {𝟏 ≤ ≤}}

f(x) имеет период 2L

для L=0,5, Period=1

 импортировать matplotlib. pyplot как plt
из квадрата импорта scipy.signal
Л=1
х=np.arange(-L,L,0,001)
y=квадрат(2*np.pi*x)
plt.plot(x,y,'r--')
plt.title("ряд Фурье для прямоугольной волны")
plt.show()
 

Сгенерированный график:

УЧАСТНИК

Bindu Sanjana T

Лицензия: Creative Commons-Attribution-ShareAlike 4.0 (CC-BY-SA 4.0)

Разложение периодической функции f(x) в (-pi,pi) в ряд Фурье

Ряд Фурье Разложение периодической функции f(x) в (-pi,pi) — ряд Фурье

• Категория: Машиностроение
• Подкатегория: Математика

• Расширение ряда Фурье
• периодические функции ряд Фурье
• периодическая функция в ряду Фурье
• инженерная математика Видео
• ряд Фурье периодической функции
• Экида
• Разложение периодической функции в ряд Фурье
• Серия Фурье
• инженерная математика Видео лекция
• ряд Фурье инженерная математика

Нет просмотров

Нет лайков

Нет не нравится

Нет Комментарии

Разложение в ряд Фурье периодической функции f(x) по (-pi,pi) из главы Ряды Фурье по инженерной математике 3 для студентов инженерных специальностей всех университетов. -x в (0,2pi) — Ряд Фурье — En 9-x in (0,2pi) — Ряды Фурье — Инженерная математика 3 — https://youtu.be/Iy8c-RAJnwc 2) Разложение в ряд Фурье f(x) = cospx in (0,2pi) — Ряд Фурье — Инженерная математика 3 — https://youtu.be/PLvieaMNTLk Смотреть следующие видео главы серии Фурье: — 1) Разложение Sinx и Cosx в ряд Фурье по (-pi,pi) — Ряды Фурье — Инженерная математика 3 — https://youtu.be/-tLIBt90ATY 2) Формула ряда Фурье четной и нечетной функции в (-pi,pi) — Ряд Фурье — Инженерная математика 3 — https://youtu.be/_sb6SuprDlU Получите доступ к полному плейлисту серий Фурье: http://gg.gg/Fourier-Series-Engg-Maths Получите доступ к полному плейлисту Engineering Mathematics 3: http://gg.gg/Engineering-Mathematics-3 Подпишитесь на канал Ekeeda, чтобы получить доступ к большему количеству видео http://gg.gg/Subscribe-Now Чтобы получить доступ к полному курсу инженерной математики — III (Университет Мумбаи — Электроника и телекоммуникации — SEM III) Нажмите здесь: — http://ekeeda.com/course/SEM-III/Мумбайский университет/Электроника-и-телекоммуникации-инжиниринг/Applied-Mathematics_III/4395 #инженернаяматематика3 #прикладнаяматематика3лекции #прикладнаяматематика3видеолекции #Прикладная математика #инженернаяматематика1лекции #appliedmaths3tutorials #прикладнаяматематика3 Спасибо за просмотр.