4.5. Разложение в ряд Фурье только по синусам или только по косинусам
Начнем с простого замечания: если заданная на отрезке интегрируемая функция является нечетной, то есть для всех выполняется равенство , то .
Для четной функции справедливо .
Напомним некоторые свойства четных и нечетных функций на :
Произведение двух четных или двух нечетных функций есть функция четная;
Произведение четной и нечетной функций есть нечетная функция.
Утверждение. Пусть определена и интегрируема на , а -ее коэффициенты Фурье. Тогда
если -нечетная, то
, а ряд Фурье имеет вид .
если — четная, то
,
а
ряд Фурье имеет вид
.
Допустим, что функция задана на отрезке . Если мы хотим найти разложение на этом отрезке в ряд Фурье, то сначала продолжим на симметричный промежуток произвольным образом, а потом воспользуемся формулами для коэффициентов Фурье.
Если продолжить функцию четным образом, то получим разложение только по косинусам, а если продолжить нечетным образом, то – только по синусам. При этом в первом случае продолженная функция будет иметь вид
,
а во втором случае
4.6. Разложение в ряд Фурье функции, заданной на произвольном промежутке
Пусть задана на отрезке , и на этом отрезке она кусочно-гладкая. Рассмотрим периодическую кусочно-гладкую функцию с периодом
,
которая совпадает с на , а -произвольная кусочно-гладкая функция.
Таким
образом,
была продолжена на симметричный отрезок.
Алгоритм разложения функции в тригонометрический ряд Фурье:
выяснить формально ряд Фурье по заданию функции;
найти коэффициенты ряда Фурье;
используя теорему о достаточном условии сходимости ряда Фурье, найти сумму ряда, построить график и . Выяснить, в каких точках совпадает с .
4.7. Контрольные вопросы и задания.
Какая функция называется периодической? Является ли функция Дирихле периодической? Чему равен период? Имеет ли эта функция основной период?
Что такое тригонометрический ряд?
Какой тригонометрический ряд называется рядом Фурье?
Являются ли тригонометрические ряды и рядами Фурье?
Сформулировать достаточные условия поточечной сходимости ряда Фурье.

Записать равенство Парсеваля и неравенство Бесселя для тригонометрического ряда Фурье.
Какой вид имеет ряд Фурье для нечетной интегрируемой функции?
Какой вид имеет ряд Фурье для -периодической функции?
4.8. Образцы решения типовых задач
При нахождении коэффициентов Фурье полезно помнить:
.
Пример 1. Разложить функцию в ряд Фурье на интервале . Построить график суммы ряда Фурье. Вычислить суммы получающихся рядов, полагая .
Построим график данной функции:
Продолжим данную функцию периодически с периодом на всю прямую.
Построим график суммы ряда Фурье
Найдём коэффициенты ряда Фурье. Так как нечётная на
Итак, .
Используя полученное разложение с учётом вида графика суммы ряда Фурье, из которого видно, к чему сходится ряд в точках разрыва, найдём суммы некоторых числовых рядов.
При получим .
При получим
.
При получим
.
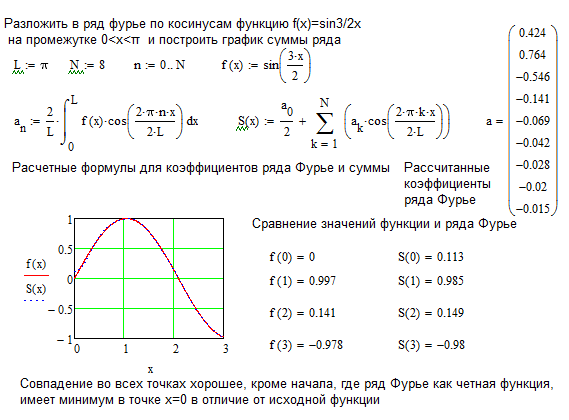
Пример 2. Разложить в ряд Фурье по косинусам функцию (полупериод функции равен )
Изобразим график заданной функции
Продолжим функцию чётным образом на промежутке , тогда коэффициенты .
Продолжим полученную функцию с периодом на всю прямую. Так как продолжение будет непрерывной функцией, то для график суммы ряда Фурье совпадает с графиком продолженной функции
Вычислим коэффициенты ряда Фурье
при .
Пример 3. Разложить в ряд Фурье по синусам функцию (полупериод функции равен )
Разложение функции в ряд по синусам — это ряд Фурье нечётного продолжения функции с промежутка на промежуток .
Изобразим график суммы ряда Фурье
Имеем .
КАТЕГОРИИ: Главная Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748) | Так как функция заданана отрезке , то ее можно доопределить на отрезок четным или нечетным образом. Если функция доопределена четным образом, то она, как четная функция может быть разложена по формулам для четной функции
, , . = (в точках непрерывности функции). Это – разложение в ряд Фурье по косинусам кратных дуг.
Если функция доопределена нечетным образом, то она, как нечетная функция может быть разложена по формулам для нечетной функции
, ,..
= (в точках непрерывности функции). Это – разложение в ряд Фурье по синусам кратных дуг.
Одну и ту же функцию, заданную на отрезке , можно разложить и по синусам, и по косинусам кратных дуг. Пример. Разложить по косинусам и синусам кратных дуг функцию , заданную на отрезке . Так как мы доопределяем функцию на отрезок при разложении по косинусам и синусам кратных дуг, то . Разложим функцию по косинусам кратных дуг. , , . Разложим функцию по синусам кратных дуг. , ,.. == , (теорема Дирихле).
Дата добавления: 2014-01-06; Просмотров: 10582; Нарушение авторских прав?; Мы поможем в написании вашей работы! Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет |
Дифференциальные уравнения. Косинусные ряды Фурье
Онлайн-заметки Пола
Главная
/
Дифференциальные уравнения
/
Краевые задачи и ряды Фурье
/ Косинусный ряд Фурье
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 8.5: Косинус Фурье, ряд
В этом разделе мы рассмотрим ряд косинусов Фурье. Мы начнем так же, как и в предыдущем разделе, где мы рассмотрели ряды синусов Фурье. Начнем с предположения, что функция \(f\left( x \right)\), с которой мы будем работать изначально, является четной функцией (
Этот ряд называется косинусным рядом Фурье и обратите внимание, что в этом случае (в отличие от синусоидального ряда Фурье) мы можем начать представление ряда с \(n = 0\), поскольку этот член не будет равен нулю, поскольку это было с синусом. Кроме того, как и в случае ряда синусов Фурье, аргумент \(\frac{{n\pi x}}{L}\) в косинусах используется только потому, что это аргумент, с которым мы столкнемся в следующем глава. Единственное реальное требование здесь состоит в том, чтобы заданный набор функций, которые мы используем, был ортогонален на интервале, над которым мы работаем. 9{L} {\ cos \ left ( {\ frac {{n \ pi x}} {L}} \ right) \ cos \ left ( {\ frac {{m \ pi x}} {L}} \ right )\,dx}} = \left\{ {\begin{array}{*{20}{l}}{2L}&{{\mbox{if}}n = m = 0}\\L&{{\ mbox{if}}n = m \ne 0}\\0&{{\mbox{if}}n \ne m}\end{массив}} \right.\]
Кроме того, как и в случае ряда синусов Фурье, аргумент \(\frac{{n\pi x}}{L}\) в косинусах используется только потому, что это аргумент, с которым мы столкнемся в следующем глава. Единственное реальное требование здесь состоит в том, чтобы заданный набор функций, которые мы используем, был ортогонален на интервале, над которым мы работаем. 9{L} {\ cos \ left ( {\ frac {{n \ pi x}} {L}} \ right) \ cos \ left ( {\ frac {{m \ pi x}} {L}} \ right )\,dx}} = \left\{ {\begin{array}{*{20}{l}}{2L}&{{\mbox{if}}n = m = 0}\\L&{{\ mbox{if}}n = m \ne 0}\\0&{{\mbox{if}}n \ne m}\end{массив}} \right.\]
Мы получим формулу для коэффициентов почти точно так же, как в предыдущем разделе. Мы начнем с представления выше и умножим обе части на \(\cos\left({\frac{{m\pi x}}{L}} \right)\), где \(m\) — фиксированное целое число в диапазоне \(\left\{ {0,1,2,3, \ldots } \right\}\). Это дает 9{{\,L}}{{\cos \left({\frac{{n\,\pi x}}{L}} \right)\cos \left({\frac{{m\,\pi x }}{L}} \right)\,dx}}} \end{align*}\]
Теперь мы знаем, что все интегралы в правой части будут равны нулю, за исключением случая \(n = m\), потому что набор косинусов образует ортогональный набор на интервале \( — L \le x \le L\ ).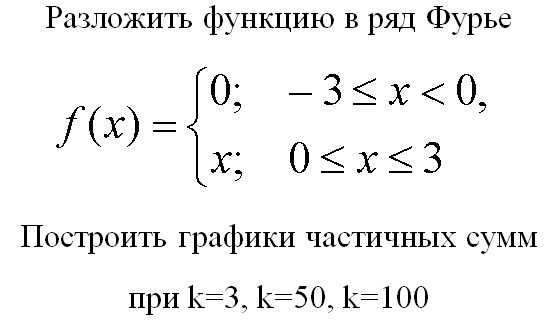 {{\,L}}{{f\left( x \right)\cos \left({\frac{{n\,\pi x}}{L}} \right) \,dx}}}&{\,\,\,\,\,n \ne 0}\end{массив}} \right.\]
92}}}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \]
{{\,L}}{{f\left( x \right)\cos \left({\frac{{n\,\pi x}}{L}} \right) \,dx}}}&{\,\,\,\,\,n \ne 0}\end{массив}} \right.\]
92}}}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \]
Обратите внимание, что мы часто будем выбрасывать \(n = 0\) из ряда, как мы сделали здесь, потому что он почти всегда будет отличаться от других коэффициентов, и это позволяет нам фактически подставлять коэффициенты в ряд .
Теперь, как и в предыдущем разделе, давайте спросим, что нам нужно сделать, чтобы найти ряд косинусов Фурье нечетной функции. Как и в случае с рядом синусов Фурье, когда мы делаем это изменение, нам нужно будет перейти на интервал \(0 \le x \le L\) теперь вместо \( — L \le x \le L\), и снова мы будем предположим, что ряд будет сходиться к \(f\left( x \right)\) в этой точке, и оставим обсуждение сходимости этого ряда в следующем разделе.
Мы могли бы выполнить работу, чтобы найти коэффициенты здесь дважды, как мы это сделали с рядами синусов Фурье, однако в этом нет реальной причины. Итак, хотя мы могли бы повторить всю работу выше, чтобы получить формулы для коэффициентов, давайте вместо этого сразу перейдем ко второму методу нахождения коэффициентов.
Итак, хотя мы могли бы повторить всю работу выше, чтобы получить формулы для коэффициентов, давайте вместо этого сразу перейдем ко второму методу нахождения коэффициентов.
В этом случае, прежде чем мы на самом деле продолжим, нам нужно определить четное расширение функции \(f\left( x \right)\) на \( — L \le x \le L\) . Итак, для данной функции \(f\left( x \right)\) мы определим четное расширение функции как
\[g\left(x\right) = \left\{ {\begin{array}{*{20}{l}}{f\left(x\right)}&{\,\,\,\, {\mbox{if}}0 \le x \le L}\\{f\left( { — x} \right)}&{\,\,\,\,{\mbox{if}} — L \ le x \le 0}\end{массив}} \right.\]
Показать, что это четная функция, достаточно просто.
\[g\left(-x \right)=f\left(-\left(-x \right) \right)=f\left( x \right)=g\left( x \right) \hspace{0.25 in} \text{для}0 , и мы можем видеть, что \(g\left( x \right) = f\left( x \right)\) на \(0 \le x \le L\) и если \(f\left( x \ right)\) уже является четной функцией, мы получаем \(g\left( x \right) = f\left( x \right)\) на \( — L \le x \le L\). Показать все решения Скрыть все решения a \(f\left( x \right) = L — x\) на \(0 \le x \le L\) Показать решение Вот еще расширение этой функции. \[\ begin{align*}g\left(x\right) & = \left\{ {\begin{array}{*{20}{l}}{f\left(x\right)}&{\ ,\,\,\,{\mbox{if}}0 \le x \le L}\\{f\left( { — x} \right)}&{\,\,\,\,{\mbox {if}} — L \le x \le 0}\end{массив}} \right.\\ & = \left\{ {\begin{array}{*{20}{l}}{L — x} &{\,\,\,\,{\mbox{if}}0 \le x \le L}\\{L + x} &{\,\,\,\,{\mbox{if}} — L \le x \le 0}\end{массив}} \right.\end{align*}\]
93}}&{\,\,\,\,{\mbox{if}} — L \le x \le 0}\end{массив}} \right. Эскиз функции и четное расширение, c \ (f \ left ( x \ right) = \ left \ { {\ begin {array} {* {20} {l}} {\ frac {L} {2}} & {\, \, \, \ ,{\mbox{if}}0 \le x \le \frac{L}{2}}\\{x — \frac{L}{2}}&{\,\,\,\,{\mbox {if }}\frac{L}{2} \le x \le L}\end{array}} \right.\) Показать решение Вот четное расширение этой функции, \[\ begin{align*}g\left(x\right) & = \left\{ {\begin{array}{*{20}{l}}{f\left(x\right)}&{\ ,\,\,\,{\mbox{if}}0 \le x \le L}\\{f\left( { — x} \right)}&{\,\,\,\,{\mbox {if}} — L \le x \le 0}\end{массив}} \right.\\ & = \left\{ {\begin{array}{*{20}{l}}{x — \frac {L} {2}} & {\, \, \, \, {\ mbox {if}} \ frac {L} {2} \ le x \ le L} \\ {\ frac {L} {2} } & {\, \, \, \, {\ mbox {if}} 0 \ le x \ le \ frac {L} {2}} \\ {\ frac {L} {2}} & {\, \ ,\,\,{\mbox{if}} — \frac{L}{2} \le x \le 0}\\{ — x — \frac{L}{2}}&{\,\,\ ,\,{\mbox{if}} — L \le x \le — \frac{L}{2}}\end{array}} \right. Эскиз функции и четное расширение: Хорошо, давайте теперь подумаем о том, как мы можем использовать четное расширение функции, чтобы найти ряд косинусов Фурье любой функции \(f\left( x \right) \) на \(0 \le x \le L\). Итак, для функции \(f\left( x \right)\) пусть \(g\left( x \right)\) будет четным расширением, как определено выше. Теперь \(g\left( x \right)\) является четной функцией на \( — L \le x \le L\), поэтому мы можем записать ее ряд косинусов Фурье. Это, 9{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}}&{ \,\,\,\,\,n \ne 0}\end{массив}} \right.\] и обратите внимание, что мы будем использовать вторую форму интегралов для вычисления констант. Теперь, поскольку мы знаем, что на \(0 \le x \le L\) мы имеем \(f\left( x \right) = g\left( x \right)\) и, следовательно, ряд косинусов Фурье \(f\left( x \right)\) на \(0 \le x \le L\) также определяется как \[f\left( x \right) = \sum\limits_{n = 0}^\infty {{A_n}\cos \left( {\frac {{n\,\pi x}}{L}} \ справа)} \ hspace {0,25 дюйма} {A_n} = \ left \ { {\ begin {array} {* {20} {l}} {\ displaystyle \ frac {1} {L} \ int_ {{\, 0 }}^{{\,L}}{{f\left( x \right)\,dx}}}&{\,\,\,\,\,n = 0}\\{\displaystyle \frac{ 2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}} {L}} \right)\,dx}}}&{\,\,\,\,\,n \ne 0}\end{массив}} \right. Наконец, давайте кратко рассмотрим кусочную функцию. Пример 5. Найдите ряд косинусов Фурье для \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\frac{L}{2}}&{ \,\,\,\,{\mbox{if}}0 \le x \le \frac{L}{2}}\\{x — \frac{L}{2}}&{\,\, \,\,{\mbox{if}}\frac{L}{2} \le x \le L}\end{array}} \right.\) на \(0 \le x \le L\). Показать решение
9{\pi/2} \cos(x)\,dx=\frac 4 \pi.$$
$$\tag{1}$$ График $\cos x$ (пунктирная линия) и $|\cos x|$ (сплошная линия) в интервале $[-\pi,\pi]$. Коэффициенты $b_n=0$ как вы заключили. Что касается коэффициентов $a_n$, то только нечетные равны $0$ (см. ниже). Функции $\cos(x)$ и $\cos(nx)$ ортогональны в интервале $[-\pi,\pi]$, но $|\cos(x)|$ и $\cos(nx) $ нет. Начиная с \begin{equation*}
\left\vert \cos (x)\right\vert =\left\{
\начать{массив}{с}
\cos (х) \\
-\cos (х)
\конец{массив}
\начать{массив}{с}
\текст{если} \\
\текст{если}
\конец{массив}
\начать{массив}{с}
0\leq х\leq \пи /2 \\
\pi /2\leq x\leq \pi,
\конец{массив}
\верно. 3}\) на \(0 \le x \le L\)
3}\) на \(0 \le x \le L\) \end{align*}\]
\end{align*}\]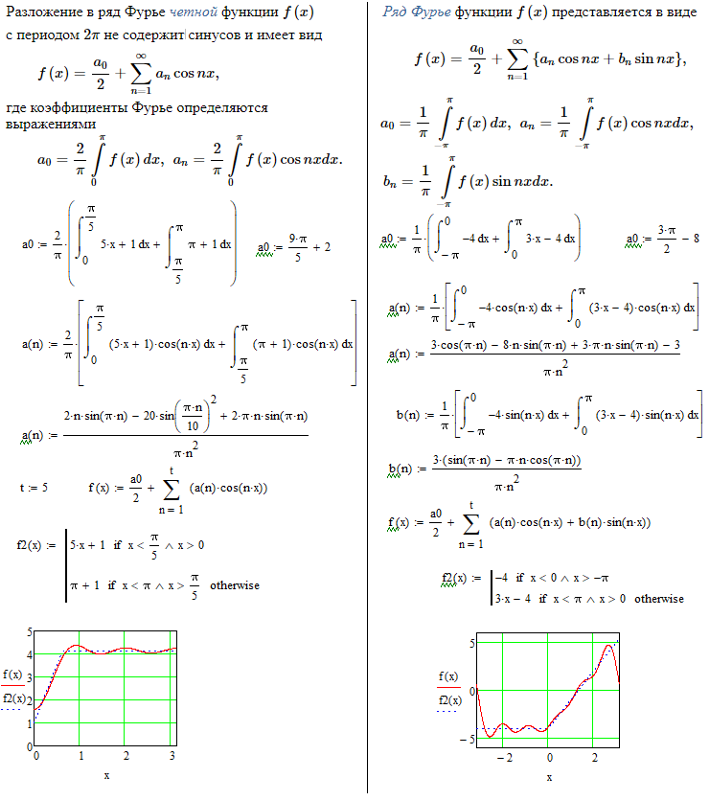 \end{align*}\]
\end{align*}\]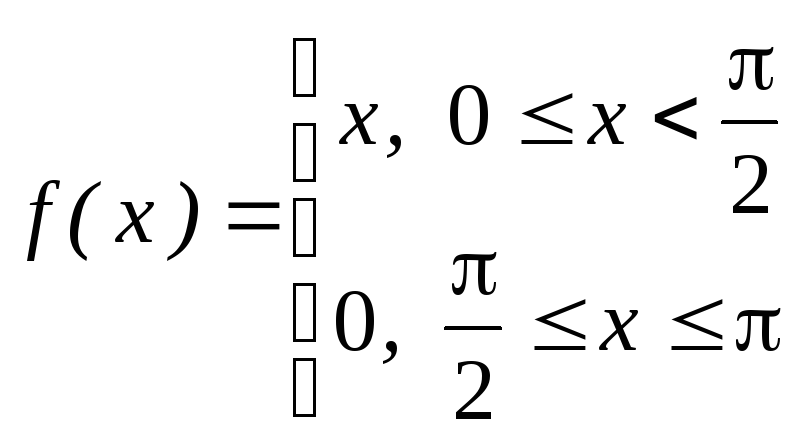 3}\) на \(0 \le x \le L\).
9n}} \right)\cos \left( {\frac {{n\,\pi x}}{L}} \right)} \]
3}\) на \(0 \le x \le L\).
9n}} \right)\cos \left( {\frac {{n\,\pi x}}{L}} \right)} \]