Разложить вектор по базису векторов: Онлайн калькулятор. Разложение вектора по базису

§ 4. Разложение вектора по базису.

Запись вида: = 𝛌₁  + 𝛌₂  + …+ 𝛌_n , где 𝛌₁, 𝛌₂, … , 𝛌_n — некоторые действительные

числа, называется разложением вектора по векторам , , …, .

Теорема (разложение по базису).

1). Пусть — базис пространства V₁. Тогда любой вектор  V₁ можно единственным

образом разложить по базису: = λ .

2). Пусть , — базис пространства V₂. Тогда любой вектор  V₂ можно

единственным образом разложить по базису: = λ₁ + λ₂ .

3). Пусть , , — базис пространства V₃. Тогда любой вектор  V₃ можно

единственным образом разложить по базису:

= λ₁ + λ₂ + λ₃ .

Коэффициенты при базисных векторах называются координатами вектора относительно

данного базиса.

= λ  — координата вектора относительно базиса { };

= λ₁ + λ₂  — координаты вектора относительно базиса { , };

= λ₁ + λ₂ + λ₃  — координаты вектора относительно базиса { , , }.

Пример.

V₁: = (-3)  ; V₂: = 2 + 5  ; V₃: = — 2  .

Теорема. (линейные действия с векторами в координатах).

При умножении вектора на число все его координаты умножаются на это число;

при сложении (вычитании) векторов их координаты складываются (вычитаются):

 λ ;

, 

+ , .

Условие коллинеарности векторов в координатной форме.

Векторы и коллинеарны тогда и только тогда, когда их

координаты пропорциональны:

Следствие.

= 0

rang = 1

 = = = 0

Пример.

,  rang = 2 ≠ 1  ;

,  rang = 1 

Пример.

Доказать, что — базис на плоскости и разложить вектор по этому базису:

, , . Построить заданные векторы в ортонормированном базисе.

= -5 ≠ 0   — базис на плоскости.

= λ₁ + λ₂  = λ₁ + λ₂  = + 

 =    =  

—

—

Условие компланарности векторов в координатной форме.

Векторы , и компланарны тогда и только тогда,

когда определитель матрицы, строки которой — координаты этих векторов, равен нулю:

, , — компланарны  = 0

Пример.

Доказать, что — базис в пространстве и разложить вектор по

этому базису: , , , .

= = = -5 ≠ 0  — базис в пространстве.

= λ₁ + λ₂ + λ₃  = λ₁ + λ₂ + λ₃ 

 = {0; λ₁; 3λ₁} + {- λ₂; 0; 2λ₂} + {λ₃; 3λ₃; 2λ₃}  = {- λ₂ + λ₃; λ₁+3λ₃; 3λ₁ +2λ₂+2λ₃}

   = 2  3  1 

Задачи по теме 1.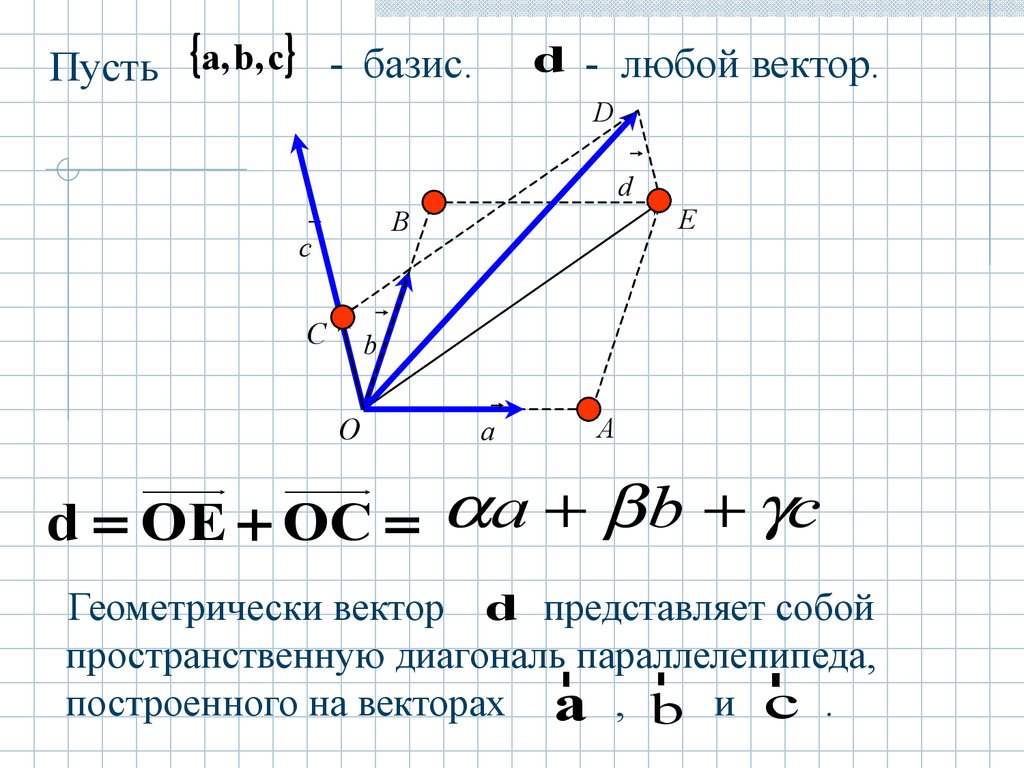

. Дан параллелограмм ABCD. Точки K, L, M, N — середины сторон параллелограмма,

= , = . Найти координаты вектора в базисе .

B

C

L

*

K

M

*

*

A

D

N

*

1. = 2. = 3. = 4. =

5. = 6. = 7. = 8. =

9. = 10. = 11. = 12. =

. Дан параллелепипед ABCD A₁B₁C₁D₁. Точка K — центр грани ABA₁B₁,

точка L — центр грани ABCD, точка M — центр грани AA₁DD₁, точка N — центр грани A₁B₁C₁D₁,

точка P — центр грани

BB₁CC₁, точка Q — центр грани CDC₁D₁, = , = , = .

Найти координаты вектора в базисе .

A₁

C₁

D₁

B₁

C

A

B

DD

1. = 2. = 3. = 4. =

5. = 6. = 7. = 8. =

9. = 10. = 11. = 12. =

13. = 14. = 15. = 16. =

. Доказать, что — базис на плоскости и разложить вектор по этому базису. Построить заданные векторы в ортонормированном базисе.

1. , , 2. , ,

3. , , 4. , ,

5. , , 6. , ,

Доказать, что — базис в пространстве и разложить вектор по этому базису.

7. , , ,

8. , , ,

9. , , ,

10. , , ,

11. , , ,

12. , , ,

Дополнительные задачи.

1. В правильном 5-угольнике ABCDE = , = .

C

Разложить вектор по базису .

B

D

A

E

2. В правильном 5-угольнике ABCDE = , = .

C

Разложить векторы и по базису .

B

D

A

E

3. Точка О — центр тяжести  ABC. Найти + + .

B

O

A

C

4. Дана пирамида ABCD, = , = , = . Точка О — центр тяжести  ABC.

Разложить вектор по базису .

D

B

A

C

O

2. Умножение векторов.

Разложение вектора по базису

Вектор вида , где () – некоторые числа, называется линейной комбинацией данных векторов . – коэффициенты линейной комбинации. Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он

разложен по этим векторам.

Справедливы следующие теоремы

Т е о р е м а 1. Пусть даны два неколлинеарных вектора и. Любой компланарный с ними векторраскладывается по ним и такое разложение единственно. Т. е.,=+, гдеиединственные для этого векторавполне определенные числа.

Т е о р е м а 2. Пусть даны три некомпланарных вектора ,и. Любой векторраскладывается по ним и такое разложение единственно. Т. е.,=++.

Базисом в пространстве называются три некомпланарных вектора, взятых в определенном порядке. Базис позволяет однозначно сопоставить вектору упорядоченную тройку чисел ,,- коэффициентов разложения этого вектора по векторам базиса. С другой стороны, каждой упорядоченной тройке чисел при помощи базиса сопоставляется единственный вектор. Если,,- базис и=++, то числа,,называются

координатами вектора в данном базисе, при этом пишут. Аналогично дается определение базиса на плоскости, когда вектор имеет две координаты.

Действия над векторами, заданными своими координатами:

1.При умножении вектора на число все его координаты умножаются

на это число. Т.е., (++)=++и{,,}.

2. При сложении векторов складываются их соответствующие координаты. Т. е., если в выбранном базисе ,, то.

Аффинные координаты

Аффинные координаты в пространстве определяются (рис. 4) заданием базиса ,,и точкиО – начала координат (affinis – смежный, соседний).

Рис. 4

Прямые, проходящие через начало координат в направлении базисных векторов, называются

осями координат: первая – ось абсцисс; вторая – ось ординат; третья – ось аппликат. Плоскости, проходящие через оси координат – координатные плоскости.

Пусть в пространстве задана точка М. —радиус-вектор точки М. Тогда разложение по векторам базиса =++.Аффинными координатами точки М называются координаты — радиус-вектора

в рассматриваемой системе координат, пишут , где- абсцисса,- ордината,- аппликата точкиМ. В заданной аффинной системе координат координаты фиксированной точки определяются однозначно. С другой стороны, если задана система координат, то в ней каждой упорядоченной тройке чисел ставится в соответствие единственная точка. Аффинная система координат на плоскости определяет такое же соответствие между точками и упорядоченными парами чисел.

З а д а ч а. Пусть в заданной аффинной системеи. Требуется найти координаты вектора.

Рис. 5

Р е ш е н и е . Из чертежа (рис. 5) видно , тогда

++++=

=.

Таким образом, , то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.

Проекция вектора на ось

Ориентированной осью называется прямая, на которой закреплена точка — начало отсчета, выбрана единица длины и направление отсчета.

Рис. 6

Проекцией вектора на осьназывается величина, численно равная длине отрезкамежду основаниями перпендикуляров, опущенных из точекА и В на l. Эта длина берется со знаком плюс, если направление от ксовпадает с направлением осиl и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.

Углом между осью и вектором называется угол, на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что .

Свойства проекции вектора на ось.

1. Проекция равна нулю тогда и только тогда, когда вектор перпендикулярен оси (говорят, вектор ортогонален оси).

2. При параллельном переносе вектора его проекция не меняется.

3. Проекция вектора на ось равна произведению длины вектора на

косинус угла между вектором и осью.

.

Рис. 7 Рис. 8

В этой формуле знак проекции регулируется знаком косинуса:

— если острый угол (рис. 7), тои;

— если тупой угол (рис. 8), тои.

4. Скалярный множитель можно выносить за знак проекции

.

5. Проекция суммы векторов равна сумме проекций слагаемых

.

Линейная алгебра

— Разложение вектора через скалярное произведение с базисным вектором: откуда следует необходимость нормализации?

Задавать вопрос

спросил 3 года 11 месяцев назад

Изменено 3 года, 11 месяцев назад

Просмотрено 581 раз 9n e_k \alpha_i e_i = a_k e_k \bullet e_k}_\text{as $e_k \bullet e_i = 0$ для всех $i \neq k$, так как все $e_i$ ортогональны. } = \alpha_k$$

Если $E$ не ортонормирован, а просто ортогонален, все $e_i$ должны быть нормализованы, поэтому мы получим

$\alpha_k = \frac{e_k \bullet v}{e_k \bullet e_k}$ для $ k$-я компонента $v$.

По крайней мере, так мне сказали. Однако я не вижу, где в доказательстве используется тот факт, что все $e_i$ имеют единичную длину. Это работает так же хорошо, если $e_i$ имеют разную длину. По-прежнему верно, что $e_k \bullet e_k = 1$ и что $e_k \bullet e_i = 0 ~ \forall ~i \neq k$. Следовательно, согласно логике доказательства, $k$-я компонента $v$ должна быть просто $v \bullet e_k$.

Однако я также понимаю, что в общем случае $v \bullet e_k \neq v \bullet c e_k$ для некоторого фактора $c$. Итак… есть ли дыра в доказательстве или я упустил момент, когда используется свойство $e_i$ быть единичной длины?

• линейная алгебра
• векторов

$\endgroup$

1

$\begingroup$

Тот факт, что $a_k e_k\cdot e_k=a_k$, объясняется тем, что $|e_k|^2=1$. Если $e_k$ не ортонормированы, а только ортогональны, то: 92\\ \подразумевает a_k=\frac{a_k e_k\cdot e_k}{|e_k\cdot e_k|}\\ \подразумевает a_k=\frac{e_k\cdot v}{|e_k\cdot e_k|} \end{выравнивание}

$\endgroup$

4

$\begingroup$

«По-прежнему верно, что $e_k \bullet e_k = 1$»

Согласно вашим предположениям ($e_k$ все еще ортогональны, но не обязательно имеют единичную длину), это в общем случае неверно. Вы можете посмотреть на этот пример:

$$ e_1 = \pmatrix{2 \\ 0}\\ e_2 = \pmatrix{0 \\ 2} $$ в котором $e_k \cdot e_k = 4$ при $k = 1, 2$.

Если попытаться разложить вектор $$ v = \pmatrix{2\\2} = e_1 + e_2 $$ используя предложенную вами формулу, вы увидите, что пойдет не так.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Как разложить вектор на неортогональные компоненты?

спросил 6 лет, 4 месяца назад

Изменено 6 лет, 4 месяца назад

Просмотрено 3к раз

$\begingroup$

Как разложить вектор на неортогональные компоненты?

У меня есть вектор с координатами (-4 , -1).