Размещение сочетание перестановки: Лекция 2. Перестановки, сочетания, размещения · Теория вероятностей и математическая статистика

Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР

РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.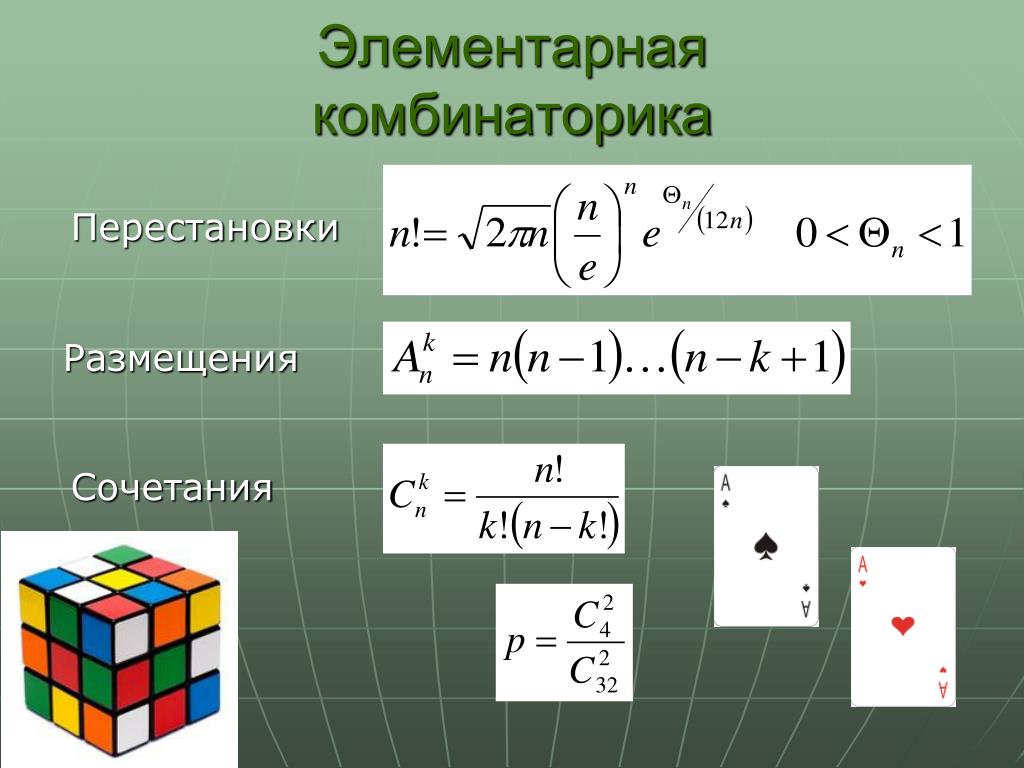
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

376111 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Владимир Александрович Кузьмин

«

Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить. Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии. Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.

В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!

«

Вячеслав Юрьевич Матыкин

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Клиентам

• Репетиторы по математике
• Репетиторы по русскому языку
• Репетиторы по химии
• Репетиторы по биологии
• Репетиторы английского языка
• Репетиторы немецкого языка

Репетиторам

• Регистрация
• Публичная оферта
• Библиотека
• Бан-лист репетиторов

Партнеры

• ChemSchool
• PREPY. RU
• Class

Дискретная математика — Формулы комбинаторики

Перестановки    

1) Перестановки без повторений.

Перестановки — это комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком расположения этих элементов. Возьмем n различных элементов a₁, a₂, a₃, … a_n; будем переставлять эти элементы всевозможными способами, оставляя без изменения число элементов и меняя только порядок их расположения. Обозначим общее число полученных таким образом перестановок P(n). P — первая буква французского словаpermutation — перестановка.

Составив таблицу перестановок для n элементов и применив (n — 1) раз правило произведения, получим число всех возможных перестановок:

P(n) = n • (n -1) • (n — 2) • … • 3 • 2 • 1 = n!

Такие перестановки называются перестановками без повторений (один и тот же элемент не может повториться в комбинации, все элементы различны).

Задача: шесть человек могут в разном порядке сесть за круглый стол, сколько существует способов разместить эти шесть человек за столом?

Решение: т.к. все люди различны и  их комбинации различаются только порядком следования, то мы имеем перестановки без повторений. Определим их число:

Р(6) = 6! = 1 • 2 • 3 • 4 • 5 • 6 = 720.

2) Перестановки с повторениями

Рассматривая различные перестановки, мы предполагали, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.

Если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., n_k элементов к-го вида, то имеем перестановки с повторениями, их число:

, где n₁+…+n_k = n.

Задача: сколько различных «слов» можно составить из букв слова ДЕД, МАТЕМАТИКА.

Решение: имеем перестановки с повторениями.

А) ДЕД    n=3, k=2, n₁=2, n₂=1

P₃(2, 1) = 3!/(2! • 1!) = 6 / 2 = 3;

Б) МАТЕМАТИКА n=10, k=6, n₁=2, n₂=3, n₃=2, n₄=n₅=n₆=1

P₁₀(2,3,2,1,1,1)=10!/(2! • 3! • 2!)=2•4•5•6•7•9•10 = 134 400.

 Размещения

1) Размещения без повторений.

Размещениями называют комбинации, составленные из n данных элементов по k элементов (k<=n, k>0), которые отличаются либо составом элементов, либо порядком расположения элементов. Обозначаются размещения A

n^k . А — первая буква французского слова arrangement, что в переводе означает «размещение», «приведение в порядок». Число всех возможных размещений находится по формуле:

.

Задача: расписание одного дня состоит из двух пар. Определить число вариантов расписания при выборе из пяти дисциплин, если не может быть одинаковых пар.

Решение: имеем размещения без повторений из пяти элементов по два, из число: .

2) Размещения с повторениями.

Пусть существуют n различных элементов. Выберем из них m штук, действуя по следующему принципу: возьмем любой элемент, но не будем устанавливать его в какой-либо ряд, а просто запишем под номером 1 его название, сам же элемент вернем к остальным элементам. Затем опять из всех n элементов выберем один, запишем его название под номером 2 и снова вернем элемент обратно. Будем выполнять эти операции, пока не получим m названий. Размещения с повторениями вычисляются по формуле:

.

Задача: сколько четырехзначных номеров можно составить из 10 цифр?

Решение: имеем размещения с повторениями из 10 элементов по 4, их число: .

Сочетания

1) Сочетания без повторений.

Сочетаниями называют комбинации, составленные из n различных элементов по k (k =< n) элементов, которые отличаются хотя бы одним элементом. Сочетания обозначаются: C_n^k C — первая буква французского слова combinasion— сочетание.

Составим из n элементов всевозможные сочетания по k элементов в каждом. Их будет C

n^k . Внутри каждого сочетания, состоящего из k элементов, образуем всевозможные комбинации, учитывающие порядок следования в них элементов. Таких комбинаций будет P_k, т.к. мы в нашем сочетании образовываем перестановки. Всего различных комбинаций из n элементов по k в каждой, отличающихся друг от друга либо составом (элементами), либо порядком их следования, будет C_n^k • P_k . Но такие комбинации называются размещениями. Таким образом, A_n^k = C_n^k • P_k, тогда:

.

Задача: в шахматном турнире участвует 7 человек; сколько партий будет сыграно, если между любыми двумя участниками должна быть сыграна партия?

Решение: имеем сочетания без повторений из 7 элементов по 2; их число:  .

2) Сочетания с повторениями.

Если в сочетаниях некоторые элементы (или все) могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями. Их число определяется по формуле:                               .

Задача: сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных?

Решение: имеем сочетания с повторениями из четырех по 7 по, их число: .

 

_{Вопросы и задания!}

 1. Города A,B,C,D,E попарно соединены дорогами. Сколько разных маршрутов путешествия из города А в город Е с посещением еще каких-то двух городов можно составить? Предполагается, что в маршруте каждый город присутствует не более одного раза, и маршруты, отличающиеся порядком следования городов, различны.

 

2. Сколькими способами можно распределить среди 20 студентов группы четыре билета в театр, если

• билеты на один спектакль, и каждый студент может получить не более одного билета; 
• билеты на один спектакль, и каждый студент может получить сколько угодно билетов;
• все билеты на разные спектакли, и каждый студент может получить не более одного билета;
• все билеты на разные спектакли, и каждый студент может получить сколько угодно билетов?  

3. Есть 4 билета на концерт, 5 билетов в театр и 7 билетов в цирк. Сколькими способами их можно распределить среди 25 студентов группы, если каждый студент может получить не более одного билета на каждое мероприятие? Билеты на одно мероприятие считаются равнозначными.

 

4. Девочка нанизала n разных бусин на английскую булавку. Сколько различных украшений может получиться таким образом? Два украшения различны, если они отличаются порядком следования бусин на булавке. 

 

5. У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если ему дадут не более трех имен из 300 возможных, и при этом

• имена могут повторяться;
• все имена различны?

Назад  В начало  Далее

Важные практические вопросы | Перестановка и комбинация

В этой статье мы обсудим основные понятия и формулы перестановки и комбинации, необходимые для решения задач на различных вступительных испытаниях и конкурсных экзаменах. Вопросы этой темы в основном сосредоточены на проверке навыков аспиранта в логический счет.

Изучите основные принципы перестановки и комбинации вместе с решенными примерами.

---

Формулы для перестановок и комбинаций

Обозначение факториала:

Пусть n — целое положительное число. Тогда факториал n, обозначаемый n! определяется как: 

н! = п(п — 1)(п — 2) … 3.2.1.

Примеры: 

— Определяем 0! = 1. 

— 4! = (4 х 3 х 2 х 1) = 24,

— 5! = (5 х 4 х 3 х 2 х 1) = 120,

Перестановки:

Различное расположение заданного количества вещей путем одновременного взятия некоторых или всех вещей называется перестановками.

Примеры: 

— Все перестановки (или расположения), выполненные с буквами a, b, c путем взятия по две за раз, составляют 

.

(ab, ba, ac, ca, bc, cb).

 — Все перестановки букв a, b, c, берущие все сразу: 

(abc, acb, bac, bca, cab, cba)

Количество перестановок: 

Количество всех перестановок n вещей, взятых по r за раз, определяется как: 

ⁿ P _r     = n! / (н — р)!

Примеры: 

— ⁶ P ₂ = (6 x 5) = 30.  

— ⁷ P ₃  = (7 x 6 x 5) = 210. 

Комбинации:

Каждая из различных групп или выборок, которые могут быть образованы путем взятия некоторых или всех объектов , называется комбинацией .

Примеры: 

— Предположим, мы хотим выбрать двух из трех мальчиков A, B, C. Возможные варианты: AB, BC и CA.

— Примечание: AB и BA представляют один и тот же выбор.

— Все комбинации, образованные a, b, c, включая аб, до н.э., ок.

— Единственная комбинация, которая может быть составлена ​​из трех букв a, b, c, взятых одновременно, — это abc.

— Различные группы из 2-х из четырех человек A, B, C, D:

—  AB, AC, AD, BC, BD, CD.

— обратите внимание, что ab ba — это две разные перестановки, но они представляют собой одну и ту же комбинацию.

Количество комбинаций: 

Количество всех комбинаций из n предметов, взятых по r за раз, равно: 

ⁿ C _r  = n! / (р !) (н — р) !

Примечание:

—  ⁿ C _n  = 1 и ⁿ C ₀  = 1.  

—  ⁿ C _r   = ⁿ C _(n-r)

Примеры: 

¹¹ C ₄  = (11 x 10 x 9 x 8) / (4 x 3 x 2 x 1) = 330. 

¹⁶ C ₁₃  = ¹⁶ C _(16-13)  =  ¹⁶ C ₁₃   = (16 x 15 x 14) / x 5 0,3 = 2

---

Практические вопросы для перестановки и комбинации

Q1) Разведывательное агентство формирует код из двух различных цифр, выбранных из 0, 1, 2, …., 9, так что первая цифра кода отлична от нуля. Однако код, написанный от руки на бланке, может создать путаницу, если читать его вверх ногами — например, код 9.1 может выглядеть как 16. Сколько существует кодов, для которых не может возникнуть такая путаница?

А) 80

Б) 78

С) 71

Г) 69

Решение:

---

В2) Если в холодильнике 12 банок, то 7 синих банок и 5 красных банок. Сколькими способами можно убрать 8 банок так, чтобы в холодильнике осталась хотя бы 1 синяя и 1 красная банки.

А) 513

Б) 455

С) 627

Д) 369

Решение:

---

Q3) В гостинице состоится собрание 20 делегатов. Сколькими способами можно рассадить этих делегатов за круглым столом, если три конкретных делегата всегда сидят вместе?

А) 17! 3!

Б) 18! 3!

С) 17! 4!

Д) 18! 4!

Решение:

---

Удалите все свои концепции способностей от экспертов с помощью курса Aptitude Cracker!- https://bit.ly/2YFn39h

---

В4) Сколькими способами можно составить четырехзначное четное число, используя цифры 2,3,5,8 ровно один раз?

А) 24

Б) 12

С) 6

Г) 18

Решение:

---

В5) В колледже учатся 10 баскетболистов. Из этих 10 игроков будет выбрана команда из 5 человек и капитан. Сколько различных выборов можно сделать?

А) 1260

Б) 210

С) 10С6 * 6!

Г) 10C5 * 6

Решение:

Из 10 игроков нужно выбрать команду из 6 человек. Это можно сделать способами 10C6 или 210.
Теперь капитана из этих 6 игроков можно выбрать 6 способами.
Таким образом, общее количество способов выбора равно 210*6 = 1260. 

---

В6) Сколько слов из 7 согласных и 4 гласных можно составить из 3 согласных и 2 гласных?

А) 24400

Б) 21300 

С) 210

Г) 25200

Решение:

Количество способов выбора 3 согласных из 7 = 7C3
Количество способов выбрать 2 гласных из 4= 4C2
Количество способов выделения 3 согласных из 7 и 2 гласных из 4
= 7C3 × 4C2
=(7×6×5/3×2×1)×(4×3/2×1)=210
Это означает, что у нас может быть 210 групп, каждая из которых содержит всего 5 букв (3 согласных и 2 9 букв).0148 гласные).
Количество способов расположения 5 букв между собой=5!=5×4×3×2×1=120 
Следовательно, требуемое количество путей=210×120=25200

---

В7) У мальчика девять брюк и 12 рубашек. Сколькими способами он может выбрать брюки и рубашку?

А) 21

Б) 12

С) 9

Г) 108

Решение:

Мальчик может выбрать одну штанину девятью способами.
Мальчик может выбрать одну рубашку 12 способами.
Количество способов, которыми он может выбрать одни брюки и одну рубашку, составляет 9 * 12 = 108 способов.

---

Ищете комплект для подготовки к размещению ALL IN ONE? Присоединяйтесь к нашему полному пакету размещения ! — https://bit.ly/2WC7tIL  

---

В8) Найдите сумму всех четырехзначных чисел, которые можно составить из цифр 3, 4, 5 и 6 

А) 119988

Б) 11988

С) 191988

D) Ничего из перечисленного

Решение:

Количество цифр = 4 Все различны; Их можно расположить в 4! = 24 способа
Каждая из цифр 3, 4, 5 и 6 встречается на единичном разряде = 3! Пути = 6 способов.
Таким образом, будет 6 чисел, оканчивающихся на 3, 4, 5 и 6 каждое. Таким образом, сумма цифр в единице
место = 6(3 + 4 + 5 + 6) = 108
Сумма чисел = 108 × 103 + 108 × 102 + 108 × 101 + 108 × 100 = 119988

---

В9) Сколькими способами можно расположить буквы слова «НАЧАЛО» так, чтобы гласные всегда совпадали?

А) 720

Б) 520

С) 700

Г) 750

Решение:

Слово «ВЕДУЩИЙ» состоит из 7 разных букв.
Когда гласные EAI всегда вместе, можно предположить, что они образуют одну букву. Затем нам нужно расставить буквы LNDG (EAI).
Теперь 5 (4 + 1) букв можно составить по 5! = 120 способов.
Гласные (EAI) можно расположить между собой по 3! = 6 способов.
Необходимое количество путей = (120 х 6) = 720.

---

В10) Сколько комбинаций студентов возможно, если группа состоит ровно из 3 первокурсников?

А) 5000

Б) 4550

С) 4000

Г) 3550

Решение:

Здесь нам нужно количество возможных комбинаций 3 из 5 первокурсников, 5С3 и число
возможных комбинаций 3 из 15 второкурсников и юниоров,
15С3. Обратите внимание, что нам нужны 3 первокурсника и 3 студента из других классов. Поэтому мы
умножьте количество возможных групп из 3 из 5 первокурсников на количество возможных
группы по 3 из 15 учеников других классов. 5С3×15С3=4550.

---

Чтобы проверить себя, нажмите на БЕСПЛАТНУЮ СЕРИЮ ТЕСТИРОВАНИЯ, предоставленную Talent Battle — https://bit.ly/3dmvTNa  

Как рассчитать перестановки и комбинации

3 апреля 2020 г.

Вам не нужно быть гением математики, чтобы быть хорошим программистом, но есть несколько приемов, которые вы захотите добавить в свою сумку для решения проблем, чтобы улучшить производительность своих алгоритмов и произвести впечатление на технических собеседованиях. В этом уроке вы узнаете, как вычислять перестановки и комбинации ряда из n целых чисел с помощью простых и легко запоминающихся уравнений.

---

Быть О(#1). Возьмите свою копию Маленькой книги Большого О.

---

В чем разница между перестановками и комбинациями?

• Перестановки, важна последовательность

Нас интересует порядок размещения предметов.

• Комбинации, последовательность не важна

Нас интересует количество групп, которые мы можем создать.

Давайте рассмотрим пример.

Сколько трехбуквенных перестановок существует для букв A, B и C?

 азбука
ACB
ВСА
БАК
ТАКСИ
ЦБ 

Есть шесть перестановок.

Как насчет комбинаций?

Ну, есть только один.

Почему?

Независимо от порядка, наша группа всегда содержит одни и те же три буквы, A, B и C.

Когда мы вычисляли перестановки для трех букв, вы заметили закономерность?

Давайте попробуем четыре буквы:

 АВСD
АБДК
ACBD
ACDB
АДБК
АДКБ
БАКД
БАДК
BCAD
BCDA
БДАК
БДКА
КАБР
CADB
КБАД
КБДА
CDAB
CDBA
DABC
DACB
DBAC
ДБКА
DCAB
DCBA 

Мы только что сделали большой скачок в количестве перестановок, которые нам нужно рассчитать!

Где мы видели это или что-то подобное раньше?

🤔

Факториал!

В первом примере с тремя буквами наши перестановки были 3! или:

 3 * 2 * 1 = 6 

Во втором примере с четырьмя буквами наши перестановки были 4! или:

 4 * 3 * 2 * 1 = 24 

Как насчет вычисления подмножеств перестановок?

Как рассчитать перестановки

Допустим, вы судья на конкурсе выпечки и вам нужно вручить золотые, серебряные и бронзовые подставки для тортов трем лучшим из 12 участников, но все пекари заслуживают награды.

Сколько вариантов нужно рассчитать?

Это проблема перестановок.

Почему?

Заказ важен.

Мы оцениваем или упорядочиваем трех лучших пекарей.

Вручаем золото Ноэлю.

Теперь на выбор осталось одиннадцать участников.

Вручаем серебро Сэнди.

Теперь на выбор осталось десять конкурсантов.

Мы вручаем бронзу Прю.

Эти трое — очевидные победители.

(Извините, Пол.)

Но если бы это не было так очевидно, сколько возможных перестановок нам пришлось бы вычислить?

Каждый раз, когда мы выбираем победителя, этот индивидуум удаляется из группы, и мы вычисляем возможные перестановки оставшихся индивидуумов.

Сколько 12!?

 12 * 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 47
00 

Много обработки!

К счастью, нам не нужно вычислять столько перестановок.

Нам нужно только рассчитать перестановки для трех победителей.

Как нам это сделать?

Мы просто останавливаемся после трех самых больших значений в нашей последовательности:

 12 * 11 * 10 = 1320 

Почему?

Нет необходимости вычислять все перестановок, только для трех наибольших значений.

Это по-прежнему много перестановок, но гораздо более управляемое число.

Что, если бы мы не знали размер нашего ввода с самого начала?

Превратим это в уравнение!

Как еще можно описать числа, которые мы не учитывали?

 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 

9!

Поскольку факториал — это произведение последовательности, мы не можем просто вычесть 9! с 12!.

Нам нужно разделить:

 12! / 9! 

Мы могли бы также записать это как:

 12! / (12 - 3)! 

Теперь нужно просто заменить значения переменными.

 н! / (н - к)! 

Как рассчитать комбинации

Допустим, мы заказываем пиццу, чтобы накормить участников хакатона.

Поскольку это программисты, они хотят знать, сколько возможных комбинаций доступно для выбора.

Местная пиццерия предлагает нам 12 вариантов начинки, но мы можем выбрать только три на пиццу.

Сколько разных пицц возможно?

Это проблема комбинаций.

Почему?

Потому что порядок не имеет значения.

Пицца с пепперони, перцем и ананасом такая же, как пицца с ананасом, перцем и пепперони.

Но поскольку порядок не имеет значения, важна избыточность.

Когда мы вычисляем перестановки, нет избыточности в заказывает элементов, но в группировке элементов много избыточности.

Как убрать лишние комбинации?

Мы просто делим на количество перестановок k или k!

 (н!/(н-к)!)/к! 

Что также:

 (н!/(н!-к!) )*1/к! 

В упрощенном виде:

 н! / (н - к)! * к! 

Это часто записывается как:

И читать как « n выбрать k », потому что существует n способов выбрать неупорядоченное подмножество k элементов из фиксированного набора n элементов.

АКА биномиальный коэффициент

Как рассчитать перестановки и комбинации

Вам не нужно быть гением математики, чтобы быть хорошим программистом, но есть несколько уравнений, которые вы захотите добавить в свой набор инструментов для решения задач.