Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376126 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
- ChemSchool
-
PREPY.
RU
- Class
RU
Перестановки. Размещения. Сочетания. Урок решения комбинаторных задач
Вы можете изучить и скачать доклад-презентацию на тему Перестановки. Размещения. Сочетания. Урок решения комбинаторных задач. Презентация на заданную тему содержит 17 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Математика» Перестановки. Размещения. Сочетания. Урок решения комбинаторных задач
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Слайд 2
Описание слайда:
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Слайд 5
Описание слайда:
Слайд 6
Описание слайда:
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Слайд 9
Описание слайда:
Слайд 10
Описание слайда:
Слайд 11
Описание слайда:
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
Слайд 14
Описание слайда:
Слайд 15
Описание слайда:
Слайд 16
Описание слайда:
Слайд 17
Описание слайда:
Tags
Перестановки.
Размещения. Сочетания. Урок решения комбинаторных задач
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Перестановки и комбинации – хитрости и важные формулы
Перестановки и комбинации – одна из самых важных глав для любых конкурсных экзаменов, таких как Placement Test, Bank PO, CAT, CMAT, XAT, SNAP, FMS, IIFT, MICA, GRE и GMAT. Вопросы из этой темы в основном проверяют умение аспиранта в логическом счете. Глубокое теоретическое понимание различных методов счета поможет вам интересно ответить на все вопросы о способностях из этой области с помощью приемов и важных формул.
Пожалуйста, прочитайте статью о методах счета, чтобы лучше понять основные навыки счета.
Нелегко ответить на вопросы по этим понятиям с вашими базовыми навыками счета. Таким образом, вы должны изучить математические приложения в этом отношении.
Здесь мы в основном рассматриваем различные применения концепции перестановки. Это опять же понятие аранжировки, но только главное отличие, повторение объектов в аранжировках недопустимо. т.е. когда вы сталкиваетесь с такой ситуацией расположения без повторения предметов, поймите, это и есть применение Перестановки.
Основные задачи этого модуля:
- Факториалы
- Свойства факториалов
- Перестановки (некруглые)
- Условные перестановки
- Сумма чисел, образованных различными способами.
- Ранг слова (или аранжировки)
- Круговая перестановка
- Комбинации
- Важные свойства и результаты комбинаций
- Геометрические приложения Комбинации
- Распределение одинаковых вещей по группам
Факториал
Рассмотрим практический пример, чтобы понять важность концепции факториала в аранжировках.
Пример: Сколькими способами можно расположить буквы в слове «ЛИЦО»?
Это в основном контекст аранжировки, но это аранжировка без повторения какой-либо буквы.
Четыре разных буквы F A, C и E.
| 1-я буква | 2-я буква | 3-я буква | 4-я буква |
|---|---|---|---|
| Любая из четырех 9006 | Любой, кроме первой буквы | Любой, кроме первых двух букв | Осталась одна буква |
| 4 выхода | 3 направления | 2 направления | односторонний |
Следовательно, общее количество аранжировок = 4 * 3 * 2 * 1 = 24
т.е. произведение первых четырех натуральных чисел.
Это часто встречающаяся ситуация в сфере договоренностей.
Здесь мы видим уместность концепции факториала.
Произведение первых 4 натуральных чисел можно выразить как 4! (4 факториал).
т. е. н! означает произведение первых n натуральных чисел.
н! = 1 * 2 * 3 * ….. * (n — 2) * (n — 1) * n
| Количество способов расположить n различных объектов в n разных местах может быть выражено как ‘n!’ |
Следовательно, количество способов расположить один предмет в одном месте = 1! = 1 способ
И количество способов расположить ‘0’ объект (нет объекта) на ‘0’ месте (нет места) можно считать за ‘0!’, т.
е. можно предположить только одним способом.
Отсюда 0! = 1
| «0! = 1 |
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| И так далее.» |
Свойства факториалов:
- Факториал любой отрицательной величины недействителен.
- н! = п * (п — 1) !
[т.е. 6! = 6 * 5! = 6 * 5 * 4! и т.д.]
- n!/n = (n — 1) !
- н!/(н — 1)! = п
Численные задачи, связанные с факториалами, описаны в теме «Числа». Здесь мы рассматриваем применение «факториалов» в «аранжировках».
Здесь у нас есть три различных вида применения факториалов в отношении некруговых схем.
- Расположение n различных объектов.
- Расположение ‘n’ объектов, в котором некоторые из них повторяются.
- Условное размещение ‘n’ объектов (различных или неразличимых объектов).
Пример для типа 1:
Сколькими способами можно расположить буквы в слове РАДУГА?
Решение:
Здесь у нас есть 7 различных букв.
Отсюда искомое количество аранжировок = 7! = 5040
| Результат: Количество способов расположить n различных букв в ряду = n! |
Пример для типа 2:
Сколькими способами можно расположить буквы слова ИНДИЯ?
Решение:
Здесь 5 букв и две из них повторяются.
т. е. повторяются два «я». Эти одинаковые буквы дублируют количество аранжировок.
Чтобы избежать дублирования при подсчете, просто разделите общее количество аранжировок (независимо от повторения) на 2!.
т.е. необходимое количество аранжировок = 5! / 2! = 120/2 = 60 способов
| Результат: Количество способов расположить «n» объектов в ряд так, чтобы «p» объектов из «n» объектов были идентичными, а «q» объектов из «n» объектов были идентичными, равно п!/(р! д!).  |
Пример для типа 3:
Сколькими способами можно переставить буквы в слове ПЕСНЯ так, чтобы слово начиналось с гласной?
Решение:
Из четырех различных букв только одна буква (О) является гласной, и расположение должно начинаться с «О».
т.е. первую букву можно расположить только одним способом, а остальные три места — тремя! способы.
Отсюда общее количество аранжировок = 1 * 3! = 6 способов.
Перестановка (некруговая)
Перестановка означает размещение без повторения отдельных объектов. Существует два разных типа перестановок.
- Нециклическая перестановка.
- Круговая перестановка.
В этой первой части мы рассматриваем нециклические перестановки. В основном это применимо в контексте расположения по рядам.
| Результат: Количество способов упорядочить ‘r’ объектов из ‘n’ различных объектов выражается как nP r .  nP r = n!/(n-r)! , где n > 0, r ≥ 0 и n ≥ r. |
Пример 1: Сколько различных трехзначных чисел можно составить так, чтобы цифры были различными простыми числами?
Однозначные простые числа: 2, 3, 5 и 7.
т. е. существует 4 различных простых числа из одной цифры.
Чтобы найти требуемые трехзначные числа, мы должны расположить в ряд любые три из четырех различных простых чисел.
Это расположение трех из четырех цифр подряд.
т.е. 4P 3 = 4!/ (4 — 3)! = 24
Следовательно, возможно 24 таких различных трехзначных числа.
Примечание. В таком расположении:
Общее количество объектов = 4 (четыре различных однозначных простых числа)
Количество мест для заполнения = 3 (трехзначное число)
| Как и в предыдущем примере, в результате nP r ; n → количество предметов r → количество мест |
Пример 2.
Сколькими способами можно припарковать 4 автомобиля на 5 разных парковочных местах?
Здесь 4 машины — это четыре различных объекта, а 5 доступных слотов — это места.
Необходимое количество соединений = 5P 4 = 5!/(5 — 4)! = 120 способов
| Согласно приведенному выше примеру, в результате nP r ; n → количество предметов r → количество мест |
Важное примечание:
Из приведенных выше двух примеров видно, что в результате nP r n и r могут быть либо объектами, либо местами, в зависимости от ситуации подсчета.
| np 0 = n!/(n-0)! = 1 np 1 = n!/(n-1)! = n(n-1)!/(n-1)! = п np n = n!/(n-n)! = п!/1 = п! Там для, 0!=1 |
Сумма чисел, образованных различными способами.
Это расширенное приложение перестановки Liner. Все вступительные экзамены в школу B часто задают вопросы из этой области.
Мы уже знакомы с методом кадрирования различных чисел посредством заданного расположения различных цифр. Здесь мы рассматриваем метод нахождения суммы всех чисел, образованных такими сочетаниями.
Пример:
Найдите сумму всех трехзначных чисел, образованных цифрами 1, 2 и 3 без повторения.
Решение:
Без повторения цифр мы можем кадрировать 3! Всего номеров, т.е. 6 номеров.
Ниже приведены возможные номера.
123
132
213
231
312
321
| Столбец 1 | Колонка 2 | столбец 3 | .0052 |
|---|---|---|---|
| 1 | 2 | 3 | |
| 1 | 3 | 2 | |
| 2 | 1 | 3 | |
| 2 | 3 | 1 | |
| 3 | 1 | 2 | |
| 3 | 2 | 1 | |
| Итого = 12 | Итого = 12 | Итого = 12 |
Из вышеприведенной таблицы легко понять, что после упомянутых расстановок в каждом столбце есть данные цифры с одинаковой частотой, но в разном порядке.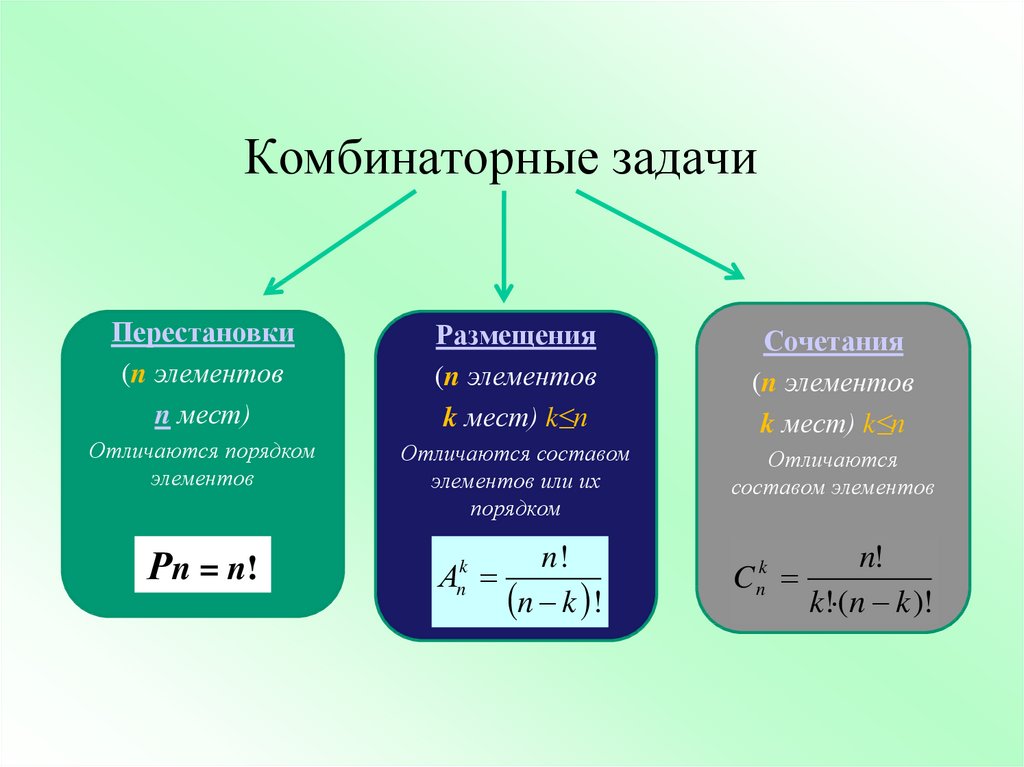
Эта частота повторения цифры в каждом столбце равна (n-1)!, где n — количество различных цифр в аранжировках. В заданном вопросе мы должны расположить три цифры, поэтому n = 3. Итак, (n-1)! = (3 — 1)! = 2
Следовательно, отдельные суммы каждого столбца равны, и сумму каждого столбца можно найти следующим образом.
Сумма в каждом столбце = сумма различных цифр в расположении * (n — 1)!
= (1 + 2 + 3) * (3 — 1)!
= 6 * 2 = 12
Сумма всех чисел = 1200 + 120 + 12 (учитывать разряды)
= 1332
Для нахождения итоговой суммы можно применить другой метод, т.е. 12 * 111 (количество единиц равно количеству мест)
Согласно приведенному выше объяснению, мы можем завершить метод следующим образом.
| Сумма всех чисел, состоящих из n ненулевых цифр = (n — 1)! * Сумма всех цифр в расположении * 1111…n раз. |
Ранг слова
Ранг слова означает при расположении слов (кодов), образованных определенной группой отдельных букв в стандартном порядке (алфавитном порядке) словаря, положение конкретного слова ( код).
Пример:
Если переставить буквы в слове «ЛИЦО» и разные слова, образованные этими перестановками, расположить в алфавитном порядке (или в порядке стандартного словаря), найти ранг слова «ЛИЦО».
Решение:
FACE — это слово из 4 букв, и все слова различны.
Алфавитный порядок букв в слове: A, C, E, F
Избегайте всех слов, начинающихся с «A».
Количество слов начинается с A = 3! {Первая буква «А», а остальные буквы можно расположить 3! способами}
Аналогично;
Количество букв начинается с ‘C’ = 3!
Количество слов, начинающихся с ‘E’ = 3!
т.е. наши обязательные приходят после всего вышеперечисленного количества договоренностей.
Рассмотрим слово, начинающееся с F.
Согласно алфавитному порядку, первое слово, которое начинается с ‘F’, это ‘FACE’, наше необходимое слово.
Следовательно, ранг слова «ЛИЦО» = 3! + 3! + 3! + 1 = 19
, т. е. 19 90 529 th 90 530 слово расположения — это «ЛИЦО».
Пример:
Найдите ранг слова ‘BOOK’, расположив слова, образованные перестановкой букв слова ‘BOOK’ в порядке стандартного словаря.
Решение:
Буквы в алфавитном порядке: B, K, O, O
Количество слов, начинающихся с ‘BK’ = 2!/ 2! = 1 {буква ‘O’ повторяется дважды}
Количество слов, начинающихся с ‘BOK’ = 1 {оставшаяся буква только ‘O’}
Следующее слово — ‘BOOK’.
Следовательно, ранг слова «КНИГА» = 1 + 1 + 1 = 3
Теперь мы рассмотрим «Круговые перестановки» и «Комбинации». Этот модуль даст вам четкое представление о различных применениях перестановок и комбинаций в различных практических ситуациях, даже в области геометрии.
Циркулярная перестановка
Случай 1: Порядок расположения является вопросом.
Если объекты расположены по кругу, то сформированная таким образом перестановка называется круговой перестановкой.
Общее количество круговых перестановок ‘n’ объектов, если порядок кругового расположения (по часовой стрелке или против часовой стрелки) значителен, определяется как (n-1)!.
Пример:
Количество способов рассадить 3 человека вокруг стола = (3 — 1)! = 2 способа
Ниже приведены возможные способы расположения.
Здесь мы рассматриваем расположение по часовой стрелке. Следовательно, возможны два различных расположения, и направление расположения имеет значение при подсчете.
Случай 2: Порядок расположения не имеет значения.
Общее количество круговых перестановок ‘n’ объектов, если нет ‘Нет разницы’ между расположением по часовой стрелке и против часовой стрелки, определяется как (n-1)!/2.
Например: расположение бусин в ожерелье.
В этом случае расположение бусин по часовой стрелке , а не отличается от расположения бусин по часовой стрелке или против часовой стрелки, потому что одно из них представляет собой просто вид сзади другого . Поэтому, учитывая порядок бусинок по часовой стрелке и против часовой стрелки, нет двух разных расположений.
Мы можем обобщить понятие круговой перестановки.
Если мы имеем дело с уникальными предметами, то круговая перестановка = (n-1)!/2
Пример:
Количество способов расположить 3 разноцветные бусины в ожерелье = (3-1)!/2 = 1
Обратитесь к следующему рисунку:
Наблюдая, мы можем легко увидеть, что вторая цифра является просто отражением первой цифры, если порядок не имеет значения.
Следовательно, имеется только одна аранжировка.
т.е. количество способов расположить 3 разноцветные бусины в ожерелье = 1 способ.
Основные понятия перестановки и комбинирования — Hitbullseye
В этой статье мы обсудим основные понятия перестановки и комбинирования и формулы, необходимые для решения задач на них. Эта тема затрагивается на всех конкурсных экзаменах, поэтому вы не можете позволить себе рисковать и избегать ее. Прочитав эту статью, вы познакомитесь с основными понятиями перестановки и комбинации.
Рекомендуемое действие
БЕСПЛАТНЫЕ живые мастер-классы от нашего Звездного факультета с более чем 20-летним опытом.
Зарегистрируйтесь сейчас
Формула перестановки и комбинации:
- Перестановка f формула: Перестановка определяется как расположение r вещей, которые можно сделать из общего количества n вещей. Это обозначается n P r , что равно n!/(n-r)!
- Комбинированная формула
- Комбинация определяется как выбор r вещей, которые можно сделать, из n вещей. Это обозначается n C r , что равно n!/r!(n-r)!
- В соответствии с основным принципом счета, если одно действие может быть выполнено 90 640 m 90 641 способами, а другое действие может быть выполнено 90 640 n 90 641 способами, то любое из двух действий может быть выполнено 90 640 m + 90 641 90 640 n 90 641 способов. способами, и оба они могут быть выполнены в 90 640 м × 90 641 90 640 n способов.
Пример 1: Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 (повторение цифр не допускается)?
Решение: Тысячное число можно заполнить 6 способами.
Место сотни можно заполнить 5 способами. Место десятки может быть заполнено 4 способами. Место юнита можно заполнить 3 способами. Итак, используя основной принцип счета, мы получаем ответ как 6 × 5 × 4 × 3 = 360. Или, используя формулу перестановок, нам нужно расположить 4 цифры из 6 цифр. Это можно сделать в 6 P 4 = 360 контактов.
Пример 2: У человека есть 6 друзей, которых нужно пригласить на ужин по пригласительным билетам, и у него есть 3 слуги. Сколькими способами он может продлить пригласительный билет?
Решение: Мы видим, что у друга 1 st есть 3 варианта получения карты, т.е. либо от слуги 1 st , либо от 2 st или 3 rd . Точно так же у 2-го друга также есть 3 варианта получения карты, т.е. либо от 1 ст слуга или 2 й или 3 й . Таким образом, можно сказать, что у каждого из 6 друзей есть 3 варианта получения карты.
Следовательно, ответ будет 3 × 3 × 3 × 3 × 3 × 3 = 3 90 529 6 90 530 = 90 607 729 способов.
Пример 3: В экзамене 10 вопросов. Сколькими способами человек может попытаться ответить хотя бы на один вопрос?
Решение: Человек может попытаться ответить на 1 вопрос или 2 вопроса или …..до всех 10 вопросов. Ответить на один вопрос из десяти можно за 9 0529 10 C 1 = 10 контактов. Точно так же на два вопроса из десяти можно ответить 90 529 10 90 530 C 90 275 2 90 276 = 45 способами. Следуя той же логике, можно попытаться ответить на все десять вопросов 10 C 10 = 1 способом. Следовательно, общее количество способов = 10 + 45 + 120 +…..10 + 1 = 1023 способа (используя формулу Комбинации).
Альтернативный метод: Или можно применить некоторую логику: У каждого вопроса есть 2 варианта, либо попытка, либо нет. Продолжая эту логику, поскольку есть 10 вопросов, и каждый вопрос имеет 2 варианта, поэтому общее количество случаев = 2 10 = 1024.