Разность это плюс или минус: Что такое разность и частное

Возведение в квадрат и куб суммы и разности двух выражений. Разложение на множители с помощью формул квадрата суммы и

88. Возведение в квадрат и куб суммы и разности двух выражений. Разложение на множители с помощью формул квадрата суммы и квадрата разности.

Мы уже знаем, как умножить многочлен на многочлен. Но для некоторых случаев есть формулы, которые помогут существенно ускорить расчеты. Это формулы сокращенного умножения. Сегодня мы познакомимся с четырьмя из них.

Возведем в квадрат сумму (a+b):

(a+b)² = (a+b)(a+b)

Применим правило умножения многочлена на многочлен:

(a+b)(a+b) = a*a+a*b+b*a+b*b = a²+ab+ab+b² = a²+2ab+b²

Мы получили формулу:

(a+b)² = a²+2ab+b²

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Аналогично выведем формулу для квадрата разности:

(a-b)² = (a-b)(a-b) = a*a-a*b-b*a+b*b = a²-ab-ab+b² = a²-2ab+b²

(a-b)² = a²-2ab+b²

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Теперь, используя эти формулы, выведем формулы для куба суммы и куба разности двух выражений:

(a+b)³ = (a+b)(a+b)² = (a+b)(a²+2ab+b²) = a*a²+a*2ab+a*b²+b*a²+b*2ab+b*b² = a³+2a²b+ab²+a²b+2ab²+b³ = a³+3a²b+3ab²+b³

(a+b)^{3= a3+3a2b+3ab2+b3}

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб третьего выражения.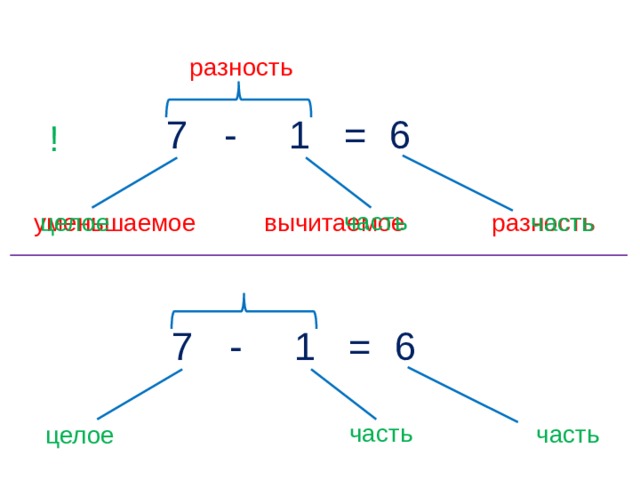

Это правило не так-то легко запомнить? Достаточно выучить формулу! Правило – это всего лишь ее словесное описание.

Аналогично найдем формулу куба разности:

(a-b)³ = (a-b)(a-b)² = (a-b)(a²-2ab+b²) = a*a²-a*2ab+a*b²-b*a²+b*2ab-b*b² = a³-2a²b+ab²-a²b+2ab²-b³ = a³-3a²b+3ab²-b³

(a-b)³ = a³-3a²b+3ab²-b³

Если в формуле для куба суммы все одночлены соединены знаками «+», что понятно – минусу просто неоткуда взяться, то в формуле для куба разности знаки между одночленами чередуются: «-» «+» «-».

Формулы сокращенного умножения используются также при разложении на множители.

Пример 1. Разложим на множители многочлен 81a²-18ab+b².

Можно ли слагаемое 81а² представить в виде квадрата одночлена? 81 – это квадрат числа 9.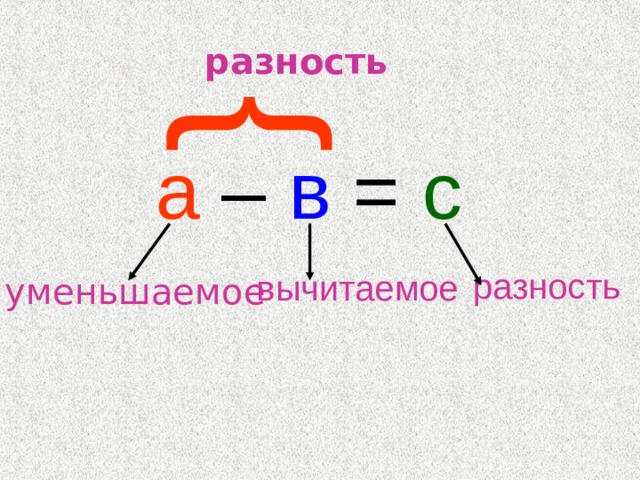 Тогда 81а² = 9²а² = (9а)². Причем -18аb = -2*9a*b.

«Свернем» многочлен, используя формулу квадрата суммы:

81a²-18ab+b^{2= (9а)2-2*9a*b+b2= (9а-b)2= (9а-b)(9а-b).}

Математика Слагаемые. Сумма. Уменьшаемое. Вычитаемое. Разность

Материалы к уроку

Конспект урока

Тема: Слагаемые. Сумма. Уменьшаемое. Вычитаемое. Разность.

 

Ход урока

 

1. Организационное начало урока

 

Математика сложна,
Но скажу с почтением:
Математика нужна
Всем без исключения!

 

2. Актуализация знаний

 

1. Целеполагание

 

— Сегодня мы узнаем, как называются числа при сложении и вычитании. Будем решать примеры и отвечать на сказочные вопросы.

9      4      8     6     7     3

Ш    И      П     У      К    Н

— Расставьте данные числа в порядке возрастания, чтобы узнать, в мир сказок какого писателя мы отправимся.

— А.С. Пушкин – великий русский писатель, произведения которого интересны и любимы и взрослыми, и детьми. Наш урок математики будет посвящён сказкам А. С. Пушкина, которые он написал, заложив в основу народные сказки, рассказанные ему любимой няней.

 

2. Устный счёт

 

1)

— Сколько стихотворных сказок было написано Александром Сергеевичем?
— Правильно, пять.

— Из какой сказки эти строки?

Белка там живёт ручная,
Да затейница какая!
Белка песенки поёт
Да орешки всё грызёт.

— Попробуйте справиться со следующим заданием и «расщёлкать» цепочку примеров, как белка – золотые орешки.

5 – 1 ○    -2  ○    +3  ○    -2  ○    +2  ○   -1 □

1 + 2  ○    -2  ○   +3  ○    +2 ○     -3   ○   +1 □

— Проверь себя.

2)

 – Помогите закончить следующие строчки:

Ветер по морю гуляет
И кораблик подгоняет;
Он бежит себе в волнах
На раздутых парусах.
По морю, по океану
В царство славного … Салтана.

— Молодцы! Вы должны отправить кораблики к нужному берегу.

— Проверь себя.

3) 

— Царица и её сын Гвидон плыли по морю в бочке 3 дня и 3 три ночи. Сколько дней и ночей  царица и её сын находились в бочке?
— Правильно, шесть. Три плюс три будет – шесть.

— Отгадайте загадку.

Я круглое и гладкое.
Но не румяное и не сладкое.
Глядят в меня,
А видят себя. (Зеркало)

— Кто из героев сказок А. С. Пушкина очень часто смотрел в зеркало?
— Правильно, царица из сказки «Сказка о мёртвой царевне и семи богатырях».

— До обеда царица смотрелась в зеркало 5 раз, а после обеда – 2раза.

Сколько раз посмотрела царица в зеркало за весь день?
— Правильно, семь раз. Потому что к пяти прибавить два будет – семь.

— В лесу жили в домике 7 богатырей и одна царевна. Сколько всего человек жило в домике?
— Совершенно верно, восемь. К семи прибавить один будет – восемь.

 

4)  

— Из каких фигур  состоит иллюстрация к сказке А. С. Пушкина «Сказка о рыбаке и рыбке»?

— Домик состоит: из синего большого квадрата и жёлтого маленького квадрата, из красного большого треугольника и зелёного маленького треугольника.
Дерево состоит из зелёного овала и коричневого четырёхугольника.
Солнышко – это жёлтый круг. Пенёк – коричневый квадрат.

 

Физкультминутка для глаз

 

Глазки видят всё вокруг,

Обведу я ими круг.
Глазкам видеть всё дано:
Где  окно и где крыльцо.
Обведу я снова круг,
Посмотрю на мир вокруг.

 

Актуализация знаний 2

3. Формирование знаний

 

— Сколько кораблей с белыми парусами? Шесть.
— Сколько кораблей с красными парусами? Два.
— Сколько всего кораблей? Восемь.
— Правильно.

— Число 6 – это первое слагаемое; число 2 – это второе слагаемое; число 8 – сумма.

— Запись чисел «шесть плюс два» читается: «Сумма чисел шесть и два».

 Таким образом, числа, которые складываются, называются слагаемыми, а результат сложения – их суммой.

Два «слагаемые» в ряд
Друг за дружкою стоят.
Вслед за ними знак «равно» —
Он известен нам давно.
Что в итоге получаем,
Словом «суммой» называем.

— Назовите второе слагаемое. Два.

— Найдите сумму чисел четыре и один. Сумма чисел четыре и один равна пяти.

— Назовите каждое число в этой записи  математическим «именем».
— Слагаемое, слагаемое, сумма.

— Сколько рыбок поймал старик? Шесть.
— Сколько рыбок кот пытается съесть? Две.
— Правильно. Шесть минус два равно – четыре.

— В математике число шесть в таких равенствах называют уменьшаемым, число два – вычитаемым, четыре – разностью.

— Запись чисел «шесть минус два» читается: «Разность чисел шесть и два». Значит, число, которое уменьшают, называется уменьшаемым, а число, которое вычитают, называется вычитаемым. Результат является разностью.

Хоть я у всех всё отнимаю,
Но это вовсе не беда.
Я роль свою ведь выполняю,
А это, верьте, не со зла.
Поэтому вы знать должны
что компоненты все важны.
Уменьшаемое, вычитаемое, разность.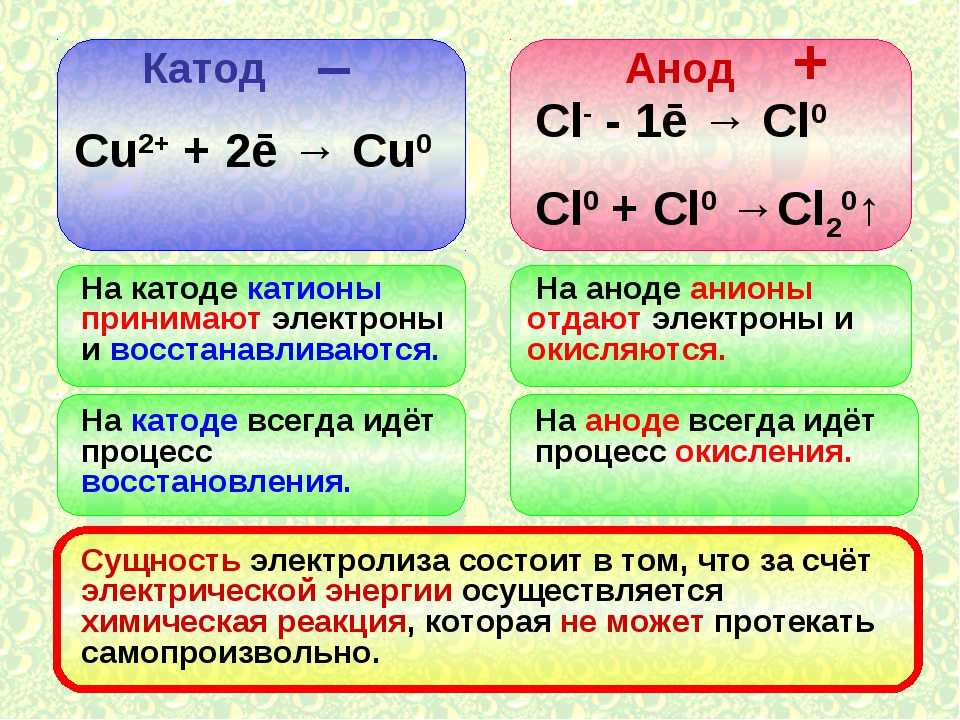

— Назовите уменьшаемое. Восемь.

— Найдите разность чисел шесть и один. Разность чисел шесть и один равна пяти.

— Назовите числа в примере их математическим «именем».

 

Физкультминутка

 

Дунул ветер – полетели.
Мы летели, мы летели
И на землю тихо сели.
Ветер снова набежал
И листочки все поднял.
Закружились, полетели

И на землю тихо сели.

 

Актуализация знаний 3

4. Закрепление знаний

 

Вдруг шатёр
Распахнулся… и девица,
Шамаханская царица,
Вся сияя, как заря,
Тихо встретила царя.

— Из какой сказки эти строки?
— Правильно, «Золотой петушок».

1)
— У Васи было три книги. Ему подарили ещё 2 книги. Сколько книг стало у Васи? Правильно, пять. Запишите этот пример. Назовите первое слагаемое –три;  второе слагаемое – два; сумму – пять.

2)

-Назовите первое и второе слагаемое и запишите, сколько получится  в сумме.

— Первое слагаемое – четыре, второе слагаемое два, сумма – шесть.
— Первое слагаемое – пять, второе слагаемое – три, сумма – восемь.

— Первое слагаемое – три, второе слагаемое – четыре, сумма – семь.

— Уменьшаемое равно девяти, вычитаемое – двум. Запиши разность этих чисел и вычисли её.

— Уменьшаемое равно четырём, вычитаемое – двум. Запиши разность и вычисли.
4 — 2 = 2

— Запиши разность чисел пять и два и найди её значение.
 5 — 2 = 3

3)
— В море плавало восемь золотых рыбок. Одна из них уплыла. Сколько рыбок осталось?
— Верно, семь.
 От восьми отнять один, будет семь.

— На ветке сидело четыре синички. К ним прилетело ещё две. Сколько птиц стало?
— Правильно, восемь. К четырём прибавить два, получится шесть.

— На полянке сидело девять зайчиков. Двое из них побежали в лес. Сколько зайчиков осталось на полянке?

— Правильно, семь. От девяти отнять два, равно семь.

Пять лодок у причала,
Волна их весело качала.
Три лодки взяли рыбаки,
Чтоб переплыть простор реки.
А сколько лодок у причала
Волна по-прежнему качала?

— Верно, две.
— От пяти отнять три равно – два.

 

4) Самостоятельная работа

 

1

6

— Запиши справа число, больше данного на один.
— Проверь себя.

1

6

 

5 — 2 = 5 — 1 — 1 = 2

3 — 2 =

6 — 2 =

7 — 2 =

— Найди разность по образцу.
— Проверь себя.

3 — 2 = 3 — 1 — 1 = 1

6 — 2 = 6 — 1 — 1 = 4

7 — 2 = 7 — 1 — 1 = 5

 

Мама-белка для детишек
Собрала десяток шишек.

Сразу все не отдала,
По одной всего дала:
Старшему  — еловую,
Среднему – сосновую,
Младшему – кедровую.

(Сколько шишек осталось у мамы-белки?) 

-Проверь себя.

 

— Начертите  отрезок  четыре сантиметра .

5) Задача на смекалку

— В корзинке три яблока. Как поделить их между тремя царевнами так, чтобы одно яблоко осталось в корзинке?
— Нужно отдать одно яблоко с корзинкой.

 

3. Подведение итогов

 

— Узнали героя сказки А.С. Пушкина? Это Балда из сказки «Сказка о попе и работнике его Балде». Помогите ему разложить равенства в корзинки.

— В первую корзинку нужно положить  разности , а во вторую — суммы.

7 — 1           6 + 4

6 — 5           3 + 6

13 — 4         9 + 9

— Надеюсь, после этого занятия вам захочется перечитать сказки А. С. Пушкина. Они многому вас научат.

Сказки Пушкина в сердце живут,
Радость и свет всем детям несут!
Вновь помогут они нам с тобой
Восхититься волшебной страной!

 

Рефлексия

 

-Продолжите фразу:

-Я узнал  …
-Я умею …
-Мне было трудно …

-Выберите картинку, которая соответствует вашему настроению.

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

алгебраическое предварительное исчисление — Плюс или Минус = Минус или Плюс Это то же самое?

спросил 4 года, 6 месяцев назад

Изменено 4 года, 6 месяцев назад

Просмотрено 426 раз

$\begingroup$

«Плюс или минус» или «Минус или плюс» — это одно и то же? 92=9 \подразумевает x = \pm 3 \quad \text{or}\quad x = \mp3$$

Эти знаки можно использовать на обычном уроке математики или на уроке алгебры?

• алгебра-предварительное исчисление
• арифметика

$\endgroup$

4

$\begingroup$

Иногда мы можем написать, например,

$$x=\pm 1 \quad y=\mp 1$$

, чтобы указать, что

• значение $x=+1$ соответствует значению $y=-1$
• значение $x=-1$ соответствует значению $y=+1$

, в противном случае они являются эквивалентными символами.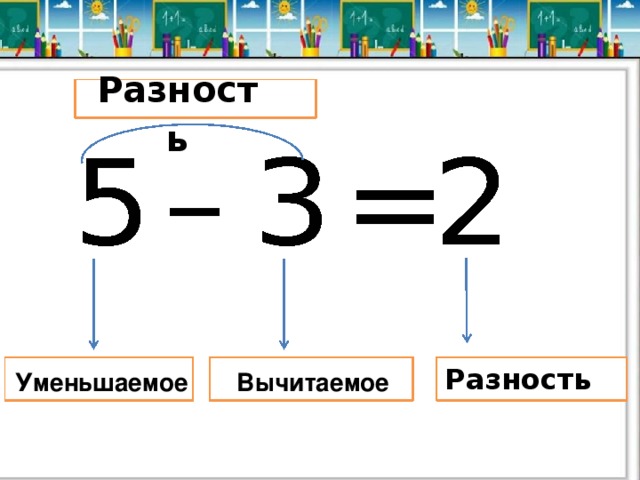

$\endgroup$

$\begingroup$

Логистически $\pm a$ означает «либо $a$, либо $-a$», а $\mp a$ означает «либо $-a$, либо $a$». Логистически они абсолютно одинаковы.

Однако $\mp a$ выглядит неестественно и криво, поэтому по соглашению мы всегда используем $\pm a$.

Итак, если мы когда-нибудь увидим $\mp a$, обычно это происходит по какой-то другой причине; что в другом месте выражения есть указание на то, что выбор нами $a$ или $-a$ зависит от чего-то еще. Например: если бы я увидел: $k = a \pm \sqrt {b \mp c}$, я бы интерпретировал это как два случая: либо $k = a + \sqrt{b — c}$, либо $ k = a — \sqrt{b + c}$.

Но это неизбежно двусмысленно. Я бы также непоследовательно интерпретировал утверждение $k = a \pm \sqrt{b \pm c}$ как имеющее четыре возможных случая: $k = a + \sqrt{b + c}; к = а -\sqrt{b+c}; к = а +\sqrt{b-c}; k = а-\sqrt{b-c}$.

Следует соблюдать осторожность, чтобы избежать потенциальной двусмысленности.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

python — Как найти разницу между двумя значениями, не зная, какое из них больше?

спросил 9 лет, 11 месяцев назад

Изменено 10 месяцев назад

Просмотрено 175 тысяч раз

Мне интересно, есть ли встроенная в Python функция, которая может определять расстояние между двумя рациональными числами, но без моего указания, какое число больше. например

 >>>расстояние(6,3)
3
>>>расстояние(3,6)
3
 

Очевидно, я мог бы написать простое определение, чтобы вычислить, что больше, а затем просто выполнить простое вычитание:

 def Distance(x, y):
    если х >= у:
        результат = х - у
    еще:
        результат = у - х
    вернуть результат
 

, но я бы предпочел не вызывать подобную пользовательскую функцию. Из моего ограниченного опыта я часто обнаруживал, что Python имеет встроенную функцию или модуль, который делает именно то, что вы хотите, и быстрее, чем ваш код. Надеюсь, кто-нибудь скажет мне, что есть встроенная функция, которая может это сделать.

• python
• функция
• числа
• расстояние

абс(х-у) сделает именно то, что вы ищете:

 В [1]: абс(1-2)
Выход[1]: 1
В [2]: абс (2-1)
Выход[2]: 1
 

1

Хотя абс(х - у) и эквивалентные абс(у - х) работают, следующие однострочники также работают:

• math. dist((x,), (y,)) (доступно в Python ≥3.8)

• math.fabs(x - y)

• макс(х - у, у - х)

• -мин(х - у, у - х)

• макс(х, у) - мин(х, у)

• (x - y) * math.copysign(1, x - y) или эквивалентно (d := x - y) * math.copysign(1, d) в Python ≥3.8

• functools.reduce(operator.sub, sorted([x, y], reverse=True))

Все они возвращают евклидово расстояние (x, y) .

1

Если у вас есть массив, вы также можете использовать numpy.diff :

 импортировать numpy как np
а = [1,5,6,8]
np.diff(a)
Выход: массив ([4, 1, 2])
 

Просто используйте абс(х - у) . Это вернет чистую разницу между ними как положительное значение, независимо от того, какое значение больше.

0

Так просто, просто используйте abs((a) — (b)).

будет работать без каких-либо дополнительных знаков (положительные, отрицательные)

 def get_distance(p1,p2):
     вернуть абс ((p1) - (p2))
получить_расстояние (0,2)
2
получить_расстояние (0,2)
2
получить_расстояние (-2,0)
2
получить_расстояние(2,-1)
3
get_distance(-2,-1)
1
 

Это не относится к первоначальному вопросу, но я решил расширить ответ, который дал Зинтурс. Если вы хотите определить расстояние между любыми двумя числами с соответствующим знаком, вы можете использовать пользовательскую функцию, подобную этой:

 импорт математики
расстояние защиты (а, б):
    если (а == б):
        вернуть 0
    elif (a < 0) и (b < 0) или (a > 0) и (b > 0):
        если (а < б):
            вернуть (абс(абс(а) - абс(б)))
        еще:
            возврат - (абс (абс (а) - абс (б)))
    еще:
        вернуть math.copysign((абс(а) + абс(б)),б)
печать(расстояние(3,-5)) # -8
печать (расстояние (-3,5)) # 8
печать (расстояние (-3,-5)) # 2
печать(расстояние(5,3)) # -2
печать (расстояние (5,5)) # 0
печать (расстояние (-5,3)) # 8
печать(расстояние(5,-3)) # -8
 

Пожалуйста, поделитесь более простыми или более питоническими подходами, если они у вас есть.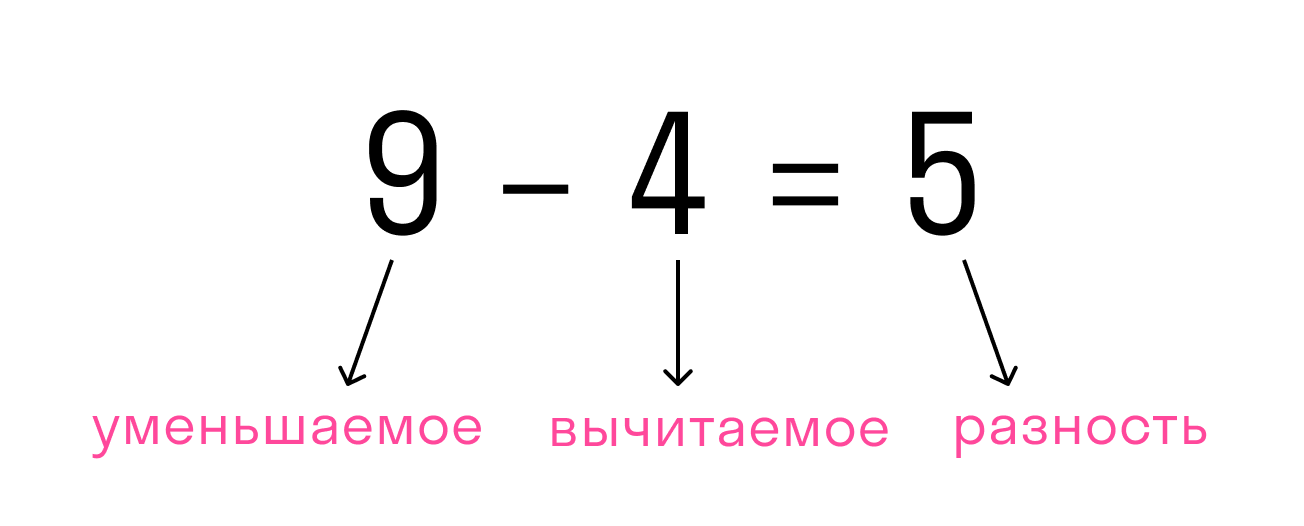

4

используйте эту функцию.

это то же соглашение, которое вы хотели. используя простую функцию abs Python.

также - иногда ответы настолько просты, что мы их пропускаем, ничего страшного 🙂

 >>> def Distance(x,y):
    вернуть абс (х-у)
 

0

Если вы планируете использовать фрагмент расчета расстояния со знаком, опубликованный phi (как и я), и ваш b может иметь значение 0, вы, вероятно, захотите исправить код, как описано ниже:

 импорт математики
расстояние защиты (а, б):
    если (а == б):
        вернуть 0
    elif (a < 0) и (b < 0) или (a > 0) и (b >= 0): # fix: b >= 0 для покрытия случая b == 0
        если (а < б):
            вернуть (абс(абс(а) - абс(б)))
        еще:
            возврат - (абс (абс (а) - абс (б)))
    еще:
        вернуть math.copysign((абс(а) + абс(б)),б)
 

Исходный фрагмент неправильно работает в отношении знака, когда a > 0 и b == 0.