Угол. Прямой и развернутый угол. Измерение углов.
На плоскости можно изобразить любую фигуру. Такими фигурами могут быть луч, отрезок, прямая.
Нанесем на плоскость произвольную точку К и проведем от нее два луча КМ и КР. Таким образом, получилась новая плоская геометрическая фигура – угол.
Определение
Угол – это часть плоскости, которую ограничивают два луча, исходящие из единого центра.
Называют угол латинскими буквами (заглавными) и обозначают при записи знаком «∠».
Лучи КМ и КР называют сторонами угла, а единую точку К – вершиной угла. Когда записывают название угла, то в середине указывают ту точку, которая является именно вершиной угла.
Таким образом, получился ∠ КР. Можно называть угол только по его вершине — ∠ К.
Если посмотреть на рисунок, то можно увидеть, что угол имеет внутреннюю часть и внешнюю.
Отсюда следует, что угол бывает
Расположим точки A, B, C, F, K, M, N в плоскости угла ∠O. На рисунке видно, что точки K, C, F размещены во внутренней части угла, точки M, N во внешней части, а точки A и B лежат на сторонах угла.
Определение
Если один угол можно наложить на другой таким образом, чтоб их вершины и стороны совпали, такие углы называют равными.
Рассмотрим произвольные углы ∠КМВ, ∠АВС, ∠LΝВ.
- Сравним углы ∠КМВ и ∠АВС, т.е. соединим вершины углов и одну из сторон. Проделав эту работу, можно отметить, что вторые стороны углов при этом не совпали, а значит ∠КМВ ≠ ∠АВС.
- Теперь сравним углы ∠КМВ и ∠LΝВ аналогичным способом. Из рисунка видно, что вершины и обе стороны углов совпали при наложении друг на друга, а значит ∠КМВ = ∠LΝВ.
Возьмем для изучения произвольный ∠COB. Из его вершины проведем дополнительный луч OA, который разделит его на два дополнительных угла — ∠AOC и ∠BOA. При этом можно отметить, что эти углы меньше ∠ COB.
Для отображения этих параметров составляют следующую запись:
∠ AOC ‹ ∠ COB
∠ BOA ‹∠ COB
Вместе эти углы образовывают ∠ COB:
∠ AOC + ∠ BOA = ∠ COB
Развернутый уголОпределение
Два дополнительных друг другу луча образуют развернутый угол.Сторонами такого угла является прямая линия, на которой лежит вершина развернутого угла.
Лучи ОA и ОB являются дополнительными друг другу. Они образуют развернутый угол ∠AOB. Точка О, вершина угла, лежит на прямой AB.
Прямой уголРассмотрим развернутый ∠АОВ.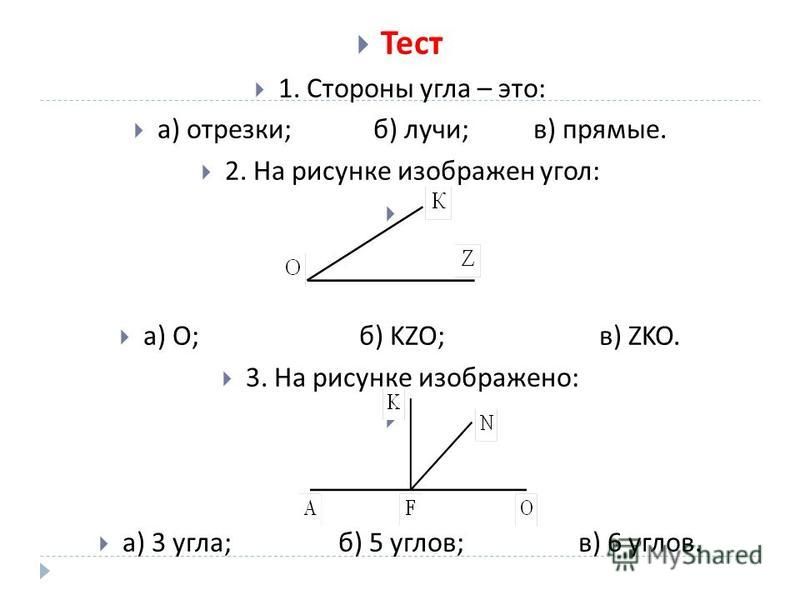
Проведем из его вершины луч СО так, чтоб этот луч разделил угол ∠ АОВ на два равных угла.
Получили углы ∠АОС и ∠СОВ. Поскольку из условия построения углов новообразованные углы равны половине развернутого угла, то можно сделать следующую запись:
∠ АОС = ∠ СОВ = ∠ АОВ
Такие углы называют прямыми, т.е. ∠ АОС и ∠ СОВ – прямые углы.
Прямой угол можно построить при помощи чертежной линейки-треугольника.
Алгоритм построения прямого углаДля того, чтоб построить прямой луч, стороной которого является луч АВ, надо:
- Расположить линейку-треугольник так, чтобы ее вершина совпала сточкой А, а одна из ее сторон пошла по лучу АВ.
- Провести луч АС вдоль второй стороны линейки-треугольника.
- Угол ∠САВ – прямой.
Для того, чтоб измерить или построить угол необходимого размера используют другой измерительный инструмент – транспортир.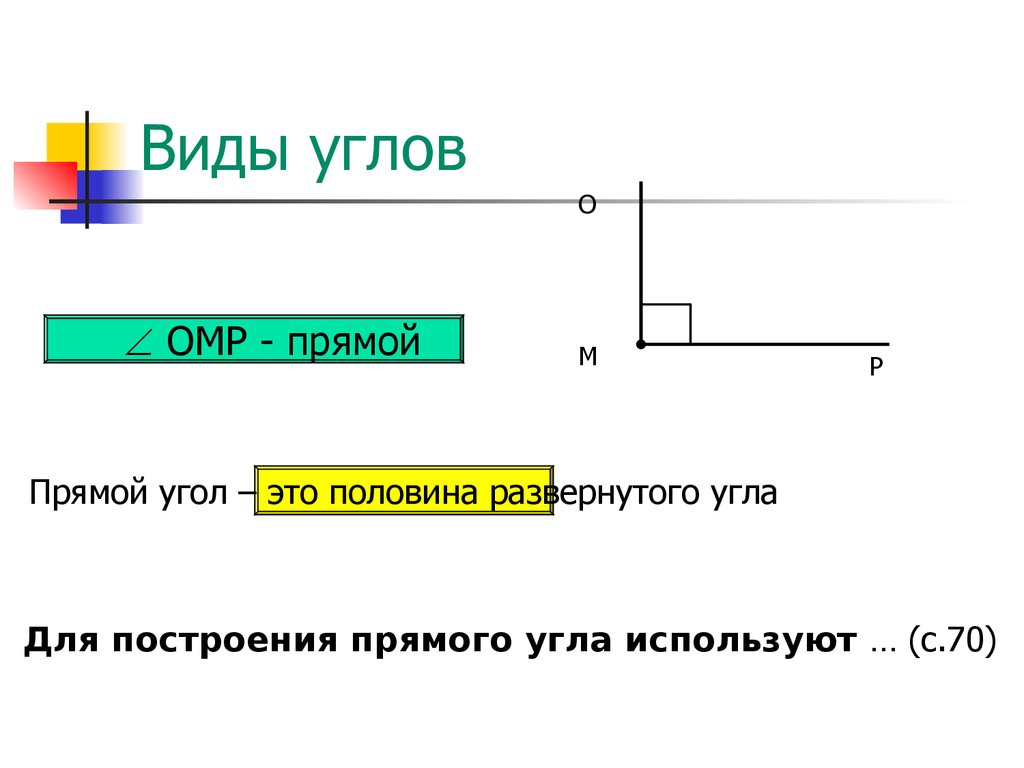
На внешней дуге транспортира нанесена шкала измерений – градусы, всего от 0 до 180˚. Таким образом, наибольший угол, который можно измерить или построить, это развернутый угол величиной 180˚.
Алгоритм измерения углов при помощи транспортира:- Прямую часть инструмента накладывают на одну из сторон измеряемого угла, также совмещают центры угла и транспортира.
- Вторая сторона угла указывает на шкалу – в месте пересечения стоит отметка о размере угла.
Поделиться статьей в соцсетях
Остались вопросы?
Наши репетиторы помогут
Остались вопросы?
Угол. Прямой и развернутый угол. Чертежный треугольник
Урок 42. Математика 5 класс
В этом уроке мы сформируем представление об угле, его вершине и сторонах, обозначении угла, сравнении углов наложением. Введем понятия развернутого и прямого угла. Научимся пользоваться чертежным треугольником.
Конспект урока «Угол. Прямой и развернутый угол. Чертежный треугольник»
На этом уроке мы узнаем, что за фигуру называют углом. Рассмотрим элементы, которыми обладает угол. А также рассмотрим взаимное расположение угла и точек.
Для начала вспомним основные плоские геометрические фигуры, которые мы с вами научились уже строить в курсе математики 5-го класса.
Напомним, что плоские геометрические фигуры – это фигуры, которые располагаются в плоскости.
Например,
А теперь давайте перейдём непосредственно к чертежам. Отметим в плоскости, в любом понравившемся вам месте, некоторую точку О. И проведём от этой точки два луча ОА и ОВ. Обратите внимание, у нас получилась новая геометрическая фигура, угол.
Определение
Угол
– это
часть плоскости, ограниченная двумя лучами, выходящими из одной точки, или
имеющими одно начало.
Угол визуально делят на «
Мы же все чаще будем работать именно с внутренними углами.
Определение
У нас получился угол АОВ. Называют его заглавными латинскими буквами и обозначают угол вот таким знаком «», который вам следует не перепутать со знаком «меньше».
Лучи ОА и ОВ – называют сторонами угла, а точку О – его вершиной. При записи угла в середине пишут его вершину.
Обратите внимание угол, который мы построили имеет вершину точку О, и в записи угла буква О стоит в середине. Также угол можно записать одной буквой, обозначающей его вершину, т.е. в нашем случае можно записать угол О.
Рассмотрим взаимное расположение угла и точек на плоскости.
На экране изображён угол ВЕС и 6 точек A, D, F, K, N, T.
Углы, как и любые геометрические фигуры можно сравнивать.
Запомните: два угла называют равными, если их можно наложить один на другой так, что их вершины и стороны совпадут.
Например
На экране изображены три угла АОВ, CED и MKN.
Давайте сравним угол АОВ с углами CED и MKN.
Изобразим следующий рисунок. Начертим угол MON и из его вершины точки О проведём луч ОК.
Обратите внимание луч ОК разделяет наш начальный угол MON на два угла МОК и КОN, каждый из этих углов меньше угла MON. Пишут так:
А вместе два этих угла образуют угол MON. Записать это можно так
Определение
Два дополнительных друг другу луча образуют развёрнутый угол.
Сторонами такого угла является прямая линия, на которой лежит вершина развёрнутого угла.
Посмотрите внимательно на экран.
Лучи ОА и ОВ являются дополнительными друг
другу.
Они образуют развёрнутый угол АОВ.
Точка О – вершина развёрнутого угла лежит на прямой АВ.
Пример развёрнутого угла вы можете встретить каждый день.
Например
Мы помним, что прямые могут пересекаться. При пересечении двух прямых образуются 6 углов, 2 из которых – развёрнутые.
Например
Прямые АВ и СD пересекаются в точке О. Угол АОВ – развёрнутый и угол СОD – развёрнутый.
Начертим развёрнутый угол MON и проведём из его вершины луч ОК, так чтобы этот луч разделил угол MON на 2 равных угла.
У нас получились углы МОК и NОК. Эти углы равны между собой и равны половине развёрнутого угла. Записывают это так:
Такие углы называют прямыми.
Для построения прямого угла пользуются чертёжным треугольником.
Запомните алгоритм построения прямого угла.
Для того чтобы построить прямой угол, стороной которого является луч EF, надо:
1) Расположить чертёжный треугольник так, чтобы его вершина совпала с точкой Е, а одна из его сторон пошла по лучу EF.
2) Провести луч ЕС вдоль второй стороны чертёжного треугольника.
3) Угол СEF, который образовался после выполнения 1–го и 2–го шага алгоритма и есть прямой.
Итоги
Итак, сегодня на уроке мы узнали, что за фигуру называют углом. Рассмотрели элементы, которыми обладает угол. Изучили взаимное расположение угла и точек в плоскости. Узнали, какие углы называют прямыми и развёрнутыми. А также научились пользоваться чертёжным треугольником.
Предыдущий урок 41 Проценты
Следующий урок 43
Измерение углов.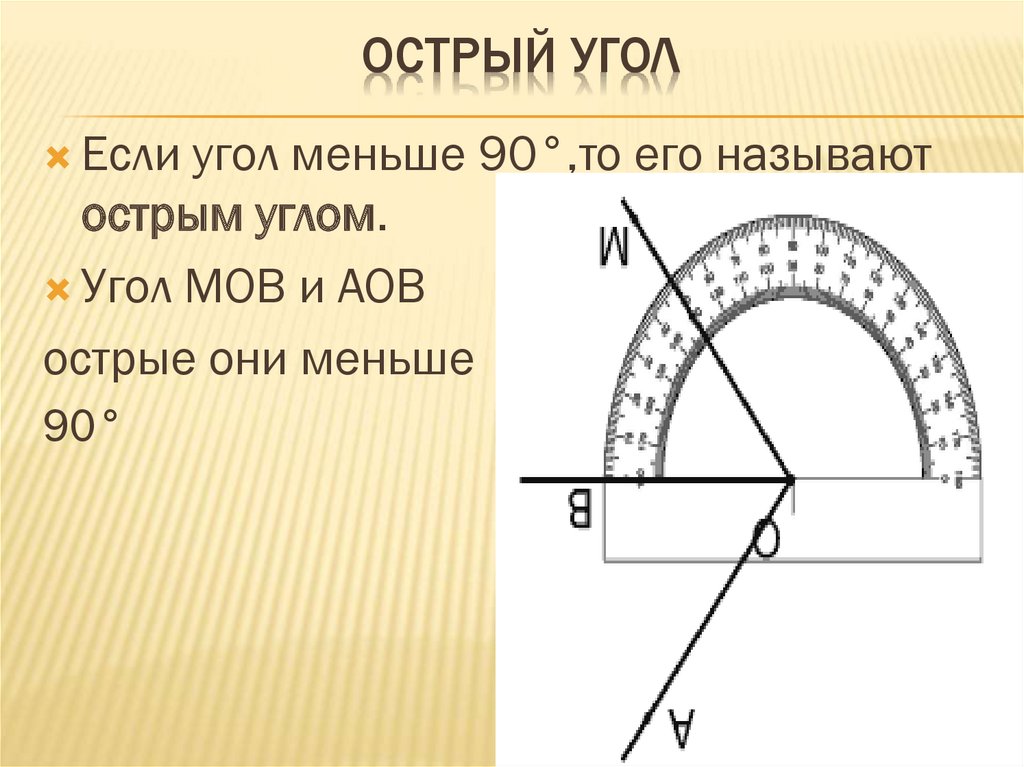
Транспортир
Получите полный комплект видеоуроков, тестов и презентаций Математика 5 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Чертеж гнутой пластины в развернутом виде | Помощь пользователям Tekla
Перейти к основному содержанию
- Home
- Tekla Structures
- Чертеж изогнутой пластины в развернутом виде
Текла Структуры
Не зависит от версии
Tekla Structures
Окружающая среда
Не зависит от среды
В начало
Назначение и описание
Используйте расширение Чертеж изогнутой пластины в развернутом виде для создания чертежа отдельной детали в развернутом виде с линией изгиба для выбранных пластин.
В начало
Системные требования
Версия Tekla Structures: не зависит от версии
Среды: все
В начало
Установка Чертеж гнутой пластины в развернутом виде
Для установки расширения:
- Загрузите установочный пакет инструментов для работы с пластинами с Tekla Warehouse . Дополнительные сведения см. в разделе Загрузка приложения из Tekla Warehouse.
- Установить пакет файлов.
В начало
Использование развернутого чертежа гнутой пластины
Чтобы использовать приложение:
- Откройте модель Tekla, в которой уже есть гнутая пластина — она работает только для гнутых пластин, смоделированных с помощью команды Присоединить к детали .
- Нажмите кнопку Приложения и компоненты
Изображение
на боковой панели, чтобы открыть каталог Приложения и компоненты . - Искать Чертеж изогнутой пластины в развернутом виде
Изображение
а затем дважды щелкните, чтобы открыть его. - Откроется диалоговое окно Чертеж изогнутой пластины в развернутом виде .
Изображение
- С помощью Выбрать объекты в компонентах , выбрать одну или несколько гнутых пластин.
Изображение
- Выберите нужные параметры и нажмите Создать .
- Если нумерация не актуальна, появится следующее сообщение: Пронумеровать выбранные объекты? . Если вы нажмете Да нумерация будет выполнена, если вы выберете Нет чертежи не будут созданы.
- В диалоговом окне отображается индикатор выполнения, показывающий ход создания.
Изображение
- При желании вы можете отменить создание чертежа, щелкнув значок Отмена кнопка
- По завершении создания в окне приложения появится следующее сообщение: Создание чертежа завершено .
Изображение
- Значение после префикса (A) представляет собой угол изгиба.
Пример:
- Если пластина сложена
Изображение
угол А = -45. - Если пластина откинута вниз
Изображение
угол А = 45,
Наверх
Свойства приложения и кнопки
Опции развернутой изогнутой пластины
| Поле | Описание | По умолчанию |
|---|---|---|
| Способ раскладывания | Определите метод развертывания. Варианты:
Изображение
Изображение | Осевая линия |
Варианты развернутого чертежа
| Поле | Описание | По умолчанию |
|---|---|---|
| Атрибуты чертежа | Определите атрибут чертежа. Параметры различаются в зависимости от среды. | стандарт |
| Атрибуты линии сгиба | Определите атрибут линии сгиба.
Изображение Примечание. Пользователь может создавать атрибуты линии в свойствах Go Line . Изображение | FoldUpLine |
| Атрибуты линии сгиба вниз | Определите атрибут линии сгиба вниз.
Изображение Примечание. Пользователь может создавать атрибуты линии в свойствах Go Line . Изображение | Сложить вниз по линии |
| Префикс на чертеже | Определите префикс изогнутого угла на чертеже. | А= |
| Атрибуты текста | Определите атрибут текста. Примечание. Если текст плохо выравнивается, установите Перенос слов в Свойства текста с по Выкл. параметр. | развернутый BPD |
| Смещение текста | Задайте смещение текста. | Х=0 мм |
| Y=(высота текста/2)*4 мм |
Кнопки приложений
| Поле | Описание |
|---|---|
| Создать | Используется для создания чертежей. Во время создания кнопка становится неактивной, и появляется индикатор выполнения, показывающий ход создания чертежа. |
| Отмена | Используется для отмены создания чертежа. |
Вернуться к началу
- Если при создании возникли ошибки Показать журнал появится кнопка, после нажатия на которую файл журнала будет открыт в текстовом редакторе по умолчанию.
Изображение
- Если деталь не выбрана, пользователь получит следующее предупреждающее сообщение: Объекты не выбраны .
В начало
Ограничения
Выберите раздел главы, соответствующий версии расширения, которую вы хотите использовать.
Инструменты для обработки пластин 3.5
Начиная с Tekla Structures 2020 расширение Чертеж гнутой пластины в развернутом виде поддерживает Диспетчер документов , поэтому вам не нужно включать список чертежей из диалогового окна Дополнительные параметры больше.
Для более ранних версий, чем Tekla Structures 2020, которые поддерживают Диспетчер документов , необходимо включить Список чертежей , установив для расширенного параметра XS_USE_OLD_DRAWING_LIST_DIALOG значение TRUE в категории Свойства чертежа диалогового окна Дополнительные параметры .
Это связано с тем, что макросы Список чертежей не поддерживаются в Диспетчере документов .
Начиная с версии Tekla Structures 2018i все команды и кнопки, которые должны были запускаться Список чертежей запустит Диспетчер документов . Диспетчер документов включен по умолчанию вместо Список чертежей .
Дополнительные сведения о xs_use_old_drawing_list_dialog см. в разделе xs_use_old_drawing_list_dialog
Дополнительные сведения о Диспетчер документов см. в разделе Диспетчер документов.
Подробнее о Список чертежей см. в разделе Список чертежей.
Инструменты для обработки пластин 3.4, 3.3
Потому что Список чертежей Макросы не поддерживаются в Диспетчере документов , необходимо включить Список чертежей , установив для расширенного параметра XS_USE_OLD_DRAWING_LIST_DIALOG значение TRUE в категории Свойства чертежа диалогового окна Дополнительные параметры .
Начиная с версии Tekla Structures 2018i, все команды и кнопки, которые должны были запустить Список чертежей , будут запускать Диспетчер документов . Диспетчер документов включен по умолчанию вместо Список чертежей .
Дополнительные сведения о xs_use_old_drawing_list_dialog см. в разделе xs_use_old_drawing_list_dialog
Дополнительные сведения о Диспетчер документов см. в разделе Диспетчер документов.
Подробнее о Список чертежей см. в разделе Список чертежей.
Вернуться к началу
См. также
Развернутая изогнутая пластина
Вернуться к началу
это было полезно?Чего не хватает?
| База ZW3D | ||
| ||
| Складывание/раскладывание деталей из листового металла | ||
Складывание/раскладывание деталей из листового металла Развернуть деталь из листового металла Сгибание листового металла Деталь Установить стационарное лицо Примечания
Панель инструментов для листового металла Используйте эти команды, чтобы развернуть и развернуть осевые сгибы в 3D-детали из листового металла.
Используйте эту команду, чтобы развернуть осевые сгибы в 3D-детали из листового металла. Размер детали соответствует характеристикам расширения изогнутого листового металла и любым вырезам, отверстиям, плоским вырезам или вырезам поперек изгибов. Полученная деталь также называется разверткой. Детали из листового металла можно повторно сгибать с помощью команды «Свернуть деталь из листового металла ». Информацию о назначении атрибутов листового металла по умолчанию и дополнительных параметров развертывания см. в разделе 9.0027 Форма атрибутов листового металла .
Используйте эту команду, чтобы согнуть осевые сгибы в 3D-детали из листового металла после того, как она была развернута с помощью
Команда «Развернуть деталь из листового металла ».
Используйте эту команду, чтобы задать неподвижную грань детали из листового металла. Эта грань остается неподвижной, когда деталь
в сложенном или разложенном виде. Если эта команда не используется, неподвижной гранью по умолчанию будет грань с наибольшей площадью поверхности. Вы также можете установить или изменить неподвижное лицо во время
Сгибание и разворачивание листового металла, часть команд.
Неподвижная грань, выбранная первой для операции развертывания, запоминается при последующих операциях складывания и развертывания. Стационарную грань нужно выбирать только в том случае, если ее необходимо изменить. Вы также можете установить эту грань с помощью команды Установить стационарную грань .
| ||
Развернув деталь, вы увидите, как изменится размер и форма развертки. Деталь также может быть детализирована на чертежном листе в развернутом состоянии. Также сюда включена команда для установки стационарного лица. Это будет определять, как часть будет разворачиваться. См. приведенные ниже команды.
Размер детали изменяется в соответствии с характеристиками расширения изогнутого листового металла и любыми выемками, отверстиями, плоскими вырезами или вырезами поперек сгибов. Для назначения атрибутов листового металла по умолчанию и дополнительных параметров фальца см.
Форма атрибутов листового металла.
